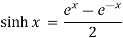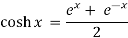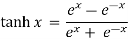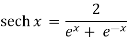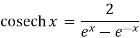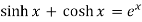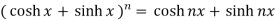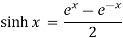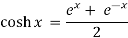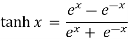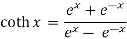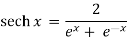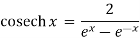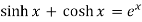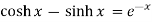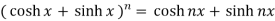Unit-3
Complex Variable (Differentiation)
De Moivre’s theorem: Power of complex numbers
Let 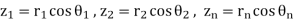 Then by the product rule in polar form, we
Then by the product rule in polar form, we
Get
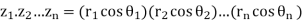
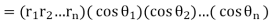
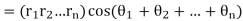
Thus
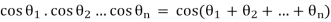
If we chose 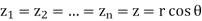 then
then 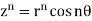 or for choice of r = 1, we get
or for choice of r = 1, we get
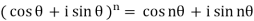
Which is known as De Moivre’s theorem.
Note-
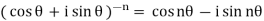
De Moivre’s theorem is valid for all rational valuesof n (including positive, negative integral values and zero).
Roots of complex number:
Let z = 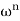 where n is an integer 1, 2, 3, . . .. This isa single-valued function which associates a uniquevalue z for each ω. Now consider the inverse function
where n is an integer 1, 2, 3, . . .. This isa single-valued function which associates a uniquevalue z for each ω. Now consider the inverse function
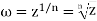
Which is multivalued, namely n valued. For any given
z  0 and the given integer n, there corresponds preciselyn distinct values of
0 and the given integer n, there corresponds preciselyn distinct values of 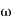 which are known as then roots of z. Thus the nth root of a complex number isanother complex number whose nth power is equalto the radicand. To determine these n roots, let
which are known as then roots of z. Thus the nth root of a complex number isanother complex number whose nth power is equalto the radicand. To determine these n roots, let  and z =
and z = 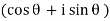 then
then
n = [ R (cos + I sin )]n
= Rn[cos n + I sin n ]
= z = r(cos θ + i sin θ)
By using De Moivre’s theorem. Since the moduli ofequal complex numbers must be equal, while theiramplitudes may circle with centre at origin and ofradius 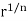 . They constitute the n vertices of a regularpolygon of n sides inscribed in the circle, spacedat equal angular intervals of
. They constitute the n vertices of a regularpolygon of n sides inscribed in the circle, spacedat equal angular intervals of 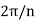 , beginning with theradius whose angle is
, beginning with theradius whose angle is  .
.
Principal value of 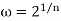 is obtained for k = 0 and by taking principal value of argument of z.
is obtained for k = 0 and by taking principal value of argument of z.
In particular, the nth roots of a real non-zero number
A also has n values since the real number A canbe expressed in trigonometric form as
A = |A|(cos θ + i sin θ) = |A| cos 0 for A > 0
And
A = |A| (cos π + i sin π) = |A| cos π for A<0
Where k is an integer. For k = 0, 1, 2, ···(n −1) weget n different roots since for these values of k, 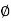 defines n distinct angles which identify n differentcomplex numbers. But as k takes n, n + 1, ···or−1, −2, . . ., the same angles
defines n distinct angles which identify n differentcomplex numbers. But as k takes n, n + 1, ···or−1, −2, . . ., the same angles 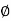 are repeated againand again, thus giving the root values that coincidewith those (already) obtained. Thus the nth root of acomplex number has n distinct values given by
are repeated againand again, thus giving the root values that coincidewith those (already) obtained. Thus the nth root of acomplex number has n distinct values given by
= z1/n = 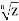 = r1/n [ cos( θ+2kπ /n) + i sin( θ+2kπ /n)] (1)
= r1/n [ cos( θ+2kπ /n) + i sin( θ+2kπ /n)] (1)
Where k = 0, 1, 2, . . . , n – 1
Geometrically, these n values are given by
x = 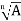 (cos 2kπ /n + i sin 2kπ /n) (2)
(cos 2kπ /n + i sin 2kπ /n) (2)
For k = 0, 1, 2, . . . , n −1 when A is a real positivenumber. In particular the nth roots of unity (for A = 1) are given by
11/n = (cos 2kπ /n + i sin 2kπ /n ), k = 0,1, . . ., n - 1
Similarly when A is a real negative number, then
x =  [cos (π+2kπ /n) + i sin (π+2kπ / n)] (3)
[cos (π+2kπ /n) + i sin (π+2kπ / n)] (3)
For k = 0, 1, 2, . . . , (n −1). In particular the nthroots of −1 (for A = −1) are given by
(-1)1/n = [cos (π+2kπ /n) + i sin (π+2kπ / n)]
For k = 0, 1, 2, . . . (n −1).
When A is a complex number, these n values of x are obtained from (1). Now the general rationalpower of a complex number is defined as
zp/q = (x1/q)p = [ r1/q cos θ+2kπ/q]p
= rp/q cos (p/q (θ + 2kπ))
For k = 0, 1, 2, . . . , q −1.
Example: Simplify-
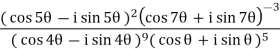
Sol:
By using De-Moivre’s theorem:
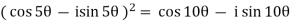

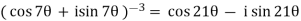
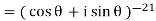
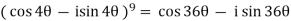
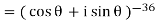
Substituting these values in given expression, we get
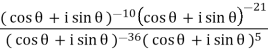
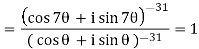
Example: If z = cos 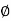 and
and 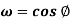 then show that
then show that
zmn + z-m-n = 2 cos(mθ + n)
Sol:
Let’s consider
zmn + z-m-n = (cis θ)m(cis )n + (cis θ)-m(cis )-n
= (cos m θ + i sin m θ)( cos n + i sin n ) + (cos m θ – i sin mθ)(cos n - i sin n )
= (cos mθ . Cos n - sin mθ . Sin n )
= cos(mθ + n)
Example: Find all solutions of the equation
z4 – (1+4i)z2 + 4i = 0
Sol:
z4 – z2 – 4iz2 + 4i =
= z2(z2 – 1) – 4i(z2 – 1) = 0
(z2 – 1)(z2 – 4i) = 0
Then z2 – 1 = 0 and z2 = 4i or z = ± 1 and z = ± 2 √i
But
√i = (eiπ/2)1/2 = eiπ/4
So z = ± 1
z = ± 2 eiπ/4 = ±2 (1/√2 + i1/√2)
The solutions are
±1, ±√2(1+i).
Example: Find all the values of (-1 + i √3)3/2
Sol:
Let
-1 + i√3 = x+iy, so x = - 1.
y = √3. Then r = √x2 + y2 = √1+3 = √4 = 2
-1 = x = r cos θ = 2 cos θ, so cos θ = - ½
√3 = y = r sin θ = 2 sin θ, so sin θ = √3/2
θ= π – π/3 = 2π/3. Thus
-1 + i √3 = reiθ = 2ei2π/3
Now
(-1 + i√3)3/2 = (2ei2π/3)3/2 = (8ei2π)1/2
= √8 ei(2π+2kπ/2) with k = 0, 1
= √8 eiπ = - √8 = -2√2 for k = 0
= √8 ei2π = + √8 = 2√2 for k = 1
Thus the solutions are 
Example: Express 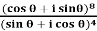 in the form of (x + iy).
in the form of (x + iy).
Sol:
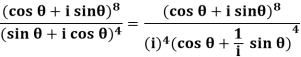
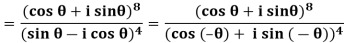
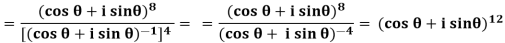
= cos 12 θ + i sin 12 θ
Circular functions:
Euler’s exponential form of circular functions:
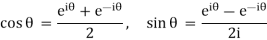
If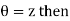
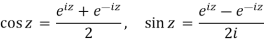
Hyperbolic functions:
Relationship between circular and hyperbolic functions:
Sin ix = i sinh x sinh ix = i sin x
Cos ix = cosh x cosh ix = cos x
Tan ix = i tanh x tanh ix = i tan x
Important formulas of hyperbolic functions:
- (1) cosh2x – sinh2 x = 1, (2) sech2 x = 1 – tanh2 x,
(3) cosech2 x = coth2x – 1
B. (1) sinh (x±y) = sinh x cosh y ± cosh x sinh y
(2) cosh (x±y) = cosh x cosh y ± sinh x sinh y
(3) tanh (x±y) = tanh x ± tanh y/ 1± tanh x tanh y
C. (1) sin h 2x = 2 sinh x coh x (2) cosh 2x = cosh2 x + sinh2 x
(3) cosh = 2 cosh2 x – 1 (4) cosh 2x = 1+2 sinh2 x
(5) tanh 2x = 2tanh x/ 1+ tanh2 x
D. (1) sinh x + sinh y = 2 sinh x+y/2 cosh x-y/2
(2) sinh x – sinh y = 2 cosh x+y/2 sinh x-y/2
(3) cosh x + cosh y = 2 cosh x+y/2 cosh x-y/2
(4) cosh x – cosh y = 2 sinh x+y/2 sinh x-y/2
Example: Prove that
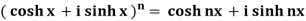
Sol:
LHS = 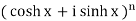
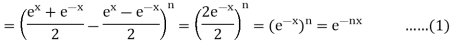
Now RHS
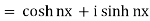
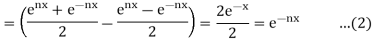
From (1) and (2), we have
LHS = RHS
Example: If cosh x = sec 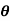 then prove that
then prove that
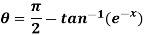
Sol:
Let
Tan-1 e-x = α
e-x = tan α and α = tan-1 (e-x ) …………..(1)
ex = cot α …………………..(2)
Now
Sec θ = cos h x = ex + e-x/2 …….............(3)
Putting the value of 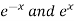 from (1) and (2) in (3), we get
from (1) and (2) in (3), we get
Sec θ = cot α + tan α/2
Sec θ = cot α + tan α = cos α/sin α + sin α/cos α = cos2α + sin2α/ sin α cos α
= 2/ 2 sin α cos α
= 2/ sin 2 α
Cos θ = sin 2 α
Cos θ = cos (π/2 -2α)
θ = π/2 - 2α = π/2 – 2 tan-1 (e-x)
In the narrow sense of the term, the theory of function of a complex variable is the theory of analytic functions (cf. Analytic function) of one or several complex variables. As an independent discipline, the theory of functions of a complex variable took shape in about the middle of the 19th century as the theory of analytic functions.
Complex function-
x + iy is a complex variable which is denoted by z
If for each value of the complex variable z = x + iy in a region R, we have one or more than one values of w = u + iv, then w is called a complex function of z.
And it is denoted as-
w = u(x , y) + iv(x , y) = f(z)
Neighbourhood of 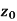
Let a point  in the complex plane and z be any positive number, then the set of points z such that-
in the complex plane and z be any positive number, then the set of points z such that-
|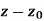 |<ε
|<ε
Is called ε- neighbourhood of 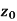
Limit of a function of a complex variable-
Suppose f(z) is a single valued function defined at all points in some neighbourhood of point 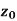 -
-
The-
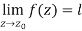
Example-1: Find-
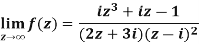
Sol. Here we have-
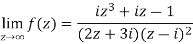
Divide numerator and denominator by  , we get-
, we get-
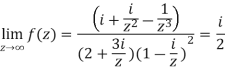
Continuity- A function w = f(z) is said to be continuous at z = 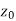 , if
, if
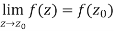
Also if w = f(z) = u(x , y) + iv(x , y) is continuous at z = 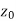 then u(x , y), v(x , y) are also continuous at z =
then u(x , y), v(x , y) are also continuous at z = 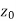 .
.
Example: Show that f(z) = Re z = x is continuous but not differentiable.
Sol.
Continuity:
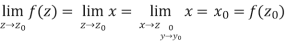
Not differentiability-
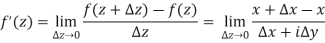
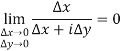
While
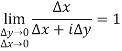
Hence limit does not exist which means function is not differentiable.
Differentiability-
Let f(z) be a single valued function of the variable z, then
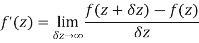
Provided that the limit exists and has the same value for all the different ways in which 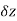 approaches to zero.
approaches to zero.
Example: if f(z) is a complex function given below, then discuss 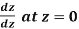

Sol. If z→0 along radius vector y = mx
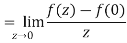
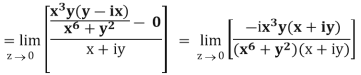
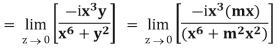
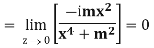
But along 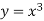 ,
,
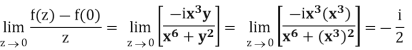
In different paths we get different value of 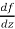 that means 0 and –i/2, in that case the function is not differentiable at z = 0.
that means 0 and –i/2, in that case the function is not differentiable at z = 0.
Key takeaways-
- Neighbourhood of
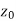
|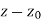 |<ε
|<ε
2. Limit of a function of a complex variable-
Suppose f(z) is a single valued function defined at all points in some neighbourhood of point 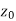 -
-
The-
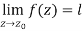
3. A function w = f(z) is said to be continuous at z = 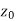 , if
, if
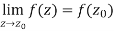
4. 
Analytic functions
A function  is said to be analytic at a point
is said to be analytic at a point 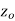 if f is differentiable not only at
if f is differentiable not only at 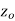 but an every point of some neighborhood at
but an every point of some neighborhood at 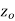 .
.
Note-
1. A point at which the function is not differentiable is called singular point.
2. A function which is analytic everywhere is called an entire function.
3. An entire function is always analytic, differentiable and continuous function.( converse is not true)
4. Analytic function is always differentiable and continuous but converse is not true.
5. A differentiable function is always continuous but converse is not true.
The necessary condition for f(z) to be analytic-
f(z) = u + i(v) is to be analytic at all the points in a region R are-
1. 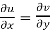 …………. (1)
…………. (1)
2. 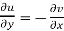 ……...…. (2)
……...…. (2)
Provided 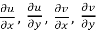 exists
exists
Equation (1) and (2) are known as Cauchy-Riemann equations.
The sufficient condition for f(z) to be analytic-
f(z) = u + i(v) is to be analytic at all the points in a region R are-
1. 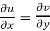 …………. (1)
…………. (1)
2. 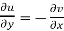 ……...…. (2)
……...…. (2)
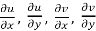 are continuous function of x and y in region R.
are continuous function of x and y in region R.
Important note-
1. If a function is analytic in a domain D, then u and v will satisfy Cauchy-Riemann conditions.
2. C-R conditions are necessary but not sufficient for analytic function.
3. C-R conditions are sufficient if the partial derivative are continuous.
State and prove sufficient condition for analytic functions
Statement – The sufficient condition for a function 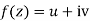 to be analytic at all points in a region R are
to be analytic at all points in a region R are
1 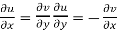
2 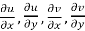 are continuous function of x and y in region R.
are continuous function of x and y in region R.
Proof:- Let f(z) be a simple valued function having 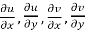 at each point in the region R. Then Cauchy-Reimann equation are satisfied by Taylor’s Theorem
at each point in the region R. Then Cauchy-Reimann equation are satisfied by Taylor’s Theorem
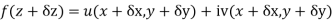
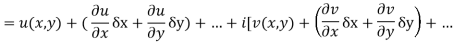

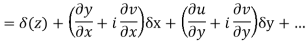
Ignoring the terms of second power and higher power
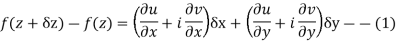
We know C-R equation
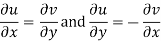
Replacing 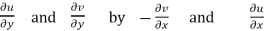
Respectively in (1) we get
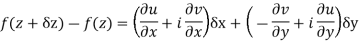
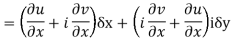

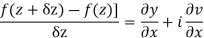
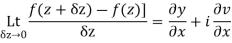

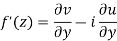
Show that 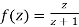 is analytic at
is analytic at 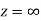
Ans The function f(z) is analytic at 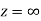 if the function
if the function 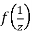 is analytic at z=0
is analytic at z=0
Since 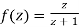
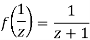
Now  is differentiable at z=0 and at all points in its neighbourhood Hence the function
is differentiable at z=0 and at all points in its neighbourhood Hence the function 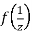 is analytic at z=0 and in turn f(z) is analytic at
is analytic at z=0 and in turn f(z) is analytic at 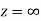
Example-1: If w = log z, then find 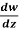 . Also determine where w is non-analytic.
. Also determine where w is non-analytic.
Sol. Here we have 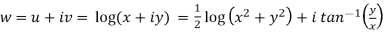
Therefore-
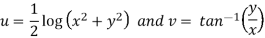
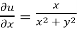 and
and
Again-

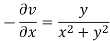
Hence the C-R conditions are satisfied also the partial derivatives are continuous except at (0 , 0).
So that w is analytic everywhere but not at z = 0
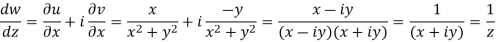
Example-2: Prove that the function 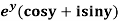 is an analytical function.
is an analytical function.
Sol. Let 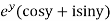 =u+iv
=u+iv
Let 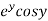 =u and
=u and 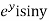 =v
=v
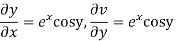
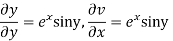
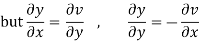
Hence C-R-Equation satisfied.
Example-3: Prove that 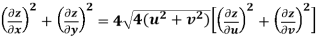
Sol. Given that
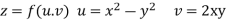

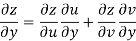
Since 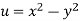

V=2xy

Now 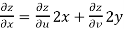
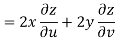
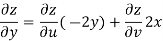
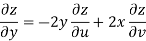
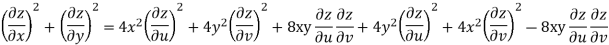
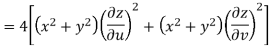
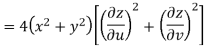
But 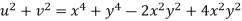
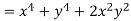
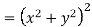

Hence 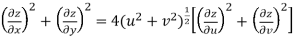
Example-4: Show that polar form of C-R equations are-
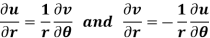
Sol. z = x + iy = 

U and v are expressed in terms of r and θ.
Differentiate it partially w.r.t. r and θ, we get-
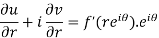
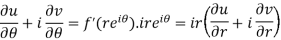
By equating real and imaginary parts, we get-
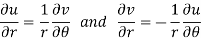
Key takeaways-
- A function
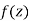 is said to be analytic at a point
is said to be analytic at a point 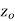 if f is differentiable not only at
if f is differentiable not only at 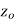 but an every point of some neighborhood at
but an every point of some neighborhood at 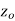 .
. - A point at which the function is not differentiable is called singular point.
- A function which is analytic everywhere is called an entire function.
- If a function is analytic in a domain D, then u and v will satisfy Cauchy-Riemann conditions.
- C-R conditions are necessary but not sufficient for analytic function.
- C-R conditions are sufficient if the partial derivative are continuous
Properties of analytic functions
Necessary condition for function f(z) to be analytic-
Theorem; The necessary condition for a function 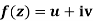 to be analytic at all the points in a region R are
to be analytic at all the points in a region R are
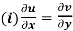 (ii)
(ii) 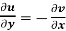
Provided, 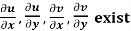
Proof:
Let 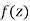 be an analytic function in region R.
be an analytic function in region R.
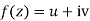
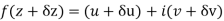
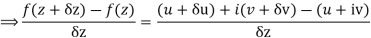
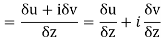
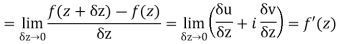
Along real axis
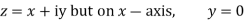
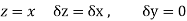
Then f’(z), becomes-
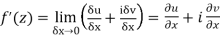 ………… (1)
………… (1)
Along imaginary axis
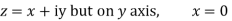
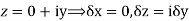
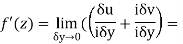

From equation (1) and (2)
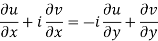
Equating real and imaginary parts
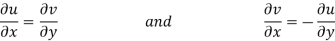
Therefore-
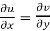 and
and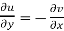
These are called Cauchy Riemann Equations.
Sufficient condition for function f(z) to be analytic-
Theorem-
The sufficient conditions of a function f(z) = u + iv to be analytic at all the points in the region R are-
1. 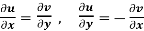
2.  are continuous functions of x and y in region R.
are continuous functions of x and y in region R.
Proof:
Suppose f(z) be a single-valued function which has-

At each point in the R region, then the Cauchy-Reimann equations are satisfied.
By Taylor’s theorem-
f(z+ δz) = u(x + δx, y+δy) + iv(x+δx, y+δy)
= u(x, y) + (u/x δx + u/y δy) + . . . + i [ v(x,y) + (v/x δx + v/y δy) + . . ]
= [u(x,y) + iv(x,y)] + [u/x δx + i v/x δx] + [u/y δy + i v/y δy] + . . .
= f(z) + (u/x + i v/x)δx + (u/y + i v/y)δy + . . .
Ignore the terms of higher power.
f(z+δz) – f(z) = (u/x + i v/x) δx + (u/y + i v/y)δy
We know that from C-R equations-

Replace 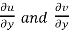 by
by 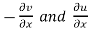
We get-
f(z+δz) – f(z) = (u/x + i v/x) δx + (-v/x + i u/x)δy
=(u/x + i v/x)δx + (iv/x + u/x) iδy = (u/x + i v/x)(δx + iδy) = (u/x + i v/x)δz
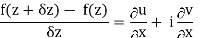
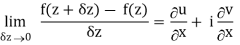
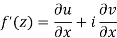
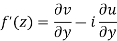
Proved
Cauchy- Riemann equations (Cartesian and Polar form)
In Cartesian form
Theorem; The necessary condition for a function 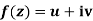 to be analytic at all the points in a region R are
to be analytic at all the points in a region R are
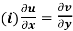 (ii)
(ii) 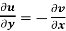
Provided, 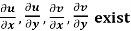
Proof:
Let 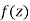 be an analytic function in region R.
be an analytic function in region R.
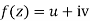
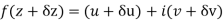

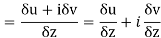
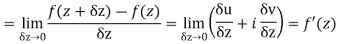
Along real axis
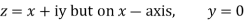
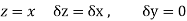
Then f’(z), becomes-
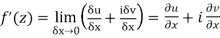 ………… (1)
………… (1)
Along imaginary axis
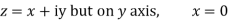
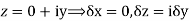
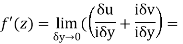
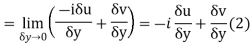
From equation (1) and (2)
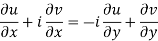
Equating real and imaginary parts

Therefore-
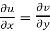 and
and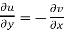
These are called Cauchy Riemann Equations.
C-R equation in polar from-
C-R equations in polar form are-
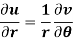

Proof:
As we know that-
x = r cos and u is the function of x and y
and u is the function of x and y
z = x + iy = r ( cos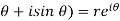
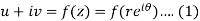
Differentiate (1) partially with respect to r, we get-
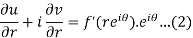
Now differentiate (1) with respect to 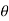 , we get-
, we get-
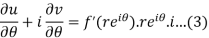
Substitute the value of 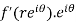 , we get-
, we get-
u/θ + iv/θ = r(u/r + i v/r)i or u/θ + i v/θ = ir u/r – r v/r
Equating real and imaginary parts, we get-

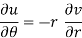
Proved
Key takeaways-
- The necessary condition for a function
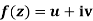 to be analytic at all the points in a region R are
to be analytic at all the points in a region R are
 (ii)
(ii) 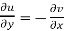
2. C-R equations in polar form are-
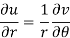
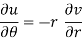
Harmonic Functions and Conjugates, Construction of Analytic Function
A function which satisfies the Laplace equation is known as a harmonic function.
Theorem- if f(z) = u + iv is an analytic function, then u and v are both harmonic functions.
Proof:
Suppose f(z) = u + iv, be an analytic function, then we have
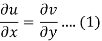
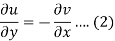
Differentiate (1) with respect to x, we get
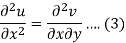
Differentiate (2) with respect to y, we get
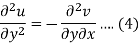
Add 3 and 4-

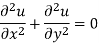
Similarly-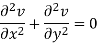
So that u and v are harmonic functions.
Example: Prove that 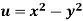 and
and 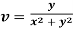 are harmonic functions of (x, y).
are harmonic functions of (x, y).
Sol.
We have 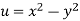
Now
u/x = 2x, 2u/x2 = 2, u/y = -2y, 2u/y2 = -2
2u/x2 + 2u/y2 = 2-2 =0
Here it satisfies Laplace equation so that u (x, y) is harmonic.
Now-
v = y/x2 + y2, v/x = - 2xy/ (x2 +y2)2
2v/x2 = (x2+y2)2(-2y) – (-2xy)2(x2+y2)2x / (x2+y2)4
= (x2+y2)(-2y)-(-2xy)4x / (x2 + y2)3 = 6x2y – 2y3 / (x2 + y2)3
v/y = (x2+y2). 1 – y(2y) / (x2+y2)2 = x2 – y2 / (x2 + y2)2
2v/y2 = (x2+y2)2 (-2y) - (x2-y2)2(x2+y2)(2y) / (x2+y2)4 = (x2+y2)(-2y)- (x2-y2)(4y) / (x2+y2)3
= -2x2y – 2y3 -4x2y +4y3 / (x2 + y2)3 = -6x2y + 2y3/(x2 + y2)3
On adding the above results-
We get-

So that v(x, y) is also a harmonic function.
Example: Find the harmonic conjugate function of the function U (x, y) = 2x (1 – y).
Sol.
We have,
U(x, y) = 2x (1 – y)
Let V is the harmonic conjugate of U.
So that by total differentiation,
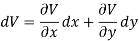
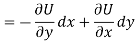
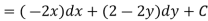
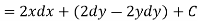
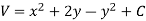
Hence the harmonic conjugate of U is 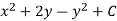
Method to find Analytic functions
Milne-Thomson method is used to construct an analytic function without finding v,
The method is given below-
Since,
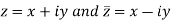
So that-
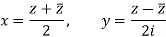
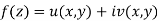
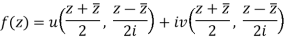
The relation above can be regarded as a formal identity in two independent variables z and 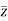
Replacing 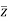 by z we get-
by z we get-
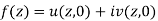
Condition-1 if u is given-
We have-
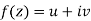

If we write-
u/x = 1(x, y) u/y = 2(x,y)
f’(z) = 1(x, y) - i2(x, y) or f’(z) = 1(z, 0) - i2(z, 0)
On integrating-
f(z) = 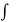 1(z, 0) dz – i
1(z, 0) dz – i 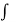 2 (z, 0)dz +c
2 (z, 0)dz +c
Condition-2: If v is given-
f(z) = u + iv
f’(z) = u/x + i v/x = v/y + i v/x = ψ1(x, y)+ i ψ2(x, y)
ψ1(x, y) = v/y, ψ2(x, y) = v/x
f(z) =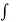 ψ1 (z, 0) dz + i
ψ1 (z, 0) dz + i 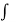 ψ2 (z, 0) dz + c
ψ2 (z, 0) dz + c
Example: If
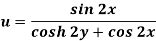
Then find f(z)
Sol.
Here-
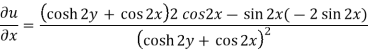
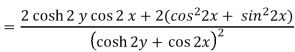
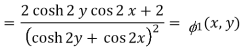
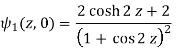
u/y = - sin 2x(2 sinh 2y) / (cosh 2y + cos 2x)2 = -2sin 2x sinh 2y / (cosh 2y + cos 2x)2 = 2(x, y)
ψ2(z, 0) = 0
f(z) = 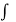 [ψ1(z, 0) – i ψ2 (z, 0)] dz + C
[ψ1(z, 0) – i ψ2 (z, 0)] dz + C
= 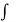 (2cos 2z + 2)/ (1+cos 2z)2 dz + C = 2
(2cos 2z + 2)/ (1+cos 2z)2 dz + C = 2 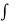 1/ 1+ cos 2z dz + C
1/ 1+ cos 2z dz + C
= 2 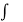 1/ 2 cos2z dz + C =
1/ 2 cos2z dz + C = 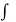 sec2 z dz + C = tan z + C
sec2 z dz + C = tan z + C
Which is the required answer.
Example: Verify if  is analytic or not?
is analytic or not?
Sol.
Here we have-
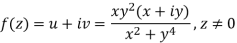
And
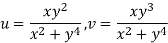
At origin-
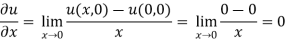

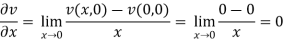

Since
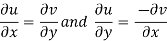
C-R equations are satisfied at the origin-
But-
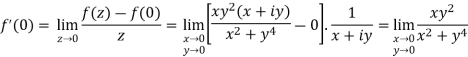
Let 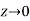 along the real axis y = 0, then
along the real axis y = 0, then
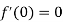
Now let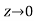 along the curve
along the curve 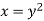 , then-
, then-
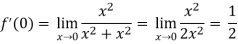
Which shows that f'(0) does not exist since the limit is not unique along two different paths. Hence f(z) is not analytic at origin but C-R equations are satisfied.
Key takeaways-
- If u is given-
f(z) = 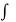 1(z, 0) dz – i
1(z, 0) dz – i 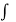 2 (z, 0) dz + c
2 (z, 0) dz + c
2. If v is given-
ψ1(x, y) = v/y, ψ2(x, y) = v/x
f(z) = 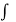 ψ1(z, 0) dz +
ψ1(z, 0) dz + 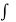 ψ2(z, 0) dz + c
ψ2(z, 0) dz + c
References:
- E. Kreyszig, “Advanced Engineering Mathematics”, John Wiley & Sons, 2006.
- P. G. Hoel, S. C. Port And C. J. Stone, “Introduction To Probability Theory”, Universal Book Stall, 2003.
- S. Ross, “A First Course in Probability”, Pearson Education India, 2002.
- W. Feller, “An Introduction To Probability Theory and Its Applications”, Vol. 1, Wiley, 1968.
- N.P. Bali and M. Goyal, “A Text Book of Engineering Mathematics”, Laxmi Publications, 2010.
- B.S. Grewal, “Higher Engineering Mathematics”, Khanna Publishers, 2000.
Unit-3
Complex Variable (Differentiation)
De Moivre’s theorem: Power of complex numbers
Let 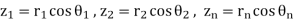 Then by the product rule in polar form, we
Then by the product rule in polar form, we
Get
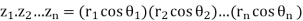
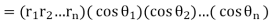
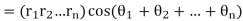
Thus

If we chose  then
then 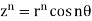 or for choice of r = 1, we get
or for choice of r = 1, we get
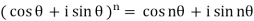
Which is known as De Moivre’s theorem.
Note-
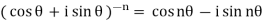
De Moivre’s theorem is valid for all rational valuesof n (including positive, negative integral values and zero).
Roots of complex number:
Let z =  where n is an integer 1, 2, 3, . . .. This isa single-valued function which associates a uniquevalue z for each ω. Now consider the inverse function
where n is an integer 1, 2, 3, . . .. This isa single-valued function which associates a uniquevalue z for each ω. Now consider the inverse function
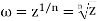
Which is multivalued, namely n valued. For any given
z  0 and the given integer n, there corresponds preciselyn distinct values of
0 and the given integer n, there corresponds preciselyn distinct values of 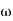 which are known as then roots of z. Thus the nth root of a complex number isanother complex number whose nth power is equalto the radicand. To determine these n roots, let
which are known as then roots of z. Thus the nth root of a complex number isanother complex number whose nth power is equalto the radicand. To determine these n roots, let 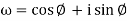 and z =
and z = 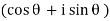 then
then
n = [ R (cos + I sin )]n
= Rn[cos n + I sin n ]
= z = r(cos θ + i sin θ)
By using De Moivre’s theorem. Since the moduli ofequal complex numbers must be equal, while theiramplitudes may circle with centre at origin and ofradius 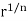 . They constitute the n vertices of a regularpolygon of n sides inscribed in the circle, spacedat equal angular intervals of
. They constitute the n vertices of a regularpolygon of n sides inscribed in the circle, spacedat equal angular intervals of 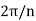 , beginning with theradius whose angle is
, beginning with theradius whose angle is 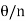 .
.
Principal value of 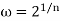 is obtained for k = 0 and by taking principal value of argument of z.
is obtained for k = 0 and by taking principal value of argument of z.
In particular, the nth roots of a real non-zero number
A also has n values since the real number A canbe expressed in trigonometric form as
A = |A|(cos θ + i sin θ) = |A| cos 0 for A > 0
And
A = |A| (cos π + i sin π) = |A| cos π for A<0
Where k is an integer. For k = 0, 1, 2, ···(n −1) weget n different roots since for these values of k, 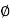 defines n distinct angles which identify n differentcomplex numbers. But as k takes n, n + 1, ···or−1, −2, . . ., the same angles
defines n distinct angles which identify n differentcomplex numbers. But as k takes n, n + 1, ···or−1, −2, . . ., the same angles 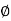 are repeated againand again, thus giving the root values that coincidewith those (already) obtained. Thus the nth root of acomplex number has n distinct values given by
are repeated againand again, thus giving the root values that coincidewith those (already) obtained. Thus the nth root of acomplex number has n distinct values given by
= z1/n = 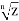 = r1/n [ cos( θ+2kπ /n) + i sin( θ+2kπ /n)] (1)
= r1/n [ cos( θ+2kπ /n) + i sin( θ+2kπ /n)] (1)
Where k = 0, 1, 2, . . . , n – 1
Geometrically, these n values are given by
x = 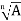 (cos 2kπ /n + i sin 2kπ /n) (2)
(cos 2kπ /n + i sin 2kπ /n) (2)
For k = 0, 1, 2, . . . , n −1 when A is a real positivenumber. In particular the nth roots of unity (for A = 1) are given by
11/n = (cos 2kπ /n + i sin 2kπ /n ), k = 0,1, . . ., n - 1
Similarly when A is a real negative number, then
x = 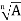 [cos (π+2kπ /n) + i sin (π+2kπ / n)] (3)
[cos (π+2kπ /n) + i sin (π+2kπ / n)] (3)
For k = 0, 1, 2, . . . , (n −1). In particular the nthroots of −1 (for A = −1) are given by
(-1)1/n = [cos (π+2kπ /n) + i sin (π+2kπ / n)]
For k = 0, 1, 2, . . . (n −1).
When A is a complex number, these n values of x are obtained from (1). Now the general rationalpower of a complex number is defined as
zp/q = (x1/q)p = [ r1/q cos θ+2kπ/q]p
= rp/q cos (p/q (θ + 2kπ))
For k = 0, 1, 2, . . . , q −1.
Example: Simplify-

Sol:
By using De-Moivre’s theorem:
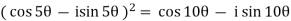
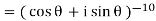
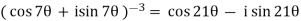
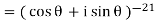
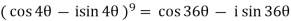

Substituting these values in given expression, we get

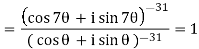
Example: If z = cos 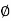 and
and 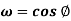 then show that
then show that
zmn + z-m-n = 2 cos(mθ + n)
Sol:
Let’s consider
zmn + z-m-n = (cis θ)m(cis )n + (cis θ)-m(cis )-n
= (cos m θ + i sin m θ)( cos n + i sin n ) + (cos m θ – i sin mθ)(cos n - i sin n )
= (cos mθ . Cos n - sin mθ . Sin n )
= cos(mθ + n)
Example: Find all solutions of the equation
z4 – (1+4i)z2 + 4i = 0
Sol:
z4 – z2 – 4iz2 + 4i =
= z2(z2 – 1) – 4i(z2 – 1) = 0
(z2 – 1)(z2 – 4i) = 0
Then z2 – 1 = 0 and z2 = 4i or z = ± 1 and z = ± 2 √i
But
√i = (eiπ/2)1/2 = eiπ/4
So z = ± 1
z = ± 2 eiπ/4 = ±2 (1/√2 + i1/√2)
The solutions are
±1, ±√2(1+i).
Example: Find all the values of (-1 + i √3)3/2
Sol:
Let
-1 + i√3 = x+iy, so x = - 1.
y = √3. Then r = √x2 + y2 = √1+3 = √4 = 2
-1 = x = r cos θ = 2 cos θ, so cos θ = - ½
√3 = y = r sin θ = 2 sin θ, so sin θ = √3/2
θ= π – π/3 = 2π/3. Thus
-1 + i √3 = reiθ = 2ei2π/3
Now
(-1 + i√3)3/2 = (2ei2π/3)3/2 = (8ei2π)1/2
= √8 ei(2π+2kπ/2) with k = 0, 1
= √8 eiπ = - √8 = -2√2 for k = 0
= √8 ei2π = + √8 = 2√2 for k = 1
Thus the solutions are 
Example: Express  in the form of (x + iy).
in the form of (x + iy).
Sol:

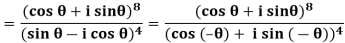

= cos 12 θ + i sin 12 θ
Circular functions:
Euler’s exponential form of circular functions:

If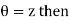

Hyperbolic functions:
Relationship between circular and hyperbolic functions:
Sin ix = i sinh x sinh ix = i sin x
Cos ix = cosh x cosh ix = cos x
Tan ix = i tanh x tanh ix = i tan x
Important formulas of hyperbolic functions:
- (1) cosh2x – sinh2 x = 1, (2) sech2 x = 1 – tanh2 x,
(3) cosech2 x = coth2x – 1
B. (1) sinh (x±y) = sinh x cosh y ± cosh x sinh y
(2) cosh (x±y) = cosh x cosh y ± sinh x sinh y
(3) tanh (x±y) = tanh x ± tanh y/ 1± tanh x tanh y
C. (1) sin h 2x = 2 sinh x coh x (2) cosh 2x = cosh2 x + sinh2 x
(3) cosh = 2 cosh2 x – 1 (4) cosh 2x = 1+2 sinh2 x
(5) tanh 2x = 2tanh x/ 1+ tanh2 x
D. (1) sinh x + sinh y = 2 sinh x+y/2 cosh x-y/2
(2) sinh x – sinh y = 2 cosh x+y/2 sinh x-y/2
(3) cosh x + cosh y = 2 cosh x+y/2 cosh x-y/2
(4) cosh x – cosh y = 2 sinh x+y/2 sinh x-y/2
Example: Prove that
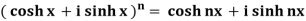
Sol:
LHS = 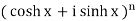
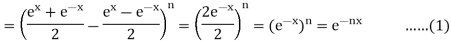
Now RHS
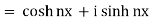

From (1) and (2), we have
LHS = RHS
Example: If cosh x = sec 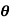 then prove that
then prove that
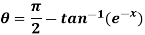
Sol:
Let
Tan-1 e-x = α
e-x = tan α and α = tan-1 (e-x ) …………..(1)
ex = cot α …………………..(2)
Now
Sec θ = cos h x = ex + e-x/2 …….............(3)
Putting the value of 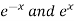 from (1) and (2) in (3), we get
from (1) and (2) in (3), we get
Sec θ = cot α + tan α/2
Sec θ = cot α + tan α = cos α/sin α + sin α/cos α = cos2α + sin2α/ sin α cos α
= 2/ 2 sin α cos α
= 2/ sin 2 α
Cos θ = sin 2 α
Cos θ = cos (π/2 -2α)
θ = π/2 - 2α = π/2 – 2 tan-1 (e-x)
In the narrow sense of the term, the theory of function of a complex variable is the theory of analytic functions (cf. Analytic function) of one or several complex variables. As an independent discipline, the theory of functions of a complex variable took shape in about the middle of the 19th century as the theory of analytic functions.
Complex function-
x + iy is a complex variable which is denoted by z
If for each value of the complex variable z = x + iy in a region R, we have one or more than one values of w = u + iv, then w is called a complex function of z.
And it is denoted as-
w = u(x , y) + iv(x , y) = f(z)
Neighbourhood of 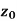
Let a point 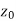 in the complex plane and z be any positive number, then the set of points z such that-
in the complex plane and z be any positive number, then the set of points z such that-
|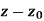 |<ε
|<ε
Is called ε- neighbourhood of 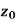
Limit of a function of a complex variable-
Suppose f(z) is a single valued function defined at all points in some neighbourhood of point 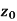 -
-
The-
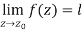
Example-1: Find-
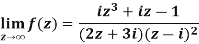
Sol. Here we have-
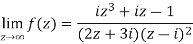
Divide numerator and denominator by 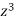 , we get-
, we get-
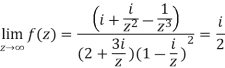
Continuity- A function w = f(z) is said to be continuous at z = 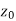 , if
, if
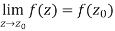
Also if w = f(z) = u(x , y) + iv(x , y) is continuous at z = 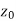 then u(x , y), v(x , y) are also continuous at z =
then u(x , y), v(x , y) are also continuous at z = 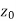 .
.
Example: Show that f(z) = Re z = x is continuous but not differentiable.
Sol.
Continuity:
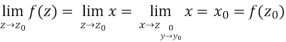
Not differentiability-

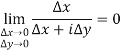
While

Hence limit does not exist which means function is not differentiable.
Differentiability-
Let f(z) be a single valued function of the variable z, then
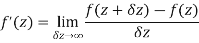
Provided that the limit exists and has the same value for all the different ways in which 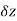 approaches to zero.
approaches to zero.
Example: if f(z) is a complex function given below, then discuss 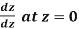
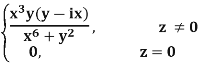
Sol. If z→0 along radius vector y = mx
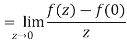
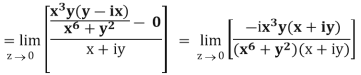
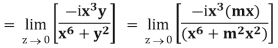
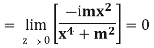
But along  ,
,

In different paths we get different value of  that means 0 and –i/2, in that case the function is not differentiable at z = 0.
that means 0 and –i/2, in that case the function is not differentiable at z = 0.
Key takeaways-
- Neighbourhood of
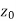
|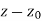 |<ε
|<ε
2. Limit of a function of a complex variable-
Suppose f(z) is a single valued function defined at all points in some neighbourhood of point  -
-
The-

3. A function w = f(z) is said to be continuous at z = 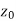 , if
, if
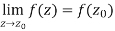
4. 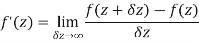
Analytic functions
A function 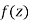 is said to be analytic at a point
is said to be analytic at a point  if f is differentiable not only at
if f is differentiable not only at 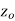 but an every point of some neighborhood at
but an every point of some neighborhood at 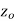 .
.
Note-
1. A point at which the function is not differentiable is called singular point.
2. A function which is analytic everywhere is called an entire function.
3. An entire function is always analytic, differentiable and continuous function.( converse is not true)
4. Analytic function is always differentiable and continuous but converse is not true.
5. A differentiable function is always continuous but converse is not true.
The necessary condition for f(z) to be analytic-
f(z) = u + i(v) is to be analytic at all the points in a region R are-
1. 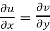 …………. (1)
…………. (1)
2. 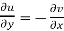 ……...…. (2)
……...…. (2)
Provided 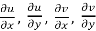 exists
exists
Equation (1) and (2) are known as Cauchy-Riemann equations.
The sufficient condition for f(z) to be analytic-
f(z) = u + i(v) is to be analytic at all the points in a region R are-
1.  …………. (1)
…………. (1)
2. 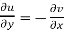 ……...…. (2)
……...…. (2)
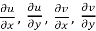 are continuous function of x and y in region R.
are continuous function of x and y in region R.
Important note-
1. If a function is analytic in a domain D, then u and v will satisfy Cauchy-Riemann conditions.
2. C-R conditions are necessary but not sufficient for analytic function.
3. C-R conditions are sufficient if the partial derivative are continuous.
State and prove sufficient condition for analytic functions
Statement – The sufficient condition for a function 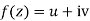 to be analytic at all points in a region R are
to be analytic at all points in a region R are
1 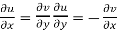
2 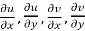 are continuous function of x and y in region R.
are continuous function of x and y in region R.
Proof:- Let f(z) be a simple valued function having 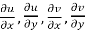 at each point in the region R. Then Cauchy-Reimann equation are satisfied by Taylor’s Theorem
at each point in the region R. Then Cauchy-Reimann equation are satisfied by Taylor’s Theorem
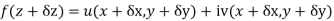
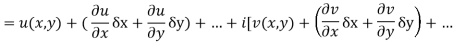
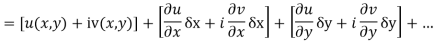
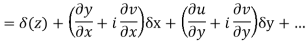
Ignoring the terms of second power and higher power
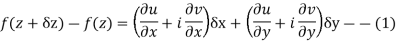
We know C-R equation
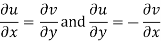
Replacing 
Respectively in (1) we get
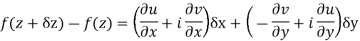
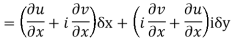
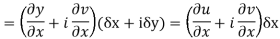
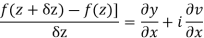
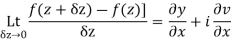
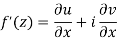
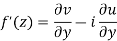
Show that 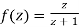 is analytic at
is analytic at 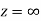
Ans The function f(z) is analytic at 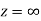 if the function
if the function 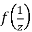 is analytic at z=0
is analytic at z=0
Since 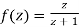
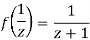
Now 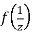 is differentiable at z=0 and at all points in its neighbourhood Hence the function
is differentiable at z=0 and at all points in its neighbourhood Hence the function  is analytic at z=0 and in turn f(z) is analytic at
is analytic at z=0 and in turn f(z) is analytic at 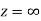
Example-1: If w = log z, then find 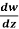 . Also determine where w is non-analytic.
. Also determine where w is non-analytic.
Sol. Here we have 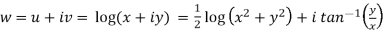
Therefore-
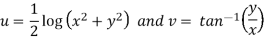
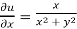 and
and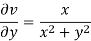
Again-

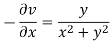
Hence the C-R conditions are satisfied also the partial derivatives are continuous except at (0 , 0).
So that w is analytic everywhere but not at z = 0
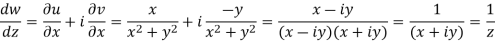
Example-2: Prove that the function 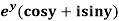 is an analytical function.
is an analytical function.
Sol. Let 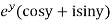 =u+iv
=u+iv
Let 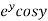 =u and
=u and 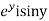 =v
=v
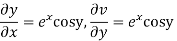
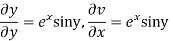
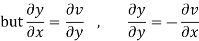
Hence C-R-Equation satisfied.
Example-3: Prove that 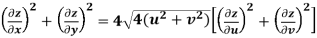
Sol. Given that
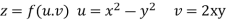
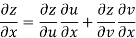

Since 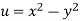

V=2xy

Now 
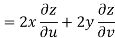
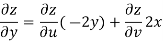
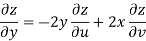
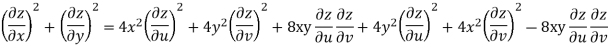
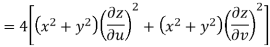
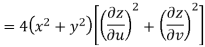
But 
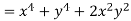
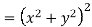
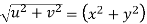
Hence 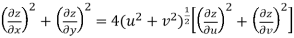
Example-4: Show that polar form of C-R equations are-
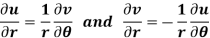
Sol. z = x + iy = 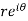
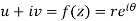
U and v are expressed in terms of r and θ.
Differentiate it partially w.r.t. r and θ, we get-
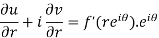
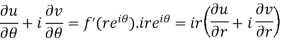
By equating real and imaginary parts, we get-
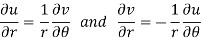
Key takeaways-
- A function
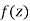 is said to be analytic at a point
is said to be analytic at a point 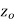 if f is differentiable not only at
if f is differentiable not only at 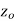 but an every point of some neighborhood at
but an every point of some neighborhood at 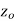 .
. - A point at which the function is not differentiable is called singular point.
- A function which is analytic everywhere is called an entire function.
- If a function is analytic in a domain D, then u and v will satisfy Cauchy-Riemann conditions.
- C-R conditions are necessary but not sufficient for analytic function.
- C-R conditions are sufficient if the partial derivative are continuous
Properties of analytic functions
Necessary condition for function f(z) to be analytic-
Theorem; The necessary condition for a function 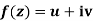 to be analytic at all the points in a region R are
to be analytic at all the points in a region R are
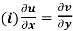 (ii)
(ii) 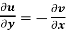
Provided, 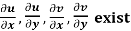
Proof:
Let 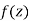 be an analytic function in region R.
be an analytic function in region R.

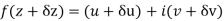
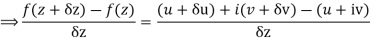
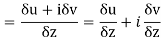

Along real axis
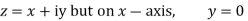
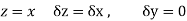
Then f’(z), becomes-
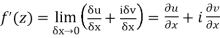 ………… (1)
………… (1)
Along imaginary axis
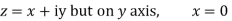
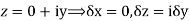
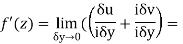

From equation (1) and (2)
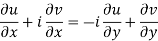
Equating real and imaginary parts
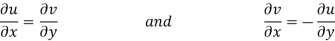
Therefore-
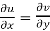 and
and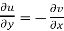
These are called Cauchy Riemann Equations.
Sufficient condition for function f(z) to be analytic-
Theorem-
The sufficient conditions of a function f(z) = u + iv to be analytic at all the points in the region R are-
1. 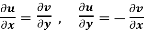
2. 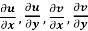 are continuous functions of x and y in region R.
are continuous functions of x and y in region R.
Proof:
Suppose f(z) be a single-valued function which has-
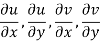
At each point in the R region, then the Cauchy-Reimann equations are satisfied.
By Taylor’s theorem-
f(z+ δz) = u(x + δx, y+δy) + iv(x+δx, y+δy)
= u(x, y) + (u/x δx + u/y δy) + . . . + i [ v(x,y) + (v/x δx + v/y δy) + . . ]
= [u(x,y) + iv(x,y)] + [u/x δx + i v/x δx] + [u/y δy + i v/y δy] + . . .
= f(z) + (u/x + i v/x)δx + (u/y + i v/y)δy + . . .
Ignore the terms of higher power.
f(z+δz) – f(z) = (u/x + i v/x) δx + (u/y + i v/y)δy
We know that from C-R equations-
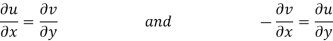
Replace  by
by 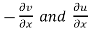
We get-
f(z+δz) – f(z) = (u/x + i v/x) δx + (-v/x + i u/x)δy
=(u/x + i v/x)δx + (iv/x + u/x) iδy = (u/x + i v/x)(δx + iδy) = (u/x + i v/x)δz
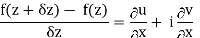
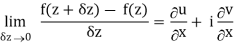
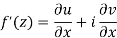
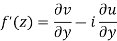
Proved
Cauchy- Riemann equations (Cartesian and Polar form)
In Cartesian form
Theorem; The necessary condition for a function 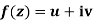 to be analytic at all the points in a region R are
to be analytic at all the points in a region R are
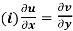 (ii)
(ii) 
Provided, 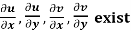
Proof:
Let  be an analytic function in region R.
be an analytic function in region R.
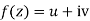
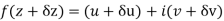

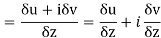
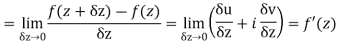
Along real axis
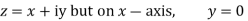

Then f’(z), becomes-
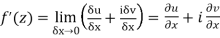 ………… (1)
………… (1)
Along imaginary axis
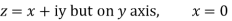
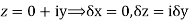
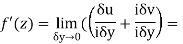
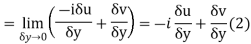
From equation (1) and (2)
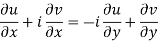
Equating real and imaginary parts
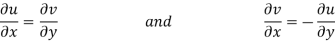
Therefore-
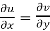 and
and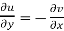
These are called Cauchy Riemann Equations.
C-R equation in polar from-
C-R equations in polar form are-
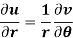
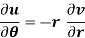
Proof:
As we know that-
x = r cos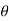 and u is the function of x and y
and u is the function of x and y
z = x + iy = r ( cos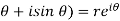

Differentiate (1) partially with respect to r, we get-
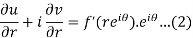
Now differentiate (1) with respect to 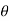 , we get-
, we get-
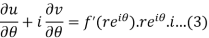
Substitute the value of 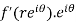 , we get-
, we get-
u/θ + iv/θ = r(u/r + i v/r)i or u/θ + i v/θ = ir u/r – r v/r
Equating real and imaginary parts, we get-
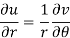
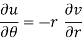
Proved
Key takeaways-
- The necessary condition for a function
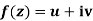 to be analytic at all the points in a region R are
to be analytic at all the points in a region R are
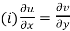 (ii)
(ii) 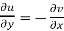
2. C-R equations in polar form are-
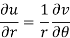
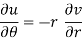
Harmonic Functions and Conjugates, Construction of Analytic Function
A function which satisfies the Laplace equation is known as a harmonic function.
Theorem- if f(z) = u + iv is an analytic function, then u and v are both harmonic functions.
Proof:
Suppose f(z) = u + iv, be an analytic function, then we have

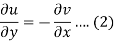
Differentiate (1) with respect to x, we get
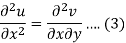
Differentiate (2) with respect to y, we get
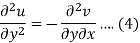
Add 3 and 4-
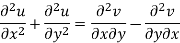
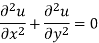
Similarly-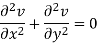
So that u and v are harmonic functions.
Example: Prove that 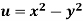 and
and 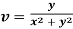 are harmonic functions of (x, y).
are harmonic functions of (x, y).
Sol.
We have 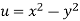
Now
u/x = 2x, 2u/x2 = 2, u/y = -2y, 2u/y2 = -2
2u/x2 + 2u/y2 = 2-2 =0
Here it satisfies Laplace equation so that u (x, y) is harmonic.
Now-
v = y/x2 + y2, v/x = - 2xy/ (x2 +y2)2
2v/x2 = (x2+y2)2(-2y) – (-2xy)2(x2+y2)2x / (x2+y2)4
= (x2+y2)(-2y)-(-2xy)4x / (x2 + y2)3 = 6x2y – 2y3 / (x2 + y2)3
v/y = (x2+y2). 1 – y(2y) / (x2+y2)2 = x2 – y2 / (x2 + y2)2
2v/y2 = (x2+y2)2 (-2y) - (x2-y2)2(x2+y2)(2y) / (x2+y2)4 = (x2+y2)(-2y)- (x2-y2)(4y) / (x2+y2)3
= -2x2y – 2y3 -4x2y +4y3 / (x2 + y2)3 = -6x2y + 2y3/(x2 + y2)3
On adding the above results-
We get-

So that v(x, y) is also a harmonic function.
Example: Find the harmonic conjugate function of the function U (x, y) = 2x (1 – y).
Sol.
We have,
U(x, y) = 2x (1 – y)
Let V is the harmonic conjugate of U.
So that by total differentiation,

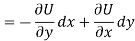

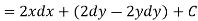
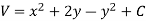
Hence the harmonic conjugate of U is 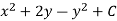
Method to find Analytic functions
Milne-Thomson method is used to construct an analytic function without finding v,
The method is given below-
Since,
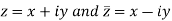
So that-
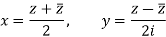
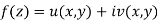
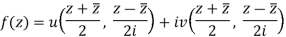
The relation above can be regarded as a formal identity in two independent variables z and 
Replacing  by z we get-
by z we get-

Condition-1 if u is given-
We have-
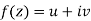
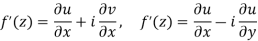
If we write-
u/x = 1(x, y) u/y = 2(x,y)
f’(z) = 1(x, y) - i2(x, y) or f’(z) = 1(z, 0) - i2(z, 0)
On integrating-
f(z) = 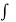 1(z, 0) dz – i
1(z, 0) dz – i 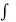 2 (z, 0)dz +c
2 (z, 0)dz +c
Condition-2: If v is given-
f(z) = u + iv
f’(z) = u/x + i v/x = v/y + i v/x = ψ1(x, y)+ i ψ2(x, y)
ψ1(x, y) = v/y, ψ2(x, y) = v/x
f(z) = ψ1 (z, 0) dz + i
ψ1 (z, 0) dz + i 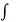 ψ2 (z, 0) dz + c
ψ2 (z, 0) dz + c
Example: If
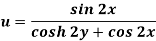
Then find f(z)
Sol.
Here-
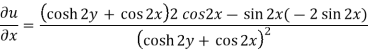
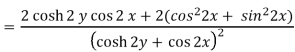
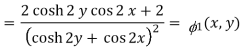
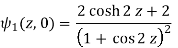
u/y = - sin 2x(2 sinh 2y) / (cosh 2y + cos 2x)2 = -2sin 2x sinh 2y / (cosh 2y + cos 2x)2 = 2(x, y)
ψ2(z, 0) = 0
f(z) = 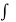 [ψ1(z, 0) – i ψ2 (z, 0)] dz + C
[ψ1(z, 0) – i ψ2 (z, 0)] dz + C
= 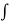 (2cos 2z + 2)/ (1+cos 2z)2 dz + C = 2
(2cos 2z + 2)/ (1+cos 2z)2 dz + C = 2 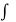 1/ 1+ cos 2z dz + C
1/ 1+ cos 2z dz + C
= 2 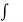 1/ 2 cos2z dz + C =
1/ 2 cos2z dz + C = 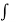 sec2 z dz + C = tan z + C
sec2 z dz + C = tan z + C
Which is the required answer.
Example: Verify if 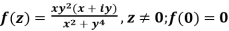 is analytic or not?
is analytic or not?
Sol.
Here we have-
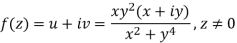
And

At origin-
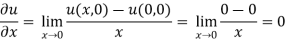
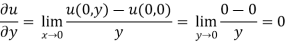

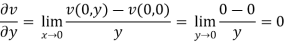
Since
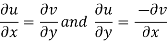
C-R equations are satisfied at the origin-
But-
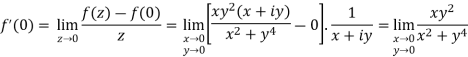
Let  along the real axis y = 0, then
along the real axis y = 0, then
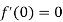
Now let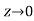 along the curve
along the curve 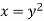 , then-
, then-
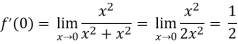
Which shows that f'(0) does not exist since the limit is not unique along two different paths. Hence f(z) is not analytic at origin but C-R equations are satisfied.
Key takeaways-
- If u is given-
f(z) = 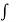 1(z, 0) dz – i
1(z, 0) dz – i  2 (z, 0) dz + c
2 (z, 0) dz + c
2. If v is given-
ψ1(x, y) = v/y, ψ2(x, y) = v/x
f(z) = 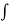 ψ1(z, 0) dz +
ψ1(z, 0) dz + 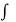 ψ2(z, 0) dz + c
ψ2(z, 0) dz + c
References:
- E. Kreyszig, “Advanced Engineering Mathematics”, John Wiley & Sons, 2006.
- P. G. Hoel, S. C. Port And C. J. Stone, “Introduction To Probability Theory”, Universal Book Stall, 2003.
- S. Ross, “A First Course in Probability”, Pearson Education India, 2002.
- W. Feller, “An Introduction To Probability Theory and Its Applications”, Vol. 1, Wiley, 1968.
- N.P. Bali and M. Goyal, “A Text Book of Engineering Mathematics”, Laxmi Publications, 2010.
- B.S. Grewal, “Higher Engineering Mathematics”, Khanna Publishers, 2000.