Unit - 1
Higher order linear differential equations and applications
1.1 Basic definition, differential operator, complimentary functions, particular integral, Shortcut methods for standard functions like  , sin(ax+ b), cos(ax+ b),,
, sin(ax+ b), cos(ax+ b),,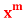 ,
, 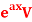 V and xV
V and xV
Linear differential equations are those in which the independent variable and its derivative occur only in the first degree and are not multiplied together.
Thus the general linear differential equation of the n’th order is of the form
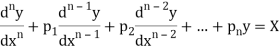
Where  and X are function of x.
and X are function of x.
Linear differential equation with constant co-efficient are of the form-
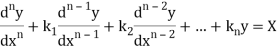
Where  are constants.
are constants.
Rules to find the complementary function-
To solve the equation-

This can be written as in symbolic form-
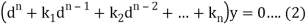
Or-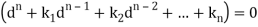
It is called the auxiliary equation.
Let 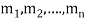 be the roots-
be the roots-
Case-1: If all the roots are real and distinct, then equation (2) becomes,

Now this equation will be satisfied by the solution of 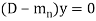
This is a Leibnitz’s linear and I.F. = 
Its solution is-
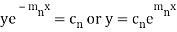
The complete solution will be-
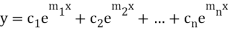
Case-2: If two roots are equal 
Then complete solution is given by-

Case-3: If one pair of roots be imaginary, i.e. 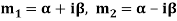 then the complete solution is-
then the complete solution is-
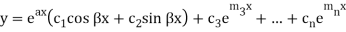
Where 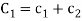 and
and 
Case-4: If two points of imaginary roots be equal-

Then the complete solution is-
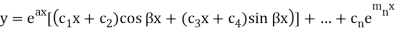
Example-Solve 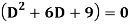
Sol.
Its auxiliary equation is-
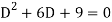
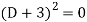
Where-
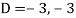
Therefore the complete solution is-
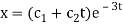
Inverse operator-
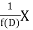 is that function of x, not containing arbitrary constants which when operated upon gives X.
is that function of x, not containing arbitrary constants which when operated upon gives X.
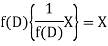
So that 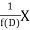 satisfies the equation f(D)y = X and is, therefore, its P.I.
satisfies the equation f(D)y = X and is, therefore, its P.I.
f(D) and 1/f(D) are inverse operator.
Note-
1. 
2. 
Rules for finding the particular integral-
Let us consider the equation-
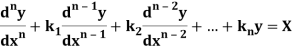
Or in symbolic form-
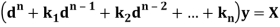
So that-

Now-
Case-1: When X = 
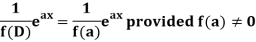
In case f(a) = 0, then we see that the above rule will not work,
So that-

Example: Find the P.I. Of (D + 2)
Sol.
P.I. = 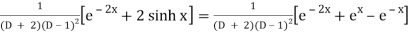
Now we will evaluate each term separately-
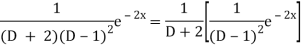
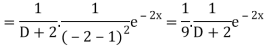


And

Therefore-

Example: Solve (D – D’ – 2 ) (D – D’ – 3) z = 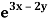
Sol.
The C.F. Will be given by-

Particular integral-



Therefore the complete solution is-
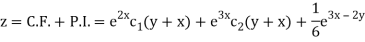
Case-2: when X = sin(ax + b) or cos (ax + b)

In case 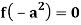 then the above rule fails.
then the above rule fails.
Now-

And if 
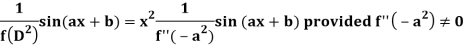
Similarly-


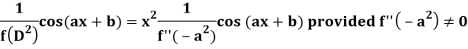
Example: Find the P.I. Of 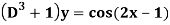
Sol.
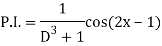

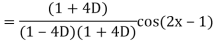

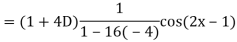
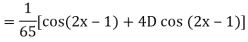
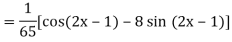
Example: Find the P.I. Of (D + 1) (D + D’ – 1)z = sin (x + 2y)
Sol.
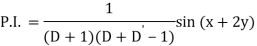
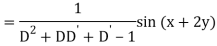
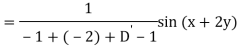

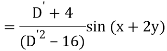
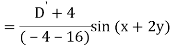
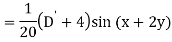
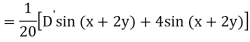

Example: Find P.I. Of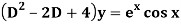
Sol. P.I = 
Replace D by D+1


Put 

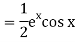
Polynomials in x, 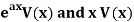
Let us consider the equation-
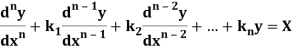
Or in symbolic form-
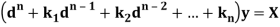
So that-
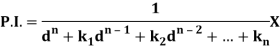
Now-
Case-1: When 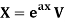 , V is the function of x.
, V is the function of x.
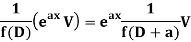
Case-2: When X is any other function of x.
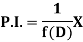
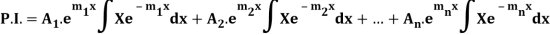
Example: Find P.I. Of 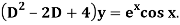
Sol.
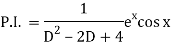
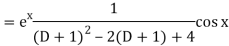

Put 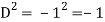
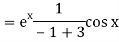

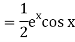
Working method to find the complete solution of an equation-
Example: Solve 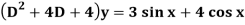
Sol.
Here first we will find the C.F.-
Its auxiliary equation will be-

Here we get-
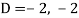
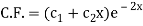
Now we will find P.I.-
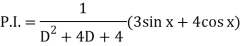
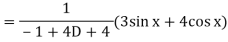

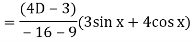
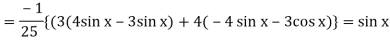
Now the complete solution is-


Example: Solve-
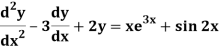
Sol.
The given equation can be written as-
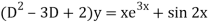
Its auxiliary equation is-
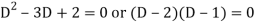
We get-

So that the C.F. Will be-

Now we will find P.I.-
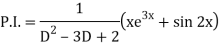
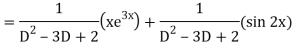
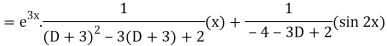

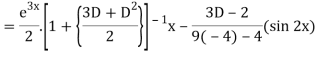
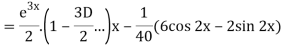
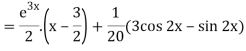
Therefore the complete solution is-
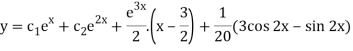
Method of variation of parameters-
Consider a second order LDE with constant co-efficients given by

Then let the complimentary function  is given by
is given by
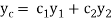
Then the particular integral is
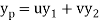
Where u and v are unknown and to be calculated using the formula
u=
Example-1: Solve the following DE by using variation of parameters-
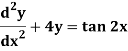
Sol. We can write the given equation in symbolic form as-
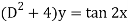
To find CF-
It’s A.E. Is 
So that CF is- 
To find PI-
Here 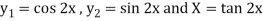
Now 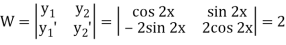
Thus PI = 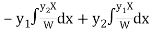
= 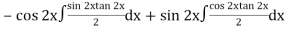
= 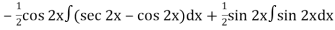
= 
= 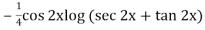
So that the complete solution is-

Example-2: Solve the following by using the method of variation of parameters.
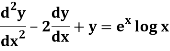
Sol. This can be written as-
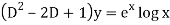
C.F.-
Auxiliary equation is- 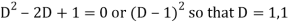
So that the C.F. Will be- 
P.I.-
Here 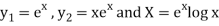
Now 
Thus PI = 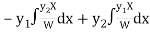
= 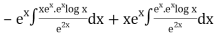
= 
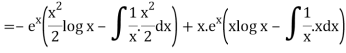
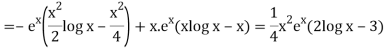
So that the complete solution is-

Key takeaways-
- Linear differential equation with constant co-efficient are of the form-

Where  are constants.
are constants.
2. 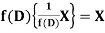
3. 
4. 
A general method of finding the PI of any function 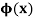
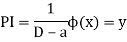
Or
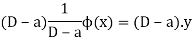
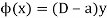
Or
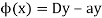

It is the LDE.
The solution will be-

Example:
Solve 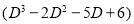

Solution:
Auxiliary equation 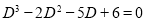
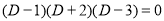
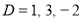
Complementary function 
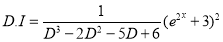

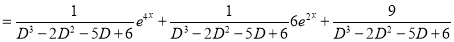

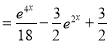
Complete Solution is 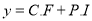
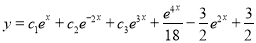
Example:
Solve 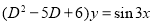
Solution:
Auxiliary equation 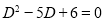

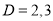
C.F is 
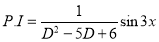
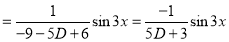
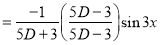
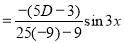


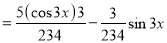 [
[ ]
]
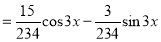
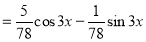
 The Complete Solution is
The Complete Solution is 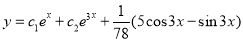
Example
Solve 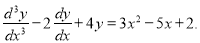
Solution:
The Auxiliary equation is 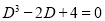
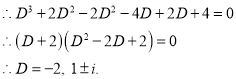
 The C.F is
The C.F is 

P.I 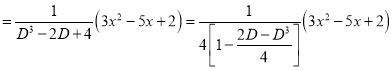

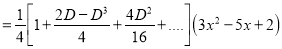

 The Complete Solution is
The Complete Solution is 
Example
Solve 
Solution:
The Auxiliary equation is 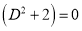

 The C.F is
The C.F is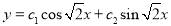
P.I 
Now, 

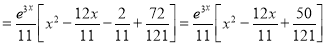
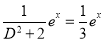
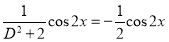
 The Complete Solution is
The Complete Solution is
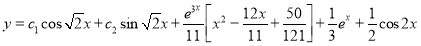
Example
Solve 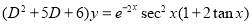
Solution:
The auxiliary equation is 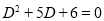
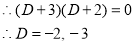
 The C.F is
The C.F is 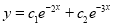
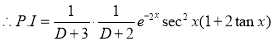
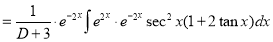 [Put
[Put 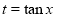 ]
]
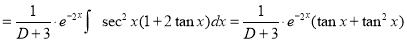
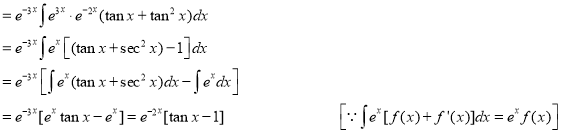
 The Complete Solution is
The Complete Solution is 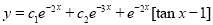
Example
Solve 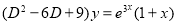
Solution:
The auxiliary equation is 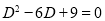

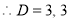
 The C.F is
The C.F is
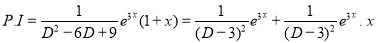
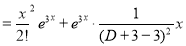
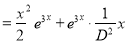
But 
 The Complete Solution is
The Complete Solution is 
Example
Solve 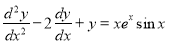
Solution:
The auxiliary equation is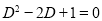

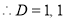
 The C.F is
The C.F is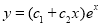


 [By parts]
[By parts]
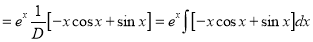


 The Complete Solution is
The Complete Solution is 
Example
Solve 
Solution:
The auxiliary equation is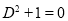
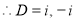
 The C.F is
The C.F is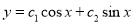
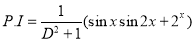
Now, 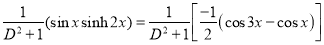

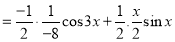
And 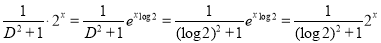
 The Complete Solution
The Complete Solution 
A homogeneous linear ordinary differential equation with constant coefficients is an ordinary differential equation in which coefficients are constants, all terms are linear, and the entire differential equation is equal to zero,
The form of second order linear differential equation with constant coefficients is,

Where a,b,c are the constants.
Let, aD²y+bDy+cy = f(x), where d² =  , D =
, D = 
∅(D)y = f(x) , where ∅(D)y = aD²y+bDy+cy
Here first we solve, ∅(D)y = 0, which is called complementary function(C.F)
Then we find particular integral (P.I)
P.I. = 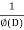 f(x)
f(x)
General solution = C.F. +P.I.
Let’s do an examples to understand the concept,
Example1: Solve (4D² +4D -3)y = 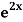
Solution: Auxiliary equation is 4m² +4m – 3 = 0
We get, (2m+3)(2m – 1) = 0
m =  ,
, 
Complementary function: CF is A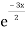 + B
+ B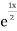
Now we will find particular integral,
P.I. = 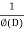 f(x)
f(x)
=  .
. 
=  .
. 
= 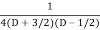 .
. 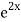
=  .
. 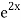 =
= 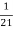 .
. 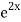
General solution is y = CF + PI
= A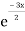 + B
+ B .
. 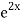
Differential operators
D stands for operation of differential i.e.

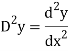
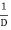 stands for the operator of integration.
stands for the operator of integration.
 stands for operation of integration twice.
stands for operation of integration twice.
Thus, 
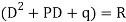
Note:-Complete solution = complementary function + Particular integral
i.e. y=CF + PI
Method for finding the CF
Step1:- In finding the CF right hand side of the given equation is replaced by zero.
Step 2:- Let 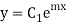 be the CF of
be the CF of

Putting the value of  in equation (1) we get
in equation (1) we get


It is called auxiliary equation.
Step 3:- Roots Real and Different
If 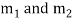 are the roots the CF is
are the roots the CF is 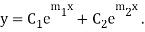
If  are the roots then
are the roots then 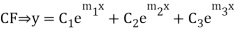
Step 4- Roots Real and Equal
If both the roots are 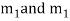 then CF is
then CF is
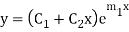
If roots are 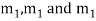

Example: Solve 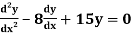
Ans. Given, 
Here Auxiliary equation is


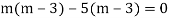
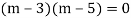
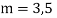

Example: Solve
Or,
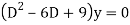
Ans. Auxiliary equation are 
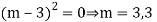
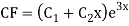
Note: If roots are in complex form i.e. 

Example: Solve 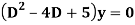
Ans. Auxiliary equation are 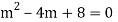
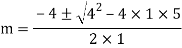
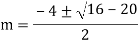


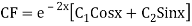
Rules to find Particular Integral
Case 1: 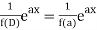
If, 
If, 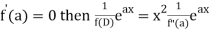
Example: Solve
Ans. Given, 
Auxiliary equation is 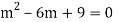
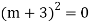
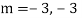
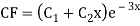
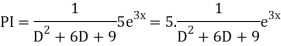

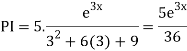
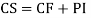

Case2: 
Expand  by the
by the
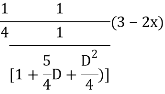
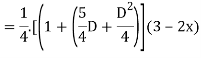
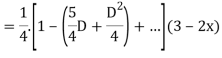
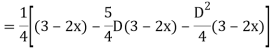

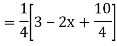
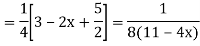
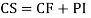
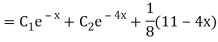
Case 3: 
Or,
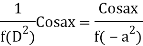
Example: 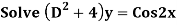
Ans. Auxiliary equation are 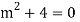
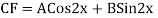
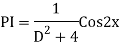

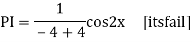
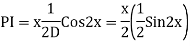

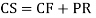

Case 4: 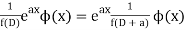
Example: Solve 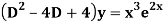
Ans. AE= 
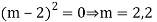
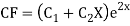
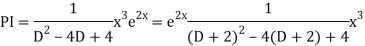
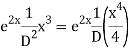
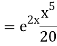
Complete solution is 
Example: Solve 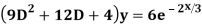
Ans. The AE is 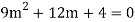
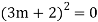
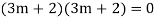
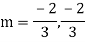
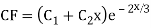
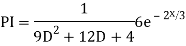
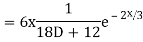
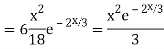
Complete solution y= CF + PI
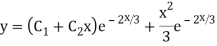
Example: Solve 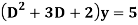
Ans. The AE is 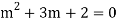
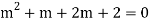
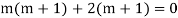
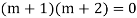
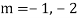

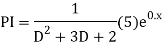
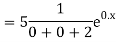
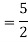
Complete solution = CF + PI
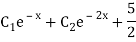
Example: Solve
Ans. The AE is 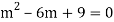

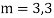
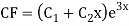
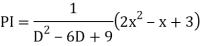
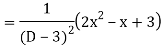

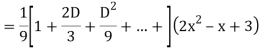

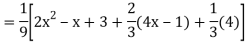

Complete solutio0n is y= CF + PI
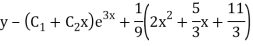
Example: Find the PI of 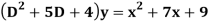
Ans. 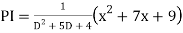


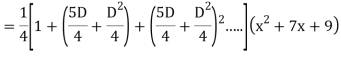

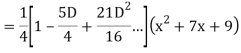
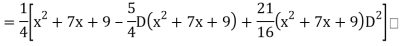

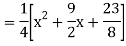
Example: solve
Ans. Given equation in symbolic form is
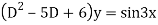
Its Auxiliary equation is 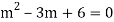
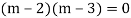
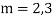
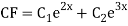
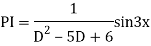
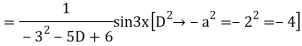
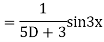


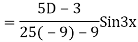
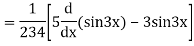
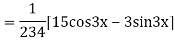
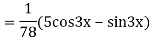
Complete solution is y= CF + PI
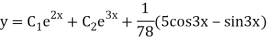
Example: Solve
Ans. The AE is 

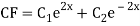
We know, 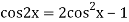
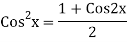
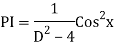
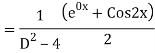
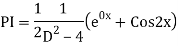
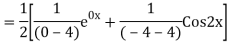

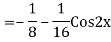
Complete solution is y= CF + PI
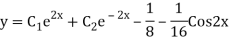
Example: Find the PI of(D2-4D+3)y=ex cos2x
Ans. 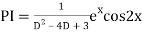

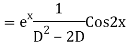

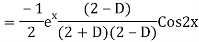




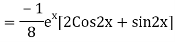
Example. Solve(D3-7D-6) y=e2x (1+x)
Ans. The auxiliary equation i9s
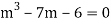

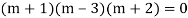
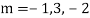
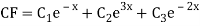
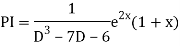
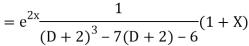
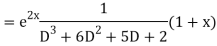
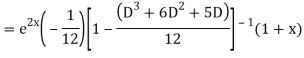


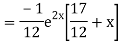
Hence complete solution is y= CF + PI

Key takeaways-
- The second order linear differential equation with constant coefficients is,

Where a,b,c are the constants.
2. General solution = C.F. +P.I.
3. 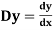
4. 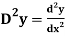
5. Roots Real and Equal-

6. Roots Real and Different-
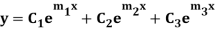
7. If roots are in complex form i.e. 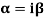
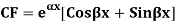

Where,  are constant is called Cauchy’s homogenous linear equation.
are constant is called Cauchy’s homogenous linear equation.
Put, 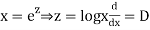
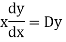

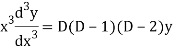
Example.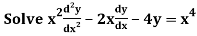
Ans. Putting, 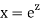
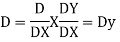
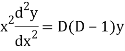
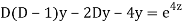

AE is 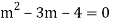
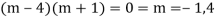
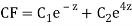

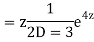

CS = CF + PI

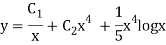
Example: Solve 
Ans. Let, 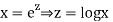
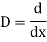
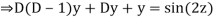

AE is 
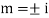
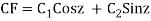
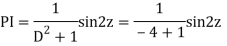
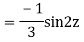
y= CF + PI
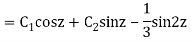
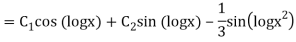
Example: Solve 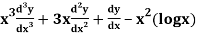
Ans. Let,  so that z = log x
so that z = log x

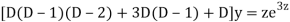

AE is 
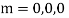

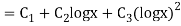

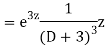

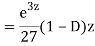
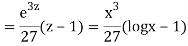

Legendre’s differential equation-
A differential equation of the form-

Where k is the constants and X is a function of x, is known as Legendre’s linear differential equation.
We can reduce such type of equations to linear equations with constant coefficient by the substitution as-

i.e.
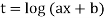
Example: Solve 
Sol. As we see that this is Legendre’s linear equation.
Now put 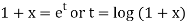
So that- 
And 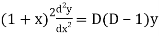
Then the equation becomes- D (D – 1)y+ Dy + y = 2 sin t

Its auxiliary equation is- 
And particular integral-
P.I. = 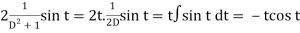
Note - 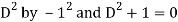
Hence the solution is - 
Key takeaways-
- Cauchy’s linear equation-
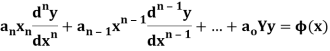
2. Legendre’s linear differential equation-
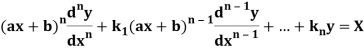
Introduction
In “real-world,” there are many physical quantities that can be represented by functions. Involving only one of the four variables e.g., (x, y, z, t). Equations involving highest order derivatives of order one = 1st order differential equations. Examples Function σ(x) = the stress in a uni – axial stretched tapered metal rod.
Function v(x) =the velocity of fluid flowing a straight channel with varying cross-section.
Solution Method of First Order ODEs Solution of Linear (Homogeneous Equation)
Typical form of the equation
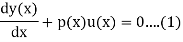
The solution u(x) in eq(1) is given by,
U(x) =
Where k= constant to be determined by given condition and the function F(x) has the form:
F(x)=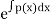 ...(3)
...(3)
In which p(x) is given in differential equation.
Type 2
Solution Method of First Order ODEs Solution of Linear (Non-Homogeneous Equation)
Typical form of the equation
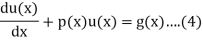
The appearance of g(x) in eq(4) tends to non-homogenous
The solution u(x) in eq(4) is given by,
U(x) =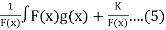
Where k= constant to be determined by given condition and the function F(x) has the form:
F(x)=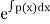
Some important terms to be considered to solve the electrical circuit problems:
*If a current i(t) is flowing through a resistor R ohms, then the voltage  across
across
*the resistor is given by 
*for an inductor of L Hentry, the voltage-current relationship is given by
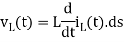
*For a capacity of c faraday, the voltage current relationship is given by
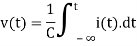
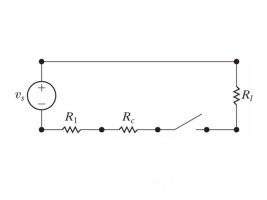
Example-1:
Finding the optimal current of an electrical circuit(RL circuits) in which the initial
Condition is i=0 at t=0
Solution:
By Kirchhoff voltage law(KVL) method, we get
The differential equation for the RL circuit will be 
In which initial conditions are i=0 at t=0
The standard form of the equation is,
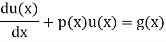
Dividing the differential equation by L to obtain

The integrating factor is

Multiplying the above equation with standard form gives rise to
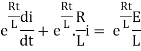
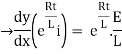
By applying integration on both sides we get
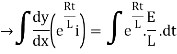
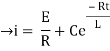
Now applying i=0 at t-0 gives us
0=
 C=-
C=-
NOW
i=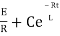
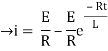
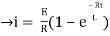 = t
= t 
Therefore by finding current of the RL circuits is i=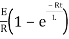
Hence we complete the solution by first order differential equation of first order and even several types of networking circuits and fluid mechanics uses this method.
Example-2:
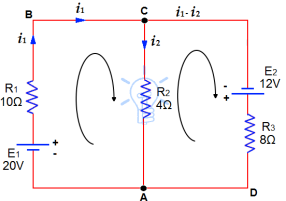
Resistors of R1= 10Ω, R2 = 4Ω and R3 = 8Ω are connected up to two batteries (of negligible resistance) as shown. Find the current through each resistor.
Solution:
Assume currents to flow in directions indicated by arrows
Apply KCL on junctions C and A
Therefore, current in mesh ABC = i1
Current in Mesh CA = i2
Then current in mesh is = i1- i2
Now, apply KVL on mesh ABC,20V are acting in clockwise direction, equating the sum of IR products, we get
10i1 +4i2 = 20.....(1)
In mesh ACD 12 volts are acting in clock-wise direction, then
8( i1 - i2)-4i2 = 12
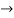 8 i1 - 8 i2-4i2 = 12
8 i1 - 8 i2-4i2 = 12
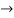 8 i1 - 12 i2 = 12...(2)
8 i1 - 12 i2 = 12...(2)
Multiplying eq(1) by 3 we get
30 i1 + 12 i2 = 60
By solving equation 1 and 2 we get,
38i1 = 72
The above equation can be also simplified by elimination or cramer’sruke
I1 = 72/38 = 1.895 Amperes = current in 10 ohms resistor
Substituting this value in (1) we get,
10(1.895)+4i2 = 20
4i2 = 20-18.95
I2 = 0.263 Amperes=current in 4 ohms resistors
Now,
i1- i2 = 1.895-0.263=1.632 Amperes
Note-
L-C circuit-
Suppose we have an electric circuit which has an inductance L and capacitance C.
Let i is the current and q is the charge in the condenser plate at time t, so that the voltage drop across-
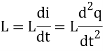
And the voltage drop across-


By Kirchhoff’s first law-
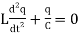 ………….. (1)
………….. (1)
Divide by L and replacing 1/LC =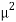 , equation (1) becomes-
, equation (1) becomes-

It represents the free electric oscillations of the current having period  .
.
L-C-R circuit-
Let us consider the discharge of a condenser C through an inductance L and the resistance R.
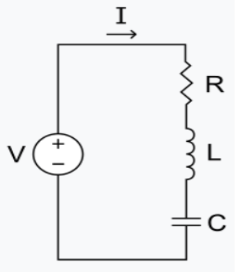
Since the voltage drop across L,C and R are respectively.
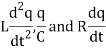
So that by Kirchhoff’s law- we have
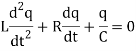
On replacing R/L by 2λ and 1/LC by μ², we get-

Key takeaways-
- The voltage current relationship is given by
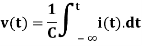
2. Kirchhoff’s first law-
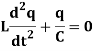
3. Free electric oscillations of the current having period 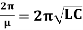 .
.
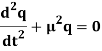
4. For an inductor of L Hentry, the voltage-current relationship is given by

References:
- E. Kreyszig, “Advanced Engineering Mathematics”, John Wiley & Sons, 2006.
- P. G. Hoel, S. C. Port And C. J. Stone, “Introduction To Probability Theory”, Universal Book Stall, 2003.
- S. Ross, “A First Course in Probability”, Pearson Education India, 2002.
- W. Feller, “An Introduction To Probability Theory and Its Applications”, Vol. 1, Wiley, 1968.
- N.P. Bali and M. Goyal, “A Text Book of Engineering Mathematics”, Laxmi Publications, 2010.
- B.S. Grewal, “Higher Engineering Mathematics”, Khanna Publishers, 2000.
- T. Veerarajan, “Engineering Mathematics”, Tata Mcgraw-Hill, New Delhi, 2010