Unit - 3

Fourier series

3.1 Introduction, Definition and Eular’s formula

Introduction:
Fourier series was given by Fourier(Jean-Baptiste Joseph Fourier (1768–1830, French physicist and mathematician) in 1907. It is known as an important development in applied mathematics.

It is very useful in the study of heat conduction, mechanics, concentrations of chemicals and pollutants, electrostatics, acoustics and in areas unheard of in Fourier’s day such as computing and computer assisted tomography scan. This series is an infinite series representation of periodic function in terms of the trigonometric sine and cosine functions. Harmonic analysis is the theory of expanding functions in Fourier series.

Periodic function

If the value of the function (y-axis) repeats itself on x-axis, then the function is called periodic function.

Suppose f(x) is a function, then

If   f(x) = f(x + t) = f (x + 2t) =    …………….

Then t is called the periodic of the function f(x).

Suppose if we take sin x, then it repeats its value after the period of 2such that, we write this as

Sin x = sin (x + 2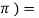 sin ( x + 4) ………….

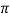We can say that sin x is a periodic function with the period of 2.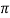

Note-

1. Cos x, sinx , sex x, cosec x are periodic functions with period 2.
2. Tan x and cot x are periodic with period
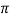
3. Suppose T is the period of f(x) then nT is also periodic of f for any integer n.

Some important integrals:

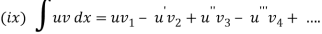
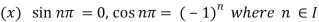
A series of the form,

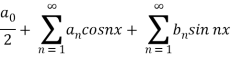
Is called fourier series , where

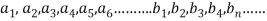are constants.

Any periodic function can be expanded in the form of fourier series.

Determination of 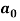 ,  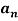 , 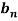of Fourier series-

We know that, the fourier series,

f(x) = 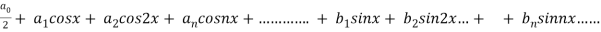  ------------ eq.(1)

To find –

Intergrate equation (1) on both sides, from 0 to 2π

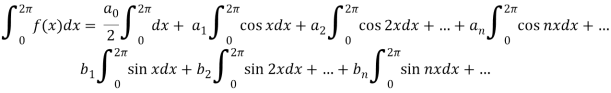
Which gives,

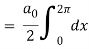
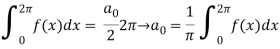
To find -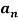

Multiply each side of eq. (1) by cos nx and integrate from 0 to 2π

We get,

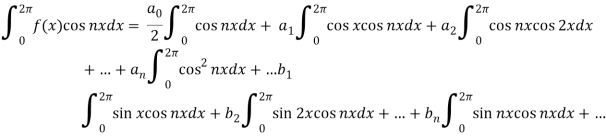
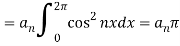
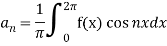
Similarly we can find 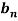by, multiplying eq. (1) by sin nx and integrating from 0 to  2π

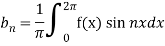
Euler’s Formulae-

Euler’s formulae can be defined as-

The Fourier series for the function f(x) in the interval is given by-

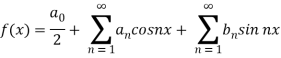
Here-

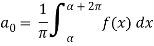
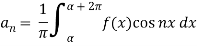
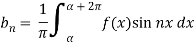
Where-

are called Euler’s formulae.

Example: Find the Fourier series of

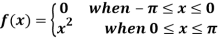
Which is assumed to be periodic with period 2π

Sol:

The Fourier series is given by-

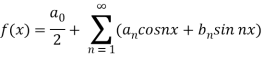
Here

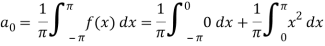
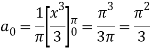
Now

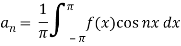
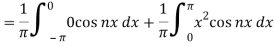
Integrating by parts,

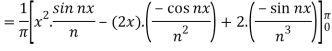
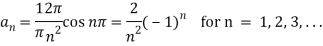
Similarly we get,

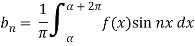
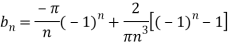
Substituting 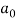, 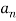and 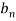we get the required Fourier series of f (x) in the internal (−π, π ) as

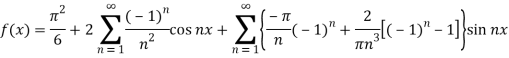
Which is the required answer.

Example: Find the fourier series of the function f(x) = x      where 0 < x < 2 π

Sol. We know that, from fourier series,

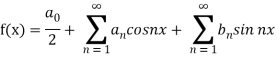
First we will find ,

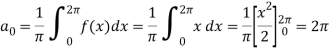
Now,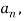

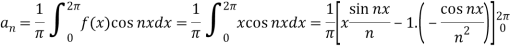
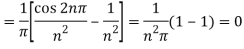
And ,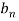

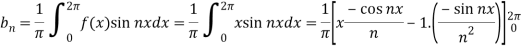
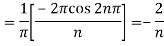
Put these value in Fourier series, we get

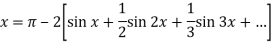
Example: Find the Fourier series for f(x) = x / 2 over the interval 0 < x < 2π

And has period 2π

Sol. First we will find

=

=

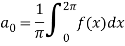
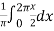
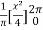
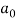= π

   =   π

Similarly,

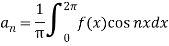
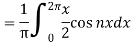
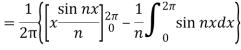
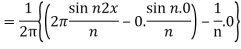
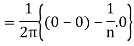
Which gives, 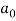  =   0

Now,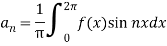
 

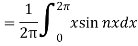
We get,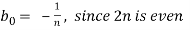

We know that, the Fourier series

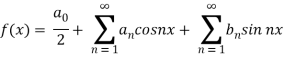
Put these values in Fourier series, we get

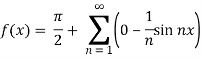
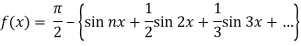
Example: Find the Fourier series for f(x) = 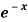in the interval .

Sol.

Suppose

Then-

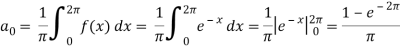
And

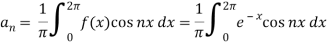
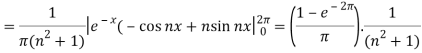
So that-

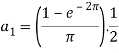
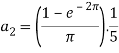
And then-

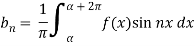
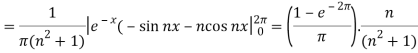
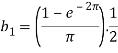
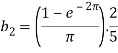
Now put these value in equations (1), we get-

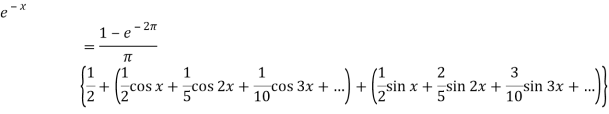
Key takeaways-

1. If the value of the function (y-axis) repeats itself on x-axis, then the function is called periodic function
2. Cos x, sinx , sex x, cosec x are periodic functions with period 2.
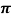3. A series of the form,

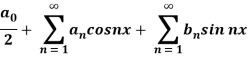
Is called fourier series, where

3.2 Fourier series of periodic functions with period 2π and 2L, Dirichlet’s theorem (Only statement)

In engineering problems the period of the given function is not always 2π but 2c.

This interval must be converted into length 2π.

Suppose a function f(x) which is periodic defined in (.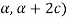

Now to change the problem to period 2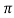

Put,

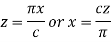
Thus the function f(x) of period 2c is transformed to the function-

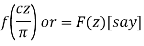
Of period 2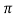 in (.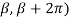

So that the function can be expressed as the Fourier series-

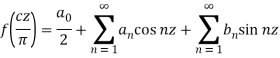
Where

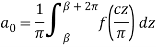
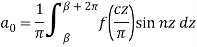
By the inverse substitution z = 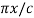 , dz = ( 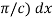in the above, the Fourier expansion of f(x) in the interval ( 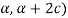is given by-

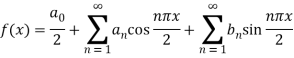
Where-

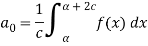
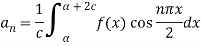
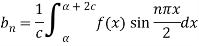
Example: A periodic function of period 4 is defined as below-

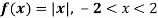
Find its Fourier series.

Sol. Here

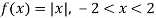
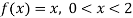
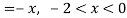
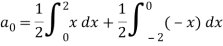
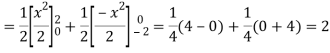
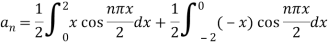
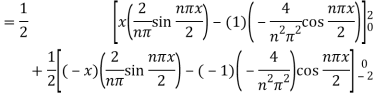
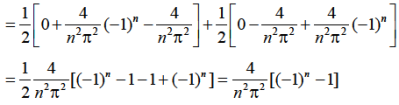
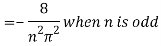
as function is even.

The Fourier series is-

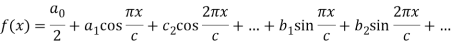
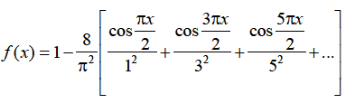
Example: Find the Fourier series for the function-

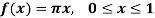
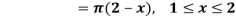
Sol.

The series if of the form,

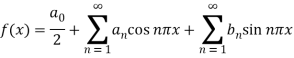
Then-

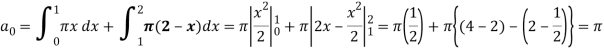
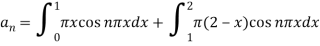
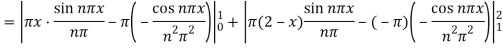
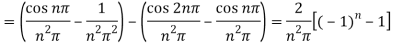
= 0 when n is even and 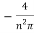when n is odd.

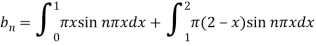
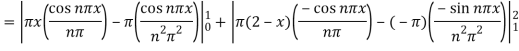
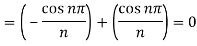
Therefore-

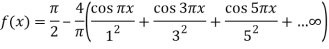
Fourier series of the function f(x) of period 2L is-

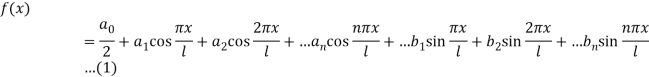
We know that

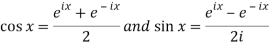
On putting these values in equation (1), we get

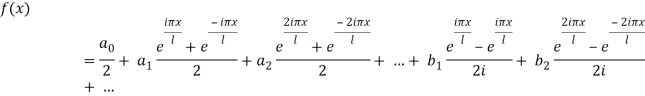
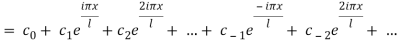
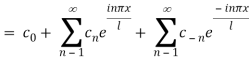
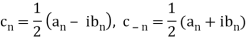
Where,

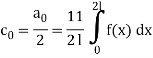
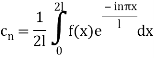
It is also known as the complex form of Fourier series.

Example:

Obtain the complex form of the Fourier series of the function

Sol:

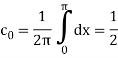
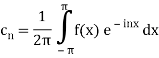
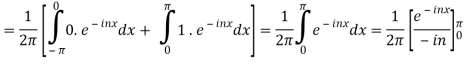
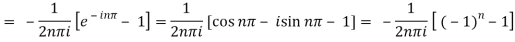
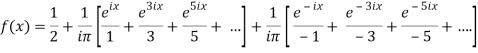
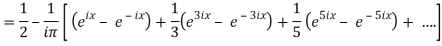
Dirichlet’s conditions for representation by a Fourier series-

Let f(x) be a function defined in C < x < C + 2L such that

1)     f(x) is defined and single valued in the given internal also. 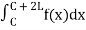exist.

2)     f(x) may have finite number of finite discontinuities in the interval.

3)     f(x) may have finite number of maxima or minima in the given interval.

3.3 Even and odd functions, half range sine and cosine series.

Fourier series of even and odd function

Odd function

A function f(x), which is written as,

f( - x ) = - f(x)

Is known as odd function.

The graph of the odd function looks like-

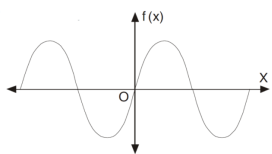
The graph of the function is symmetric about x-axis.

And the area under the curve from -π to π is always zero.(see fig)

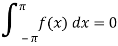
Important notes:

1. The graph of f (x) is symmetric about the origin (lies in opposite quadrants Ist and IIIrd).
2. f (x) contains only odd powers of x and may contain only sin x, cosec x.
3. The sum of two odd functions is odd i.e., h(x) = f (x) + g(x) is odd when both f (x) and g(x) are odd (or 0 + 0 = 0).
4. Product of an odd function and even function is odd i.e., h(x) = f (x)g(x) is odd when f is even and g is odd or vice versa (or) 0 · e = 0.
5. Product of two odd functions is even i.e., 0 · 0 = e.

Note- Most functions are neither even nor odd. But any function f (x) can be written as the arithmetic mean of an even and odd function as

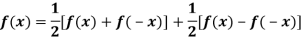
Even function-

If f(-x) = f(x) then the function is known as even function.

The graph of the function f(x) looks like-

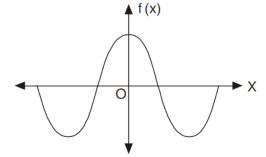
Area under the curve from -π to π  will always be double the area from 0 to π

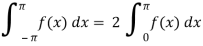
Expansion of an even function-

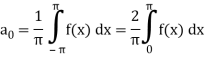
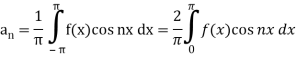
Here cosnx and f(x) are both even functions.

As we know that the product of two even numbers will be even.

Such as product of f(x) and cosnx will always be even.

Now,

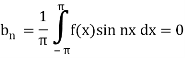
Here we see that sin nx is an odd function.

So that we do not need to find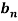

That means the series of an even function contains cosine terms only.

Expansion of an odd function-

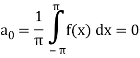
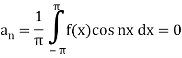
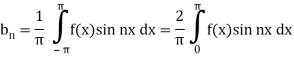
The series of the odd function contains only sine terms.

Example: Find the fourier expression of f(x) = x³ for –π< x <π.

Sol.

Here, we can see that f(x) Is an odd function

So that,

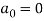and

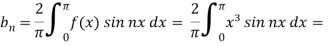
We will use here ,

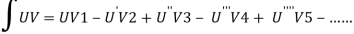
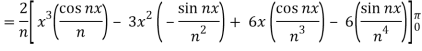
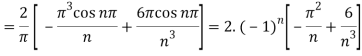
We get the value of f(x),

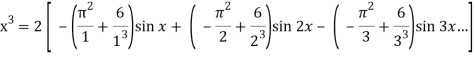
Example: Find the Fourier series expansion of the periodic function of period 2π.

f(x) = x² ,    -π≤x≤π

Sol. The given function is even, so that,

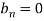
We will find

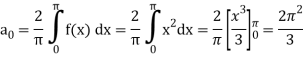
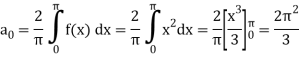
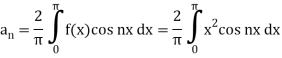
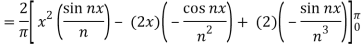
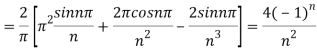
The fourier series will be ,

f(x) = a0/2 + a1 cos x + a2 cos 2x + a3 cos 3x + . . . + an cos nx + . . .

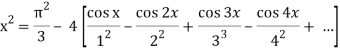
Example: Expand the function f (x) = 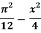in Fourier series in the interval (−π, π )

Sol:

f (x) is even since f (−x) = f (x). The Fourier series reduces to Fourier cosine series given by

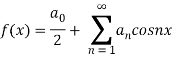
Where

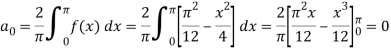
Now

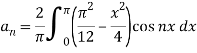
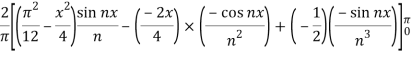
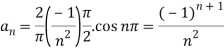
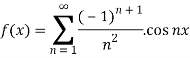
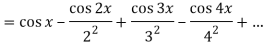
Half range sine and cosine series

Half range sine and cosine series

The function is defined in the interval (0,π) and it is immaterial whatever the function may be outside the interval (0,π) to get the series of cosines only we suppose that f(x) is an even function in the interval (-π,π)

And bn = 0

To expand the as a sine series in the same interval and as an odd function.

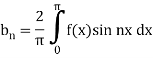
Bn = 0.

Example- Find a Fourier series for

f(x) = x2 – 2;   -2 ≤ x ≤ 2

Solution:

Here

f(x) = x2 – 2 ;      -2 ≤ x ≤ 2

Since f(x) is even function hence bn = 0

It’s Fourier series is

f(x) = a0/2 +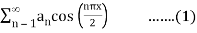

Where

a0 = 2/2

=

=

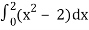
= [ 8/3 – 4 – 0 ]

= - 4/3

=

=

=

=

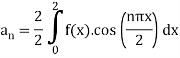
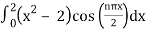
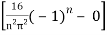
Hence equation (1) becomes,

Find half range cosine series of f(x) = x(π – x) in the interval (0, π) and hence deduce that

a)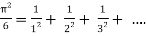    

b)   

Solution:

Here

f(x) = x(π – x);  (0, π)

Hence it’s half range cosine series is,

f(x) = a0/2 +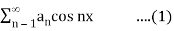

Where

a0 = 2/π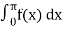 

= 2/π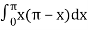

= 2/π

= 2/π [ π3/2 – π3/3 – 0]

= 2/π [ π3/6]

= π2/3

a0 = 2/π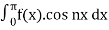 

= 2/π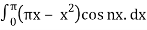 

= 2/π

= 2/π [ -π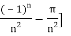

= -2 [ (1 + (-1)n)/n2]

Hence equation (1) becomes,

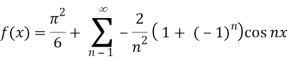
= π2/6 – 2 [ 2/22  cos 2x + 2/42  cos 4x + 2/62  cos 6x+ …..]

= π/6 – 4 [ cos 2x/22 + cos 4x/42 + cos 6x/62 + …..]       …..(2)

Put x = 0, we get

0 = π2/6 – 4 [ ½2 + 1/42 + 1/62 +  …..]

  π2/6 = 1/12 + ½2 + 1/32 + …..

Hence the result

Put x = π/2 we get,

π2/4 = π2/6 – 4 [ -1/22 + 1/42 - 1/62 +  …..]

i.e. π2/12 = 1/12 – ½2 + 1/32 – ¼2 + ….

Example: Find the Fourier sine series for the function-

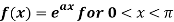
Where ‘a’ is a constant.

Sol.

Here we know-

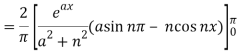
We know that-

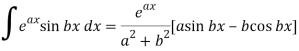
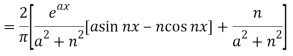
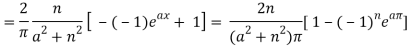
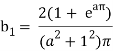
And

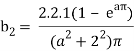
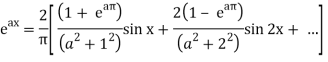
References:

1. E. Kreyszig, “Advanced Engineering Mathematics”, John Wiley & Sons, 2006.
2. P. G. Hoel, S. C. Port And C. J. Stone, “Introduction To Probability Theory”, Universal Book Stall, 2003.
3. S. Ross, “A First Course in Probability”, Pearson Education India, 2002.
4. W. Feller, “An Introduction To Probability Theory and Its Applications”, Vol. 1, Wiley, 1968.
5. N.P. Bali and M. Goyal, “A Text Book of Engineering Mathematics”, Laxmi Publications, 2010.
6. B.S. Grewal, “Higher Engineering Mathematics”, Khanna Publishers, 2000.
7. T. Veerarajan, “Engineering Mathematics”, Tata Mcgraw-Hill, New Delhi, 2010