Unit - 4
Laplace transform
Differential equations with boundary values can be solved by using Laplace transform without finding general solutions and the values of the arbitrary constants.
Let f(t) be any function of t defined for all positive values of t. Then the Laplace transform of the function f(t) is defined as-
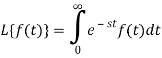
Provided that the integral exists, here ‘s’ is the parameter which could be real or complex.
The inverse of the Laplace transform can be defined as below-
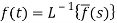
Here 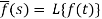
f(t) is called the inverse Laplace transform of 
L is called the Laplace transformation operator.
Applications of LT:
Laplace transform is very useful in obtaining solution of linear differential equations, both ordinary and partial, solution of system of simultaneous differential equations, solution of integral equations, solution of linear difference equations and in the evaluation of definite integrals.
Advantages of LT:
1. With the application of Laplace transform, particular solution of differential equation (D.E.) is obtained directly without the necessity of first determining general solution and then obtaining the particular solution (by substitution of initial conditions).
2. L.T. Solves non-homogeneous D.E. Without the necessity of first solving the corresponding homogeneous D.E.
3. L.T. Is applicable not only to continuous functions but also to piecewise continuous functions, complicated periodic functions, step functions and impulse functions.
Conditions for the existence of Laplace transforms-
The Laplace transform of f(t) exists for s>a, if
1. f(t) is a discontinuous function.
2. 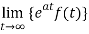 is finite.
is finite.
Important formulae-
1. 
2. 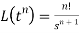
3. 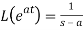
4. 
5. 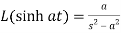
6. 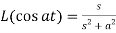
7. 
Example-1: Find the Laplace transform of the following functions-
1.  2.
2. 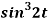
Sol. 1.
Here 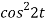
So that we can write it as-
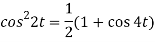
Now-
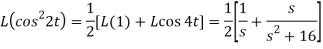
2. Since 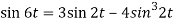
Or 
Now-
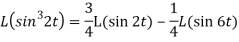
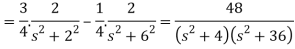
Example-2: Find the Laplace transform of (1 + cos 2t)
Sol. 
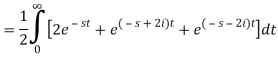
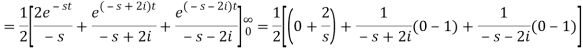
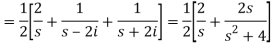
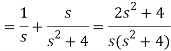
So that-
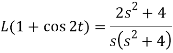
LT of standard functions-
1. 
Proof: by the definition of Laplace transform-
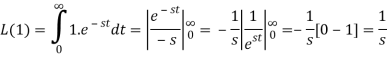
So that-
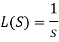
2. 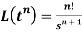
Proof: by the definition of Laplace transform-
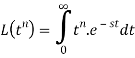
Let 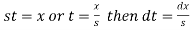
So that-
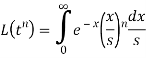
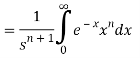
We know that-
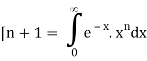
Then-
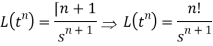
3.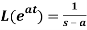
Proof: by the definition of Laplace transform-

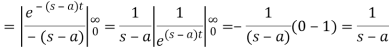
4. 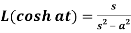
Proof: here we know that,
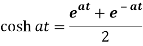
So that-
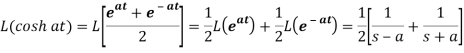

5. 
Proof: here we know that,
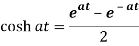
So that-
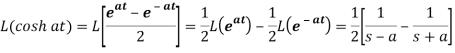
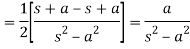
6. 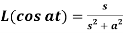
Proof: here we know that,
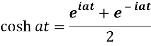
So that-
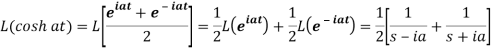
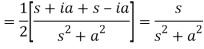
7. 
Proof: here we know that,
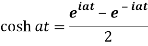
So that-
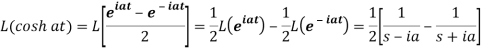
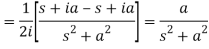
Properties and theorems of LT
1. Linearity property-
Let a and b be any two constants and 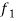 ,
, 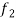 any two functions of t, then-
any two functions of t, then-

Proof: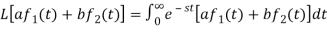
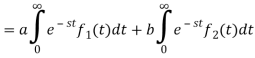
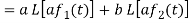
Hence proved.
2. First shifting property (Theorem)- If 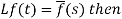
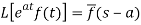
Proof: By definition-
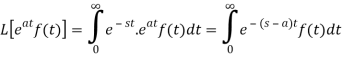
Let (s – a) = r

Hence proved.
We can find the following results with the help of the above theorem-
1. 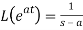
2. 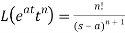
4. 
5. 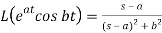
6. 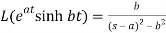
7. 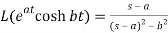
Here s>a in each case.
Example-1: Find the Laplace transform of t sin at.
Sol. Here-
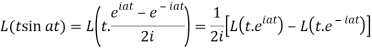
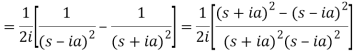
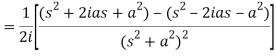

Example-2: Find the Laplace transform of 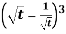
Sol. Here-
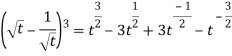
So that-
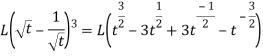
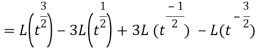
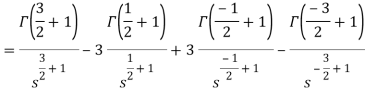
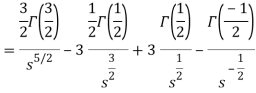
As we know that- 
So that-

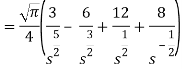
Hence-
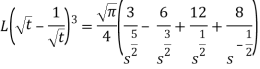
Example-3: Find the Laplace transform of the following function-
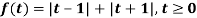
Sol. The given function f(t) can be written as-
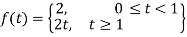
So that, by definition,

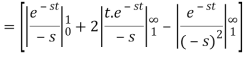
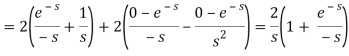
Change of scale property-
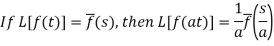
Example: Find-

Given that,
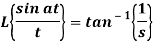
Sol.
By using change of scale property-
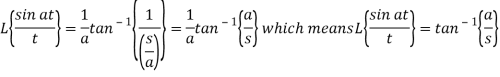
Existence theorem-
The Laplace transform of f(t) exists for s>a if –
- F(t) is continuous
 is finite.
is finite.
The above conditions are not necessary but sufficient.
Laplace transform of the derivative of f(t)-
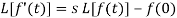
Here 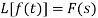
Proof: by the definition of Laplace transform-
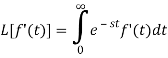
On integrating by parts, we get-
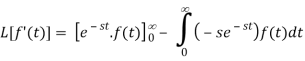
Since 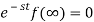
Then-

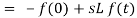
So that-
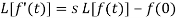
Laplace transform of integral of f(t) -
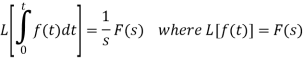
Proof: Suppose
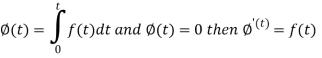
We know that-
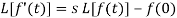
So that-
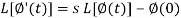

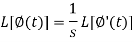
Putting the values of 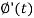 and
and 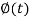 , we get-
, we get-
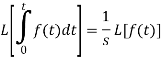
Laplace transform of the function  multiplied by t
multiplied by t
If 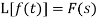 , then-
, then-
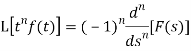
Proof: 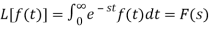
Differentiate w.r.t. x, we get-
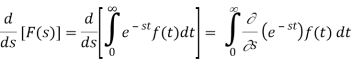
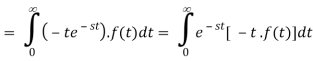
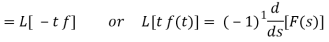
Similarly-
L[t2 f(t)] = (-1)2 d2/ds2 [F(s)]
L[t3 f(t)] = (-1)3 d3/ds3 [F(s)]
And
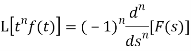
Example: Find the Laplace transform of 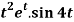 .
.
Sol. Here-
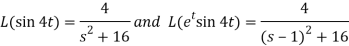
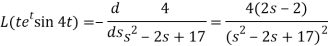
Now-
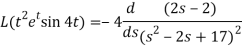
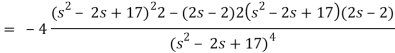

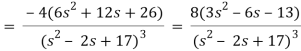
Example: Find the Laplace transform of the function f(t) = 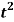 using the theorem of transform of derivative.
using the theorem of transform of derivative.
Sol:
f (0) = 0, f ‘(0) = 0, f’’ (t ) = 2
By theorem
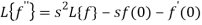
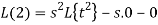
So that
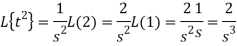
Example: Find the Laplace transform of the function f(t) = t.cos at using the theorem of transform of derivative.
Sol:
f’ = −at · sin at + cos at
f’’ = −a(at cos at + sin at ) − a sin at
f’’ = − t cos at − 2a sin at
t cos at − 2a sin at
f (0) = 0, f’(0) = 1
Using theorem for 2nd derivative
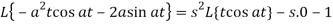
Rearranging
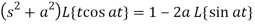
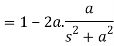
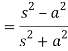
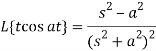
Example: Find-
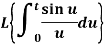
Sol:
The integrand is –

We know that
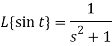
Using division by ‘t’

Using theorem on LT of integral:
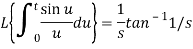
Inverse Laplace transforms-
The inverse of the Laplace transform can be defined as below-
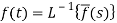
Here 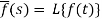
f(t) is called the inverse Laplace transform of 
L is called the Laplace transformation operator.
Important formulae-
1. 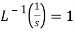 2.
2. 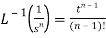
3. 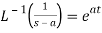 4.
4. 
5.  6.
6. 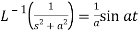
7.  8.
8. 
9. 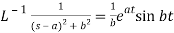 10.
10. 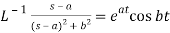
11.  12.
12. 
13. 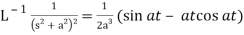 14.
14. 
15. 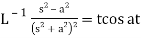 16.
16. 
17.  18.
18. 
General properties of inverse Laplace theorem:
- Linearity property:
Let L{f (t )} = F (s) and L {g(t )} = G(s) then
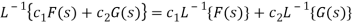
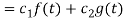
Where 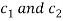 are any two constants
are any two constants
Proof:
From the Linearity property for L.T., we
Know that
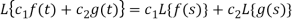
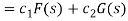
Taking inverse L.T. On either side, we get
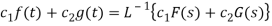
Since f(t) = 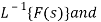 g(t) =
g(t) = 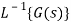 we have
we have
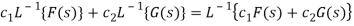
2. First shift or translation theorem
If 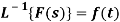 then
then

Proof: From the first translation property on L.T., we have
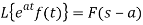
Then
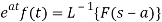
3. Change of scale property:

Proof:
From change of scale property for L.T.
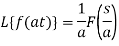
Take a = 1/k then
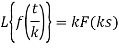
Or
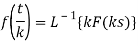
Thus
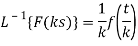
Example: (Linearity property): Find the inverse Laplace transform of the following:
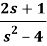
Sol:
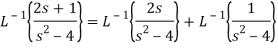
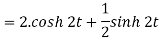
Example: (Linearity property): Find the inverse Laplace transform of the following:
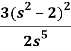
Sol:

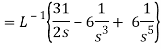

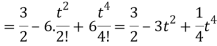
Example: (Change of scale property): Find
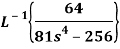
Sol:
We know that

Rewriting
 with a = 4
with a = 4
Where
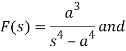
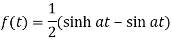
Thus applying change of scale property (with a = 3)
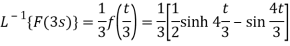
Example: (First shift theorem): Find the inverse LT of
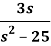
Sol:
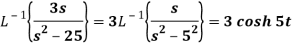
Example: (First shift theorem): Find the inverse LT of
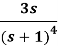
Sol:
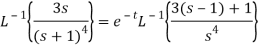
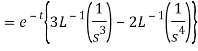
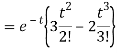
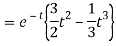
Example: Find the inverse Laplace transform of the following functions-
1. 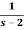
2. 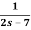
Sol.
1.

2.
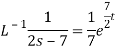
Example: Find the inverse Laplace transform of-
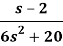
Sol.
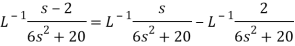
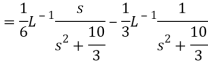
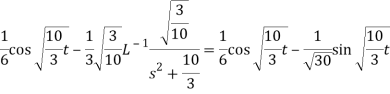
Multiplication by ‘s’ –
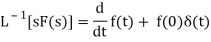
Example: Find the inverse Laplace transform of-
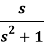
Sol.
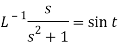
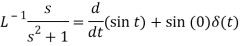
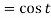
Division by s-
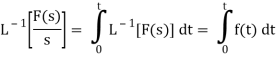
Example: Find the inverse Laplace transform of-
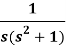
Sol.
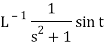
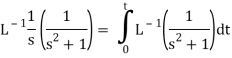
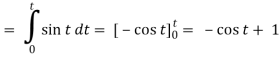
Inverse Laplace transform of derivative-
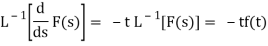
Example: Find 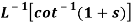
Sol.
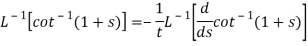
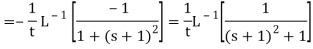
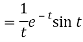
Inverse Laplace transform by using partial fraction
We can find the inverse Laplace transform by using partial fractions method described below-
Example: Find the Laplace inverse of-
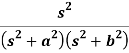
Sol.
We will convert the function into partial fractions-
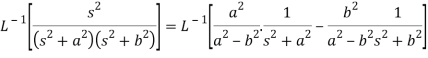
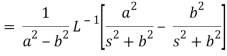
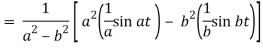
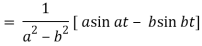
Example: Find the inverse transform of-

Sol.
First we will convert it into partial fractions-
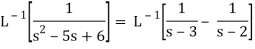
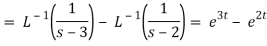
Inverse Laplace transform by convolution theorem-
According to the convolution theorem-
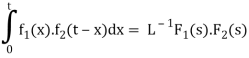
Example: Find
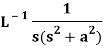
Sol.

Therefore by the convolution theorem-
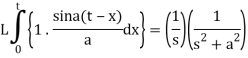
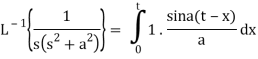
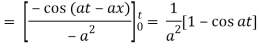
Inverse transform of logarithmic & inverse trigonometric functions
We can find the inverse LT of logarithmic and inverse trigonometric function functions as below:
Example: Find the inverse LT of-
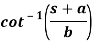
Sol:
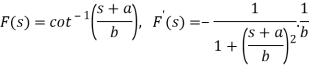
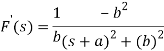
So that
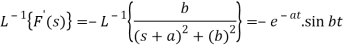
Since
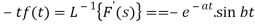
Thus
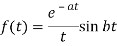
Example: Find the inverse LT of
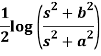
Sol:
Here
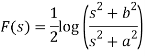
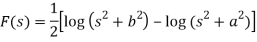
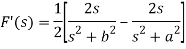
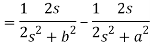

Now
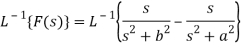
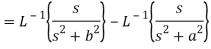

By using inverse Laplace theorem of derivatives,

Thus
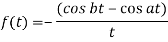
Example: Evaluate the following-

Sol:
Here
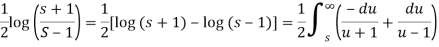
We know that
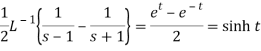
Thus applying inverse LT of integrals, we get

Convolution theorem
Convolution is used to find inverse Laplace transforms in solving differential equations and integral equations.
If 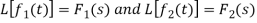
Then

Proof:
We have
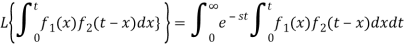
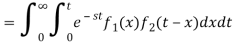
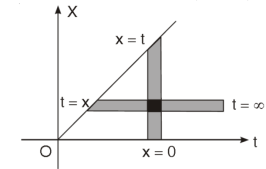
Where the double integral is taken over the infinite region in the first quadrant lying between the lines x = 0 and x = t.
If we change the order of integration, the above integrals changes to-
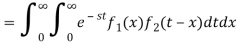
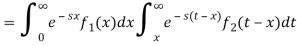
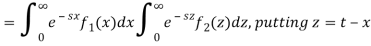
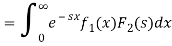
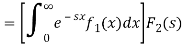
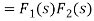
Hence proved.
Example: Apply convolution theorem to evaluate-
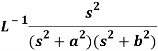
Sol.
Since
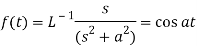
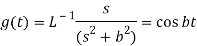
By convolution theorem, we get-
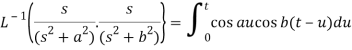
Because- f(u) = cos au, g(t-u) = cos b(t – u)

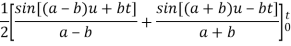
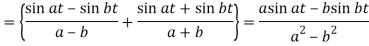
Example: Obtain
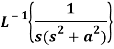
Sol:
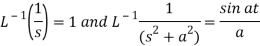
By using convolution theorem:
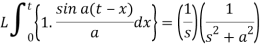
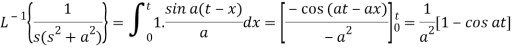
Step by step procedure to solve a linear differential equation by using Laplace transform-
1. Take Laplace transform of both sides of the given differential equation.
2. Transpose the terms with negative sign to the right.
3. Divide by the coefficient of  , getting
, getting 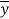 as a known function of s.
as a known function of s.
4. Resolve the function of s into partial fractions and take the inverse transform of both sides.
We will get y as a function of t. Which is the required solution.
Example-1: Use Laplace transform method to solve the following equation-
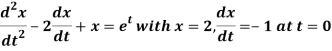
Sol. Here we have-
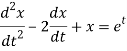
Take Laplace transform of both sides, we get-
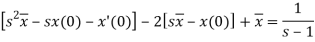
It becomes-
(
So that-
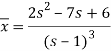
Now breaking it into partial fractions-
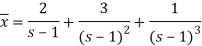
We get the following results on inversion-
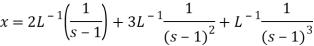
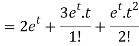
Example-2: Use Laplace transform method to solve the following equation-
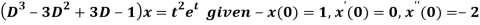
Sol.
Here, taking the Laplace transform of both sides, we get
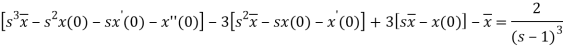
It becomes-
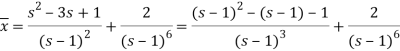

On inversion, we get-
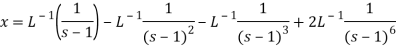
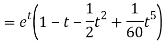
Example-3: Use Laplace transform method to solve the following equation-
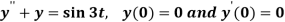
Sol. Here we have-
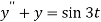
Taking Laplace transform of both sides, we get-

We get on putting given values-

On inversion, we get-
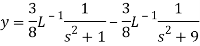

Example-4: Find the solution of the initial value problem by using Laplace transform-
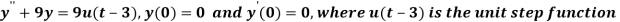
Sol. Here we have-
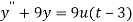
Taking Laplace transform, we get-
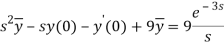
Putting the given values, we get-
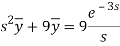
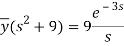

On inversion, we get-
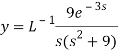
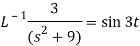
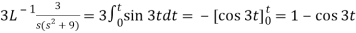 4
4
Now-
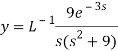

References:
- E. Kreyszig, “Advanced Engineering Mathematics”, John Wiley & Sons, 2006.
- P. G. Hoel, S. C. Port And C. J. Stone, “Introduction To Probability Theory”, Universal Book Stall, 2003.
- S. Ross, “A First Course in Probability”, Pearson Education India, 2002.
- W. Feller, “An Introduction To Probability Theory and Its Applications”, Vol. 1, Wiley, 1968.
- N.P. Bali and M. Goyal, “A Text Book of Engineering Mathematics”, Laxmi Publications, 2010.
- B.S. Grewal, “Higher Engineering Mathematics”, Khanna Publishers, 2000.
- T. Veerarajan, “Engineering Mathematics”, Tata Mcgraw-Hill, New Delhi, 2010