Unit - 1
Solution of Algebraic and Transcendental Equations
Introduction of numerical analysis-
Numerical analysis is a branch of mathematics that deal with solving the difficult mathematical problems by using efficient methods
Sometime the mathematical problems are very hard then an approximation to a difficult Mathematical problem is very important to make it more easy to solve numerical approximation has become more popular and a modern tool there are three parts of numerical analysis. The first part of the subject is about the development of a method to a problem. The second part deals with the analysis of the method, which includes the error analysis and the efficiency analysis. Error analysis gives us the understanding of how accurate the result will be if we use the method and the efficiency analysis tells us how fast we can compute the result
The third part of the subject is the development of an efficient algorithm to implement the method as a computer code.
Concept of roots of an equation-
There are two types of equations Linear and Non linear equations. Linear equations are those in which dependent variable y is directly proportional to independent variable x and is of degree one. On the other hand non linear equation are those in which y does not directly proportional to x and of degree more than one.
Ex:  +b, where a and b are constant is a linear equation.
+b, where a and b are constant is a linear equation.
 is a non linear equation.
is a non linear equation.

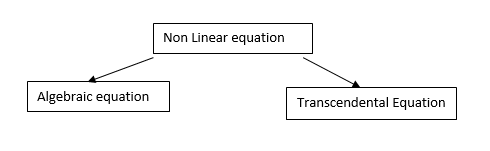
Algebraic Equation: If f(x) is a pure polynomial, then the equation 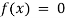 is called an algebraic equation in x.
is called an algebraic equation in x.
Ex: 
Transcendental Equation: If f(x) is an expression contain function as trigonometric, exponential and logarithmic etc. Then 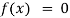 is called transcendental equation.
is called transcendental equation.
Ex 
Non –linear equation can be solved by using various analytical methods. The transcendental equations and higher order algebraic equations are difficult to solve even sometime are impossible. Finding solution of equation means just to calculate its roots.
Numerical methods are often repetitive in nature. They consist of repetitive calculation of the same process where in each step the result of preceding values are used (substitute). This is known as iteration process and is repeated till the result is obtained to desired accuracy.
The analytical methods used to solve equation; exact value of the root is obtained whereas in numerical method approximate value is obtained.
Newton-Raphson Method:
Let 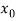 be the approximate root of the equation
be the approximate root of the equation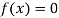 .
.
By Newton Raphson formula 
In general,

Where n=1, 2, 3…… we keep on calculating until we get desired root to the correct decimal places.
Example1Using Newton-Raphson method, find a root of the following equation correct to 3 decimal places: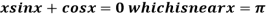 .
.
Given 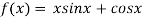
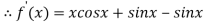

By Newton Raphson Method

= 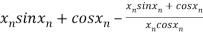
=
The initial approximation is  in radian.
in radian.
For n =0, the first approximation 
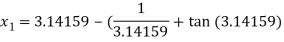
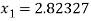
For n =1, the second approximation 
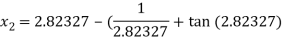
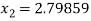
For n =2, the third approximation 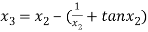


For n =3, the fourth approximation 
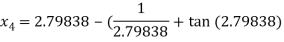

Hence the root of the given equation correct to five decimal place 2.79838.
Example 2 Using Newton-Raphson method, find a root of the following equation correct to 3 decimal places: 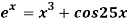 near to 4.5
near to 4.5
Let
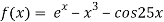
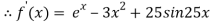
The initial approximation 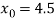
By Newton Raphson Method

For n =0, the first approximation 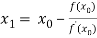
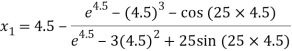
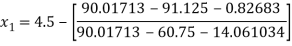
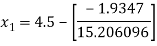
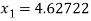
For n =1, the second approximation 


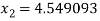
For n =2, the third approximation 


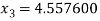
For n =3, the fourth approximation 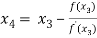


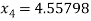
Hence the root of the equation correct to three decimal places is 4.5579
Example 3 Using Newton-Raphson method, find a root of the following equation correct to 4 decimal places: 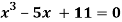
Let 
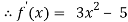
By Newton Raphson Method



Let the initial approximation be 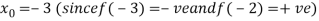
For n=0, the first approximation 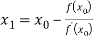


For n=1, the second approximation 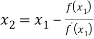
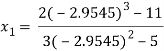
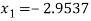
For n=2, the third approximation 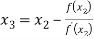
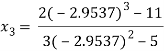

Since 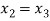 therefore the root of the given equation correct to four decimal places is -2.9537
therefore the root of the given equation correct to four decimal places is -2.9537
Key takeaways-
Newton-Raphson Method-
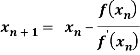
Iteration method-
To find the roots of equation f(x) = 0 by successive approximations,
We will write it as-

Now let 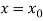 be an initial approx. Of the root(desired)
be an initial approx. Of the root(desired)  , then the first approx. Is given as-
, then the first approx. Is given as-

The second approximation is-

Same as the n’th approximation is given as-
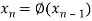
Example: Find the real root of the equation cos x = 3x – 1 correct to three decimal points by using iteration method.
Here we have-
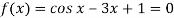
Now,
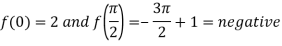
A root lies between 0 and  .
.
We can rewrite the equation as-

We have-

And

Here we can apply iteration method, starting with 
Then the successive approximation are-
x1 = (x0) = 1/3 (cos 0 + 1) = 0.6667
x2 = (x1) = 1/3 (cos 0.6667 + 1) = 0.5953
x3 = (x2) = 1/3 (cos (0.5953) + 1) = 0.6093
x4 = (x3) = 0.6067
x5 = (x4) = 0.6072
x6 = (x5) = 0.6071
Here last two approximations are almost same, the root is 0.607 correct to 3 decimal places.
Example: Starting with x = 0.12, solve x = 0.21 sin (0.5 + x) by using the iteration method.
Here

First approximation of x is gives as-
x(1) = 0.21 sin (0.5 + 0.12) = 0.122
x(2) = 0.21 sin (0.5 + 0.122) = 0.1224
x(3) = 0.12242 , x(4) = 0.12242
Here last two approx are same, hence required root is 0.12242.
There are two methods for non-linear equations:
- The method of iterations
- Newton-Raphson method
But here we will only discuss the Newton-Raphson method
Suppose the equations be given by
f(x, y) = 0, g(x, y) = 0 …… (1)
Whose real roots are required within a specified accuracy.
Let (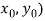 be an initial approximation to the root of the system (1).
be an initial approximation to the root of the system (1).
If 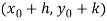 is the root of the system, the we must have,
is the root of the system, the we must have,


Assuming that f and g are sufficiently differentiable, we expand above equations by using Taylor’s series to obtain,

Where
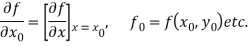
Neglecting the second and higher order terms, we get the following system of linear equations:

If the Jacobian
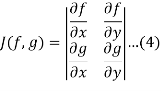
Does not vanish, then the linear equations (3) possesses a unique solution given by

The new approximations are then given by
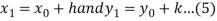
We repeat the process till we get the desired roots with accuracy.
Example: Find the roots of the equations

Sol:
Before proceeding towards the solution, we take y = x as our first approximation. This gives
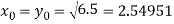
And therefore
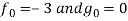
Where

Further

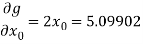

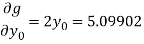
Hence
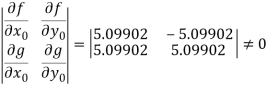
And therefore the convergence criterion is satisfied.
We then have

These equations gives,
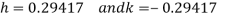
Hence the first approximation to the root is given by

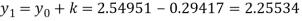
For the second approximation, we have

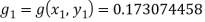
Then


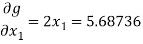
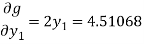
Clearly the condition of convergence is satisfied and we have the simultaneous equations,


Solving these equations, we get

And the second approximation therefore given by

And
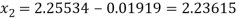
The values above may be compared with the true values, which are given by
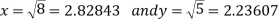
References:
- E. Kreyszig, “Advanced Engineering Mathematics”, John Wiley & Sons, 2006.
- P. G. Hoel, S. C. Port And C. J. Stone, “Introduction To Probability Theory”, Universal Book Stall, 2003.
- S. Ross, “A First Course in Probability”, Pearson Education India, 2002.
- W. Feller, “An Introduction To Probability Theory and Its Applications”, Vol. 1, Wiley, 1968.
- N.P. Bali and M. Goyal, “A Text Book of Engineering Mathematics”, Laxmi Publications, 2010.
- B.S. Grewal, “Higher Engineering Mathematics”, Khanna Publishers, 2000.
Unit - 1
Solution of Algebraic and Transcendental Equations
Introduction of numerical analysis-
Numerical analysis is a branch of mathematics that deal with solving the difficult mathematical problems by using efficient methods
Sometime the mathematical problems are very hard then an approximation to a difficult Mathematical problem is very important to make it more easy to solve numerical approximation has become more popular and a modern tool there are three parts of numerical analysis. The first part of the subject is about the development of a method to a problem. The second part deals with the analysis of the method, which includes the error analysis and the efficiency analysis. Error analysis gives us the understanding of how accurate the result will be if we use the method and the efficiency analysis tells us how fast we can compute the result
The third part of the subject is the development of an efficient algorithm to implement the method as a computer code.
Concept of roots of an equation-
There are two types of equations Linear and Non linear equations. Linear equations are those in which dependent variable y is directly proportional to independent variable x and is of degree one. On the other hand non linear equation are those in which y does not directly proportional to x and of degree more than one.
Ex: 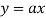 +b, where a and b are constant is a linear equation.
+b, where a and b are constant is a linear equation.
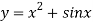 is a non linear equation.
is a non linear equation.
Algebraic Equation: If f(x) is a pure polynomial, then the equation 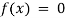 is called an algebraic equation in x.
is called an algebraic equation in x.
Ex: 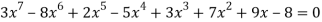
Transcendental Equation: If f(x) is an expression contain function as trigonometric, exponential and logarithmic etc. Then 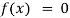 is called transcendental equation.
is called transcendental equation.
Ex 
Non –linear equation can be solved by using various analytical methods. The transcendental equations and higher order algebraic equations are difficult to solve even sometime are impossible. Finding solution of equation means just to calculate its roots.
Numerical methods are often repetitive in nature. They consist of repetitive calculation of the same process where in each step the result of preceding values are used (substitute). This is known as iteration process and is repeated till the result is obtained to desired accuracy.
The analytical methods used to solve equation; exact value of the root is obtained whereas in numerical method approximate value is obtained.
Newton-Raphson Method:
Let  be the approximate root of the equation
be the approximate root of the equation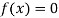 .
.
By Newton Raphson formula 
In general,
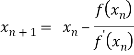
Where n=1, 2, 3…… we keep on calculating until we get desired root to the correct decimal places.
Example1Using Newton-Raphson method, find a root of the following equation correct to 3 decimal places: .
.
Given 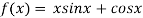
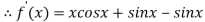

By Newton Raphson Method

= 
=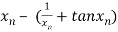
The initial approximation is  in radian.
in radian.
For n =0, the first approximation 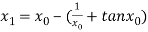

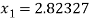
For n =1, the second approximation 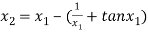
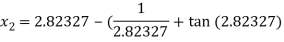
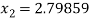
For n =2, the third approximation 

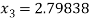
For n =3, the fourth approximation 


Hence the root of the given equation correct to five decimal place 2.79838.
Example 2 Using Newton-Raphson method, find a root of the following equation correct to 3 decimal places: 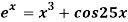 near to 4.5
near to 4.5
Let
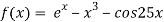

The initial approximation 
By Newton Raphson Method

For n =0, the first approximation 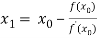
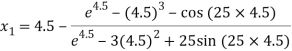



For n =1, the second approximation 



For n =2, the third approximation 


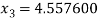
For n =3, the fourth approximation 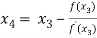


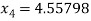
Hence the root of the equation correct to three decimal places is 4.5579
Example 3 Using Newton-Raphson method, find a root of the following equation correct to 4 decimal places: 
Let 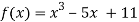
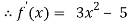
By Newton Raphson Method
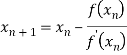
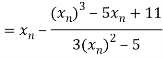
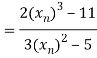
Let the initial approximation be 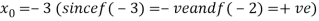
For n=0, the first approximation 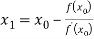
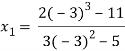
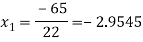
For n=1, the second approximation 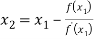
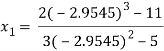
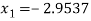
For n=2, the third approximation 
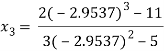

Since  therefore the root of the given equation correct to four decimal places is -2.9537
therefore the root of the given equation correct to four decimal places is -2.9537
Key takeaways-
Newton-Raphson Method-

Iteration method-
To find the roots of equation f(x) = 0 by successive approximations,
We will write it as-

Now let 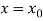 be an initial approx. Of the root(desired)
be an initial approx. Of the root(desired)  , then the first approx. Is given as-
, then the first approx. Is given as-

The second approximation is-
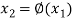
Same as the n’th approximation is given as-
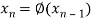
Example: Find the real root of the equation cos x = 3x – 1 correct to three decimal points by using iteration method.
Here we have-
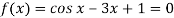
Now,
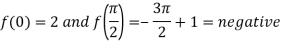
A root lies between 0 and  .
.
We can rewrite the equation as-

We have-

And
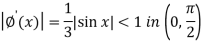
Here we can apply iteration method, starting with 
Then the successive approximation are-
x1 = (x0) = 1/3 (cos 0 + 1) = 0.6667
x2 = (x1) = 1/3 (cos 0.6667 + 1) = 0.5953
x3 = (x2) = 1/3 (cos (0.5953) + 1) = 0.6093
x4 = (x3) = 0.6067
x5 = (x4) = 0.6072
x6 = (x5) = 0.6071
Here last two approximations are almost same, the root is 0.607 correct to 3 decimal places.
Example: Starting with x = 0.12, solve x = 0.21 sin (0.5 + x) by using the iteration method.
Here

First approximation of x is gives as-
x(1) = 0.21 sin (0.5 + 0.12) = 0.122
x(2) = 0.21 sin (0.5 + 0.122) = 0.1224
x(3) = 0.12242 , x(4) = 0.12242
Here last two approx are same, hence required root is 0.12242.
There are two methods for non-linear equations:
- The method of iterations
- Newton-Raphson method
But here we will only discuss the Newton-Raphson method
Suppose the equations be given by
f(x, y) = 0, g(x, y) = 0 …… (1)
Whose real roots are required within a specified accuracy.
Let (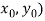 be an initial approximation to the root of the system (1).
be an initial approximation to the root of the system (1).
If 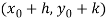 is the root of the system, the we must have,
is the root of the system, the we must have,

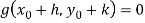
Assuming that f and g are sufficiently differentiable, we expand above equations by using Taylor’s series to obtain,
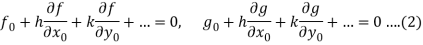
Where

Neglecting the second and higher order terms, we get the following system of linear equations:
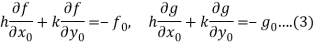
If the Jacobian
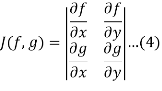
Does not vanish, then the linear equations (3) possesses a unique solution given by
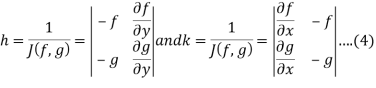
The new approximations are then given by
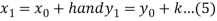
We repeat the process till we get the desired roots with accuracy.
Example: Find the roots of the equations
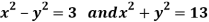
Sol:
Before proceeding towards the solution, we take y = x as our first approximation. This gives

And therefore
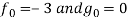
Where

Further
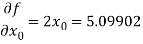
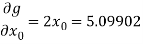
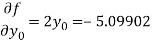
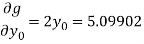
Hence
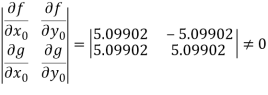
And therefore the convergence criterion is satisfied.
We then have

These equations gives,
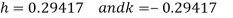
Hence the first approximation to the root is given by
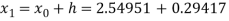

For the second approximation, we have
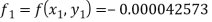

Then

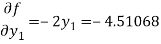

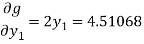
Clearly the condition of convergence is satisfied and we have the simultaneous equations,

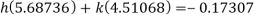
Solving these equations, we get
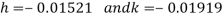
And the second approximation therefore given by

And
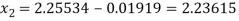
The values above may be compared with the true values, which are given by
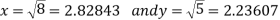
References:
- E. Kreyszig, “Advanced Engineering Mathematics”, John Wiley & Sons, 2006.
- P. G. Hoel, S. C. Port And C. J. Stone, “Introduction To Probability Theory”, Universal Book Stall, 2003.
- S. Ross, “A First Course in Probability”, Pearson Education India, 2002.
- W. Feller, “An Introduction To Probability Theory and Its Applications”, Vol. 1, Wiley, 1968.
- N.P. Bali and M. Goyal, “A Text Book of Engineering Mathematics”, Laxmi Publications, 2010.
- B.S. Grewal, “Higher Engineering Mathematics”, Khanna Publishers, 2000.
Unit - 1
Solution of Algebraic and Transcendental Equations
Introduction of numerical analysis-
Numerical analysis is a branch of mathematics that deal with solving the difficult mathematical problems by using efficient methods
Sometime the mathematical problems are very hard then an approximation to a difficult Mathematical problem is very important to make it more easy to solve numerical approximation has become more popular and a modern tool there are three parts of numerical analysis. The first part of the subject is about the development of a method to a problem. The second part deals with the analysis of the method, which includes the error analysis and the efficiency analysis. Error analysis gives us the understanding of how accurate the result will be if we use the method and the efficiency analysis tells us how fast we can compute the result
The third part of the subject is the development of an efficient algorithm to implement the method as a computer code.
Concept of roots of an equation-
There are two types of equations Linear and Non linear equations. Linear equations are those in which dependent variable y is directly proportional to independent variable x and is of degree one. On the other hand non linear equation are those in which y does not directly proportional to x and of degree more than one.
Ex: 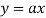 +b, where a and b are constant is a linear equation.
+b, where a and b are constant is a linear equation.
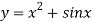 is a non linear equation.
is a non linear equation.
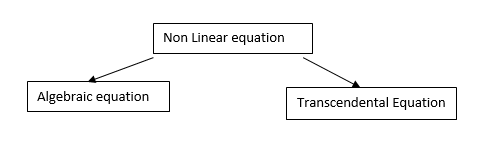
Algebraic Equation: If f(x) is a pure polynomial, then the equation 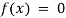 is called an algebraic equation in x.
is called an algebraic equation in x.
Ex: 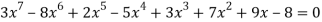
Transcendental Equation: If f(x) is an expression contain function as trigonometric, exponential and logarithmic etc. Then 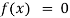 is called transcendental equation.
is called transcendental equation.
Ex 
Non –linear equation can be solved by using various analytical methods. The transcendental equations and higher order algebraic equations are difficult to solve even sometime are impossible. Finding solution of equation means just to calculate its roots.
Numerical methods are often repetitive in nature. They consist of repetitive calculation of the same process where in each step the result of preceding values are used (substitute). This is known as iteration process and is repeated till the result is obtained to desired accuracy.
The analytical methods used to solve equation; exact value of the root is obtained whereas in numerical method approximate value is obtained.
Unit - 1
Solution of Algebraic and Transcendental Equations
Unit - 1
Solution of Algebraic and Transcendental Equations
Unit - 1
Solution of Algebraic and Transcendental Equations
Introduction of numerical analysis-
Numerical analysis is a branch of mathematics that deal with solving the difficult mathematical problems by using efficient methods
Sometime the mathematical problems are very hard then an approximation to a difficult Mathematical problem is very important to make it more easy to solve numerical approximation has become more popular and a modern tool there are three parts of numerical analysis. The first part of the subject is about the development of a method to a problem. The second part deals with the analysis of the method, which includes the error analysis and the efficiency analysis. Error analysis gives us the understanding of how accurate the result will be if we use the method and the efficiency analysis tells us how fast we can compute the result
The third part of the subject is the development of an efficient algorithm to implement the method as a computer code.
Concept of roots of an equation-
There are two types of equations Linear and Non linear equations. Linear equations are those in which dependent variable y is directly proportional to independent variable x and is of degree one. On the other hand non linear equation are those in which y does not directly proportional to x and of degree more than one.
Ex: 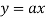 +b, where a and b are constant is a linear equation.
+b, where a and b are constant is a linear equation.
 is a non linear equation.
is a non linear equation.
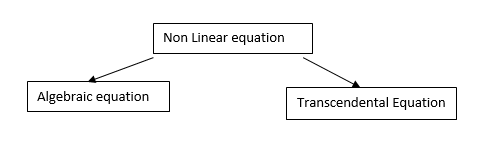
Algebraic Equation: If f(x) is a pure polynomial, then the equation  is called an algebraic equation in x.
is called an algebraic equation in x.
Ex: 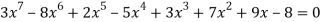
Transcendental Equation: If f(x) is an expression contain function as trigonometric, exponential and logarithmic etc. Then 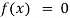 is called transcendental equation.
is called transcendental equation.
Ex 
Non –linear equation can be solved by using various analytical methods. The transcendental equations and higher order algebraic equations are difficult to solve even sometime are impossible. Finding solution of equation means just to calculate its roots.
Numerical methods are often repetitive in nature. They consist of repetitive calculation of the same process where in each step the result of preceding values are used (substitute). This is known as iteration process and is repeated till the result is obtained to desired accuracy.
The analytical methods used to solve equation; exact value of the root is obtained whereas in numerical method approximate value is obtained.
Newton-Raphson Method:
Let 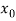 be the approximate root of the equation
be the approximate root of the equation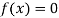 .
.
By Newton Raphson formula 
In general,
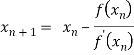
Where n=1, 2, 3…… we keep on calculating until we get desired root to the correct decimal places.
Example1Using Newton-Raphson method, find a root of the following equation correct to 3 decimal places: .
.
Given 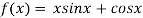
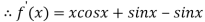

By Newton Raphson Method

= 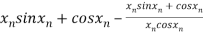
=
The initial approximation is 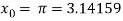 in radian.
in radian.
For n =0, the first approximation 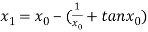
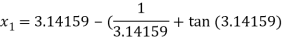

For n =1, the second approximation 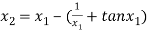


For n =2, the third approximation 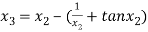


For n =3, the fourth approximation 
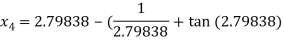
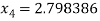
Hence the root of the given equation correct to five decimal place 2.79838.
Example 2 Using Newton-Raphson method, find a root of the following equation correct to 3 decimal places:  near to 4.5
near to 4.5
Let


The initial approximation 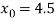
By Newton Raphson Method

For n =0, the first approximation 

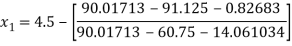


For n =1, the second approximation 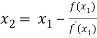


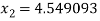
For n =2, the third approximation 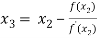

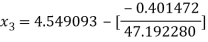

For n =3, the fourth approximation 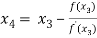

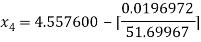

Hence the root of the equation correct to three decimal places is 4.5579
Example 3 Using Newton-Raphson method, find a root of the following equation correct to 4 decimal places: 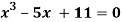
Let 

By Newton Raphson Method
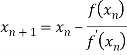
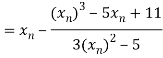

Let the initial approximation be 
For n=0, the first approximation 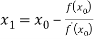
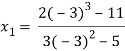
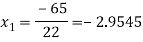
For n=1, the second approximation 
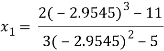
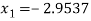
For n=2, the third approximation 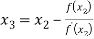
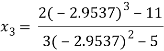
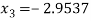
Since 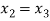 therefore the root of the given equation correct to four decimal places is -2.9537
therefore the root of the given equation correct to four decimal places is -2.9537
Key takeaways-
Newton-Raphson Method-
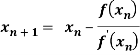
Iteration method-
To find the roots of equation f(x) = 0 by successive approximations,
We will write it as-

Now let  be an initial approx. Of the root(desired)
be an initial approx. Of the root(desired) 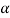 , then the first approx. Is given as-
, then the first approx. Is given as-
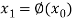
The second approximation is-
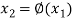
Same as the n’th approximation is given as-

Example: Find the real root of the equation cos x = 3x – 1 correct to three decimal points by using iteration method.
Here we have-
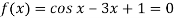
Now,

A root lies between 0 and  .
.
We can rewrite the equation as-
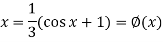
We have-

And

Here we can apply iteration method, starting with 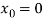
Then the successive approximation are-
x1 = (x0) = 1/3 (cos 0 + 1) = 0.6667
x2 = (x1) = 1/3 (cos 0.6667 + 1) = 0.5953
x3 = (x2) = 1/3 (cos (0.5953) + 1) = 0.6093
x4 = (x3) = 0.6067
x5 = (x4) = 0.6072
x6 = (x5) = 0.6071
Here last two approximations are almost same, the root is 0.607 correct to 3 decimal places.
Example: Starting with x = 0.12, solve x = 0.21 sin (0.5 + x) by using the iteration method.
Here
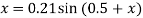
First approximation of x is gives as-
x(1) = 0.21 sin (0.5 + 0.12) = 0.122
x(2) = 0.21 sin (0.5 + 0.122) = 0.1224
x(3) = 0.12242 , x(4) = 0.12242
Here last two approx are same, hence required root is 0.12242.
Unit - 1
Solution of Algebraic and Transcendental Equations
Introduction of numerical analysis-
Numerical analysis is a branch of mathematics that deal with solving the difficult mathematical problems by using efficient methods
Sometime the mathematical problems are very hard then an approximation to a difficult Mathematical problem is very important to make it more easy to solve numerical approximation has become more popular and a modern tool there are three parts of numerical analysis. The first part of the subject is about the development of a method to a problem. The second part deals with the analysis of the method, which includes the error analysis and the efficiency analysis. Error analysis gives us the understanding of how accurate the result will be if we use the method and the efficiency analysis tells us how fast we can compute the result
The third part of the subject is the development of an efficient algorithm to implement the method as a computer code.
Concept of roots of an equation-
There are two types of equations Linear and Non linear equations. Linear equations are those in which dependent variable y is directly proportional to independent variable x and is of degree one. On the other hand non linear equation are those in which y does not directly proportional to x and of degree more than one.
Ex:  +b, where a and b are constant is a linear equation.
+b, where a and b are constant is a linear equation.
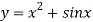 is a non linear equation.
is a non linear equation.

Algebraic Equation: If f(x) is a pure polynomial, then the equation 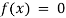 is called an algebraic equation in x.
is called an algebraic equation in x.
Ex: 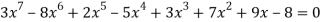
Transcendental Equation: If f(x) is an expression contain function as trigonometric, exponential and logarithmic etc. Then  is called transcendental equation.
is called transcendental equation.
Ex 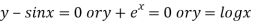
Non –linear equation can be solved by using various analytical methods. The transcendental equations and higher order algebraic equations are difficult to solve even sometime are impossible. Finding solution of equation means just to calculate its roots.
Numerical methods are often repetitive in nature. They consist of repetitive calculation of the same process where in each step the result of preceding values are used (substitute). This is known as iteration process and is repeated till the result is obtained to desired accuracy.
The analytical methods used to solve equation; exact value of the root is obtained whereas in numerical method approximate value is obtained.
Newton-Raphson Method:
Let  be the approximate root of the equation
be the approximate root of the equation .
.
By Newton Raphson formula 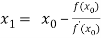
In general,
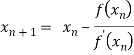
Where n=1, 2, 3…… we keep on calculating until we get desired root to the correct decimal places.
Example1Using Newton-Raphson method, find a root of the following equation correct to 3 decimal places: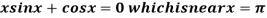 .
.
Given 


By Newton Raphson Method

= 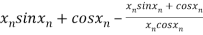
=
The initial approximation is  in radian.
in radian.
For n =0, the first approximation 


For n =1, the second approximation 

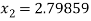
For n =2, the third approximation 


For n =3, the fourth approximation 
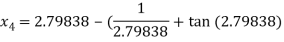
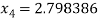
Hence the root of the given equation correct to five decimal place 2.79838.
Example 2 Using Newton-Raphson method, find a root of the following equation correct to 3 decimal places: 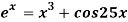 near to 4.5
near to 4.5
Let


The initial approximation 
By Newton Raphson Method

For n =0, the first approximation 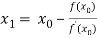
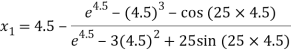

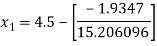

For n =1, the second approximation 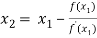

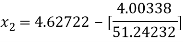

For n =2, the third approximation 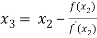



For n =3, the fourth approximation 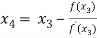

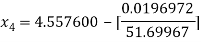

Hence the root of the equation correct to three decimal places is 4.5579
Example 3 Using Newton-Raphson method, find a root of the following equation correct to 4 decimal places: 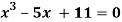
Let 
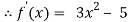
By Newton Raphson Method



Let the initial approximation be 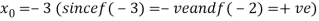
For n=0, the first approximation 


For n=1, the second approximation 
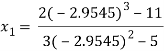

For n=2, the third approximation 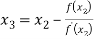
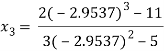
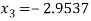
Since  therefore the root of the given equation correct to four decimal places is -2.9537
therefore the root of the given equation correct to four decimal places is -2.9537
Key takeaways-
Newton-Raphson Method-
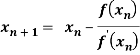
Iteration method-
To find the roots of equation f(x) = 0 by successive approximations,
We will write it as-
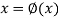
Now let 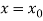 be an initial approx. Of the root(desired)
be an initial approx. Of the root(desired)  , then the first approx. Is given as-
, then the first approx. Is given as-

The second approximation is-

Same as the n’th approximation is given as-

Example: Find the real root of the equation cos x = 3x – 1 correct to three decimal points by using iteration method.
Here we have-

Now,
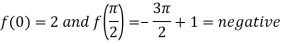
A root lies between 0 and  .
.
We can rewrite the equation as-
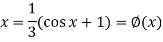
We have-

And
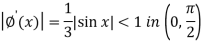
Here we can apply iteration method, starting with 
Then the successive approximation are-
x1 = (x0) = 1/3 (cos 0 + 1) = 0.6667
x2 = (x1) = 1/3 (cos 0.6667 + 1) = 0.5953
x3 = (x2) = 1/3 (cos (0.5953) + 1) = 0.6093
x4 = (x3) = 0.6067
x5 = (x4) = 0.6072
x6 = (x5) = 0.6071
Here last two approximations are almost same, the root is 0.607 correct to 3 decimal places.
Example: Starting with x = 0.12, solve x = 0.21 sin (0.5 + x) by using the iteration method.
Here
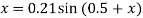
First approximation of x is gives as-
x(1) = 0.21 sin (0.5 + 0.12) = 0.122
x(2) = 0.21 sin (0.5 + 0.122) = 0.1224
x(3) = 0.12242 , x(4) = 0.12242
Here last two approx are same, hence required root is 0.12242.
There are two methods for non-linear equations:
- The method of iterations
- Newton-Raphson method
But here we will only discuss the Newton-Raphson method
Suppose the equations be given by
f(x, y) = 0, g(x, y) = 0 …… (1)
Whose real roots are required within a specified accuracy.
Let ( be an initial approximation to the root of the system (1).
be an initial approximation to the root of the system (1).
If 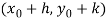 is the root of the system, the we must have,
is the root of the system, the we must have,
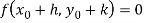

Assuming that f and g are sufficiently differentiable, we expand above equations by using Taylor’s series to obtain,

Where

Neglecting the second and higher order terms, we get the following system of linear equations:
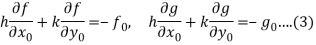
If the Jacobian
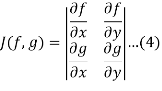
Does not vanish, then the linear equations (3) possesses a unique solution given by

The new approximations are then given by

We repeat the process till we get the desired roots with accuracy.
Example: Find the roots of the equations

Sol:
Before proceeding towards the solution, we take y = x as our first approximation. This gives
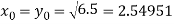
And therefore

Where
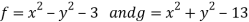
Further



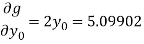
Hence

And therefore the convergence criterion is satisfied.
We then have
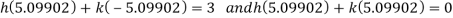
These equations gives,
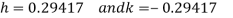
Hence the first approximation to the root is given by

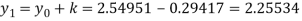
For the second approximation, we have


Then
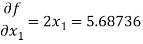

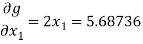
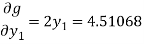
Clearly the condition of convergence is satisfied and we have the simultaneous equations,

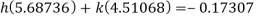
Solving these equations, we get

And the second approximation therefore given by
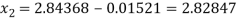
And

The values above may be compared with the true values, which are given by

References:
- E. Kreyszig, “Advanced Engineering Mathematics”, John Wiley & Sons, 2006.
- P. G. Hoel, S. C. Port And C. J. Stone, “Introduction To Probability Theory”, Universal Book Stall, 2003.
- S. Ross, “A First Course in Probability”, Pearson Education India, 2002.
- W. Feller, “An Introduction To Probability Theory and Its Applications”, Vol. 1, Wiley, 1968.
- N.P. Bali and M. Goyal, “A Text Book of Engineering Mathematics”, Laxmi Publications, 2010.
- B.S. Grewal, “Higher Engineering Mathematics”, Khanna Publishers, 2000.