Unit - 3
Numerical solutions of Ordinary Differential Equations
Consider the differential equation of first order
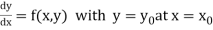
Let 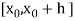 be the first interval.
be the first interval.
A second order Runge Kutta formula

Where 
Rewrite as
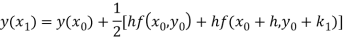
A fourth order Runge Kutta formula:

Where 
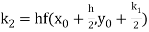

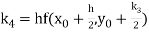
Example1: Use Runge Kutta method to find y when x=1.2 in step of h=0.1 given that

Given equation 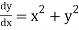
Here 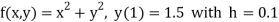
Also 
By Runge Kutta formula for first interval
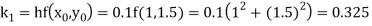
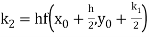
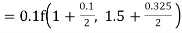

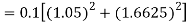



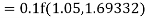
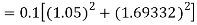

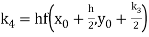
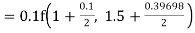
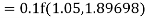

Again 
A fourth order Runge Kutta formula:


To find y at 



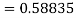
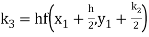

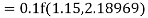




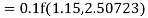

A fourth order Runge Kutta formula:


Example 2: Apply Runge Kutta fourth order method to find an approximate value of y for x=0.2 in step of 0.1, if

Given equation 
Here 
Also 
By Runge Kutta formula for first interval
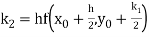
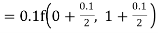

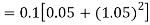
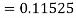
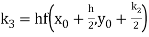
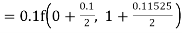
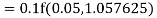
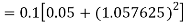




A fourth order Runge Kutta formula:


Again 


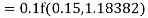

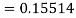

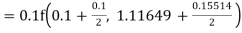


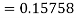


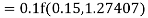


A fourth order Runge Kutta formula:

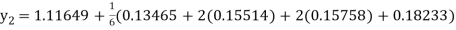

Example 3: Using Runge Kutta method of fourth order, solve

Given equation 
Here 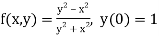
Also 
By Runge Kutta formula for first interval
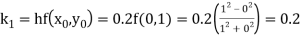



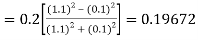
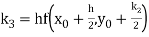
 )
)

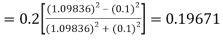



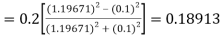
A fourth order Runge Kutta formula:
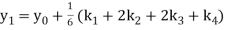
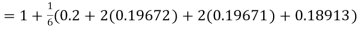

Hence at x = 0.2 then y = 1.196
To find the value of y at x=0.4. In this case 
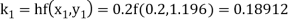
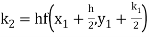

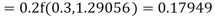
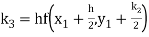
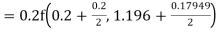

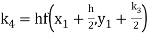

A fourth order Runge Kutta formula:

Hence at x = 0.4 then y=1.37527
Picard’s method:
The general first order differential equation
 ….(1)
….(1)
With the initial condition  …(2)
…(2)
In general, the solution of first order differential equation in one of the two forms:
a) A series for y in terms of power of x, from which the value of y can be obtained by direct solution.
b) A set of tabulated values of x and y.
The case (a) is solved by Taylor’s Series or Picard method whereas case (b) is solved by Euler’s, Runge Kutta Methods etc.
Picard’s method-
Let us suppose the first order equation-
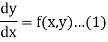
It is required to find out that particular solution of equation (1) which assumes the value 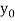 when
when  ,
,
Now integrate (1) between limits, we get-

This is equivalent to equation (1),
For it contains the not-known y under the integral sign,
As a first approximation  to the solution, put
to the solution, put 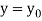 in f(x, y) and integrate (2),
in f(x, y) and integrate (2),
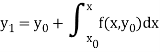
For second approximation-
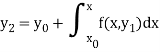
Similarly-
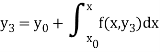
And so on.
Example: Find the value of y for x = 0.1 by using Picard’s method, given that-
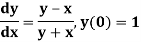
Sol.
We have-

For first approximation, we put y = 1, then-

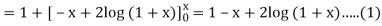
Second approximation-
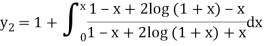
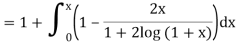
We find it very hard to integrate.
Hence we use the first approximation and take x = 0.1 in (1)
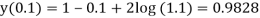
Example: Obtain the picard’s second approximation for the given initial value problem-
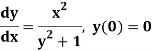
Find y(1).
Sol.
The first approximation will be-
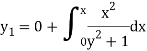
Replace y by 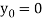 , we get-
, we get-
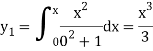
The second approximation is-
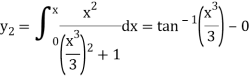
The third approximation-
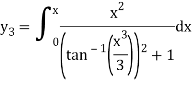
It is very difficult to solve the integration-
This is the disadvantage of the method.
Now we get from the second approximation-
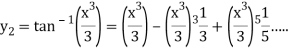
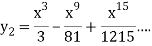
At x = 1-

Simultaneous equation using Runge Kutta method of 2 orders:
The second order differential equation
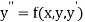
Let 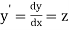 then the above equation reduces to first order simultaneous differential equation
then the above equation reduces to first order simultaneous differential equation
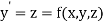
Then 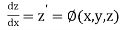
This can be solved as we discuss above by Runge Kutta Method. Here  for
for  and
and 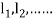 for
for  .
.
A fourth order Runge Kutta formula:
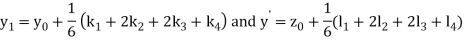
Where 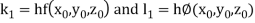

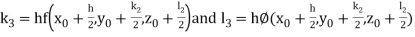

Example1: Using Runge Kutta method of order four , solve 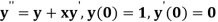 to find
to find 
Given second order differential equation is
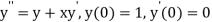
Let 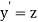 then above equation reduces to
then above equation reduces to
Or 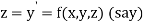
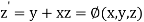 (say)
(say)
Or 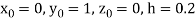 .
.
By Runge Kutta Method we have
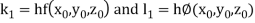
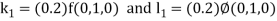



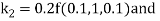

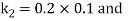
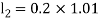
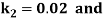
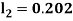
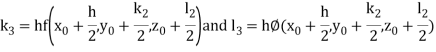







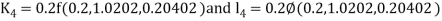
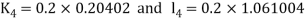
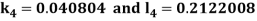
A fourth order Runge Kutta formula:
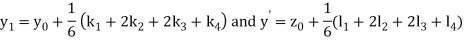
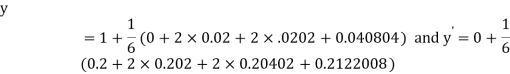
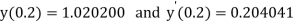
Example 2: Using Runge Kutta method, solve
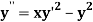 for
for 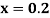 correct to four decimal places with initial condition
correct to four decimal places with initial condition  .
.
Given second order differential equation is
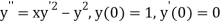
Let 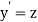 then above equation reduces to
then above equation reduces to
Or 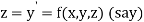
 (say)
(say)
Or  .
.
By Runge Kutta Method we have


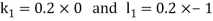
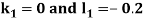

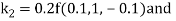

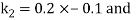

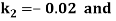

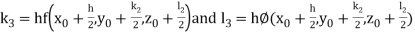
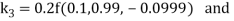

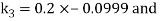



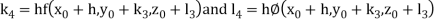
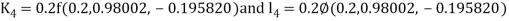
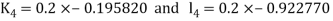
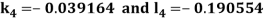
A fourth order Runge Kutta formula:
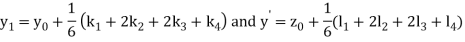

And
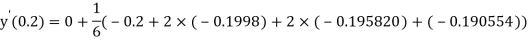
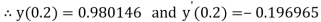 .
.
Example 3: Solve the differential equations
 for
for 
Using four order Runge Kutta method with initial conditions 
Given differential equation are
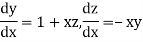
Let 
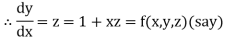
And 
Also 
By Runge Kutta Method we have







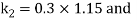

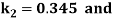
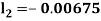


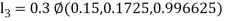
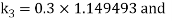
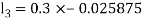






A fourth order Runge Kutta formula:
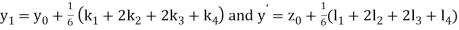

And 
 .
.
Key takeaways-
Runge-kutta methods-
A second order Runge Kutta formula
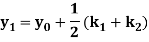
Where 
A fourth order Runge Kutta formula:
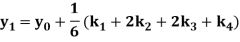
Where 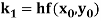
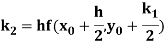
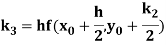
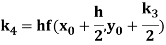
References:
- E. Kreyszig, “Advanced Engineering Mathematics”, John Wiley & Sons, 2006.
- P. G. Hoel, S. C. Port And C. J. Stone, “Introduction To Probability Theory”, Universal Book Stall, 2003.
- S. Ross, “A First Course in Probability”, Pearson Education India, 2002.
- W. Feller, “An Introduction To Probability Theory and Its Applications”, Vol. 1, Wiley, 1968.
- N.P. Bali and M. Goyal, “A Text Book of Engineering Mathematics”, Laxmi Publications, 2010.
- B.S. Grewal, “Higher Engineering Mathematics”, Khanna Publishers, 2000.
Unit - 3
Numerical solutions of Ordinary Differential Equations
Consider the differential equation of first order

Let 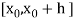 be the first interval.
be the first interval.
A second order Runge Kutta formula

Where 
Rewrite as

A fourth order Runge Kutta formula:

Where 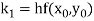



Example1: Use Runge Kutta method to find y when x=1.2 in step of h=0.1 given that
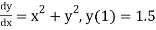
Given equation 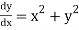
Here 
Also 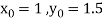
By Runge Kutta formula for first interval
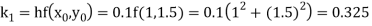
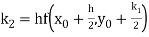


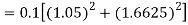

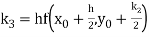

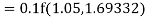
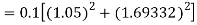
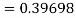
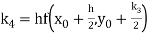




Again 
A fourth order Runge Kutta formula:

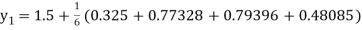

To find y at 


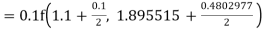


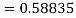
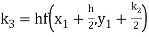
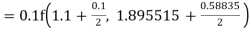

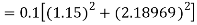
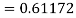

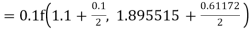

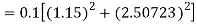

A fourth order Runge Kutta formula:



Example 2: Apply Runge Kutta fourth order method to find an approximate value of y for x=0.2 in step of 0.1, if
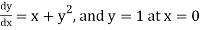
Given equation 
Here 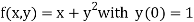
Also 
By Runge Kutta formula for first interval

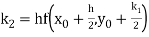

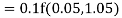

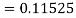


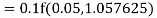


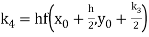

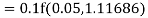
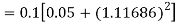

A fourth order Runge Kutta formula:
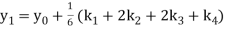


Again 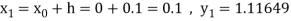

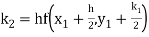
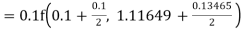







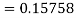
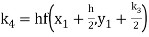




A fourth order Runge Kutta formula:



Example 3: Using Runge Kutta method of fourth order, solve
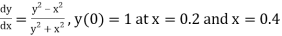
Given equation 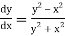
Here 
Also 
By Runge Kutta formula for first interval
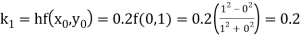



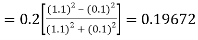

 )
)

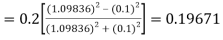
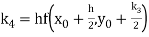



A fourth order Runge Kutta formula:

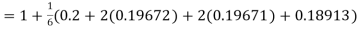

Hence at x = 0.2 then y = 1.196
To find the value of y at x=0.4. In this case 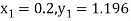

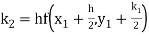
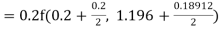





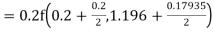

A fourth order Runge Kutta formula:



Hence at x = 0.4 then y=1.37527
Picard’s method:
The general first order differential equation
 ….(1)
….(1)
With the initial condition 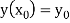 …(2)
…(2)
In general, the solution of first order differential equation in one of the two forms:
a) A series for y in terms of power of x, from which the value of y can be obtained by direct solution.
b) A set of tabulated values of x and y.
The case (a) is solved by Taylor’s Series or Picard method whereas case (b) is solved by Euler’s, Runge Kutta Methods etc.
Picard’s method-
Let us suppose the first order equation-

It is required to find out that particular solution of equation (1) which assumes the value 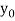 when
when  ,
,
Now integrate (1) between limits, we get-
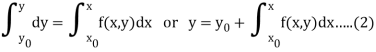
This is equivalent to equation (1),
For it contains the not-known y under the integral sign,
As a first approximation 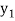 to the solution, put
to the solution, put  in f(x, y) and integrate (2),
in f(x, y) and integrate (2),
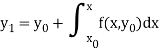
For second approximation-
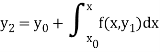
Similarly-
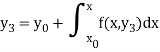
And so on.
Example: Find the value of y for x = 0.1 by using Picard’s method, given that-

Sol.
We have-

For first approximation, we put y = 1, then-
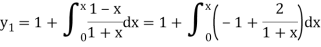
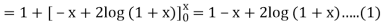
Second approximation-
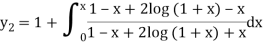
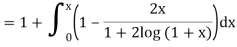
We find it very hard to integrate.
Hence we use the first approximation and take x = 0.1 in (1)
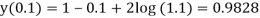
Example: Obtain the picard’s second approximation for the given initial value problem-
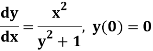
Find y(1).
Sol.
The first approximation will be-
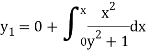
Replace y by  , we get-
, we get-
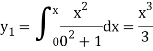
The second approximation is-
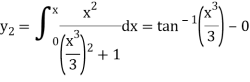
The third approximation-
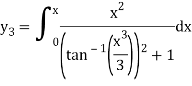
It is very difficult to solve the integration-
This is the disadvantage of the method.
Now we get from the second approximation-
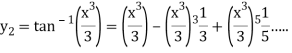
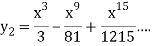
At x = 1-

Simultaneous equation using Runge Kutta method of 2 orders:
The second order differential equation
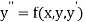
Let 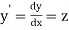 then the above equation reduces to first order simultaneous differential equation
then the above equation reduces to first order simultaneous differential equation

Then 
This can be solved as we discuss above by Runge Kutta Method. Here 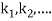 for
for  and
and  for
for 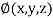 .
.
A fourth order Runge Kutta formula:
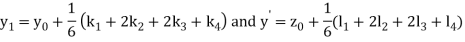
Where 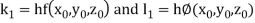


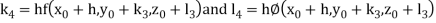
Example1: Using Runge Kutta method of order four , solve  to find
to find 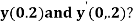
Given second order differential equation is
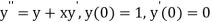
Let 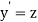 then above equation reduces to
then above equation reduces to
Or 
 (say)
(say)
Or  .
.
By Runge Kutta Method we have
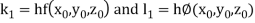
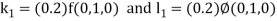
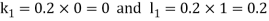
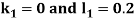
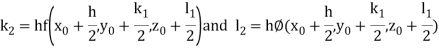
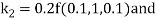





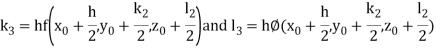




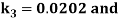


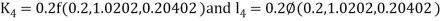
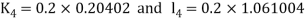
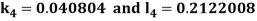
A fourth order Runge Kutta formula:
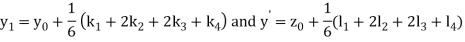
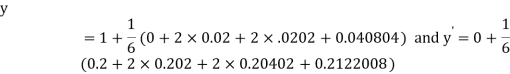
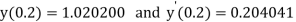
Example 2: Using Runge Kutta method, solve
 for
for  correct to four decimal places with initial condition
correct to four decimal places with initial condition 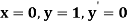 .
.
Given second order differential equation is
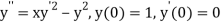
Let 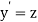 then above equation reduces to
then above equation reduces to
Or 
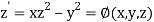 (say)
(say)
Or 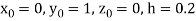 .
.
By Runge Kutta Method we have
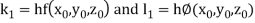
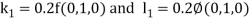
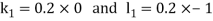







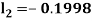
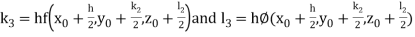

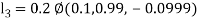
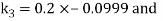

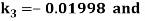

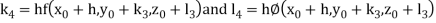
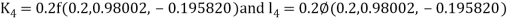


A fourth order Runge Kutta formula:
And
 .
.
Example 3: Solve the differential equations
 for
for 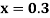
Using four order Runge Kutta method with initial conditions 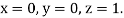
Given differential equation are
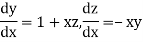
Let 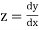

And 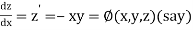
Also 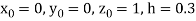
By Runge Kutta Method we have
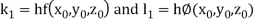
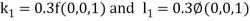
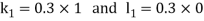



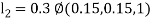






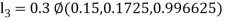

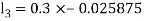
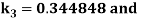
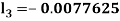
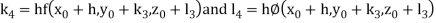
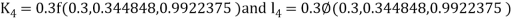

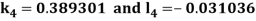
A fourth order Runge Kutta formula:
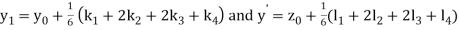

And 
 .
.
Key takeaways-
Runge-kutta methods-
A second order Runge Kutta formula
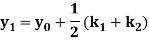
Where 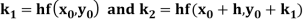
A fourth order Runge Kutta formula:
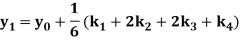
Where 
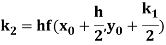
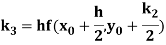
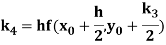
References:
- E. Kreyszig, “Advanced Engineering Mathematics”, John Wiley & Sons, 2006.
- P. G. Hoel, S. C. Port And C. J. Stone, “Introduction To Probability Theory”, Universal Book Stall, 2003.
- S. Ross, “A First Course in Probability”, Pearson Education India, 2002.
- W. Feller, “An Introduction To Probability Theory and Its Applications”, Vol. 1, Wiley, 1968.
- N.P. Bali and M. Goyal, “A Text Book of Engineering Mathematics”, Laxmi Publications, 2010.
- B.S. Grewal, “Higher Engineering Mathematics”, Khanna Publishers, 2000.
Unit - 3
Numerical solutions of Ordinary Differential Equations
Unit - 3
Numerical solutions of Ordinary Differential Equations
Unit - 3
Numerical solutions of Ordinary Differential Equations
Unit - 3
Numerical solutions of Ordinary Differential Equations
Unit - 3
Numerical solutions of Ordinary Differential Equations
Unit - 3
Numerical solutions of Ordinary Differential Equations
Consider the differential equation of first order

Let  be the first interval.
be the first interval.
A second order Runge Kutta formula

Where 
Rewrite as
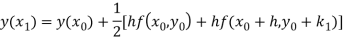
A fourth order Runge Kutta formula:

Where 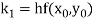
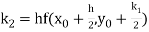


Example1: Use Runge Kutta method to find y when x=1.2 in step of h=0.1 given that

Given equation 
Here 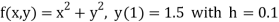
Also 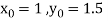
By Runge Kutta formula for first interval






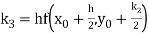


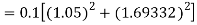
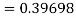
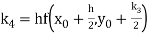

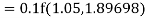
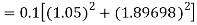
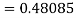
Again 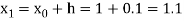
A fourth order Runge Kutta formula:



To find y at 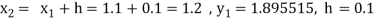

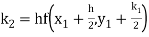

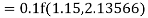






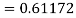

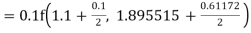
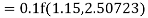
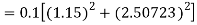
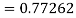
A fourth order Runge Kutta formula:

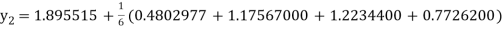

Example 2: Apply Runge Kutta fourth order method to find an approximate value of y for x=0.2 in step of 0.1, if
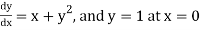
Given equation 
Here 
Also 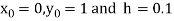
By Runge Kutta formula for first interval


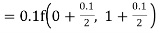



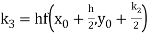
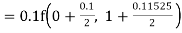

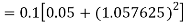




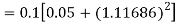

A fourth order Runge Kutta formula:
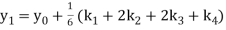


Again 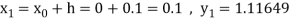



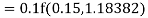
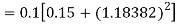
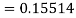
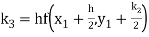
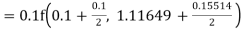
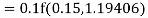


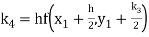
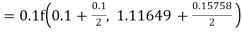
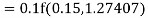


A fourth order Runge Kutta formula:
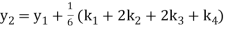
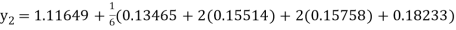
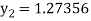
Example 3: Using Runge Kutta method of fourth order, solve

Given equation 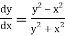
Here 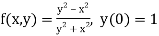
Also 
By Runge Kutta formula for first interval
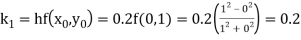

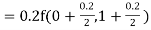
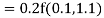


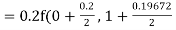 )
)
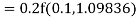
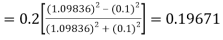
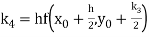
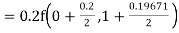

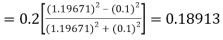
A fourth order Runge Kutta formula:

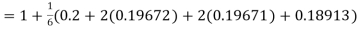

Hence at x = 0.2 then y = 1.196
To find the value of y at x=0.4. In this case 
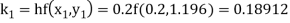
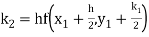




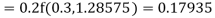


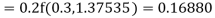
A fourth order Runge Kutta formula:
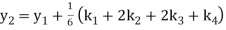


Hence at x = 0.4 then y=1.37527
Picard’s method:
The general first order differential equation
 ….(1)
….(1)
With the initial condition 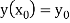 …(2)
…(2)
In general, the solution of first order differential equation in one of the two forms:
a) A series for y in terms of power of x, from which the value of y can be obtained by direct solution.
b) A set of tabulated values of x and y.
The case (a) is solved by Taylor’s Series or Picard method whereas case (b) is solved by Euler’s, Runge Kutta Methods etc.
Picard’s method-
Let us suppose the first order equation-
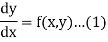
It is required to find out that particular solution of equation (1) which assumes the value 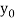 when
when  ,
,
Now integrate (1) between limits, we get-

This is equivalent to equation (1),
For it contains the not-known y under the integral sign,
As a first approximation 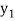 to the solution, put
to the solution, put 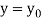 in f(x, y) and integrate (2),
in f(x, y) and integrate (2),
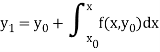
For second approximation-

Similarly-
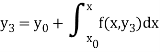
And so on.
Example: Find the value of y for x = 0.1 by using Picard’s method, given that-
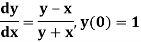
Sol.
We have-
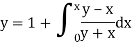
For first approximation, we put y = 1, then-
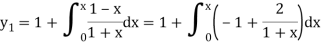
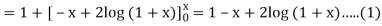
Second approximation-

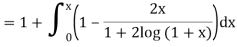
We find it very hard to integrate.
Hence we use the first approximation and take x = 0.1 in (1)
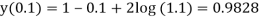
Example: Obtain the picard’s second approximation for the given initial value problem-
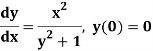
Find y(1).
Sol.
The first approximation will be-
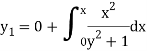
Replace y by 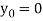 , we get-
, we get-
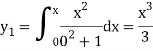
The second approximation is-
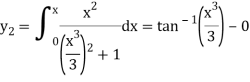
The third approximation-
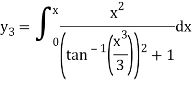
It is very difficult to solve the integration-
This is the disadvantage of the method.
Now we get from the second approximation-
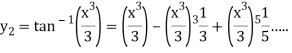
At x = 1-
Simultaneous equation using Runge Kutta method of 2 orders:
The second order differential equation

Let  then the above equation reduces to first order simultaneous differential equation
then the above equation reduces to first order simultaneous differential equation

Then 
This can be solved as we discuss above by Runge Kutta Method. Here  for
for  and
and  for
for  .
.
A fourth order Runge Kutta formula:
Where 


Example1: Using Runge Kutta method of order four , solve  to find
to find 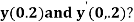
Given second order differential equation is
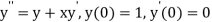
Let 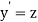 then above equation reduces to
then above equation reduces to
Or 
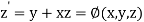 (say)
(say)
Or  .
.
By Runge Kutta Method we have
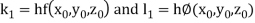
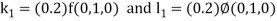
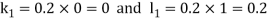
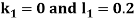
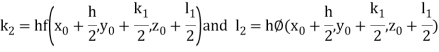

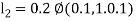

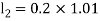


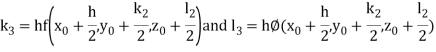
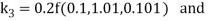
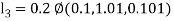



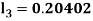
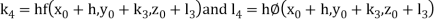

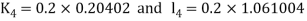
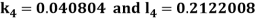
A fourth order Runge Kutta formula:
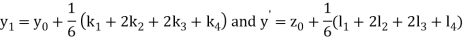
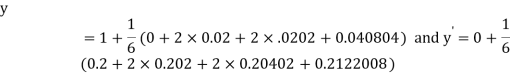

Example 2: Using Runge Kutta method, solve
 for
for 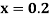 correct to four decimal places with initial condition
correct to four decimal places with initial condition  .
.
Given second order differential equation is
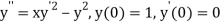
Let  then above equation reduces to
then above equation reduces to
Or 
 (say)
(say)
Or  .
.
By Runge Kutta Method we have


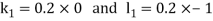



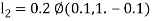



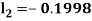


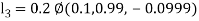
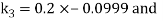



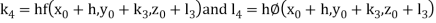
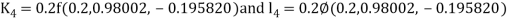
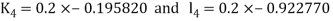
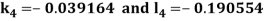
A fourth order Runge Kutta formula:
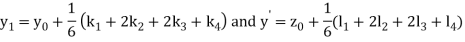

And
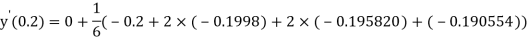
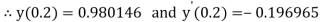 .
.
Example 3: Solve the differential equations
 for
for 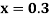
Using four order Runge Kutta method with initial conditions 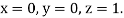
Given differential equation are

Let 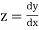
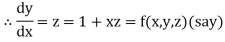
And 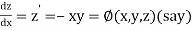
Also 
By Runge Kutta Method we have

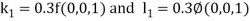



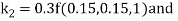




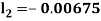



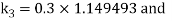





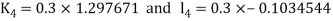

A fourth order Runge Kutta formula:
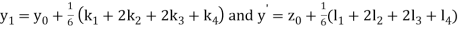
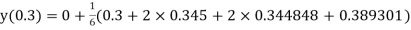
And 
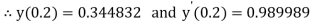 .
.
Key takeaways-
Runge-kutta methods-
A second order Runge Kutta formula
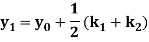
Where 
A fourth order Runge Kutta formula:
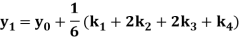
Where 
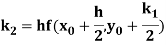
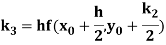
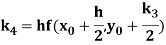
References:
- E. Kreyszig, “Advanced Engineering Mathematics”, John Wiley & Sons, 2006.
- P. G. Hoel, S. C. Port And C. J. Stone, “Introduction To Probability Theory”, Universal Book Stall, 2003.
- S. Ross, “A First Course in Probability”, Pearson Education India, 2002.
- W. Feller, “An Introduction To Probability Theory and Its Applications”, Vol. 1, Wiley, 1968.
- N.P. Bali and M. Goyal, “A Text Book of Engineering Mathematics”, Laxmi Publications, 2010.
- B.S. Grewal, “Higher Engineering Mathematics”, Khanna Publishers, 2000.