Unit - 4
Numerical Integration
Numerical Integration
Numerical integration is a process of evaluating or obtaining a definite integral  from a set of numerical values of the integrand f(x).In case of function of single variable, the process is called quadrature
from a set of numerical values of the integrand f(x).In case of function of single variable, the process is called quadrature
Newton cotes formula-
Suppose  where y takes the values
where y takes the values 
And let the integration interval (a,b) is divided into n equal sub-intervals, each of width h = b – a /n, so that,
x0 = a, x1 = x0 + h, x2 = x0 + 2h, . . . , xn = x0 + nh = b.
I = 
The above formula is known as Newton’s cotes formula.
This is also known as general quadrature formula.
Trapezoidal Method:
Let the interval 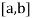 be divided into n equal intervals such that
be divided into n equal intervals such that 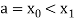 <
<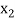 <….<
<….< =b.
=b.
Here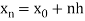 .
.
To find the value of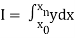 .
.
Setting n=1, we get

Or I = 
The above is known as Trapezoidal method.
Note: In this method second and higher difference are neglected and so f(x) is a polynomial of degree 1.
Geometrical Significance: The curve y=f(x),is replaced by n straight lines with the points  (
( );(
);(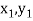 ) and (
) and (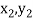 );…….;(
);…….;( ) and (
) and ( ).
).
The area bounded by the curve y=f(x), the ordinates , and the x axis is approximately equivalent to the sum of the area of the n trapeziums obtained.
, and the x axis is approximately equivalent to the sum of the area of the n trapeziums obtained.
Example1: State the trapezoidal rule for finding an approximate area under the given curve. A curve is given by the points (x, y) given below:

Estimate the area bounded by the curve, the x axis and the extreme ordinates.
We construct the data table:
X | 0 | 0.5 | 1.0 | 1.5 | 2.0 | 2.5 | 3.0 | 3.5 | 4.0 |
Y | 23 | 19 | 14 | 11 | 12.5 | 16 | 19 | 20 | 20 |
Here length of interval h =0.5, initial value a = 0 and final value b = 4
By Trapezoidal method
Area of curve bounded on x axis =
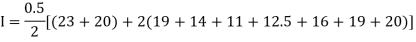
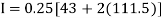

Example 2: Compute the value of 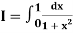 ?
?
Using the trapezoidal rule with h=0.5, 0.25 and 0.125.
Here 
For h=0.5, we construct the data table:
X | 0 | 0.5 | 1 |
Y | 1 | 0.8 | 0.5 |
By Trapezoidal rule

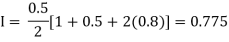
For h=0.25, we construct the data table:
X | 0 | 0.25 | 0.5 | 0.75 | 1 |
Y | 1 | 0.94117 | 0.8 | 0.64 | 0.5 |
By Trapezoidal rule


For h = 0.125, we construct the data table:
X | 0 | 0.125 | 0.25 | 0.375 | 0.5 | 0.625 | 0.75 | 0.875 | 1 |
Y | 1 | 0.98461 | 0.94117 | 0.87671 | 0.8 | 0.71910 | 0.64 | 0.56637 | 0.5 |
By Trapezoidal rule

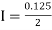 [(1+0.5)+2(0.98461+0.94117+0.87671+0.8+0.71910+0.64+0.56637)]
[(1+0.5)+2(0.98461+0.94117+0.87671+0.8+0.71910+0.64+0.56637)]

Example 3: Evaluate, using trapezoidal rule with five ordinates

Here 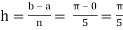
We construct the data table:
X | 0 |  |  |  | 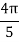 | 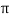 |
Y | 0 | 0.3693161 | 1.195328 | 1.7926992 | 1.477265 | 0 |


Simpson’s Rule:
Let the interval  be divided into n equal intervals such that
be divided into n equal intervals such that 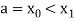 <
< <….<
<….< =b.
=b.
Here .
.
To find the value of .
.
Setting n = 2,

Which is known as Simpson’s 1/3- rule or Simpson’s rule.
Note: In this rule third and higher differences are neglected a so f(x) is a polynomial of degree 2.
Example 1: Estimate the value of the integral
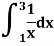
By Simpson’s rule with 4 strips and 8 strips respectively.
For n=4, we have 
Construct the data table:
X | 1.0 | 1.5 | 2.0 | 2.5 | 3.0 |
Y=1/x | 1 | 0.66666 | 0.5 | 0.4 | 0.33333 |
By Simpson’s Rule
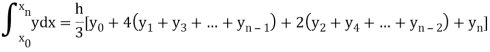
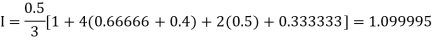
For n = 8, we have 
X | 1 | 1.25 | 1.50 | 1.75 | 2.0 | 2.25 | 2.50 | 2.75 | 3.0 |
Y=1/x | 1 | 0.8 | 0.66666 | 0.571428 | 0.5 | 0.444444 | 0.4 | 0.3636363 | 0.333333 |
By Simpson’s Rule
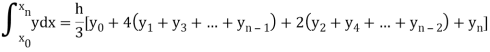


Example 2: Evaluate 
Using Simpson’s 1/3 rule with 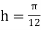 .
.
For  , we construct the data table:
, we construct the data table:
X | 0 |  |  |  |  | 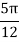 |  |
 | 0 | 0.50874 | 0.707106 | 0.840896 | 0.930604 | 0.98281 | 1 |
By Simpson’s Rule



Example 3: Using Simpson’s 1/3 rule with h = 1, evaluate
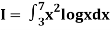
For h = 1, we construct the data table:
X | 3 | 4 | 5 | 6 | 7 |
 | 9.88751 | 22.108709 | 40.23594 | 64.503340 | 95.34959 |
By Simpson’s Rule
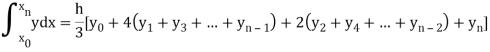
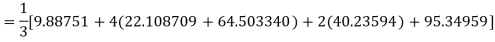
= 177.3853
Simpson’s 3/8 rule
Let the interval  be divided into n equal intervals such that
be divided into n equal intervals such that  <
< <….<
<….<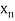 =b.
=b.
Here .
.
To find the value of  .
.
Setting n=3 , we get

Is known as Simpson’s 3/8 rule which is not as accurate as Simpson’s rule.
Note: In this rule the fourth and higher differences are neglected and so f(x) is a polynomial of degree 3.
Example 1: Evaluate 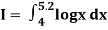
By Simpson’s 3/8 rule.
Let us divide the range of the interval [4, 5.2] into six equal parts.
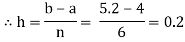
For h=0.2, we construct the data table:
X | 4.0 | 4.2 | 4.4 | 4.6 | 4.8 | 5.0 | 5.2 |
 | 1.3863 | 1.4351 | 1.4816 | 1.5261 | 1.5686 | 1.6094 | 1.6487 |
By Simpson’s 3/8 rule


= 1.8278475
Example 2: Evaluate 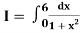
Let us divide the range of the interval [0,6] into six equal parts.

For h=1, we construct the data table:
X | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
 | 1 | 0.5 | 0.2 | 0.1 | 0.0588 | 0.0385 | 0.027 |
By Simpson’s 3/8 rule

 +3(0.0385)+0.027]
+3(0.0385)+0.027]
=1.3571
Error in Integration
Error in Trapezoidal method
The total error in trapezoidal method is given by

Let  is the largest value of the n quantities on the right hand side of the above equation then
is the largest value of the n quantities on the right hand side of the above equation then

Error in Simpson’s Rule
The error in the Simpson’s rule is given by

Where 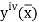 is the largest value of the fourth derivative of y(x).
is the largest value of the fourth derivative of y(x).
Error in Simpson’s 3/8 Rule
The error in this rule is given by

Where 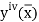 is the largest value of the derivative of y(x).
is the largest value of the derivative of y(x).
Boole’s rule & Waddle’s rule-
The formula given below is known as Boole’s rule-

And the waddle’s rules is defined as-
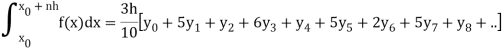
Example: A river is 80 m wide. The depth ‘b’ of the river at a distance ‘a’ from one bank is given by the table-
a | 0 | 10 | 20 | 30 | 40 | 50 | 60 | 70 | 80 |
B | 0 | 4 | 7 | 9 | 12 | 15 | 14 | 8 | 3 |
Find the approximate area of cross-section of the river using Boole’s rule.
Sol.
The area of the cross-section of the river will be-

The number of sub-intervals here is 8.
Then by Boole’s rule-

= 2(10)/45 [ 7(0) + 32(4) + 12(7) + 32(9) + 7(12) + 7(12) + 32(15) + 12(14) + 32(8) +7(3)]
= 708
So that the area of of the cross-section of the river is 708 square meter.
Example: Evaluate  by using Boole’s.
by using Boole’s.
Sol.
Take h = 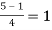 , so that there four sub intervals-
, so that there four sub intervals-
X | 1 | 2 | 3 | 4 | 5 |
F(x) | 1 | ½ | 1/3 | ¼ | 1/5 |
Using Boole’s method-


Romberg integration:
In order to obtain accurate results, we compute the integrals by trapezium or Simpson’s rules for a number of values of step lengths, each time reducing the step length. We stop the computation, when convergence is attained (usually, the magnitude of the difference in successive values of the integrals obtained by reducing values of the step lengths is less than a given accuracy). Convergence may be obtained after computing the value of the integral with a number of step lengths. While computing the value of the integral with a particular step length, the values of the integral obtained earlier by using larger step lengths were not used. Further, convergence may be slow. Romberg method is a powerful tool which uses the method of extrapolation.
We compute the value of the integral with a number of step lengths using the same method. Usually, we start with a coarse step length, then reduce the step lengths and recomputed the value of the integral. The sequence of these values converges to the exact value of the integral. Romberg method uses these values of the integral obtained with various step lengths, to refine the solution such that the new values are of higher order. That is, as if the results are obtained using a higher order method than the order of the method used. The extrapolation method is derived by studying the error of the method that is being used.
Lets consider the definite integral,

And evaluate it by the trapezoidal rule with two different subintervals of width 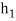 and
and  to obtain the approximate values
to obtain the approximate values 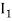 and
and 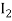 respectively,
respectively,
Then

And

Since the term  is also the largest value of
is also the largest value of 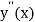 , it is reasonable to assume that the quantities
, it is reasonable to assume that the quantities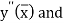
 are very nearly the same.
are very nearly the same.
We therefore have

And hence

Since 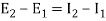 , this gives
, this gives

We therefore obtain a new approximation  defined by
defined by
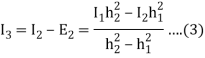
Which in general, would be closer to the actual value- provided that the errors decrease monotonically and are the same sign.
If we now set
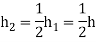
Equation (3) can be written as-

Where I(h) = 

In table form it can be written as,
I(h) I(h, ½ h) I(1/2 h) I(h, ½ h, ¼ h) I( ½ h, ¼ h) I(h, ½ h, ¼ h, 1/8 h) I(1/4 h) I( ½ h, ¼ h, 1/8 h) I( ¼ h, 1/8 h) I(1/8 h) |
Example: Compute the following integral upto three decimal places by using Romberg’s method.

Sol:
We take h = 0.5, 0.25 and 0.125 successively and use the results as below
I(h) = 0.7084, I(1/2h) = 0.6970 and I(1/4 h) = 0.6941
Hence,
We get


Finally,

The table of values,
0.7084
0.6932
0.6970 0.6931
0.6931
0.6941
References:
- E. Kreyszig, “Advanced Engineering Mathematics”, John Wiley & Sons, 2006.
- P. G. Hoel, S. C. Port And C. J. Stone, “Introduction To Probability Theory”, Universal Book Stall, 2003.
- S. Ross, “A First Course in Probability”, Pearson Education India, 2002.
- W. Feller, “An Introduction To Probability Theory and Its Applications”, Vol. 1, Wiley, 1968.
- N.P. Bali and M. Goyal, “A Text Book of Engineering Mathematics”, Laxmi Publications, 2010.
- B.S. Grewal, “Higher Engineering Mathematics”, Khanna Publishers, 2000.
Unit - 4
Numerical Integration
Numerical Integration
Numerical integration is a process of evaluating or obtaining a definite integral  from a set of numerical values of the integrand f(x).In case of function of single variable, the process is called quadrature
from a set of numerical values of the integrand f(x).In case of function of single variable, the process is called quadrature
Newton cotes formula-
Suppose 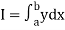 where y takes the values
where y takes the values 
And let the integration interval (a,b) is divided into n equal sub-intervals, each of width h = b – a /n, so that,
x0 = a, x1 = x0 + h, x2 = x0 + 2h, . . . , xn = x0 + nh = b.
I = 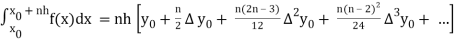
The above formula is known as Newton’s cotes formula.
This is also known as general quadrature formula.
Trapezoidal Method:
Let the interval 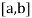 be divided into n equal intervals such that
be divided into n equal intervals such that  <
<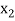 <….<
<….< =b.
=b.
Here .
.
To find the value of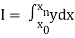 .
.
Setting n=1, we get
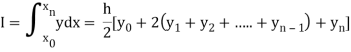
Or I = 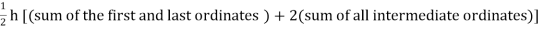
The above is known as Trapezoidal method.
Note: In this method second and higher difference are neglected and so f(x) is a polynomial of degree 1.
Geometrical Significance: The curve y=f(x),is replaced by n straight lines with the points  (
( );(
);( ) and (
) and ( );…….;(
);…….;(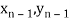 ) and (
) and ( ).
).
The area bounded by the curve y=f(x), the ordinates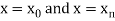 , and the x axis is approximately equivalent to the sum of the area of the n trapeziums obtained.
, and the x axis is approximately equivalent to the sum of the area of the n trapeziums obtained.
Example1: State the trapezoidal rule for finding an approximate area under the given curve. A curve is given by the points (x, y) given below:
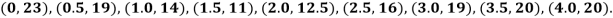
Estimate the area bounded by the curve, the x axis and the extreme ordinates.
We construct the data table:
X | 0 | 0.5 | 1.0 | 1.5 | 2.0 | 2.5 | 3.0 | 3.5 | 4.0 |
Y | 23 | 19 | 14 | 11 | 12.5 | 16 | 19 | 20 | 20 |
Here length of interval h =0.5, initial value a = 0 and final value b = 4
By Trapezoidal method
Area of curve bounded on x axis =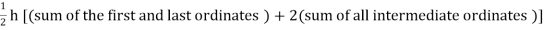

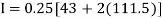
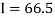
Example 2: Compute the value of  ?
?
Using the trapezoidal rule with h=0.5, 0.25 and 0.125.
Here 
For h=0.5, we construct the data table:
X | 0 | 0.5 | 1 |
Y | 1 | 0.8 | 0.5 |
By Trapezoidal rule


For h=0.25, we construct the data table:
X | 0 | 0.25 | 0.5 | 0.75 | 1 |
Y | 1 | 0.94117 | 0.8 | 0.64 | 0.5 |
By Trapezoidal rule

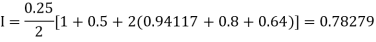
For h = 0.125, we construct the data table:
X | 0 | 0.125 | 0.25 | 0.375 | 0.5 | 0.625 | 0.75 | 0.875 | 1 |
Y | 1 | 0.98461 | 0.94117 | 0.87671 | 0.8 | 0.71910 | 0.64 | 0.56637 | 0.5 |
By Trapezoidal rule

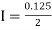 [(1+0.5)+2(0.98461+0.94117+0.87671+0.8+0.71910+0.64+0.56637)]
[(1+0.5)+2(0.98461+0.94117+0.87671+0.8+0.71910+0.64+0.56637)]
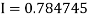
Example 3: Evaluate, using trapezoidal rule with five ordinates

Here 
We construct the data table:
X | 0 |  | 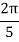 | 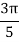 | 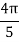 |  |
Y | 0 | 0.3693161 | 1.195328 | 1.7926992 | 1.477265 | 0 |
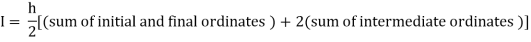
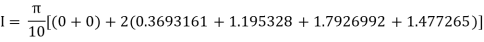
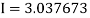
Simpson’s Rule:
Let the interval  be divided into n equal intervals such that
be divided into n equal intervals such that 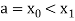 <
<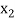 <….<
<….< =b.
=b.
Here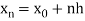 .
.
To find the value of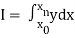 .
.
Setting n = 2,

Which is known as Simpson’s 1/3- rule or Simpson’s rule.
Note: In this rule third and higher differences are neglected a so f(x) is a polynomial of degree 2.
Example 1: Estimate the value of the integral

By Simpson’s rule with 4 strips and 8 strips respectively.
For n=4, we have 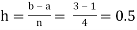
Construct the data table:
X | 1.0 | 1.5 | 2.0 | 2.5 | 3.0 |
Y=1/x | 1 | 0.66666 | 0.5 | 0.4 | 0.33333 |
By Simpson’s Rule

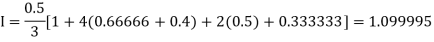
For n = 8, we have 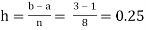
X | 1 | 1.25 | 1.50 | 1.75 | 2.0 | 2.25 | 2.50 | 2.75 | 3.0 |
Y=1/x | 1 | 0.8 | 0.66666 | 0.571428 | 0.5 | 0.444444 | 0.4 | 0.3636363 | 0.333333 |
By Simpson’s Rule


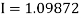
Example 2: Evaluate 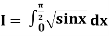
Using Simpson’s 1/3 rule with  .
.
For  , we construct the data table:
, we construct the data table:
X | 0 | 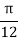 |  |  |  |  |  |
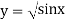 | 0 | 0.50874 | 0.707106 | 0.840896 | 0.930604 | 0.98281 | 1 |
By Simpson’s Rule



Example 3: Using Simpson’s 1/3 rule with h = 1, evaluate

For h = 1, we construct the data table:
X | 3 | 4 | 5 | 6 | 7 |
 | 9.88751 | 22.108709 | 40.23594 | 64.503340 | 95.34959 |
By Simpson’s Rule


= 177.3853
Simpson’s 3/8 rule
Let the interval  be divided into n equal intervals such that
be divided into n equal intervals such that 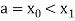 <
< <….<
<….<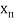 =b.
=b.
Here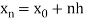 .
.
To find the value of 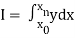 .
.
Setting n=3 , we get
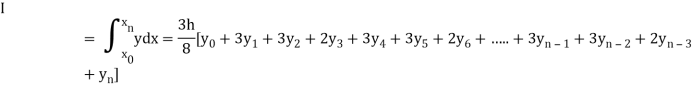
Is known as Simpson’s 3/8 rule which is not as accurate as Simpson’s rule.
Note: In this rule the fourth and higher differences are neglected and so f(x) is a polynomial of degree 3.
Example 1: Evaluate 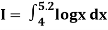
By Simpson’s 3/8 rule.
Let us divide the range of the interval [4, 5.2] into six equal parts.
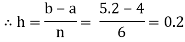
For h=0.2, we construct the data table:
X | 4.0 | 4.2 | 4.4 | 4.6 | 4.8 | 5.0 | 5.2 |
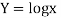 | 1.3863 | 1.4351 | 1.4816 | 1.5261 | 1.5686 | 1.6094 | 1.6487 |
By Simpson’s 3/8 rule
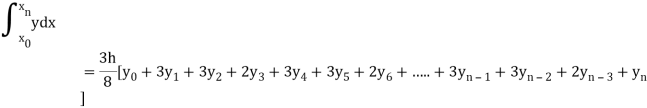

= 1.8278475
Example 2: Evaluate 
Let us divide the range of the interval [0,6] into six equal parts.

For h=1, we construct the data table:
X | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
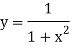 | 1 | 0.5 | 0.2 | 0.1 | 0.0588 | 0.0385 | 0.027 |
By Simpson’s 3/8 rule
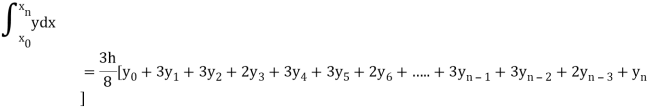
 +3(0.0385)+0.027]
+3(0.0385)+0.027]
=1.3571
Error in Integration
Error in Trapezoidal method
The total error in trapezoidal method is given by
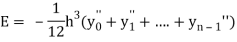
Let  is the largest value of the n quantities on the right hand side of the above equation then
is the largest value of the n quantities on the right hand side of the above equation then
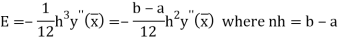
Error in Simpson’s Rule
The error in the Simpson’s rule is given by
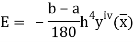
Where  is the largest value of the fourth derivative of y(x).
is the largest value of the fourth derivative of y(x).
Error in Simpson’s 3/8 Rule
The error in this rule is given by

Where  is the largest value of the derivative of y(x).
is the largest value of the derivative of y(x).
Boole’s rule & Waddle’s rule-
The formula given below is known as Boole’s rule-
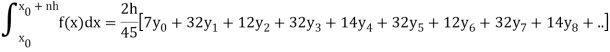
And the waddle’s rules is defined as-
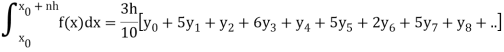
Example: A river is 80 m wide. The depth ‘b’ of the river at a distance ‘a’ from one bank is given by the table-
a | 0 | 10 | 20 | 30 | 40 | 50 | 60 | 70 | 80 |
B | 0 | 4 | 7 | 9 | 12 | 15 | 14 | 8 | 3 |
Find the approximate area of cross-section of the river using Boole’s rule.
Sol.
The area of the cross-section of the river will be-

The number of sub-intervals here is 8.
Then by Boole’s rule-

= 2(10)/45 [ 7(0) + 32(4) + 12(7) + 32(9) + 7(12) + 7(12) + 32(15) + 12(14) + 32(8) +7(3)]
= 708
So that the area of of the cross-section of the river is 708 square meter.
Example: Evaluate 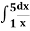 by using Boole’s.
by using Boole’s.
Sol.
Take h = 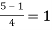 , so that there four sub intervals-
, so that there four sub intervals-
X | 1 | 2 | 3 | 4 | 5 |
F(x) | 1 | ½ | 1/3 | ¼ | 1/5 |
Using Boole’s method-


Romberg integration:
In order to obtain accurate results, we compute the integrals by trapezium or Simpson’s rules for a number of values of step lengths, each time reducing the step length. We stop the computation, when convergence is attained (usually, the magnitude of the difference in successive values of the integrals obtained by reducing values of the step lengths is less than a given accuracy). Convergence may be obtained after computing the value of the integral with a number of step lengths. While computing the value of the integral with a particular step length, the values of the integral obtained earlier by using larger step lengths were not used. Further, convergence may be slow. Romberg method is a powerful tool which uses the method of extrapolation.
We compute the value of the integral with a number of step lengths using the same method. Usually, we start with a coarse step length, then reduce the step lengths and recomputed the value of the integral. The sequence of these values converges to the exact value of the integral. Romberg method uses these values of the integral obtained with various step lengths, to refine the solution such that the new values are of higher order. That is, as if the results are obtained using a higher order method than the order of the method used. The extrapolation method is derived by studying the error of the method that is being used.
Lets consider the definite integral,

And evaluate it by the trapezoidal rule with two different subintervals of width 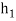 and
and  to obtain the approximate values
to obtain the approximate values  and
and  respectively,
respectively,
Then

And
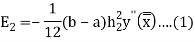
Since the term  is also the largest value of
is also the largest value of  , it is reasonable to assume that the quantities
, it is reasonable to assume that the quantities
 are very nearly the same.
are very nearly the same.
We therefore have

And hence

Since  , this gives
, this gives
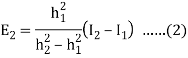
We therefore obtain a new approximation 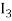 defined by
defined by

Which in general, would be closer to the actual value- provided that the errors decrease monotonically and are the same sign.
If we now set

Equation (3) can be written as-

Where I(h) = 

In table form it can be written as,
I(h) I(h, ½ h) I(1/2 h) I(h, ½ h, ¼ h) I( ½ h, ¼ h) I(h, ½ h, ¼ h, 1/8 h) I(1/4 h) I( ½ h, ¼ h, 1/8 h) I( ¼ h, 1/8 h) I(1/8 h) |
Example: Compute the following integral upto three decimal places by using Romberg’s method.

Sol:
We take h = 0.5, 0.25 and 0.125 successively and use the results as below
I(h) = 0.7084, I(1/2h) = 0.6970 and I(1/4 h) = 0.6941
Hence,
We get


Finally,

The table of values,
0.7084
0.6932
0.6970 0.6931
0.6931
0.6941
References:
- E. Kreyszig, “Advanced Engineering Mathematics”, John Wiley & Sons, 2006.
- P. G. Hoel, S. C. Port And C. J. Stone, “Introduction To Probability Theory”, Universal Book Stall, 2003.
- S. Ross, “A First Course in Probability”, Pearson Education India, 2002.
- W. Feller, “An Introduction To Probability Theory and Its Applications”, Vol. 1, Wiley, 1968.
- N.P. Bali and M. Goyal, “A Text Book of Engineering Mathematics”, Laxmi Publications, 2010.
- B.S. Grewal, “Higher Engineering Mathematics”, Khanna Publishers, 2000.
Unit - 4
Numerical Integration
Numerical Integration
Numerical integration is a process of evaluating or obtaining a definite integral  from a set of numerical values of the integrand f(x).In case of function of single variable, the process is called quadrature
from a set of numerical values of the integrand f(x).In case of function of single variable, the process is called quadrature
Newton cotes formula-
Suppose  where y takes the values
where y takes the values 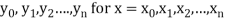
And let the integration interval (a,b) is divided into n equal sub-intervals, each of width h = b – a /n, so that,
x0 = a, x1 = x0 + h, x2 = x0 + 2h, . . . , xn = x0 + nh = b.
I = 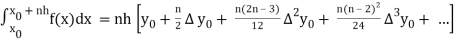
The above formula is known as Newton’s cotes formula.
This is also known as general quadrature formula.
Trapezoidal Method:
Let the interval  be divided into n equal intervals such that
be divided into n equal intervals such that 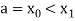 <
< <….<
<….< =b.
=b.
Here .
.
To find the value of .
.
Setting n=1, we get

Or I = 
The above is known as Trapezoidal method.
Note: In this method second and higher difference are neglected and so f(x) is a polynomial of degree 1.
Geometrical Significance: The curve y=f(x),is replaced by n straight lines with the points  (
( );(
);( ) and (
) and ( );…….;(
);…….;(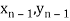 ) and (
) and ( ).
).
The area bounded by the curve y=f(x), the ordinates , and the x axis is approximately equivalent to the sum of the area of the n trapeziums obtained.
, and the x axis is approximately equivalent to the sum of the area of the n trapeziums obtained.
Example1: State the trapezoidal rule for finding an approximate area under the given curve. A curve is given by the points (x, y) given below:

Estimate the area bounded by the curve, the x axis and the extreme ordinates.
We construct the data table:
X | 0 | 0.5 | 1.0 | 1.5 | 2.0 | 2.5 | 3.0 | 3.5 | 4.0 |
Y | 23 | 19 | 14 | 11 | 12.5 | 16 | 19 | 20 | 20 |
Here length of interval h =0.5, initial value a = 0 and final value b = 4
By Trapezoidal method
Area of curve bounded on x axis =
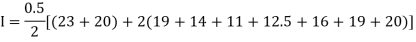

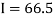
Example 2: Compute the value of 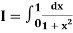 ?
?
Using the trapezoidal rule with h=0.5, 0.25 and 0.125.
Here 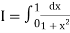
For h=0.5, we construct the data table:
X | 0 | 0.5 | 1 |
Y | 1 | 0.8 | 0.5 |
By Trapezoidal rule
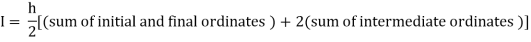
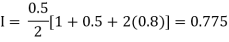
For h=0.25, we construct the data table:
X | 0 | 0.25 | 0.5 | 0.75 | 1 |
Y | 1 | 0.94117 | 0.8 | 0.64 | 0.5 |
By Trapezoidal rule
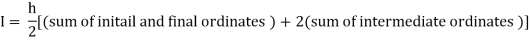

For h = 0.125, we construct the data table:
X | 0 | 0.125 | 0.25 | 0.375 | 0.5 | 0.625 | 0.75 | 0.875 | 1 |
Y | 1 | 0.98461 | 0.94117 | 0.87671 | 0.8 | 0.71910 | 0.64 | 0.56637 | 0.5 |
By Trapezoidal rule
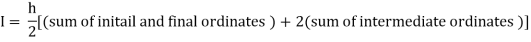
 [(1+0.5)+2(0.98461+0.94117+0.87671+0.8+0.71910+0.64+0.56637)]
[(1+0.5)+2(0.98461+0.94117+0.87671+0.8+0.71910+0.64+0.56637)]

Example 3: Evaluate, using trapezoidal rule with five ordinates
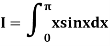
Here 
We construct the data table:
X | 0 |  | 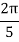 |  |  | 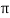 |
Y | 0 | 0.3693161 | 1.195328 | 1.7926992 | 1.477265 | 0 |


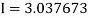
Simpson’s Rule:
Let the interval  be divided into n equal intervals such that
be divided into n equal intervals such that  <
< <….<
<….< =b.
=b.
Here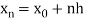 .
.
To find the value of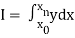 .
.
Setting n = 2,

Which is known as Simpson’s 1/3- rule or Simpson’s rule.
Note: In this rule third and higher differences are neglected a so f(x) is a polynomial of degree 2.
Example 1: Estimate the value of the integral

By Simpson’s rule with 4 strips and 8 strips respectively.
For n=4, we have 
Construct the data table:
X | 1.0 | 1.5 | 2.0 | 2.5 | 3.0 |
Y=1/x | 1 | 0.66666 | 0.5 | 0.4 | 0.33333 |
By Simpson’s Rule
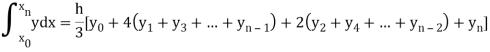

For n = 8, we have 
X | 1 | 1.25 | 1.50 | 1.75 | 2.0 | 2.25 | 2.50 | 2.75 | 3.0 |
Y=1/x | 1 | 0.8 | 0.66666 | 0.571428 | 0.5 | 0.444444 | 0.4 | 0.3636363 | 0.333333 |
By Simpson’s Rule

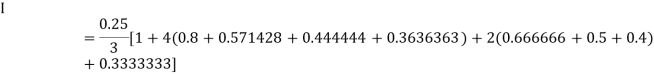

Example 2: Evaluate 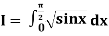
Using Simpson’s 1/3 rule with  .
.
For 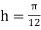 , we construct the data table:
, we construct the data table:
X | 0 |  |  |  |  |  |  |
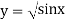 | 0 | 0.50874 | 0.707106 | 0.840896 | 0.930604 | 0.98281 | 1 |
By Simpson’s Rule



Example 3: Using Simpson’s 1/3 rule with h = 1, evaluate
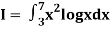
For h = 1, we construct the data table:
X | 3 | 4 | 5 | 6 | 7 |
 | 9.88751 | 22.108709 | 40.23594 | 64.503340 | 95.34959 |
By Simpson’s Rule


= 177.3853
Simpson’s 3/8 rule
Let the interval  be divided into n equal intervals such that
be divided into n equal intervals such that  <
<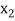 <….<
<….< =b.
=b.
Here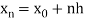 .
.
To find the value of 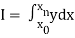 .
.
Setting n=3 , we get
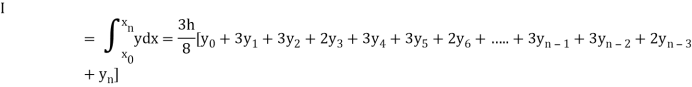
Is known as Simpson’s 3/8 rule which is not as accurate as Simpson’s rule.
Note: In this rule the fourth and higher differences are neglected and so f(x) is a polynomial of degree 3.
Example 1: Evaluate 
By Simpson’s 3/8 rule.
Let us divide the range of the interval [4, 5.2] into six equal parts.

For h=0.2, we construct the data table:
X | 4.0 | 4.2 | 4.4 | 4.6 | 4.8 | 5.0 | 5.2 |
 | 1.3863 | 1.4351 | 1.4816 | 1.5261 | 1.5686 | 1.6094 | 1.6487 |
By Simpson’s 3/8 rule


= 1.8278475
Example 2: Evaluate 
Let us divide the range of the interval [0,6] into six equal parts.

For h=1, we construct the data table:
X | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
 | 1 | 0.5 | 0.2 | 0.1 | 0.0588 | 0.0385 | 0.027 |
By Simpson’s 3/8 rule
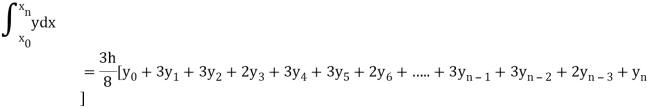
 +3(0.0385)+0.027]
+3(0.0385)+0.027]
=1.3571
Error in Integration
Error in Trapezoidal method
The total error in trapezoidal method is given by

Let  is the largest value of the n quantities on the right hand side of the above equation then
is the largest value of the n quantities on the right hand side of the above equation then

Error in Simpson’s Rule
The error in the Simpson’s rule is given by
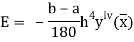
Where  is the largest value of the fourth derivative of y(x).
is the largest value of the fourth derivative of y(x).
Error in Simpson’s 3/8 Rule
The error in this rule is given by
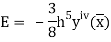
Where  is the largest value of the derivative of y(x).
is the largest value of the derivative of y(x).
Boole’s rule & Waddle’s rule-
The formula given below is known as Boole’s rule-

And the waddle’s rules is defined as-

Example: A river is 80 m wide. The depth ‘b’ of the river at a distance ‘a’ from one bank is given by the table-
a | 0 | 10 | 20 | 30 | 40 | 50 | 60 | 70 | 80 |
B | 0 | 4 | 7 | 9 | 12 | 15 | 14 | 8 | 3 |
Find the approximate area of cross-section of the river using Boole’s rule.
Sol.
The area of the cross-section of the river will be-

The number of sub-intervals here is 8.
Then by Boole’s rule-
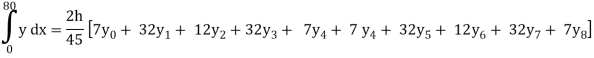
= 2(10)/45 [ 7(0) + 32(4) + 12(7) + 32(9) + 7(12) + 7(12) + 32(15) + 12(14) + 32(8) +7(3)]
= 708
So that the area of of the cross-section of the river is 708 square meter.
Example: Evaluate  by using Boole’s.
by using Boole’s.
Sol.
Take h =  , so that there four sub intervals-
, so that there four sub intervals-
X | 1 | 2 | 3 | 4 | 5 |
F(x) | 1 | ½ | 1/3 | ¼ | 1/5 |
Using Boole’s method-


Romberg integration:
In order to obtain accurate results, we compute the integrals by trapezium or Simpson’s rules for a number of values of step lengths, each time reducing the step length. We stop the computation, when convergence is attained (usually, the magnitude of the difference in successive values of the integrals obtained by reducing values of the step lengths is less than a given accuracy). Convergence may be obtained after computing the value of the integral with a number of step lengths. While computing the value of the integral with a particular step length, the values of the integral obtained earlier by using larger step lengths were not used. Further, convergence may be slow. Romberg method is a powerful tool which uses the method of extrapolation.
We compute the value of the integral with a number of step lengths using the same method. Usually, we start with a coarse step length, then reduce the step lengths and recomputed the value of the integral. The sequence of these values converges to the exact value of the integral. Romberg method uses these values of the integral obtained with various step lengths, to refine the solution such that the new values are of higher order. That is, as if the results are obtained using a higher order method than the order of the method used. The extrapolation method is derived by studying the error of the method that is being used.
Lets consider the definite integral,

And evaluate it by the trapezoidal rule with two different subintervals of width 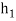 and
and  to obtain the approximate values
to obtain the approximate values  and
and 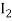 respectively,
respectively,
Then
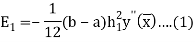
And
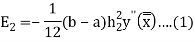
Since the term 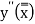 is also the largest value of
is also the largest value of  , it is reasonable to assume that the quantities
, it is reasonable to assume that the quantities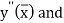
 are very nearly the same.
are very nearly the same.
We therefore have

And hence

Since  , this gives
, this gives

We therefore obtain a new approximation  defined by
defined by
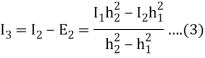
Which in general, would be closer to the actual value- provided that the errors decrease monotonically and are the same sign.
If we now set

Equation (3) can be written as-

Where I(h) = 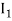

In table form it can be written as,
I(h) I(h, ½ h) I(1/2 h) I(h, ½ h, ¼ h) I( ½ h, ¼ h) I(h, ½ h, ¼ h, 1/8 h) I(1/4 h) I( ½ h, ¼ h, 1/8 h) I( ¼ h, 1/8 h) I(1/8 h) |
Example: Compute the following integral upto three decimal places by using Romberg’s method.

Sol:
We take h = 0.5, 0.25 and 0.125 successively and use the results as below
I(h) = 0.7084, I(1/2h) = 0.6970 and I(1/4 h) = 0.6941
Hence,
We get
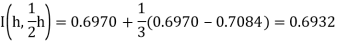

Finally,
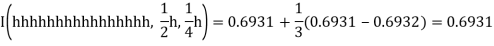
The table of values,
0.7084
0.6932
0.6970 0.6931
0.6931
0.6941
References:
- E. Kreyszig, “Advanced Engineering Mathematics”, John Wiley & Sons, 2006.
- P. G. Hoel, S. C. Port And C. J. Stone, “Introduction To Probability Theory”, Universal Book Stall, 2003.
- S. Ross, “A First Course in Probability”, Pearson Education India, 2002.
- W. Feller, “An Introduction To Probability Theory and Its Applications”, Vol. 1, Wiley, 1968.
- N.P. Bali and M. Goyal, “A Text Book of Engineering Mathematics”, Laxmi Publications, 2010.
- B.S. Grewal, “Higher Engineering Mathematics”, Khanna Publishers, 2000.
Unit - 4
Numerical Integration
Unit - 4
Numerical Integration
Unit - 4
Numerical Integration
Unit - 4
Numerical Integration
Numerical Integration
Numerical integration is a process of evaluating or obtaining a definite integral 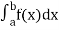 from a set of numerical values of the integrand f(x).In case of function of single variable, the process is called quadrature
from a set of numerical values of the integrand f(x).In case of function of single variable, the process is called quadrature
Newton cotes formula-
Suppose  where y takes the values
where y takes the values 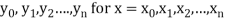
And let the integration interval (a,b) is divided into n equal sub-intervals, each of width h = b – a /n, so that,
x0 = a, x1 = x0 + h, x2 = x0 + 2h, . . . , xn = x0 + nh = b.
I = 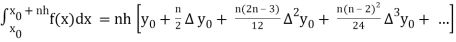
The above formula is known as Newton’s cotes formula.
This is also known as general quadrature formula.
Trapezoidal Method:
Let the interval  be divided into n equal intervals such that
be divided into n equal intervals such that  <
< <….<
<….<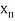 =b.
=b.
Here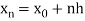 .
.
To find the value of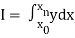 .
.
Setting n=1, we get

Or I = 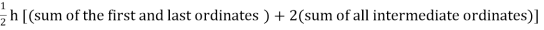
The above is known as Trapezoidal method.
Note: In this method second and higher difference are neglected and so f(x) is a polynomial of degree 1.
Geometrical Significance: The curve y=f(x),is replaced by n straight lines with the points  (
(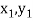 );(
);( ) and (
) and ( );…….;(
);…….;( ) and (
) and ( ).
).
The area bounded by the curve y=f(x), the ordinates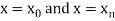 , and the x axis is approximately equivalent to the sum of the area of the n trapeziums obtained.
, and the x axis is approximately equivalent to the sum of the area of the n trapeziums obtained.
Example1: State the trapezoidal rule for finding an approximate area under the given curve. A curve is given by the points (x, y) given below:
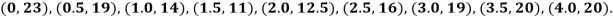
Estimate the area bounded by the curve, the x axis and the extreme ordinates.
We construct the data table:
X | 0 | 0.5 | 1.0 | 1.5 | 2.0 | 2.5 | 3.0 | 3.5 | 4.0 |
Y | 23 | 19 | 14 | 11 | 12.5 | 16 | 19 | 20 | 20 |
Here length of interval h =0.5, initial value a = 0 and final value b = 4
By Trapezoidal method
Area of curve bounded on x axis =

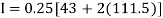
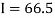
Example 2: Compute the value of 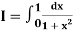 ?
?
Using the trapezoidal rule with h=0.5, 0.25 and 0.125.
Here 
For h=0.5, we construct the data table:
X | 0 | 0.5 | 1 |
Y | 1 | 0.8 | 0.5 |
By Trapezoidal rule
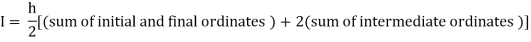

For h=0.25, we construct the data table:
X | 0 | 0.25 | 0.5 | 0.75 | 1 |
Y | 1 | 0.94117 | 0.8 | 0.64 | 0.5 |
By Trapezoidal rule

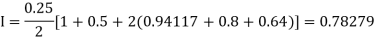
For h = 0.125, we construct the data table:
X | 0 | 0.125 | 0.25 | 0.375 | 0.5 | 0.625 | 0.75 | 0.875 | 1 |
Y | 1 | 0.98461 | 0.94117 | 0.87671 | 0.8 | 0.71910 | 0.64 | 0.56637 | 0.5 |
By Trapezoidal rule

 [(1+0.5)+2(0.98461+0.94117+0.87671+0.8+0.71910+0.64+0.56637)]
[(1+0.5)+2(0.98461+0.94117+0.87671+0.8+0.71910+0.64+0.56637)]
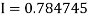
Example 3: Evaluate, using trapezoidal rule with five ordinates
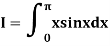
Here 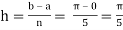
We construct the data table:
X | 0 |  |  | 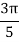 |  |  |
Y | 0 | 0.3693161 | 1.195328 | 1.7926992 | 1.477265 | 0 |

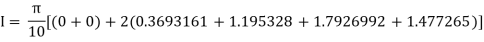

Unit - 4
Numerical Integration
Numerical Integration
Numerical integration is a process of evaluating or obtaining a definite integral 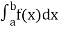 from a set of numerical values of the integrand f(x).In case of function of single variable, the process is called quadrature
from a set of numerical values of the integrand f(x).In case of function of single variable, the process is called quadrature
Newton cotes formula-
Suppose 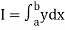 where y takes the values
where y takes the values 
And let the integration interval (a,b) is divided into n equal sub-intervals, each of width h = b – a /n, so that,
x0 = a, x1 = x0 + h, x2 = x0 + 2h, . . . , xn = x0 + nh = b.
I = 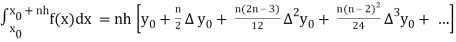
The above formula is known as Newton’s cotes formula.
This is also known as general quadrature formula.
Trapezoidal Method:
Let the interval 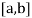 be divided into n equal intervals such that
be divided into n equal intervals such that  <
< <….<
<….< =b.
=b.
Here .
.
To find the value of .
.
Setting n=1, we get
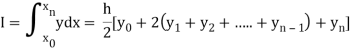
Or I = 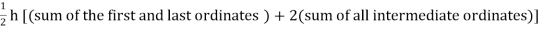
The above is known as Trapezoidal method.
Note: In this method second and higher difference are neglected and so f(x) is a polynomial of degree 1.
Geometrical Significance: The curve y=f(x),is replaced by n straight lines with the points  (
( );(
);( ) and (
) and ( );…….;(
);…….;(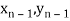 ) and (
) and ( ).
).
The area bounded by the curve y=f(x), the ordinates , and the x axis is approximately equivalent to the sum of the area of the n trapeziums obtained.
, and the x axis is approximately equivalent to the sum of the area of the n trapeziums obtained.
Example1: State the trapezoidal rule for finding an approximate area under the given curve. A curve is given by the points (x, y) given below:

Estimate the area bounded by the curve, the x axis and the extreme ordinates.
We construct the data table:
X | 0 | 0.5 | 1.0 | 1.5 | 2.0 | 2.5 | 3.0 | 3.5 | 4.0 |
Y | 23 | 19 | 14 | 11 | 12.5 | 16 | 19 | 20 | 20 |
Here length of interval h =0.5, initial value a = 0 and final value b = 4
By Trapezoidal method
Area of curve bounded on x axis =
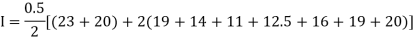


Example 2: Compute the value of  ?
?
Using the trapezoidal rule with h=0.5, 0.25 and 0.125.
Here 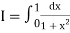
For h=0.5, we construct the data table:
X | 0 | 0.5 | 1 |
Y | 1 | 0.8 | 0.5 |
By Trapezoidal rule


For h=0.25, we construct the data table:
X | 0 | 0.25 | 0.5 | 0.75 | 1 |
Y | 1 | 0.94117 | 0.8 | 0.64 | 0.5 |
By Trapezoidal rule


For h = 0.125, we construct the data table:
X | 0 | 0.125 | 0.25 | 0.375 | 0.5 | 0.625 | 0.75 | 0.875 | 1 |
Y | 1 | 0.98461 | 0.94117 | 0.87671 | 0.8 | 0.71910 | 0.64 | 0.56637 | 0.5 |
By Trapezoidal rule

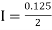 [(1+0.5)+2(0.98461+0.94117+0.87671+0.8+0.71910+0.64+0.56637)]
[(1+0.5)+2(0.98461+0.94117+0.87671+0.8+0.71910+0.64+0.56637)]

Example 3: Evaluate, using trapezoidal rule with five ordinates

Here 
We construct the data table:
X | 0 |  | 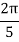 |  |  |  |
Y | 0 | 0.3693161 | 1.195328 | 1.7926992 | 1.477265 | 0 |


Simpson’s Rule:
Let the interval 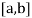 be divided into n equal intervals such that
be divided into n equal intervals such that  <
< <….<
<….< =b.
=b.
Here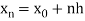 .
.
To find the value of .
.
Setting n = 2,

Which is known as Simpson’s 1/3- rule or Simpson’s rule.
Note: In this rule third and higher differences are neglected a so f(x) is a polynomial of degree 2.
Example 1: Estimate the value of the integral

By Simpson’s rule with 4 strips and 8 strips respectively.
For n=4, we have 
Construct the data table:
X | 1.0 | 1.5 | 2.0 | 2.5 | 3.0 |
Y=1/x | 1 | 0.66666 | 0.5 | 0.4 | 0.33333 |
By Simpson’s Rule
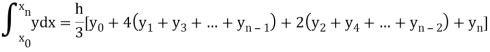

For n = 8, we have 
X | 1 | 1.25 | 1.50 | 1.75 | 2.0 | 2.25 | 2.50 | 2.75 | 3.0 |
Y=1/x | 1 | 0.8 | 0.66666 | 0.571428 | 0.5 | 0.444444 | 0.4 | 0.3636363 | 0.333333 |
By Simpson’s Rule


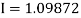
Example 2: Evaluate 
Using Simpson’s 1/3 rule with  .
.
For  , we construct the data table:
, we construct the data table:
X | 0 |  |  |  |  |  |  |
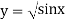 | 0 | 0.50874 | 0.707106 | 0.840896 | 0.930604 | 0.98281 | 1 |
By Simpson’s Rule



Example 3: Using Simpson’s 1/3 rule with h = 1, evaluate

For h = 1, we construct the data table:
X | 3 | 4 | 5 | 6 | 7 |
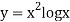 | 9.88751 | 22.108709 | 40.23594 | 64.503340 | 95.34959 |
By Simpson’s Rule


= 177.3853
Simpson’s 3/8 rule
Let the interval 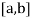 be divided into n equal intervals such that
be divided into n equal intervals such that  <
< <….<
<….<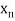 =b.
=b.
Here .
.
To find the value of  .
.
Setting n=3 , we get

Is known as Simpson’s 3/8 rule which is not as accurate as Simpson’s rule.
Note: In this rule the fourth and higher differences are neglected and so f(x) is a polynomial of degree 3.
Example 1: Evaluate 
By Simpson’s 3/8 rule.
Let us divide the range of the interval [4, 5.2] into six equal parts.

For h=0.2, we construct the data table:
X | 4.0 | 4.2 | 4.4 | 4.6 | 4.8 | 5.0 | 5.2 |
 | 1.3863 | 1.4351 | 1.4816 | 1.5261 | 1.5686 | 1.6094 | 1.6487 |
By Simpson’s 3/8 rule
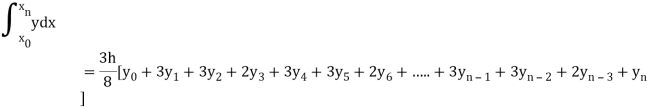

= 1.8278475
Example 2: Evaluate 
Let us divide the range of the interval [0,6] into six equal parts.

For h=1, we construct the data table:
X | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
 | 1 | 0.5 | 0.2 | 0.1 | 0.0588 | 0.0385 | 0.027 |
By Simpson’s 3/8 rule
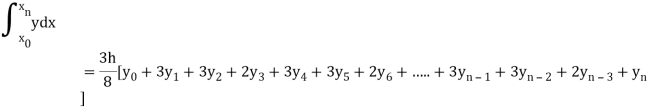
 +3(0.0385)+0.027]
+3(0.0385)+0.027]
=1.3571
Error in Integration
Error in Trapezoidal method
The total error in trapezoidal method is given by

Let 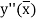 is the largest value of the n quantities on the right hand side of the above equation then
is the largest value of the n quantities on the right hand side of the above equation then

Error in Simpson’s Rule
The error in the Simpson’s rule is given by

Where  is the largest value of the fourth derivative of y(x).
is the largest value of the fourth derivative of y(x).
Error in Simpson’s 3/8 Rule
The error in this rule is given by

Where  is the largest value of the derivative of y(x).
is the largest value of the derivative of y(x).
Boole’s rule & Waddle’s rule-
The formula given below is known as Boole’s rule-
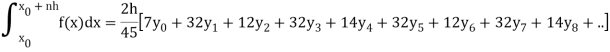
And the waddle’s rules is defined as-

Example: A river is 80 m wide. The depth ‘b’ of the river at a distance ‘a’ from one bank is given by the table-
a | 0 | 10 | 20 | 30 | 40 | 50 | 60 | 70 | 80 |
B | 0 | 4 | 7 | 9 | 12 | 15 | 14 | 8 | 3 |
Find the approximate area of cross-section of the river using Boole’s rule.
Sol.
The area of the cross-section of the river will be-
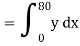
The number of sub-intervals here is 8.
Then by Boole’s rule-
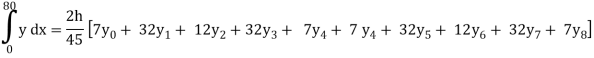
= 2(10)/45 [ 7(0) + 32(4) + 12(7) + 32(9) + 7(12) + 7(12) + 32(15) + 12(14) + 32(8) +7(3)]
= 708
So that the area of of the cross-section of the river is 708 square meter.
Example: Evaluate 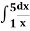 by using Boole’s.
by using Boole’s.
Sol.
Take h =  , so that there four sub intervals-
, so that there four sub intervals-
X | 1 | 2 | 3 | 4 | 5 |
F(x) | 1 | ½ | 1/3 | ¼ | 1/5 |
Using Boole’s method-


Romberg integration:
In order to obtain accurate results, we compute the integrals by trapezium or Simpson’s rules for a number of values of step lengths, each time reducing the step length. We stop the computation, when convergence is attained (usually, the magnitude of the difference in successive values of the integrals obtained by reducing values of the step lengths is less than a given accuracy). Convergence may be obtained after computing the value of the integral with a number of step lengths. While computing the value of the integral with a particular step length, the values of the integral obtained earlier by using larger step lengths were not used. Further, convergence may be slow. Romberg method is a powerful tool which uses the method of extrapolation.
We compute the value of the integral with a number of step lengths using the same method. Usually, we start with a coarse step length, then reduce the step lengths and recomputed the value of the integral. The sequence of these values converges to the exact value of the integral. Romberg method uses these values of the integral obtained with various step lengths, to refine the solution such that the new values are of higher order. That is, as if the results are obtained using a higher order method than the order of the method used. The extrapolation method is derived by studying the error of the method that is being used.
Lets consider the definite integral,

And evaluate it by the trapezoidal rule with two different subintervals of width  and
and  to obtain the approximate values
to obtain the approximate values 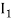 and
and  respectively,
respectively,
Then
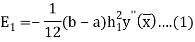
And
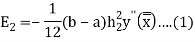
Since the term 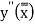 is also the largest value of
is also the largest value of  , it is reasonable to assume that the quantities
, it is reasonable to assume that the quantities
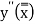 are very nearly the same.
are very nearly the same.
We therefore have

And hence
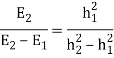
Since  , this gives
, this gives

We therefore obtain a new approximation  defined by
defined by

Which in general, would be closer to the actual value- provided that the errors decrease monotonically and are the same sign.
If we now set

Equation (3) can be written as-

Where I(h) = 
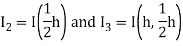
In table form it can be written as,
I(h) I(h, ½ h) I(1/2 h) I(h, ½ h, ¼ h) I( ½ h, ¼ h) I(h, ½ h, ¼ h, 1/8 h) I(1/4 h) I( ½ h, ¼ h, 1/8 h) I( ¼ h, 1/8 h) I(1/8 h) |
Example: Compute the following integral upto three decimal places by using Romberg’s method.
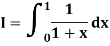
Sol:
We take h = 0.5, 0.25 and 0.125 successively and use the results as below
I(h) = 0.7084, I(1/2h) = 0.6970 and I(1/4 h) = 0.6941
Hence,
We get
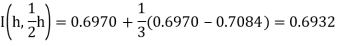

Finally,

The table of values,
0.7084
0.6932
0.6970 0.6931
0.6931
0.6941
References:
- E. Kreyszig, “Advanced Engineering Mathematics”, John Wiley & Sons, 2006.
- P. G. Hoel, S. C. Port And C. J. Stone, “Introduction To Probability Theory”, Universal Book Stall, 2003.
- S. Ross, “A First Course in Probability”, Pearson Education India, 2002.
- W. Feller, “An Introduction To Probability Theory and Its Applications”, Vol. 1, Wiley, 1968.
- N.P. Bali and M. Goyal, “A Text Book of Engineering Mathematics”, Laxmi Publications, 2010.
- B.S. Grewal, “Higher Engineering Mathematics”, Khanna Publishers, 2000.