Unit - 6
Vector space
Definition-
Let ‘F’ be any given field, then a given set V is said to be a vector space if-
1. There is a defined composition in ‘V’. This composition called addition of vectors which is denoted by ‘+’
2. There is a defined an external composition in ‘V’ over ‘F’. That will be denoted by scalar multiplication.
3. The two compositions satisfy the following conditions-
(a) 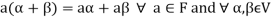
(b) 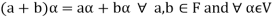
(c) 
(d) If  then 1 is the unity element of the field F.
then 1 is the unity element of the field F.
If V is a vector space over the field F, then we will denote vector space as V(F).
Note that each member of V(F) will be referred as a vector and each member of F as a scalar
Note- Here we have denoted the addition of the vectors by the symbol ‘+’. This symbol also be used for the addition of scalars.
If 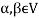 then
then  represents addition in vectors(V).
represents addition in vectors(V).
If 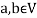 then a+b represents the addition of the scalars or addition in the field F.
then a+b represents the addition of the scalars or addition in the field F.
Note- For V to be an abelian group with respect to addition vectors, the following conditions must be followed-
1. 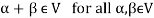
2. 
3.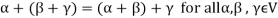
4. There exists an element  which is also called the zero vector. Such that-
which is also called the zero vector. Such that-
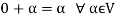
It is the additive identity in V.
5. There exists a  to every vector
to every vector 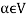 such that
such that
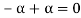
This is the additive inverse of V
Note- All the properties of an abelian group will hold in V if (V,+) is an abelian group.
These properties are-
1. 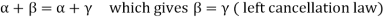
2. 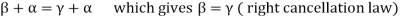
3. 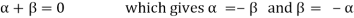
4. 
5. The additive identity 0 will be unique.
6. The additive inverse will be unique.
7. 
Note- The Greek letters 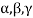 are used to denote elements of vectors and Latin letters a , b , c etc. for scalars that means the elements of field F.
are used to denote elements of vectors and Latin letters a , b , c etc. for scalars that means the elements of field F.
Note- Suppose C is the field of complex numbers and R is the field of real numbers, then C is a vector space over R, here R is the subfield of C.
Here note that R is not a vector space over C.
Example-: The set of all 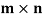 matrices with their elements as real numbers is a vector space over the field F of real numbers with respect to addition of matrices as addition of vectors and multiplication of a matrix by a scalar as scalar multiplication.
matrices with their elements as real numbers is a vector space over the field F of real numbers with respect to addition of matrices as addition of vectors and multiplication of a matrix by a scalar as scalar multiplication.
Sol. V is an abelian group with respect to addition of matrices in groups.
The null matrix of m by n is the additive identity of this group.
If 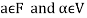 then
then 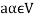 as
as  is also the matrix of m by n with elements of real numbers.
is also the matrix of m by n with elements of real numbers.
So that V is closed with respect to scalar multiplication.
We conclude that from matrices-
1. 
2. 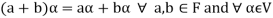
3. 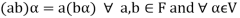
4.  Where 1 is the unity element of F.
Where 1 is the unity element of F.
Therefore we can say that V (F) is a vector space.
Example-2: The vector space of all polynomials over a field F.
Suppose F[x] represents the set of all polynomials in indeterminate x over a field F. The F[x] is vector space over F with respect to addition of two polynomials as addition of vectors and the product of a polynomial by a constant polynomial.
Example-3: The vector space of all real valued continuous (differentiable or integrable) functions defined in some interval [0,1]
Suppose f and g are two functions, and V denotes the set of all real valued continuous functions of x defined in the interval [0,1]
Then V is a vector space over the filed R with vector addition and multiplication as:
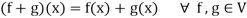
And
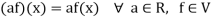
Here we will first prove that V is an abelian group with respect to addition composition as in rings.
V is closed with respect to scalar multiplication since af is also a real valued continuous function
We observe that-
1. If 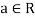 and f,g
and f,g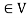 , then
, then
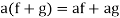
2. If  and
and 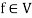 , then
, then
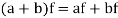
3. If 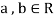 and
and 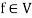 , then
, then
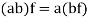
4. If 1 is the unity element of R and 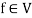 , then
, then
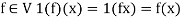
So that V is a vector space over R.
Some important theorems on vector spaces-
Theorem-1: Suppose V(F) is a vector space and 0 be the zero vector of V. Then-
1. 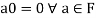
2. 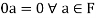
3. 
4. 
5. 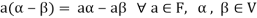
6. 
Proof-
1. We have
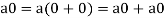
We can write 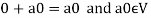
So that,
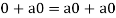
Now V is an abelian group with respect to addition.
So that by right cancellation law, we get-
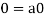
2. We have
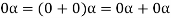
We can write 
So that,
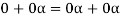
Now V is an abelian group with respect to addition.
So that by right cancellation law, we get-
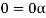
3. We have 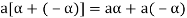
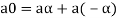
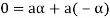
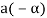 is the additive inverse of
is the additive inverse of 
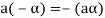
4. We have 
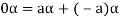

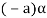 is the additive inverse of
is the additive inverse of 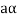
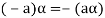
5. We have-
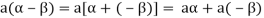
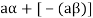
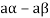
6. Suppose  the inverse of ‘a’ exists because ‘a’ is non-zero element of the field.
the inverse of ‘a’ exists because ‘a’ is non-zero element of the field.
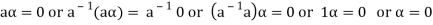
Again let-
 , then to prove
, then to prove 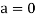 let
let  then inverse of ‘a’ exists
then inverse of ‘a’ exists
We get a contradiction that  must be a zero vector. Therefore ‘a’ must be equal to zero.
must be a zero vector. Therefore ‘a’ must be equal to zero.
So that
Vector sub-space-
Definition
Suppose V is a vector space over the field F and  . Then W is called subspace of V if W itself a vector space over F with respect to the operations of vector addition and scalar multiplication in V.
. Then W is called subspace of V if W itself a vector space over F with respect to the operations of vector addition and scalar multiplication in V.
Theorem-1-The necessary and sufficient conditions for a non-empty sub-set W of a vector space V(F) to be a subspace of V are-
1. 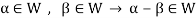
2. 
Proof:
Necessary conditions-
W is an abelian group with respect to vector addition If W is a subspace of V.
So that 
Here W must be closed under a scalar multiplication so that the second condition is also necessary.
Sufficient conditions-
Let W is a non-empty subset of V satisfying the two given conditions.
From first condition-
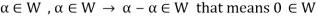
So that we can say that zero vector of V belongs to W. It is a zero vector of W as well.
Now 
So that the additive inverse of each element of W is also in W.
So that-
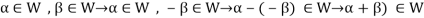
Thus W is closed with respect to vector addition.
Theorem-2:
The intersection of any two subspaces 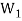 and
and  of a vector space V(F) is also a subspace of V(F).
of a vector space V(F) is also a subspace of V(F).
Proof: As we know that  therefore
therefore  is not empty.
is not empty.
Suppose  and
and 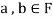
Now, 
And 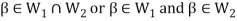
Since 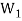 is a subspace, therefore-
is a subspace, therefore-
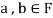 and
and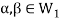 then
then 
Similarly, 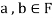
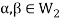 then
then
Now 
Thus,
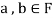 And
And 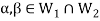
Then 
So that 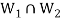 is a subspace of V(F).
is a subspace of V(F).
Example-1: If 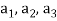 are fixed elements of a field F, then set of W of all ordered triads (
are fixed elements of a field F, then set of W of all ordered triads (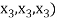 of elements of F,
of elements of F,
Such that-
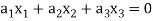
Is a subspace of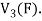
Sol. Suppose 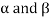 are any two elements of W.
are any two elements of W.
Such that 
And these are the elements of F, such that-
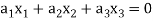 …………………….. (1)
…………………….. (1)
 ……………………. (2)
……………………. (2)
If a and b are two elements of F, we have
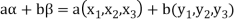
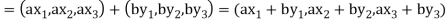
Now
= 
= 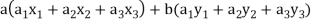
= 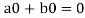
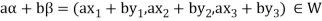
So that W is subspace of 
Example-2: Let R be a field of real numbers. Now check whether which one of the following are subspaces of 
1. { 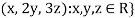
2. { 
3. { 
Solution- 1. Suppose W = { 
Let  be any two elements of W.
be any two elements of W.
If a and b are two real numbers, then-
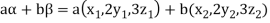
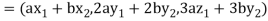
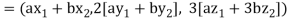
Since  are real numbers.
are real numbers.
So that  and
and 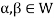 or
or 
So that W is a subspace of 
2. Let W = { 
Let 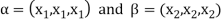 be any two elements of W.
be any two elements of W.
If a and b are two real numbers, then-
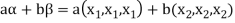
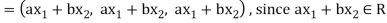
So that W is a subspace of 
3. Let W ={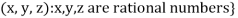
Now  is an element of W. Also
is an element of W. Also 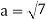 is an element of R.
is an element of R.
But  which do not belong to W.
which do not belong to W.
Since  are not rational numbers.
are not rational numbers.
So that W is not closed under scalar multiplication.
W is not a subspace of 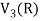
Key takeaways:
- Each member of V(F) will be referred as a vector and each member of F as a scalar
- All the properties of an abelian group will hold in V if (V,+) is an abelian group.
- The Greek letters
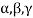 are used to denote elements of vectors and Latin letters a , b , c etc. for scalars that means the elements of field F.
are used to denote elements of vectors and Latin letters a , b , c etc. for scalars that means the elements of field F. - Suppose C is the field of complex numbers and R is the field of real numbers, then C is a vector space over R, here R is the subfield of C.
- Here note that R is not a vector space over C.
- Suppose V is a vector space over the field F and
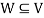 . Then W is called subspace of V if W itself a vector space over F with respect to the operations of vector addition and scalar multiplication in V.
. Then W is called subspace of V if W itself a vector space over F with respect to the operations of vector addition and scalar multiplication in V.
Algebra of subs paces, quotient spaces
Another definition of subspace:
A subset W of a vector space V over a field F is called a subspace of V if W is a vector space over F with the operations of addition and scalar multiplication defined on V.
In any vector space V, note that V and {0 } are subspaces. The latter is called the zero subspace of V.
Note- A subset W of a vector space V is a subspace of V if and only if the following four properties hold.
1. x + y ∈ W whenever x ∈ W and y ∈ W. (W is closed under addition.)
2. c x ∈ W whenever c ∈ F and x ∈ W. (W is closed under scalar multiplication.)
3. W has a zero vector.
4. Each vector in W has an additive inverse in W.
Note- Let V be a vector space and W a subset of V. Then W is a subspace of V if and only if the following three conditions hold for the operations defined in V.
(a) 0 ∈ W.
(b) x + y ∈ W whenever x ∈ W and y ∈ W.
(c) cx ∈ W whenever c ∈ F and x ∈ W.
The transpose  of an m × n matrix A is the n × m matrix obtained from A by interchanging the rows with the columns
of an m × n matrix A is the n × m matrix obtained from A by interchanging the rows with the columns
Suppose,
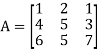
Then
Transpose of this matrix,
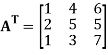
A symmetric matrix is a matrix A such that  = A.
= A.
A skew- symmetric matrix is a matrix A such that 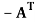 = A.
= A.
Note- the set of symmetric matrices is closed under addition and scalar multiplication.
Example: An n×n matrix M is called a diagonal matrix if 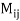 = 0 whenever i
= 0 whenever i  j, that is, if all its nondiagonal entries are zero. Clearly the zero matrix is a diagonal matrix because all of its entries are 0. Moreover, if A and B are diagonal n × n matrices, then whenever i
j, that is, if all its nondiagonal entries are zero. Clearly the zero matrix is a diagonal matrix because all of its entries are 0. Moreover, if A and B are diagonal n × n matrices, then whenever i  j,
j,
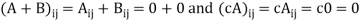
For any scalar c. Hence A + B and cA are diagonal matrices for any scalar c. Therefore the set of diagonal matrices is a subspace of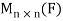 .
.
Theorem: Any intersection of subspaces of a vector space V is a subspace of V.
Proof:
Let C be a collection of subspaces of V, and let W denote the intersection of the subspaces in C. Since every subspace contains the zero vector, 0 ∈ W. Let a ∈ F and x, y ∈ W. Then x and y are contained in each subspace in C. Because each subspace in C is closed under addition and scalar multiplication, it follows that x+y and ax are contained in each subspace in C. Hence x+y and ax are also contained in W, so that W is a subspace of V
Note- The union of subspaces must contain the zero vector and be closed under scalar multiplication, but in general the union of subspaces of V need not be closed under addition.
Definition of sum and direct sum:
Sum- If S1 and S2 are nonempty subsets of a vector space V, then the sum of S1 and S2, denoted S1+S2, is the set {x + y : x ∈ S1 and y ∈ S2}.
Direct sum- A vector space V is called the direct sum of W1 and W2 if W1 and W2 are subspaces of V such that W1 ∩W2 = {0} and W1 +W2 = V. We denote that V is the direct sum of W1 and W2 by writing V = W1 ⊕ W2.
Key takeaways:
1. A subset W of a vector space V is a subspace of V if and only if the following four properties hold.
1. x + y ∈ W whenever x ∈ W and y ∈ W. (W is closed under addition.)
2. c x ∈ W whenever c ∈ F and x ∈ W. (W is closed under scalar multiplication.)
3. W has a zero vector.
4. Each vector in W has an additive inverse in W.
2. The transpose 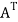 of an m × n matrix A is the n × m matrix obtained from A by interchanging the rows with the columns
of an m × n matrix A is the n × m matrix obtained from A by interchanging the rows with the columns
3. A symmetric matrix is a matrix A such that 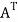 = A.
= A.
4. A skew- symmetric matrix is a matrix A such that 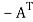 = A.
= A.
5. The set of symmetric matrices is closed under addition and scalar multiplication.
Definition-
Suppose U(F) and V(F) are two vector spaces, then a mapping 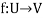 is called a linear transformation of U into V, if:
is called a linear transformation of U into V, if:
1. 
2. 
It is also called homomorphism.
Kernel(null space) of a linear transformation-
Let f be a linear transformation of a vector space U(F) into a vector space V(F).
The kernel W of f is defined as-

The kernel W of f is a subset of U consisting of those elements of U which are mapped under f onto the zero vector V.
Since f(0) = 0, therefore atleast 0 belong to W. So that W is not empty.
Another definition of null space and range:
Let V and W be vector spaces, and let T: V → W be linear. We define the null space (or kernel) N(T) of T to be the set of all vectors x in V such that T(x) = 0; that is, N(T) = {x ∈ V: T(x) = 0 }.
We define the range (or image) R(T) of T to be the subset of W consisting of all images (under T) of vectors in V; that is, R(T) = {T(x) : x ∈ V}.
Example: The mapping  defined by-
defined by-
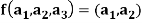
Is a linear transformation  .
.
What is the kernel of this linear transformation.
Sol. Let  be any two elements of
be any two elements of 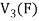
Let a, b be any two elements of F.
We have
 (
(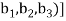
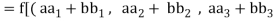
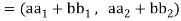
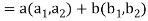 =
= 
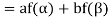
So that f is a linear transformation.
To show that f is onto 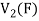 . Let
. Let  be any elements
be any elements 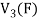 .
.
Then  and we have
and we have 
So that f is onto 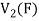
Therefore f is homomorphism of  onto
onto 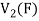 .
.
If W is the kernel of this homomorphism then 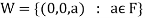
We have
∀
Also if  then
then 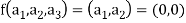
Implies 
Therefore 
Hence W is the kernel of f.
Theorem: Let V and W be vector spaces and T: V → W be linear. Then N(T) and R(T) are subspaces of V and W, respectively.
Proof:
Here we will use the symbols 0 V and 0W to denote the zero vectors of V and W, respectively.
Since T(0 V) = 0W, we have that 0 V ∈ N(T). Let x, y ∈ N(T) and c ∈ F.
Then T(x + y) = T(x)+T(y) = 0W+0W = 0W, and T(c x) = c T(x) = c0W = 0W. Hence x + y ∈ N(T) and c x ∈ N(T), so that N(T) is a subspace of V. Because T(0 V) = 0W, we have that 0W ∈ R(T). Now let x, y ∈ R(T) and c ∈ F. Then there exist v and w in V such that T(v) = x and T(w) = y. So T(v + w) = T(v)+T(w) = x + y, and T(c v) = c T(v) = c x. Thus x+ y ∈ R(T) and c x ∈ R(T), so R(T) is a subspace of W.
Key takeaways:
1. Suppose U(F) and V(F) are two vector spaces, then a mapping  is called a linear transformation of U into V, if:
is called a linear transformation of U into V, if:
1. 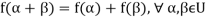
2. 
2. Let V and W be vector spaces, and let T: V → W be linear. We define the null space (or kernel) N(T) of T to be the set of all vectors x in V such that T(x) = 0; that is, N(T) = {x ∈ V: T(x) = 0 }.
Rank and nullity of a linear transformation
Definition:
Let V and W be vector spaces, and let T: V → W be linear. If N(T) and R(T) are finite-dimensional, then we define the nullity of T, denoted nullity(T), and the rank of T, denoted rank(T), to be the dimensions of N(T) and R(T), respectively.
Theorem: Let A is a matrix of order m by n, then-
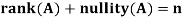
Proof:
If rank (A) = n, then the only solution to Ax = 0 is the trivial solution x = 0by using invertible matrix.
So that in this case null-space (A) = {0}, so nullity (A) = 0.
Now suppose rank (A) = r < n, in this case there are n – r > 0 free variable in the solution to Ax = 0.
Let 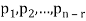 represent these free variables and let
represent these free variables and let 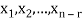 denote the solution obtained by sequentially setting each free variable to 1 and the remaining free variables to zero.
denote the solution obtained by sequentially setting each free variable to 1 and the remaining free variables to zero.
Here  is linearly independent.
is linearly independent.
Moreover every solution is to Ax = 0 is a linear combination of 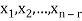
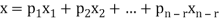
Which shows that 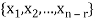 spans null-space (A).
spans null-space (A).
Thus  is a basis for null-space(A) and nullity (A) = n – r.
is a basis for null-space(A) and nullity (A) = n – r.
Theorem: Let V and W be vector spaces, and let T: V → W be linear. Then T is one-to-one if and only if N(T) = {0 }.
Proof:
Suppose that T is one-to-one and x ∈ N(T). Then T(x) = 0 = T(0 ). Since T is one-to-one, we have x = 0 . Hence N(T) = {0 }.
Now assume that N(T) = {0 }, and suppose that T(x) = T(y). Then 0 = T(x) − T(y) = T(x − y).
Therefore x − y ∈ N(T) = {0 }. So x − y = 0, or x = y. This means that T is one-to-one.
Note- Let V and W be vector spaces of equal (finite) dimension, and let T: V → W be linear. Then the following are equivalent.
(a) T is one-to-one.
(b) T is onto.
(c) rank(T) = dim(V).
Key takeaways:
- Let A is a matrix of order m by n, then-
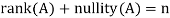
Suppose V(F) be a vector space. If 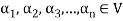 , then any vector-
, then any vector-
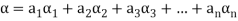
Where 
Is called a linear combination of the vectors 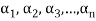
Linear Span-
Definition- Let V(F) be a vector space and S be a non-empty subset of V. Then the linear span of S is the set of all linear combinations of finite sets of elements of S and it is denoted by L(S). Thus we have-
L(S) = 
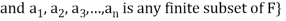
Theorem:
The linear span L(S) of any subset S of a vector space V(F) is s subspace of V generated by S.
Proof: Suppose 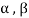 be any two elements of L(S).
be any two elements of L(S).
Then
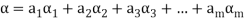
And 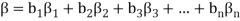
Where a and b are the elements of F and 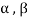 are the elements of S.
are the elements of S.
If a,b be any two elements of F, then-
 (
( (
(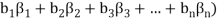
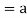 (
( (
(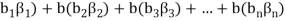
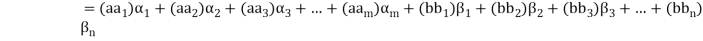
Thus 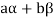 has been expressed as a linear combination of a finite set
has been expressed as a linear combination of a finite set  of the elements of S.
of the elements of S.
Consequently 
Thus,  and
and 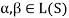 so that
so that 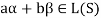
Hence L(S) is a subspace of V(F).
Linear dependence-
Let V(F) be a vector space.
A finite set 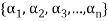 of vector of V is said to be linearly dependent if there exists scalars
of vector of V is said to be linearly dependent if there exists scalars 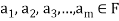 (not all of them as some of them might be zero)
(not all of them as some of them might be zero)
Such that-
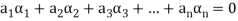
Linear independence-
Let V(F) be a vector space.
A finite set  of vector of V is said to be linearly independent if every relation if the form-
of vector of V is said to be linearly independent if every relation if the form-
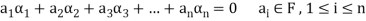
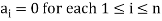
Theorem:
The set of non-zero vectors  of V(F) is linearly dependent if some
of V(F) is linearly dependent if some 
Is a linear combination of the preceding ones.
Proof: if some 
Is a linear combination of the preceding ones, 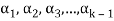 then ∃ scalars
then ∃ scalars 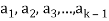 such that-
such that-
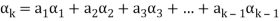 …… (1)
…… (1)
The set {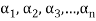 } is linearly dependent because the linear combination (1) the scalar coefficient
} is linearly dependent because the linear combination (1) the scalar coefficient 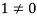
Hence the set {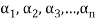 } of which {
} of which {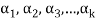 } is a subset must be linearly dependent.
} is a subset must be linearly dependent.
Example-1: If the set S =  of vector V(F) is linearly independent, then none of the vectors
of vector V(F) is linearly independent, then none of the vectors 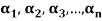 can be zero vector.
can be zero vector.
Sol. Let 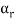 be equal to zero vector where
be equal to zero vector where 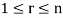
Then 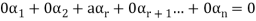
For any  in F.
in F.
Here 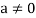 therefore from this relation we can say that S is linearly dependent. This is the contradiction because it is given that S is linearly independent.
therefore from this relation we can say that S is linearly dependent. This is the contradiction because it is given that S is linearly independent.
Hence none of the vectors can be zero.
We can conclude that a set of vectors which contains the zero vector is necessarily linear dependent.
Example-2: Show that S = {(1 , 2 , 4) , (1 , 0 , 0) , (0 , 1 , 0) , (0 , 0 , 1)} is linearly dependent subset of the vector space 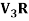 . Where R is the field of real numbers.
. Where R is the field of real numbers.
Sol. Here we have-
1 (1 , 2 , 4) + (-1) (1 , 0 , 0) + (-2) (0 ,1, 0) + (-4) (0, 0, 1)
= (1, 2 , 4) + (-1 , 0 , 0) + (0 ,-2, 0) + (0, 0, -4)
= (0, 0, 0)
That means it is a zero vector.
In this relation the scalar coefficients 1 , -1 , -2, -4 are all not zero.
So that we can conclude that S is linearly dependent.
Example-3: If  are linearly independent vectors of V(F).where F is the field of complex numbers, then so also are
are linearly independent vectors of V(F).where F is the field of complex numbers, then so also are 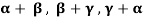 .
.
Sol. Suppose a, b, c are scalars such that-
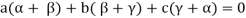
 …………….. (1)
…………….. (1)
But  are linearly independent vectors of V(F), so that equations (1) implies that-
are linearly independent vectors of V(F), so that equations (1) implies that-
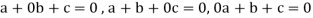
The coefficient matrix A of these equations will be-
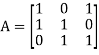
Here we get rank of A = 3, so that a = 0, b = 0, c = 0 is the only solution of the given equations, so that  are also linearly independent.
are also linearly independent.
Key takeaways:
- Suppose V(F) be a vector space. If
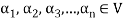 , then any vector-
, then any vector-
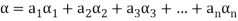
Where 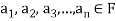
Is called a linear combination of the vectors 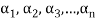
2. Let V(F) be a vector space and S be a non-empty subset of V. Then the linear span of S is the set of all linear combinations of finite sets of elements of S and it is denoted by L(S).
3. A finite set  of vector of V is said to be linearly independent if every relation if the form-
of vector of V is said to be linearly independent if every relation if the form-
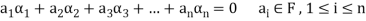
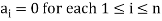
Definition:
A subset S of a vector space V(F) is said to be a basis of V(F), if-
1. S consists of linearly independent vectors
2. Each vector in V is a linear combination of a finite number of elements of S.
Finite dimensional vector spaces
The vector space V(F) is said to be finite dimensional if there exists a finite subset S of V such that V = L(S).
Dimension theorem for vector spaces-
Statement- If V(F) is a finite dimensional vector spaces, then any two bases of V have the same number of elements.
Proof: Let V(F) is a finite dimensional vector space. Then V possesses a basis.
Let  and
and  be two bases of V.
be two bases of V.
We shall prove that m = n
Since V = L( and
and 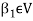 therefore
therefore  can be expressed as a linear combination of
can be expressed as a linear combination of 
Consequently the set  which also generates V(F) is linearly dependent. So that there exists a member
which also generates V(F) is linearly dependent. So that there exists a member 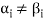 of this set. Such that
of this set. Such that  is the linear combination of the preceding vectors
is the linear combination of the preceding vectors 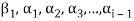
If we omit the vector  from
from 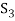 then V is also generated by the remaining set.
then V is also generated by the remaining set.
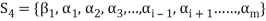
Since V = L( and
and 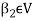 therefore
therefore 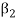 can be expressed as a linear combination of the vectors belonging to
can be expressed as a linear combination of the vectors belonging to 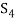
Consequently the set-
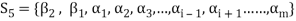
Is linearly dependent.
Therefore there exists a member 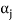 of this set such that
of this set such that 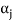 is a linear combination of the preceding vectors. Obviously
is a linear combination of the preceding vectors. Obviously 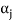 will be different from
will be different from 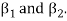
Since { } is a linearly independent set
} is a linearly independent set
If we exclude the vector 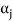 from
from 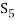 then the remaining set will generate V(F).
then the remaining set will generate V(F).
We may continue to proceed in this manner. Here each step consists in the exclusion of an 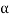 and the inclusion of
and the inclusion of  in the set
in the set 
Obviously the set 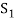 of all
of all  can not be exhausted before the set
can not be exhausted before the set 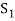 and
and 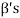
Otherwise V(F) will be a linear span of a proper subset of 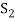 thus
thus  become linearly dependent. Therefore we must have-
become linearly dependent. Therefore we must have-
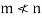
Now interchanging the roles of  we shall get that
we shall get that 
Hence,
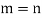
Extension theorem-
Every linearly independent subset of a finitely generated vector space V(F) forms of a part of a basis of V.
Proof: Suppose  be a linearly independent subset of a finite dimensional vector space V(F) if dim V = n, then V has a finite basis, say
be a linearly independent subset of a finite dimensional vector space V(F) if dim V = n, then V has a finite basis, say 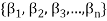
Let us consider a set-
 …………. (1)
…………. (1)
Obviously L( , since there
, since there 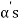 can be expressed as linear combination of
can be expressed as linear combination of 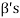 therefore the set
therefore the set  is linearly dependent.
is linearly dependent.
So that there is some vector of  which is linear combination of its preceding vectors. This vector can not be any of the
which is linear combination of its preceding vectors. This vector can not be any of the 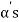 since the
since the  are linearly independent.
are linearly independent.
Therefore this vector must be some 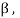 say
say 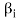
Now omit the vector 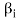 from (1) and consider the set-
from (1) and consider the set-
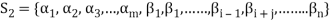
Obviously L( . If
. If 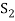 is linearly independent, then
is linearly independent, then  will be a basis of V and it is the required extended set which is a basis of V.
will be a basis of V and it is the required extended set which is a basis of V.
If 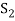 is not linearly independent, then repeating the above process a finite number of times. We shall get a linearly independent set containing
is not linearly independent, then repeating the above process a finite number of times. We shall get a linearly independent set containing 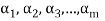 and spanning V. This set will be a basis of V contains the same number of elements, so that exactly n-m elements of the set of
and spanning V. This set will be a basis of V contains the same number of elements, so that exactly n-m elements of the set of 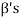 will be adjoined to S so as to form a basis of V.
will be adjoined to S so as to form a basis of V.
Example-1: Show that the vectors (1, 2, 1), (2, 1, 0) and (1, -1, 2) form a basis of 
Sol. We know that set {(1,0,0) , (0,1,0) , (0,0,1)} forms a basis of 
So that dim 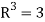 .
.
Now if we show that the set S = {(1, 2, 1), (2, 1, 0) , (1, -1, 2)} is linearly independent, then this set will form a basis of 
We have,
 (1, 2, 1)+
(1, 2, 1)+ (2, 1, 0)+
(2, 1, 0)+ (1, -1, 2) = (0, 0, 0)
(1, -1, 2) = (0, 0, 0)
(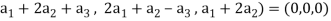
Which gives-
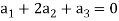
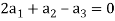
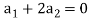
On solving these equations we get,
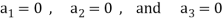
So we can say that the set S is linearly independent.
Therefore it forms a basis of 
Key takeaways:
- The vector space V(F) is said to be finite dimensional if there exists a finite subset S of V such that V = L(S).
- If V(F) is a finite dimensional vector spaces, then any two bases of V have the same number of elements.
- Every linearly independent subset of a finitely generated vector space V(F) forms of a part of a basis of V.
Let A be any m  n matrix over a field K. Recall that the rows of A may be viewed as vectors in
n matrix over a field K. Recall that the rows of A may be viewed as vectors in 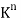 and that the row space of A, written rowsp(A), is the subspace of
and that the row space of A, written rowsp(A), is the subspace of 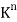 spanned by the rows of A. The following definition applies.
spanned by the rows of A. The following definition applies.
Def:
The rank of a matrix A, written rank(A), is equal to the maximum number of linearly independent rows of A or, equivalently, the dimension of the row space of A.
Recall, on the other hand, that the columns of an m  n matrix A may be viewed as vectors in
n matrix A may be viewed as vectors in 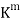 and that the column space of A, written colsp(A), is the subspace of
and that the column space of A, written colsp(A), is the subspace of 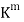 spanned by the columns of A.
spanned by the columns of A.
Although m may not be equal to n—that is, the rows and columns of A may belong to different vector spaces—we have the following fundamental result.
Theorem: The maximum number of linearly independent rows of any matrix A is equal to the maximum number of linearly independent columns of A. Thus, the dimension of the row space of A is equal to the dimension of the column space of A.
Basis-Finding Problems:
We will shows how an echelon form of any matrix A gives us the solution to certain problems about A itself. Specifically, let A and B be the following matrices, where the echelon matrix B (whose pivots are circled) is an echelon form of A:
A =  and B =
and B = 
We solve the following four problems about the matrix A, where C1; C2; . . . ; C6 denote its columns:
(a) Find a basis of the row space of A.
(b) Find each column Ck of A that is a linear combination of preceding columns of A.
(c) Find a basis of the column space of A.
(d) Find the rank of A.
(a) We are given that A and B are row equivalent, so they have the same row space. Moreover, B is in echelon form, so its nonzero rows are linearly independent and hence form a basis of the row space of B. Thus, they also form a basis of the row space of A. That is,
Basis of rowsp(A): (1, 2, 1, 3, 1, 2), (0, 1, 3, 1, 2, 1), (0, 0, 0, 1, 1, 2)
(b) Let  [
[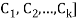 , the submatrix of A consisting of the first k columns of A. Then
, the submatrix of A consisting of the first k columns of A. Then  and
and
Mk are, respectively, the coefficient matrix and augmented matrix of the vector equation
x1C1 + x2C2 + . . . + xk – 1Ck – 1 = Ck
The system has a solution, or, equivalently, Ck is a linear combination of the preceding columns of A if and only if rank( = rank(
= rank(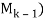 , where rank(
, where rank(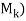 means the number of pivots in an echelon form of
means the number of pivots in an echelon form of 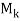 . Now the first k column of the echelon matrix B is also an echelon form of
. Now the first k column of the echelon matrix B is also an echelon form of  . Accordingly,
. Accordingly,
Rank (M2) = rank (M3) = 2 and rank(M4) = rank(M5) = rank(M6) = 3
Thus, C3, C5, C6 are each a linear combination of the preceding columns of A.
c) The fact that the remaining columns C1, C2, C4 are not linear combinations of their respective preceding columns also tells us that they are linearly independent. Thus, they form a basis of the column space of A. That is,
Basis of colsp(A): [1, 2, 3, 1, 2]T , [2, 5, 7, 5, 6]T, [3, 6, 11, 8, 11]T
Observe that C1, C2, C4 may also be characterized as those columns of A that contain the pivots in any echelon form of A.
(d) Here we see that three possible definitions of the rank of A yield the same value.
(i) There are three pivots in B, which is an echelon form of A.
(ii) The three pivots in B correspond to the nonzero rows of B, which form a basis of the row space of A.
(iii) The three pivots in B correspond to the columns of A, which form a basis of the column space of A.
Thus, rank(A) = 3.
References:
- E. Kreyszig, “Advanced Engineering Mathematics”, John Wiley & Sons, 2006.
- P. G. Hoel, S. C. Port And C. J. Stone, “Introduction To Probability Theory”, Universal Book Stall, 2003.
- S. Ross, “A First Course in Probability”, Pearson Education India, 2002.
- W. Feller, “An Introduction To Probability Theory and Its Applications”, Vol. 1, Wiley, 1968.
- N.P. Bali and M. Goyal, “A Text Book of Engineering Mathematics”, Laxmi Publications, 2010.
- B.S. Grewal, “Higher Engineering Mathematics”, Khanna Publishers, 2000.
Unit - 6
Vector space
Definition-
Let ‘F’ be any given field, then a given set V is said to be a vector space if-
1. There is a defined composition in ‘V’. This composition called addition of vectors which is denoted by ‘+’
2. There is a defined an external composition in ‘V’ over ‘F’. That will be denoted by scalar multiplication.
3. The two compositions satisfy the following conditions-
(a) 
(b) 
(c) 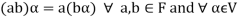
(d) If 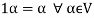 then 1 is the unity element of the field F.
then 1 is the unity element of the field F.
If V is a vector space over the field F, then we will denote vector space as V(F).
Note that each member of V(F) will be referred as a vector and each member of F as a scalar
Note- Here we have denoted the addition of the vectors by the symbol ‘+’. This symbol also be used for the addition of scalars.
If 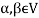 then
then  represents addition in vectors(V).
represents addition in vectors(V).
If 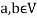 then a+b represents the addition of the scalars or addition in the field F.
then a+b represents the addition of the scalars or addition in the field F.
Note- For V to be an abelian group with respect to addition vectors, the following conditions must be followed-
1. 
2. 
3.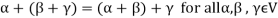
4. There exists an element 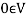 which is also called the zero vector. Such that-
which is also called the zero vector. Such that-
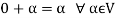
It is the additive identity in V.
5. There exists a  to every vector
to every vector  such that
such that
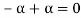
This is the additive inverse of V
Note- All the properties of an abelian group will hold in V if (V,+) is an abelian group.
These properties are-
1. 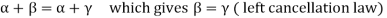
2. 
3. 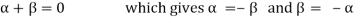
4. 
5. The additive identity 0 will be unique.
6. The additive inverse will be unique.
7. 
Note- The Greek letters 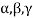 are used to denote elements of vectors and Latin letters a , b , c etc. for scalars that means the elements of field F.
are used to denote elements of vectors and Latin letters a , b , c etc. for scalars that means the elements of field F.
Note- Suppose C is the field of complex numbers and R is the field of real numbers, then C is a vector space over R, here R is the subfield of C.
Here note that R is not a vector space over C.
Example-: The set of all 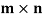 matrices with their elements as real numbers is a vector space over the field F of real numbers with respect to addition of matrices as addition of vectors and multiplication of a matrix by a scalar as scalar multiplication.
matrices with their elements as real numbers is a vector space over the field F of real numbers with respect to addition of matrices as addition of vectors and multiplication of a matrix by a scalar as scalar multiplication.
Sol. V is an abelian group with respect to addition of matrices in groups.
The null matrix of m by n is the additive identity of this group.
If 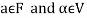 then
then  as
as  is also the matrix of m by n with elements of real numbers.
is also the matrix of m by n with elements of real numbers.
So that V is closed with respect to scalar multiplication.
We conclude that from matrices-
1. 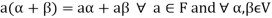
2. 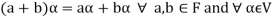
3. 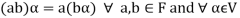
4.  Where 1 is the unity element of F.
Where 1 is the unity element of F.
Therefore we can say that V (F) is a vector space.
Example-2: The vector space of all polynomials over a field F.
Suppose F[x] represents the set of all polynomials in indeterminate x over a field F. The F[x] is vector space over F with respect to addition of two polynomials as addition of vectors and the product of a polynomial by a constant polynomial.
Example-3: The vector space of all real valued continuous (differentiable or integrable) functions defined in some interval [0,1]
Suppose f and g are two functions, and V denotes the set of all real valued continuous functions of x defined in the interval [0,1]
Then V is a vector space over the filed R with vector addition and multiplication as:
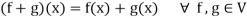
And
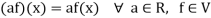
Here we will first prove that V is an abelian group with respect to addition composition as in rings.
V is closed with respect to scalar multiplication since af is also a real valued continuous function
We observe that-
1. If  and f,g
and f,g , then
, then
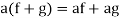
2. If  and
and  , then
, then
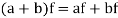
3. If 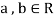 and
and  , then
, then
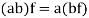
4. If 1 is the unity element of R and 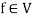 , then
, then
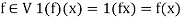
So that V is a vector space over R.
Some important theorems on vector spaces-
Theorem-1: Suppose V(F) is a vector space and 0 be the zero vector of V. Then-
1. 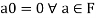
2. 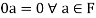
3. 
4. 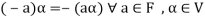
5. 
6. 
Proof-
1. We have
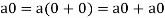
We can write 
So that,
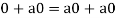
Now V is an abelian group with respect to addition.
So that by right cancellation law, we get-
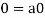
2. We have
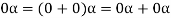
We can write 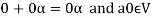
So that,
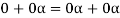
Now V is an abelian group with respect to addition.
So that by right cancellation law, we get-
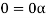
3. We have 
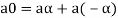
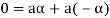
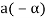 is the additive inverse of
is the additive inverse of 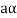
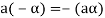
4. We have 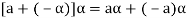
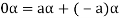

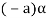 is the additive inverse of
is the additive inverse of 
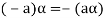
5. We have-
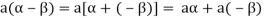
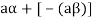
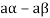
6. Suppose  the inverse of ‘a’ exists because ‘a’ is non-zero element of the field.
the inverse of ‘a’ exists because ‘a’ is non-zero element of the field.
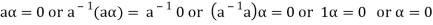
Again let-
 , then to prove
, then to prove  let
let 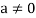 then inverse of ‘a’ exists
then inverse of ‘a’ exists
We get a contradiction that  must be a zero vector. Therefore ‘a’ must be equal to zero.
must be a zero vector. Therefore ‘a’ must be equal to zero.
So that
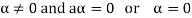
Vector sub-space-
Definition
Suppose V is a vector space over the field F and 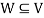 . Then W is called subspace of V if W itself a vector space over F with respect to the operations of vector addition and scalar multiplication in V.
. Then W is called subspace of V if W itself a vector space over F with respect to the operations of vector addition and scalar multiplication in V.
Theorem-1-The necessary and sufficient conditions for a non-empty sub-set W of a vector space V(F) to be a subspace of V are-
1. 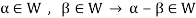
2. 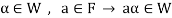
Proof:
Necessary conditions-
W is an abelian group with respect to vector addition If W is a subspace of V.
So that 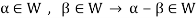
Here W must be closed under a scalar multiplication so that the second condition is also necessary.
Sufficient conditions-
Let W is a non-empty subset of V satisfying the two given conditions.
From first condition-
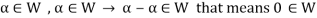
So that we can say that zero vector of V belongs to W. It is a zero vector of W as well.
Now 
So that the additive inverse of each element of W is also in W.
So that-
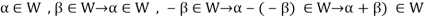
Thus W is closed with respect to vector addition.
Theorem-2:
The intersection of any two subspaces 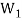 and
and 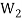 of a vector space V(F) is also a subspace of V(F).
of a vector space V(F) is also a subspace of V(F).
Proof: As we know that 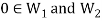 therefore
therefore 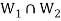 is not empty.
is not empty.
Suppose  and
and 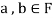
Now, 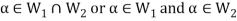
And 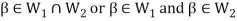
Since  is a subspace, therefore-
is a subspace, therefore-
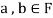 and
and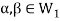 then
then 
Similarly, 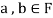
 then
then
Now 
Thus,
 And
And 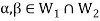
Then 
So that 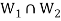 is a subspace of V(F).
is a subspace of V(F).
Example-1: If 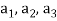 are fixed elements of a field F, then set of W of all ordered triads (
are fixed elements of a field F, then set of W of all ordered triads (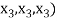 of elements of F,
of elements of F,
Such that-
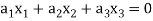
Is a subspace of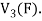
Sol. Suppose  are any two elements of W.
are any two elements of W.
Such that 
And these are the elements of F, such that-
 …………………….. (1)
…………………….. (1)
 ……………………. (2)
……………………. (2)
If a and b are two elements of F, we have
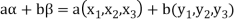
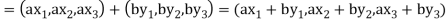
Now
= 
= 
= 
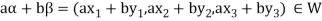
So that W is subspace of 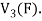
Example-2: Let R be a field of real numbers. Now check whether which one of the following are subspaces of 
1. { 
2. { 
3. { 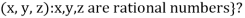
Solution- 1. Suppose W = { 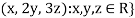
Let 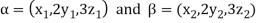 be any two elements of W.
be any two elements of W.
If a and b are two real numbers, then-
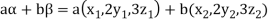
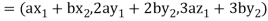
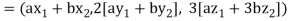
Since 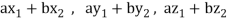 are real numbers.
are real numbers.
So that 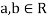 and
and  or
or 
So that W is a subspace of 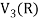
2. Let W = { 
Let  be any two elements of W.
be any two elements of W.
If a and b are two real numbers, then-
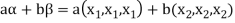
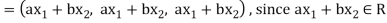
So that W is a subspace of 
3. Let W ={
Now 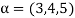 is an element of W. Also
is an element of W. Also  is an element of R.
is an element of R.
But  which do not belong to W.
which do not belong to W.
Since 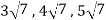 are not rational numbers.
are not rational numbers.
So that W is not closed under scalar multiplication.
W is not a subspace of 
Key takeaways:
- Each member of V(F) will be referred as a vector and each member of F as a scalar
- All the properties of an abelian group will hold in V if (V,+) is an abelian group.
- The Greek letters
 are used to denote elements of vectors and Latin letters a , b , c etc. for scalars that means the elements of field F.
are used to denote elements of vectors and Latin letters a , b , c etc. for scalars that means the elements of field F. - Suppose C is the field of complex numbers and R is the field of real numbers, then C is a vector space over R, here R is the subfield of C.
- Here note that R is not a vector space over C.
- Suppose V is a vector space over the field F and
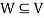 . Then W is called subspace of V if W itself a vector space over F with respect to the operations of vector addition and scalar multiplication in V.
. Then W is called subspace of V if W itself a vector space over F with respect to the operations of vector addition and scalar multiplication in V.
Algebra of subs paces, quotient spaces
Another definition of subspace:
A subset W of a vector space V over a field F is called a subspace of V if W is a vector space over F with the operations of addition and scalar multiplication defined on V.
In any vector space V, note that V and {0 } are subspaces. The latter is called the zero subspace of V.
Note- A subset W of a vector space V is a subspace of V if and only if the following four properties hold.
1. x + y ∈ W whenever x ∈ W and y ∈ W. (W is closed under addition.)
2. c x ∈ W whenever c ∈ F and x ∈ W. (W is closed under scalar multiplication.)
3. W has a zero vector.
4. Each vector in W has an additive inverse in W.
Note- Let V be a vector space and W a subset of V. Then W is a subspace of V if and only if the following three conditions hold for the operations defined in V.
(a) 0 ∈ W.
(b) x + y ∈ W whenever x ∈ W and y ∈ W.
(c) cx ∈ W whenever c ∈ F and x ∈ W.
The transpose 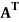 of an m × n matrix A is the n × m matrix obtained from A by interchanging the rows with the columns
of an m × n matrix A is the n × m matrix obtained from A by interchanging the rows with the columns
Suppose,
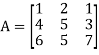
Then
Transpose of this matrix,
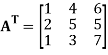
A symmetric matrix is a matrix A such that 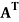 = A.
= A.
A skew- symmetric matrix is a matrix A such that  = A.
= A.
Note- the set of symmetric matrices is closed under addition and scalar multiplication.
Example: An n×n matrix M is called a diagonal matrix if  = 0 whenever i
= 0 whenever i  j, that is, if all its nondiagonal entries are zero. Clearly the zero matrix is a diagonal matrix because all of its entries are 0. Moreover, if A and B are diagonal n × n matrices, then whenever i
j, that is, if all its nondiagonal entries are zero. Clearly the zero matrix is a diagonal matrix because all of its entries are 0. Moreover, if A and B are diagonal n × n matrices, then whenever i 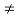 j,
j,
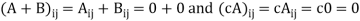
For any scalar c. Hence A + B and cA are diagonal matrices for any scalar c. Therefore the set of diagonal matrices is a subspace of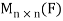 .
.
Theorem: Any intersection of subspaces of a vector space V is a subspace of V.
Proof:
Let C be a collection of subspaces of V, and let W denote the intersection of the subspaces in C. Since every subspace contains the zero vector, 0 ∈ W. Let a ∈ F and x, y ∈ W. Then x and y are contained in each subspace in C. Because each subspace in C is closed under addition and scalar multiplication, it follows that x+y and ax are contained in each subspace in C. Hence x+y and ax are also contained in W, so that W is a subspace of V
Note- The union of subspaces must contain the zero vector and be closed under scalar multiplication, but in general the union of subspaces of V need not be closed under addition.
Definition of sum and direct sum:
Sum- If S1 and S2 are nonempty subsets of a vector space V, then the sum of S1 and S2, denoted S1+S2, is the set {x + y : x ∈ S1 and y ∈ S2}.
Direct sum- A vector space V is called the direct sum of W1 and W2 if W1 and W2 are subspaces of V such that W1 ∩W2 = {0} and W1 +W2 = V. We denote that V is the direct sum of W1 and W2 by writing V = W1 ⊕ W2.
Key takeaways:
1. A subset W of a vector space V is a subspace of V if and only if the following four properties hold.
1. x + y ∈ W whenever x ∈ W and y ∈ W. (W is closed under addition.)
2. c x ∈ W whenever c ∈ F and x ∈ W. (W is closed under scalar multiplication.)
3. W has a zero vector.
4. Each vector in W has an additive inverse in W.
2. The transpose  of an m × n matrix A is the n × m matrix obtained from A by interchanging the rows with the columns
of an m × n matrix A is the n × m matrix obtained from A by interchanging the rows with the columns
3. A symmetric matrix is a matrix A such that 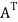 = A.
= A.
4. A skew- symmetric matrix is a matrix A such that  = A.
= A.
5. The set of symmetric matrices is closed under addition and scalar multiplication.
Definition-
Suppose U(F) and V(F) are two vector spaces, then a mapping 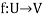 is called a linear transformation of U into V, if:
is called a linear transformation of U into V, if:
1. 
2. 
It is also called homomorphism.
Kernel(null space) of a linear transformation-
Let f be a linear transformation of a vector space U(F) into a vector space V(F).
The kernel W of f is defined as-

The kernel W of f is a subset of U consisting of those elements of U which are mapped under f onto the zero vector V.
Since f(0) = 0, therefore atleast 0 belong to W. So that W is not empty.
Another definition of null space and range:
Let V and W be vector spaces, and let T: V → W be linear. We define the null space (or kernel) N(T) of T to be the set of all vectors x in V such that T(x) = 0; that is, N(T) = {x ∈ V: T(x) = 0 }.
We define the range (or image) R(T) of T to be the subset of W consisting of all images (under T) of vectors in V; that is, R(T) = {T(x) : x ∈ V}.
Example: The mapping  defined by-
defined by-
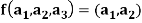
Is a linear transformation  .
.
What is the kernel of this linear transformation.
Sol. Let  be any two elements of
be any two elements of 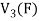
Let a, b be any two elements of F.
We have
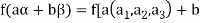 (
(
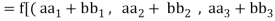
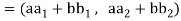
 =
= 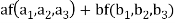
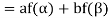
So that f is a linear transformation.
To show that f is onto  . Let
. Let 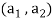 be any elements
be any elements  .
.
Then 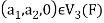 and we have
and we have 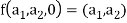
So that f is onto 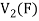
Therefore f is homomorphism of 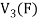 onto
onto 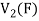 .
.
If W is the kernel of this homomorphism then 
We have
∀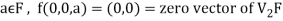
Also if  then
then 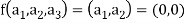
Implies 
Therefore 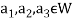
Hence W is the kernel of f.
Theorem: Let V and W be vector spaces and T: V → W be linear. Then N(T) and R(T) are subspaces of V and W, respectively.
Proof:
Here we will use the symbols 0 V and 0W to denote the zero vectors of V and W, respectively.
Since T(0 V) = 0W, we have that 0 V ∈ N(T). Let x, y ∈ N(T) and c ∈ F.
Then T(x + y) = T(x)+T(y) = 0W+0W = 0W, and T(c x) = c T(x) = c0W = 0W. Hence x + y ∈ N(T) and c x ∈ N(T), so that N(T) is a subspace of V. Because T(0 V) = 0W, we have that 0W ∈ R(T). Now let x, y ∈ R(T) and c ∈ F. Then there exist v and w in V such that T(v) = x and T(w) = y. So T(v + w) = T(v)+T(w) = x + y, and T(c v) = c T(v) = c x. Thus x+ y ∈ R(T) and c x ∈ R(T), so R(T) is a subspace of W.
Key takeaways:
1. Suppose U(F) and V(F) are two vector spaces, then a mapping 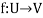 is called a linear transformation of U into V, if:
is called a linear transformation of U into V, if:
1. 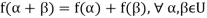
2. 
2. Let V and W be vector spaces, and let T: V → W be linear. We define the null space (or kernel) N(T) of T to be the set of all vectors x in V such that T(x) = 0; that is, N(T) = {x ∈ V: T(x) = 0 }.
Rank and nullity of a linear transformation
Definition:
Let V and W be vector spaces, and let T: V → W be linear. If N(T) and R(T) are finite-dimensional, then we define the nullity of T, denoted nullity(T), and the rank of T, denoted rank(T), to be the dimensions of N(T) and R(T), respectively.
Theorem: Let A is a matrix of order m by n, then-
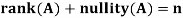
Proof:
If rank (A) = n, then the only solution to Ax = 0 is the trivial solution x = 0by using invertible matrix.
So that in this case null-space (A) = {0}, so nullity (A) = 0.
Now suppose rank (A) = r < n, in this case there are n – r > 0 free variable in the solution to Ax = 0.
Let  represent these free variables and let
represent these free variables and let  denote the solution obtained by sequentially setting each free variable to 1 and the remaining free variables to zero.
denote the solution obtained by sequentially setting each free variable to 1 and the remaining free variables to zero.
Here  is linearly independent.
is linearly independent.
Moreover every solution is to Ax = 0 is a linear combination of 
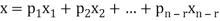
Which shows that  spans null-space (A).
spans null-space (A).
Thus  is a basis for null-space(A) and nullity (A) = n – r.
is a basis for null-space(A) and nullity (A) = n – r.
Theorem: Let V and W be vector spaces, and let T: V → W be linear. Then T is one-to-one if and only if N(T) = {0 }.
Proof:
Suppose that T is one-to-one and x ∈ N(T). Then T(x) = 0 = T(0 ). Since T is one-to-one, we have x = 0 . Hence N(T) = {0 }.
Now assume that N(T) = {0 }, and suppose that T(x) = T(y). Then 0 = T(x) − T(y) = T(x − y).
Therefore x − y ∈ N(T) = {0 }. So x − y = 0, or x = y. This means that T is one-to-one.
Note- Let V and W be vector spaces of equal (finite) dimension, and let T: V → W be linear. Then the following are equivalent.
(a) T is one-to-one.
(b) T is onto.
(c) rank(T) = dim(V).
Key takeaways:
- Let A is a matrix of order m by n, then-
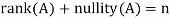
Suppose V(F) be a vector space. If 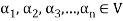 , then any vector-
, then any vector-
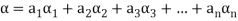
Where 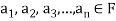
Is called a linear combination of the vectors 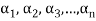
Linear Span-
Definition- Let V(F) be a vector space and S be a non-empty subset of V. Then the linear span of S is the set of all linear combinations of finite sets of elements of S and it is denoted by L(S). Thus we have-
L(S) = 
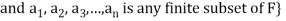
Theorem:
The linear span L(S) of any subset S of a vector space V(F) is s subspace of V generated by S.
Proof: Suppose  be any two elements of L(S).
be any two elements of L(S).
Then
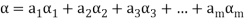
And 
Where a and b are the elements of F and 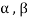 are the elements of S.
are the elements of S.
If a,b be any two elements of F, then-
 (
( (
(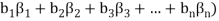
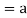 (
(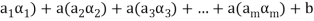 (
(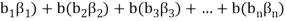
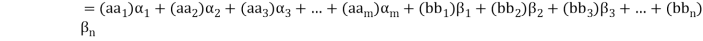
Thus 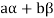 has been expressed as a linear combination of a finite set
has been expressed as a linear combination of a finite set 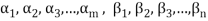 of the elements of S.
of the elements of S.
Consequently 
Thus, 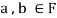 and
and 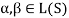 so that
so that 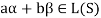
Hence L(S) is a subspace of V(F).
Linear dependence-
Let V(F) be a vector space.
A finite set  of vector of V is said to be linearly dependent if there exists scalars
of vector of V is said to be linearly dependent if there exists scalars  (not all of them as some of them might be zero)
(not all of them as some of them might be zero)
Such that-
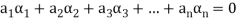
Linear independence-
Let V(F) be a vector space.
A finite set 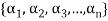 of vector of V is said to be linearly independent if every relation if the form-
of vector of V is said to be linearly independent if every relation if the form-
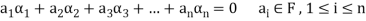
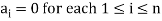
Theorem:
The set of non-zero vectors 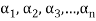 of V(F) is linearly dependent if some
of V(F) is linearly dependent if some 
Is a linear combination of the preceding ones.
Proof: if some 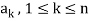
Is a linear combination of the preceding ones,  then ∃ scalars
then ∃ scalars  such that-
such that-
 …… (1)
…… (1)
The set {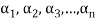 } is linearly dependent because the linear combination (1) the scalar coefficient
} is linearly dependent because the linear combination (1) the scalar coefficient 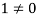
Hence the set {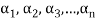 } of which {
} of which { } is a subset must be linearly dependent.
} is a subset must be linearly dependent.
Example-1: If the set S = 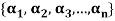 of vector V(F) is linearly independent, then none of the vectors
of vector V(F) is linearly independent, then none of the vectors 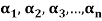 can be zero vector.
can be zero vector.
Sol. Let 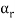 be equal to zero vector where
be equal to zero vector where 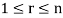
Then 
For any 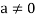 in F.
in F.
Here 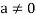 therefore from this relation we can say that S is linearly dependent. This is the contradiction because it is given that S is linearly independent.
therefore from this relation we can say that S is linearly dependent. This is the contradiction because it is given that S is linearly independent.
Hence none of the vectors can be zero.
We can conclude that a set of vectors which contains the zero vector is necessarily linear dependent.
Example-2: Show that S = {(1 , 2 , 4) , (1 , 0 , 0) , (0 , 1 , 0) , (0 , 0 , 1)} is linearly dependent subset of the vector space  . Where R is the field of real numbers.
. Where R is the field of real numbers.
Sol. Here we have-
1 (1 , 2 , 4) + (-1) (1 , 0 , 0) + (-2) (0 ,1, 0) + (-4) (0, 0, 1)
= (1, 2 , 4) + (-1 , 0 , 0) + (0 ,-2, 0) + (0, 0, -4)
= (0, 0, 0)
That means it is a zero vector.
In this relation the scalar coefficients 1 , -1 , -2, -4 are all not zero.
So that we can conclude that S is linearly dependent.
Example-3: If 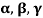 are linearly independent vectors of V(F).where F is the field of complex numbers, then so also are
are linearly independent vectors of V(F).where F is the field of complex numbers, then so also are 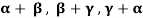 .
.
Sol. Suppose a, b, c are scalars such that-
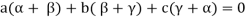
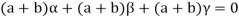 …………….. (1)
…………….. (1)
But 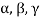 are linearly independent vectors of V(F), so that equations (1) implies that-
are linearly independent vectors of V(F), so that equations (1) implies that-
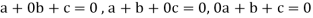
The coefficient matrix A of these equations will be-
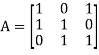
Here we get rank of A = 3, so that a = 0, b = 0, c = 0 is the only solution of the given equations, so that 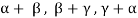 are also linearly independent.
are also linearly independent.
Key takeaways:
- Suppose V(F) be a vector space. If
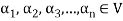 , then any vector-
, then any vector-
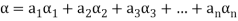
Where 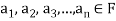
Is called a linear combination of the vectors 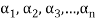
2. Let V(F) be a vector space and S be a non-empty subset of V. Then the linear span of S is the set of all linear combinations of finite sets of elements of S and it is denoted by L(S).
3. A finite set 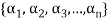 of vector of V is said to be linearly independent if every relation if the form-
of vector of V is said to be linearly independent if every relation if the form-
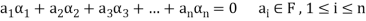
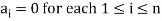
Definition:
A subset S of a vector space V(F) is said to be a basis of V(F), if-
1. S consists of linearly independent vectors
2. Each vector in V is a linear combination of a finite number of elements of S.
Finite dimensional vector spaces
The vector space V(F) is said to be finite dimensional if there exists a finite subset S of V such that V = L(S).
Dimension theorem for vector spaces-
Statement- If V(F) is a finite dimensional vector spaces, then any two bases of V have the same number of elements.
Proof: Let V(F) is a finite dimensional vector space. Then V possesses a basis.
Let 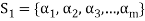 and
and  be two bases of V.
be two bases of V.
We shall prove that m = n
Since V = L( and
and 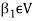 therefore
therefore 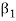 can be expressed as a linear combination of
can be expressed as a linear combination of 
Consequently the set  which also generates V(F) is linearly dependent. So that there exists a member
which also generates V(F) is linearly dependent. So that there exists a member  of this set. Such that
of this set. Such that 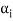 is the linear combination of the preceding vectors
is the linear combination of the preceding vectors 
If we omit the vector 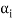 from
from 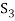 then V is also generated by the remaining set.
then V is also generated by the remaining set.
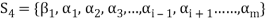
Since V = L(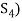 and
and 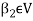 therefore
therefore  can be expressed as a linear combination of the vectors belonging to
can be expressed as a linear combination of the vectors belonging to 
Consequently the set-
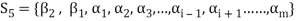
Is linearly dependent.
Therefore there exists a member  of this set such that
of this set such that  is a linear combination of the preceding vectors. Obviously
is a linear combination of the preceding vectors. Obviously 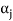 will be different from
will be different from 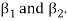
Since { } is a linearly independent set
} is a linearly independent set
If we exclude the vector  from
from  then the remaining set will generate V(F).
then the remaining set will generate V(F).
We may continue to proceed in this manner. Here each step consists in the exclusion of an 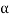 and the inclusion of
and the inclusion of  in the set
in the set 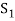
Obviously the set 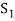 of all
of all 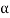 can not be exhausted before the set
can not be exhausted before the set 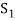 and
and 
Otherwise V(F) will be a linear span of a proper subset of  thus
thus 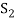 become linearly dependent. Therefore we must have-
become linearly dependent. Therefore we must have-
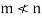
Now interchanging the roles of 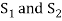 we shall get that
we shall get that 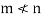
Hence,
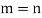
Extension theorem-
Every linearly independent subset of a finitely generated vector space V(F) forms of a part of a basis of V.
Proof: Suppose  be a linearly independent subset of a finite dimensional vector space V(F) if dim V = n, then V has a finite basis, say
be a linearly independent subset of a finite dimensional vector space V(F) if dim V = n, then V has a finite basis, say 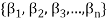
Let us consider a set-
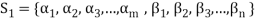 …………. (1)
…………. (1)
Obviously L( , since there
, since there 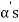 can be expressed as linear combination of
can be expressed as linear combination of 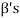 therefore the set
therefore the set  is linearly dependent.
is linearly dependent.
So that there is some vector of  which is linear combination of its preceding vectors. This vector can not be any of the
which is linear combination of its preceding vectors. This vector can not be any of the 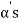 since the
since the 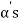 are linearly independent.
are linearly independent.
Therefore this vector must be some  say
say 
Now omit the vector  from (1) and consider the set-
from (1) and consider the set-
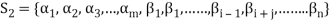
Obviously L(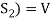 . If
. If  is linearly independent, then
is linearly independent, then  will be a basis of V and it is the required extended set which is a basis of V.
will be a basis of V and it is the required extended set which is a basis of V.
If 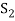 is not linearly independent, then repeating the above process a finite number of times. We shall get a linearly independent set containing
is not linearly independent, then repeating the above process a finite number of times. We shall get a linearly independent set containing  and spanning V. This set will be a basis of V contains the same number of elements, so that exactly n-m elements of the set of
and spanning V. This set will be a basis of V contains the same number of elements, so that exactly n-m elements of the set of 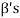 will be adjoined to S so as to form a basis of V.
will be adjoined to S so as to form a basis of V.
Example-1: Show that the vectors (1, 2, 1), (2, 1, 0) and (1, -1, 2) form a basis of 
Sol. We know that set {(1,0,0) , (0,1,0) , (0,0,1)} forms a basis of 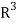
So that dim  .
.
Now if we show that the set S = {(1, 2, 1), (2, 1, 0) , (1, -1, 2)} is linearly independent, then this set will form a basis of 
We have,
 (1, 2, 1)+
(1, 2, 1)+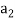 (2, 1, 0)+
(2, 1, 0)+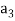 (1, -1, 2) = (0, 0, 0)
(1, -1, 2) = (0, 0, 0)
(
Which gives-
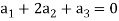
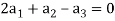
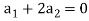
On solving these equations we get,
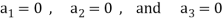
So we can say that the set S is linearly independent.
Therefore it forms a basis of 
Key takeaways:
- The vector space V(F) is said to be finite dimensional if there exists a finite subset S of V such that V = L(S).
- If V(F) is a finite dimensional vector spaces, then any two bases of V have the same number of elements.
- Every linearly independent subset of a finitely generated vector space V(F) forms of a part of a basis of V.
Let A be any m  n matrix over a field K. Recall that the rows of A may be viewed as vectors in
n matrix over a field K. Recall that the rows of A may be viewed as vectors in  and that the row space of A, written rowsp(A), is the subspace of
and that the row space of A, written rowsp(A), is the subspace of 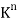 spanned by the rows of A. The following definition applies.
spanned by the rows of A. The following definition applies.
Def:
The rank of a matrix A, written rank(A), is equal to the maximum number of linearly independent rows of A or, equivalently, the dimension of the row space of A.
Recall, on the other hand, that the columns of an m  n matrix A may be viewed as vectors in
n matrix A may be viewed as vectors in  and that the column space of A, written colsp(A), is the subspace of
and that the column space of A, written colsp(A), is the subspace of 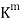 spanned by the columns of A.
spanned by the columns of A.
Although m may not be equal to n—that is, the rows and columns of A may belong to different vector spaces—we have the following fundamental result.
Theorem: The maximum number of linearly independent rows of any matrix A is equal to the maximum number of linearly independent columns of A. Thus, the dimension of the row space of A is equal to the dimension of the column space of A.
Basis-Finding Problems:
We will shows how an echelon form of any matrix A gives us the solution to certain problems about A itself. Specifically, let A and B be the following matrices, where the echelon matrix B (whose pivots are circled) is an echelon form of A:
A =  and B =
and B = 
We solve the following four problems about the matrix A, where C1; C2; . . . ; C6 denote its columns:
(a) Find a basis of the row space of A.
(b) Find each column Ck of A that is a linear combination of preceding columns of A.
(c) Find a basis of the column space of A.
(d) Find the rank of A.
(a) We are given that A and B are row equivalent, so they have the same row space. Moreover, B is in echelon form, so its nonzero rows are linearly independent and hence form a basis of the row space of B. Thus, they also form a basis of the row space of A. That is,
Basis of rowsp(A): (1, 2, 1, 3, 1, 2), (0, 1, 3, 1, 2, 1), (0, 0, 0, 1, 1, 2)
(b) Let 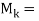 [
[ , the submatrix of A consisting of the first k columns of A. Then
, the submatrix of A consisting of the first k columns of A. Then  and
and
Mk are, respectively, the coefficient matrix and augmented matrix of the vector equation
x1C1 + x2C2 + . . . + xk – 1Ck – 1 = Ck
The system has a solution, or, equivalently, Ck is a linear combination of the preceding columns of A if and only if rank(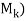 = rank(
= rank(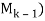 , where rank(
, where rank(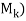 means the number of pivots in an echelon form of
means the number of pivots in an echelon form of 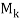 . Now the first k column of the echelon matrix B is also an echelon form of
. Now the first k column of the echelon matrix B is also an echelon form of  . Accordingly,
. Accordingly,
Rank (M2) = rank (M3) = 2 and rank(M4) = rank(M5) = rank(M6) = 3
Thus, C3, C5, C6 are each a linear combination of the preceding columns of A.
c) The fact that the remaining columns C1, C2, C4 are not linear combinations of their respective preceding columns also tells us that they are linearly independent. Thus, they form a basis of the column space of A. That is,
Basis of colsp(A): [1, 2, 3, 1, 2]T , [2, 5, 7, 5, 6]T, [3, 6, 11, 8, 11]T
Observe that C1, C2, C4 may also be characterized as those columns of A that contain the pivots in any echelon form of A.
(d) Here we see that three possible definitions of the rank of A yield the same value.
(i) There are three pivots in B, which is an echelon form of A.
(ii) The three pivots in B correspond to the nonzero rows of B, which form a basis of the row space of A.
(iii) The three pivots in B correspond to the columns of A, which form a basis of the column space of A.
Thus, rank(A) = 3.
References:
- E. Kreyszig, “Advanced Engineering Mathematics”, John Wiley & Sons, 2006.
- P. G. Hoel, S. C. Port And C. J. Stone, “Introduction To Probability Theory”, Universal Book Stall, 2003.
- S. Ross, “A First Course in Probability”, Pearson Education India, 2002.
- W. Feller, “An Introduction To Probability Theory and Its Applications”, Vol. 1, Wiley, 1968.
- N.P. Bali and M. Goyal, “A Text Book of Engineering Mathematics”, Laxmi Publications, 2010.
- B.S. Grewal, “Higher Engineering Mathematics”, Khanna Publishers, 2000.
Unit - 6
Vector space
Unit - 6
Vector space
Definition-
Let ‘F’ be any given field, then a given set V is said to be a vector space if-
1. There is a defined composition in ‘V’. This composition called addition of vectors which is denoted by ‘+’
2. There is a defined an external composition in ‘V’ over ‘F’. That will be denoted by scalar multiplication.
3. The two compositions satisfy the following conditions-
(a) 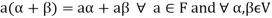
(b) 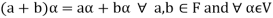
(c) 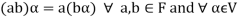
(d) If 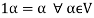 then 1 is the unity element of the field F.
then 1 is the unity element of the field F.
If V is a vector space over the field F, then we will denote vector space as V(F).
Note that each member of V(F) will be referred as a vector and each member of F as a scalar
Note- Here we have denoted the addition of the vectors by the symbol ‘+’. This symbol also be used for the addition of scalars.
If  then
then  represents addition in vectors(V).
represents addition in vectors(V).
If  then a+b represents the addition of the scalars or addition in the field F.
then a+b represents the addition of the scalars or addition in the field F.
Note- For V to be an abelian group with respect to addition vectors, the following conditions must be followed-
1. 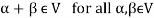
2. 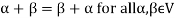
3.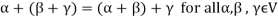
4. There exists an element  which is also called the zero vector. Such that-
which is also called the zero vector. Such that-
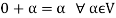
It is the additive identity in V.
5. There exists a  to every vector
to every vector 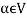 such that
such that
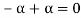
This is the additive inverse of V
Note- All the properties of an abelian group will hold in V if (V,+) is an abelian group.
These properties are-
1. 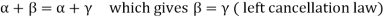
2. 
3. 
4. 
5. The additive identity 0 will be unique.
6. The additive inverse will be unique.
7. 
Note- The Greek letters  are used to denote elements of vectors and Latin letters a , b , c etc. for scalars that means the elements of field F.
are used to denote elements of vectors and Latin letters a , b , c etc. for scalars that means the elements of field F.
Note- Suppose C is the field of complex numbers and R is the field of real numbers, then C is a vector space over R, here R is the subfield of C.
Here note that R is not a vector space over C.
Example-: The set of all  matrices with their elements as real numbers is a vector space over the field F of real numbers with respect to addition of matrices as addition of vectors and multiplication of a matrix by a scalar as scalar multiplication.
matrices with their elements as real numbers is a vector space over the field F of real numbers with respect to addition of matrices as addition of vectors and multiplication of a matrix by a scalar as scalar multiplication.
Sol. V is an abelian group with respect to addition of matrices in groups.
The null matrix of m by n is the additive identity of this group.
If 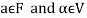 then
then 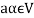 as
as 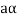 is also the matrix of m by n with elements of real numbers.
is also the matrix of m by n with elements of real numbers.
So that V is closed with respect to scalar multiplication.
We conclude that from matrices-
1. 
2. 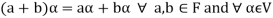
3. 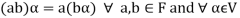
4. 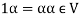 Where 1 is the unity element of F.
Where 1 is the unity element of F.
Therefore we can say that V (F) is a vector space.
Example-2: The vector space of all polynomials over a field F.
Suppose F[x] represents the set of all polynomials in indeterminate x over a field F. The F[x] is vector space over F with respect to addition of two polynomials as addition of vectors and the product of a polynomial by a constant polynomial.
Example-3: The vector space of all real valued continuous (differentiable or integrable) functions defined in some interval [0,1]
Suppose f and g are two functions, and V denotes the set of all real valued continuous functions of x defined in the interval [0,1]
Then V is a vector space over the filed R with vector addition and multiplication as:
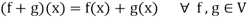
And
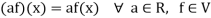
Here we will first prove that V is an abelian group with respect to addition composition as in rings.
V is closed with respect to scalar multiplication since af is also a real valued continuous function
We observe that-
1. If 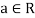 and f,g
and f,g , then
, then
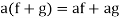
2. If 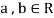 and
and  , then
, then
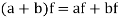
3. If 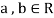 and
and 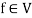 , then
, then
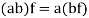
4. If 1 is the unity element of R and  , then
, then
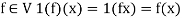
So that V is a vector space over R.
Some important theorems on vector spaces-
Theorem-1: Suppose V(F) is a vector space and 0 be the zero vector of V. Then-
1. 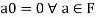
2. 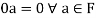
3. 
4. 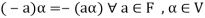
5. 
6. 
Proof-
1. We have
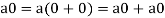
We can write 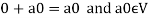
So that,
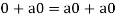
Now V is an abelian group with respect to addition.
So that by right cancellation law, we get-
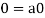
2. We have
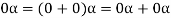
We can write 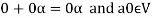
So that,
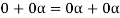
Now V is an abelian group with respect to addition.
So that by right cancellation law, we get-
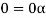
3. We have 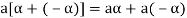
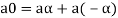
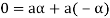
 is the additive inverse of
is the additive inverse of 
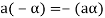
4. We have 
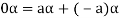

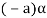 is the additive inverse of
is the additive inverse of 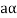
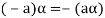
5. We have-
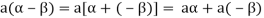
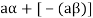
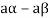
6. Suppose  the inverse of ‘a’ exists because ‘a’ is non-zero element of the field.
the inverse of ‘a’ exists because ‘a’ is non-zero element of the field.
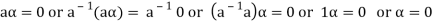
Again let-
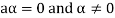 , then to prove
, then to prove 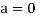 let
let  then inverse of ‘a’ exists
then inverse of ‘a’ exists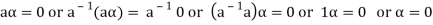
We get a contradiction that 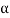 must be a zero vector. Therefore ‘a’ must be equal to zero.
must be a zero vector. Therefore ‘a’ must be equal to zero.
So that
Vector sub-space-
Definition
Suppose V is a vector space over the field F and 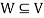 . Then W is called subspace of V if W itself a vector space over F with respect to the operations of vector addition and scalar multiplication in V.
. Then W is called subspace of V if W itself a vector space over F with respect to the operations of vector addition and scalar multiplication in V.
Theorem-1-The necessary and sufficient conditions for a non-empty sub-set W of a vector space V(F) to be a subspace of V are-
1. 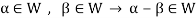
2. 
Proof:
Necessary conditions-
W is an abelian group with respect to vector addition If W is a subspace of V.
So that 
Here W must be closed under a scalar multiplication so that the second condition is also necessary.
Sufficient conditions-
Let W is a non-empty subset of V satisfying the two given conditions.
From first condition-
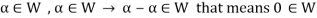
So that we can say that zero vector of V belongs to W. It is a zero vector of W as well.
Now 
So that the additive inverse of each element of W is also in W.
So that-
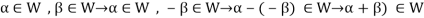
Thus W is closed with respect to vector addition.
Theorem-2:
The intersection of any two subspaces 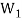 and
and  of a vector space V(F) is also a subspace of V(F).
of a vector space V(F) is also a subspace of V(F).
Proof: As we know that  therefore
therefore  is not empty.
is not empty.
Suppose  and
and 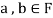
Now, 
And 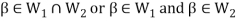
Since  is a subspace, therefore-
is a subspace, therefore-
 and
and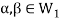 then
then 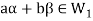
Similarly, 
 then
then
Now 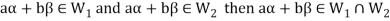
Thus,
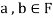 And
And 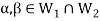
Then 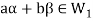
So that 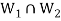 is a subspace of V(F).
is a subspace of V(F).
Example-1: If 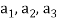 are fixed elements of a field F, then set of W of all ordered triads (
are fixed elements of a field F, then set of W of all ordered triads ( of elements of F,
of elements of F,
Such that-
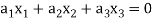
Is a subspace of
Sol. Suppose 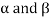 are any two elements of W.
are any two elements of W.
Such that 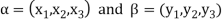
And these are the elements of F, such that-
 …………………….. (1)
…………………….. (1)
 ……………………. (2)
……………………. (2)
If a and b are two elements of F, we have
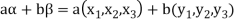
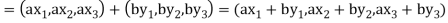
Now
= 
= 
= 
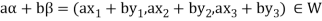
So that W is subspace of 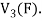
Example-2: Let R be a field of real numbers. Now check whether which one of the following are subspaces of 
1. { 
2. { 
3. { 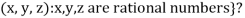
Solution- 1. Suppose W = { 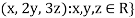
Let 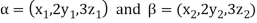 be any two elements of W.
be any two elements of W.
If a and b are two real numbers, then-
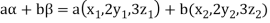
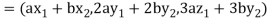
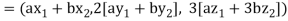
Since  are real numbers.
are real numbers.
So that 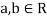 and
and  or
or 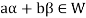
So that W is a subspace of 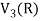
2. Let W = { 
Let 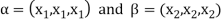 be any two elements of W.
be any two elements of W.
If a and b are two real numbers, then-
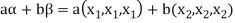
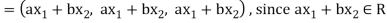
So that W is a subspace of 
3. Let W ={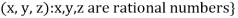
Now 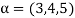 is an element of W. Also
is an element of W. Also 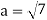 is an element of R.
is an element of R.
But 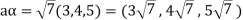 which do not belong to W.
which do not belong to W.
Since  are not rational numbers.
are not rational numbers.
So that W is not closed under scalar multiplication.
W is not a subspace of 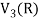
Key takeaways:
- Each member of V(F) will be referred as a vector and each member of F as a scalar
- All the properties of an abelian group will hold in V if (V,+) is an abelian group.
- The Greek letters
 are used to denote elements of vectors and Latin letters a , b , c etc. for scalars that means the elements of field F.
are used to denote elements of vectors and Latin letters a , b , c etc. for scalars that means the elements of field F. - Suppose C is the field of complex numbers and R is the field of real numbers, then C is a vector space over R, here R is the subfield of C.
- Here note that R is not a vector space over C.
- Suppose V is a vector space over the field F and
 . Then W is called subspace of V if W itself a vector space over F with respect to the operations of vector addition and scalar multiplication in V.
. Then W is called subspace of V if W itself a vector space over F with respect to the operations of vector addition and scalar multiplication in V.
Algebra of subs paces, quotient spaces
Another definition of subspace:
A subset W of a vector space V over a field F is called a subspace of V if W is a vector space over F with the operations of addition and scalar multiplication defined on V.
In any vector space V, note that V and {0 } are subspaces. The latter is called the zero subspace of V.
Note- A subset W of a vector space V is a subspace of V if and only if the following four properties hold.
1. x + y ∈ W whenever x ∈ W and y ∈ W. (W is closed under addition.)
2. c x ∈ W whenever c ∈ F and x ∈ W. (W is closed under scalar multiplication.)
3. W has a zero vector.
4. Each vector in W has an additive inverse in W.
Note- Let V be a vector space and W a subset of V. Then W is a subspace of V if and only if the following three conditions hold for the operations defined in V.
(a) 0 ∈ W.
(b) x + y ∈ W whenever x ∈ W and y ∈ W.
(c) cx ∈ W whenever c ∈ F and x ∈ W.
The transpose  of an m × n matrix A is the n × m matrix obtained from A by interchanging the rows with the columns
of an m × n matrix A is the n × m matrix obtained from A by interchanging the rows with the columns
Suppose,
Then
Transpose of this matrix,
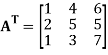
A symmetric matrix is a matrix A such that  = A.
= A.
A skew- symmetric matrix is a matrix A such that 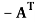 = A.
= A.
Note- the set of symmetric matrices is closed under addition and scalar multiplication.
Example: An n×n matrix M is called a diagonal matrix if  = 0 whenever i
= 0 whenever i  j, that is, if all its nondiagonal entries are zero. Clearly the zero matrix is a diagonal matrix because all of its entries are 0. Moreover, if A and B are diagonal n × n matrices, then whenever i
j, that is, if all its nondiagonal entries are zero. Clearly the zero matrix is a diagonal matrix because all of its entries are 0. Moreover, if A and B are diagonal n × n matrices, then whenever i  j,
j,
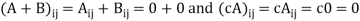
For any scalar c. Hence A + B and cA are diagonal matrices for any scalar c. Therefore the set of diagonal matrices is a subspace of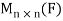 .
.
Theorem: Any intersection of subspaces of a vector space V is a subspace of V.
Proof:
Let C be a collection of subspaces of V, and let W denote the intersection of the subspaces in C. Since every subspace contains the zero vector, 0 ∈ W. Let a ∈ F and x, y ∈ W. Then x and y are contained in each subspace in C. Because each subspace in C is closed under addition and scalar multiplication, it follows that x+y and ax are contained in each subspace in C. Hence x+y and ax are also contained in W, so that W is a subspace of V
Note- The union of subspaces must contain the zero vector and be closed under scalar multiplication, but in general the union of subspaces of V need not be closed under addition.
Definition of sum and direct sum:
Sum- If S1 and S2 are nonempty subsets of a vector space V, then the sum of S1 and S2, denoted S1+S2, is the set {x + y : x ∈ S1 and y ∈ S2}.
Direct sum- A vector space V is called the direct sum of W1 and W2 if W1 and W2 are subspaces of V such that W1 ∩W2 = {0} and W1 +W2 = V. We denote that V is the direct sum of W1 and W2 by writing V = W1 ⊕ W2.
Key takeaways:
1. A subset W of a vector space V is a subspace of V if and only if the following four properties hold.
1. x + y ∈ W whenever x ∈ W and y ∈ W. (W is closed under addition.)
2. c x ∈ W whenever c ∈ F and x ∈ W. (W is closed under scalar multiplication.)
3. W has a zero vector.
4. Each vector in W has an additive inverse in W.
2. The transpose 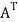 of an m × n matrix A is the n × m matrix obtained from A by interchanging the rows with the columns
of an m × n matrix A is the n × m matrix obtained from A by interchanging the rows with the columns
3. A symmetric matrix is a matrix A such that 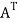 = A.
= A.
4. A skew- symmetric matrix is a matrix A such that  = A.
= A.
5. The set of symmetric matrices is closed under addition and scalar multiplication.
Unit - 6
Vector space
Unit - 6
Vector space
Unit - 6
Vector space
Definition-
Let ‘F’ be any given field, then a given set V is said to be a vector space if-
1. There is a defined composition in ‘V’. This composition called addition of vectors which is denoted by ‘+’
2. There is a defined an external composition in ‘V’ over ‘F’. That will be denoted by scalar multiplication.
3. The two compositions satisfy the following conditions-
(a) 
(b) 
(c) 
(d) If  then 1 is the unity element of the field F.
then 1 is the unity element of the field F.
If V is a vector space over the field F, then we will denote vector space as V(F).
Note that each member of V(F) will be referred as a vector and each member of F as a scalar
Note- Here we have denoted the addition of the vectors by the symbol ‘+’. This symbol also be used for the addition of scalars.
If 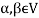 then
then  represents addition in vectors(V).
represents addition in vectors(V).
If 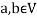 then a+b represents the addition of the scalars or addition in the field F.
then a+b represents the addition of the scalars or addition in the field F.
Note- For V to be an abelian group with respect to addition vectors, the following conditions must be followed-
1. 
2. 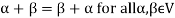
3.
4. There exists an element  which is also called the zero vector. Such that-
which is also called the zero vector. Such that-
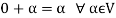
It is the additive identity in V.
5. There exists a  to every vector
to every vector 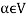 such that
such that
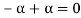
This is the additive inverse of V
Note- All the properties of an abelian group will hold in V if (V,+) is an abelian group.
These properties are-
1. 
2. 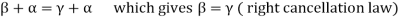
3. 
4. 
5. The additive identity 0 will be unique.
6. The additive inverse will be unique.
7. 
Note- The Greek letters 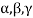 are used to denote elements of vectors and Latin letters a , b , c etc. for scalars that means the elements of field F.
are used to denote elements of vectors and Latin letters a , b , c etc. for scalars that means the elements of field F.
Note- Suppose C is the field of complex numbers and R is the field of real numbers, then C is a vector space over R, here R is the subfield of C.
Here note that R is not a vector space over C.
Example-: The set of all 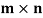 matrices with their elements as real numbers is a vector space over the field F of real numbers with respect to addition of matrices as addition of vectors and multiplication of a matrix by a scalar as scalar multiplication.
matrices with their elements as real numbers is a vector space over the field F of real numbers with respect to addition of matrices as addition of vectors and multiplication of a matrix by a scalar as scalar multiplication.
Sol. V is an abelian group with respect to addition of matrices in groups.
The null matrix of m by n is the additive identity of this group.
If 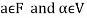 then
then 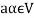 as
as  is also the matrix of m by n with elements of real numbers.
is also the matrix of m by n with elements of real numbers.
So that V is closed with respect to scalar multiplication.
We conclude that from matrices-
1. 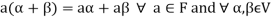
2. 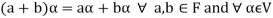
3. 
4. 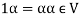 Where 1 is the unity element of F.
Where 1 is the unity element of F.
Therefore we can say that V (F) is a vector space.
Example-2: The vector space of all polynomials over a field F.
Suppose F[x] represents the set of all polynomials in indeterminate x over a field F. The F[x] is vector space over F with respect to addition of two polynomials as addition of vectors and the product of a polynomial by a constant polynomial.
Example-3: The vector space of all real valued continuous (differentiable or integrable) functions defined in some interval [0,1]
Suppose f and g are two functions, and V denotes the set of all real valued continuous functions of x defined in the interval [0,1]
Then V is a vector space over the filed R with vector addition and multiplication as:
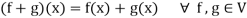
And
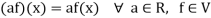
Here we will first prove that V is an abelian group with respect to addition composition as in rings.
V is closed with respect to scalar multiplication since af is also a real valued continuous function
We observe that-
1. If  and f,g
and f,g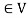 , then
, then
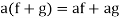
2. If 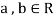 and
and  , then
, then
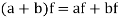
3. If  and
and 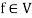 , then
, then
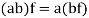
4. If 1 is the unity element of R and 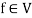 , then
, then
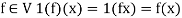
So that V is a vector space over R.
Some important theorems on vector spaces-
Theorem-1: Suppose V(F) is a vector space and 0 be the zero vector of V. Then-
1. 
2. 
3. 
4. 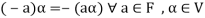
5. 
6. 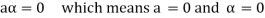
Proof-
1. We have
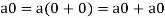
We can write 
So that,
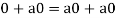
Now V is an abelian group with respect to addition.
So that by right cancellation law, we get-
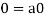
2. We have
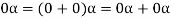
We can write 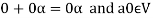
So that,
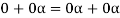
Now V is an abelian group with respect to addition.
So that by right cancellation law, we get-
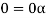
3. We have 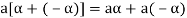
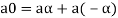
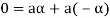
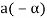 is the additive inverse of
is the additive inverse of 
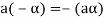
4. We have 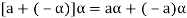
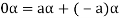

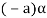 is the additive inverse of
is the additive inverse of 
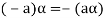
5. We have-
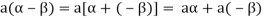
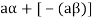
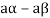
6. Suppose 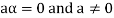 the inverse of ‘a’ exists because ‘a’ is non-zero element of the field.
the inverse of ‘a’ exists because ‘a’ is non-zero element of the field.
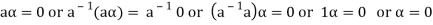
Again let-
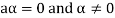 , then to prove
, then to prove 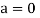 let
let  then inverse of ‘a’ exists
then inverse of ‘a’ exists
We get a contradiction that 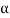 must be a zero vector. Therefore ‘a’ must be equal to zero.
must be a zero vector. Therefore ‘a’ must be equal to zero.
So that
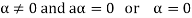
Vector sub-space-
Definition
Suppose V is a vector space over the field F and  . Then W is called subspace of V if W itself a vector space over F with respect to the operations of vector addition and scalar multiplication in V.
. Then W is called subspace of V if W itself a vector space over F with respect to the operations of vector addition and scalar multiplication in V.
Theorem-1-The necessary and sufficient conditions for a non-empty sub-set W of a vector space V(F) to be a subspace of V are-
1. 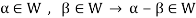
2. 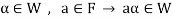
Proof:
Necessary conditions-
W is an abelian group with respect to vector addition If W is a subspace of V.
So that 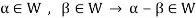
Here W must be closed under a scalar multiplication so that the second condition is also necessary.
Sufficient conditions-
Let W is a non-empty subset of V satisfying the two given conditions.
From first condition-
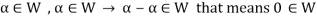
So that we can say that zero vector of V belongs to W. It is a zero vector of W as well.
Now 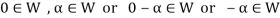
So that the additive inverse of each element of W is also in W.
So that-
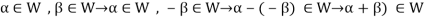
Thus W is closed with respect to vector addition.
Theorem-2:
The intersection of any two subspaces  and
and 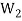 of a vector space V(F) is also a subspace of V(F).
of a vector space V(F) is also a subspace of V(F).
Proof: As we know that 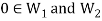 therefore
therefore  is not empty.
is not empty.
Suppose  and
and 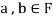
Now, 
And 
Since  is a subspace, therefore-
is a subspace, therefore-
 and
and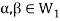 then
then 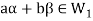
Similarly, 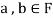
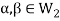 then
then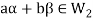
Now 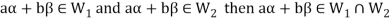
Thus,
 And
And 
Then 
So that 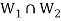 is a subspace of V(F).
is a subspace of V(F).
Example-1: If 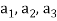 are fixed elements of a field F, then set of W of all ordered triads (
are fixed elements of a field F, then set of W of all ordered triads (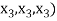 of elements of F,
of elements of F,
Such that-
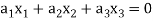
Is a subspace of
Sol. Suppose 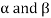 are any two elements of W.
are any two elements of W.
Such that 
And these are the elements of F, such that-
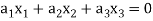 …………………….. (1)
…………………….. (1)
 ……………………. (2)
……………………. (2)
If a and b are two elements of F, we have
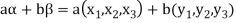
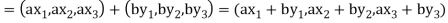
Now
= 
= 
= 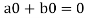
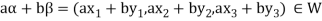
So that W is subspace of 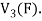
Example-2: Let R be a field of real numbers. Now check whether which one of the following are subspaces of 
1. { 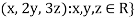
2. { 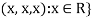
3. { 
Solution- 1. Suppose W = { 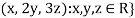
Let  be any two elements of W.
be any two elements of W.
If a and b are two real numbers, then-
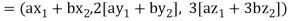
Since  are real numbers.
are real numbers.
So that 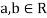 and
and  or
or 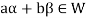
So that W is a subspace of 
2. Let W = { 
Let 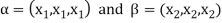 be any two elements of W.
be any two elements of W.
If a and b are two real numbers, then-
So that W is a subspace of 
3. Let W ={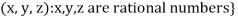
Now  is an element of W. Also
is an element of W. Also 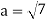 is an element of R.
is an element of R.
But 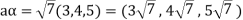 which do not belong to W.
which do not belong to W.
Since 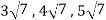 are not rational numbers.
are not rational numbers.
So that W is not closed under scalar multiplication.
W is not a subspace of 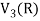
Key takeaways:
- Each member of V(F) will be referred as a vector and each member of F as a scalar
- All the properties of an abelian group will hold in V if (V,+) is an abelian group.
- The Greek letters
 are used to denote elements of vectors and Latin letters a , b , c etc. for scalars that means the elements of field F.
are used to denote elements of vectors and Latin letters a , b , c etc. for scalars that means the elements of field F. - Suppose C is the field of complex numbers and R is the field of real numbers, then C is a vector space over R, here R is the subfield of C.
- Here note that R is not a vector space over C.
- Suppose V is a vector space over the field F and
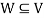 . Then W is called subspace of V if W itself a vector space over F with respect to the operations of vector addition and scalar multiplication in V.
. Then W is called subspace of V if W itself a vector space over F with respect to the operations of vector addition and scalar multiplication in V.
Algebra of subs paces, quotient spaces
Another definition of subspace:
A subset W of a vector space V over a field F is called a subspace of V if W is a vector space over F with the operations of addition and scalar multiplication defined on V.
In any vector space V, note that V and {0 } are subspaces. The latter is called the zero subspace of V.
Note- A subset W of a vector space V is a subspace of V if and only if the following four properties hold.
1. x + y ∈ W whenever x ∈ W and y ∈ W. (W is closed under addition.)
2. c x ∈ W whenever c ∈ F and x ∈ W. (W is closed under scalar multiplication.)
3. W has a zero vector.
4. Each vector in W has an additive inverse in W.
Note- Let V be a vector space and W a subset of V. Then W is a subspace of V if and only if the following three conditions hold for the operations defined in V.
(a) 0 ∈ W.
(b) x + y ∈ W whenever x ∈ W and y ∈ W.
(c) cx ∈ W whenever c ∈ F and x ∈ W.
The transpose 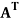 of an m × n matrix A is the n × m matrix obtained from A by interchanging the rows with the columns
of an m × n matrix A is the n × m matrix obtained from A by interchanging the rows with the columns
Suppose,
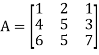
Then
Transpose of this matrix,
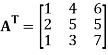
A symmetric matrix is a matrix A such that  = A.
= A.
A skew- symmetric matrix is a matrix A such that  = A.
= A.
Note- the set of symmetric matrices is closed under addition and scalar multiplication.
Example: An n×n matrix M is called a diagonal matrix if  = 0 whenever i
= 0 whenever i  j, that is, if all its nondiagonal entries are zero. Clearly the zero matrix is a diagonal matrix because all of its entries are 0. Moreover, if A and B are diagonal n × n matrices, then whenever i
j, that is, if all its nondiagonal entries are zero. Clearly the zero matrix is a diagonal matrix because all of its entries are 0. Moreover, if A and B are diagonal n × n matrices, then whenever i  j,
j,
For any scalar c. Hence A + B and cA are diagonal matrices for any scalar c. Therefore the set of diagonal matrices is a subspace of .
.
Theorem: Any intersection of subspaces of a vector space V is a subspace of V.
Proof:
Let C be a collection of subspaces of V, and let W denote the intersection of the subspaces in C. Since every subspace contains the zero vector, 0 ∈ W. Let a ∈ F and x, y ∈ W. Then x and y are contained in each subspace in C. Because each subspace in C is closed under addition and scalar multiplication, it follows that x+y and ax are contained in each subspace in C. Hence x+y and ax are also contained in W, so that W is a subspace of V
Note- The union of subspaces must contain the zero vector and be closed under scalar multiplication, but in general the union of subspaces of V need not be closed under addition.
Definition of sum and direct sum:
Sum- If S1 and S2 are nonempty subsets of a vector space V, then the sum of S1 and S2, denoted S1+S2, is the set {x + y : x ∈ S1 and y ∈ S2}.
Direct sum- A vector space V is called the direct sum of W1 and W2 if W1 and W2 are subspaces of V such that W1 ∩W2 = {0} and W1 +W2 = V. We denote that V is the direct sum of W1 and W2 by writing V = W1 ⊕ W2.
Key takeaways:
1. A subset W of a vector space V is a subspace of V if and only if the following four properties hold.
1. x + y ∈ W whenever x ∈ W and y ∈ W. (W is closed under addition.)
2. c x ∈ W whenever c ∈ F and x ∈ W. (W is closed under scalar multiplication.)
3. W has a zero vector.
4. Each vector in W has an additive inverse in W.
2. The transpose  of an m × n matrix A is the n × m matrix obtained from A by interchanging the rows with the columns
of an m × n matrix A is the n × m matrix obtained from A by interchanging the rows with the columns
3. A symmetric matrix is a matrix A such that  = A.
= A.
4. A skew- symmetric matrix is a matrix A such that  = A.
= A.
5. The set of symmetric matrices is closed under addition and scalar multiplication.
Definition-
Suppose U(F) and V(F) are two vector spaces, then a mapping  is called a linear transformation of U into V, if:
is called a linear transformation of U into V, if:
1. 
2. 
It is also called homomorphism.
Kernel(null space) of a linear transformation-
Let f be a linear transformation of a vector space U(F) into a vector space V(F).
The kernel W of f is defined as-

The kernel W of f is a subset of U consisting of those elements of U which are mapped under f onto the zero vector V.
Since f(0) = 0, therefore atleast 0 belong to W. So that W is not empty.
Another definition of null space and range:
Let V and W be vector spaces, and let T: V → W be linear. We define the null space (or kernel) N(T) of T to be the set of all vectors x in V such that T(x) = 0; that is, N(T) = {x ∈ V: T(x) = 0 }.
We define the range (or image) R(T) of T to be the subset of W consisting of all images (under T) of vectors in V; that is, R(T) = {T(x) : x ∈ V}.
Example: The mapping  defined by-
defined by-
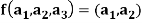
Is a linear transformation  .
.
What is the kernel of this linear transformation.
Sol. Let 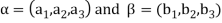 be any two elements of
be any two elements of 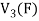
Let a, b be any two elements of F.
We have
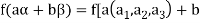 (
(
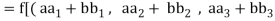
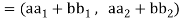
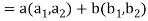 =
= 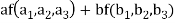
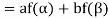
So that f is a linear transformation.
To show that f is onto  . Let
. Let 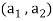 be any elements
be any elements 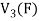 .
.
Then 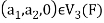 and we have
and we have 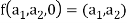
So that f is onto 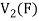
Therefore f is homomorphism of 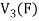 onto
onto  .
.
If W is the kernel of this homomorphism then 
We have
∀
Also if 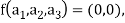 then
then 
Implies 
Therefore 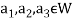
Hence W is the kernel of f.
Theorem: Let V and W be vector spaces and T: V → W be linear. Then N(T) and R(T) are subspaces of V and W, respectively.
Proof:
Here we will use the symbols 0 V and 0W to denote the zero vectors of V and W, respectively.
Since T(0 V) = 0W, we have that 0 V ∈ N(T). Let x, y ∈ N(T) and c ∈ F.
Then T(x + y) = T(x)+T(y) = 0W+0W = 0W, and T(c x) = c T(x) = c0W = 0W. Hence x + y ∈ N(T) and c x ∈ N(T), so that N(T) is a subspace of V. Because T(0 V) = 0W, we have that 0W ∈ R(T). Now let x, y ∈ R(T) and c ∈ F. Then there exist v and w in V such that T(v) = x and T(w) = y. So T(v + w) = T(v)+T(w) = x + y, and T(c v) = c T(v) = c x. Thus x+ y ∈ R(T) and c x ∈ R(T), so R(T) is a subspace of W.
Key takeaways:
1. Suppose U(F) and V(F) are two vector spaces, then a mapping  is called a linear transformation of U into V, if:
is called a linear transformation of U into V, if:
1. 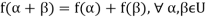
2. 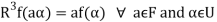
2. Let V and W be vector spaces, and let T: V → W be linear. We define the null space (or kernel) N(T) of T to be the set of all vectors x in V such that T(x) = 0; that is, N(T) = {x ∈ V: T(x) = 0 }.
Rank and nullity of a linear transformation
Definition:
Let V and W be vector spaces, and let T: V → W be linear. If N(T) and R(T) are finite-dimensional, then we define the nullity of T, denoted nullity(T), and the rank of T, denoted rank(T), to be the dimensions of N(T) and R(T), respectively.
Theorem: Let A is a matrix of order m by n, then-
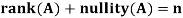
Proof:
If rank (A) = n, then the only solution to Ax = 0 is the trivial solution x = 0by using invertible matrix.
So that in this case null-space (A) = {0}, so nullity (A) = 0.
Now suppose rank (A) = r < n, in this case there are n – r > 0 free variable in the solution to Ax = 0.
Let 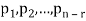 represent these free variables and let
represent these free variables and let 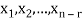 denote the solution obtained by sequentially setting each free variable to 1 and the remaining free variables to zero.
denote the solution obtained by sequentially setting each free variable to 1 and the remaining free variables to zero.
Here 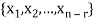 is linearly independent.
is linearly independent.
Moreover every solution is to Ax = 0 is a linear combination of 
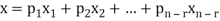
Which shows that 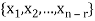 spans null-space (A).
spans null-space (A).
Thus 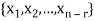 is a basis for null-space(A) and nullity (A) = n – r.
is a basis for null-space(A) and nullity (A) = n – r.
Theorem: Let V and W be vector spaces, and let T: V → W be linear. Then T is one-to-one if and only if N(T) = {0 }.
Proof:
Suppose that T is one-to-one and x ∈ N(T). Then T(x) = 0 = T(0 ). Since T is one-to-one, we have x = 0 . Hence N(T) = {0 }.
Now assume that N(T) = {0 }, and suppose that T(x) = T(y). Then 0 = T(x) − T(y) = T(x − y).
Therefore x − y ∈ N(T) = {0 }. So x − y = 0, or x = y. This means that T is one-to-one.
Note- Let V and W be vector spaces of equal (finite) dimension, and let T: V → W be linear. Then the following are equivalent.
(a) T is one-to-one.
(b) T is onto.
(c) rank(T) = dim(V).
Key takeaways:
- Let A is a matrix of order m by n, then-
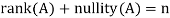
Suppose V(F) be a vector space. If 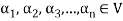 , then any vector-
, then any vector-
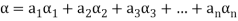
Where 
Is called a linear combination of the vectors 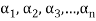
Linear Span-
Definition- Let V(F) be a vector space and S be a non-empty subset of V. Then the linear span of S is the set of all linear combinations of finite sets of elements of S and it is denoted by L(S). Thus we have-
L(S) = 
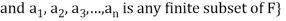
Theorem:
The linear span L(S) of any subset S of a vector space V(F) is s subspace of V generated by S.
Proof: Suppose  be any two elements of L(S).
be any two elements of L(S).
Then
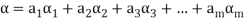
And 
Where a and b are the elements of F and  are the elements of S.
are the elements of S.
If a,b be any two elements of F, then-
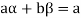 (
(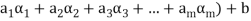 (
(
 (
(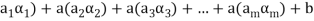 (
(
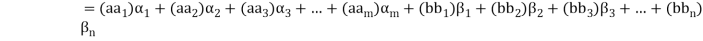
Thus 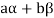 has been expressed as a linear combination of a finite set
has been expressed as a linear combination of a finite set  of the elements of S.
of the elements of S.
Consequently 
Thus,  and
and 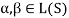 so that
so that 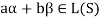
Hence L(S) is a subspace of V(F).
Linear dependence-
Let V(F) be a vector space.
A finite set  of vector of V is said to be linearly dependent if there exists scalars
of vector of V is said to be linearly dependent if there exists scalars 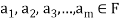 (not all of them as some of them might be zero)
(not all of them as some of them might be zero)
Such that-
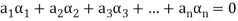
Linear independence-
Let V(F) be a vector space.
A finite set 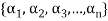 of vector of V is said to be linearly independent if every relation if the form-
of vector of V is said to be linearly independent if every relation if the form-
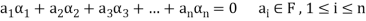
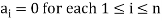
Theorem:
The set of non-zero vectors  of V(F) is linearly dependent if some
of V(F) is linearly dependent if some 
Is a linear combination of the preceding ones.
Proof: if some 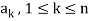
Is a linear combination of the preceding ones,  then ∃ scalars
then ∃ scalars  such that-
such that-
 …… (1)
…… (1)
The set { } is linearly dependent because the linear combination (1) the scalar coefficient
} is linearly dependent because the linear combination (1) the scalar coefficient 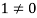
Hence the set { } of which {
} of which { } is a subset must be linearly dependent.
} is a subset must be linearly dependent.
Example-1: If the set S = 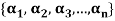 of vector V(F) is linearly independent, then none of the vectors
of vector V(F) is linearly independent, then none of the vectors  can be zero vector.
can be zero vector.
Sol. Let 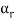 be equal to zero vector where
be equal to zero vector where 
Then 
For any 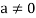 in F.
in F.
Here 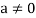 therefore from this relation we can say that S is linearly dependent. This is the contradiction because it is given that S is linearly independent.
therefore from this relation we can say that S is linearly dependent. This is the contradiction because it is given that S is linearly independent.
Hence none of the vectors can be zero.
We can conclude that a set of vectors which contains the zero vector is necessarily linear dependent.
Example-2: Show that S = {(1 , 2 , 4) , (1 , 0 , 0) , (0 , 1 , 0) , (0 , 0 , 1)} is linearly dependent subset of the vector space 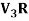 . Where R is the field of real numbers.
. Where R is the field of real numbers.
Sol. Here we have-
1 (1 , 2 , 4) + (-1) (1 , 0 , 0) + (-2) (0 ,1, 0) + (-4) (0, 0, 1)
= (1, 2 , 4) + (-1 , 0 , 0) + (0 ,-2, 0) + (0, 0, -4)
= (0, 0, 0)
That means it is a zero vector.
In this relation the scalar coefficients 1 , -1 , -2, -4 are all not zero.
So that we can conclude that S is linearly dependent.
Example-3: If 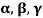 are linearly independent vectors of V(F).where F is the field of complex numbers, then so also are
are linearly independent vectors of V(F).where F is the field of complex numbers, then so also are 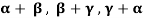 .
.
Sol. Suppose a, b, c are scalars such that-
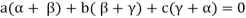
 …………….. (1)
…………….. (1)
But  are linearly independent vectors of V(F), so that equations (1) implies that-
are linearly independent vectors of V(F), so that equations (1) implies that-
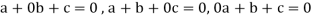
The coefficient matrix A of these equations will be-
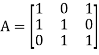
Here we get rank of A = 3, so that a = 0, b = 0, c = 0 is the only solution of the given equations, so that  are also linearly independent.
are also linearly independent.
Key takeaways:
- Suppose V(F) be a vector space. If
 , then any vector-
, then any vector-
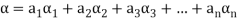
Where 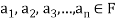
Is called a linear combination of the vectors 
2. Let V(F) be a vector space and S be a non-empty subset of V. Then the linear span of S is the set of all linear combinations of finite sets of elements of S and it is denoted by L(S).
3. A finite set 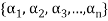 of vector of V is said to be linearly independent if every relation if the form-
of vector of V is said to be linearly independent if every relation if the form-
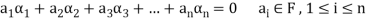
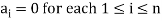
Definition:
A subset S of a vector space V(F) is said to be a basis of V(F), if-
1. S consists of linearly independent vectors
2. Each vector in V is a linear combination of a finite number of elements of S.
Finite dimensional vector spaces
The vector space V(F) is said to be finite dimensional if there exists a finite subset S of V such that V = L(S).
Dimension theorem for vector spaces-
Statement- If V(F) is a finite dimensional vector spaces, then any two bases of V have the same number of elements.
Proof: Let V(F) is a finite dimensional vector space. Then V possesses a basis.
Let  and
and  be two bases of V.
be two bases of V.
We shall prove that m = n
Since V = L(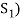 and
and  therefore
therefore 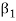 can be expressed as a linear combination of
can be expressed as a linear combination of 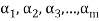
Consequently the set  which also generates V(F) is linearly dependent. So that there exists a member
which also generates V(F) is linearly dependent. So that there exists a member 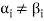 of this set. Such that
of this set. Such that  is the linear combination of the preceding vectors
is the linear combination of the preceding vectors 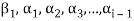
If we omit the vector  from
from 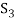 then V is also generated by the remaining set.
then V is also generated by the remaining set.
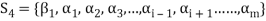
Since V = L(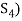 and
and  therefore
therefore 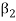 can be expressed as a linear combination of the vectors belonging to
can be expressed as a linear combination of the vectors belonging to 
Consequently the set-
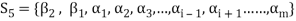
Is linearly dependent.
Therefore there exists a member 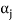 of this set such that
of this set such that  is a linear combination of the preceding vectors. Obviously
is a linear combination of the preceding vectors. Obviously  will be different from
will be different from 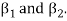
Since {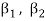 } is a linearly independent set
} is a linearly independent set
If we exclude the vector 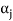 from
from  then the remaining set will generate V(F).
then the remaining set will generate V(F).
We may continue to proceed in this manner. Here each step consists in the exclusion of an 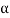 and the inclusion of
and the inclusion of  in the set
in the set 
Obviously the set 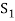 of all
of all  can not be exhausted before the set
can not be exhausted before the set 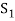 and
and 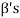
Otherwise V(F) will be a linear span of a proper subset of  thus
thus 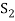 become linearly dependent. Therefore we must have-
become linearly dependent. Therefore we must have-
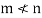
Now interchanging the roles of  we shall get that
we shall get that 
Hence,
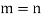
Extension theorem-
Every linearly independent subset of a finitely generated vector space V(F) forms of a part of a basis of V.
Proof: Suppose  be a linearly independent subset of a finite dimensional vector space V(F) if dim V = n, then V has a finite basis, say
be a linearly independent subset of a finite dimensional vector space V(F) if dim V = n, then V has a finite basis, say 
Let us consider a set-
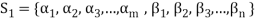 …………. (1)
…………. (1)
Obviously L( , since there
, since there  can be expressed as linear combination of
can be expressed as linear combination of  therefore the set
therefore the set 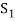 is linearly dependent.
is linearly dependent.
So that there is some vector of 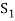 which is linear combination of its preceding vectors. This vector can not be any of the
which is linear combination of its preceding vectors. This vector can not be any of the 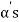 since the
since the  are linearly independent.
are linearly independent.
Therefore this vector must be some 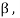 say
say 
Now omit the vector 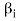 from (1) and consider the set-
from (1) and consider the set-
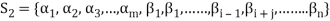
Obviously L(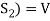 . If
. If  is linearly independent, then
is linearly independent, then 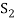 will be a basis of V and it is the required extended set which is a basis of V.
will be a basis of V and it is the required extended set which is a basis of V.
If 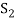 is not linearly independent, then repeating the above process a finite number of times. We shall get a linearly independent set containing
is not linearly independent, then repeating the above process a finite number of times. We shall get a linearly independent set containing 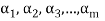 and spanning V. This set will be a basis of V contains the same number of elements, so that exactly n-m elements of the set of
and spanning V. This set will be a basis of V contains the same number of elements, so that exactly n-m elements of the set of 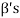 will be adjoined to S so as to form a basis of V.
will be adjoined to S so as to form a basis of V.
Example-1: Show that the vectors (1, 2, 1), (2, 1, 0) and (1, -1, 2) form a basis of 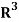
Sol. We know that set {(1,0,0) , (0,1,0) , (0,0,1)} forms a basis of 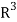
So that dim 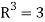 .
.
Now if we show that the set S = {(1, 2, 1), (2, 1, 0) , (1, -1, 2)} is linearly independent, then this set will form a basis of 
We have,
 (1, 2, 1)+
(1, 2, 1)+ (2, 1, 0)+
(2, 1, 0)+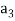 (1, -1, 2) = (0, 0, 0)
(1, -1, 2) = (0, 0, 0)
(
Which gives-
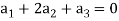
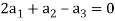
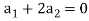
On solving these equations we get,
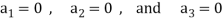
So we can say that the set S is linearly independent.
Therefore it forms a basis of 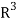
Key takeaways:
- The vector space V(F) is said to be finite dimensional if there exists a finite subset S of V such that V = L(S).
- If V(F) is a finite dimensional vector spaces, then any two bases of V have the same number of elements.
- Every linearly independent subset of a finitely generated vector space V(F) forms of a part of a basis of V.
Let A be any m  n matrix over a field K. Recall that the rows of A may be viewed as vectors in
n matrix over a field K. Recall that the rows of A may be viewed as vectors in  and that the row space of A, written rowsp(A), is the subspace of
and that the row space of A, written rowsp(A), is the subspace of  spanned by the rows of A. The following definition applies.
spanned by the rows of A. The following definition applies.
Def:
The rank of a matrix A, written rank(A), is equal to the maximum number of linearly independent rows of A or, equivalently, the dimension of the row space of A.
Recall, on the other hand, that the columns of an m  n matrix A may be viewed as vectors in
n matrix A may be viewed as vectors in  and that the column space of A, written colsp(A), is the subspace of
and that the column space of A, written colsp(A), is the subspace of 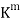 spanned by the columns of A.
spanned by the columns of A.
Although m may not be equal to n—that is, the rows and columns of A may belong to different vector spaces—we have the following fundamental result.
Theorem: The maximum number of linearly independent rows of any matrix A is equal to the maximum number of linearly independent columns of A. Thus, the dimension of the row space of A is equal to the dimension of the column space of A.
Basis-Finding Problems:
We will shows how an echelon form of any matrix A gives us the solution to certain problems about A itself. Specifically, let A and B be the following matrices, where the echelon matrix B (whose pivots are circled) is an echelon form of A:
A =  and B =
and B = 
We solve the following four problems about the matrix A, where C1; C2; . . . ; C6 denote its columns:
(a) Find a basis of the row space of A.
(b) Find each column Ck of A that is a linear combination of preceding columns of A.
(c) Find a basis of the column space of A.
(d) Find the rank of A.
(a) We are given that A and B are row equivalent, so they have the same row space. Moreover, B is in echelon form, so its nonzero rows are linearly independent and hence form a basis of the row space of B. Thus, they also form a basis of the row space of A. That is,
Basis of rowsp(A): (1, 2, 1, 3, 1, 2), (0, 1, 3, 1, 2, 1), (0, 0, 0, 1, 1, 2)
(b) Let  [
[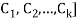 , the submatrix of A consisting of the first k columns of A. Then
, the submatrix of A consisting of the first k columns of A. Then 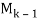 and
and
Mk are, respectively, the coefficient matrix and augmented matrix of the vector equation
x1C1 + x2C2 + . . . + xk – 1Ck – 1 = Ck
The system has a solution, or, equivalently, Ck is a linear combination of the preceding columns of A if and only if rank(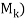 = rank(
= rank(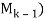 , where rank(
, where rank(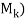 means the number of pivots in an echelon form of
means the number of pivots in an echelon form of 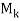 . Now the first k column of the echelon matrix B is also an echelon form of
. Now the first k column of the echelon matrix B is also an echelon form of  . Accordingly,
. Accordingly,
Rank (M2) = rank (M3) = 2 and rank(M4) = rank(M5) = rank(M6) = 3
Thus, C3, C5, C6 are each a linear combination of the preceding columns of A.
c) The fact that the remaining columns C1, C2, C4 are not linear combinations of their respective preceding columns also tells us that they are linearly independent. Thus, they form a basis of the column space of A. That is,
Basis of colsp(A): [1, 2, 3, 1, 2]T , [2, 5, 7, 5, 6]T, [3, 6, 11, 8, 11]T
Observe that C1, C2, C4 may also be characterized as those columns of A that contain the pivots in any echelon form of A.
(d) Here we see that three possible definitions of the rank of A yield the same value.
(i) There are three pivots in B, which is an echelon form of A.
(ii) The three pivots in B correspond to the nonzero rows of B, which form a basis of the row space of A.
(iii) The three pivots in B correspond to the columns of A, which form a basis of the column space of A.
Thus, rank(A) = 3.
References:
- E. Kreyszig, “Advanced Engineering Mathematics”, John Wiley & Sons, 2006.
- P. G. Hoel, S. C. Port And C. J. Stone, “Introduction To Probability Theory”, Universal Book Stall, 2003.
- S. Ross, “A First Course in Probability”, Pearson Education India, 2002.
- W. Feller, “An Introduction To Probability Theory and Its Applications”, Vol. 1, Wiley, 1968.
- N.P. Bali and M. Goyal, “A Text Book of Engineering Mathematics”, Laxmi Publications, 2010.
- B.S. Grewal, “Higher Engineering Mathematics”, Khanna Publishers, 2000.