UNIT 1

MATERIALS

1.1 Classification of engineering materials

Material is nothing but a matter of substance used to create a certain thing. Engineering materials are the materials used to for the application of engineering works. Based on the mechanical, physical, chemical and manufacturing properties materials are selected according to the application.

Mechanical properties of the materials are strength (compressive or tensile), toughness, stiffness, elasticity, plasticity, ductility, brittleness and hardness.

Physical properties of materials are density, conductivity (thermal or electrical), acoustical (sound transmission or absorption), optical, combustibility.

Chemical properties of materials are composition (oxide or compound), acidity or alkalinity, weathering corrosion.

Manufacturing properties of materials are castability, machinability rating, machining speeds and feeds and for dimensioning purpose shape and size.

The selection of material for the required functioning application is based on some of the following factors:

1. Stresses to which the work piece or component will be subjected.
2. Corrosion resistance.
3. Temperature, wear and tear resistance.
4. Flexibility and rigidity.
5. Easiness of the manufacturing process.
6. Cost effectiveness for the product development.
7. Availability of the material.

1.2.Classification of Engineering Material

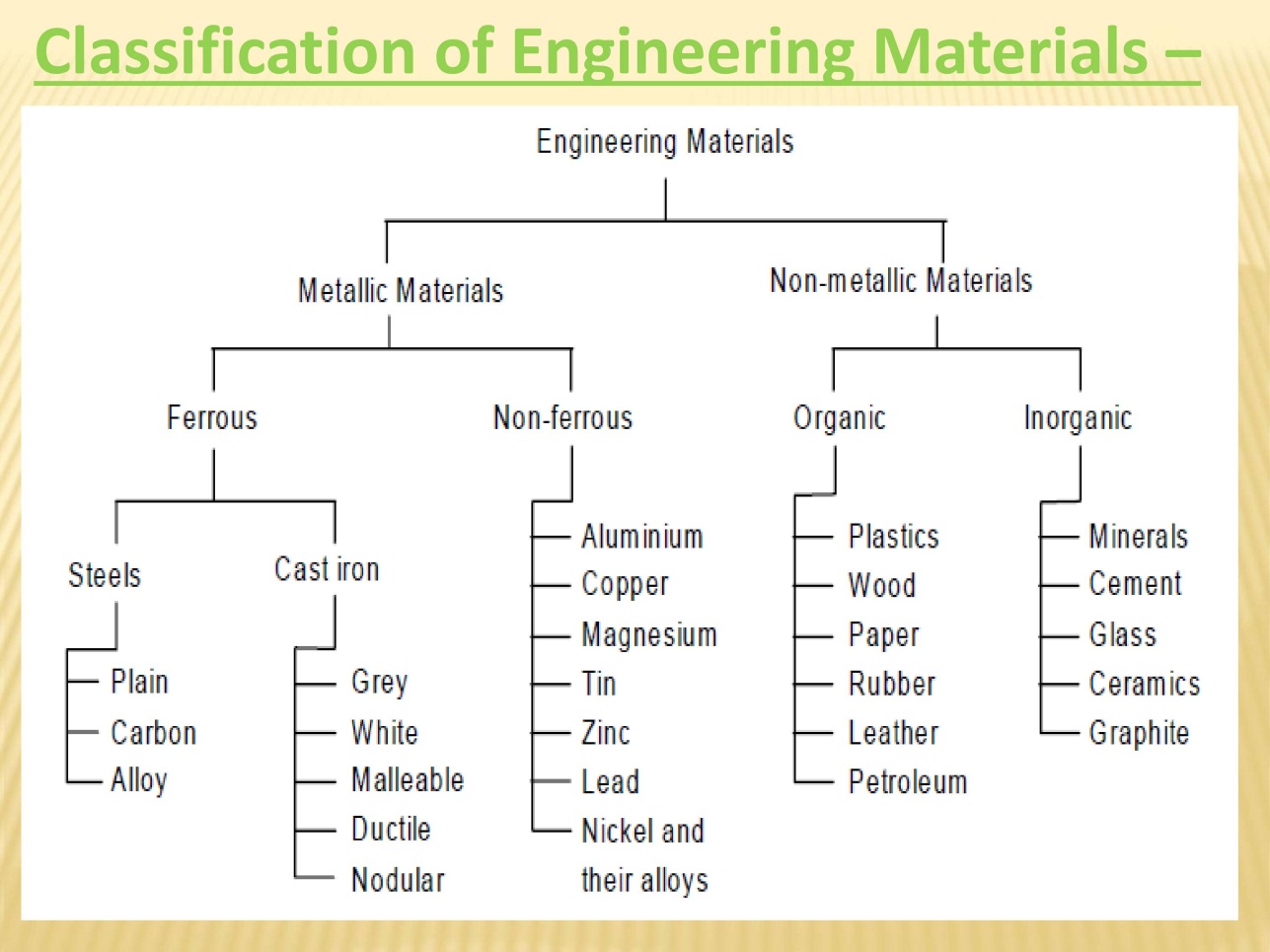
Depending upon the nature of substance materials are classified as

1. Metals and alloys
2. Ferrous metals
3. Non ferrous metals
4. Non metals
5. Ceramics
6. Polymers
7. Composites
8. Semi conductors
9. Bio materials

1. METALS AND ALLOYS

Metallic materials are combination of metallic elements.

The most prominent property of metals is electrons are non localized i.e. in atomic arrangement outer valence electrons do not belong to individual atom rather it belong to whole bulk of material. Non localized electron is free to carry charge to conduct electricity. Hence they are good conductors for electrical and thermal charge.

Metals have lustrous appearance. At normal temperature majority of the materials are in solid state, but some metals like mercury lies in liquid state.

Based upon the presence of iron content metals are named as

1. Ferrous metals
2. Non ferrous metals

Ferrous metals:

The primary content of ferrous metals is iron and carbon. Ferrous metals are magnetic and are vulnerable to rust when exposed to moisture. Wrought iron won’t rust due to purity and stainless steel due to presence of chromium.

Eg: iron, steel, etc.

Due to their magnetic property ferrous metals are used in motor and electrical applications.

Non Ferrous Metals:

Iron is not primary content. Due to the non presence of iron these metals have high resistance to rust and corrosion and they are non magnetic.

Eg: copper, brass, aluminum, tungsten, lead, zinc, gold, etc.

1.Alloy:

Alloy is a combination of two or more metals. It is named based on metallic bonding character. It is of two types’ ferrous metal alloy and non ferrous metal alloy. Cast iron is an alloy made from iron, carbon and silicon. Brass is an alloy of copper and zinc.

Applications:

1. Due to their toughness and ability to sterilize at high temperatures metals are used as needles, surgical blades.
2. Due to their strength and ability to withstand heavy weights metals like iron and steel are used in construction.
3. Metals like gold, silver, platinum, etc. are used in jewellery.
4. Metals are used in machines and automobiles as they can withstand high temperature, pressure and workloads.
5. Aluminum and titanium play important role in light weight category for aircraft alloys.
6. Tungsten is used in high temperature applications.

2. CERAMICS:

A particle or fibrous which are used in terms of making ceramic products. Ceramics have regular atomic structure and crystal structure. Ceramics are mainly oxides, nitrides and carbides. They are non conducting materials, due to its insulating property they are used as insulators. They are very hard and brittle in nature.

E.g.: alumina, silica, silicon carbide, diamond, bricks, etc.

Applications:

1. Due to the compressive strength bricks are used in construction
2. Because of their good thermal insulation ceramic tiles are used in ovens.
3. Some ceramics are transparent to radar and other electromagnetic waves are used in radomes and transmitters.
4. Glass ceramics have high temperature capabilities so they are used in optical equipment and fiber insulation.
5. Alumina, silica, silicon carbide are used in making tools.
6. Diamond is used in ornaments and cutting tool applications.

3. POLYMERS:

Polymers have chain molecule structure of carbon as back bone atoms. They are mainly made up of tough organic materials. They are low density materials and also flexible. In some cases polymers are not flexible.

Polymers are not only used as structural materials, they can be used as fiber and resins in the matrix of composite materials.

e.g.: polyester as fibers, phenolic and epoxides as resins.

Elastomers are also polymers but they are considered separately due to their specific design for certain purposes like shock and vibration absorption.

Natural polymers:

Eg : wool, silk, DNA, cellulose, proteins, etc.

Synthetic polymers:

1. Thermo plastics
2. Thermosetting plastics

Eg: nylon, polyethylene, polyester, Teflon, epoxy, Bakelite, etc.

Applications:

1. Polyethylene is used for making carry bags.
2. Polypropylene is used for making high temperature resistance products like feeding bottle.
3. Polyether ether ketone and polyethylene ketone are used in mineral water bottle concept.
4. Poly carbonate is used to make high performance polymers like transparent polymers
5. Polyaniline is a conducting polymer.
6. Bakelite used for making insulating materials. 

4. COMPOSITE:

Composite material is the composition of two or more constituent materials with different physical and chemical properties to produce a different characteristic material.

Composite material may be both metals or metal and ceramic or metal and polymer, depending upon the application requirement the combination is made.

Eg : wood, concrete, fiber glass, CFRP (carbon fiber reinforced plastic), GFRP (glass fiber reinforced plastic), etc.

Applications:

1. CFRP and GFRP are used for automotive body parts.
2. CRPF and honeycomb composites are used for chassis.
3. Some fuel tanks are made up of Kevlar reinforced fiber.
4. Reinforced thermosets are used in springs and bumper system.
5. Fiberglas reinforced plastic has been used for boat hulls, fishing rods, tennis rackets, helmets, bows and arrows.

5. SEMICONDUCTORS:

Semiconductor is an intermediate conducting material. Their conductivity is not high as like metals and low as like insulating ceramic materials. In these materials resistance decreases as their temperature increases.

The unique atomic structure allows controlling the conductivity.

Eg : silicon, germanium, gallium arsenide, selenium, etc.

Applications:

1. Gallium arsenide is widely used in low noise, high gain and weak signal amplifying devices.
2. A semi conductor device can perform the function of a vacuum tube having hundreds of times its volume.

6. BIO MATERIALS:

Bio materials are non-viable materials .Eg : alumina, zirconia, titanium, tantalum, niobium, carbon, etc.

Applications:

1. Metals are used in medicine to cure any micronutrient metal deficiency diseases in humans and animals, like iron is a part of hemoglobin a bio molecule which can be used as ferrous sulphate to cure some forms of anemia.
2. Implants in the body to repair or replace the damaged tissue.

In composite materials the name itself indicates as composite (composition), it is the composition of two or more materials. In semiconductors the name itself indicates as semi (half) and conductor (conducting) The difference between an alloy and composite is that the composite is a reinforcement of other material. Whereas alloy is a combination (mixture) of both or required number of materials in the required quantity as per the necessary product.

Both semiconductors and bio materials are substitutes in metals, ceramics and polymers in the required places

II Composition of cast iron and carbon steel

CAST IRON

Cast iron is an iron alloy containing 2 wt.% – 4 wt.% carbon, 1 wt.% – 3 wt.% silicon and smaller amounts of minor elements . In comparison, steel has a lower carbon content of up to 2 wt. % and lower silicon content.

Cast iron can also be further optimized by alloying with small quantities of manganese, molybdenum, cerium, nickel, copper, vanadium and titanium before being cast. Depending on the silicon content of the cast iron, it is classified as either white cast iron or grey cast iron and may be treated further under particular temperatures to produce malleable or ductile cast iron.

General properties of cast iron

Cast iron is highly favored for its ability to be easily cast into complex shapes when molten and for its low cost. In addition, its properties can be easily altered by adjusting the composition and cooling rate without significant changes to production methods. Its other main advantages over cast steel include ease of machining, vibration dampening, compressive strength, wear resistance and corrosion resistance. Corrosion resistance of cast iron is improved via the addition of minor elements such as silicon, nickel, chromium, molybdenum and copper.

Types of cast iron and their applications

Cast iron can be classified into grey cast iron, white cast iron, malleable cast iron and ductile cast iron, depending on its composition.

i) Grey cast iron

Grey cast iron, or gray iron, has a dark grey fracture colour due to a graphitic microstructure. The presence of graphite flakes is due to the addition of silicon, which acts to stabilize carbon in the form of graphite as opposed to iron carbide. Grey cast iron typically has a composition of 2.5 wt.% – 4.0 wt.% carbon and 1.0 wt.% – 3.0 wt.% silicon.

Grey cast iron applications

Grey cast iron is the most common form of cast iron. It is used in applications where its high stiffness, machinability, vibration dampening, high heat capacity and high thermal conductivity are of advantage, such as internal combustion engine cylinder blocks, flywheels, gearbox cases, manifolds, disk brake rotors and cookware.

A commonly used classification for grey cast iron is ASTM International standard A48. Under this system, grey cast irons are graded according to their tensile strength with class 20 grey cast iron for example, having a minimum tensile strength of 20,000 psi (140 MPa).

Ii) White cast iron

White cast iron has a white fracture colour due to the presence of iron carbide, or cementite Fe3C. The presence of carbon in this form, as opposed to graphite, is the result of a lower silicon content compared to grey cast iron. White cast iron typically contains 1.8 wt.% – 3.6 wt.% carbon, 0.5 wt.% – 1.9 wt.% silicon and 1.0 wt.% – 2.0 wt.% manganese. White cast irons are extremely wear-resistant yet brittle. They exhibit high hardness as a result of their microstructure containing large iron carbide particles and are not easily machined.

White cast iron applications

White cast irons are used in abrasion-resistant parts where its brittleness is of minimum concern such as shell liners, slurry pumps, ball mills, lifter bars, extrusion nozzles, cement mixers, pipe fittings, flanges, crushers and pump impellers. A popular grade of white iron is high chrome white irons, ASTM A532. This contains nickel and chromium for good low-impact abrasion applications .

Iii) Malleable cast iron

Malleable cast irons are formed via a slow annealing heat treatment of white cast iron. This results in the conversion of carbon, in the form of iron carbide in white iron, to graphite, with the remaining matrix being composed of ferrite or pearlite. The graphite is present in the form of spherical or nodular shapes.

Malleable cast iron exhibits good malleability and good ductility. Due to the lower silicon content compared to other cast irons, it exhibits good fracture toughness at low temperature.

Malleable cast iron applications

As a result of its good tensile strength and ductility, malleable cast iron is used for electrical fittings and equipment, hand tools, pipe fittings, washers, brackets, farm equipment, mining hardware, and machine parts.

Iv) Ductile cast iron

Ductile cast iron, also known as nodular cast iron and spheroidal graphite cast iron, is defined by the presence of graphite in the form of spherical nodules, as with malleable cast iron. Differently to malleable cast iron, ductile cast iron is formed not by heat treatment of white iron, but through a specific chemical composition.

Ductile cast iron contains 3.2 wt.% – 3.6 wt.% carbon, 2.2 wt.% – 2.8 wt.% silicon and 0.1 wt.% – 0.2 wt.% manganese, as well as smaller amounts of magnesium, phosphorus, sulfur and copper. The presence of manganese is responsible for the spherical form of the graphite inclusions.

Ductile cast iron applications

Due to its microstructure, this material is more ductile than grey or white cast irons. For this reason, it is used as ductile iron pipe for water and sewage infrastructure. It can also withstand thermal cycling and is therefore used in vehicle gears and suspension components, brakes and valves, pumps and hydraulic parts, and housings for wind turbines.

Production and processing

To produce cast iron, the iron must be extracted from iron ore. The ore is smelted in a blast furnace where it separates into pig iron and slag. The furnace is heated to around 1800 degrees Celsius in an oxygen atmosphere and the slag formed rises to the top and can be removed. The molten pig iron below contains around 3 wt.%  – 5 wt.% carbon. This is then combined with iron, steel, coke and limestone.

Once impurities are removed selectively from this iron, the carbon content is reduced. At this point, silicon may be added to convert the carbon content to graphite or cementite. The iron is then cast into various forms.

CARBON STEEL

Carbon steel is an iron-carbon alloy, which contains up to 2.1 wt.% carbon. For carbon steels, there is no minimum specified content of other alloying elements; however, they often contain manganese. The maximum manganese, silicon and copper content should be less than 1.65 wt. %, 0.6 wt. % and 0.6 wt. %, respectively.

Types of carbon steel and their properties

Carbon steel can be classified into three categories according to its carbon content: low-carbon steel (or mild-carbon steel), medium-carbon steel and high-carbon steel their carbon content, microstructure and properties compare as follows:

Low-carbon steel

Low-carbon steel is the most widely used form of carbon steel. These steels usually have a carbon content of less than 0.25 wt.%. They cannot be hardened by heat treatment (to form martensite) so this is usually achieved by cold work.

Carbon steels are usually relatively soft and have low strength. They do, however, have high ductility, making them excellent for machining, welding and low cost. High-strength, low-alloy steels (HSLA) are also often classified as low-carbon steels, however, also contains other elements such as copper, nickel, vanadium and molybdenum. Combined, these comprise up to 10 wt.% of the steel content. High-strength, low-alloy steels, as the name suggests, have higher strengths, which is achieved by heat treatment. They also retain ductility, making them easily formable and machinable. HSLA are more resistant to corrosion than plain low-carbon steels.

Medium-carbon steel

Medium-carbon steel has a carbon content of 0.25 – 0.60 wt. % and a manganese content of 0.60 – 1.65 wt. %. The mechanical properties of this steel are improved via heat treatment involving autenitising followed by quenching and tempering, giving them a martensitic microstructure. Heat treatment can only be performed on very thin sections, however, additional alloying elements, such as chromium, molybdenum and nickel, can be added to improve the steels ability to be heat treated and, thus, hardened. Hardened medium-carbon steels have greater strength than low-carbon steels, however, this comes at the expense of ductility and toughness.

High-carbon steel

High-carbon steel has a carbon content of 0.60– 1.25 wt.% and a manganese content of 0.30 – 0.90 wt.%. It has the highest hardness and toughness of the carbon steels and the lowest ductility. High-carbon steels are very wear-resistant as a result of the fact that they are almost always hardened and tempered.

Tool steels and die steels are types of high-carbon steels, which contain additional alloying elements including chromium, vanadium, molybdenum and tungsten. The addition of these elements results in the very hard wear-resistant steel, which is a result of the formation of carbide compounds such as tungsten carbide (WC).

Production and processing

Carbon steel can be produced from recycled steel, virgin steel or a combination of both. Virgin steel is made by combining iron ore, coke (produced by heating coal in the absence of air) and lime in a blast furnace at around 1650 °C. The molten iron extracted from the iron ore is enriched with carbon from the burning coke. The remaining impurities combine with the lime to form slag, which floats on top of the molten metal where it can be extracted.

The resulting molten steel contains roughly 4 wt.% carbon. This carbon content is then reduced to the desired amount in a process called decarburization. This is achieved by passing oxygen through the melt, which oxidizes the carbon in the steel, producing carbon monoxide and carbon dioxide.

Examples & Applications

Low-carbon steel

Low carbon steels are often used in automobile body components, structural shapes (I-beams, channel and angle iron), pipes, construction and bridge components, and food cans.

Medium-carbon steel

As a result of their high strength, resistance to wear and toughness, medium-carbon steels are often used for railway tracks, train wheels, crankshafts, and gears and machinery parts requiring this combination of properties.

High-carbon steel

Due to their high wear-resistance and hardness, high-carbon steels are used in cutting tools, springs high strength wire and dies.

III) Iron carbon diagram:

Iron-carbon phase diagram describes the iron-carbon system of alloys containing up to 6.67% of carbon, discloses the phase’s compositions and their transformations occurring with the alloys during their cooling or heating.

Carbon content 6.67% corresponds to the fixed composition of the iron carbide Fe3C.

The diagram is presented in the picture:

The following phases are involved in the transformation, occurring with iron-carbon alloys:

• L - Liquid solution of carbon in iron;

• δ-ferrite – Solid solution of carbon in iron.

Maximum concentration of carbon in δ-ferrite is 0.09% at 2719 ºF (1493ºC) – temperature of the peritectic transformation.

The crystal structure of δ-ferrite is BCC (cubic body centered).

• Austenite – interstitial solid solution of carbon in γ-iron.

Austenite has FCC (cubic face centered) crystal structure, permitting high solubility of carbon – up to 2.06% at 2097 ºF (1147 ºC).

Austenite does not exist below 1333 ºF (723ºC) and maximum carbon concentration at this temperature is 0.83%.

• α-ferrite – solid solution of carbon in α-iron.

α-ferrite has BCC crystal structure and low solubility of carbon – up to 0.025% at 1333 ºF (723ºC). α-ferrite exists at room temperature.

• Cementite – iron carbide, intermetallic compound, having fixed composition Fe3C. Cementite is a hard and brittle substance, influencing on the properties of steels and cast irons.

The following phase transformations occur with iron-carbon alloys:

Alloys, containing up to 0.51% of carbon, start solidification with formation of crystals of δ-ferrite. Carbon content in δ-ferrite increases up to 0.09% in course solidification, and at 2719 ºF (1493ºC) remaining liquid phase and δ-ferrite perform peritectic transformation, resulting in formation of austenite. Alloys, containing carbon more than 0.51%, but less than 2.06%, form primary austenite crystals in the beginning of solidification and when the temperature reaches the curve ACM primary cementite stars to form.

Iron-carbon alloys, containing up to 2.06% of carbon, are called steels.

Alloys, containing from 2.06 to 6.67% of carbon, experience eutectic transformation at 2097 ºF (1147 ºC). The eutectic concentration of carbon is 4.3%.

In practice only hypoeutectic alloys are used. These alloys (carbon content from 2.06% to 4.3%) are called cast irons. When temperature of an alloy from this range reaches 2097 ºF (1147 ºC), it contains primary austenite crystals and some amount of the liquid phase. The latter decomposes by eutectic mechanism to a fine mixture of austenite and cementite, called leduburite.

All iron-carbon alloys (steels and cast irons) experience eutectoid transformation at 1333 ºF (723ºC). The eutectoid concentration of carbon is 0.83%.

When the temperature of an alloy reaches 1333 ºF (733ºC), austenite transforms to pearlite (fine ferrite-cementite structure, forming as a result of decomposition of austenite at slow cooling conditions).

Critical temperatures

• Upper critical temperature (point) A3 is the temperature, below which ferrite starts to form as a result of ejection from austenite in the hypo eutectoid alloys.

• Upper critical temperature (point) ACM is the temperature, below which cementite starts to form as a result of ejection from austenite in the hypereutectoid alloys.

• Lower critical temperature (point) A1 is the temperature of the austenite-to-pearlite eutectoid transformation. Below this temperature austenite does not exist.

• Magnetic transformation temperature A2 is the temperature below which α-ferrite is ferromagnetic.

Phase compositions of the iron-carbon alloys at room temperature

• Hypo eutectoid steels (carbon content from 0 to 0.83%) consist of primary (proeutectoid) ferrite (according to the curve A3) and pearlite.

• Eutectoid steel (carbon content 0.83%) entirely consists of pearlite.

• Hypereutectoid steels (carbon content from 0.83 to 2.06%) consist of primary (proeutectoid) cementite (according to the curve ACM) and pearlite.

• Cast irons (carbon content from 2.06% to 4.3%) consist of proeutectoid cementite C2 ejected from austenite according to the curve ACM , pearlite and transformed ledeburite (ledeburite in which austenite transformed to pearlite).

IV) Alloy steels their applications:

Alloy steel is a class of steel that, in addition to carbon, is alloyed with other elements, ranging from 1 wt.% to 50 wt.%, which are used to enhance the material’s various properties.

These elements commonly include manganese, nickel, chromium, molybdenum, vanadium, silicon, and boron. Less common elements include aluminium, cobalt, copper, cerium, niobium, titanium, tungsten, tin, zinc, lead, and zirconium.

There are multiple subcategories of alloy steel. These include:

• Low-alloy steel
• High-strength low alloy (HSLA) steel
• High-alloy steel
• Stainless steel

• Micro alloyed steel
• Advanced high-strength steel (AHSS)
• Maraging steel
• Tool steel

Low alloy steels generally contain less than 8 wt.% non-iron elements, whereas high-alloy steels contain more than 8 wt.% non-iron elements [2]. Both typically have superior mechanical properties in comparison to carbon steels [3].

Alloy steels can contain a wide variety of elements, each of which can enhance various properties of the material, such as mechanical thermal and corrosion resistance. Elements added in low quantities of less than around 5 wt.% tend to improve mechanical properties, for example increasing hardenability and strength, whereas larger additions of up to 20 wt.% increase corrosion resistance and stability at high or low temperatures.

The effects of adding various elements to steel, along with the typical amounts in weight fraction, is summarised in the table below.

Overall, in comparison to carbon steels, alloy steels can exhibit increased strength, ductility and toughness. The disadvantages, however, are that alloy steels usually have lower machinability, weld ability and formability.

Production & processing

The alloying and processing methods for alloy steel depend on the desired result. The required combination of elements is first melted together in a furnace at over 1600°C for 8 to 12 hours. The steel is then annealed at over 500°C in order to remove impurities and to alter the physical and chemical properties.

Next, mill scale (a mixture of iron oxides), which results from the annealing process, is removed from the surface of the steel with hydrofluoric acid before repeating the annealing and descaling process. Finally, the steel is melted and cast into for rolling and shaping into the final form.

Applications & examples

As the term alloy steel encompasses numerous types of steel, its application area is broad.

Low alloy steels are used in a wide range of industries due to their extreme strength, machinability, cost-effectiveness and availability. They are found in military vehicles, construction equipment, ships, pipelines, pressure vessels oil drilling platforms and in structural components. Examples include HY80 and HY100.

High-alloy steels can be expensive to manufacture and difficult to process. Nevertheless, their superior hardness, toughness and corrosion resistance make them ideal for structural components, automotive applications, chemical processing and power generating equipment. Examples of high-alloy steels include the grades HE, HF, HH, HI, HK, and HL.

V) Mechanical properties of material:

Mechanical properties are how the metal performs when different forces are applied to them. That includes things like strength, ductility, wear resistance, etc.   

The mechanical and physical properties of materials are determined by their chemical composition and their internal structure, like grain size or crystal structure. Mechanical properties may be greatly affected by processing due to rearrangement of the internal structure. Metalworking processes or heat treatment might play a role in affecting some physical properties like density and electrical conductivity, but those effects are usually insignificant.

Mechanical and physical properties are a key determinant for which alloy is considered suitable for a given application when multiple alloys satisfy the service conditions. In almost every instance, the engineer designs the part to perform within a given range of properties. Many of the mechanical properties are interdependent high performance in one category may be coupled with lower performance in another.  Higher strength, as an example, may be achieved at the expense of lower ductility. So a broad understanding of the product’s environment will lead to the selection of the best material for the application.

Here are some of the most common mechanical properties that define different types of metal:

1.      Strength

The measurement of how much load a material can withstand before failure. The more load a material can bear, the more strength it has.

There are different types of strength based on loading types, which are:

a.      Compressive strength

b.      Shear strength

c.       Tensile strength

In regards to deformation before fracture, the following types of strength are:

a.      Elastic strength

b.      Ultimate strength

c.       Yield strength

Strength – Shear

Shear strength is a consideration in applications like bolts or beams where the direction as well as the magnitude of the stress is important. Shear occurs when directional forces cause the internal structure of the metal to slide against itself, at the granular level.

 Strength – Tensile

One of the most common metal property measures is Tensile, or Ultimate, Strength. Tensile strength refers to the amount of load a section of metal can withstand before it breaks.  In lab testing, the metal will elongate but return to its original shape through the area of elastic deformation. When it reaches the point of permanent or plastic deformation (measured as Yield), it retains the elongated shape even when load is removed.  At the Tensile point, the load causes the metal to ultimately fracture.  This measure helps differentiate between materials that are brittle from those that are more ductile. Tensile or ultimate tensile strength is measured in Newton’s per square millimeter (Mega Pascals or MPa) or pounds per square inch.

Strength – Yield

Similar in concept and measure to Tensile Strength, Yield Strength describes the point after which the material under load will no longer return to its original position or shape. Deformation moves from elastic to plastic.  Design calculations include the Yield Point to understand the limits of dimensional integrity under load.  Like Tensile strength, Yield strength is measured in Newtons per square millimeter (Mega Pascal’s or MPa) or pounds per square inch.

2.      Fatigue Strength

The amount of cycles a material can withstand under fluctuating stress (cyclic loading) upon reaching failure. Fatigue refers to the failure of a material under cyclic loading prior to reaching its ultimate limit.

Fatigue can lead to fracture under repeated or fluctuating stresses (for example loading or unloading) that have a maximum value less than the tensile strength of the material. Higher stresses will accelerate the time to failure, and vice versa, so there is a relationship between the stress and cycles to failure.  Fatigue limit, then, refers to the maximum stress the metal can withstand (the variable) in a given number of cycles.  Conversely, the fatigue life measure holds the load fixed and measures how many load cycles the material can withstand before failure.  Fatigue strength is an important consideration when designing components subjected to repetitive load conditions. 

3.      Brittleness

Brittleness is when a material breaks suddenly under stress, without exhibiting much elastic deformation or changes in dimension.

4.      Stiffness

A material’s ability to resist significant elastic deformation while loading. The less deformation a material exhibits during loading, the stiffer it is.

The stiffness of a metal is often measured by the Young’s Modulus, which compares the relationship between stress (the force applied) and strain (the resulting deformation). The higher the Modulus – meaning greater stress results in proportionally lesser deformation – the stiffer the material.  Glass would be an example of a stiff/high Modulus material, where rubber would be a material that exhibits low stiffness/low Modulus.  This is an important design consideration for applications where stiffness is required under load.

5.      Hardness

Hardness is defined by a material’s ability to resist various forms of deformation, indentation and penetration. Also refers to its resistance to scratching, scraping, drilling, chipping and wear and tear.

Hardness is defined as a material’s ability to resist permanent indentation (that is plastic deformation). Typically, the harder the material, the better it resists wear or deformation. The term hardness, thus, also refers to local surface stiffness of a material or its resistance to scratching, abrasion, or cutting.  Hardness is measured by employing such methods as Brinell, Rockwell, and Vickers, which measure the depth and area of a depression by a harder material, including a steel ball, diamond, or other indenter.

6.      Toughness

Toughness is defined by the material’s capacity to withstand elastic and plastic deformation without failure. Typically measured by the amount of energy a material can absorb before fracturing.

Measured using the Charpy impact test similar to Impact Resistance, toughness represents a material’s ability to absorb impact without fracturing at a given temperature. Since impact resistance is often lower at low temperatures, materials may become more brittle.  Charpy values are commonly prescribed in ferrous alloys where the possibilities of low temperatures exist in the application (e.g. Offshore oil platforms, oil pipelines, etc.) or where instantaneous loading is a consideration (e.g. Ballistic containment in military or aircraft applications).

7.      Embrittlement

The result of metal losing’s its ductility and becoming brittle due to chemical or physical changes.

8.      Homogeneity

Any material that has the same properties throughout its entire geometry. A homogeneous material cannot be mechanically separated or identified individually. Certain types of homogeneous material include plastics, metals, glass, paper, resins and coatings.

9.      Isotropy

Often confused with homogeneity, isotropic materials exhibit the same properties in any direction or orientation, whereas homogeneous materials have the same properties regardless of direction.

10.  Anisotropy

A material that exhibits different properties based on its direction or orientation. For example, in computer graphics, an anisotropic surface changes in appearance depending on the angle it’s being displayed at.

11.  Elasticity

Materials that rebound back to their original dimensions after deformation, or being removed from its load. Every material has a certain elastic limit before becoming deformed permanently, otherwise known as plasticity deformation.

12.  Plasticity

A type of permanent deformation that occurs under stress before resulting in failure. Commonly used in metal shaping to achieve certain shapes and forms.

Plasticity, the converse of elasticity, describes the tendency of a certain solid material to hold its new shape when subjected to forming forces. It is the quality that allows materials to be bent or worked into a permanent new shape.  Materials transition from elastic behavior to plastic at the yield point. 

13.  Ductility

Ductility is the result of solid material becoming stretched due to tensile stress. A common application of this process is turning metal into wiring.

Ductility is the ability of a material to deform plastically (that is, stretch) without fracturing and retain the new shape when the load is removed. Think of it as the ability to stretch a given metal into a wire. Ductility is often measured using a tensile test as a percentage of elongation, or the reduction in the cross sectional area of the sample before failure. A tensile test can also be used to determine the Young’s Modulus or modulus of elasticity, an important stress/strain ratio used in many design calculations.  The tendency of a material to resist cracking or breaking under stress makes ductile materials appropriate for other metalworking processes including rolling or drawing.  Certain other processes like cold-working tend to make a metal less ductile. 

14.  Malleability

The ability to plastically deform a material or significantly change its shape without becoming fractured.

15.   Machinability

The ease of which a metal part can be cut without sacrificing the quality of the finish. Malleability, a physical property, describes a metal’s ability to be formed without breaking. Pressure, or compressive stress, is used to press or roll the material into thinner sheets.  A material with high malleability will be able to withstand higher pressure without breaking. 

16.  Creep

A slow and gradual deformation (or change in dimensions) of materials under a certain applied load. Measured by the influence of time and temperature. Typically occurs at high temperatures, but can also occur at room temperature, albeit much more slowly.

17.  Resilience

The ability to absorb energy while being elastically deformed, and releasing that energy after being unloaded. Proof resilience is the maximum amount of energy a material can absorb before permanent deformation.

18.  Damping

Damping refers to dissipating the amount of energy used to create vibration, oscillation or stress. A material with a good damping property, such as cast iron, is capable of absorbing high amounts of vibration.

19.  Thermal Expansion

A change in shape, volume or area caused by changes in temperature. The coefficient of thermal expansion refers to the amount a material’s shape or size will change during exposure to a change in temperature.

VI) Tensile test-stress strain diagram of ductile and brittle materials

One of the most fundamental mechanical tests that can be performed on a material is the tensile test. A test sample is loaded in tension when it experiences opposing forces acting upon opposite faces both located on the same axis that attempt to pull the specimen apart. These tests are simple to setup and complete and reveal many characteristics of the material that is tested. Tensile tests are considered to be essentially the opposite of a compression test.

Purpose of tensile testing:

Generally, a tensile test is designed to be run until the sample fails or breaks under the load. The values that may be measured from this type of test can range from but are not limited to tensile strength, ultimate strength, elongation, modulus of elasticity, yield strength, Poisson’s ratio, and strain hardening. The measurements taken during the test reveals the characteristics of a material while it is under a tensile load.

Many types of tensile tests: There many different variants of tensile tests but a few of the more common tests are tension, tensile adhesion, tensile shear, tensile grab, tensile pulling, tension fatigue, and tensile creep. In most of these tests the specimen is loaded until it fails or fractures with the main difference in the type of specimen geometry and associated tensile test fixture used. Tension fatigue testing differs not only in the type of grip but also in the test machine type. It is performed by loading the material to a positive force and then reducing the load to zero and repeating this process until the sample fails with the number of cycles till failure as the desired value to be measured. Tensile creep is similar to this except that the load is not altered but rather steadily applied until the sample fails.

Types of materials:

Nearly all materials can be tested in tension in one manner or another, but the more popular materials include metals, plastics, woods, polymers and textiles. The test sample often take the shapes of bars, strings, strands, coupons, dog bones, and dumbbells depending upon the material, the tensile grip, and test performed on the sample. Materials with high compressive strength values have relatively low tensile strength, such as brick and aerospace composites. These are not generally tested in tension as their applications do not normally require them to withstand tensile loads.

Stress strain diagram

The relationship between stress and strain in a material is determined by subjecting a material specimen to a tension or compression test. In this test, a steadily increasing axial force is applied to a test specimen, and the deflection is measured as the load is increased. These values can be plotted as a load-deflection curve. The deflection in the test specimen is dependent on both the material's elastic modulus as well as the geometry of the specimen (area and length). Since we are interested material behavior without regard to geometry, it is useful to generalize the data to remove the effect of geometry. This is done by converting the load values to stress values and converting the deflection values to strain values:

σ=P/A0

ε=L-L0/L0
In the equation for stress, P is the load and A0 is the original cross-sectional area of the test specimen. In the equation for strain, L is the current length of the specimen and L0 is the original length.

Stress-Strain Curve

The values of stress and strain determined from the tensile test can be plotted as a stress-strain curve, as shown below:

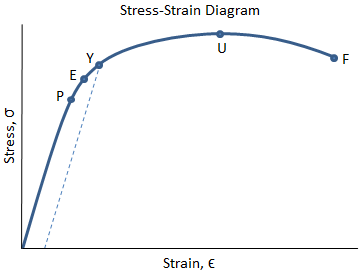
There are several points of interest in the diagram above:

• P: This is the proportionality limit, which represents the maximum value of stress at which the stress-strain curve is linear.
• E: This is the elastic limit, which represents the maximum value of stress at which there is no permanent set. Even though the curve is not linear between the proportionality limit and the elastic limit, the material is still elastic in this region and if the load is removed at or below this point the specimen will return to its original length.
• Y: This is the yield point, which represents the value of stress above which the strain will begin to increase rapidly. The stress at the yield point is called the yield strength, Sty. For materials without a well-defined yield point, it is typically defined using the 0.2% offset method in which a line parallel to the linear portion of the curve is drawn that intersects the x-axis at a strain value of 0.002. The point at which the line intersects the stress-strain curve is designated as the yield point.
• U: This point corresponds to the ultimate strength, Stu, which is the maximum value of stress on the stress-strain diagram. The ultimate strength is also referred to as the tensile strength. After reaching the ultimate stress, specimens of ductile materials will exhibit necking, in which the cross-sectional area in a localized region of the specimen reduces significantly.
• F: This is the fracture point or the break point, which is the point at which the material fails and separates into two pieces.

True Stress and Strain

Engineers typically work with engineering stress, which is the force divided by the original area of the specimen before loading: σ = P/A0. However, as a material is loaded, the area decreases. The true stress, , is the value of stress in the material considering the actual area of the specimen. Because the area decreases as a material is loaded, true stress is higher than engineering stress.

The figure below shows an engineering stress-strain curve as compared to a true stress-strain curve. Because the engineering stress is calculated as force divided by original area (which is a constant), the engineering stress-strain curve has the same shape as the load-deflection curve. The engineering stress-strain curve drops after the ultimate strength is reached because the force that can be supported by the material drops as it begins to neck down. However, the stress value in the true stress-strain curve always increases as the strain increases. This is because the instantaneous value of area is used when calculating true stress. Even when the force supported by the material drops, the reduction in the specimen area outweighs the reduction in force, and the stress continues to increase.

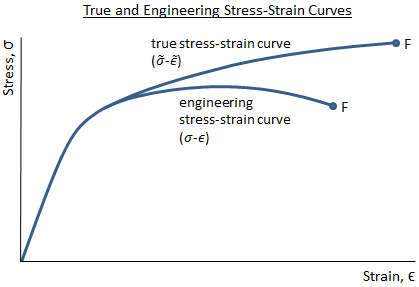
It should be noted that the engineering stress and the true stress are essentially the same in the linear-elastic region of the stress-strain curve. Because engineers typically operate within this linear-elastic region (it is uncommon to design a structure that is intended to operate beyond the elastic limit), it is valid to work with engineering stress as opposed to true stress.

Engineering strain is the change in length divided by the original length: ε = ΔL/L0. Instead of just calculating a single value of ΔL, consider that the change in length is divided among many small increments, ΔLj. The strain is also calculated in small increments: εj = ΔLj/Lj, where ΔLj is the change in length for an increment, and Lj is the length at the start of the increment. As these increments become infinitesimally small, the summation of the strains approaches the true strain:

f it is assumed that the volume is constant throughout the deflection, then true stress and strain can be calculated as:

σ and ε are the engineering stress and strain.

VI) Hooks law and modulus of elasticity:

Hooks law:

When force is applied to a material, we know that it either stretches or compresses in response to the applied force. In mechanics, the force applied per unit area is known as stress and is denoted by the symbol σ. The extent to which the material compresses or stretches is known as strain. Different materials respond differently to applied stress. 

In 19th-century while studying springs and elasticity English scientist Robert Hooke noticed that many materials exhibited a similar property when the stress-strain relationship was studied There was a linear region where the force required to stretch the material was proportional to the extension of the material. This is known as Hooke’s Law.

Hooke’s law states that the strain of the material is proportional to the applied stress within the elastic limit of that material.

When the elastic materials are stretched, the atoms and molecules deform until stress is been applied and when the stress is removed they return to their initial state.

Mathematically, Hooke’s law is commonly expressed as:

F = –k.x

In the equation,

Hooke’s Law Graph

The figure below shows the stress-strain curve for low carbon steel.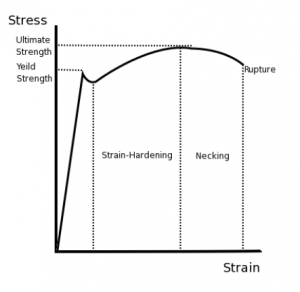        

The material exhibits elastic behaviour up to the yield strength point, after which the material loses elasticity and exhibits plasticity.

From the origin till the proportional limit nearing yield strength, the straight line implies that the material follows Hooke’s law. Beyond the elastic limit between proportional limit and yield strength, the material loses its elastic nature and starts exhibiting plasticity. The area under the curve from origin to the proportional limit falls under the elastic range. The area under the curve from a proportional limit to the rupture/fracture point falls under the plastic range.

The ultimate strength of a material is defined based on the maximum ordinate value given by the stress-strain curve (from origin to rupture). The rupture strength is given by the value at a point of rupture.

The applications of Hooke’s Law are as follows:

• Hooke’s Law is used all branches of science and engineering
• It is used as a fundamental principle behind manometer, spring scale, and balance wheel of the clock.
• Foundation for seismology, acoustics and molecular mechanics.

The disadvantages of Hooke’s Law are as follows:

• The law ceases to apply past the elastic limit of a material.
• The law is accurate only for solid bodies if the forces and deformations are small.
• The law isn’t a universal principle and only applies to the materials as long as they aren’t stretched way past their capacity.

MODULUS OF ELASTICITY:

Young’s modulus is also known as modulus of elasticity and is defined as:

The mechanical property of a material to withstand the compression or the elongation with respect to its length.

It is denoted as E or Y.

Young’s Modulus (also referred to as the Elastic Modulus or Tensile Modulus), is a measure of mechanical properties of linear elastic solids like rods, wires, and such. There are other numbers that give us a measure of elastic properties of a material, like Bulk modulus and shear modulus, but the value of Young’s Modulus is most commonly used. This is because it gives us information about the tensile elasticity of a material (ability to deform along an axis).

Young’s modulus describes the relationship between stress (force per unit area) and strain (proportional deformation in an object. The Young’s modulus is named after the British scientist Thomas Young. A solid object deforms when a particular load is applied to it. If the object is elastic, the body regains its original shape when the pressure is removed. Many materials are not linear and elastic beyond a small amount of deformation. The constant Young’s modulus applies only to linear elastic substances.

Young’s Modulus Formula

E=σ / ϵ

Young’s Modulus Formula From Other Quantities

E ≡ σ (ϵ) / ϵ= (F /A) / (ΔL/ L0) =FL0 / AΔL

Notations Used in the Young’s Modulus Formula

• E is Young’s modulus in Pa
• 𝞂 is the uniaxial stress in Pa
• ε is the strain or proportional deformation
• F is the force exerted by the object under tension
• A is the actual cross-sectional area
• ΔL is the change in the length
• L0 is the actual length

Units and Dimension

The Young’s Modulus of such a material is given by the ratio of stress and strain, corresponding to the stress of the material. The relation is given below.

E = σ / ϵ

Where,

• E is the Young’s Modulus of the material given in N/m2
• σ is the stress applied to the material
• ϵ is the strain corresponding to applied stress in the material

With the value of Young’s modulus for a material, the rigidity of the body can be determined. This is because it tells us about the body’s ability to resist deformation on the application of force.

The Young’s Modulus values (x109N/m2) of different material are given below:

• Steel – 200
• Glass – 65
• Wood – 13
• Plastic (Polystyrene) – 3

Young’s Modulus Factors

Quite obviously we can claim that Steel is a lot more rigid in nature than wood or polystyrene, as in its tendency to experience deformation under applied load is less. Young’s modulus is also used to determine how much a material will deform under a certain applied load.

Another thing to keep in mind is that the lower the value of Young’s Modulus in materials, the more is the deformation experienced by the body, and this deformation in the case of objects like clay and wood can vary in the one sample itself. One part of the clay sample deforms more than the other whereas a steel bar will experience an equal deformation throughout.

VII) Hardness and impact of testing of materials:

Hardness is a characteristic of a material, not a fundamental physical property. It is defined as the resistance to indentation, and it is determined by measuring the permanent depth of the indentation.

More simply put, when using a fixed force (load)* and a given indenter, the smaller the indentation, the harder the material. Indentation hardness value is obtained by measuring the depth or the area of the indentation using one of over 12 different test methods.
 

Hardness testing is used for two general characterizations

1.Material Characteristics
• Test to check material
• Test hardenability
• Test to confirm process 
• Can be used to predict Tensile strength

2. Functionality
• Test to confirm ability to function as designed.
• Wear Resistance
• Toughness
• Resistance to impact

Hardness Testing Considerations
The following sample characteristics should be consider prior to selecting the hardness testing method to use:
• Material
• Sample Size
• Thickness
• Scale
• Shape of sample, round, cylindrical, flat, irregular
• Gage R & R
 

Material
The type of material and expected hardness will determine test method. Materials such as hardened bearing steels have small grain size and can be measured using the Rockwell scale due to the use of diamond indenters and high PSI loading. Materials such as cast irons and powder metals will need a much larger indenter such as used with Brinell scales. Very small parts or small sections may need to be measured on a micro hardness tester using the Vickers or Knoop Scale.

When selecting a hardness scale, a general guide is to select the scale that specifies the largest load and the largest indenter possible without exceeding defined operation conditions and accounting for conditions that may influence the test result.  

Sample Size 

The smaller the part, the lighter the load required to produce the required indentation. On small parts, it is particularly important to be sure to meet minimum thickness requirements and properly space indentations away from inside and outside edges. Larger parts need to be fixture properly to ensure secure placement during the test process without the chance for movement or slippage. Parts that either overhang the anvil or are not easily supported on the anvil should be clamped into place or properly supported.

Cylindrical  Samples

A correction to a test result is needed when testing on cylinder shapes with small diameters due to a difference between axial and radial material flow. Roundness correction factors are added to your testing result based on the diameter of convex cylinder surfaces. Additionally, it is important to maintain a minimum spacing equal to 2~1/2 times the indentation's diameter from an edge or another indentation.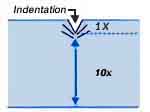 




Sample Thickness

Your sample should have a minimal thickness that is at least 10x (ten times) the indentation depth that is expected to be attained. There are minimum, allowable thickness recommendations for regular and superficial Rockwell methods 

Scales 
Sometimes it is necessary to test in one scale and report in another scale. Conversions have been established that have some validity, but it is important to note that unless an actual correlation has been completed by testing in different scales, established conversions may or may not provide reliable information. Refer to ASTM scale conversion charts for non-austenitic metals in the high hardness range and low hardness range. Also refer to ASTM standard E140 for more scale conversion information.

Gage R&R 

Gage Repeatability and Reproducibility Studies were developed to calculate the ability of operators and their instruments to test accordingly within the tolerances of a given test piece. In hardness testing, there are inherent variables that preclude using standard Gage R&R procedures and formulas with actual test pieces. Material variation and the inability to retest the same area on depth measuring testers are two significant factors that affect GR&R results. In order to minimize these effects,  it is best to do the study on highly consistent test blocks in order to minimize these built in variations.  Operate are ideally suited for these studies. Unfortunately, since these studies can only be effectively done on test blocks, their value does not necessarily translate into actual testing operations. There are a host of factors that can be introduced when testing under real conditions. Newage testers excel at testing in real-world conditions by reducing the effects of vibration, operator influence, part deflection due to dirt, scale, a specimen flexing under load.

Brinell hardness test

The Brinell hardness test method as used to determine Brinell hardness is defined in ASTM E10. Most commonly it is used to test materials that have a structure that is too coarse or that have a surface that is too rough to be tested using another test method, e.g., castings and forgings. Brinell testing often use a very high test load (3000 kgf) and a 10mm diameter indenter so that the resulting indentation averages out most surface and sub-surface inconsistencies.

The Brinell method applies a predetermined test load (F) to a carbide ball of fixed diameter (D) which is held for a predetermined time period and then removed. The resulting impression is measured with a specially designed Brinell microscope or optical system across at least two diameters – usually at right angles to each other and these results are averaged (d). Although the calculation below can be used to generate the Brinell number, most often a chart is then used to convert the averaged diameter measurement to a Brinell hardness number.

Common test forces range from 500kgf often used for non-ferrous materials to 3000kgf usually used for steels and cast iron. There are other Brinell scales with load as low as 1kgf and 1mm diameter indenters but these are infrequently used. 

                                                 

Typically the greatest source of error in Brinell testing is the measurement of the indentation. Due to disparities in operators making the measurements, the results will vary even under perfect conditions. Less than perfect conditions can cause the variation to increase greatly. Frequently the test surface is prepared with a grinder to remove surface conditions.

The jagged edge makes interpretation of the indentation difficult. Furthermore, when operators know the specifications limits for rejects, they may often be influenced to see the measurements in a way that increases the percentage of “good” tests and less re-testing.

Two types of technological remedies for countering Brinell measurement error problems have been developed over the years. Automatic optical Brinell scopes, such as the B.O.S.S. System, use computers and image analysis to read the indentations in a consistent manner. This standardization helps eliminate operator subjectivity so operators are less-prone to automatically view in-tolerance results when the sample’s result may be out-of-tolerance. 

Brinell units, which measure according to ASTM E103, measure the samples using Brinell hardness parameters together with a Rockwell hardness method. This method provides the most repeatable results (and greater speed) since the vagaries of optical interpretations are removed through the use of an automatic mechanical depth measurement.

Using this method, however, results may not be strictly consistent with Brinell results due to the different test methods – an offset to the results may be required for some materials. It is easy to establish the correct values in those cases where this may be a problem.

ROCKWELL HARDNESS TEST

In addition to a Rockwell Hardness Test, there is a Superficial Rockwell. For each test, a minor load is applied to either a diamond cone or a steel ball indenter positioned on the test material’s surface to establish a zero reference position. Next, a major load is applied for a specified amount of time, leaving the minor load applied upon release. The Rockwell hardness number will be the difference in depth between the zero reference position and the indent due to the major load.

The choice of indenter is dependent upon the characteristics of the test material. The Rockwell Hardness Test applies larger minor and major load values than the Superficial Rockwell, yet both tests offer three different major load options. More than thirty different scales are used between Rockwell and Superficial Rockwell hardness testing due to the various choices and combinations of tests, indenters and major loads.

KNOOP HARDNESS TEST

This Micro hardness Test is used on very small parts and material features that are unable to be tested by the other methods and employs a test load of 1000 grams or less. The Knoop Test is performed like Brinell hardness by applying controlled force for a specific amount of time to an indenter in a rhombus-shape. The impression is measured microscopically and is used along with the test load to calculate the hardness value on the Knoop scale.

VICKERS HARDNESS TEST

The Vickers Hardness Test can be performed on both the micro and macro hardness scales with a maximum test load of 50 kilograms. This type of hardness test is also performed by applying controlled force for a specific amount of time to an indenter, which in this case is a square-based diamond pyramid. The impression measurement and test load are used in the appropriate formula to calculate the Vickers hardness value. Like Brinell and Knoop, this method has one scale that covers its entire hardness range.

IMPACT TESTING:

An impact test is used to observe the mechanics that a material will exhibit when it experiences a shock loading that causes the specimen to immediately deform, fracture or rupture completely. To perform this test the sample is placed into a holding fixture with the geometry and orientation determined by the type of test that is used and then a known weight generally but not always in the shape of a pendulum is released from a known height so that it collides with the specimen with a sudden force. This collision between the weight and specimen generally results in the destruction of the specimen but the transfer of energy between the two is used to determine the fracture mechanics of the material.

Purpose of impact testing:

The purpose of an impact test is to determine the ability of the material to absorb energy during a collision. This energy may be used to determine the toughness, impact strength, fracture resistance, impact resistance or fracture resistance of the material depending on the test that was performed and the characteristic that is to be determined. These values are important for the selection of materials that will be used in applications that require the material to undergo very rapid loading processes such as in vehicular collisions.

Types of impact tests:

For a single impact test the three most popular types of test are the Charpy V-notch test, the Izod test and the Tensile Impact test. These three tests all essentially determine the same characteristics of the material but differ in the orientation of the test sample which causes the sample to be stressed in different directions and involve a known weight released from a known height colliding with the specimen in its test fixture. All of these tests are useful in determining the impact mechanics of the test specimen.

Types of materials for impact testing:

Nearly all materials may benefit from impact testing, but the most common types used are metals, plastics, woods, composites, ceramics, and polymers. Generally these materials take the form of sheets of varying thicknesses or short rods depending on the test. However, most materials will experience either ductile or brittle failure depending of the type of test, the rate of loading and the temperature of the sample. Brittle failure of a material requires a small amount of energy to begin the crack or to cause the crack to grow until the sample fails. On the other hand, ductile failure of a material requires a much higher load to initiate and propagate the crack until failure.

Charpy impact testing:

The Charpy impact test, also known as the Charpy V-notch test, is a test which determines the amount of energy absorbed by a material during impact. Charpy impact testing involves striking a specially machined and notched specimen with a calibrated controlled weight pendulum swung from specific height. The standard Charpy-V notch specimen is to very precise dimensions prior to testing. The amount of energy absorbed in fracturing the test-piece is measured and this gives an indication of the toughness of the material being tested. Charpy impact testing show whether a metal can be classified as being either brittle or ductile. This is particularly useful for ferritic steels that show a ductile to brittle transition with decreasing temperature. A brittle metal will absorb only a small amount of energy when impact tested; a tough ductile metal absorbs a large amount of energy.

Izod test:

The Izod test is has become the standard testing procedure for comparing the impact resistances of plastics.  While being the standard for plastics it is also used on other materials. The Izod test is most commonly used to evaluate the relative toughness or impact toughness of materials and as such is often used in quality control applications where it is a fast and economical test. It is used more as a comparative test rather than a definitive test. This is also in part due to the fact that the values do not relate accurately to the impact strength of molded parts or actual components under actual operational conditions.

Izod Test Specimens

Izod test specimens vary depending on what material is being tested. Metallic samples tend to be square in cross section, while polymeric test specimens are often rectangular, being struck parallel to the long axis of the rectangle. Izod test sample usually have a V-notch cut into them, although specimens with no notch as also used on occasion.

What Does the Izod Test Involve

The Izod test involves striking a suitable test piece with a striker, mounted at the end of a pendulum. The test piece is clamped vertically with the notch facing the striker. The striker swings downwards impacting the test piece at the bottom of its swing.

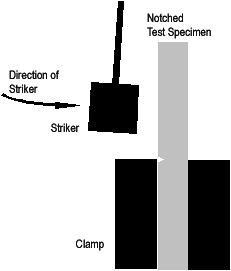Figure 1. Schematic of the Izod impact test.

Some Izod impact testers are equipped to be able to utilise different sized strikers, which impart different amounts of energy. Often a series of strikers may be used to determine the impact energy, starting with small strikers and working up until failure occurs.

Izod Tests at Different Temperatures

Tests are often performed at different temperatures to more closely simulate the actual service conditions. In the case of low temperature tests, specimens may are kept in a freezer until their temperature has equilibrated. They are then immediately removed and tested within seconds of removal from the freezer.

Determination of Izod Impact Energy

At the point of impact, the striker has a known amount of kinetic energy. The impact energy is calculated based on the height to which the striker would have risen, if no test specimen was in place, and this compared to the height to which the striker actually rises. Tough materials absorb a lot of energy, whilst brittle materials tend to absorb very little energy prior to fracture.