Unit - 2
Data representation
Digital Computers use a Binary number system to represent all types of information inside the computers. Alphanumeric characters are represented using binary bits (i. e., 0 and 1). Digital representations are easier to design, storage is easy, accuracy and precision are greater.
There are various types of number representation techniques for digital number representation, for example, Binary number system, octal number system, decimal number system, and hexadecimal number system, etc. But the Binary number system is most relevant and popular for representing numbers in the digital computer system.
Storing Real Number
These are structures as below −

There are two major approaches to store real numbers (i. e., numbers with fractional component) in modern computing. These are (i) Fixed-Point Notation and (ii) Floating Point Notation. In fixed-point notation, there are a fixed number of digits after the decimal point, whereas a floating-point number allows for a varying number of digits after the decimal point.
Fixed-Point Representation −
This representation has a fixed number of bits for the integer part and fractional part. For example, if given fixed-point representation is IIII. FFFF, then you can store the minimum value is 0000. 0001 and the maximum value is 9999. 9999. There are three parts of a fixed-point number representation: the sign field, integer field, and fractional field.
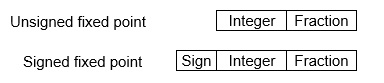
We can represent these numbers using:
- Signed representation: range from -(2(k-1)-1) to (2(k-1)-1), for k bits.
- 1’s complement representation: range from -(2(k-1)-1) to (2(k-1)-1), for k bits.
- 2’s complementation representation: range from -(2(k-1)) to (2(k-1)-1), for k bits.
2’s complementation representation is preferred in the computer system because of its unambiguous property and easier of arithmetic operations.
Example −Assume number is using a 32-bit format which reserves 1 bit for the sign, 15 bits for the integer part, and 16 bits for the fractional part.
Then, -43. 625 is represented as follows:

Where 0 is used to represent + and 1 is used to represent. 000000000101011 is a 15-bit binary value for decimal 43 and 1010000000000000 is a 16-bit binary value for fractional 0. 625.
The advantage of using a fixed-point representation is performance and the disadvantage is a relatively limited range of values that they can represent. So, it is usually inadequate for numerical analysis as it does not allow enough numbers and accuracy. A number whose representation exceeds 32 bits would have to be stored inexactly.

These are above the smallest positive number and largest positive number which can be store in 32-bit representation as given above format. Therefore, the smallest positive number is 2-16 ≈ 0. 000015 approximate and the largest positive number is (215-1)+(1-2-16)=215(1-2-16) =32768, and the gap between these numbers is 2-16.
We can move the radix point either left or right with the help of only integer field is 1.
Floating-Point Representation −
This representation does not reserve a specific number of bits for the integer part or the fractional part. Instead, it reserves a certain number of bits for the number (called the mantissa or significand) and a certain number of bits to say where within that number the decimal place sits (called the exponent).
The floating number representation of a number has two-part: the first part represents a signed fixed-point number called the mantissa. The second part of designates the position of the decimal (or binary) point and is called the exponent. The fixed point mantissa may be a fraction of an integer. Floating -point is always interpreted to represent a number in the following form: Mxre.
Only the mantissa m and the exponent e are physically represented in the register (including their sign). A floating-point binary number is represented similarly except that it uses base 2 for the exponent. A floating-point number is said to be normalized if the most significant digit of the mantissa is 1.
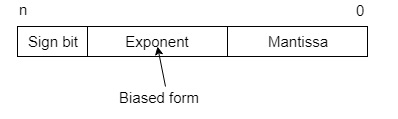
So, the actual number is (-1)s(1+m)x2(e-Bias), where s is the sign bit, m is the mantissa, e is the exponent value, and Bias is the bias number.
Note that signed integers and exponents are represented by either sign representation, or one’s complement representation, or two’s complement representation.
The floating-point representation is more flexible. Any non-zero number can be represented in the normalized form of ±(1. b1b2b3 . . . )2x2n This is the normalized form of a number x.
Example −Suppose the number is using the 32-bit format: the 1-bit sign bit, 8 bits for the signed exponent, and 23 bits for the fractional part. The leading bit 1 is not stored (as it is always 1 for a normalized number) and is referred to as a “hidden bit”.
Then −53.5 is normalized as -53.5=(-110101.1)2=(-1.101011)x25, which is represented as below,

Where 00000101 is the 8-bit binary value of exponent value +5.
Note that 8-bit exponent field is used to store integer exponents -126 ≤ n ≤ 127.
The smallest normalized positive number that fits into 32 bits is (1. 00000000000000000000000)2x2-126=2-126≈1.18x10-38 and the largest normalized positive number that fits into 32 bits is (1. 11111111111111111111111)2x2127=(224-1)x2104 ≈ 3.40x1038. These numbers are represented as below,

The precision of a floating-point format is the number of positions reserved for binary digits plus one (for the hidden bit). In the examples considered here, the precision is 23+1=24.
The gap between 1 and the next normalized floating-point number is known as machine epsilon. The gap is (1+2-23)-1=2-23for the above example, but this is the same as the smallest positive floating-point number because of non-uniform spacing unlike in the fixed-point scenario.
Note that non-terminating binary numbers can be represented in floating-point representation, e. g., 1/3 = (0. 010101 . . . )2 cannot be a floating-point number as its binary representation is non-terminating.
IEEE Floating point Number Representation −
IEEE (Institute of Electrical and Electronics Engineers) has standardized Floating-Point Representation as the following diagram.
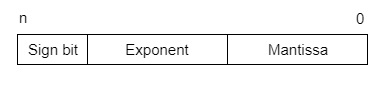
So, the actual number is (-1)s(1+m)x2(e-Bias), where s is the sign bit, m is the mantissa, e is the exponent value, and Bias is the bias number. The sign bit is 0 for a positive number and 1 for a negative number. Exponents are represented by or two’s complement representation.
According to IEEE 754 standard, the floating-point number is represented in the following ways:
- Half Precision (16 bit): 1 sign bit, 5-bit exponent, and 10-bit mantissa
- Single Precision (32 bit): 1 sign bit, 8-bit exponent, and 23-bit mantissa
- Double Precision (64 bit): 1 sign bit, 11-bit exponent, and 52-bit mantissa
- Quadruple Precision (128 bit): 1 sign bit, 15-bit exponent, and 112-bit mantissa
Special Value Representation −
Some special values depended upon different values of the exponent and mantissa in the IEEE 754 standard.
- All the exponent bits 0 with all mantissa bits 0 represents 0. If the sign bit is 0, then +0, else -0.
- All the exponent bits 1 with all mantissa bits 0 represents infinity. If the sign bit is 0, then +∞, else -∞.
- All the exponent bits 0 and mantissa bits non-zero represents a denormalized number.
- All the exponent bits 1 and mantissa bits non-zero represents error.
Key takeaway
Digital Computers use a Binary number system to represent all types of information inside the computers. Alphanumeric characters are represented using binary bits (i. e. , 0 and 1). Digital representations are easier to design, storage is easy, accuracy and precision are greater.
There are various types of number representation techniques for digital number representation, for example, Binary number system, octal number system, decimal number system, and hexadecimal number system, etc. But the Binary number system is most relevant and popular for representing numbers in the digital computer system.
Operations we'll get to know:
- Addition
- Subtraction
- Multiplication
- Division
- Logical operations (not, and, or, nand, nor, xor, xnor)
- Shifting
The rules for doing the arithmetic operations vary depending on what representation is implied.
A LITTLE BIT ON ADDING
----------------------
an overview.
Carry in a b | sum carry out
---------------+----------------
0 0 0 | 0 0
0 0 1 | 1 0
0 1 0 | 1 0
0 1 1 | 0 1
1 0 0 | 1 0
1 0 1 | 0 1
1 1 0 | 0 1
1 1 1 | 1 1
|
a 0011
+b +0001
-- -----
sum 0100
it's just like we do for decimal!
0 + 0 = 0
1 + 0 = 1
1 + 1 = 2 which is 10 in binary, sum is 0 and carry the 1.
1 + 1 + 1 = 3 sum is 1, and carry a 1.
ADDITION
--------
Unsigned:
just like the simple addition given.
examples:
100001 00001010 (10)
+011101 +00001110 (14)
------- ---------
111110 00011000 (24)
Ignore (throw away) carry out of the msb.
Why? Because computers ALWAYS work with fixed precision.
Sign-magnitude:
rules:
- add magnitudes only (do not carry into the sign bit)
- throw away any carry out of the msb of the magnitude
(Due, again, to the fixed precision constraints. )
- add only integers of like sign ( + to + or - to -)
- sign of the result is the same as the sign of the addends
examples:
0 0101 (5) 1 1010 (-10)
+ 0 0011 (3) + 1 0011 (-3)
--------- ---------
0 1000 (8) 1 1101 (-13)
0 01011 (11)
+ 1 01110 (-14)
----------------
don't add! must do subtraction!
One's complement:
by example

so it seems that if there is a carry out (of 1) from the msb, then
the result will be off by 1, so add 1 again to get the correct
result. (Implementation in HW called an "end around carrry.")
Two's complement:
rules:
- just add all the bits
- throw away any carry out of the msb
- (same as for unsigned!)
examples
00011 (3) 101000 111111 (-1)
+ 11100 (-4) + 010000 + 001000 (8)
------------ -------- --------
11111 (-1) 111000 1 000111 (7)
After seeing examples for all these representations, you may see
Why 2's complement addition requires simpler hardware than
Sign mag. Or one's complement addition.
SUBTRACTION
-----------
general rules:
1 - 1 = 0
0 - 0 = 0
1 - 0 = 1
10 - 1 = 1
0 - 1 = borrow!
Unsigned:
- it only makes sense to subtract a smaller number from a larger one
examples
1011 (11) must borrow
- 0111 (7)
------------
0100 (4)
Sign-magnitude:
- if the signs are the same, then do subtraction
- if signs are different, then change the problem to addition
- compare magnitudes, then subtract smaller from larger
- if the order is switched, then switch the sign too.
- when the integers are of the opposite sign, then do
a - b becomes a + (-b)
a + b becomes a - (-b)
examples
0 00111 (7) 1 11000 (-24)
- 0 11000 (24) - 1 00010 (-2)
-------------- --------------
1 10110 (-22)
Do 0 11000 (24)
- 0 00111 (7)
--------------
1 10001 (-17)
(switch sign since the order of the subtraction was reversed)
One's complement:
figure it out on your own
Two's complement:
- change the problem to addition!
a - b becomes a + (-b)
- so, get the additive inverse of b, and do addition.
examples

so do
10110 (-10)
+ 11101 (-3)
------------
1 10011 (-13)
(throw away carry out)
OVERFLOW DETECTION IN ADDITION
unsigned -- when there is a carry out of the msb
1000 (8)
+1001 (9)
-----
1 0001 (1)
sign-magnitude -- when there is a carry out of the msb of the magnitude
1 1000 (-8)
+ 1 1001 (-9)
-----
1 0001 (-1) (carry out of msb of magnitude)
2's complement -- when the signs of the addends are the same, and the sign of the result is different
0011 (3)
+ 0110 (6)
----------
1001 (-7) (note that a correct answer would be 9, but 9 cannot be represented in 4 bit 2's complement)
a detail -- you will never get overflow when adding 2 numbers of opposite signs
OVERFLOW DETECTION IN SUBTRACTION
unsigned -- never
sign-magnitude -- never happen when doing subtraction
2's complement -- we never do subtraction, so use the addition rule
on the addition operation done.
MULTIPLICATION of integers
0 x 0 = 0
0 x 1 = 0
1 x 0 = 0
1 x 1 = 1
-- longhand, it looks just like decimal
-- the result can require 2x as many bits as the larger multiplicand
-- in 2's complement, to always get the right answer without
Thinking about the problem, sign extend both multiplicands to
2x as many bits (as the larger). Then take the correct number
Of result bits from the least significant portion of the result.
2's complement example:

11111111
11111111
11111111
11111111
+ 11111111
----------------
1 00000000111
-------- (correct answer underlined)

Take the least significant 8 bits 11110001 = -15
DIVISION of integers
unsigned only!
example of 15 / 3 1111 / 011
To do this longhand, use the same algorithm as for decimal integers.
LOGICAL OPERATIONS
done bitwise
X = 0011
Y = 1010
X AND Y is 0010
X OR Y is 1011
X NOR Y is 0100
X XOR Y is 1001
Etc.
SHIFT OPERATIONS
A way of moving bits around within a word
3 types: logical, arithmetic and rotate (each type can go either left or right)
logical left - move bits to the left, same order
- throw away the bit that pops off the msb
- introduce a 0 into the lsb
00110101
01101010 (logically left shifted by 1 bit)
logical right - move bits to the right, same order
- throw away the bit that pops off the lsb
- introduce a 0 into the msb
00110101
00011010 (logically right-shifted by 1 bit)
arithmetic left - move bits to the left, same order
- throw away the bit that pops off the msb
- introduce a 0 into the lsb
- SAME AS LOGICAL LEFT SHIFT!
arithmetic right - move bits to the right, same order
- throw away the bit that pops off the lsb
- reproduce the original msb into the new msb
- another way of thinking about it: shift the
Bits, and then do sign extension
00110101 -> 00011010 (arithmetically right-shifted by 1 bit)
1100 -> 1110 (arithmetically right-shifted by 1 bit)
rotate left - move bits to the left, same order
- put the bit that pops off the msb into the lsb,
So no bits are thrown away or lost.
00110101 -> 01101010 (rotated left by 1 place)
1100 -> 1001 (rotated left by 1 place)
rotate right - move bits to the right, same order
- put the bit that pops off the lsb into the msb,
So no bits are thrown away or lost.
00110101 -> 10011010 (rotated right by 1 place)
1100 -> 0110 (rotated right by 1 place)
SASM INSTRUCTIONS FOR LOGICAL AND SHIFT OPERATIONS
SASM has instructions that do bitwise logical operations and shifting operations.
Lnot x x <- NOT (x)
Land x, y x <- (x) AND (y)
Lor x, y x <- (x) OR (y)
Lxor x, y x <- (x) XOR (y)
Llsh x x <- (x), logically left shifted by 1 bit
Rlsh x x <- (x), logically right shifted by 1 bit
Rash x x <- (x), arithmetically right shifted by 1 bit
Rror x x <- (x), rotated right by 1 bit
Key takeaway
Carry in a b | sum carry out
---------------+----------------
0 0 0 | 0 0
0 0 1 | 1 0
0 1 0 | 1 0
0 1 1 | 0 1
1 0 0 | 1 0
1 0 1 | 0 1
1 1 0 | 0 1
1 1 1 | 1 1
|
a 0011
+b +0001
-- -----
sum 0100
It's just like we do for decimal!
0 + 0 = 0
1 + 0 = 1
1 + 1 = 2 which is 10 in binary, sum is 0 and carry the 1.
1 + 1 + 1 = 3 sum is 1, and carry a 1.
In the case of parallel adders, the binary addition of two numbers is initiated when all the bits of the augend and the addend must be available at the same time to perform the computation. In a parallel adder circuit, the carry output of each full adder stage is connected to the carry input of the next higher-order stage, hence it is also called a ripple carry type adder.
In such adder circuits, it is not possible to produce the sum and carry outputs of any stage until the input carry occurs. So there will be a considerable time delay in the addition process, which is known as, carry propagation delay. In any combinational circuit, the signal must propagate through the gates before the correct output sum is available in the output terminals.
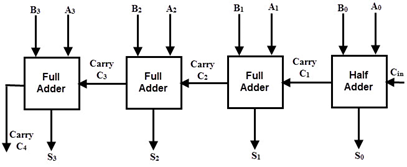
Fig 1 – Example
Consider the above figure, in which the sum S4 is produced by the corresponding full adder as soon as the input signals are applied to it. But the carry input C4 is not available on its final steady-state value until carry c3 is available at its steady-state value. Similarly, C3 depends on C2 and C2 on C1. Therefore, carry must propagate to all the stages so that output S4 and carry C5 settle their final steady-state value.
The propagation time is equal to the propagation delay of the typical gate times the number of gate levels in the circuit. For example, if each full adder stage has a propagation delay of 20n seconds, then S4 will reach its final correct value after 80n (20 × 4) seconds. If we extend the number of stages for adding more bits then this situation becomes much worse.
So the speed at which the number of bits added in the parallel adder depends on the carry propagation time. However, signals must be propagated through the gates at a given enough time to produce the correct or desired output.
The following are the methods to get the high speed in the parallel adder to produce the binary addition.
- By employing faster gates with reduced delays, we can reduce the propagation delay. But there will be a capability limit for every physical logic gate.
- Another way is to increase the circuit complexity to reduce the carry delay time. There are several methods available to speed up the parallel adder, one commonly used method employs the principle of look ahead-carry addition by eliminating inter stage carry logic.
Carry-Lookahead Adder
A carry-Lookahead adder is a fast parallel adder as it reduces the propagation delay by more complex hardware, hence it is costlier. In this design, the carry logic over fixed groups of bits of the adder is reduced to two-level logic, which is nothing but a transformation of the ripple carry design.
This method makes use of logic gates to look at the lower order bits of the augend and addend to see whether a higher-order carry is to be generated or not. Let us discuss this in detail.
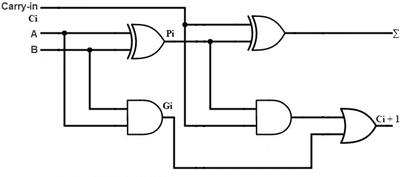
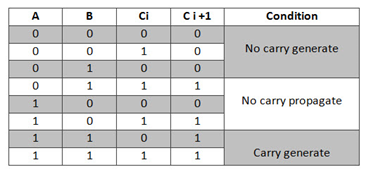
Fig 2 – Example
Consider the full adder circuit shown above with the corresponding truth table. If we define two variables as carry generate Gi and carry propagate Pi then,
Pi = Ai ⊕ Bi
Gi = Ai Bi
The sum output and carry output can be expressed as
Si = Pi ⊕ Ci
C i +1 = Gi + Pi Ci
Where Gi is a carry generate which produces the carry when both Ai, Bi are one regardless of the input carry. Pi is a carry propagate and it is associate with the propagation of carrying from Ci to Ci +1.
The carry output Boolean function of each stage in a 4 stage carry-Lookahead adder can be expressed as
C1 = G0 + P0 Cin
C2 = G1 + P1 C1
= G1 + P1 G0 + P1 P0 Cin
C3 = G2 + P2 C2
= G2 + P2 G1+ P2 P1 G0 + P2 P1 P0 Cin
C4 = G3 + P3 C3
= G3 + P3 G2+ P3 P2 G1 + P3 P2 P1 G0 + P3 P2 P1 P0 Cin
From the above Boolean equations, we can observe that C4 does not have to wait for C3 and C2 to propagate but C4 is propagated at the same time as C3 and C2. Since the Boolean expression for each carry output is the sum of products so these can be implemented with one level of AND gates followed by an OR gate.
The implementation of three Boolean functions for each carry output (C2, C3, and C4) for a carry-Lookahead carry generator is shown in the below figure.

Fig 3 – Look ahead carry generator
Therefore, a 4-bit parallel adder can be implemented with the carry-Lookahead scheme to increase the speed of binary addition as shown below figure. In this, two Ex-OR gates are required by each sum output. The first Ex-OR gate generates Pi variable output and the AND gate generates the Gi variable.
Hence, in two gates levels, all these P’s and G’s are generated. The carry-Lookahead generators allow all these P and G signals to propagate after they settle into their steady-state values and produces the output carriers at a delay of two levels of gates. Therefore, the sum outputs S2 to S4 have equal propagation delay times.
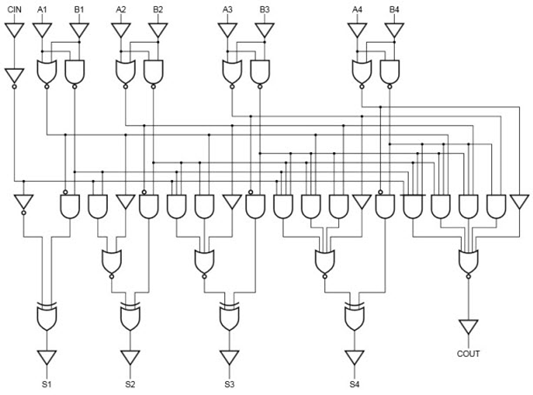
Fig 4 – Example
It is also possible to construct 16 bit and 32 bit parallel adders by cascading the number of 4-bit adders with carry logic. A 16-bit carry-Lookahead adder is constructed by cascading the four 4 bit adders with two more gate delays, whereas the 32-bit carry-Lookahead adder is formed by cascading of two 16 bit adders.
In a 16 bit carry-Lookahead adder, 5 and 8 gate delays are required to get C16 and S15 respectively, which are less as compared to the 9 and 10 gate delay for C16 and S15 respectively in cascaded four-bit carry-Lookahead adder blocks. Similarly, in 32-bit adders, 7 and 10 gate delays are required by C32 and S31 which are less compared to 18 and 17 gate delays for the same outputs if the 32-bit adder is implemented by eight 4 bit adders.
Carry-Lookahead Adder ICS
The high-speed carry-Lookahead adders are integrated on integrated circuits in different bit configurations by several manufacturers. There are several individual carry generator ICs are available so that we have to make the connection with logic gates to perform the addition operation.
A typical carry-Lookahead generator IC is 74182 which accepts four pairs of active low carry propagate (as P0, P1, P2, and P3) and carry generate (Go, G1, G2, and G3) signals and an active high input (Cn).
It provides active high carriers (Cn+x, Cn+y, Cn+z) across the four groups of binary adders. This IC also facilitates the other levels of look-ahead by active low propagate and carry generate outputs.
The logic expressions provided by the IC 74182 are
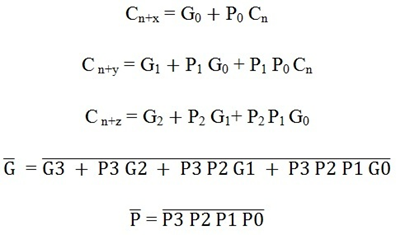
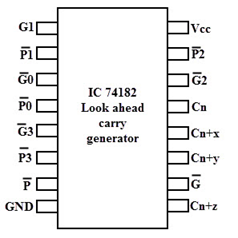
On the other hand, there are many high-speed adder ICs that combine a set of full adders with carry-Lookahead circuitry. The most popular form of such IC is 74LS83/74S283 which is a 4-bit parallel adder high-speed IC that contains four interconnected full adders with a carry-Lookahead circuitry.
The functional symbol for this type of IC is shown below figure. It accepts the two 4 bit numbers as A3A2A1A0 and B3B2B1B0 and input carry Cin0 into the LSB position. This IC produces output sum bits as S3S2S1S0 and the carry output Cout3 into the MSB position.
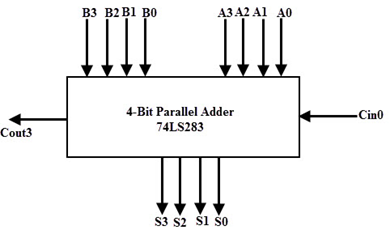
By cascading two or more parallel adder ICs we can perform the addition of larger binary numbers such as 8 bit, 24-bit, and 32-bit addition.
Key takeaway
In the case of parallel adders, the binary addition of two numbers is initiated when all the bits of the augend and the addend must be available at the same time to perform the computation. In a parallel adder circuit, the carry output of each full adder stage is connected to the carry input of the next higher-order stage, hence it is also called a ripple carry type adder.
In such adder circuits, it is not possible to produce the sum and carry outputs of any stage until the input carry occurs. So there will be a considerable time delay in the addition process, which is known as, carry propagation delay. In any combinational circuit, the signal must propagate through the gates before the correct output sum is available in the output terminals.
Booth algorithm gives a procedure for multiplying binary integers in signed 2’s complement representation in the efficient way, i. e. , less number of additions/subtractions required. It operates on the fact that strings of 0’s in the multiplier require no addition but just shifting and a string of 1’s in the multiplier from bit weight 2^k to weight 2^m can be treated as 2^(k+1 ) to 2^m.
As in all multiplication schemes, the booth algorithm requires examination of the multiplier bits and shifting of the partial product. Before the shifting, the multiplicand may be added to the partial product, subtracted from the partial product, or left unchanged according to the following rules:
- The multiplicand is subtracted from the partial product upon encountering the first least significant 1 in a string of 1’s in the multiplier
- The multiplicand is added to the partial product upon encountering the first 0 (provided that there was a previous ‘1’) in a string of 0’s in the multiplier.
- The partial product does not change when the multiplier bit is identical to the previous multiplier bit.
Hardware Implementation of Booths Algorithm – The hardware implementation of the booth algorithm requires the register configuration shown in the figure below.
Booth’s Algorithm Flowchart –
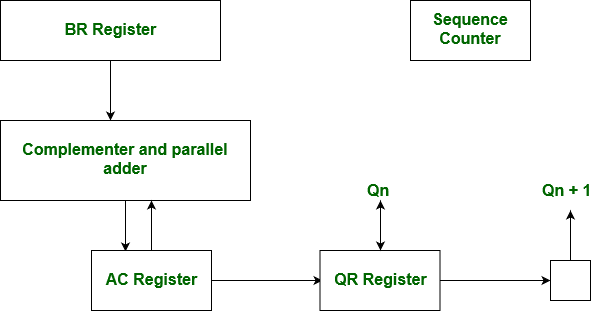
Fig 5 – Booths flowchart
We name the register as A, B, and Q, AC, BR, and QR respectively. Qn designates the least significant bit of multiplier in the register QR. An extra flip-flop Qn+1is appended to QR to facilitate a double inspection of the multiplier. The flowchart for the booth algorithm is shown below.
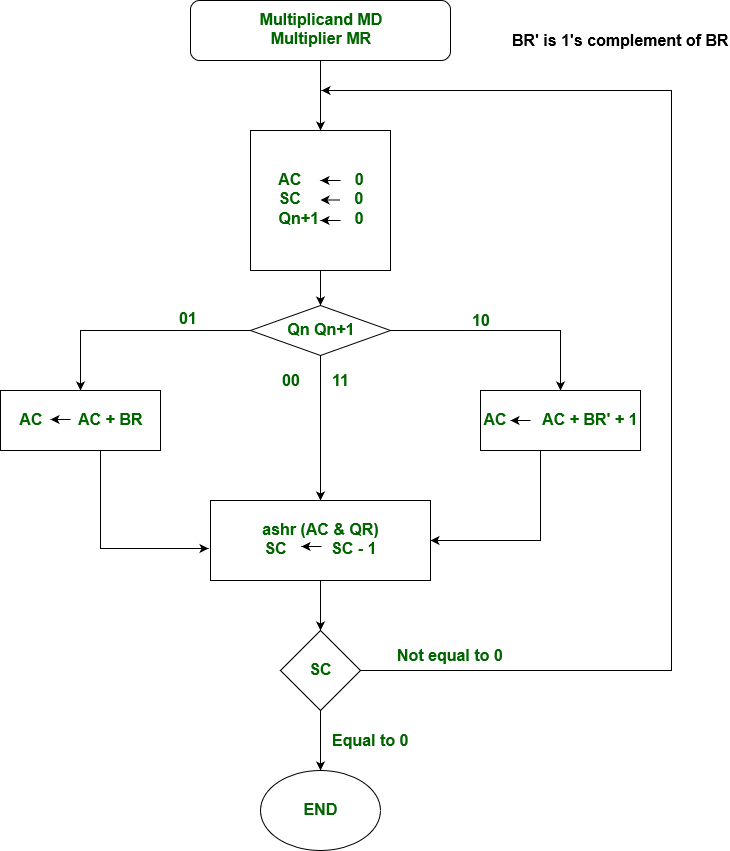
Fig 6 – Booth’s algorithm
AC and the appended bit Qn+1 are initially cleared to 0 and the sequence SC is set to a number n equal to the number of bits in the multiplier. The two bits of the multiplier in Qn and Qn+1are inspected. If the two bits are equal to 10, it means that the first 1 in a string has been encountered. This requires subtraction of the multiplicand from the partial product in AC. If the 2 bits are equal to 01, it means that the first 0 in a string of 0’s has been encountered. This requires the addition of the multiplicand to the partial product in AC.
When the two bits are equal, the partial product does not change. An overflow cannot occur because the addition and subtraction of the multiplicand follow each other. As a consequence, the 2 numbers that are added always have opposite signs, a condition that excludes an overflow. The next step is to shift right the partial product and the multiplier (including Qn+1). This is an arithmetic shift right (ashr) operation in which AC and QR to the right and leaves the sign bit in AC unchanged. The sequence counter is decremented and the computational loop is repeated n times.
Example – A numerical example of the booth’s algorithm is shown below for n = 4. It shows the step by step multiplication of -5 and -7.
MD = -5 = 1011, MD = 1011, MD'+1 = 0101
MR = -7 = 1001
The explanation of the first step is as follows: Qn+1
AC = 0000, MR = 1001, Qn+1 = 0, SC = 4
Qn Qn+1 = 10
So, we do AC + (MD)'+1, which gives AC = 0101
On right shifting AC and MR, we get
AC = 0010, MR = 1100 and Qn+1 = 1
OPERATION | AC | MR | Qn+1 | SC |
| 0000 | 1001 | 0 | 4 |
AC + MD’ + 1 | 0101 | 1001 | 0 |
|
ASHR | 0010 | 1100 | 1 | 3 |
AC + MR | 1101 | 1100 | 1 |
|
ASHR | 1110 | 1110 | 0 | 2 |
ASHR | 1111 | 0111 | 0 | 1 |
AC + MD’ + 1 | 0010 | 0011 | 1 | 0 |
The product is calculated as follows:
Product = AC MR
Product = 0010 0011 = 35
Best Case and Worst Case Occurrence:
Best case is when there is a large block of consecutive 1’s and 0’s in the multipliers so that there is a minimum number of logical operations taking place, as in addition and subtraction.
The worst case is when there are pairs of alternate 0’s and 1’s, either 01 or 10 in the multipliers, so that maximum number of additions and subtractions are required.
Key takeaway
Booth algorithm gives a procedure for multiplying binary integers in signed 2’s complement representation in the efficient way, i. e. , less number of additions/subtractions required. It operates on the fact that strings of 0’s in the multiplier require no addition but just shifting and a string of 1’s in the multiplier from bit weight 2^k to weight 2^m can be treated as 2^(k+1 ) to 2^m.
As in all multiplication schemes, the booth algorithm requires examination of the multiplier bits and shifting of the partial product.
In an earlier post Restoring Division learned about restoring division. Now, here perform Non-Restoring division, it is less complex than the restoring one because the simpler operation is involved i. e. Addition, and subtraction, also now restoring step is performed. In the method, rely on the sign bit of the register which initially contains zero named as A.
Here is the flow chart is given below.
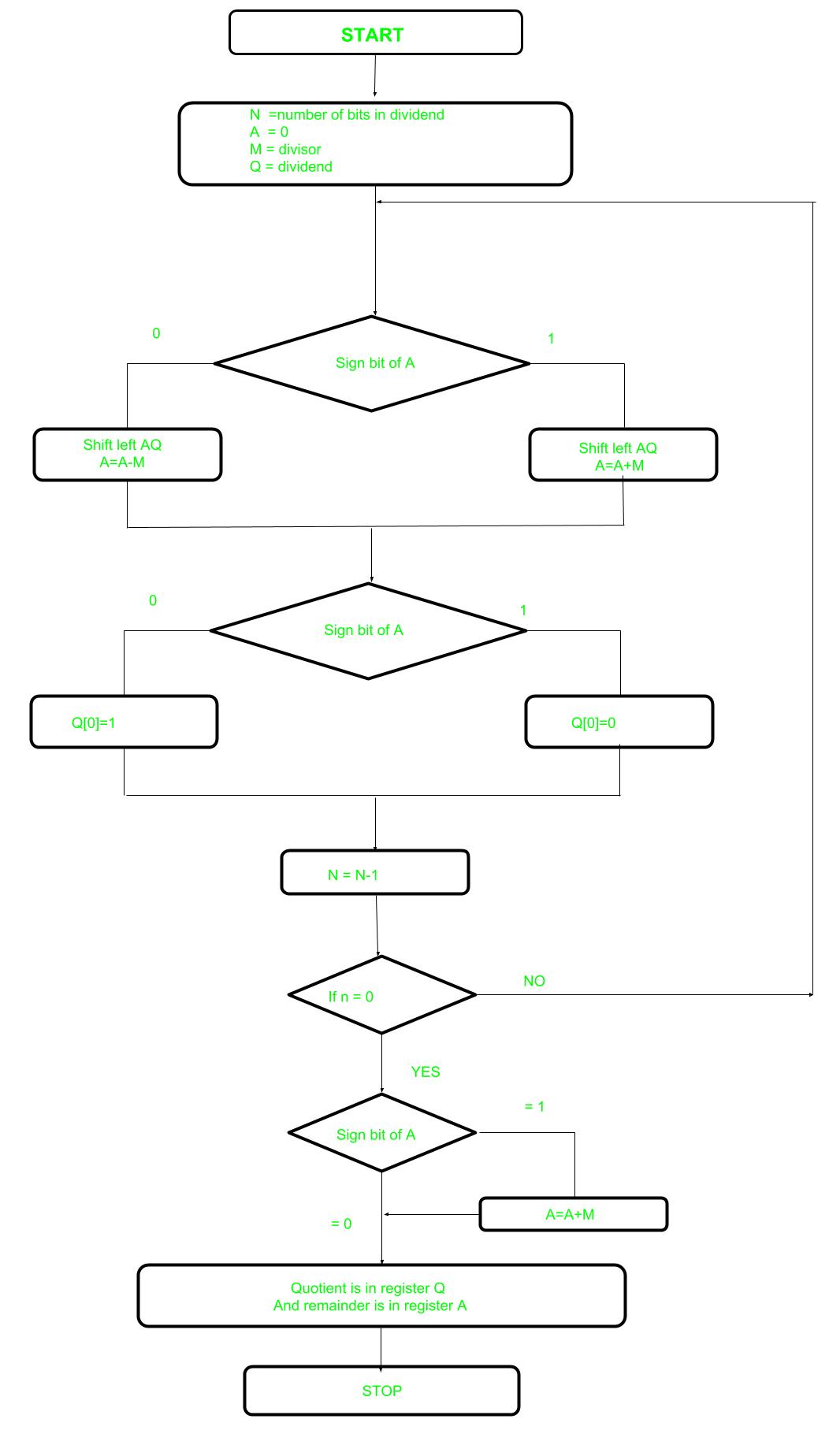
Fig 7 – Flowchart
Let’s pick the step involved:
- Step-1: First the registers are initialized with corresponding values (Q = Dividend, M = Divisor, A = 0, n = number of bits in dividend)
- Step-2: Check the sign bit of register A
- Step-3: If it is 1 shift left the content of AQ and perform A = A+M, otherwise shift left AQ and perform A = A-M (means add 2’s complement of M to A and store it to A)
- Step-4: Again the sign bit of register A
- Step-5: If the sign bit is 1 Q[0] become 0 otherwise Q[0] become 1 (Q[0] means the least significant bit of register Q)
- Step-6: Decrements value of N by 1
- Step-7: If N is not equal to zero go to Step 2 otherwise go to the next step
- Step-8: If sign bit of A is 1 then perform A = A+M
- Step-9: Register Q contain quotient and A contain remainder
Examples: Perform Non_Restoring Division for Unsigned Integer
Dividend =11
Divisor =3
-M =11101
N | M | A | Q | Action |
4 | 00011 | 00000 | 1011 | Start |
|
| 00001 | 011_ | Left shift AQ |
|
| 11110 | 011_ | A=A-M |
3 |
| 11110 | 0110 | Q[0]=0 |
|
| 11100 | 110_ | Left shift AQ |
|
| 11111 | 110_ | A=A+M |
2 |
| 11111 | 1100 | Q[0]=0 |
|
| 11111 | 100_ | Left Shift AQ |
|
| 00010 | 100_ | A=A+M |
1 |
| 00010 | 1001 | Q[0]=1 |
|
| 00101 | 001_ | Left Shift AQ |
|
| 00010 | 001_ | A=A-M |
0 |
| 00010 | 0011 | Q[0]=1 |
Quotient = 3 (Q)
Remainder = 2 (A)
Restoring Division Algorithm For Unsigned Integer
A division algorithm provides a quotient and a remainder when we divide two numbers. They are generally of two types slow algorithm and fast algorithm. Slow division algorithms are restoring, non-restoring, non-performing restoring, SRT algorithm, and under fast comes to Newton–Raphson, and Goldschmidt.
In this article, will be performing restoring algorithm for an unsigned integer. Restoring term is due to fact that the value of register A is restored after each iteration.

Fig 8 – Example
Here, register Q contains quotient and register A contain remainder. Here, the n-bit dividend is loaded in Q, and the divisor is loaded in M. Value of Register is initially kept 0 and this is the register whose value is restored during iteration due to which it is named Restoring.
Let’s pick the step involved:
- Step-1: First the registers are initialized with corresponding values (Q = Dividend, M = Divisor, A = 0, n = number of bits in dividend)
- Step-2: Then the content of register A and Q is shifted left as if they are a single unit
- Step-3: Then the content of register M is subtracted from A and the result is stored in A
- Step-4: Then the most significant bit of the A is checked if it is 0 the least significant bit of Q is set to 1 otherwise if it is 1 the least significant bit of Q is set to 0 and the value of register A is restored i. e the value of A before the subtraction with M
- Step-5: The value of counter n is decremented
- Step-6: If the value of n becomes zero we get of the loop otherwise we repeat from step 2
- Step-7: Finally, the register Q contains the quotient, and A contain remainder
Examples:
Perform Division Restoring Algorithm
Dividend = 11
Divisor = 3
n | M | A | Q | Operation |
4 | 00011 | 00000 | 1011 | Initialize |
| 00011 | 00001 | 011_ | Shift left AQ |
| 00011 | 11110 | 011_ | A=A-M |
| 00011 | 00001 | 0110 | Q[0]=0 And restore A |
3 | 00011 | 00010 | 110_ | Shift left AQ |
| 00011 | 11111 | 110_ | A=A-M |
| 00011 | 00010 | 1100 | Q[0]=0 |
2 | 00011 | 00101 | 100_ | Shift left AQ |
| 00011 | 00010 | 100_ | A=A-M |
| 00011 | 00010 | 1001 | Q[0]=1 |
1 | 00011 | 00101 | 001_ | Shift left AQ |
| 00011 | 00010 | 001_ | A=A-M |
| 00011 | 00010 | 0011 | Q[0]=1 |
Remember to restore the value of A most significant bit of A is 1. As that register Q contains the quotient, i. e. 3 and register A contain remainder 2.
Key takeaway
In an earlier post Restoring Division learned about restoring division. Now, here perform Non-Restoring division, it is less complex than the restoring one because the simpler operation is involved i. e. Addition, and subtraction, also now restoring step is performed. In the method, rely on the sign bit of the register which initially contains zero named as A.
References:
1. “Computer Organization and Design: The Hardware/Software Interface”, 5th Edition by David A. Patterson and John L. Hennessy, Elsevier.
2. “Computer Organization and Embedded Systems”, 6th Edition by Carl Hamacher, McGraw Hill Higher Education.
3. “Computer Architecture and Organization”, 3rd Edition by John P. Hayes, WCB/McGraw-Hill
4. “Computer Organization and Architecture: Designing for Performance”, 10th Edition by William Stallings, Pearson Education.
5. “Computer System Design and Architecture”, 2nd Edition by Vincent P. Heuring and Harry F. Jordan, Pearson Education.