Unit - 3
Linked Lists
Each node in singly linked list points to next node and it appears to move in one direction. Thus SLL is unidirectional. Fig. 6.3 shows schematic diagram of singly linked list with 4 nodes.
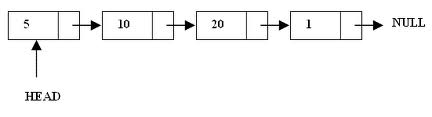
Fig: Singly Linked List
Implementation in C:
Typedef struct node
{
Int data;
Struct node *next;
}node;
A node is defined by structures in C. This structure is called as self referential structure. This node stores integer value in data field of node. Next stores address of next node and hence declared as a pointer variable.
Creation of First Node:
Step 1 : node *P;
Step 2 : P = (node*)malloc(sizeof(node));
Step 3 : P->data = 10;
Step 4 : P->next=NULL;
- Step 1 declares P as a node.
- Step 2 allocates memory to node P with c standard function malloc. The malloc function returns void pointer and hence typecasted before assigning to P.
- Step 3 stores value 10 in data field of node P. This is done with the help of arrow operator .It is also called as structure member operator.
- Step 4 stores NULL value in address field of node P.
P1: Program to create a Linked List
#include <stdio.h>
#include<conio.h>
Typedef struct node
{
Int data;
Struct node *next;
}node;
Void main()
{
Node *HEAD, *P ;
Int n,i;
Printf(“Enter no of nodes to be inserted ”)
Scanf(“%d”, &n);
HEAD = (node*)malloc(sizeof(node));//get the first node
Scanf(“%d”, &(HEAD->data));// get data in first node
HEAD->next= NULL;
P=HEAD;// currently HEAD and P points to same node
For(i=1;i<n;i++)// for n nodes
{
P->next= (node*)malloc(sizeof(node));
P=P->next;
P->next= NULL;
Scanf(“%d”, &(P->data));
}
}
Explanation:
Declare node with self referential structure.
Create HEAD node which is first node in Linked List.
HEAD = (node*)malloc(sizeof(node));
Store data in First node .
Scanf(“%d”, &(HEAD->data));//
Currently there is only one node in Linked List. So *next contains Null value and HEAD and P points to same node.
HEAD next=NULL;
P=HEAD;
Now create remaining nodes with the help of following code.
For(i=1;i<n;i++)// for n nodes
{
P->next= (node*)malloc(sizeof(node));
P=P->next;
P->next= NULL;
Scanf(“%d”, &(P->data));
}
P2: Program to create and display the Linked List using function. This program also counts total number of nodes in Linked List
#include <stdio.h>
#include<conio.h>
Typedef struct node
{
Int data;
Struct node *next;
}node;
Node *create(int);
Void display(node*);
Int count(node *);
Void main()
{
Node *HEAD;
Int n, x;
Printf(“Enter number of nodes”);
Scanf(“%d”, &n);
HEAD = create(n) ;
Display(HEAD);
x= count(HEAD);
Printf(“Total number of nodes =”+x);
Getch();
}
Node *create(int n)
{
Node *start, *P;
Int i;
HEAD= (node*)malloc(sizeof(node));
Start-> next = NULL;
Scanf(“%d”, &(start->data));
P= start;
For(i=1;i<n;i++)
{
P->next = (node*)malloc(sizeof(node));
P=P->next;
Scanf(“%d”, &(P->data));
P->next= NULL;
}
Return(start);
}
Void display(node *P)
{
Printf(“Nodes are”)
While(P!=NULL)
{
Printf(“ %d ”P->data);
P=P->next;
}
}
Int count(node *P)
{
Int i=0;
While(P!=NULL)
{
P=P->next;
i++;
}
Return(i)
}
Output:
Enter number of nodes: 3
10 20 30
Nodes are
10 20 30
Total number of nodes: 3
Traversing is the most common operation that is performed in almost every scenario of singly linked list. Traversing means visiting each node of the list once in order to perform some operation on that. This will be done by using the following statements.
Ptr = head;
while (ptr!=NULL)
{
ptr = ptr -> next;
}
Algorithm
STEP 1: SET PTR = HEAD
STEP 2: IF PTR = NULL
WRITE "EMPTY LIST"
GOTO STEP 7
END OF IF
STEP 4: REPEAT STEP 5 AND 6 UNTIL PTR != NULL
STEP 5: PRINT PTR→ DATA
STEP 6: PTR = PTR → NEXT
[END OF LOOP]
STEP 7: EXIT
C function
#include<stdio.h>
#include<stdlib.h>
Void create(int);
Void traverse();
Struct node
{
int data;
struct node *next;
};
Struct node *head;
Void main ()
{
int choice,item;
do
{
printf("\n1.Append List\n2.Traverse\n3.Exit\n4.Enter your choice?");
scanf("%d",&choice);
switch(choice)
{
case 1:
printf("\nEnter the item\n");
scanf("%d",&item);
create(item);
break;
case 2:
traverse();
break;
case 3:
exit(0);
break;
default:
printf("\nPlease enter valid choice\n");
}
}while(choice != 3);
}
Void create(int item)
{
struct node *ptr = (struct node *)malloc(sizeof(struct node *));
if(ptr == NULL)
{
printf("\nOVERFLOW\n");
}
else
{
ptr->data = item;
ptr->next = head;
head = ptr;
printf("\nNode inserted\n");
}
}
Void traverse()
{
struct node *ptr;
ptr = head;
if(ptr == NULL)
{
printf("Empty list..");
}
else
{
printf("printing values . . . . .\n");
while (ptr!=NULL)
{
printf("\n%d",ptr->data);
ptr = ptr -> next;
}
}
}
Output
1.Append List
2.Traverse
3.Exit
4.Enter your choice?1
Enter the item
23
Node inserted
1.Append List
2.Traverse
3.Exit
4.Enter your choice?1
Enter the item
233
Node inserted
1.Append List
2.Traverse
3.Exit
4.Enter your choice?2
Printing values . . . . .
233
23
Searching an element (Iterative approach)
1) Initialize a node pointer, temp = head
2) Do following while temp is not NULL
Temp->data is equal to the data being searched, return true.
Temp = temp->next
3) Return false
Now, let us see a program to search element in a linked list using the iterative approach.
Iterative C Program to search for an element in the Linked List
#include <stdio.h>
#include <stdlib.h>
// Creating node with data and a pointer
Struct node {
Int data;
Struct node *next;
}*head;
Void createList(int n);
Void search_element(int data);
Void displayList();
Int main()
{
Int n, data, element;
Printf("\nEnter the total number of nodes: ");
Scanf("%d", &n);
CreateList(n);
Printf("\nThe List is \n");
DisplayList();
Printf("\nEnter the element to be searched in the list : "); // value of the element to be searched in the list
Scanf("%d",&element);
Search_element(element);
Return 0;
}
Void createList(int n)
{
Struct node *newNode, *temp;
Int data, i;
Head = (struct node *)malloc(sizeof(struct node));
// When the list is empty
If(head == NULL)
{
Printf("Unable to allocate memory.");
}
Else
{
Printf("\nEnter the data of node 1: ");
Scanf("%d", &data);
Head->data = data;
Head->next = NULL;
Temp = head;
For(i=2; i<=n; i++)
{
NewNode = (struct node *)malloc(sizeof(struct node));
If(newNode == NULL)
{
Printf("Unable to allocate memory.");
Break;
}
Else
{
Printf("\nEnter the data of node %d: ", i);
Scanf("%d", &data);
NewNode->data = data;
NewNode->next = NULL;
Temp->next = newNode;
Temp = temp->next;
}}}}
Void search_element(int data)
{
Int count = 0;
Struct node* temp;
Temp = head;
While(temp != NULL) // Start traversing from head node
{
If(temp -> data == data)
{
Printf("\nElement found at position %d",count);
Break;
}
Else
{
Count = count + 1;
Temp = temp -> next;
}}
Printf("\n Element %d is not found in the list\n",data);
}
Void displayList()
{
Struct node *temp;
If(head == NULL)
{
Printf("List is empty.");
}
Else
{
Temp = head;
While(temp != NULL)
{
Printf("%d\t", temp->data);
Temp = temp->next;
}
Printf("\n");
}}
OUTPUT
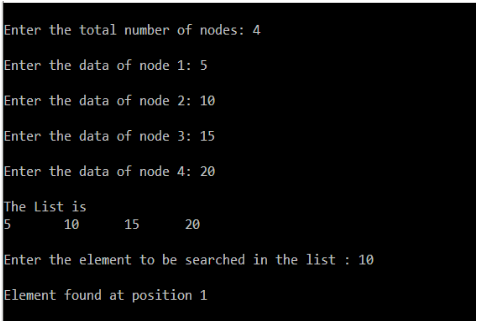
Insertion is a three- step process −
- Create a new Link with provided data.
- Point New Link to old First Link.
- Point First Link to this New Link.
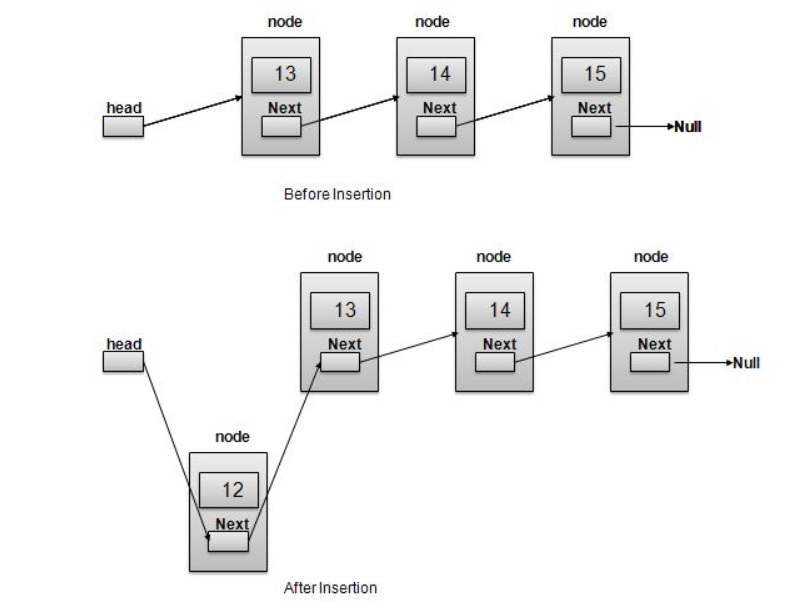
//insert link at the first location
Void insertFirst(int key, int data){
//create a link
struct node *link = (struct node*) malloc(sizeof(struct node));
link->key = key;
link->data = data;
//point it to old first node
link->next = head;
//point first to new first node
head = link;
}
Deletion is a two step process −
- Get the Link pointed by First Link as Temp Link.
- Point First Link to Temp Link's Next Link.
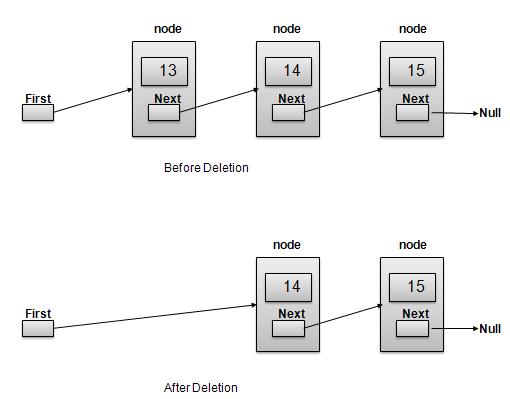
//delete first item
Struct node* deleteFirst(){
//save reference to first link
struct node *tempLink = head;
//mark next to first link as first
head = head->next;
//return the deleted link
return tempLink;
}
A Double ended queue is a queue in which elements can be inserted or deleted from either front or rear. New elements can be added at either the front or the rear. Likewise, existing items can be removed from either end. This abstract data structure often abbreviated as deque and is also known as head-tail linked list. Deques are useful when we need both random access, and ability to delete/insert at both the ends. This hybrid linear structure provides all the capabilities of stacks and queues in a single data structure.
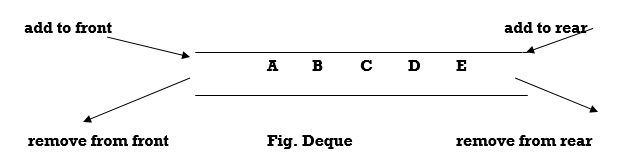
DeQueue can be categorized in two types
1) Input restricted DeQueue: It allows insertions at only one end
2) output restricted DeQueue: It allows deletions from only one end
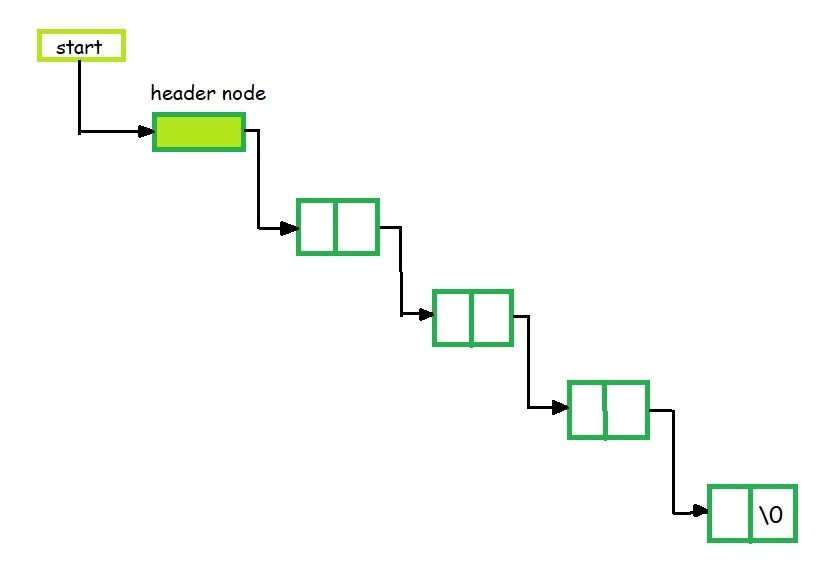
A header node is a special node that is found at the beginning of the list. A list that contains this type of node, is called the header-linked list. This type of list is useful when information other than that found in each node is needed.
For example, suppose there is an application in which the number of items in a list is often calculated. Usually, a list is always traversed to find the length of the list. However, if the current length is maintained in an additional header node that information can be easily obtained.
Types of Header Linked List
Grounded Header Linked List
It is a list whose last node contains the NULL pointer. In the header linked list the start pointer always points to the header node. start -> next = NULL indicates that the grounded header linked list is empty. The operations that are possible on this type of linked list are Insertion, Deletion, and Traversing.
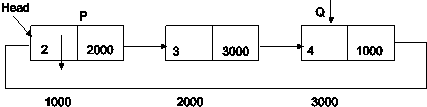
Construction of doubly linked list:
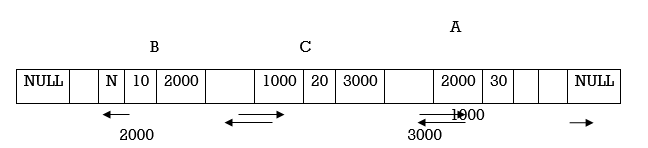
Fig.: Doubly Linked List
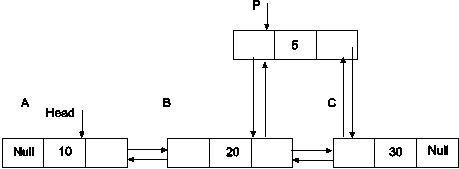
Fig. Shows example of doubly linked list. Assume Our Doubly linked List contains 3 nodes and let us denote it by A, B,and C.
Node A starts at memory address 1000.It does not have any predecessor node so left link points to NULL. Data field contains integer value ‘10’.Right Link of node in doubly linked list always stores memory address of its successor node. Hence right link of node A contains 2000 i.e memory address of node B.
Left Link of node in doubly linked list contains memory address of predecessor node. A is predecessor node of B so left link of B contains 1000 i.e. memory address of A. Data field contains value’20’ and right link contains 3000 i.e memory address of node C.
Same strategy is applied for all nodes in doubly linked list.
Node in doubly linked list is defined as
Typedef struct node
{
Int data;
Struct node *next,*prev;
}node;
Node is defined as self referential structure which contains one data field denoted as ‘data’ and two pointers ‘*next’, ‘*prev’.*next points to successor node and *prev points to predecessor node.
C Implementation of Doubly Linked List:
P6: Program to create and display doubly linked list
#include<stdio.h>
#include<conio.h>
#include<stdlib.h>
Typedef struct node
{
Int data;
Struct node *next,*prev;
}node;
Node *create();
Void display(node*);
Void main()
{
Node *head;
Head= NULL;
Head=create();
Printf(“Elements of Doubly Linked List”);
Display(head);
}
Node *create()
{
Node *p, *q, *r;
Int i,n,x;
p=NULL;
Printf(“Enter number of elements”);
Scanf(“%d”,&n);
For(i=0;i<n;i++)
{
Printf(“Enter data”);
Scanf(“%d”,&x);
r= (node*)malloc(sizeof(node));
r->data=x;
r->prev=q->next=NULL;
If(p==NULL)
q=p=r;
Else
q->next=r;
r->prev=q;
q=r;
}
Return(p);
}
Void display()
{
While(p!=NULL)
{
printf(“ %d ”, p->data);
p=p->next;
}
}
Operations On Doubly Linked List
1. Insertion of Node
2.Deletion of Node
3.Traversing
Insertion of Node
Node can be inserted in doubly linked list at 3 positions.
(A)At the beginning
(B)In the middle
(C)At the end
Algorithms:
Assume node to be inserted is pointed by P.
(A)Insertion of node at the beginning of Doubly Linked List
Suppose our DLL consists of 3 nodes.
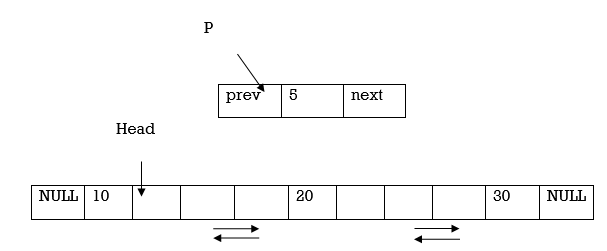
Insertion can be done in following steps
1.Allocate memory to node pointed by P
P= (node*)malloc(sizeof(node))
2.Update the next pointer of the node P to the Head node and make prev pointer as NULL
P->next=Head
P->prev= NULL

3.Now update Head node’s prev pointer to point to node P and make node P as head node.
Head->prev=P
P = Head

Insertion of node in the middle of Doubly Linked List
To insert a node in the middle of DLL we must know the data value of node after which node is to be inserted. Once we get the data value of node, traverse to that node.
Let us represent data value in a node by variable ‘data’ and value of node after which new node is to be inserted is ‘val’. Suppose we want to insert new node after 2nd node.
2.Initially Q points to first node.
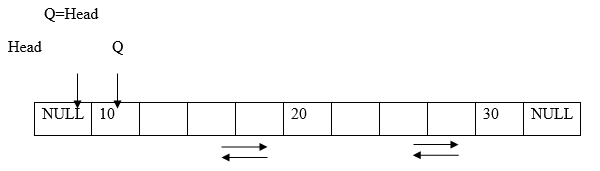
Traverse to the node after which node is to be inserted.
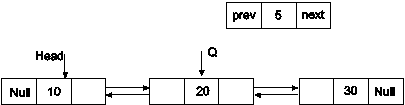
While(Q!=NULL)
{
If(Q->data==val)
Break;
Q=Q->next
}
Now Q points to 2nd node.
 P
P
Make the next pointer of node P to point to node next to Q. Also make the prev point of node P to point to node 2nd node.
P->next=Q->next
P->prev=Q
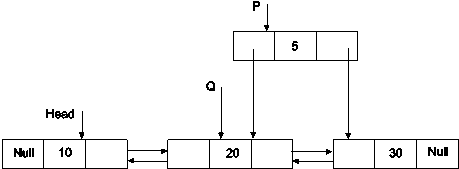
Now point Q’s next to P
Q->next=P
Insertion of node at the last of Doubly Linked List
1.Traverse the list to end.
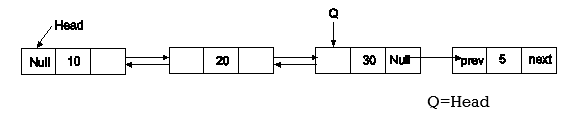
While(Q->next!=Null)
Q=Q->next
2.Update next pointer of Q to point to P.
Q->next=P

3.Make next pointer of P to point to NULL and prev pointer to point to Q
P->prev=Q
P->next=NULL
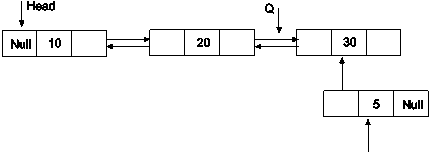
Deletion Of Node From Dll
Node can be deleted from doubly linked list at 3 positions
(A)At the beginning
(B)In the middle
(C)At the end
Algorithms:
(A)Deletion of node from the beginning of Doubly Linked List
Assume P points to node to be deleted.
1.P and Head points to the first node in DLL.
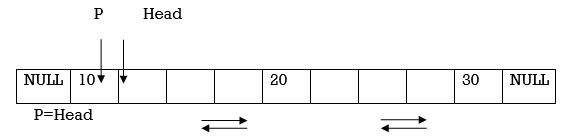
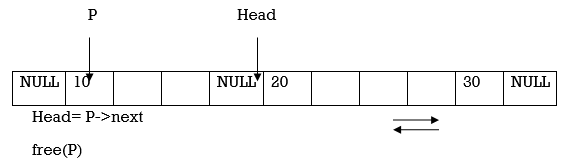
2.Now move the Head pointer to point to the next node. Also change the Head’s prev and P’s next to NULL. Then dispose the node pointed by P.
(B)Deletion of node from the middle of Doubly Linked List
To delete a node in the middle of DLL we must know the data value of node after which node is to be deleted. Once we get the data value of node, traverse to that node.
Let us represent data value in a node by variable ‘data’ and value of node after which new node is to be inserted is ‘val’. Suppose we want to delete 3rd node
1.Initially P and Head points to first node.

2.Traverse to the node after which node is to be deleted.
While(P!=NULL)
{
If(P->data==val)
Break;
Q=P;
P=P->next
}
Now Q points to 2nd node and P points to 3rd node i.e. node to be deleted.

3.Set next of Q to next of P and prev of next of P to Q.
P->next=Q->next
P->next->prev=Q

Dispose P.
Free(P)
(c)Deletion of node from the end of Doubly Linked List
1.Position pointer Q to the node previous to P. In order to find this position, list should be traversed first, beginning from the head.
Q=Head
While(Q->next->next!=NuLL)
Q=Q->next
P=Q->next

2.Set next link of the Q and prev link of P to NULL.
Q->next=NuLL

3.Dispose off the Last Node.
Free(P)
P7: Program to perform following operations on doubly linked list
(A)Create a doubly linked list
(B)Insertion of a node
1.At the beginning of doubly Linked List
2.In the middle of doubly Linked List
3.At the end of doubly Linked List
(C)Deletion of a node
1.beginning of doubly Linked List
2.the middle of doubly Linked List
3.end of doubly Linked List
(D)Display doubly Linked List
#include <stdio.h>
#include<conio.h>
#include<stdlib.h>
Typedef struct node
{
Char data;
Struct node *next, *prev;
}node;
Node *create();
Node *insert_s(node *head, char x)
Node *insert_b(node *head, char x)
Node *insert_e(node *head, char x);
Node *delete_s(node *head );
Node *delete_b(node *head );
Node *delete_e(node *head );
Void display(node*);
Void main()
{
Int c,op;
Char x;
Node *head=NULL;
Do
{
Printf(“1.create\n2.insert\n3.delete\n4.display\n5.Quit”);
Printf(“Enter your choice”);
Scanf(“%d”, &c);
Switch(c)
{
Case 1:head=create();
Break;
Case 2:printf(“\n 1.Beginning\n2. Middle\n3.end”);
Printf(“Enter your choice”);
Scanf(“%d”,&op);
Printf(“Enter data to be inserted”);
Flushall();
x=getchar();
Switch(op)
{
Case 1:head=insert_s(head,x);
Break;
Case 2:head=insert_m(head,x);
Break;
Case 3:head=insert_e(head,x);
Break;
}
Break;
Case 3:printf(“\n 1.Beginning\n2. Middle\n3.end”);
Printf(“Enter your choice”);
Scanf(“%d”,&op);
Switch(op)
{
Case 1:head=delete_s(head);
Break;
Case 2:head=delete_m(head);
Break;
Case 3:head=delete_e(head);
Break;
}
Break;
Case 4:display(head);
Break;
}
}while(op!=5);
}
Node *create()
{
Node *head,*p;
Char x;
Head=NULL;
Printf(“Enter string”);
Flushall();
While(x=getchar()!=’\n’)
{
If(head==NULL)
{
Head=p=(node *)malloc(sizeof(node));
Head->next=head->prev=NULL;
}
Else
{
p->next=(node*)malloc(sizeof(node));
p->next->prev=p;
p=p->next;
p->next=NULL;
}
p->data=x;
}
Return(head);
}
Node *insert_s(node *head, char x)
{
Node *p;
p= (node*)malloc(sizeof(node));
p->data=x;
If(head==NULL)
{
Head=p;
Head->next=head->prev=NULL;
}
Else
{
p->next=head;
Head->prev=p;
p->prev=NULL;
Head=p;
}
Return(head);
}
Node *insert_m(node *head, char x)
{
Node *p,*q;
Char y;
p= (node*)malloc(sizeof(node));
p->data=x;
Printf(“Insert after which character”);
Flushall();
y=getchar();
For(q=head;q!=NULL && q->data!=y;q=q->next)
{
If(q->data==y)
{
p->next=q->next;
p->prev=q;
p->next->prev=p;
p->prev->next=p;
}
Else
Printf(“data not found”);
Return(head);
}
}
Node *insert_e(node *head, char x)
{
Node *p,*q;
p= (node*)malloc(sizeof(node));
p->data=x;
If(head==NULL)
{
Head=p;
Head->next=head->prev=NULL;
}
Else
{
For(q=head;q->next!=NULL;q=q->next)
{
q->next=p;
p->prev=q;
p->next=NULL;
}
Return(head);
}
Node *delete_s(node *head)
{
Node *p,*q;
If(head==NULL)
{
Printf(“Linked list is empty”);
Return(head);
}
If(head->next==NULL)
{
p=head;
Free(p);
Head=NULL;
}
Else
{
P=head;
Head=head->next;
Head->prev=NULL;
Free(p);
}
Return(head);
}
Node *delete_m(node *head)
{
Node *p,*q;
Char x;
If(head==NULL)
{
Printf(“List is empty”);
Return(head);
}
Printf(“Enter data to be deleted”);
Flushall();
x=getchar();
For(p=head;p!=NULL && p->data!=x;p=p->next)
{
If(p->data!=x)
{
Printf(“data not found”);
Return(head);
}
If(p==head)
{
Head=head->next;
If(head!=NULL)
Head->prev=NULL;
Free(p);
}
Else
{
p->prev->next=p->next;
p->next->prev=p->prev;
Free(p);
}
Return(head);
}
}
Void display(node *head)
{
Node *p;
If(head!=NULL)
{
For(p=head;p!=NULL;p=p->next)
Printf(“%c”, p->data);
}
}
Output:
Create
Insert
Delete
Display
Quit
Enter choice: 1
Enter a string: abcde
1. Create
2. Insert
3. Delete
4. Display
5. Quit
Enter choice: 2
Beginning
Middle
End
Enter choice: 2
Enter data to be inserted:f
Insert after which character: c
1. Create
2. Insert
3. Delete
4. Display
5. Quit
Enter choice: 4
Abcfde
1. Create
2. Insert
3. Delete
4. Display
5. Quit
Enter choice:3
Beginning
Middle
End
Enter choice: 1
1. Create
2. Insert
3. Delete
4. Display
5. Quit
Enter choice:4
Bcfde
Reverse of Doubly Linked List:
C Function to reverse a doubly linked list:
Void reverse(node *head)
{
Node *p;
If(head!=NULL)
{
For(p=head;p->next!=NULL;p=p->next)
{
For(;p!=NULL;p=p->prev)
Printf(“%c”, p->data);
}
}
}
Analysis is the theoretical way to study performance of computer program. Analysis of an algorithm is helpful to decide the complexity of an algorithm. There are three ways to analyze an algorithm which are stated as below.
1. Worst case: In worst case analysis of an algorithm, upper bound of an algorithm is calculated. This case considers the maximum number of operation on algorithm. For example if user want to search a word in English dictionary which is not present in the dictionary. In this case user has to check all the words in dictionary for desired word.
2. Best case: In best case analysis of an algorithm, lower bound of an algorithm is calculated. This case considers the minimum number of operation on algorithm. For example if user want to search a word in English dictionary which is found at the first attempt. In this case there is no need to check other words in dictionary.
3. Average case: In average case analysis of an algorithm, all possible inputs are consider and computing time is calculated for all inputs. Average case analysis is performed by summation of all calculated value which is divided by total number of inputs. In average case analysis user must be aware about the all types of input so average case analyses are very rarely used in practical cases.
Circular Linked List
A circular linked list is a linked list in which last node points to first node i.e next pointer of last node points to first node. Circular linked list does not contain NULL pointers.

Here A is the first node and C is the last node. C points to A and hence C stores address of A.
Operations On Circular Linked List
1.Insertion of a node
2.Deletion of a node
3.Traversing
Insertion of a node
Node can be inserted at 3 positions i.e. at the beginning, in the middle and at the end of circular linked list.
Insertion at the beginning:
Assume node to be inserted is pointed by P. Insertion can be done in following steps.
1.Position pointer Q to the last node of CLL. For this traverse the list to the end of list.
Q=Head
While(Q->next!=NULL)
Q=Q->next
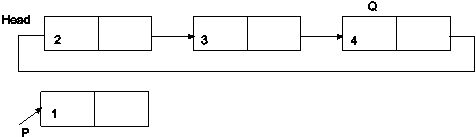
2.Set next link of Q to P and next link of P to Head of CLL.
Q->next=P
P->next=Head
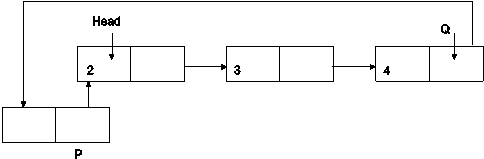
3.Make P as Head of CLL
Head=P
Insertion in the middle
Insertion of node in the middle of CLL is same as that of Singly linked List.
Insertion at the end
1.Position pointer Q to the last node of CLL. For this traverse the list to the end of list.
Q= Head
While(Q->next!=Head)
Q=Q->next

2.Set next link of Q to P and next link of P to Head.
P= Q->next
Head= P->next

Deletion Of Node From Cll
Node can be deleted at the beginning, from the middle and end of CLL.
Deletion at the beginning
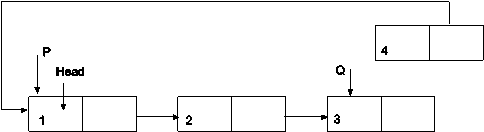
Assume node to be deleted is pointed by P. Deletion can be done in following steps.
1.Position pointer P to point to Head Node and Q to the last node.
P=Q= Head
While(Q->next!=Head)
Q=Q->next
2.Position pointer Head to the next of P. Set next link of Q to point to new Head.
Head=Head->next
Head= Q->next
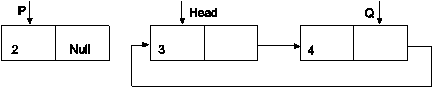
3.Dispose P.
Free(P)
Deletion in the middle of CLL
Deletion of node in middle of CLL is same as that of Singly linked list.
Deletion at the end of CLL
1. Position pointer Q to last but one node of CLL.
Q=Head
While(Q->next->next!=Head)
Q=Q->next

2.Set next link of Q to Head and P to NULL. Dispose P.
Q->next=Head
Free(P)
3.Set next link of Q to Head and P to NULL. Dispose P.
Q->next=Head
Free(P)

P8: Program to create add remove & display element from circular linked list
#include<stdio.h>
#include<alloc.h>
#include<conio.h>
Struct node
{
Int data;
Struct node *next;
};
Struct node *head=NULL;
Struct node *tail=NULL;
Void main()
{
Void addrecord();
Void deleterecord();
Void disrecord();
Int ch;
Clrscr();
Do
{
Printf("\n 1. To add records\n");
Printf("\n 2. To delete a records\n");
Printf("\n 3. To view the records\n");
Printf("\n 4. To exit\n");
Printf("\n Enter your choice\n");
Scanf("%d",&ch);
Fflush(stdin);
switch(ch)
{
case 1:addrecord();
break;
case 2:deleterecord();
break;
case 3: disrecord();
break;
case 4:exit(0);
}
} while (ch!=4);
}
Void addrecord()
{
Int new_data;
Char ans='y';
Struct node *ptr,*prev,*temp;
Clrscr();
while (ans=='y')
{
Temp=(struct node*)malloc(sizeof(struct node));
Printf("\n Enter the new element:\n");
Scanf("%d",&new_data);
Fflush(stdin);
Temp->data=new_data;
Temp->next=NULL;
If (head==NULL)
{
head=tail=temp;
Temp->next=head;
}
Else
{
Tail->next=temp;
Tail=temp;
}
Printf("\n Would you like to enter another data(y\\n): \n");
Ans = getchar();
Fflush(stdin);
}
}
Void deleterecord()
{
struct node *ptr,*prev,*delnode;
Int elt;
Printf("\n Enter the enrollment number to be deleted \n");
Scanf("%d",&elt);
Fflush(stdin);
if (head==NULL)
{
printf("\n No elements in the list \n");
Return;
}
Else
{
If (head->data==elt)
{
Delnode=head;
If (head==tail)
Head=tail=NULL;
Else
{
Head=head->next;
Tail->next=head;
}
}
else if (tail->data==elt)
{
for(ptr=head;(ptr!=tail);prev=ptr,ptr=ptr->next);
Delnode=tail;
Tail=prev;
Tail->next=head;
}
Else
{
For(prev=ptr=head;(ptr->data!=elt)&&(ptr!=tail);
Prev=ptr,ptr=ptr->next);
If(ptr->data==elt)
{
Delnode=ptr;
Prev->next=ptr->next;
Printf("yes...");
}
else
{
printf("Given element not found in the list");
Getch();
return;
}
}
}
free(delnode);
}
Void disrecord()
{
Struct node *ptr,*prev=NULL;
If (head==NULL)
{
printf("\n No records to view\n");
Return;
}
Printf("\n The elements in the circular list are\n");
For (ptr=head;prev!=tail;prev=ptr,ptr=ptr->next)
Printf("\n\n %d",ptr->data);
Printf(" NULL\n\n ");
Getch();
}
Complexity of an algorithm is the function which gives the running time and space requirement of an algorithm in terms of size of input data. Frequency count refers to the number of times particular instructions executed in a block of code. Frequency count plays important role in the performance analysis of an algorithm. Each instruction in algorithm is incremented by one as its execution. Frequency count analysis is the form of priori analysis. Frequency count analysis produces output in terms of time complexity and space complexity.
- Time complexity: Time complexity is about to number of times compiler execute basic operations in instruction. That is because basic operations are so defined that the time for the other operations is much less than or at most proportional to the time for the basic operations. To determine time complexity user need to calculate frequency count and express it in terms of notations. Total time taken by program is the summation of compile time and running time. Out of these two main point to take care about is running time as it depends upon the number and magnitude of input and output.
- Space complexity: Space complexity is about to maximum amount of memory required for algorithm. To determine space complexity user need to calculate frequency count and express it in terms of notations.
Frequency count analysis for this code is as follows
Sr. No. | Instructions | Frequency count |
#include<stdio.h> |
| |
2. | #include<conio.h> |
|
3. | Void main() { |
|
4. | Int marks; |
|
5. | Printf(“enter a marks”); | Add 1 to the time count |
6. | Scanf(“%d”,&marks); | Add 1 to the space count |
7. | Printf(“your marks is %d”,marks); | Add 1 to the time count |
8. | Getch(); } |
|
In the above example, for the first four instructions there is no frequency count. For data declaration and the inclusion of header file there is no frequency count. So, for this example has a frequency count for time is 2 and a frequency count for space is 1. So, total frequency count is 3.
Consider the following example
Sr. No. | Instructions | Frequency count |
#include<stdio.h> |
| |
2. | #include<conio.h> |
|
3. | Void main() { |
|
4. | Int sum=0; | 1 |
5. | For(i=0;i<5;i++) | 6 |
6. | Sum=sum+i; | 5 |
7. | Printf(“Addition is %d”,sum); | 1 |
8. | Getch(); } |
|
Explanation: In the above example, one is add to frequency count for instruction four and seven after that in fifth instruction is check from zero to five so it will add value six to frequency count. ‘For’ loop executed for five times so for sixth instruction frequency count is five. Total frequency count for above program is 1+6+5+1 =13.
Consider the following example
Sr. No. | Instructions | Frequency count |
1. | #include<stdio.h> |
|
2. | #include<conio.h> |
|
3. | Void main() { |
|
4. | Int a[2][3],b[2][3],c[2][3]] |
|
5. | For(i=0;i<m;i++) | m+1 |
6. | { |
|
7. | For(j=0;j<n;j++) | m(n+1) |
8. | { |
|
9. | c[i][j]=a[i][j]*b[i][j]; | m.n |
10. | }} |
|
11. | Getch(); } |
|
Explanation: In the above example, in instruction five value of ‘i’ is check from 0 to ‘m’ so frequency count is ‘m+1’ for fifth instruction. In instruction five value of ‘j’ is check from 0 to ‘n’ so frequency count is ‘n+1’ but this instruction is in the for loop which execute for ‘m’ times, so for seventh instruction is m*(n+1). Ninth instruction is in the two for loops, out of which first for loop execute for m times and second ‘for’ loop execute for ‘n’ times. So for ninth instruction frequency count is m*n. The total frequency count for the above program is (m+1)+m(n+1)+mn=2m+2mn+1=2m(1+n)+1.
Consider the following example
Sr. No. | Instructions | Frequency count |
1. | #include<stdio.h> |
|
2. | #include<conio.h> |
|
3. | Void main() { |
|
4. | Int a[2][3],b[2][3],c[2][3]] |
|
5. | For(i=0;i<m;i++) | m+1 |
6. | { |
|
7. | For(j=0;j<n;j++) | m(n+1) |
8. | { |
|
9. | a[i][j]=n; | m.n |
10. | For(k=0;k<n;k++) | Mn(n+1) |
11. | c[i][j]=a[i][j]*b[i][j]; | m.n.n |
12. | }} |
|
13. | Getch(); } |
|
Explanation: For above program total frequency count
=(m+1)+m(n+1)+mn+mn(n+1)+mn
=m+1+mn+m+mn+mn2 +mn+mn2
=2 mn2+3mn+2m+1
=mn(2n+3)+2m+1
Consider the following example
Sr. No. | Instructions | Frequency count |
1. | #include<stdio.h> |
|
2. | #include<conio.h> |
|
3. | Void main() { |
|
4. | Int n=1,m; | 1 |
5. | Do |
|
6. | { |
|
7. | Printf(“hi”); | 10 |
8. | If(n==10) | 10 |
9. | Break; | 1 |
10. | n++; | 9 |
11. | } |
|
12. | While(n<15); | 10 |
13. | Getch(); } |
|
Explanation: the above example, one is add to frequency count for instruction four. The loop will execute till value of n is incremented to 10 from 1, so for loop statements ie instructions seven and eight is execute for tem times. When the value of ‘n’ is ten then ‘break’ statement will execute for one time and it will skip the tenth execution of tenth instruction. Tenth instruction will add value nine to frequency count. Total frequency count for above program is 10+10+1+9+10 = 40.
References:
1. Algorithms, Data Structures, and Problem Solving with C++”, Illustrated Edition by Mark Allen Weiss, Addison-Wesley Publishing Company.
2. “How to Solve it by Computer”, 2nd Impression by R.G. Dromey, Pearson Education.
3. “Fundamentals of Data Structures”, Illustrated Edition by Ellis Horowitz, Sartaj Sahni, Computer Science Press.