Unit - 2
Search Techniques
The uninformed search does not contain any domain knowledge such as closeness, the location of the goal. It operates in a brute-force way as it only includes information about how to traverse the tree and how to identify leaf and goal nodes. Uninformed search applies a way in which search tree is searched without any information about the search space like initial state operators and test for the goal, so it is also called blind search. It examines each node of the tree until it achieves the goal node.
It can be divided into five main types:
● Breadth-first search
● Uniform cost search
● Depth-first search
● Iterative deepening depth-first search
● Bidirectional Search
1. Breadth-first Search:
● Breadth-first search is the most common search strategy for traversing a tree or graph. This algorithm searches breadthwise in a tree or graph, so it is called breadth-first search.
● BFS algorithm starts searching from the root node of the tree and expands all successor node at the current level before moving to nodes of next level.
● The breadth-first search algorithm is an example of a general-graph search algorithm.
● Breadth-first search implemented using FIFO queue data structure.
Advantages:
● BFS will provide a solution if any solution exists.
● If there are more than one solutions for a given problem, then BFS will provide the minimal solution which requires the least number of steps.
Disadvantages:
● It requires lots of memory since each level of the tree must be saved into memory to expand the next level.
● BFS needs lots of time if the solution is far away from the root node.
Example:
In the below tree structure, we have shown the traversing of the tree using BFS algorithm from the root node S to goal node K. BFS search algorithm traverse in layers, so it will follow the path which is shown by the dotted arrow, and the traversed path will be:
S---> A--->B---->C--->D---->G--->H--->E---->F---->I---->K
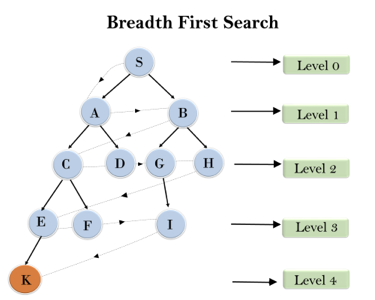
Fig 1: Breadth first search
Time Complexity: Time Complexity of BFS algorithm can be obtained by the number of nodes traversed in BFS until the shallowest Node. Where the d= depth of shallowest solution and b is a node at every state.
T (b) = 1+b2+b3+.......+ bd= O (bd)
Space Complexity: Space complexity of BFS algorithm is given by the Memory size of frontier which is O(bd).
Completeness: BFS is complete, which means if the shallowest goal node is at some finite depth, then BFS will find a solution.
Optimality: BFS is optimal if path cost is a non-decreasing function of the depth of the node.
2. Depth-first Search
● Depth-first search is a recursive algorithm for traversing a tree or graph data structure.
● It is called the depth-first search because it starts from the root node and follows each path to its greatest depth node before moving to the next path.
● DFS uses a stack data structure for its implementation.
● The process of the DFS algorithm is similar to the BFS algorithm.
Advantage:
● DFS requires very less memory as it only needs to store a stack of the nodes on the path from root node to the current node.
● It takes less time to reach to the goal node than BFS algorithm (if it traverses in the right path).
‘
Disadvantage:
● There is the possibility that many states keep reoccurring, and there is no guarantee of finding the solution.
● DFS algorithm goes for deep down searching and sometime it may go to the infinite loop.
Example:
In the below search tree, we have shown the flow of depth-first search, and it will follow the order as:
Root node--->Left node ----> right node.
It will start searching from root node S, and traverse A, then B, then D and E, after traversing E, it will backtrack the tree as E has no other successor and still goal node is not found. After backtracking it will traverse node C and then G, and here it will terminate as it found goal node.
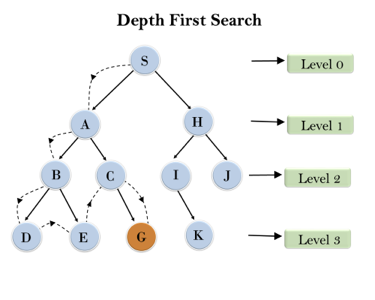
Fig 2: Depth first search
Completeness: DFS search algorithm is complete within finite state space as it will expand every node within a limited search tree.
Time Complexity: Time complexity of DFS will be equivalent to the node traversed by the algorithm. It is given by:
T(n)= 1+ n2+ n3 +.........+ nm=O(nm)
Where, m= maximum depth of any node and this can be much larger than d (Shallowest solution depth)
Space Complexity: DFS algorithm needs to store only single path from the root node, hence space complexity of DFS is equivalent to the size of the fringe set, which is O(bm).
Optimal: DFS search algorithm is non-optimal, as it may generate a large number of steps or high cost to reach to the goal node.
3. Depth-Limited Search Algorithm:
A depth-limited search algorithm is similar to depth-first search with a predetermined limit. Depth-limited search can solve the drawback of the infinite path in the Depth-first search. In this algorithm, the node at the depth limit will treat as it has no successor nodes further.
Depth-limited search can be terminated with two Conditions of failure:
● Standard failure value: It indicates that problem does not have any solution.
● Cutoff failure value: It defines no solution for the problem within a given depth limit.
Advantages:
Depth-limited search is Memory efficient.
Disadvantages:
● Depth-limited search also has a disadvantage of incompleteness.
● It may not be optimal if the problem has more than one solution.
Example:
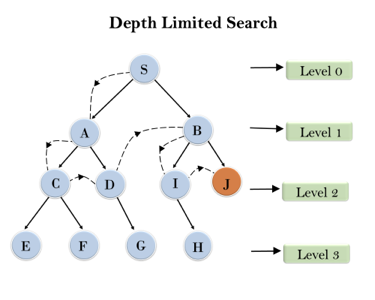
Fig 3: Depth limited search
Completeness: DLS search algorithm is complete if the solution is above the depth-limit.
Time Complexity: Time complexity of DLS algorithm is O(bℓ).
Space Complexity: Space complexity of DLS algorithm is O(b×ℓ).
Optimal: Depth-limited search can be viewed as a special case of DFS, and it is also not optimal even if ℓ>d.
4. Uniform-cost Search Algorithm:
Uniform-cost search is a searching algorithm used for traversing a weighted tree or graph. This algorithm comes into play when a different cost is available for each edge. The primary goal of the uniform-cost search is to find a path to the goal node which has the lowest cumulative cost. Uniform-cost search expands nodes according to their path costs form the root node. It can be used to solve any graph/tree where the optimal cost is in demand. A uniform-cost search algorithm is implemented by the priority queue. It gives maximum priority to the lowest cumulative cost. Uniform cost search is equivalent to BFS algorithm if the path cost of all edges is the same.
Advantages:
● Uniform cost search is optimal because at every state the path with the least cost is chosen.
Disadvantages:
● It does not care about the number of steps involve in searching and only concerned about path cost. Due to which this algorithm may be stuck in an infinite loop.
Example:

Fig 4: Uniform cost search
Completeness: Uniform-cost search is complete, such as if there is a solution, UCS will find it.
Time Complexity: Let C* is Cost of the optimal solution, and ε is each step to get closer to the goal node. Then the number of steps is = C*/ε+1. Here we have taken +1, as we start from state 0 and end to C*/ε.
Hence, the worst-case time complexity of Uniform-cost search isO(b1 + [C*/ε])/.
Space Complexity: The same logic is for space complexity so, the worst-case space complexity of Uniform-cost search is O(b1 + [C*/ε]).
Optimal: Uniform-cost search is always optimal as it only selects a path with the lowest path cost.
5. Iterative deepening depth-first Search:
The iterative deepening algorithm is a combination of DFS and BFS algorithms. This search algorithm finds out the best depth limit and does it by gradually increasing the limit until a goal is found.
This algorithm performs depth-first search up to a certain "depth limit", and it keeps increasing the depth limit after each iteration until the goal node is found.
This Search algorithm combines the benefits of Breadth-first search's fast search and depth-first search's memory efficiency.
The iterative search algorithm is useful uninformed search when search space is large, and depth of goal node is unknown.
Advantages:
● It Combines the benefits of BFS and DFS search algorithm in terms of fast search and memory efficiency.
Disadvantages:
● The main drawback of IDDFS is that it repeats all the work of the previous phase.
Example:
Following tree structure is showing the iterative deepening depth-first search. IDDFS algorithm performs various iterations until it does not find the goal node. The iteration performed by the algorithm is given as:
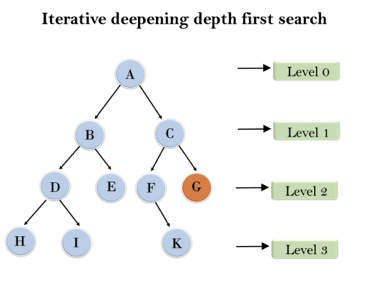
Fig 5: Iterative deepening depth first search
1'st Iteration-----> A
2'nd Iteration----> A, B, C
3'rd Iteration------>A, B, D, E, C, F, G
4'th Iteration------>A, B, D, H, I, E, C, F, K, G
In the fourth iteration, the algorithm will find the goal node.
Completeness: This algorithm is complete is if the branching factor is finite.
Time Complexity: Let's suppose b is the branching factor and depth is d then the worst-case time complexity is O(bd).
Space Complexity: The space complexity of IDDFS will be O(bd).
Optimal: IDDFS algorithm is optimal if path cost is a non- decreasing function of the depth of the node.
6. Bidirectional Search Algorithm:
Bidirectional search algorithm runs two simultaneous searches, one form initial state called as forward-search and other from goal node called as backward-search, to find the goal node. Bidirectional search replaces one single search graph with two small subgraphs in which one starts the search from an initial vertex and other starts from goal vertex. The search stops when these two graphs intersect each other.
Bidirectional search can use search techniques such as BFS, DFS, DLS, etc.
Advantages:
● Bidirectional search is fast.
● Bidirectional search requires less memory
Disadvantages:
● Implementation of the bidirectional search tree is difficult.
● In bidirectional search, one should know the goal state in advance.
Example:
In the below search tree, bidirectional search algorithm is applied. This algorithm divides one graph/tree into two sub-graphs. It starts traversing from node 1 in the forward direction and starts from goal node 16 in the backward direction.
The algorithm terminates at node 9 where two searches meet.
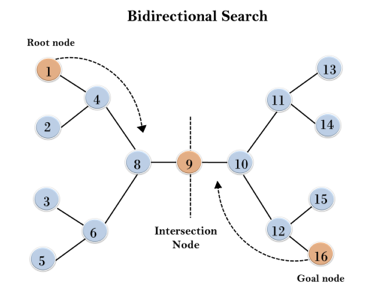
Fig 6: Bidirectional search
Completeness: Bidirectional Search is complete if we use BFS in both searches.
Time Complexity: Time complexity of bidirectional search using BFS is O(bd).
Space Complexity: Space complexity of bidirectional search is O(bd).
Optimal: Bidirectional search is Optimal.
A heuristic is a technique for making our search process more efficient. Some heuristics assist in the direction of a search process without claiming completeness, whereas others do. A heuristic is a piece of problem-specific knowledge that helps you spend less time looking for answers. It's a strategy that works on occasion, but not all of the time.
The heuristic search algorithm uses the problem information to help steer the way over the search space. These searches make use of a number of functions that, assuming the function is efficient, estimate the cost of going from where you are now to where you want to go.
A heuristic function is a function that converts problem situation descriptions into numerical measures of desirability. The heuristic function's objective is to direct the search process in the most profitable routes by recommending which path to take first when there are multiple options.
The following procedures should be followed when using the heuristic technique to identify a solution:
1. Add domain—specific information to select what is the best path to continue searching along.
2. Define a heuristic function h(n) that estimates the ‘goodness’ of a node n. Specifically, h(n) = estimated cost(or distance) of minimal cost path from n to a goal state.
3. The term heuristic means ‘serving to aid discovery’ and is an estimate, based on domain specific information that is computable from the current state description of how close we are to a goal.
A search problem in which multiple search orders and the use of heuristic knowledge are clearly understood is finding a path from one city to another.
1. State: The current city in which the traveler is located.
2. Operators: Roads linking the current city to other cities.
3. Cost Metric: The cost of taking a given road between cities.
4. Heuristic information: The search could be guided by the direction of the goal city from the current city, or we could use airline distance as an estimate of the distance to the goal.
Key takeaway
Informed Search also called heuristic or intelligent search, this uses information about the problem to guide the search—usually guesses the distance to a goal state and is therefore efficient, but the search may not always be possible.
The purpose of heuristic function is to guide the search process in the most profitable directions by suggesting which path to follow first when more than is available.
Generate and Test Search is a heuristic search technique based on Depth First Search with Backtracking that, if done correctly, assures the discovery of a solution. In this method, all possible solutions are developed and examined to find the best one. It ensures that the best answer is compared to all other solutions that may have been provided.
It's also known as the British Museum Search Algorithm because it's similar to randomly looking for an exhibit or finding an object in the British Museum.
The heuristic function does the evaluation since all of the solutions are generated systematically in the generate and test process, but if there are any paths that are highly improbable to lead us to a result, they are ignored. The heuristic accomplishes this by ranking all of the options and is frequently successful in doing so.
When it comes to solving difficult problems, systematic Generate and Test may be unproductive. However, in complex circumstances, there is a strategy for reducing the search space by combining generate and test search with other strategies.
For example, in the Artificial Intelligence Program DENDRAL, we use two techniques to work on a smaller search space, the first of which is Constraint Satisfaction Techniques, followed by Generate and Test Procedure to produce an effective result by working on a smaller number of lists generated in the first step.
Algorithm
- Generate a possible solution. For example, generating a particular point in the problem space or generating a path for a start state.
- Test to see if this is a actual solution by comparing the chosen point or the endpoint of the chosen path to the set of acceptable goal states
- If a solution is found, quit. Otherwise go to Step 1
Key takeaway
Generate and Test Search is a heuristic search technique based on Depth First Search with Backtracking that, if done correctly, assures the discovery of a solution. In this method, all possible solutions are developed and examined to find the best one.
Hill climbing search is a local search problem. The purpose of the hill climbing search is to climb a hill and reach the topmost peak/ point of that hill. It is based on the heuristic search technique where the person who is climbing up on the hill estimates the direction which will lead him to the highest peak.
The hill climbing algorithm is a local search algorithm that proceeds in the direction of rising elevation/value in order to find the mountain's peak or the best solution to the problem. When it hits a peak value, it stops since no neighbor has a greater value.
The hill climbing algorithm is a strategy for optimizing mathematical problems. The Traveling-salesman algorithm is one of the most well-known examples of a hill climbing algorithm. We have a problem where we need to reduce the salesman's trip distance. It's also known as greedy local search because it just considers its good immediate neighbor state and nothing else.
The state and value of a node in a hill climbing algorithm are the two components. When a decent heuristic is available, hill climbing is usually used. We don't need to maintain or handle the search tree or graph in this technique because it simply preserves a single current state.
Features of Hill climbing algorithm
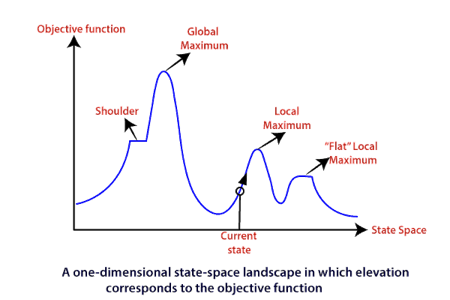
To understand the concept of hill climbing algorithm, consider the below landscape representing the goal state/peak and the current state of the climber. The topographical regions shown in the figure can be defined as:
● Global Maximum: It is the highest point on the hill, which is the goal state.
● Local Maximum: It is the peak higher than all other peaks but lower than the global maximum.
● Flat local maximum: It is the flat area over the hill where it has no uphill or downhill. It is a saturated point of the hill.
● Shoulder: It is also a flat area where the summit is possible.
● Current state: It is the current position of the person.
Types of Hill climbing search algorithm
There are following types of hill-climbing search:
● Simple hill climbing
● Steepest-ascent hill climbing
● Stochastic hill climbing
● Random-restart hill climbing
Simple hill climbing search
Simple hill climbing is the simplest technique to climb a hill. The task is to reach the highest peak of the mountain. Here, the movement of the climber depends on his move/steps. If he finds his next step better than the previous one, he continues to move else remain in the same state. This search focus only on his previous and next step.
Simple hill climbing Algorithm
- Create a CURRENT node, NEIGHBOUR node, and a GOAL node.
- If the CURRENT node=GOAL node, return GOAL and terminate the search.
- Else CURRENT node<= NEIGHBOUR node, move ahead.
- Loop until the goal is not reached or a point is not found.
Steepest-ascent hill climbing
Steepest-ascent hill climbing is different from simple hill climbing search. Unlike simple hill climbing search, It considers all the successive nodes, compares them, and choose the node which is closest to the solution. Steepest hill climbing search is similar to best-first search because it focuses on each node instead of one.
Note: Both simple, as well as steepest-ascent hill climbing search, fails when there is no closer node.
Steepest-ascent hill climbing algorithm
- Create a CURRENT node and a GOAL node.
- If the CURRENT node=GOAL node, return GOAL and terminate the search.
- Loop until a better node is not found to reach the solution.
- If there is any better successor node present, expand it.
- When the GOAL is attained, return GOAL and terminate.
Stochastic hill climbing
Stochastic hill climbing does not focus on all the nodes. It selects one node at random and decides whether it should be expanded or search for a better one.
Random-restart hill climbing
Random-restart algorithm is based on try and try strategy. It iteratively searches the node and selects the best one at each step until the goal is not found. The success depends most commonly on the shape of the hill. If there are few plateaus, local maxima, and ridges, it becomes easy to reach the destination.
Limitations of Hill climbing algorithm
Hill climbing algorithm is a fast and furious approach. It finds the solution state rapidly because it is quite easy to improve a bad state. But, there are following limitations of this search:
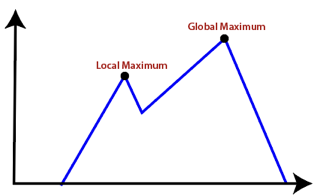
● Local Maxima: It is that peak of the mountain which is highest than all its neighboring states but lower than the global maxima. It is not the goal peak because there is another peak higher than it.
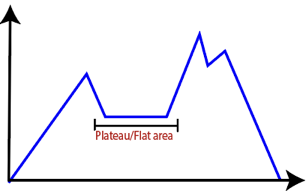
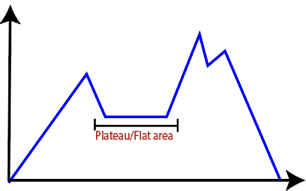
● Plateau: It is a flat surface area where no uphill exists. It becomes difficult for the climber to decide that in which direction he should move to reach the goal point. Sometimes, the person gets lost in the flat area.
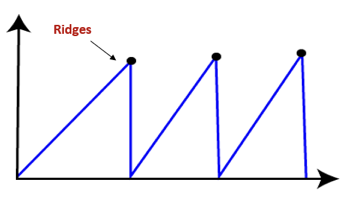
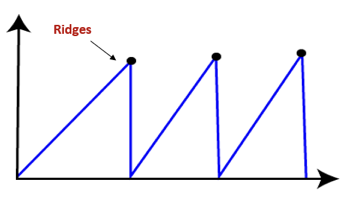
● Ridges: It is a challenging problem where the person finds two or more local maxima of the same height commonly. It becomes difficult for the person to navigate the right point and stuck to that point itself.
Simulated Annealing
Simulated annealing is similar to the hill climbing algorithm. It works on the current situation. It picks a random move instead of picking the best move. If the move leads to the improvement of the current situation, it is always accepted as a step towards the solution state, else it accepts the move having a probability less than 1.
This search technique was first used in 1980 to solve VLSI layout problems. It is also applied for factory scheduling and other large optimization tasks.
Local Beam Search
Local beam search is quite different from random-restart search. It keeps track of k states instead of just one. It selects k randomly generated states, and expand them at each step. If any state is a goal state, the search stops with success. Else it selects the best k successors from the complete list and repeats the same process.
In random-restart search where each search process runs independently, but in local beam search, the necessary information is shared between the parallel search processes.
Disadvantages of Local Beam search
● This search can suffer from a lack of diversity among the k states.
● It is an expensive version of hill climbing search.
Key takeaway
Hill climbing search is a local search problem. The purpose of the hill climbing search is to climb a hill and reach the topmost peak/ point of that hill. It is based on the heuristic search technique where the person who is climbing up on the hill estimates the direction which will lead him to the highest peak.
The technique of this method is very similar to that of the best first search algorithm. It's a simple best-first search that reduces the expected cost of accomplishing the goal. It basically chooses the node that appears to be closest to the goal. Before assessing the change in the score, this search starts with the initial matrix and makes all possible adjustments. The modification is then applied until the best result is achieved. The search will go on until no further improvements can be made. A lateral move is never made by the greedy search.
It reduces the search time by using the least estimated cost h (n) to the goal state as a measure, however the technique is neither comprehensive nor optimal. The key benefit of this search is that it is straightforward and results in speedy results. The downsides include the fact that it is not ideal and is prone to false starts.
Fig 7: Greedy search
The best first search algorithm is a graph search method that chooses a node for expansion based on an evaluation function f. (n). Because the assessment measures the distance to the goal, the explanation is generally given to the node with the lowest score. Within a general search framework, a priority queue, which is a data structure that keeps the fringe in ascending order of f values, can be utilized to achieve best first search. This search algorithm combines the depth first and breadth first search techniques.
Algorithm:
Step 1: Place the starting node or root node into the queue.
Step 2: If the queue is empty, then stop and return failure.
Step 3: If the first element of the queue is our goal node, then stop and return success.
Step 4: Else, remove the first element from the queue. Expand it and compute the estimated goal distance for each child. Place the children in the queue in ascending order to the goal distance.
Step 5: Go to step-3.
Step 6: Exit
Key takeaway
The main advantage of this search is that it is simple and finds solutions quickly.
The disadvantages are that it is not optimal, susceptible to false start.
We've all heard of the divide and conquer technique, which involves breaking down a problem into smaller subproblems to find a solution. The sub-problems can then be solved to obtain their sub-solutions. These sub-solutions can then be combined to form a complete solution. This is referred to as "Problem Reduction." This method creates AND arcs, which are a type of arc. A single AND arc can point to any number of successor nodes, all of which must be solved in order for the arc to point to a solution.
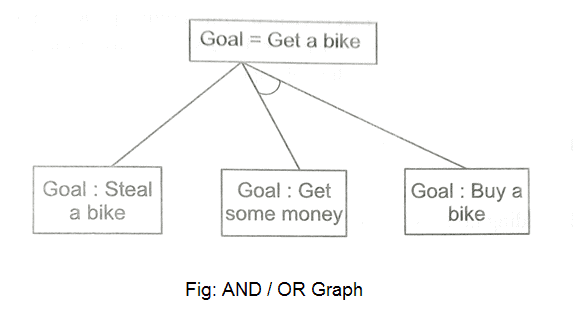
Fig 8: AND/OR graph
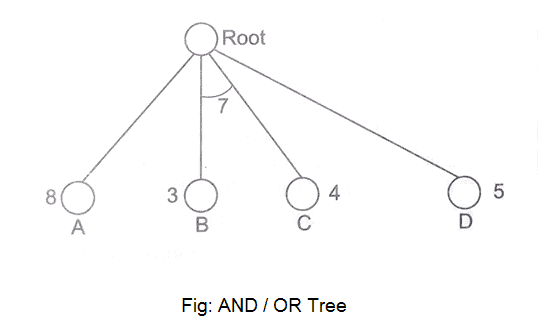
Fig 9: AND/OR tree
Problem reduction algorithm
1. Initialize the graph to the starting node.
2. Loop until the starting node is labeled SOLVED or until its cost goes above FUTILITY:
(i) Traverse the graph, starting at the initial node and following the current best path and accumulate the set of nodes that are on that path and have not yet been expanded.
(ii) Pick one of these unexpanded nodes and expand it. If there are no successors, assign FUTILITY as the value of this node. Otherwise, add its successors to the graph and for each of them compute f'(n). If f'(n) of any node is O, mark that node as SOLVED.
(iii) Change the f'(n) estimate of the newly expanded node to reflect the new information provided by its successors. Propagate this change backwards through the graph. If any node contains a successor arc whose descendants are all solved, label the node itself as SOLVED.
Constraint satisfaction
A constraint satisfaction problem (CSP) consists of
● a set of variables,
● a domain for each variable, and
● a set of constraints.
The goal is to pick a value for each variable so that the resulting alternative world fulfills the constraints; we're looking for a constraint model.
CSPs are mathematical problems in which the state of a group of objects must conform to a set of rules.
P = {X, D, C}
X = {x1,…..,xn}
D = {D1,…..,Dn}
C = {c1,…..cm}
A CSP over finite domains is depicted in the diagram. We have a collection of variables (X), a set of domains (D), and a set of constraints (C) to work with.
The values assigned to variables in X must fall into one of D's domains.
xi Di
A constraint restricts the possible values of a subset of variables from X.
A finite CSP has a finite number of variables and each variable has a finite domain. Although several of the approaches discussed in this chapter are designed for infinite, even continuous domains, many of them only operate for finite CSPs.
Given a CSP, there are a number of tasks that can be performed:
● Determine whether or not there is a model.
● Find a model.
● Find all of the models or enumerate the models.
● Count the number of models.
● Find the best model, given a measure of how good models are
● Determine whether some statement holds in all models.
Example
A cryptographic issue: The next pattern is as follows:

To make the sum correct, we must change each letter with a different numeral.
References:
- E.Rich and K. Knight, Artificial Intelligence, Tata McGraw Hill, 2008.
- Artificial intelligence and soft computing for beginners by Anandita Das Bhattachargee, Shroff Publishers
- Artificial Intelligence – A Practical Approach: Patterson , Tata McGraw Hill, 3rd Edition
Unit - 2
Search Techniques
Unit - 2
Search Techniques
The uninformed search does not contain any domain knowledge such as closeness, the location of the goal. It operates in a brute-force way as it only includes information about how to traverse the tree and how to identify leaf and goal nodes. Uninformed search applies a way in which search tree is searched without any information about the search space like initial state operators and test for the goal, so it is also called blind search. It examines each node of the tree until it achieves the goal node.
It can be divided into five main types:
● Breadth-first search
● Uniform cost search
● Depth-first search
● Iterative deepening depth-first search
● Bidirectional Search
1. Breadth-first Search:
● Breadth-first search is the most common search strategy for traversing a tree or graph. This algorithm searches breadthwise in a tree or graph, so it is called breadth-first search.
● BFS algorithm starts searching from the root node of the tree and expands all successor node at the current level before moving to nodes of next level.
● The breadth-first search algorithm is an example of a general-graph search algorithm.
● Breadth-first search implemented using FIFO queue data structure.
Advantages:
● BFS will provide a solution if any solution exists.
● If there are more than one solutions for a given problem, then BFS will provide the minimal solution which requires the least number of steps.
Disadvantages:
● It requires lots of memory since each level of the tree must be saved into memory to expand the next level.
● BFS needs lots of time if the solution is far away from the root node.
Example:
In the below tree structure, we have shown the traversing of the tree using BFS algorithm from the root node S to goal node K. BFS search algorithm traverse in layers, so it will follow the path which is shown by the dotted arrow, and the traversed path will be:
S---> A--->B---->C--->D---->G--->H--->E---->F---->I---->K
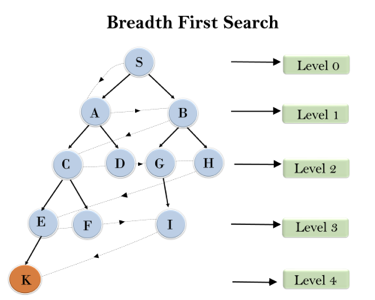
Fig 1: Breadth first search
Time Complexity: Time Complexity of BFS algorithm can be obtained by the number of nodes traversed in BFS until the shallowest Node. Where the d= depth of shallowest solution and b is a node at every state.
T (b) = 1+b2+b3+.......+ bd= O (bd)
Space Complexity: Space complexity of BFS algorithm is given by the Memory size of frontier which is O(bd).
Completeness: BFS is complete, which means if the shallowest goal node is at some finite depth, then BFS will find a solution.
Optimality: BFS is optimal if path cost is a non-decreasing function of the depth of the node.
2. Depth-first Search
● Depth-first search is a recursive algorithm for traversing a tree or graph data structure.
● It is called the depth-first search because it starts from the root node and follows each path to its greatest depth node before moving to the next path.
● DFS uses a stack data structure for its implementation.
● The process of the DFS algorithm is similar to the BFS algorithm.
Advantage:
● DFS requires very less memory as it only needs to store a stack of the nodes on the path from root node to the current node.
● It takes less time to reach to the goal node than BFS algorithm (if it traverses in the right path).
‘
Disadvantage:
● There is the possibility that many states keep reoccurring, and there is no guarantee of finding the solution.
● DFS algorithm goes for deep down searching and sometime it may go to the infinite loop.
Example:
In the below search tree, we have shown the flow of depth-first search, and it will follow the order as:
Root node--->Left node ----> right node.
It will start searching from root node S, and traverse A, then B, then D and E, after traversing E, it will backtrack the tree as E has no other successor and still goal node is not found. After backtracking it will traverse node C and then G, and here it will terminate as it found goal node.
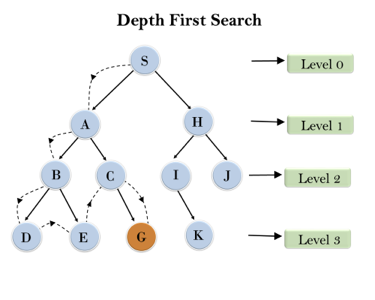
Fig 2: Depth first search
Completeness: DFS search algorithm is complete within finite state space as it will expand every node within a limited search tree.
Time Complexity: Time complexity of DFS will be equivalent to the node traversed by the algorithm. It is given by:
T(n)= 1+ n2+ n3 +.........+ nm=O(nm)
Where, m= maximum depth of any node and this can be much larger than d (Shallowest solution depth)
Space Complexity: DFS algorithm needs to store only single path from the root node, hence space complexity of DFS is equivalent to the size of the fringe set, which is O(bm).
Optimal: DFS search algorithm is non-optimal, as it may generate a large number of steps or high cost to reach to the goal node.
3. Depth-Limited Search Algorithm:
A depth-limited search algorithm is similar to depth-first search with a predetermined limit. Depth-limited search can solve the drawback of the infinite path in the Depth-first search. In this algorithm, the node at the depth limit will treat as it has no successor nodes further.
Depth-limited search can be terminated with two Conditions of failure:
● Standard failure value: It indicates that problem does not have any solution.
● Cutoff failure value: It defines no solution for the problem within a given depth limit.
Advantages:
Depth-limited search is Memory efficient.
Disadvantages:
● Depth-limited search also has a disadvantage of incompleteness.
● It may not be optimal if the problem has more than one solution.
Example:

Fig 3: Depth limited search
Completeness: DLS search algorithm is complete if the solution is above the depth-limit.
Time Complexity: Time complexity of DLS algorithm is O(bℓ).
Space Complexity: Space complexity of DLS algorithm is O(b×ℓ).
Optimal: Depth-limited search can be viewed as a special case of DFS, and it is also not optimal even if ℓ>d.
4. Uniform-cost Search Algorithm:
Uniform-cost search is a searching algorithm used for traversing a weighted tree or graph. This algorithm comes into play when a different cost is available for each edge. The primary goal of the uniform-cost search is to find a path to the goal node which has the lowest cumulative cost. Uniform-cost search expands nodes according to their path costs form the root node. It can be used to solve any graph/tree where the optimal cost is in demand. A uniform-cost search algorithm is implemented by the priority queue. It gives maximum priority to the lowest cumulative cost. Uniform cost search is equivalent to BFS algorithm if the path cost of all edges is the same.
Advantages:
● Uniform cost search is optimal because at every state the path with the least cost is chosen.
Disadvantages:
● It does not care about the number of steps involve in searching and only concerned about path cost. Due to which this algorithm may be stuck in an infinite loop.
Example:
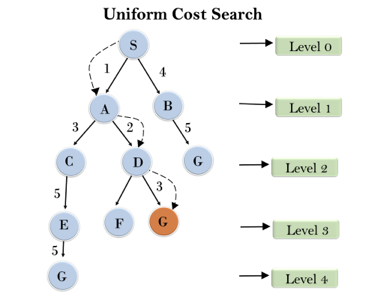
Fig 4: Uniform cost search
Completeness: Uniform-cost search is complete, such as if there is a solution, UCS will find it.
Time Complexity: Let C* is Cost of the optimal solution, and ε is each step to get closer to the goal node. Then the number of steps is = C*/ε+1. Here we have taken +1, as we start from state 0 and end to C*/ε.
Hence, the worst-case time complexity of Uniform-cost search isO(b1 + [C*/ε])/.
Space Complexity: The same logic is for space complexity so, the worst-case space complexity of Uniform-cost search is O(b1 + [C*/ε]).
Optimal: Uniform-cost search is always optimal as it only selects a path with the lowest path cost.
5. Iterative deepening depth-first Search:
The iterative deepening algorithm is a combination of DFS and BFS algorithms. This search algorithm finds out the best depth limit and does it by gradually increasing the limit until a goal is found.
This algorithm performs depth-first search up to a certain "depth limit", and it keeps increasing the depth limit after each iteration until the goal node is found.
This Search algorithm combines the benefits of Breadth-first search's fast search and depth-first search's memory efficiency.
The iterative search algorithm is useful uninformed search when search space is large, and depth of goal node is unknown.
Advantages:
● It Combines the benefits of BFS and DFS search algorithm in terms of fast search and memory efficiency.
Disadvantages:
● The main drawback of IDDFS is that it repeats all the work of the previous phase.
Example:
Following tree structure is showing the iterative deepening depth-first search. IDDFS algorithm performs various iterations until it does not find the goal node. The iteration performed by the algorithm is given as:

Fig 5: Iterative deepening depth first search
1'st Iteration-----> A
2'nd Iteration----> A, B, C
3'rd Iteration------>A, B, D, E, C, F, G
4'th Iteration------>A, B, D, H, I, E, C, F, K, G
In the fourth iteration, the algorithm will find the goal node.
Completeness: This algorithm is complete is if the branching factor is finite.
Time Complexity: Let's suppose b is the branching factor and depth is d then the worst-case time complexity is O(bd).
Space Complexity: The space complexity of IDDFS will be O(bd).
Optimal: IDDFS algorithm is optimal if path cost is a non- decreasing function of the depth of the node.
6. Bidirectional Search Algorithm:
Bidirectional search algorithm runs two simultaneous searches, one form initial state called as forward-search and other from goal node called as backward-search, to find the goal node. Bidirectional search replaces one single search graph with two small subgraphs in which one starts the search from an initial vertex and other starts from goal vertex. The search stops when these two graphs intersect each other.
Bidirectional search can use search techniques such as BFS, DFS, DLS, etc.
Advantages:
● Bidirectional search is fast.
● Bidirectional search requires less memory
Disadvantages:
● Implementation of the bidirectional search tree is difficult.
● In bidirectional search, one should know the goal state in advance.
Example:
In the below search tree, bidirectional search algorithm is applied. This algorithm divides one graph/tree into two sub-graphs. It starts traversing from node 1 in the forward direction and starts from goal node 16 in the backward direction.
The algorithm terminates at node 9 where two searches meet.

Fig 6: Bidirectional search
Completeness: Bidirectional Search is complete if we use BFS in both searches.
Time Complexity: Time complexity of bidirectional search using BFS is O(bd).
Space Complexity: Space complexity of bidirectional search is O(bd).
Optimal: Bidirectional search is Optimal.
A heuristic is a technique for making our search process more efficient. Some heuristics assist in the direction of a search process without claiming completeness, whereas others do. A heuristic is a piece of problem-specific knowledge that helps you spend less time looking for answers. It's a strategy that works on occasion, but not all of the time.
The heuristic search algorithm uses the problem information to help steer the way over the search space. These searches make use of a number of functions that, assuming the function is efficient, estimate the cost of going from where you are now to where you want to go.
A heuristic function is a function that converts problem situation descriptions into numerical measures of desirability. The heuristic function's objective is to direct the search process in the most profitable routes by recommending which path to take first when there are multiple options.
The following procedures should be followed when using the heuristic technique to identify a solution:
1. Add domain—specific information to select what is the best path to continue searching along.
2. Define a heuristic function h(n) that estimates the ‘goodness’ of a node n. Specifically, h(n) = estimated cost(or distance) of minimal cost path from n to a goal state.
3. The term heuristic means ‘serving to aid discovery’ and is an estimate, based on domain specific information that is computable from the current state description of how close we are to a goal.
A search problem in which multiple search orders and the use of heuristic knowledge are clearly understood is finding a path from one city to another.
1. State: The current city in which the traveler is located.
2. Operators: Roads linking the current city to other cities.
3. Cost Metric: The cost of taking a given road between cities.
4. Heuristic information: The search could be guided by the direction of the goal city from the current city, or we could use airline distance as an estimate of the distance to the goal.
Key takeaway
Informed Search also called heuristic or intelligent search, this uses information about the problem to guide the search—usually guesses the distance to a goal state and is therefore efficient, but the search may not always be possible.
The purpose of heuristic function is to guide the search process in the most profitable directions by suggesting which path to follow first when more than is available.
Generate and Test Search is a heuristic search technique based on Depth First Search with Backtracking that, if done correctly, assures the discovery of a solution. In this method, all possible solutions are developed and examined to find the best one. It ensures that the best answer is compared to all other solutions that may have been provided.
It's also known as the British Museum Search Algorithm because it's similar to randomly looking for an exhibit or finding an object in the British Museum.
The heuristic function does the evaluation since all of the solutions are generated systematically in the generate and test process, but if there are any paths that are highly improbable to lead us to a result, they are ignored. The heuristic accomplishes this by ranking all of the options and is frequently successful in doing so.
When it comes to solving difficult problems, systematic Generate and Test may be unproductive. However, in complex circumstances, there is a strategy for reducing the search space by combining generate and test search with other strategies.
For example, in the Artificial Intelligence Program DENDRAL, we use two techniques to work on a smaller search space, the first of which is Constraint Satisfaction Techniques, followed by Generate and Test Procedure to produce an effective result by working on a smaller number of lists generated in the first step.
Algorithm
- Generate a possible solution. For example, generating a particular point in the problem space or generating a path for a start state.
- Test to see if this is a actual solution by comparing the chosen point or the endpoint of the chosen path to the set of acceptable goal states
- If a solution is found, quit. Otherwise go to Step 1
Key takeaway
Generate and Test Search is a heuristic search technique based on Depth First Search with Backtracking that, if done correctly, assures the discovery of a solution. In this method, all possible solutions are developed and examined to find the best one.
Hill climbing search is a local search problem. The purpose of the hill climbing search is to climb a hill and reach the topmost peak/ point of that hill. It is based on the heuristic search technique where the person who is climbing up on the hill estimates the direction which will lead him to the highest peak.
The hill climbing algorithm is a local search algorithm that proceeds in the direction of rising elevation/value in order to find the mountain's peak or the best solution to the problem. When it hits a peak value, it stops since no neighbor has a greater value.
The hill climbing algorithm is a strategy for optimizing mathematical problems. The Traveling-salesman algorithm is one of the most well-known examples of a hill climbing algorithm. We have a problem where we need to reduce the salesman's trip distance. It's also known as greedy local search because it just considers its good immediate neighbor state and nothing else.
The state and value of a node in a hill climbing algorithm are the two components. When a decent heuristic is available, hill climbing is usually used. We don't need to maintain or handle the search tree or graph in this technique because it simply preserves a single current state.
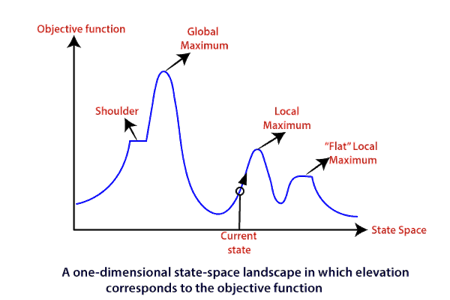
Features of Hill climbing algorithm
To understand the concept of hill climbing algorithm, consider the below landscape representing the goal state/peak and the current state of the climber. The topographical regions shown in the figure can be defined as:
● Global Maximum: It is the highest point on the hill, which is the goal state.
● Local Maximum: It is the peak higher than all other peaks but lower than the global maximum.
● Flat local maximum: It is the flat area over the hill where it has no uphill or downhill. It is a saturated point of the hill.
● Shoulder: It is also a flat area where the summit is possible.
● Current state: It is the current position of the person.
Types of Hill climbing search algorithm
There are following types of hill-climbing search:
● Simple hill climbing
● Steepest-ascent hill climbing
● Stochastic hill climbing
● Random-restart hill climbing

Simple hill climbing search
Simple hill climbing is the simplest technique to climb a hill. The task is to reach the highest peak of the mountain. Here, the movement of the climber depends on his move/steps. If he finds his next step better than the previous one, he continues to move else remain in the same state. This search focus only on his previous and next step.
Simple hill climbing Algorithm
- Create a CURRENT node, NEIGHBOUR node, and a GOAL node.
- If the CURRENT node=GOAL node, return GOAL and terminate the search.
- Else CURRENT node<= NEIGHBOUR node, move ahead.
- Loop until the goal is not reached or a point is not found.
Steepest-ascent hill climbing
Steepest-ascent hill climbing is different from simple hill climbing search. Unlike simple hill climbing search, It considers all the successive nodes, compares them, and choose the node which is closest to the solution. Steepest hill climbing search is similar to best-first search because it focuses on each node instead of one.
Note: Both simple, as well as steepest-ascent hill climbing search, fails when there is no closer node.
Steepest-ascent hill climbing algorithm
- Create a CURRENT node and a GOAL node.
- If the CURRENT node=GOAL node, return GOAL and terminate the search.
- Loop until a better node is not found to reach the solution.
- If there is any better successor node present, expand it.
- When the GOAL is attained, return GOAL and terminate.
Stochastic hill climbing
Stochastic hill climbing does not focus on all the nodes. It selects one node at random and decides whether it should be expanded or search for a better one.
Random-restart hill climbing
Random-restart algorithm is based on try and try strategy. It iteratively searches the node and selects the best one at each step until the goal is not found. The success depends most commonly on the shape of the hill. If there are few plateaus, local maxima, and ridges, it becomes easy to reach the destination.
Limitations of Hill climbing algorithm
Hill climbing algorithm is a fast and furious approach. It finds the solution state rapidly because it is quite easy to improve a bad state. But, there are following limitations of this search:
● Local Maxima: It is that peak of the mountain which is highest than all its neighboring states but lower than the global maxima. It is not the goal peak because there is another peak higher than it.
● Plateau: It is a flat surface area where no uphill exists. It becomes difficult for the climber to decide that in which direction he should move to reach the goal point. Sometimes, the person gets lost in the flat area.
● Ridges: It is a challenging problem where the person finds two or more local maxima of the same height commonly. It becomes difficult for the person to navigate the right point and stuck to that point itself.
Simulated Annealing
Simulated annealing is similar to the hill climbing algorithm. It works on the current situation. It picks a random move instead of picking the best move. If the move leads to the improvement of the current situation, it is always accepted as a step towards the solution state, else it accepts the move having a probability less than 1.
This search technique was first used in 1980 to solve VLSI layout problems. It is also applied for factory scheduling and other large optimization tasks.
Local Beam Search
Local beam search is quite different from random-restart search. It keeps track of k states instead of just one. It selects k randomly generated states, and expand them at each step. If any state is a goal state, the search stops with success. Else it selects the best k successors from the complete list and repeats the same process.
In random-restart search where each search process runs independently, but in local beam search, the necessary information is shared between the parallel search processes.
Disadvantages of Local Beam search
● This search can suffer from a lack of diversity among the k states.
● It is an expensive version of hill climbing search.
Key takeaway
Hill climbing search is a local search problem. The purpose of the hill climbing search is to climb a hill and reach the topmost peak/ point of that hill. It is based on the heuristic search technique where the person who is climbing up on the hill estimates the direction which will lead him to the highest peak.
The technique of this method is very similar to that of the best first search algorithm. It's a simple best-first search that reduces the expected cost of accomplishing the goal. It basically chooses the node that appears to be closest to the goal. Before assessing the change in the score, this search starts with the initial matrix and makes all possible adjustments. The modification is then applied until the best result is achieved. The search will go on until no further improvements can be made. A lateral move is never made by the greedy search.
It reduces the search time by using the least estimated cost h (n) to the goal state as a measure, however the technique is neither comprehensive nor optimal. The key benefit of this search is that it is straightforward and results in speedy results. The downsides include the fact that it is not ideal and is prone to false starts.
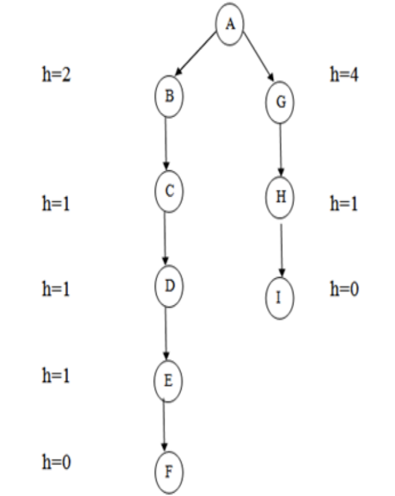
Fig 7: Greedy search
The best first search algorithm is a graph search method that chooses a node for expansion based on an evaluation function f. (n). Because the assessment measures the distance to the goal, the explanation is generally given to the node with the lowest score. Within a general search framework, a priority queue, which is a data structure that keeps the fringe in ascending order of f values, can be utilized to achieve best first search. This search algorithm combines the depth first and breadth first search techniques.
Algorithm:
Step 1: Place the starting node or root node into the queue.
Step 2: If the queue is empty, then stop and return failure.
Step 3: If the first element of the queue is our goal node, then stop and return success.
Step 4: Else, remove the first element from the queue. Expand it and compute the estimated goal distance for each child. Place the children in the queue in ascending order to the goal distance.
Step 5: Go to step-3.
Step 6: Exit
Key takeaway
The main advantage of this search is that it is simple and finds solutions quickly.
The disadvantages are that it is not optimal, susceptible to false start.
We've all heard of the divide and conquer technique, which involves breaking down a problem into smaller subproblems to find a solution. The sub-problems can then be solved to obtain their sub-solutions. These sub-solutions can then be combined to form a complete solution. This is referred to as "Problem Reduction." This method creates AND arcs, which are a type of arc. A single AND arc can point to any number of successor nodes, all of which must be solved in order for the arc to point to a solution.
Fig 8: AND/OR graph
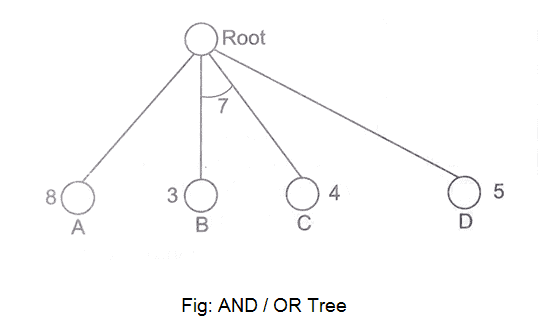
Fig 9: AND/OR tree
Problem reduction algorithm
1. Initialize the graph to the starting node.
2. Loop until the starting node is labeled SOLVED or until its cost goes above FUTILITY:
(i) Traverse the graph, starting at the initial node and following the current best path and accumulate the set of nodes that are on that path and have not yet been expanded.
(ii) Pick one of these unexpanded nodes and expand it. If there are no successors, assign FUTILITY as the value of this node. Otherwise, add its successors to the graph and for each of them compute f'(n). If f'(n) of any node is O, mark that node as SOLVED.
(iii) Change the f'(n) estimate of the newly expanded node to reflect the new information provided by its successors. Propagate this change backwards through the graph. If any node contains a successor arc whose descendants are all solved, label the node itself as SOLVED.
Constraint satisfaction
A constraint satisfaction problem (CSP) consists of
● a set of variables,
● a domain for each variable, and
● a set of constraints.
The goal is to pick a value for each variable so that the resulting alternative world fulfills the constraints; we're looking for a constraint model.
CSPs are mathematical problems in which the state of a group of objects must conform to a set of rules.
P = {X, D, C}
X = {x1,…..,xn}
D = {D1,…..,Dn}
C = {c1,…..cm}
A CSP over finite domains is depicted in the diagram. We have a collection of variables (X), a set of domains (D), and a set of constraints (C) to work with.
The values assigned to variables in X must fall into one of D's domains.
xi Di
A constraint restricts the possible values of a subset of variables from X.
A finite CSP has a finite number of variables and each variable has a finite domain. Although several of the approaches discussed in this chapter are designed for infinite, even continuous domains, many of them only operate for finite CSPs.
Given a CSP, there are a number of tasks that can be performed:
● Determine whether or not there is a model.
● Find a model.
● Find all of the models or enumerate the models.
● Count the number of models.
● Find the best model, given a measure of how good models are
● Determine whether some statement holds in all models.
Example
A cryptographic issue: The next pattern is as follows:

To make the sum correct, we must change each letter with a different numeral.
References:
- E.Rich and K. Knight, Artificial Intelligence, Tata McGraw Hill, 2008.
- Artificial intelligence and soft computing for beginners by Anandita Das Bhattachargee, Shroff Publishers
- Artificial Intelligence – A Practical Approach: Patterson , Tata McGraw Hill, 3rd Edition
Unit - 2
Search Techniques
The uninformed search does not contain any domain knowledge such as closeness, the location of the goal. It operates in a brute-force way as it only includes information about how to traverse the tree and how to identify leaf and goal nodes. Uninformed search applies a way in which search tree is searched without any information about the search space like initial state operators and test for the goal, so it is also called blind search. It examines each node of the tree until it achieves the goal node.
It can be divided into five main types:
● Breadth-first search
● Uniform cost search
● Depth-first search
● Iterative deepening depth-first search
● Bidirectional Search
1. Breadth-first Search:
● Breadth-first search is the most common search strategy for traversing a tree or graph. This algorithm searches breadthwise in a tree or graph, so it is called breadth-first search.
● BFS algorithm starts searching from the root node of the tree and expands all successor node at the current level before moving to nodes of next level.
● The breadth-first search algorithm is an example of a general-graph search algorithm.
● Breadth-first search implemented using FIFO queue data structure.
Advantages:
● BFS will provide a solution if any solution exists.
● If there are more than one solutions for a given problem, then BFS will provide the minimal solution which requires the least number of steps.
Disadvantages:
● It requires lots of memory since each level of the tree must be saved into memory to expand the next level.
● BFS needs lots of time if the solution is far away from the root node.
Example:
In the below tree structure, we have shown the traversing of the tree using BFS algorithm from the root node S to goal node K. BFS search algorithm traverse in layers, so it will follow the path which is shown by the dotted arrow, and the traversed path will be:
S---> A--->B---->C--->D---->G--->H--->E---->F---->I---->K
Fig 1: Breadth first search
Time Complexity: Time Complexity of BFS algorithm can be obtained by the number of nodes traversed in BFS until the shallowest Node. Where the d= depth of shallowest solution and b is a node at every state.
T (b) = 1+b2+b3+.......+ bd= O (bd)
Space Complexity: Space complexity of BFS algorithm is given by the Memory size of frontier which is O(bd).
Completeness: BFS is complete, which means if the shallowest goal node is at some finite depth, then BFS will find a solution.
Optimality: BFS is optimal if path cost is a non-decreasing function of the depth of the node.
2. Depth-first Search
● Depth-first search is a recursive algorithm for traversing a tree or graph data structure.
● It is called the depth-first search because it starts from the root node and follows each path to its greatest depth node before moving to the next path.
● DFS uses a stack data structure for its implementation.
● The process of the DFS algorithm is similar to the BFS algorithm.
Advantage:
● DFS requires very less memory as it only needs to store a stack of the nodes on the path from root node to the current node.
● It takes less time to reach to the goal node than BFS algorithm (if it traverses in the right path).
‘
Disadvantage:
● There is the possibility that many states keep reoccurring, and there is no guarantee of finding the solution.
● DFS algorithm goes for deep down searching and sometime it may go to the infinite loop.
Example:
In the below search tree, we have shown the flow of depth-first search, and it will follow the order as:
Root node--->Left node ----> right node.
It will start searching from root node S, and traverse A, then B, then D and E, after traversing E, it will backtrack the tree as E has no other successor and still goal node is not found. After backtracking it will traverse node C and then G, and here it will terminate as it found goal node.

Fig 2: Depth first search
Completeness: DFS search algorithm is complete within finite state space as it will expand every node within a limited search tree.
Time Complexity: Time complexity of DFS will be equivalent to the node traversed by the algorithm. It is given by:
T(n)= 1+ n2+ n3 +.........+ nm=O(nm)
Where, m= maximum depth of any node and this can be much larger than d (Shallowest solution depth)
Space Complexity: DFS algorithm needs to store only single path from the root node, hence space complexity of DFS is equivalent to the size of the fringe set, which is O(bm).
Optimal: DFS search algorithm is non-optimal, as it may generate a large number of steps or high cost to reach to the goal node.
3. Depth-Limited Search Algorithm:
A depth-limited search algorithm is similar to depth-first search with a predetermined limit. Depth-limited search can solve the drawback of the infinite path in the Depth-first search. In this algorithm, the node at the depth limit will treat as it has no successor nodes further.
Depth-limited search can be terminated with two Conditions of failure:
● Standard failure value: It indicates that problem does not have any solution.
● Cutoff failure value: It defines no solution for the problem within a given depth limit.
Advantages:
Depth-limited search is Memory efficient.
Disadvantages:
● Depth-limited search also has a disadvantage of incompleteness.
● It may not be optimal if the problem has more than one solution.
Example:
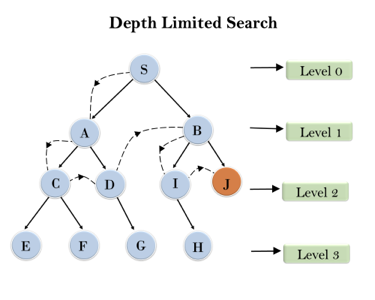
Fig 3: Depth limited search
Completeness: DLS search algorithm is complete if the solution is above the depth-limit.
Time Complexity: Time complexity of DLS algorithm is O(bℓ).
Space Complexity: Space complexity of DLS algorithm is O(b×ℓ).
Optimal: Depth-limited search can be viewed as a special case of DFS, and it is also not optimal even if ℓ>d.
4. Uniform-cost Search Algorithm:
Uniform-cost search is a searching algorithm used for traversing a weighted tree or graph. This algorithm comes into play when a different cost is available for each edge. The primary goal of the uniform-cost search is to find a path to the goal node which has the lowest cumulative cost. Uniform-cost search expands nodes according to their path costs form the root node. It can be used to solve any graph/tree where the optimal cost is in demand. A uniform-cost search algorithm is implemented by the priority queue. It gives maximum priority to the lowest cumulative cost. Uniform cost search is equivalent to BFS algorithm if the path cost of all edges is the same.
Advantages:
● Uniform cost search is optimal because at every state the path with the least cost is chosen.
Disadvantages:
● It does not care about the number of steps involve in searching and only concerned about path cost. Due to which this algorithm may be stuck in an infinite loop.
Example:
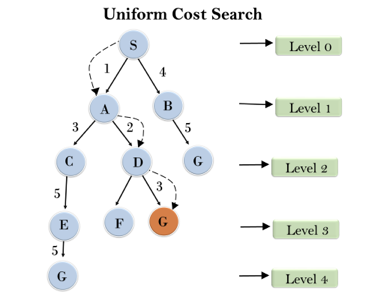
Fig 4: Uniform cost search
Completeness: Uniform-cost search is complete, such as if there is a solution, UCS will find it.
Time Complexity: Let C* is Cost of the optimal solution, and ε is each step to get closer to the goal node. Then the number of steps is = C*/ε+1. Here we have taken +1, as we start from state 0 and end to C*/ε.
Hence, the worst-case time complexity of Uniform-cost search isO(b1 + [C*/ε])/.
Space Complexity: The same logic is for space complexity so, the worst-case space complexity of Uniform-cost search is O(b1 + [C*/ε]).
Optimal: Uniform-cost search is always optimal as it only selects a path with the lowest path cost.
5. Iterative deepening depth-first Search:
The iterative deepening algorithm is a combination of DFS and BFS algorithms. This search algorithm finds out the best depth limit and does it by gradually increasing the limit until a goal is found.
This algorithm performs depth-first search up to a certain "depth limit", and it keeps increasing the depth limit after each iteration until the goal node is found.
This Search algorithm combines the benefits of Breadth-first search's fast search and depth-first search's memory efficiency.
The iterative search algorithm is useful uninformed search when search space is large, and depth of goal node is unknown.
Advantages:
● It Combines the benefits of BFS and DFS search algorithm in terms of fast search and memory efficiency.
Disadvantages:
● The main drawback of IDDFS is that it repeats all the work of the previous phase.
Example:
Following tree structure is showing the iterative deepening depth-first search. IDDFS algorithm performs various iterations until it does not find the goal node. The iteration performed by the algorithm is given as:
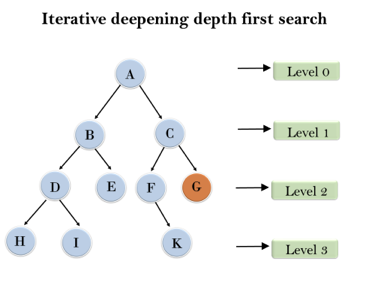
Fig 5: Iterative deepening depth first search
1'st Iteration-----> A
2'nd Iteration----> A, B, C
3'rd Iteration------>A, B, D, E, C, F, G
4'th Iteration------>A, B, D, H, I, E, C, F, K, G
In the fourth iteration, the algorithm will find the goal node.
Completeness: This algorithm is complete is if the branching factor is finite.
Time Complexity: Let's suppose b is the branching factor and depth is d then the worst-case time complexity is O(bd).
Space Complexity: The space complexity of IDDFS will be O(bd).
Optimal: IDDFS algorithm is optimal if path cost is a non- decreasing function of the depth of the node.
6. Bidirectional Search Algorithm:
Bidirectional search algorithm runs two simultaneous searches, one form initial state called as forward-search and other from goal node called as backward-search, to find the goal node. Bidirectional search replaces one single search graph with two small subgraphs in which one starts the search from an initial vertex and other starts from goal vertex. The search stops when these two graphs intersect each other.
Bidirectional search can use search techniques such as BFS, DFS, DLS, etc.
Advantages:
● Bidirectional search is fast.
● Bidirectional search requires less memory
Disadvantages:
● Implementation of the bidirectional search tree is difficult.
● In bidirectional search, one should know the goal state in advance.
Example:
In the below search tree, bidirectional search algorithm is applied. This algorithm divides one graph/tree into two sub-graphs. It starts traversing from node 1 in the forward direction and starts from goal node 16 in the backward direction.
The algorithm terminates at node 9 where two searches meet.
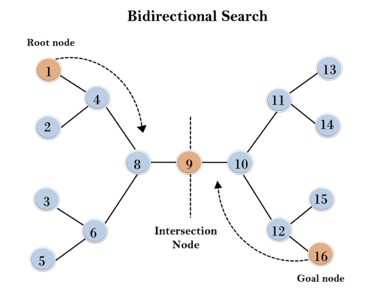
Fig 6: Bidirectional search
Completeness: Bidirectional Search is complete if we use BFS in both searches.
Time Complexity: Time complexity of bidirectional search using BFS is O(bd).
Space Complexity: Space complexity of bidirectional search is O(bd).
Optimal: Bidirectional search is Optimal.
A heuristic is a technique for making our search process more efficient. Some heuristics assist in the direction of a search process without claiming completeness, whereas others do. A heuristic is a piece of problem-specific knowledge that helps you spend less time looking for answers. It's a strategy that works on occasion, but not all of the time.
The heuristic search algorithm uses the problem information to help steer the way over the search space. These searches make use of a number of functions that, assuming the function is efficient, estimate the cost of going from where you are now to where you want to go.
A heuristic function is a function that converts problem situation descriptions into numerical measures of desirability. The heuristic function's objective is to direct the search process in the most profitable routes by recommending which path to take first when there are multiple options.
The following procedures should be followed when using the heuristic technique to identify a solution:
1. Add domain—specific information to select what is the best path to continue searching along.
2. Define a heuristic function h(n) that estimates the ‘goodness’ of a node n. Specifically, h(n) = estimated cost(or distance) of minimal cost path from n to a goal state.
3. The term heuristic means ‘serving to aid discovery’ and is an estimate, based on domain specific information that is computable from the current state description of how close we are to a goal.
A search problem in which multiple search orders and the use of heuristic knowledge are clearly understood is finding a path from one city to another.
1. State: The current city in which the traveler is located.
2. Operators: Roads linking the current city to other cities.
3. Cost Metric: The cost of taking a given road between cities.
4. Heuristic information: The search could be guided by the direction of the goal city from the current city, or we could use airline distance as an estimate of the distance to the goal.
Key takeaway
Informed Search also called heuristic or intelligent search, this uses information about the problem to guide the search—usually guesses the distance to a goal state and is therefore efficient, but the search may not always be possible.
The purpose of heuristic function is to guide the search process in the most profitable directions by suggesting which path to follow first when more than is available.
Generate and Test Search is a heuristic search technique based on Depth First Search with Backtracking that, if done correctly, assures the discovery of a solution. In this method, all possible solutions are developed and examined to find the best one. It ensures that the best answer is compared to all other solutions that may have been provided.
It's also known as the British Museum Search Algorithm because it's similar to randomly looking for an exhibit or finding an object in the British Museum.
The heuristic function does the evaluation since all of the solutions are generated systematically in the generate and test process, but if there are any paths that are highly improbable to lead us to a result, they are ignored. The heuristic accomplishes this by ranking all of the options and is frequently successful in doing so.
When it comes to solving difficult problems, systematic Generate and Test may be unproductive. However, in complex circumstances, there is a strategy for reducing the search space by combining generate and test search with other strategies.
For example, in the Artificial Intelligence Program DENDRAL, we use two techniques to work on a smaller search space, the first of which is Constraint Satisfaction Techniques, followed by Generate and Test Procedure to produce an effective result by working on a smaller number of lists generated in the first step.
Algorithm
- Generate a possible solution. For example, generating a particular point in the problem space or generating a path for a start state.
- Test to see if this is a actual solution by comparing the chosen point or the endpoint of the chosen path to the set of acceptable goal states
- If a solution is found, quit. Otherwise go to Step 1
Key takeaway
Generate and Test Search is a heuristic search technique based on Depth First Search with Backtracking that, if done correctly, assures the discovery of a solution. In this method, all possible solutions are developed and examined to find the best one.
Hill climbing search is a local search problem. The purpose of the hill climbing search is to climb a hill and reach the topmost peak/ point of that hill. It is based on the heuristic search technique where the person who is climbing up on the hill estimates the direction which will lead him to the highest peak.
The hill climbing algorithm is a local search algorithm that proceeds in the direction of rising elevation/value in order to find the mountain's peak or the best solution to the problem. When it hits a peak value, it stops since no neighbor has a greater value.
The hill climbing algorithm is a strategy for optimizing mathematical problems. The Traveling-salesman algorithm is one of the most well-known examples of a hill climbing algorithm. We have a problem where we need to reduce the salesman's trip distance. It's also known as greedy local search because it just considers its good immediate neighbor state and nothing else.
The state and value of a node in a hill climbing algorithm are the two components. When a decent heuristic is available, hill climbing is usually used. We don't need to maintain or handle the search tree or graph in this technique because it simply preserves a single current state.
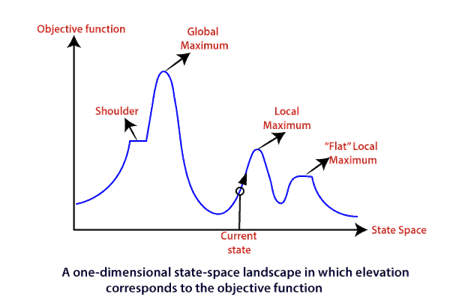
Features of Hill climbing algorithm
To understand the concept of hill climbing algorithm, consider the below landscape representing the goal state/peak and the current state of the climber. The topographical regions shown in the figure can be defined as:
● Global Maximum: It is the highest point on the hill, which is the goal state.
● Local Maximum: It is the peak higher than all other peaks but lower than the global maximum.
● Flat local maximum: It is the flat area over the hill where it has no uphill or downhill. It is a saturated point of the hill.
● Shoulder: It is also a flat area where the summit is possible.
● Current state: It is the current position of the person.
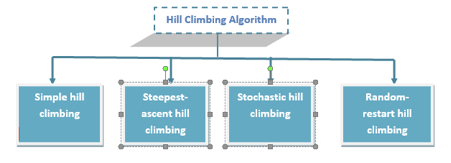
Types of Hill climbing search algorithm
There are following types of hill-climbing search:
● Simple hill climbing
● Steepest-ascent hill climbing
● Stochastic hill climbing
● Random-restart hill climbing
Simple hill climbing search
Simple hill climbing is the simplest technique to climb a hill. The task is to reach the highest peak of the mountain. Here, the movement of the climber depends on his move/steps. If he finds his next step better than the previous one, he continues to move else remain in the same state. This search focus only on his previous and next step.
Simple hill climbing Algorithm
- Create a CURRENT node, NEIGHBOUR node, and a GOAL node.
- If the CURRENT node=GOAL node, return GOAL and terminate the search.
- Else CURRENT node<= NEIGHBOUR node, move ahead.
- Loop until the goal is not reached or a point is not found.
Steepest-ascent hill climbing
Steepest-ascent hill climbing is different from simple hill climbing search. Unlike simple hill climbing search, It considers all the successive nodes, compares them, and choose the node which is closest to the solution. Steepest hill climbing search is similar to best-first search because it focuses on each node instead of one.
Note: Both simple, as well as steepest-ascent hill climbing search, fails when there is no closer node.
Steepest-ascent hill climbing algorithm
- Create a CURRENT node and a GOAL node.
- If the CURRENT node=GOAL node, return GOAL and terminate the search.
- Loop until a better node is not found to reach the solution.
- If there is any better successor node present, expand it.
- When the GOAL is attained, return GOAL and terminate.
Stochastic hill climbing
Stochastic hill climbing does not focus on all the nodes. It selects one node at random and decides whether it should be expanded or search for a better one.
Random-restart hill climbing
Random-restart algorithm is based on try and try strategy. It iteratively searches the node and selects the best one at each step until the goal is not found. The success depends most commonly on the shape of the hill. If there are few plateaus, local maxima, and ridges, it becomes easy to reach the destination.
Limitations of Hill climbing algorithm
Hill climbing algorithm is a fast and furious approach. It finds the solution state rapidly because it is quite easy to improve a bad state. But, there are following limitations of this search:
● Local Maxima: It is that peak of the mountain which is highest than all its neighboring states but lower than the global maxima. It is not the goal peak because there is another peak higher than it.
● Plateau: It is a flat surface area where no uphill exists. It becomes difficult for the climber to decide that in which direction he should move to reach the goal point. Sometimes, the person gets lost in the flat area.
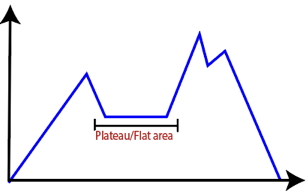
● Ridges: It is a challenging problem where the person finds two or more local maxima of the same height commonly. It becomes difficult for the person to navigate the right point and stuck to that point itself.
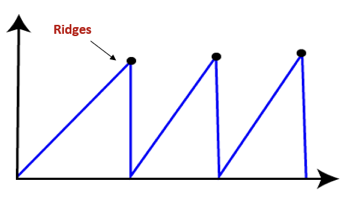
Simulated Annealing
Simulated annealing is similar to the hill climbing algorithm. It works on the current situation. It picks a random move instead of picking the best move. If the move leads to the improvement of the current situation, it is always accepted as a step towards the solution state, else it accepts the move having a probability less than 1.
This search technique was first used in 1980 to solve VLSI layout problems. It is also applied for factory scheduling and other large optimization tasks.
Local Beam Search
Local beam search is quite different from random-restart search. It keeps track of k states instead of just one. It selects k randomly generated states, and expand them at each step. If any state is a goal state, the search stops with success. Else it selects the best k successors from the complete list and repeats the same process.
In random-restart search where each search process runs independently, but in local beam search, the necessary information is shared between the parallel search processes.
Disadvantages of Local Beam search
● This search can suffer from a lack of diversity among the k states.
● It is an expensive version of hill climbing search.
Key takeaway
Hill climbing search is a local search problem. The purpose of the hill climbing search is to climb a hill and reach the topmost peak/ point of that hill. It is based on the heuristic search technique where the person who is climbing up on the hill estimates the direction which will lead him to the highest peak.
The technique of this method is very similar to that of the best first search algorithm. It's a simple best-first search that reduces the expected cost of accomplishing the goal. It basically chooses the node that appears to be closest to the goal. Before assessing the change in the score, this search starts with the initial matrix and makes all possible adjustments. The modification is then applied until the best result is achieved. The search will go on until no further improvements can be made. A lateral move is never made by the greedy search.
It reduces the search time by using the least estimated cost h (n) to the goal state as a measure, however the technique is neither comprehensive nor optimal. The key benefit of this search is that it is straightforward and results in speedy results. The downsides include the fact that it is not ideal and is prone to false starts.
Fig 7: Greedy search
The best first search algorithm is a graph search method that chooses a node for expansion based on an evaluation function f. (n). Because the assessment measures the distance to the goal, the explanation is generally given to the node with the lowest score. Within a general search framework, a priority queue, which is a data structure that keeps the fringe in ascending order of f values, can be utilized to achieve best first search. This search algorithm combines the depth first and breadth first search techniques.
Algorithm:
Step 1: Place the starting node or root node into the queue.
Step 2: If the queue is empty, then stop and return failure.
Step 3: If the first element of the queue is our goal node, then stop and return success.
Step 4: Else, remove the first element from the queue. Expand it and compute the estimated goal distance for each child. Place the children in the queue in ascending order to the goal distance.
Step 5: Go to step-3.
Step 6: Exit
Key takeaway
The main advantage of this search is that it is simple and finds solutions quickly.
The disadvantages are that it is not optimal, susceptible to false start.
We've all heard of the divide and conquer technique, which involves breaking down a problem into smaller subproblems to find a solution. The sub-problems can then be solved to obtain their sub-solutions. These sub-solutions can then be combined to form a complete solution. This is referred to as "Problem Reduction." This method creates AND arcs, which are a type of arc. A single AND arc can point to any number of successor nodes, all of which must be solved in order for the arc to point to a solution.

Fig 8: AND/OR graph
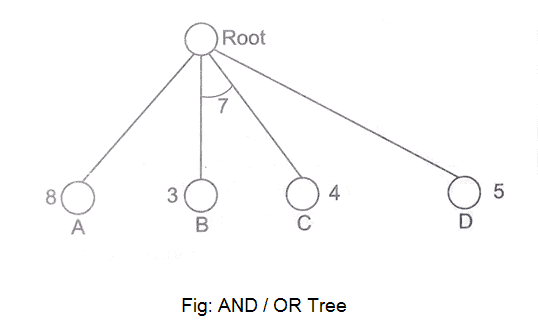
Fig 9: AND/OR tree
Problem reduction algorithm
1. Initialize the graph to the starting node.
2. Loop until the starting node is labeled SOLVED or until its cost goes above FUTILITY:
(i) Traverse the graph, starting at the initial node and following the current best path and accumulate the set of nodes that are on that path and have not yet been expanded.
(ii) Pick one of these unexpanded nodes and expand it. If there are no successors, assign FUTILITY as the value of this node. Otherwise, add its successors to the graph and for each of them compute f'(n). If f'(n) of any node is O, mark that node as SOLVED.
(iii) Change the f'(n) estimate of the newly expanded node to reflect the new information provided by its successors. Propagate this change backwards through the graph. If any node contains a successor arc whose descendants are all solved, label the node itself as SOLVED.
Constraint satisfaction
A constraint satisfaction problem (CSP) consists of
● a set of variables,
● a domain for each variable, and
● a set of constraints.
The goal is to pick a value for each variable so that the resulting alternative world fulfills the constraints; we're looking for a constraint model.
CSPs are mathematical problems in which the state of a group of objects must conform to a set of rules.
P = {X, D, C}
X = {x1,…..,xn}
D = {D1,…..,Dn}
C = {c1,…..cm}
A CSP over finite domains is depicted in the diagram. We have a collection of variables (X), a set of domains (D), and a set of constraints (C) to work with.
The values assigned to variables in X must fall into one of D's domains.
xi Di
A constraint restricts the possible values of a subset of variables from X.
A finite CSP has a finite number of variables and each variable has a finite domain. Although several of the approaches discussed in this chapter are designed for infinite, even continuous domains, many of them only operate for finite CSPs.
Given a CSP, there are a number of tasks that can be performed:
● Determine whether or not there is a model.
● Find a model.
● Find all of the models or enumerate the models.
● Count the number of models.
● Find the best model, given a measure of how good models are
● Determine whether some statement holds in all models.
Example
A cryptographic issue: The next pattern is as follows:

To make the sum correct, we must change each letter with a different numeral.
References:
- E.Rich and K. Knight, Artificial Intelligence, Tata McGraw Hill, 2008.
- Artificial intelligence and soft computing for beginners by Anandita Das Bhattachargee, Shroff Publishers
- Artificial Intelligence – A Practical Approach: Patterson , Tata McGraw Hill, 3rd Edition