Unit - 3
Knowledge representation
Humans excel in comprehending, reasoning, and interpreting information. Humans have knowledge about things and use that knowledge to accomplish various activities in the real world. However, knowledge representation and reasoning deal with how robots achieve all of these things. As a result, the following is a description of knowledge representation:
● Knowledge representation and reasoning (KR, KRR) is a branch of artificial intelligence that studies how AI agents think and how their thinking influences their behavior.
● It is in charge of encoding information about the real world in such a way that a computer can comprehend it and use it to solve complicated real-world problems like diagnosing a medical condition or conversing with humans in natural language.
● It's also a means of describing how artificial intelligence can represent knowledge. Knowledge representation is more than just storing data in a database; it also allows an intelligent machine to learn from its knowledge and experiences in order to act intelligently like a person.
What to Represent:
The types of knowledge that must be represented in AI systems are as follows:
● Object - All of the information on items in our universe. Guitars, for example, have strings, while trumpets are brass instruments.
● Events - Events are the actions that take place in our world.
● Performance - Performance is a term used to describe behaviour that entails knowing how to perform things.
● Meta-knowledge - It is information about what we already know.
● Facts - The truths about the real world and what we represent are known as facts.
● Knowledge-Base - The knowledge base is the most important component of the knowledge-based agents. It's abbreviated as KB. The Sentences are grouped together in the Knowledgebase (Here, sentences are used as a technical term and not identical with the English language).
Types of knowledge
The numerous categories of knowledge are as follows:
1. Declarative Knowledge
● Declarative knowledge is the ability to understand something.
● It contains ideas, facts, and objects.
● It's also known as descriptive knowledge, and it's communicated using declarative statements.
● It is less complicated than procedural programming.
2. Procedural Knowledge
● It's sometimes referred to as "imperative knowledge."
● Procedure knowledge is a form of knowledge that entails knowing how to do something.
● It can be used to complete any assignment.
● It has rules, plans, procedures, and agendas, among other things.
● The use of procedural knowledge is contingent on the job at hand.
3. Meta-knowledge
● Meta-knowledge is information about other sorts of knowledge.
4. Heuristic knowledge
● Heuristic knowledge is the sum of the knowledge of a group of specialists in a certain field or subject.
● Heuristic knowledge refers to rules of thumb that are based on prior experiences, awareness of methodologies, and are likely to work but not guaranteed.
5. Structural knowledge
● Basic problem-solving knowledge is structural knowledge.
● It describes the connections between distinct concepts such as kind, part of, and grouping.
● It is a term that describes the relationship between two or more concepts or objects.
The relation between knowledge and intelligence they are as follows:
Knowledge of real-worlds plays a very important role in the intelligence and the same for creating the artificial intelligence. Knowledge plays an important role in that of the demonstrating intelligent behaviour in the AI agents. An agent is the only able to accurately act on some of the input when he has some of the knowledge or the experience about that of the input.
Let's suppose if you met some of the person who is speaking in that of a language which you don't know, then how you will able to act on that. The same thing applies to that of the intelligent behaviour of the agents.
As we can see in below diagram, there is one decision maker which act by sensing that of the environment and using the knowledge. But if the knowledge part will not present then, it cannot display intelligent behaviour.
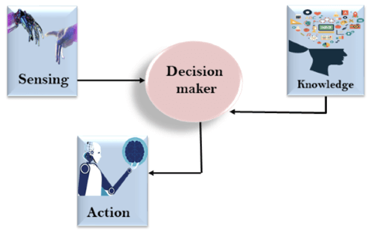
AI knowledge cycle:
An Artificial intelligence system has that of the following components for displaying intelligent behaviour they are as follows:
● Perception
● Learning
● Knowledge Representation and Reasoning
● Planning
● Execution
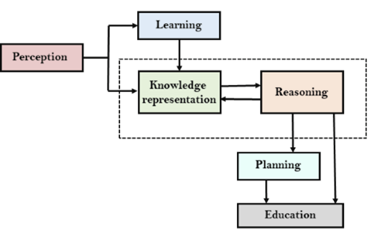
The above diagram is showing how that of an AI system can interacts with that of the real world and what the components help it to show the intelligence. AI system has the Perception component by which it retrieves information from that of its environment. It can be visual, audio or another form of the sensory input. The learning component is that the responsible for learning from data captured by the Perception comportment.
In the complete cycle, the main components are the knowledge representation and the Reasoning. These two components are involved in showing that of the intelligence in machine-like humans. These two components are independent with each other but also coupled together. The planning and execution depend on analysis of that of the Knowledge representation and the reasoning.
Approaches to knowledge representation:
There are mainly four approaches to knowledge representation, which are given below:
1. Simple relational knowledge:
● It is the simplest way of that of the storing facts which uses that of the relational method and each fact about that of a set of the object is set out systematically in that of the columns.
● This approach of the knowledge representation is famous in the database systems where the relationship between that of the different entities is represented.
● This approach has little opportunity for that of the inference.
Example: The following is the simple relational knowledge representation.
Player | Weight | Age |
Player1 | 65 | 23 |
Player2 | 58 | 18 |
Player3 | 75 | 24
|
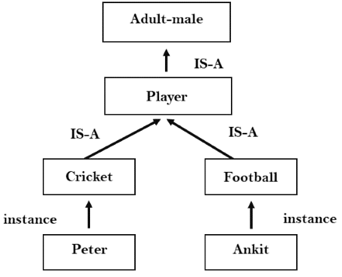
2.Inheritable knowledge:
● In the inheritable knowledge approach, all the data must be stored into that of a hierarchy of the classes.
● All classes should be arranged in that of a generalized form or a hierarchal manner.
● In this approach, we apply the inheritance property.
● Elements inherit values from the other members of a class.
● This approach contains the inheritable knowledge which shows that of a relation between instance and the class, and it is known as instance relation.
● Every individual frame can represent that of the collection of attributes and its value.
● In this approach, objects and the values are represented in the Boxed nodes.
● We use Arrows which point from that of the objects to their values.
Example:
3. Inferential knowledge:
● Inferential knowledge approach represents the knowledge in the form of the formal logics.
● This approach can be used to derive more that of the facts.
● It guaranteed the correctness.
● Example: Let's suppose there are two statements:
- Marcus is a man
- All men are mortal
Then it can represent as;
Man(Marcus)
∀x = man (x) ----------> mortal (x)s
4. Procedural knowledge:
● Procedural knowledge approach uses that of the small programs and codes which describes how to do specific things, and how to proceed.
● In this approach, one important rule is used which is If-Then rule.
● In this knowledge, we can use various coding languages such as LISP language and Prolog language.
● We can easily represent heuristic or domain-specific knowledge using this approach.
● But it is not necessary that we can represent all cases in this approach.
Requirements for knowledge Representation system:
A good knowledge representation system must possess the following properties.
- Representational Accuracy:
KR system should have that of the ability to represent that the all kind of the required knowledge.
2. Inferential Adequacy:
KR system should have ability to manipulate that of the representational structures to produce that of the new knowledge corresponding to the existing structure.
3. Inferential Efficiency:
The ability to direct the inferential knowledge mechanism into the most productive directions by storing appropriate guides.
4. Acquisitioned efficiency- The ability to acquire the new knowledge easily using automatic methods.
Key takeaway
Humans excel in comprehending, reasoning, and interpreting information. Humans have knowledge about things and use that knowledge to accomplish various activities in the real world. However, knowledge representation and reasoning deal with how robots achieve all of these things
● First-order logic is a type of knowledge representation used in artificial intelligence. It's a propositional logic variation.
● FOL is expressive enough to convey natural language statements in a concise manner.
● First-order logic is sometimes known as predicate logic or first-order predicate logic. First-order logic is a complex language for constructing information about objects and expressing relationships between them.
● First-order logic (as does natural language) assumes not just that the world contains facts, as propositional logic does, but also that the world has the following:
● Objects: People, numbers, colors, conflicts, theories, squares, pits, wumpus,
● Relation: It can be a unary relation like red, round, or nearby, or an n-any relation like sister of, brother of, has color, or comes between.
● Functions: Father of, best friend, third inning of, last inning of......
● First-order logic contains two basic pieces as a natural language:
● Syntax
● Semantics
Syntax
Syntax has to do with what ‘things’ (symbols, notations) one is allowed to use in the language and in what way; there is/are a(n):
● Alphabet
● Language constructs
● Sentences to assert knowledge
Logical connectives (⇒, ∧, ∨, and ⇐⇒ ), negation (¬), and parentheses. These will be used to recursively build complex formulas, just as was done for propositional logic.
Constants symbols are strings that will be interpreted as representing objects, e.g. Bob might be a constant.
Variable symbols will be used as “place holders” for quantifying over objects.
Predicate symbols Each has an arity (number of arguments) associated with it, which can be zero or some other finite value. Predicates will be used to represent object characteristics and relationships.
Zero-arity Because predicate symbols are viewed as propositions in first-order logic, propositional logic is subsumed. These assertions can be thought of as world properties.
Predicates with a single parameter can be thought of as specifying object attributes. If Rich is a single-arity predicate, then Rich(Bob) is used to indicate that Bob is wealthy. Multi-arity predicates are used to describe relationships between items.

Fig 1: Syntax of first order logic
Function symbols Each has a specific arity (number of input arguments) and is understood as a function that maps the stated number of input objects to objects. Allowing FatherOf to be a single-arity function symbol, the natural interpretation of FatherOf(Bob) is Bob's father.
Zero-arity function symbols are considered to be constants.
Universal and existential quantifier symbols will be used to quantify over objects. For example, ∀ x Alive(x) ⇒ Breathing(x) is a universally quantified statement that uses the variable x as a placeholder.
Semantics of First-Order Logic
As with all logics, the first step in determining the semantics of first-order logic is to define the models of first-order logic. Remember that one of the benefits of using first-order logic is that it allows us to freely discuss objects and their relationships. As a result, our models will comprise objects as well as information about their properties and interactions with other items.
First order model
A first-order model is a tuple hD, Ii, where D denotes a non-empty object domain and I denotes an interpretation function. D is nothing more than a collection of items or elements that can be finite, infinite, or uncountable. The interpretation function I gives each of the available constant, function, and predicate symbols a meaning or interpretation as follows:
● If c is a constant symbol, then I(c) is an object in D. Thus, given a model, a constant can be viewed as naming an object in the domain.
● If f is a function symbol of arity n, then I(f) is a total function from Dn to D. That is the interpretation of f is a function that maps n domain objects to the domain D.
● If p is a predicate symbol of arity n > 0, then I(p) is a subset of Dn; that is, a predicate symbol is interpreted as a set of tuples from the domain. If a tuple O = (o1, · · · , on) is in I(p) then we say that p is true for the object tuple O.
● If p is a predicate symbol of arity 0, i.e. a simple proposition, then I(p) is equal to either true or false.
Assume we have a single predicate TallerThan, a single function FatherOf, and a single constant Bob. The following could be a model M1 for these symbols:
D = { BOB, JON, NULL }
I(Bob) = BOB
I(TallerThan) = { hBOB, JONi }
Because I(FatherOf) is a function, we'll only show the value for each argument to give the FatherOf meaning.
I(FatherOf)(BOB) = JON
I(FatherOf)(JON) = NULL
I(FatherOf)(NULL) = NULL
M2 could also be interpreted as follows,
D = { BOB, JON }
I(Bob) = BOB
I(TallerThan) = { hBOB, JONi,hJON, BOBi }
I(FatherOf)(BOB) = BOB
I(FatherOf)(JON) = JON
It's vital to highlight the difference between Bob, which is a constant (a syntactic entity), and BOB, which is a domain object (a semantic entity). The second interpretation isn't exactly what we're looking for (the objects are dads of themselves, and TallerThan is inconsistent), but it's still a viable model. By imposing proper limitations on the symbols, the knowledge base can rule out such unexpected models from consideration.
Key takeaway
- The syntax of FOL determines which collection of symbols is a logical expression in first-order logic.
- The basic syntactic elements of first-order logic are symbols. We write statements in short-hand notation in FOL.
Predicate Logic is concerned with predicates, or propositions that contain variables.
A predicate is a set of one or more variables that are decided on a particular domain. A variable-based predicate can be turned into a proposition by assigning a value to the variable or quantifying it.
Predicates can be found in the following examples.
● Consider E(x, y) denote "x = y"
● Consider X(a, b, c) denote "a + b + c = 0"
● Consider M(x, y) denote "x is married to y."
Quantifier:
Predicate Logic is concerned with predicates, or propositions that contain variables.
Existential Quantifier:
If p(x) is a proposition over the universe U, it is written as ∃x p(x) and reads as "There exists at least one value of variable x in the universe such that p(x) is true." The quantifier ∃ is called the existential quantifier.
Predicates can be found in the following examples.
(∃x∈A)p(x) or ∃x∈A such that p (x) or (∃x)p(x) or p(x) is true for some x ∈A.
Universal Quantifier:
If p(x) is a proposition with respect to the universe U. Then it's written as x,p(x), which means "For every x∈U,p(x) is true." The Universal Quantifier ∀ is the name of the quantifier.
With a universal quantifier, there are various ways to write a proposition.
∀x∈A,p(x) or p(x), ∀x ∈A Or ∀x,p(x) or p(x) is true for all x ∈A.
Backward-chaining is also known as backward deduction or backward reasoning when using an inference engine. A backward chaining algorithm is a style of reasoning that starts with the goal and works backwards through rules to find facts that support it.
It's an inference approach that starts with the goal. We look for implication phrases that will help us reach a conclusion and justify its premises. It is an approach for proving theorems that is goal-oriented.
Example: Fritz, a pet that croaks and eats flies, needs his color determined. The Knowledge Base contains the following rules:
If X croaks and eats flies — → Then X is a frog.
If X sings — → Then X is a bird.
If X is a frog — → Then X is green.
If x is a bird — -> Then X is blue.
The third and fourth rules were chosen because they best fit our goal of determining the color of the pet. For example, X may be green or blue. Both the antecedents of the rules, X is a frog and X is a bird, are added to the target list. The first two rules were chosen because their implications correlate to the newly added goals, namely, X is a frog or X is a bird.
Because the antecedent (If X croaks and eats flies) is true/given, we can derive that Fritz is a frog. If it's a frog, Fritz is green, and if it's a bird, Fritz is blue, completing the goal of determining the pet's color.
Properties of backward chaining
● A top-down strategy is what it's called.
● Backward-chaining employs the modus ponens inference rule.
● In backward chaining, the goal is broken down into sub-goals or sub-goals to ensure that the facts are true.
● Because a list of objectives decides which rules are chosen and implemented, it's known as a goal-driven strategy.
● The backward-chaining approach is utilized in game theory, automated theorem proving tools, inference engines, proof assistants, and other AI applications.
● The backward-chaining method relied heavily on a depth-first search strategy for proof.
It's a type of inference technique. The following steps are carried out.
1. Analyze data and make logical assertions from it (propositional or predicate logic).
2. Put them in the normal Conjunctive form (CNF).
3. Make an argument in opposition to the conclusion.
4. To locate a solution, use the resolution tree.
For instance: If the jewelry was taken by the maid, the butler was not to blame.
Either the maid took the jewels or she milked the animal.
The butler received the cream if the cow was milked by the maid.
If the butler was at fault, he received his cream as a result.
Step1: Expressing as propositional logic.
P= maid stole the jewelry.
Q= butler is guilty.
R= maid milked the cow.
S= butler got the cream.
Step 2: Convert to propositional logic.
1. P — -> ~Q
2. P v R
3. R — -> S
4. Q — -> S (Conclusion)
Step 3: Converting to CNF.
1. ~P v ~Q
2. P v R
3. ~R v S
4. ~Q v S (Conclusion)
Step 4: Negate the conclusion.
~(~Q v S) = Q ^ ~S
It is not in CNF due to the presence of ‘^’. Thus we break it into two parts: Q and ~S. We start with Q and resolve using the resolution tree.
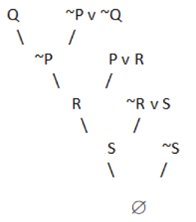
Fig 2: Resolution tree
A null value is obtained by negating the conclusion. As a result, our conclusion has been proven.
Example:
We can resolve two clauses which are given below:
[Animal (g(x) V Loves (f(x), x)] and [¬ Loves(a, b) V ¬Kills(a, b)]
Where two complimentary literals are: Loves (f(x), x) and ¬ Loves (a, b)
These literals can be unified with unifier θ= [a/f(x), and b/x], and it will generate a resolvent clause:
[Animal (g(x) V ¬ Kills(f(x), x)].
Steps for Resolution:
- Conversion of facts into first-order logic.
- Convert FOL statements into CNF
- Negate the statement which needs to prove (proof by contradiction)
- Draw resolution graph (unification).
To better understand all the above steps, we will take an example in which we will apply resolution.
Example:
John likes all kind of food.
Apple and vegetable are food
Anything anyone eats and not killed is food.
Anil eats peanuts and still alive
- Harry eats everything that Anil eats.
Prove by resolution that:
John likes peanuts.
Step-1: Conversion of Facts into FOL
In the first step we will convert all the given statements into its first order logic.

Here f and g are added predicates.
Step-2: Conversion of FOL into CNF
In First order logic resolution, it is required to convert the FOL into CNF as CNF form makes easier for resolution proofs.
Eliminate all implication (→) and rewrite
- ∀x ¬ food(x) V likes(John, x)
- Food(Apple) Λ food(vegetables)
- ∀x ∀y ¬ [eats(x, y) Λ¬ killed(x)] V food(y)
- Eats (Anil, Peanuts) Λ alive(Anil)
- ∀x ¬ eats(Anil, x) V eats(Harry, x)
- ∀x¬ [¬ killed(x) ] V alive(x)
- ∀x ¬ alive(x) V ¬ killed(x)
- Likes(John, Peanuts).
Move negation (¬)inwards and rewrite
9. ∀x ¬ food(x) V likes(John, x)
10. Food(Apple) Λ food(vegetables)
11. ∀x ∀y ¬ eats(x, y) V killed(x) V food(y)
12. Eats (Anil, Peanuts) Λ alive(Anil)
13. ∀x ¬ eats(Anil, x) V eats(Harry, x)
14. ∀x ¬killed(x) ] V alive(x)
15. ∀x ¬ alive(x) V ¬ killed(x)
16. Likes(John, Peanuts).
Rename variables or standardize variables
17. ∀x ¬ food(x) V likes(John, x)
18. Food(Apple) Λ food(vegetables)
19. ∀y ∀z ¬ eats(y, z) V killed(y) V food(z)
20. Eats (Anil, Peanuts) Λ alive(Anil)
21. ∀w¬ eats(Anil, w) V eats(Harry, w)
22. ∀g ¬killed(g) ] V alive(g)
23. ∀k ¬ alive(k) V ¬ killed(k)
24. Likes(John, Peanuts).
● Eliminate existential instantiation quantifier by elimination.
In this step, we will eliminate existential quantifier ∃, and this process is known as Skolemization. But in this example problem since there is no existential quantifier so all the statements will remain same in this step.
● Drop Universal quantifiers.
In this step we will drop all universal quantifier since all the statements are not implicitly quantified so we don't need it.
- ¬ food(x) V likes(John, x)
- Food(Apple)
- Food(vegetables)
- ¬ eats(y, z) V killed(y) V food(z)
- Eats (Anil, Peanuts)
- Alive(Anil)
- ¬ eats(Anil, w) V eats(Harry, w)
- Killed(g) V alive(g)
- ¬ alive(k) V ¬ killed(k)
- Likes(John, Peanuts).
Note: Statements "food(Apple) Λ food(vegetables)" and "eats (Anil, Peanuts) Λ alive(Anil)" can be written in two separate statements.
● Distribute conjunction ∧ over disjunction ¬.
This step will not make any change in this problem.
Step-3: Negate the statement to be proved
In this statement, we will apply negation to the conclusion statements, which will be written as ¬likes(John, Peanuts)
Step-4: Draw Resolution graph:
Now in this step, we will solve the problem by resolution tree using substitution. For the above problem, it will be given as follows:
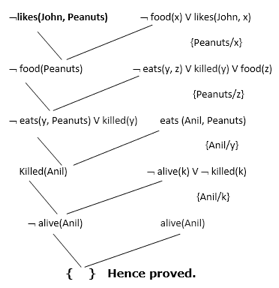
Hence the negation of the conclusion has been proved as a complete contradiction with the given set of statements.
Explanation of Resolution graph:
● In the first step of resolution graph, ¬likes(John, Peanuts) , and likes(John, x) get resolved(cancelled) by substitution of {Peanuts/x}, and we are left with ¬ food(Peanuts)
● In the second step of the resolution graph, ¬ food(Peanuts) , and food(z) get resolved (cancelled) by substitution of { Peanuts/z}, and we are left with ¬ eats(y, Peanuts) V killed(y) .
● In the third step of the resolution graph, ¬ eats(y, Peanuts) and eats (Anil, Peanuts) get resolved by substitution {Anil/y}, and we are left with Killed(Anil) .
● In the fourth step of the resolution graph, Killed(Anil) and ¬ killed(k) get resolve by substitution {Anil/k}, and we are left with ¬ alive(Anil) .
● In the last step of the resolution graph ¬ alive(Anil) and alive(Anil) get resolved.
Key takeaway
Resolution is a theorem proving technique that proceeds by building refutation proofs, i.e., proofs by contradictions. It was invented by Mathematician John Alan Robinson in 1965.
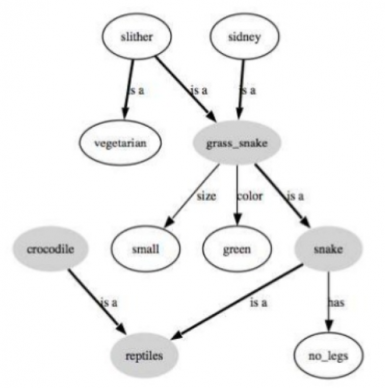
Semantic Networks, also known as Semantic Nets, are a type of knowledge representation technique for propositional data. Though it has long been utilised in philosophy, cognitive science (in the form of semantic memory), and linguistics, the Semantic Network was initially developed in computer science for artificial intelligence and machine learning. It is a knowledge base that represents the structured relationships between concepts in a network.
A semantic network is a visual representation of knowledge in the form of patterns of interconnected nodes. Only because semantic networks reflect knowledge or facilitate reasoning did they become prominent in artificial intelligence and natural language processing. In terms of knowledge representation, these serve as an alternative to predicate logic.
A semantic network is a graph with vertices that can be directed or undirected. These vertices represent concepts, whereas the edges reflect semantic relationships between concepts, as well as mapping or connecting semantic fields. Furthermore, it is known as Associative Networks because it processes information about recognised meanings in nearby locations.
Knowledge can be kept in the form of graphs, with nodes representing objects in the world and arcs expressing links between those objects, according to the structural notion.
● Nodes, links, and link labels make up semantic nets. Nodes appear in the form of circles, ellipses, or even rectangles in these network diagrams, and they represent objects such as real objects, concepts, or circumstances.
● To indicate the relationships between objects, links appear as arrows, while link labels specify the relationships.
● Because relationships provide the foundation for organising information, the items and relationships involved do not need to be concrete.
● Because the nodes are linked to each other, semantic nets are also known as associative networks.
Main Components Of Semantic Networks
● Lexical component - Relationships between objects are represented by nodes, which symbolise physical items, and labels, which denote specific objects and relationships.
● Structural component - the nodes or linkages in a diagram that are directed.
● Semantic component - The definitions are solely concerned with the links and labels of nodes, while the facts are determined by the approval regions.
● Procedural part - Constructors allow new linkages and nodes to be created. Destructors allow for the elimination of linkages and nodes.
Types of Semantic net:
Richard H. R. Of the Cambridge Language Research Unit (CLRU) created semantic networks for computers in 1956 for machine translation of natural languages. However, it is currently utilised for a wide range of purposes, including knowledge representation. There are now six different forms of semantic networks that enable declarative graphic representation, which is then utilised to represent knowledge and help automated systems that reason about it. These are the six different types of semantic networks:
Definitional Networks - These networks focus on and deal only with the subtype, or they are a link between a concept type and a newly formed subtype. A generalisation hierarchy is a type of production network. It adheres to the inheritance rule when it comes to duplicate characteristics.
Assertion Networks – It is intended to provide recommendations and is designed to assert propositions. Unless it is indicated with a modal administrator, most data in an assertion network is authentic. Some assertion systems are even regarded as models for the logical structures that underpin the semantic natural languages.
Implicational Networks – Implication is used as the principal connection between nodes. These networks can also be utilised to explain conviction patterns, causality, and deductions.
Executable Network - Contains methods that can induce changes to the network by incorporating techniques such as attached procedures or marker passing, which can conduct path messages, as well as associations and pattern searches.
Learning Networks – These are the networks that acquire knowledge from examples to develop and enhance their representations. Contain mechanisms in such networks cause changes inside the network by representing information and securing it. Adjusting fresh information from the previous system by including and excluding nodes and arcs, or changing numerical qualities termed weights and related with the arcs and nodes, is a famous example.
Hybrid Networks – Networks that integrate two or more of the preceding strategies, either in a single network or in a distinct but tightly interconnected network Some hybrid networks are specifically designed to apply theories about human cognitive functions, while others are designed for computer performance in general.
Advantages
● The semantic network is more natural than the logical representation, and it allows for the use of an efficient inference process (graphical algorithm)
● They are straightforward and simple to apply and comprehend.
● The semantic network can be used as a standard linking application between diverse domains of knowledge, such as computer science and anthropology, for example.
● The semantic network enables a straightforward investigation of the problem space.
● The semantic network provides a method for creating linked component branches.
● The semantic network also reverberates with people's data processing methods.
Disadvantages
● There is no universally accepted definition for link names.
● Semantic Nets are not intelligent, and they are completely reliant on their inventor.
● Links differ in function and appearance, causing misunderstanding in the assertion of linkages and structural links.
● Individual items are represented by undifferentiated nodes that represent classes.
● Only binary relationships are represented via links on objects.
● Negation, disjunction, and taxonomic knowledge are difficult to articulate.
Frames
A frame is a record-like structure that contains a set of properties and their values to describe a physical thing. Frames are a sort of artificial intelligence data structure that splits knowledge into substructures by depicting stereotyped situations. It is made up of a set of slots and slot values. These slots can come in any shape or size. Facets are the names and values assigned to slots.
Facets - Facets are the many characteristics of a slot. Facets are characteristics of frames that allow us to constrain them. When data from a certain slot is required, IF-NEEDED facts are called. A frame can have any number of slots, each of which can contain any number of facets, each of which can have any number of values. In artificial intelligence, a frame is also known as slot-filter knowledge representation.
There are two different kinds of frames:
● Declarative Frames: These are frames that only contain descriptive knowledge.
● Procedural Frames: A frame that is aware of a certain action or procedure.
Semantic networks gave rise to frames, which later evolved into our modern-day classes and objects. A single frame is of limited utility. A frames system is made up of a group of interconnected frames. Knowledge about an object or event can be kept in the knowledge base in the frame. The frame is a technique that is widely utilised in a variety of applications, such as natural language processing and machine vision.
Description of Frames
● A class or an instance is represented by each frame.
● Instance frame describes a specific occurrence of the class instance, whereas class frame represents a broad concept.
● Default values are usually set in class frames, but they can be changed at lower levels.
● If a class frame has an actual value facet, descendant frames cannot change it.
● For subclasses and instances, the value remains the same.
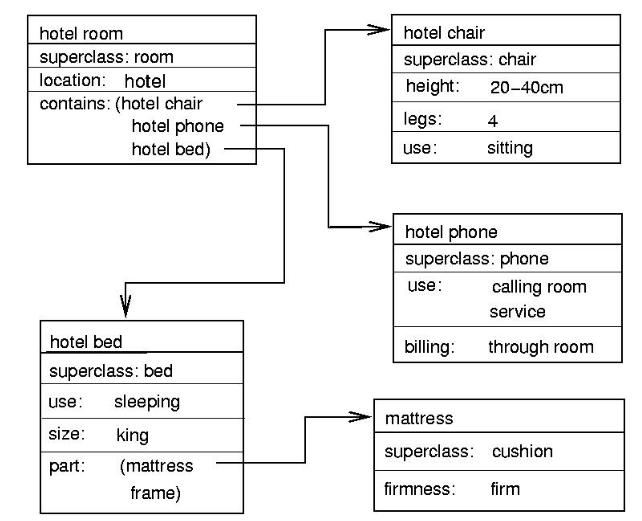
Fig 3: Part of a frame description of a hotel room. “Specialization” indicates a pointer to a superclass
Difference between Semantic net and frames
Semantic Nets | Frames |
In a network, a knowledge base that represents structured relationships between concepts. | Represent related knowledge about a specific issue that is already well-known. |
It has nodes that represent items and arcs, as well as relationships between them. | It has slots with values, which are referred to as facets. |
Adding data and drawing inferences is simple and quick using Semantic Networks. | Frames have a procedural attachment and inherit generic frame attributes. |
It categorises and connects objects in various formats. | By grouping related data, it makes programming languages easier. |
Semantic networks come in a variety of shapes and sizes, and they can represent a wide range of systems. | It's widely utilised in natural language processing and information retrieval. |
Scripts
A script is a structure that specifies a series of events that are likely to occur one after the other. It's akin to a chain of events that can be predicted. The structure of the script is defined in terms of (a) Actors (b) Roles (c) Props (d) Scenes– just like a playscript.
A script is a logical representation of a standardised sequence of events in a certain setting.
In natural language understanding systems, scripts are used to arrange a knowledge base in terms of the circumstances that the system should be able to comprehend. Scripts employ a frame-like framework to portray everyday experiences like as going to the movies, eating at a restaurant, shopping at a supermarket, or seeing an ophthalmologist.
As a result, a script is a framework that specifies a series of events that are likely to occur in succession.
Why Scripts are very useful?
i. Events tend to repeat themselves in predictable ways.
Ii. There are entry requirements for an event to take place.
Iii. There are unintentional connections between events.
Iv. There are prerequisites.
Components of a script
A script consists of the following elements:
● Entry conditions: These are basic requirements that must be met before the script's events can take place.
● Results: The condition that will be true after the script's events have occurred.
● Props: Props are slots that represent items that are engaged in events.
● Roles: Individual participants' activities are defined by their roles.
● Track: Variations on the script are being tracked. Components of the same scripts may be shared between tracks.
● Scenes: The order in which events occur.
Advantages of Scripts
● The ability to foresee occurrences.
● A combination of observations could lead to a single consistent interpretation.
Disadvantages of Scripts
● Frames are more general.
● It might not be appropriate to represent all types of knowledge.
Ontology
Ontology is a term used in AI to describe a shared vocabulary across researchers. It offers machine-readable definitions of fundamental concepts and their relationships. Ontology-based AI allows the system to make conclusions that mimic human behaviour by using contents and their relationships. It is capable of delivering tailored outcomes and does not require training sets to operate.
Ontology makes it easier for software agents to share a common concept of information structure, reuse domain knowledge, analyse domain knowledge, and separate domain knowledge from operational knowledge.
Why do we need ontology in AI?
Creating an ontology is akin to creating a set of data and its structure that can be used by other applications. Knowledge bases constructed from ontologies are used as data in problem-solving methodologies, software agents, and domain-specific applications.
The size of machine learning and deep learning systems is growing. A prevalent fallacy is that as more data is collected, a machine learning model improves. This idea, however, has been debunked by numerous researchers. As companies approach the data ceiling, they gradually realise that too much data can be burdensome to analyse, resulting in value-destroying complexity and more time and financial expenditure. According to studies, up to 85% of AI programmes fail. This is mostly due to a lack of knowledge about how to make use of massive amounts of data. In this regard, ontologies can make a big difference.
By widening the scope of an AI system, ontological modelling can assist it. It can hold any type of data and can be in an unstructured, semi-structured, or organised manner. It allows for more seamless data integration. It can address the large data given as input since it can incorporate every part of the data modelling process. Ontology can be used by a variety of organisations in a variety of industries to achieve a variety of objectives.
Ontologies can also aid in the improvement of training dataset data quality. They make the ontological structure more coherent and easier to navigate. A knowledge graph can also be created using an ontology data model.
Key takeaways
A frame is a record-like structure that contains a set of properties and their values to describe a physical thing. Frames are a sort of artificial intelligence data structure that splits knowledge into substructures by depicting stereotyped situations.
A script is a logical representation of a standardised sequence of events in a certain setting.
Ontology is a term used in AI to describe a shared vocabulary across researchers. It offers machine-readable definitions of fundamental concepts and their relationships.
References:
- Elaine Rich, Kevin Knight and Shivashankar B Nair, “Artificial Intelligence”, Mc Graw Hill Publication, 2009.
- Dan W. Patterson, “Introduction to Artificial Intelligence and Expert System”, Pearson Publication,2015.
- Saroj Kaushik, “Artificial Intelligence”, Cengage Learning, 2011.
Unit - 3
Knowledge representation
Humans excel in comprehending, reasoning, and interpreting information. Humans have knowledge about things and use that knowledge to accomplish various activities in the real world. However, knowledge representation and reasoning deal with how robots achieve all of these things. As a result, the following is a description of knowledge representation:
● Knowledge representation and reasoning (KR, KRR) is a branch of artificial intelligence that studies how AI agents think and how their thinking influences their behavior.
● It is in charge of encoding information about the real world in such a way that a computer can comprehend it and use it to solve complicated real-world problems like diagnosing a medical condition or conversing with humans in natural language.
● It's also a means of describing how artificial intelligence can represent knowledge. Knowledge representation is more than just storing data in a database; it also allows an intelligent machine to learn from its knowledge and experiences in order to act intelligently like a person.
What to Represent:
The types of knowledge that must be represented in AI systems are as follows:
● Object - All of the information on items in our universe. Guitars, for example, have strings, while trumpets are brass instruments.
● Events - Events are the actions that take place in our world.
● Performance - Performance is a term used to describe behaviour that entails knowing how to perform things.
● Meta-knowledge - It is information about what we already know.
● Facts - The truths about the real world and what we represent are known as facts.
● Knowledge-Base - The knowledge base is the most important component of the knowledge-based agents. It's abbreviated as KB. The Sentences are grouped together in the Knowledgebase (Here, sentences are used as a technical term and not identical with the English language).
Types of knowledge
The numerous categories of knowledge are as follows:
1. Declarative Knowledge
● Declarative knowledge is the ability to understand something.
● It contains ideas, facts, and objects.
● It's also known as descriptive knowledge, and it's communicated using declarative statements.
● It is less complicated than procedural programming.
2. Procedural Knowledge
● It's sometimes referred to as "imperative knowledge."
● Procedure knowledge is a form of knowledge that entails knowing how to do something.
● It can be used to complete any assignment.
● It has rules, plans, procedures, and agendas, among other things.
● The use of procedural knowledge is contingent on the job at hand.
3. Meta-knowledge
● Meta-knowledge is information about other sorts of knowledge.
4. Heuristic knowledge
● Heuristic knowledge is the sum of the knowledge of a group of specialists in a certain field or subject.
● Heuristic knowledge refers to rules of thumb that are based on prior experiences, awareness of methodologies, and are likely to work but not guaranteed.
5. Structural knowledge
● Basic problem-solving knowledge is structural knowledge.
● It describes the connections between distinct concepts such as kind, part of, and grouping.
● It is a term that describes the relationship between two or more concepts or objects.
The relation between knowledge and intelligence they are as follows:
Knowledge of real-worlds plays a very important role in the intelligence and the same for creating the artificial intelligence. Knowledge plays an important role in that of the demonstrating intelligent behaviour in the AI agents. An agent is the only able to accurately act on some of the input when he has some of the knowledge or the experience about that of the input.
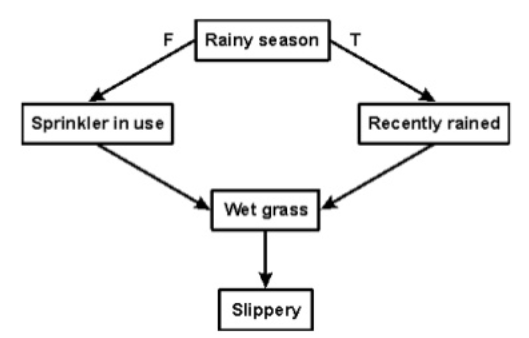
Let's suppose if you met some of the person who is speaking in that of a language which you don't know, then how you will able to act on that. The same thing applies to that of the intelligent behaviour of the agents.
As we can see in below diagram, there is one decision maker which act by sensing that of the environment and using the knowledge. But if the knowledge part will not present then, it cannot display intelligent behaviour.
AI knowledge cycle:
An Artificial intelligence system has that of the following components for displaying intelligent behaviour they are as follows:
● Perception
● Learning
● Knowledge Representation and Reasoning
● Planning
● Execution
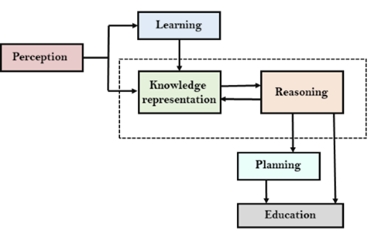
The above diagram is showing how that of an AI system can interacts with that of the real world and what the components help it to show the intelligence. AI system has the Perception component by which it retrieves information from that of its environment. It can be visual, audio or another form of the sensory input. The learning component is that the responsible for learning from data captured by the Perception comportment.
In the complete cycle, the main components are the knowledge representation and the Reasoning. These two components are involved in showing that of the intelligence in machine-like humans. These two components are independent with each other but also coupled together. The planning and execution depend on analysis of that of the Knowledge representation and the reasoning.
Approaches to knowledge representation:
There are mainly four approaches to knowledge representation, which are given below:
1. Simple relational knowledge:
● It is the simplest way of that of the storing facts which uses that of the relational method and each fact about that of a set of the object is set out systematically in that of the columns.
● This approach of the knowledge representation is famous in the database systems where the relationship between that of the different entities is represented.
● This approach has little opportunity for that of the inference.
Example: The following is the simple relational knowledge representation.
Player | Weight | Age |
Player1 | 65 | 23 |
Player2 | 58 | 18 |
Player3 | 75 | 24
|
2.Inheritable knowledge:
● In the inheritable knowledge approach, all the data must be stored into that of a hierarchy of the classes.
● All classes should be arranged in that of a generalized form or a hierarchal manner.
● In this approach, we apply the inheritance property.
● Elements inherit values from the other members of a class.
● This approach contains the inheritable knowledge which shows that of a relation between instance and the class, and it is known as instance relation.
● Every individual frame can represent that of the collection of attributes and its value.
● In this approach, objects and the values are represented in the Boxed nodes.
● We use Arrows which point from that of the objects to their values.
Example:
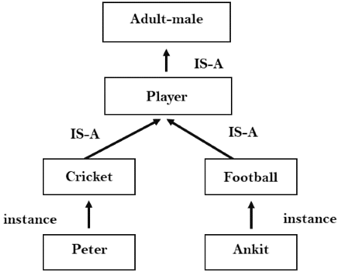
3. Inferential knowledge:
● Inferential knowledge approach represents the knowledge in the form of the formal logics.
● This approach can be used to derive more that of the facts.
● It guaranteed the correctness.
● Example: Let's suppose there are two statements:
- Marcus is a man
- All men are mortal
Then it can represent as;
Man(Marcus)
∀x = man (x) ----------> mortal (x)s
4. Procedural knowledge:
● Procedural knowledge approach uses that of the small programs and codes which describes how to do specific things, and how to proceed.
● In this approach, one important rule is used which is If-Then rule.
● In this knowledge, we can use various coding languages such as LISP language and Prolog language.
● We can easily represent heuristic or domain-specific knowledge using this approach.
● But it is not necessary that we can represent all cases in this approach.
Requirements for knowledge Representation system:
A good knowledge representation system must possess the following properties.
- Representational Accuracy:
KR system should have that of the ability to represent that the all kind of the required knowledge.
2. Inferential Adequacy:
KR system should have ability to manipulate that of the representational structures to produce that of the new knowledge corresponding to the existing structure.
3. Inferential Efficiency:
The ability to direct the inferential knowledge mechanism into the most productive directions by storing appropriate guides.
4. Acquisitioned efficiency- The ability to acquire the new knowledge easily using automatic methods.
Key takeaway
Humans excel in comprehending, reasoning, and interpreting information. Humans have knowledge about things and use that knowledge to accomplish various activities in the real world. However, knowledge representation and reasoning deal with how robots achieve all of these things
● First-order logic is a type of knowledge representation used in artificial intelligence. It's a propositional logic variation.
● FOL is expressive enough to convey natural language statements in a concise manner.
● First-order logic is sometimes known as predicate logic or first-order predicate logic. First-order logic is a complex language for constructing information about objects and expressing relationships between them.
● First-order logic (as does natural language) assumes not just that the world contains facts, as propositional logic does, but also that the world has the following:
● Objects: People, numbers, colors, conflicts, theories, squares, pits, wumpus,
● Relation: It can be a unary relation like red, round, or nearby, or an n-any relation like sister of, brother of, has color, or comes between.
● Functions: Father of, best friend, third inning of, last inning of......
● First-order logic contains two basic pieces as a natural language:
● Syntax
● Semantics
Syntax
Syntax has to do with what ‘things’ (symbols, notations) one is allowed to use in the language and in what way; there is/are a(n):
● Alphabet
● Language constructs
● Sentences to assert knowledge
Logical connectives (⇒, ∧, ∨, and ⇐⇒ ), negation (¬), and parentheses. These will be used to recursively build complex formulas, just as was done for propositional logic.
Constants symbols are strings that will be interpreted as representing objects, e.g. Bob might be a constant.
Variable symbols will be used as “place holders” for quantifying over objects.
Predicate symbols Each has an arity (number of arguments) associated with it, which can be zero or some other finite value. Predicates will be used to represent object characteristics and relationships.
Zero-arity Because predicate symbols are viewed as propositions in first-order logic, propositional logic is subsumed. These assertions can be thought of as world properties.
Predicates with a single parameter can be thought of as specifying object attributes. If Rich is a single-arity predicate, then Rich(Bob) is used to indicate that Bob is wealthy. Multi-arity predicates are used to describe relationships between items.

Fig 1: Syntax of first order logic
Function symbols Each has a specific arity (number of input arguments) and is understood as a function that maps the stated number of input objects to objects. Allowing FatherOf to be a single-arity function symbol, the natural interpretation of FatherOf(Bob) is Bob's father.
Zero-arity function symbols are considered to be constants.
Universal and existential quantifier symbols will be used to quantify over objects. For example, ∀ x Alive(x) ⇒ Breathing(x) is a universally quantified statement that uses the variable x as a placeholder.
Semantics of First-Order Logic
As with all logics, the first step in determining the semantics of first-order logic is to define the models of first-order logic. Remember that one of the benefits of using first-order logic is that it allows us to freely discuss objects and their relationships. As a result, our models will comprise objects as well as information about their properties and interactions with other items.
First order model
A first-order model is a tuple hD, Ii, where D denotes a non-empty object domain and I denotes an interpretation function. D is nothing more than a collection of items or elements that can be finite, infinite, or uncountable. The interpretation function I gives each of the available constant, function, and predicate symbols a meaning or interpretation as follows:
● If c is a constant symbol, then I(c) is an object in D. Thus, given a model, a constant can be viewed as naming an object in the domain.
● If f is a function symbol of arity n, then I(f) is a total function from Dn to D. That is the interpretation of f is a function that maps n domain objects to the domain D.
● If p is a predicate symbol of arity n > 0, then I(p) is a subset of Dn; that is, a predicate symbol is interpreted as a set of tuples from the domain. If a tuple O = (o1, · · · , on) is in I(p) then we say that p is true for the object tuple O.
● If p is a predicate symbol of arity 0, i.e. a simple proposition, then I(p) is equal to either true or false.
Assume we have a single predicate TallerThan, a single function FatherOf, and a single constant Bob. The following could be a model M1 for these symbols:
D = { BOB, JON, NULL }
I(Bob) = BOB
I(TallerThan) = { hBOB, JONi }
Because I(FatherOf) is a function, we'll only show the value for each argument to give the FatherOf meaning.
I(FatherOf)(BOB) = JON
I(FatherOf)(JON) = NULL
I(FatherOf)(NULL) = NULL
M2 could also be interpreted as follows,
D = { BOB, JON }
I(Bob) = BOB
I(TallerThan) = { hBOB, JONi,hJON, BOBi }
I(FatherOf)(BOB) = BOB
I(FatherOf)(JON) = JON
It's vital to highlight the difference between Bob, which is a constant (a syntactic entity), and BOB, which is a domain object (a semantic entity). The second interpretation isn't exactly what we're looking for (the objects are dads of themselves, and TallerThan is inconsistent), but it's still a viable model. By imposing proper limitations on the symbols, the knowledge base can rule out such unexpected models from consideration.
Key takeaway
- The syntax of FOL determines which collection of symbols is a logical expression in first-order logic.
- The basic syntactic elements of first-order logic are symbols. We write statements in short-hand notation in FOL.
Predicate Logic is concerned with predicates, or propositions that contain variables.
A predicate is a set of one or more variables that are decided on a particular domain. A variable-based predicate can be turned into a proposition by assigning a value to the variable or quantifying it.
Predicates can be found in the following examples.
● Consider E(x, y) denote "x = y"
● Consider X(a, b, c) denote "a + b + c = 0"
● Consider M(x, y) denote "x is married to y."
Quantifier:
Predicate Logic is concerned with predicates, or propositions that contain variables.
Existential Quantifier:
If p(x) is a proposition over the universe U, it is written as ∃x p(x) and reads as "There exists at least one value of variable x in the universe such that p(x) is true." The quantifier ∃ is called the existential quantifier.
Predicates can be found in the following examples.
(∃x∈A)p(x) or ∃x∈A such that p (x) or (∃x)p(x) or p(x) is true for some x ∈A.
Universal Quantifier:
If p(x) is a proposition with respect to the universe U. Then it's written as x,p(x), which means "For every x∈U,p(x) is true." The Universal Quantifier ∀ is the name of the quantifier.
With a universal quantifier, there are various ways to write a proposition.
∀x∈A,p(x) or p(x), ∀x ∈A Or ∀x,p(x) or p(x) is true for all x ∈A.
Backward-chaining is also known as backward deduction or backward reasoning when using an inference engine. A backward chaining algorithm is a style of reasoning that starts with the goal and works backwards through rules to find facts that support it.
It's an inference approach that starts with the goal. We look for implication phrases that will help us reach a conclusion and justify its premises. It is an approach for proving theorems that is goal-oriented.
Example: Fritz, a pet that croaks and eats flies, needs his color determined. The Knowledge Base contains the following rules:
If X croaks and eats flies — → Then X is a frog.
If X sings — → Then X is a bird.
If X is a frog — → Then X is green.
If x is a bird — -> Then X is blue.
The third and fourth rules were chosen because they best fit our goal of determining the color of the pet. For example, X may be green or blue. Both the antecedents of the rules, X is a frog and X is a bird, are added to the target list. The first two rules were chosen because their implications correlate to the newly added goals, namely, X is a frog or X is a bird.
Because the antecedent (If X croaks and eats flies) is true/given, we can derive that Fritz is a frog. If it's a frog, Fritz is green, and if it's a bird, Fritz is blue, completing the goal of determining the pet's color.
Properties of backward chaining
● A top-down strategy is what it's called.
● Backward-chaining employs the modus ponens inference rule.
● In backward chaining, the goal is broken down into sub-goals or sub-goals to ensure that the facts are true.
● Because a list of objectives decides which rules are chosen and implemented, it's known as a goal-driven strategy.
● The backward-chaining approach is utilized in game theory, automated theorem proving tools, inference engines, proof assistants, and other AI applications.
● The backward-chaining method relied heavily on a depth-first search strategy for proof.
It's a type of inference technique. The following steps are carried out.
1. Analyze data and make logical assertions from it (propositional or predicate logic).
2. Put them in the normal Conjunctive form (CNF).
3. Make an argument in opposition to the conclusion.
4. To locate a solution, use the resolution tree.
For instance: If the jewelry was taken by the maid, the butler was not to blame.
Either the maid took the jewels or she milked the animal.
The butler received the cream if the cow was milked by the maid.
If the butler was at fault, he received his cream as a result.
Step1: Expressing as propositional logic.
P= maid stole the jewelry.
Q= butler is guilty.
R= maid milked the cow.
S= butler got the cream.
Step 2: Convert to propositional logic.
1. P — -> ~Q
2. P v R
3. R — -> S
4. Q — -> S (Conclusion)
Step 3: Converting to CNF.
1. ~P v ~Q
2. P v R
3. ~R v S
4. ~Q v S (Conclusion)
Step 4: Negate the conclusion.
~(~Q v S) = Q ^ ~S
It is not in CNF due to the presence of ‘^’. Thus we break it into two parts: Q and ~S. We start with Q and resolve using the resolution tree.
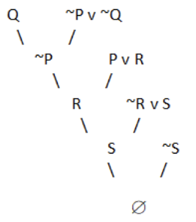
Fig 2: Resolution tree
A null value is obtained by negating the conclusion. As a result, our conclusion has been proven.
Example:
We can resolve two clauses which are given below:
[Animal (g(x) V Loves (f(x), x)] and [¬ Loves(a, b) V ¬Kills(a, b)]
Where two complimentary literals are: Loves (f(x), x) and ¬ Loves (a, b)
These literals can be unified with unifier θ= [a/f(x), and b/x], and it will generate a resolvent clause:
[Animal (g(x) V ¬ Kills(f(x), x)].
Steps for Resolution:
- Conversion of facts into first-order logic.
- Convert FOL statements into CNF
- Negate the statement which needs to prove (proof by contradiction)
- Draw resolution graph (unification).
To better understand all the above steps, we will take an example in which we will apply resolution.
Example:
John likes all kind of food.
Apple and vegetable are food
Anything anyone eats and not killed is food.
Anil eats peanuts and still alive
- Harry eats everything that Anil eats.
Prove by resolution that:
John likes peanuts.
Step-1: Conversion of Facts into FOL
In the first step we will convert all the given statements into its first order logic.

Here f and g are added predicates.
Step-2: Conversion of FOL into CNF
In First order logic resolution, it is required to convert the FOL into CNF as CNF form makes easier for resolution proofs.
Eliminate all implication (→) and rewrite
- ∀x ¬ food(x) V likes(John, x)
- Food(Apple) Λ food(vegetables)
- ∀x ∀y ¬ [eats(x, y) Λ¬ killed(x)] V food(y)
- Eats (Anil, Peanuts) Λ alive(Anil)
- ∀x ¬ eats(Anil, x) V eats(Harry, x)
- ∀x¬ [¬ killed(x) ] V alive(x)
- ∀x ¬ alive(x) V ¬ killed(x)
- Likes(John, Peanuts).
Move negation (¬)inwards and rewrite
9. ∀x ¬ food(x) V likes(John, x)
10. Food(Apple) Λ food(vegetables)
11. ∀x ∀y ¬ eats(x, y) V killed(x) V food(y)
12. Eats (Anil, Peanuts) Λ alive(Anil)
13. ∀x ¬ eats(Anil, x) V eats(Harry, x)
14. ∀x ¬killed(x) ] V alive(x)
15. ∀x ¬ alive(x) V ¬ killed(x)
16. Likes(John, Peanuts).
Rename variables or standardize variables
17. ∀x ¬ food(x) V likes(John, x)
18. Food(Apple) Λ food(vegetables)
19. ∀y ∀z ¬ eats(y, z) V killed(y) V food(z)
20. Eats (Anil, Peanuts) Λ alive(Anil)
21. ∀w¬ eats(Anil, w) V eats(Harry, w)
22. ∀g ¬killed(g) ] V alive(g)
23. ∀k ¬ alive(k) V ¬ killed(k)
24. Likes(John, Peanuts).
● Eliminate existential instantiation quantifier by elimination.
In this step, we will eliminate existential quantifier ∃, and this process is known as Skolemization. But in this example problem since there is no existential quantifier so all the statements will remain same in this step.
● Drop Universal quantifiers.
In this step we will drop all universal quantifier since all the statements are not implicitly quantified so we don't need it.
- ¬ food(x) V likes(John, x)
- Food(Apple)
- Food(vegetables)
- ¬ eats(y, z) V killed(y) V food(z)
- Eats (Anil, Peanuts)
- Alive(Anil)
- ¬ eats(Anil, w) V eats(Harry, w)
- Killed(g) V alive(g)
- ¬ alive(k) V ¬ killed(k)
- Likes(John, Peanuts).
Note: Statements "food(Apple) Λ food(vegetables)" and "eats (Anil, Peanuts) Λ alive(Anil)" can be written in two separate statements.
● Distribute conjunction ∧ over disjunction ¬.
This step will not make any change in this problem.
Step-3: Negate the statement to be proved
In this statement, we will apply negation to the conclusion statements, which will be written as ¬likes(John, Peanuts)
Step-4: Draw Resolution graph:
Now in this step, we will solve the problem by resolution tree using substitution. For the above problem, it will be given as follows:
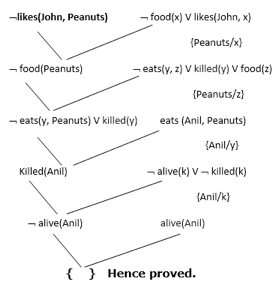
Hence the negation of the conclusion has been proved as a complete contradiction with the given set of statements.
Explanation of Resolution graph:
● In the first step of resolution graph, ¬likes(John, Peanuts) , and likes(John, x) get resolved(cancelled) by substitution of {Peanuts/x}, and we are left with ¬ food(Peanuts)
● In the second step of the resolution graph, ¬ food(Peanuts) , and food(z) get resolved (cancelled) by substitution of { Peanuts/z}, and we are left with ¬ eats(y, Peanuts) V killed(y) .
● In the third step of the resolution graph, ¬ eats(y, Peanuts) and eats (Anil, Peanuts) get resolved by substitution {Anil/y}, and we are left with Killed(Anil) .
● In the fourth step of the resolution graph, Killed(Anil) and ¬ killed(k) get resolve by substitution {Anil/k}, and we are left with ¬ alive(Anil) .
● In the last step of the resolution graph ¬ alive(Anil) and alive(Anil) get resolved.
Key takeaway
Resolution is a theorem proving technique that proceeds by building refutation proofs, i.e., proofs by contradictions. It was invented by Mathematician John Alan Robinson in 1965.
Unit - 3
Knowledge representation
Unit - 3
Knowledge representation
Humans excel in comprehending, reasoning, and interpreting information. Humans have knowledge about things and use that knowledge to accomplish various activities in the real world. However, knowledge representation and reasoning deal with how robots achieve all of these things. As a result, the following is a description of knowledge representation:
● Knowledge representation and reasoning (KR, KRR) is a branch of artificial intelligence that studies how AI agents think and how their thinking influences their behavior.
● It is in charge of encoding information about the real world in such a way that a computer can comprehend it and use it to solve complicated real-world problems like diagnosing a medical condition or conversing with humans in natural language.
● It's also a means of describing how artificial intelligence can represent knowledge. Knowledge representation is more than just storing data in a database; it also allows an intelligent machine to learn from its knowledge and experiences in order to act intelligently like a person.
What to Represent:
The types of knowledge that must be represented in AI systems are as follows:
● Object - All of the information on items in our universe. Guitars, for example, have strings, while trumpets are brass instruments.
● Events - Events are the actions that take place in our world.
● Performance - Performance is a term used to describe behaviour that entails knowing how to perform things.
● Meta-knowledge - It is information about what we already know.
● Facts - The truths about the real world and what we represent are known as facts.
● Knowledge-Base - The knowledge base is the most important component of the knowledge-based agents. It's abbreviated as KB. The Sentences are grouped together in the Knowledgebase (Here, sentences are used as a technical term and not identical with the English language).
Types of knowledge
The numerous categories of knowledge are as follows:
1. Declarative Knowledge
● Declarative knowledge is the ability to understand something.
● It contains ideas, facts, and objects.
● It's also known as descriptive knowledge, and it's communicated using declarative statements.
● It is less complicated than procedural programming.
2. Procedural Knowledge
● It's sometimes referred to as "imperative knowledge."
● Procedure knowledge is a form of knowledge that entails knowing how to do something.
● It can be used to complete any assignment.
● It has rules, plans, procedures, and agendas, among other things.
● The use of procedural knowledge is contingent on the job at hand.
3. Meta-knowledge
● Meta-knowledge is information about other sorts of knowledge.
4. Heuristic knowledge
● Heuristic knowledge is the sum of the knowledge of a group of specialists in a certain field or subject.
● Heuristic knowledge refers to rules of thumb that are based on prior experiences, awareness of methodologies, and are likely to work but not guaranteed.
5. Structural knowledge
● Basic problem-solving knowledge is structural knowledge.
● It describes the connections between distinct concepts such as kind, part of, and grouping.
● It is a term that describes the relationship between two or more concepts or objects.
The relation between knowledge and intelligence they are as follows:
Knowledge of real-worlds plays a very important role in the intelligence and the same for creating the artificial intelligence. Knowledge plays an important role in that of the demonstrating intelligent behaviour in the AI agents. An agent is the only able to accurately act on some of the input when he has some of the knowledge or the experience about that of the input.
Let's suppose if you met some of the person who is speaking in that of a language which you don't know, then how you will able to act on that. The same thing applies to that of the intelligent behaviour of the agents.
As we can see in below diagram, there is one decision maker which act by sensing that of the environment and using the knowledge. But if the knowledge part will not present then, it cannot display intelligent behaviour.
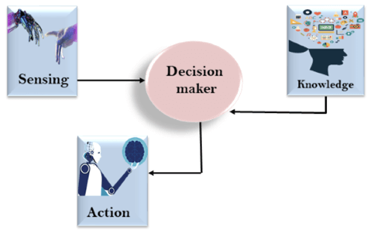
AI knowledge cycle:
An Artificial intelligence system has that of the following components for displaying intelligent behaviour they are as follows:
● Perception
● Learning
● Knowledge Representation and Reasoning
● Planning
● Execution
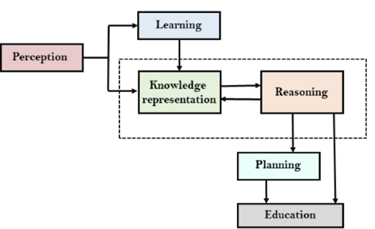
The above diagram is showing how that of an AI system can interacts with that of the real world and what the components help it to show the intelligence. AI system has the Perception component by which it retrieves information from that of its environment. It can be visual, audio or another form of the sensory input. The learning component is that the responsible for learning from data captured by the Perception comportment.
In the complete cycle, the main components are the knowledge representation and the Reasoning. These two components are involved in showing that of the intelligence in machine-like humans. These two components are independent with each other but also coupled together. The planning and execution depend on analysis of that of the Knowledge representation and the reasoning.
Approaches to knowledge representation:
There are mainly four approaches to knowledge representation, which are given below:
1. Simple relational knowledge:
● It is the simplest way of that of the storing facts which uses that of the relational method and each fact about that of a set of the object is set out systematically in that of the columns.
● This approach of the knowledge representation is famous in the database systems where the relationship between that of the different entities is represented.
● This approach has little opportunity for that of the inference.
Example: The following is the simple relational knowledge representation.
Player | Weight | Age |
Player1 | 65 | 23 |
Player2 | 58 | 18 |
Player3 | 75 | 24
|
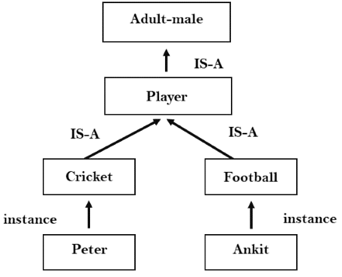
2.Inheritable knowledge:
● In the inheritable knowledge approach, all the data must be stored into that of a hierarchy of the classes.
● All classes should be arranged in that of a generalized form or a hierarchal manner.
● In this approach, we apply the inheritance property.
● Elements inherit values from the other members of a class.
● This approach contains the inheritable knowledge which shows that of a relation between instance and the class, and it is known as instance relation.
● Every individual frame can represent that of the collection of attributes and its value.
● In this approach, objects and the values are represented in the Boxed nodes.
● We use Arrows which point from that of the objects to their values.
Example:
3. Inferential knowledge:
● Inferential knowledge approach represents the knowledge in the form of the formal logics.
● This approach can be used to derive more that of the facts.
● It guaranteed the correctness.
● Example: Let's suppose there are two statements:
- Marcus is a man
- All men are mortal
Then it can represent as;
Man(Marcus)
∀x = man (x) ----------> mortal (x)s
4. Procedural knowledge:
● Procedural knowledge approach uses that of the small programs and codes which describes how to do specific things, and how to proceed.
● In this approach, one important rule is used which is If-Then rule.
● In this knowledge, we can use various coding languages such as LISP language and Prolog language.
● We can easily represent heuristic or domain-specific knowledge using this approach.
● But it is not necessary that we can represent all cases in this approach.
Requirements for knowledge Representation system:
A good knowledge representation system must possess the following properties.
- Representational Accuracy:
KR system should have that of the ability to represent that the all kind of the required knowledge.
2. Inferential Adequacy:
KR system should have ability to manipulate that of the representational structures to produce that of the new knowledge corresponding to the existing structure.
3. Inferential Efficiency:
The ability to direct the inferential knowledge mechanism into the most productive directions by storing appropriate guides.
4. Acquisitioned efficiency- The ability to acquire the new knowledge easily using automatic methods.
Key takeaway
Humans excel in comprehending, reasoning, and interpreting information. Humans have knowledge about things and use that knowledge to accomplish various activities in the real world. However, knowledge representation and reasoning deal with how robots achieve all of these things
● First-order logic is a type of knowledge representation used in artificial intelligence. It's a propositional logic variation.
● FOL is expressive enough to convey natural language statements in a concise manner.
● First-order logic is sometimes known as predicate logic or first-order predicate logic. First-order logic is a complex language for constructing information about objects and expressing relationships between them.
● First-order logic (as does natural language) assumes not just that the world contains facts, as propositional logic does, but also that the world has the following:
● Objects: People, numbers, colors, conflicts, theories, squares, pits, wumpus,
● Relation: It can be a unary relation like red, round, or nearby, or an n-any relation like sister of, brother of, has color, or comes between.
● Functions: Father of, best friend, third inning of, last inning of......
● First-order logic contains two basic pieces as a natural language:
● Syntax
● Semantics
Syntax
Syntax has to do with what ‘things’ (symbols, notations) one is allowed to use in the language and in what way; there is/are a(n):
● Alphabet
● Language constructs
● Sentences to assert knowledge
Logical connectives (⇒, ∧, ∨, and ⇐⇒ ), negation (¬), and parentheses. These will be used to recursively build complex formulas, just as was done for propositional logic.
Constants symbols are strings that will be interpreted as representing objects, e.g. Bob might be a constant.
Variable symbols will be used as “place holders” for quantifying over objects.
Predicate symbols Each has an arity (number of arguments) associated with it, which can be zero or some other finite value. Predicates will be used to represent object characteristics and relationships.
Zero-arity Because predicate symbols are viewed as propositions in first-order logic, propositional logic is subsumed. These assertions can be thought of as world properties.
Predicates with a single parameter can be thought of as specifying object attributes. If Rich is a single-arity predicate, then Rich(Bob) is used to indicate that Bob is wealthy. Multi-arity predicates are used to describe relationships between items.

Fig 1: Syntax of first order logic
Function symbols Each has a specific arity (number of input arguments) and is understood as a function that maps the stated number of input objects to objects. Allowing FatherOf to be a single-arity function symbol, the natural interpretation of FatherOf(Bob) is Bob's father.
Zero-arity function symbols are considered to be constants.
Universal and existential quantifier symbols will be used to quantify over objects. For example, ∀ x Alive(x) ⇒ Breathing(x) is a universally quantified statement that uses the variable x as a placeholder.
Semantics of First-Order Logic
As with all logics, the first step in determining the semantics of first-order logic is to define the models of first-order logic. Remember that one of the benefits of using first-order logic is that it allows us to freely discuss objects and their relationships. As a result, our models will comprise objects as well as information about their properties and interactions with other items.
First order model
A first-order model is a tuple hD, Ii, where D denotes a non-empty object domain and I denotes an interpretation function. D is nothing more than a collection of items or elements that can be finite, infinite, or uncountable. The interpretation function I gives each of the available constant, function, and predicate symbols a meaning or interpretation as follows:
● If c is a constant symbol, then I(c) is an object in D. Thus, given a model, a constant can be viewed as naming an object in the domain.
● If f is a function symbol of arity n, then I(f) is a total function from Dn to D. That is the interpretation of f is a function that maps n domain objects to the domain D.
● If p is a predicate symbol of arity n > 0, then I(p) is a subset of Dn; that is, a predicate symbol is interpreted as a set of tuples from the domain. If a tuple O = (o1, · · · , on) is in I(p) then we say that p is true for the object tuple O.
● If p is a predicate symbol of arity 0, i.e. a simple proposition, then I(p) is equal to either true or false.
Assume we have a single predicate TallerThan, a single function FatherOf, and a single constant Bob. The following could be a model M1 for these symbols:
D = { BOB, JON, NULL }
I(Bob) = BOB
I(TallerThan) = { hBOB, JONi }
Because I(FatherOf) is a function, we'll only show the value for each argument to give the FatherOf meaning.
I(FatherOf)(BOB) = JON
I(FatherOf)(JON) = NULL
I(FatherOf)(NULL) = NULL
M2 could also be interpreted as follows,
D = { BOB, JON }
I(Bob) = BOB
I(TallerThan) = { hBOB, JONi,hJON, BOBi }
I(FatherOf)(BOB) = BOB
I(FatherOf)(JON) = JON
It's vital to highlight the difference between Bob, which is a constant (a syntactic entity), and BOB, which is a domain object (a semantic entity). The second interpretation isn't exactly what we're looking for (the objects are dads of themselves, and TallerThan is inconsistent), but it's still a viable model. By imposing proper limitations on the symbols, the knowledge base can rule out such unexpected models from consideration.
Key takeaway
- The syntax of FOL determines which collection of symbols is a logical expression in first-order logic.
- The basic syntactic elements of first-order logic are symbols. We write statements in short-hand notation in FOL.
Predicate Logic is concerned with predicates, or propositions that contain variables.
A predicate is a set of one or more variables that are decided on a particular domain. A variable-based predicate can be turned into a proposition by assigning a value to the variable or quantifying it.
Predicates can be found in the following examples.
● Consider E(x, y) denote "x = y"
● Consider X(a, b, c) denote "a + b + c = 0"
● Consider M(x, y) denote "x is married to y."
Quantifier:
Predicate Logic is concerned with predicates, or propositions that contain variables.
Existential Quantifier:
If p(x) is a proposition over the universe U, it is written as ∃x p(x) and reads as "There exists at least one value of variable x in the universe such that p(x) is true." The quantifier ∃ is called the existential quantifier.
Predicates can be found in the following examples.
(∃x∈A)p(x) or ∃x∈A such that p (x) or (∃x)p(x) or p(x) is true for some x ∈A.
Universal Quantifier:
If p(x) is a proposition with respect to the universe U. Then it's written as x,p(x), which means "For every x∈U,p(x) is true." The Universal Quantifier ∀ is the name of the quantifier.
With a universal quantifier, there are various ways to write a proposition.
∀x∈A,p(x) or p(x), ∀x ∈A Or ∀x,p(x) or p(x) is true for all x ∈A.
Backward-chaining is also known as backward deduction or backward reasoning when using an inference engine. A backward chaining algorithm is a style of reasoning that starts with the goal and works backwards through rules to find facts that support it.
It's an inference approach that starts with the goal. We look for implication phrases that will help us reach a conclusion and justify its premises. It is an approach for proving theorems that is goal-oriented.
Example: Fritz, a pet that croaks and eats flies, needs his color determined. The Knowledge Base contains the following rules:
If X croaks and eats flies — → Then X is a frog.
If X sings — → Then X is a bird.
If X is a frog — → Then X is green.
If x is a bird — -> Then X is blue.
The third and fourth rules were chosen because they best fit our goal of determining the color of the pet. For example, X may be green or blue. Both the antecedents of the rules, X is a frog and X is a bird, are added to the target list. The first two rules were chosen because their implications correlate to the newly added goals, namely, X is a frog or X is a bird.
Because the antecedent (If X croaks and eats flies) is true/given, we can derive that Fritz is a frog. If it's a frog, Fritz is green, and if it's a bird, Fritz is blue, completing the goal of determining the pet's color.
Properties of backward chaining
● A top-down strategy is what it's called.
● Backward-chaining employs the modus ponens inference rule.
● In backward chaining, the goal is broken down into sub-goals or sub-goals to ensure that the facts are true.
● Because a list of objectives decides which rules are chosen and implemented, it's known as a goal-driven strategy.
● The backward-chaining approach is utilized in game theory, automated theorem proving tools, inference engines, proof assistants, and other AI applications.
● The backward-chaining method relied heavily on a depth-first search strategy for proof.
It's a type of inference technique. The following steps are carried out.
1. Analyze data and make logical assertions from it (propositional or predicate logic).
2. Put them in the normal Conjunctive form (CNF).
3. Make an argument in opposition to the conclusion.
4. To locate a solution, use the resolution tree.
For instance: If the jewelry was taken by the maid, the butler was not to blame.
Either the maid took the jewels or she milked the animal.
The butler received the cream if the cow was milked by the maid.
If the butler was at fault, he received his cream as a result.
Step1: Expressing as propositional logic.
P= maid stole the jewelry.
Q= butler is guilty.
R= maid milked the cow.
S= butler got the cream.
Step 2: Convert to propositional logic.
1. P — -> ~Q
2. P v R
3. R — -> S
4. Q — -> S (Conclusion)
Step 3: Converting to CNF.
1. ~P v ~Q
2. P v R
3. ~R v S
4. ~Q v S (Conclusion)
Step 4: Negate the conclusion.
~(~Q v S) = Q ^ ~S
It is not in CNF due to the presence of ‘^’. Thus we break it into two parts: Q and ~S. We start with Q and resolve using the resolution tree.
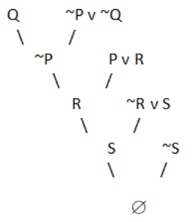
Fig 2: Resolution tree
A null value is obtained by negating the conclusion. As a result, our conclusion has been proven.
Example:
We can resolve two clauses which are given below:
[Animal (g(x) V Loves (f(x), x)] and [¬ Loves(a, b) V ¬Kills(a, b)]
Where two complimentary literals are: Loves (f(x), x) and ¬ Loves (a, b)
These literals can be unified with unifier θ= [a/f(x), and b/x], and it will generate a resolvent clause:
[Animal (g(x) V ¬ Kills(f(x), x)].
Steps for Resolution:
- Conversion of facts into first-order logic.
- Convert FOL statements into CNF
- Negate the statement which needs to prove (proof by contradiction)
- Draw resolution graph (unification).
To better understand all the above steps, we will take an example in which we will apply resolution.
Example:
John likes all kind of food.
Apple and vegetable are food
Anything anyone eats and not killed is food.
Anil eats peanuts and still alive
- Harry eats everything that Anil eats.
Prove by resolution that:
John likes peanuts.
Step-1: Conversion of Facts into FOL
In the first step we will convert all the given statements into its first order logic.

Here f and g are added predicates.
Step-2: Conversion of FOL into CNF
In First order logic resolution, it is required to convert the FOL into CNF as CNF form makes easier for resolution proofs.
Eliminate all implication (→) and rewrite
- ∀x ¬ food(x) V likes(John, x)
- Food(Apple) Λ food(vegetables)
- ∀x ∀y ¬ [eats(x, y) Λ¬ killed(x)] V food(y)
- Eats (Anil, Peanuts) Λ alive(Anil)
- ∀x ¬ eats(Anil, x) V eats(Harry, x)
- ∀x¬ [¬ killed(x) ] V alive(x)
- ∀x ¬ alive(x) V ¬ killed(x)
- Likes(John, Peanuts).
Move negation (¬)inwards and rewrite
9. ∀x ¬ food(x) V likes(John, x)
10. Food(Apple) Λ food(vegetables)
11. ∀x ∀y ¬ eats(x, y) V killed(x) V food(y)
12. Eats (Anil, Peanuts) Λ alive(Anil)
13. ∀x ¬ eats(Anil, x) V eats(Harry, x)
14. ∀x ¬killed(x) ] V alive(x)
15. ∀x ¬ alive(x) V ¬ killed(x)
16. Likes(John, Peanuts).
Rename variables or standardize variables
17. ∀x ¬ food(x) V likes(John, x)
18. Food(Apple) Λ food(vegetables)
19. ∀y ∀z ¬ eats(y, z) V killed(y) V food(z)
20. Eats (Anil, Peanuts) Λ alive(Anil)
21. ∀w¬ eats(Anil, w) V eats(Harry, w)
22. ∀g ¬killed(g) ] V alive(g)
23. ∀k ¬ alive(k) V ¬ killed(k)
24. Likes(John, Peanuts).
● Eliminate existential instantiation quantifier by elimination.
In this step, we will eliminate existential quantifier ∃, and this process is known as Skolemization. But in this example problem since there is no existential quantifier so all the statements will remain same in this step.
● Drop Universal quantifiers.
In this step we will drop all universal quantifier since all the statements are not implicitly quantified so we don't need it.
- ¬ food(x) V likes(John, x)
- Food(Apple)
- Food(vegetables)
- ¬ eats(y, z) V killed(y) V food(z)
- Eats (Anil, Peanuts)
- Alive(Anil)
- ¬ eats(Anil, w) V eats(Harry, w)
- Killed(g) V alive(g)
- ¬ alive(k) V ¬ killed(k)
- Likes(John, Peanuts).
Note: Statements "food(Apple) Λ food(vegetables)" and "eats (Anil, Peanuts) Λ alive(Anil)" can be written in two separate statements.
● Distribute conjunction ∧ over disjunction ¬.
This step will not make any change in this problem.
Step-3: Negate the statement to be proved
In this statement, we will apply negation to the conclusion statements, which will be written as ¬likes(John, Peanuts)
Step-4: Draw Resolution graph:
Now in this step, we will solve the problem by resolution tree using substitution. For the above problem, it will be given as follows:
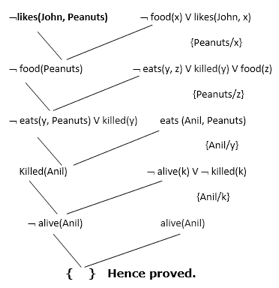
Hence the negation of the conclusion has been proved as a complete contradiction with the given set of statements.
Explanation of Resolution graph:
● In the first step of resolution graph, ¬likes(John, Peanuts) , and likes(John, x) get resolved(cancelled) by substitution of {Peanuts/x}, and we are left with ¬ food(Peanuts)
● In the second step of the resolution graph, ¬ food(Peanuts) , and food(z) get resolved (cancelled) by substitution of { Peanuts/z}, and we are left with ¬ eats(y, Peanuts) V killed(y) .
● In the third step of the resolution graph, ¬ eats(y, Peanuts) and eats (Anil, Peanuts) get resolved by substitution {Anil/y}, and we are left with Killed(Anil) .
● In the fourth step of the resolution graph, Killed(Anil) and ¬ killed(k) get resolve by substitution {Anil/k}, and we are left with ¬ alive(Anil) .
● In the last step of the resolution graph ¬ alive(Anil) and alive(Anil) get resolved.
Key takeaway
Resolution is a theorem proving technique that proceeds by building refutation proofs, i.e., proofs by contradictions. It was invented by Mathematician John Alan Robinson in 1965.
Semantic Networks, also known as Semantic Nets, are a type of knowledge representation technique for propositional data. Though it has long been utilised in philosophy, cognitive science (in the form of semantic memory), and linguistics, the Semantic Network was initially developed in computer science for artificial intelligence and machine learning. It is a knowledge base that represents the structured relationships between concepts in a network.
A semantic network is a visual representation of knowledge in the form of patterns of interconnected nodes. Only because semantic networks reflect knowledge or facilitate reasoning did they become prominent in artificial intelligence and natural language processing. In terms of knowledge representation, these serve as an alternative to predicate logic.
A semantic network is a graph with vertices that can be directed or undirected. These vertices represent concepts, whereas the edges reflect semantic relationships between concepts, as well as mapping or connecting semantic fields. Furthermore, it is known as Associative Networks because it processes information about recognised meanings in nearby locations.
Knowledge can be kept in the form of graphs, with nodes representing objects in the world and arcs expressing links between those objects, according to the structural notion.
● Nodes, links, and link labels make up semantic nets. Nodes appear in the form of circles, ellipses, or even rectangles in these network diagrams, and they represent objects such as real objects, concepts, or circumstances.
● To indicate the relationships between objects, links appear as arrows, while link labels specify the relationships.
● Because relationships provide the foundation for organising information, the items and relationships involved do not need to be concrete.
● Because the nodes are linked to each other, semantic nets are also known as associative networks.
Main Components Of Semantic Networks
● Lexical component - Relationships between objects are represented by nodes, which symbolise physical items, and labels, which denote specific objects and relationships.
● Structural component - the nodes or linkages in a diagram that are directed.
● Semantic component - The definitions are solely concerned with the links and labels of nodes, while the facts are determined by the approval regions.
● Procedural part - Constructors allow new linkages and nodes to be created. Destructors allow for the elimination of linkages and nodes.
Types of Semantic net:
Richard H. R. Of the Cambridge Language Research Unit (CLRU) created semantic networks for computers in 1956 for machine translation of natural languages. However, it is currently utilised for a wide range of purposes, including knowledge representation. There are now six different forms of semantic networks that enable declarative graphic representation, which is then utilised to represent knowledge and help automated systems that reason about it. These are the six different types of semantic networks:
Definitional Networks - These networks focus on and deal only with the subtype, or they are a link between a concept type and a newly formed subtype. A generalisation hierarchy is a type of production network. It adheres to the inheritance rule when it comes to duplicate characteristics.
Assertion Networks – It is intended to provide recommendations and is designed to assert propositions. Unless it is indicated with a modal administrator, most data in an assertion network is authentic. Some assertion systems are even regarded as models for the logical structures that underpin the semantic natural languages.
Implicational Networks – Implication is used as the principal connection between nodes. These networks can also be utilised to explain conviction patterns, causality, and deductions.
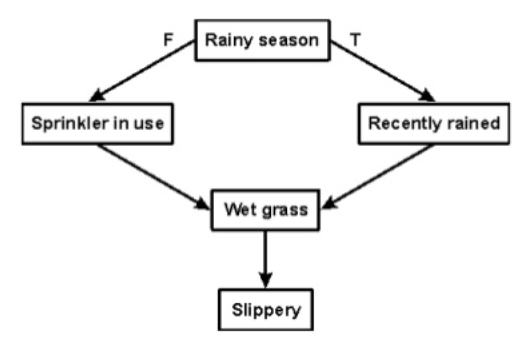
Executable Network - Contains methods that can induce changes to the network by incorporating techniques such as attached procedures or marker passing, which can conduct path messages, as well as associations and pattern searches.
Learning Networks – These are the networks that acquire knowledge from examples to develop and enhance their representations. Contain mechanisms in such networks cause changes inside the network by representing information and securing it. Adjusting fresh information from the previous system by including and excluding nodes and arcs, or changing numerical qualities termed weights and related with the arcs and nodes, is a famous example.
Hybrid Networks – Networks that integrate two or more of the preceding strategies, either in a single network or in a distinct but tightly interconnected network Some hybrid networks are specifically designed to apply theories about human cognitive functions, while others are designed for computer performance in general.
Advantages
● The semantic network is more natural than the logical representation, and it allows for the use of an efficient inference process (graphical algorithm)
● They are straightforward and simple to apply and comprehend.
● The semantic network can be used as a standard linking application between diverse domains of knowledge, such as computer science and anthropology, for example.
● The semantic network enables a straightforward investigation of the problem space.
● The semantic network provides a method for creating linked component branches.
● The semantic network also reverberates with people's data processing methods.
Disadvantages
● There is no universally accepted definition for link names.
● Semantic Nets are not intelligent, and they are completely reliant on their inventor.
● Links differ in function and appearance, causing misunderstanding in the assertion of linkages and structural links.
● Individual items are represented by undifferentiated nodes that represent classes.
● Only binary relationships are represented via links on objects.
● Negation, disjunction, and taxonomic knowledge are difficult to articulate.
Frames
A frame is a record-like structure that contains a set of properties and their values to describe a physical thing. Frames are a sort of artificial intelligence data structure that splits knowledge into substructures by depicting stereotyped situations. It is made up of a set of slots and slot values. These slots can come in any shape or size. Facets are the names and values assigned to slots.
Facets - Facets are the many characteristics of a slot. Facets are characteristics of frames that allow us to constrain them. When data from a certain slot is required, IF-NEEDED facts are called. A frame can have any number of slots, each of which can contain any number of facets, each of which can have any number of values. In artificial intelligence, a frame is also known as slot-filter knowledge representation.
There are two different kinds of frames:
● Declarative Frames: These are frames that only contain descriptive knowledge.
● Procedural Frames: A frame that is aware of a certain action or procedure.
Semantic networks gave rise to frames, which later evolved into our modern-day classes and objects. A single frame is of limited utility. A frames system is made up of a group of interconnected frames. Knowledge about an object or event can be kept in the knowledge base in the frame. The frame is a technique that is widely utilised in a variety of applications, such as natural language processing and machine vision.
Description of Frames
● A class or an instance is represented by each frame.
● Instance frame describes a specific occurrence of the class instance, whereas class frame represents a broad concept.
● Default values are usually set in class frames, but they can be changed at lower levels.
● If a class frame has an actual value facet, descendant frames cannot change it.
● For subclasses and instances, the value remains the same.
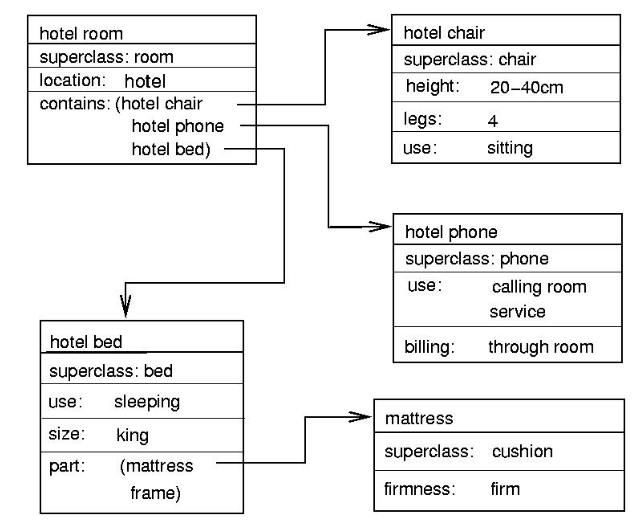
Fig 3: Part of a frame description of a hotel room. “Specialization” indicates a pointer to a superclass
Difference between Semantic net and frames
Semantic Nets | Frames |
In a network, a knowledge base that represents structured relationships between concepts. | Represent related knowledge about a specific issue that is already well-known. |
It has nodes that represent items and arcs, as well as relationships between them. | It has slots with values, which are referred to as facets. |
Adding data and drawing inferences is simple and quick using Semantic Networks. | Frames have a procedural attachment and inherit generic frame attributes. |
It categorises and connects objects in various formats. | By grouping related data, it makes programming languages easier. |
Semantic networks come in a variety of shapes and sizes, and they can represent a wide range of systems. | It's widely utilised in natural language processing and information retrieval. |
Scripts
A script is a structure that specifies a series of events that are likely to occur one after the other. It's akin to a chain of events that can be predicted. The structure of the script is defined in terms of (a) Actors (b) Roles (c) Props (d) Scenes– just like a playscript.
A script is a logical representation of a standardised sequence of events in a certain setting.
In natural language understanding systems, scripts are used to arrange a knowledge base in terms of the circumstances that the system should be able to comprehend. Scripts employ a frame-like framework to portray everyday experiences like as going to the movies, eating at a restaurant, shopping at a supermarket, or seeing an ophthalmologist.
As a result, a script is a framework that specifies a series of events that are likely to occur in succession.
Why Scripts are very useful?
i. Events tend to repeat themselves in predictable ways.
Ii. There are entry requirements for an event to take place.
Iii. There are unintentional connections between events.
Iv. There are prerequisites.
Components of a script
A script consists of the following elements:
● Entry conditions: These are basic requirements that must be met before the script's events can take place.
● Results: The condition that will be true after the script's events have occurred.
● Props: Props are slots that represent items that are engaged in events.
● Roles: Individual participants' activities are defined by their roles.
● Track: Variations on the script are being tracked. Components of the same scripts may be shared between tracks.
● Scenes: The order in which events occur.
Advantages of Scripts
● The ability to foresee occurrences.
● A combination of observations could lead to a single consistent interpretation.
Disadvantages of Scripts
● Frames are more general.
● It might not be appropriate to represent all types of knowledge.
Ontology
Ontology is a term used in AI to describe a shared vocabulary across researchers. It offers machine-readable definitions of fundamental concepts and their relationships. Ontology-based AI allows the system to make conclusions that mimic human behaviour by using contents and their relationships. It is capable of delivering tailored outcomes and does not require training sets to operate.
Ontology makes it easier for software agents to share a common concept of information structure, reuse domain knowledge, analyse domain knowledge, and separate domain knowledge from operational knowledge.
Why do we need ontology in AI?
Creating an ontology is akin to creating a set of data and its structure that can be used by other applications. Knowledge bases constructed from ontologies are used as data in problem-solving methodologies, software agents, and domain-specific applications.
The size of machine learning and deep learning systems is growing. A prevalent fallacy is that as more data is collected, a machine learning model improves. This idea, however, has been debunked by numerous researchers. As companies approach the data ceiling, they gradually realise that too much data can be burdensome to analyse, resulting in value-destroying complexity and more time and financial expenditure. According to studies, up to 85% of AI programmes fail. This is mostly due to a lack of knowledge about how to make use of massive amounts of data. In this regard, ontologies can make a big difference.
By widening the scope of an AI system, ontological modelling can assist it. It can hold any type of data and can be in an unstructured, semi-structured, or organised manner. It allows for more seamless data integration. It can address the large data given as input since it can incorporate every part of the data modelling process. Ontology can be used by a variety of organisations in a variety of industries to achieve a variety of objectives.
Ontologies can also aid in the improvement of training dataset data quality. They make the ontological structure more coherent and easier to navigate. A knowledge graph can also be created using an ontology data model.
Key takeaways
A frame is a record-like structure that contains a set of properties and their values to describe a physical thing. Frames are a sort of artificial intelligence data structure that splits knowledge into substructures by depicting stereotyped situations.
A script is a logical representation of a standardised sequence of events in a certain setting.
Ontology is a term used in AI to describe a shared vocabulary across researchers. It offers machine-readable definitions of fundamental concepts and their relationships.
References:
- Elaine Rich, Kevin Knight and Shivashankar B Nair, “Artificial Intelligence”, Mc Graw Hill Publication, 2009.
- Dan W. Patterson, “Introduction to Artificial Intelligence and Expert System”, Pearson Publication,2015.
- Saroj Kaushik, “Artificial Intelligence”, Cengage Learning, 2011.