Unit - 2
Regular sets
● A Regular Set is any set that represents the value of a Regular Expression.
● Sets that are approved by FA are called regular sets (finite automata).
For example:
L = {ε, 11, 1111, 111111, 11111111...}
L stands for a language set with an even number of 1s.
For the above-mentioned language L, finite automata is,
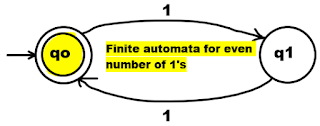
Because we may describe it with finite automata, the given set L is a regular set.
● Simple expressions called Regular Expressions can readily define the language adopted by finite automata. This is the most powerful way of expressing any language.
● Regular languages are referred to as the languages recognised by certain regular expressions.
● A regular expression may also be defined as a pattern sequence that defines a series.
● For matching character combinations in strings, regular expressions are used. This pattern is used by the string search algorithm to locate operations on a string.
A Regular Expression can be recursively defined as follows −
● ε is a Regular Expression indicates the language containing an empty string. (L (ε) = {ε})
● φ is a Regular Expression denoting an empty language. (L (φ) = { })
● x is a Regular Expression where L = {x}
● If X is a Regular Expression denoting the language L(X) and Y is a Regular
● Expression denoting the language L(Y), then
● X + Y is a Regular Expression corresponding to the language L(X) ∪
L(Y) where L(X+Y) = L(X) ∪ L(Y).
● X . Y is a Regular Expression corresponding to the language L(X) .
L(Y) where L(X.Y) = L(X) . L(Y)
● R* is a Regular Expression corresponding to the language L(R*)
Where L(R*) = (L(R))*
● If we apply any of the rules several times from 1 to 5, they are Regular
Expressions.
Unix Operator Extensions
Regular expressions are used frequently in Unix:
● In the command line
● Within text editors
● In the context of pattern matching programs such as grep and egrep
Additional operators are recognized by unix. These operators are used for convenience only.
● character classes: ‘[‘ <list of chars> ‘]’
● start of a line: ‘^’
● end of a line: ‘$’
● wildcard matching any character except newline: ‘.’
● optional instance: R? = epsilon | R
● one or more instances: R+ == RR*
Key takeaway:
Regular languages are referred to as the languages recognised by certain regular expressions.
A regular expression may also be defined as a pattern sequence that defines a series.
Given L, M, N as regular expressions, the following identities hold −
- L + M = M + L
- (L + M) + N = L + (M + N)
- (LM)N = L(MN)
- ∅ + L = L + ∅ = L
- L = L = L
- ∅L = L∅ = ∅
- L(M + N) = LM + LN
- (M + N)L = ML + NL
- L + L = L
- (L ∗ ) ∗ = L ∗
- ∅ ∗ =
- ∗ =
- (xy) ∗x = x(yx) ∗
- The following are all equivalent:
(a) (x + y) ∗
(b) (x ∗ + y) ∗
(c) x ∗ (x + y) ∗
(d) (x + yx∗ ) ∗
(e) (x ∗ y ∗ ) ∗
(f) x ∗ (yx∗ ) ∗
(g) (x ∗ y) ∗x ∗
Associativity law
Let's look at the Regular Expression Associativity Laws.
A + (B + C) = (A + B) + C and A.(B.C) = (A.B).C.
Commutativity for regular expression
Let's look at the Regular Expression Commutativity Laws.
A + B = B + A. However, A.B 6= B.A in general.
Identity for regular expression
Let's look at the Regular Expression Identity.
∅ + A = A + ∅ = A and ε.A = A.ε = A
Distributivity
Let's look at the Regular Expression Distributivity.
Left distributivity: A.(B + C) = A.B + A.C.
Right distributivity: (B + C).A = B.A + C.A.
Idempotent A + A = A.
Closure laws
Let's look at the Regular Expression Closure laws.
(A*)* = A*, ∅* = ε, ε* = ε, A+ = AA* = A*A, and A* = A + + ε.
DeMorgan Type law
Let's look at the Regular Expression DeMorgan laws.
(L + B)* = (L*B*)*
Union - R1 | R2 (sometimes written as R1 U R2 or R1 + R2) is a regular expression if R1 and R2 are regular expressions.
L(R1|R2) = L(R1) U L(R2).
Concatenation - R1R2 (sometimes written as R1.R2) is a regular expression if R1 and R2 are regular expressions.
L(R1R2) = L(R1) concatenated with L(R2).
Kleene closure - R1* (the Kleene closure of R1) is a regular expression if R1 is a regular expression.
L(R1*) = epsilon U L(R1) U L(R1R1) U L(R1R1R1) U ...
Closure takes precedence over concatenation, which takes precedence over union.
Example
Over the set ∑ = {a}, write the regular expression for the language that accepts all combinations of a's.
A can be zero, single, double, and so on in any combination of a's. If the letter an appears zero times, the string is null. That is, the set of {ε, a, aa, aaa, ....}. As a result, we can write this as a regular expression:
R = a*
That's how a Kleen closure works.
Theorem -
Let L be a regular language. Then a constant c' exists such that for every string w in L
|w| ≥ c
We are able to split w into three strings, w=xyz, so that
● |y| > 0
● |xy| ≤ c
● For all k ≥ 0, the string xyKz is also in L
Application of Pumping Lemma
It is important to apply Pumping Lemma to show that certain languages are not normal. It can never be used to illustrate the regularity of a language.
● If L is regular, it satisfies Pumping Lemma.
● If L does not satisfy Pumping Lemma, it is non-regular.
Method for demonstrating that a language L is not regular
● We have to assume that L is regular.
● The pumping lemma should hold for L.
● Use the pumping lemma to obtain a contradiction −
● Select w such that |w| ≥ c
● Select y such that |y| ≥ 1
● Select x such that |xy| ≤ c
● Assign the remaining string to z.
● Select k such that the resulting string is not in L.
Therefore, L is not regular.
Example:
Prove that L = {aibi | i ≥ 0} is not regular.
Sol:
● At first, we assume that L is regular and n is the number of states.
● Let w = anbn. Thus |w| = 2n ≥ n.
● By pumping lemma, let w = xyz, where |xy| ≤ n.
● Let x = ap , y = aq , and z = arbn , where p + q + r = n, p ≠ 0, q ≠ 0, r ≠ 0. Thus |y| ≠ 0.
● Let k = 2. Then xy2z = apa2qarbn.
● Number of as = (p + 2q + r) = (p + q + r) + q = n + q
● Hence, xy2z = an+q bn . Since q ≠ 0, xy2z is not of the form anbn .
● Thus, xy2z is not in L.
Hence L is not regular.
Regular sets contain the following characteristics:
Property 1: A regular set is formed by the union of two regular sets.
Proof −
Take a look at two regular expressions.
RE1 = a(aa)* and RE2 = (aa)*
So, L1 = {a, aaa, aaaaa,.....} (Strings of odd length excluding Null)
And L2 ={ ε, aa, aaaa, aaaaaa,.......} (Strings of even length including Null)
L1 ∪ L2 = { ε, a, aa, aaa, aaaa, aaaaa, aaaaaa,.......}
(Strings of all possible lengths including Null)
RE (L1 ∪ L2) = a* (which is a regular expression itself)
Hence proved.
Property 2: It's regular when two regular sets intersect.
Proof -
Take a look at two regular expressions.
RE1 = a(a*) and RE2 = (aa)*
So, L1 = { a,aa, aaa, aaaa, ....} (Strings of all possible lengths excluding Null)
L2 = { ε, aa, aaaa, aaaaaa,.......} (Strings of even length including Null)
L1 ∩ L2 = { aa, aaaa, aaaaaa,.......} (Strings of even length excluding Null)
RE (L1 ∩ L2) = aa(aa)* which is a regular expression itself.
Hence proved.
Property 3: A regular set's complement is also regular.
Proof -
Let's look at an example of a regular expression:
RE = (aa)*
So, L = {ε, aa, aaaa, aaaaaa, .......} (Strings of even length including Null)
L's complement is made up of all strings that aren't in L.
So, L’ = {a, aaa, aaaaa, .....} (Strings of odd length excluding Null)
RE (L’) = a(aa)* which is a regular expression itself.
Hence proved.
Property 4: The difference between two regular sets is regular.
Proof -
Take a look at two regular expressions.
RE1 = a (a*) and RE2 = (aa)*
So, L1 = {a, aa, aaa, aaaa, ....} (Strings of all possible lengths excluding Null)
L2 = { ε, aa, aaaa, aaaaaa,.......} (Strings of even length including Null)
L1 – L2 = {a, aaa, aaaaa, aaaaaaa, ....}
(Strings of all odd lengths excluding Null)
RE (L1 – L2) = a (aa)* which is a regular expression.
Hence proved.
Property 5: A regular set's reversal is also regular.
Proof -
If L is a regular set, we must show that LR is also regular.
Let, L = {01, 10, 11, 10}
RE (L) = 01 + 10 + 11 + 10
LR = {10, 01, 11, 01}
RE (LR) = 01 + 10 + 11 + 10 which is regular
Hence proved.
Property 6: The closure of a regular set is regular.
Proof -
If L = {a, aaa, aaaaa, .......} (Strings of odd length excluding Null)
i.e., RE (L) = a (aa)*
L* = {a, aa, aaa, aaaa , aaaaa,……………} (Strings of all lengths excluding Null)
RE (L*) = a (a)*
Hence proved.
Property 7: The concatenation of two regular sets is regular.
Proof -
Let RE1 = (0+1)*0 and RE2 = 01(0+1)*
Here, L1 = {0, 00, 10, 000, 010, ......} (Set of strings ending in 0)
And L2 = {01, 010,011,.....} (Set of strings beginning with 01)
Then, L1 L2 = {001,0010,0011,0001,00010,00011,1001,10010,.............}
Set of strings containing 001 as a substring which can be represented by an RE − (0 + 1)*001(0 + 1)*
Hence, proved.
The Chomsky Hierarchy describes the class of languages that the various machines embrace. The language group in Chomsky's Hierarchy is as follows:
- Type 0 known as Unrestricted Grammar.
- Type 1 known as Context Sensitive Grammar.
- Type 2 known as Context Free Grammar.
- Type 3 Regular Grammar.
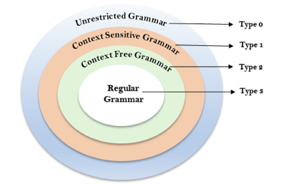
Fig: Chomsky hierarchy
The above diagram shows the hierarchy of chomsky. Each language of type 3 is therefore also of type 2, 1 and 0 respectively. Similarly, every language of type 2 is also of type 1 and type 0 likewise.
● Type 0 grammar -
Type 0 grammar is known as Unrestricted grammar.The grammar rules of these types of languages are unregulated. Turing machines can model these languages efficiently.
Example:
- BAa → aa
- P → p
● Type 1 grammar -
Type 1 grammar is known as Context Sensitive Grammar.Context-sensitive grammar is used to describe language that is sensitive to context. The context-sensitive grammar follows the rules below:
● There may be more than one symbol on the left side of their development rules for context-sensitive grammar.
● The number of left-hand symbols does not surpass the number of right-hand symbols.
● The A → ε type rule is not permitted unless A is a beginning symbol. It does not occur on the right-hand side of any rule.
● The Type 1 grammar should be Type 0. Production is in the form of V →T in type1
Key takeaway:
● Where the number of symbols in V is equal to or less than T
Example:
- S → AT
- T → xy
- A → a
● Type 2 grammar -
Type 2 Grammar is called Context Free Grammar. Context free languages are the languages which can be represented by the CNF (context free grammar) Type 2 should be type 1. The production rule is:
A → α
Key takeaway:
● Where A is any single non-terminal and is any combination of terminals and non-terminals.
Example:
- A → aBb
- A → b
- B → a
● Type 3 grammar -
Type 3 Grammar is called Regular Grammar. Those languages that can be represented using regular expressions are regular languages. These languages may be NFA or DFA-modeled.
Type3 has to be in the form of -
V → T*V / T*
Example:
A → xy
Key takeaway:
● The most limited form of grammar is Type3. Type2 and Type1 should be the grammar of Type3.
If it has rules of form A -> an or A -> aB or A -> ⁇ where ⁇ is a special symbol called NULL, grammar is natural. Standard grammar is formal grammar, i.e. regular right or regular left. Regular language is defined in every periodic grammar
Right linear grammar
Right linear grammar is also called right regular grammar is a formal grammar N, Σ, P, S such that all the production rules in P are of one of the following forms:
- A → a, where A is a non-terminal in N and a is a terminal in Σ.
- A → aB, where A and B are non-terminals in N and a is in Σ
- A → ε, where A is in N and ε denotes the empty string, i.e. the string of length 0.
Left linear grammar
Left linear grammar is also called left regular grammar. There are some rules to follow:
- A → a, where A in N is a non-terminal and an in Σ is a terminal.
- A → Ba, where A and B in N are non-terminals and an in Σ is
- A → ε, where A is N and ε denotes the empty string, i.e. the longitudinal string 0.
Key takeaway
Right linear grammar, also called right regular grammar, is a formal grammar.
Left linear grammar is also called left regular grammar.
The equivalence of regular grammar and finite automata is the subject of the following theorems.
Theorem 1: There is one finite automaton M for each right linear grammar GR (or left linear grammar GL), where
L (M) = L (GR) (or L (M) = G (GL))
Here is the proof of correctness and the construction algorithm from regular grammar to finite automata. It has two cases, one from right linear grammar to finite automata and the other from left linear grammar to finite automata.
Construction Algorithm 1.
For a given linear grammar, 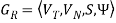 there is a corresponding NFA.
there is a corresponding NFA.
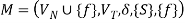
The transition function δ is specified by the following rules, where f is a newly added final state with 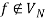 holding.
holding.
1) For any 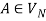 and
and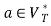 , if
, if 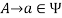 holds, then let
holds, then let 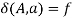 hold; or 2) For any
hold; or 2) For any 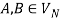 and
and 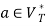 , if
, if 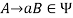 holds, then let
holds, then let 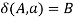 hold.
hold.
Proof. Using A→aB once in the leftmost derivation of S =>*ω (ω ∈ ∑*) for a right linear grammar GR is equivalent to the scenario that the current state A meeting with a will be transited to the subsequent state B in M. Using A→a once in the last derivation is equivalent to the current state A meeting with a being transited to f, the final state in M. Here we let 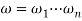 where
where 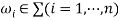 , then S =>*ω if and only if
, then S =>*ω if and only if
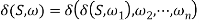
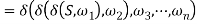
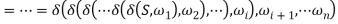
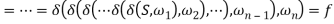
Holds.
The sufficient and necessary criteria of S =>*ω for GR are that there is only one path from S, the initial state, to f, the conclusion state in M. During the transition, all of the conditions that are met one by one are simply equivalent to ω, viz., 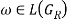 if and only if
if and only if 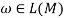 Therefore, it is evident that
Therefore, it is evident that 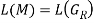 holds.
holds.
Construction Algorithm 2
For a given linear grammar, 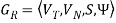 there is a corresponding NFA.
there is a corresponding NFA.
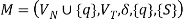
The transition function δ is described by the following rules, where q is a newly inserted start state with 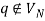 holding.
holding.
1) For any 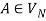 and
and 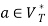 , if
, if 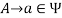 holds, then let
holds, then let 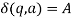 hold; or 2) for any
hold; or 2) for any 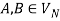 and
and 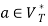 , if
, if 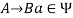 holds, then let
holds, then let 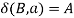 hold.
hold.
The proof of construction Algorithm 2 is the same as the proof of construction Algorithm 1, and we get the same result.
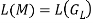
Theorem 2: There is a right linear grammar GR or a left linear grammar GL for each finite automaton M, where
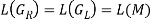
References:
- Harry R. Lewis and Christos H. Papadimitriou, Elements of the Theory of Computation, Pearson Education Asia.
- Dexter C. Kozen, Automata and Computability, Undergraduate Texts in Computer Science, Springer.
- Michael Sipser, Introduction to the Theory of Computation, PWS Publishing.
- John Martin, “Introduction to Languages and The Theory of Computation”, 2nd Edition, McGraw Hill Education, ISBN-13: 978-1-25-900558-9, ISBN-10: 1-25-900558-5
- J.Carroll & D Long, “Theory of Finite Automata”, Prentice Hall, ISBN 0-13-913708-45
Unit - 2
Regular sets
● A Regular Set is any set that represents the value of a Regular Expression.
● Sets that are approved by FA are called regular sets (finite automata).
For example:
L = {ε, 11, 1111, 111111, 11111111...}
L stands for a language set with an even number of 1s.
For the above-mentioned language L, finite automata is,
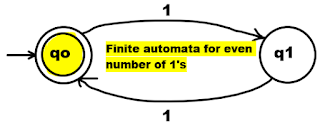
Because we may describe it with finite automata, the given set L is a regular set.
● Simple expressions called Regular Expressions can readily define the language adopted by finite automata. This is the most powerful way of expressing any language.
● Regular languages are referred to as the languages recognised by certain regular expressions.
● A regular expression may also be defined as a pattern sequence that defines a series.
● For matching character combinations in strings, regular expressions are used. This pattern is used by the string search algorithm to locate operations on a string.
A Regular Expression can be recursively defined as follows −
● ε is a Regular Expression indicates the language containing an empty string. (L (ε) = {ε})
● φ is a Regular Expression denoting an empty language. (L (φ) = { })
● x is a Regular Expression where L = {x}
● If X is a Regular Expression denoting the language L(X) and Y is a Regular
● Expression denoting the language L(Y), then
● X + Y is a Regular Expression corresponding to the language L(X) ∪
L(Y) where L(X+Y) = L(X) ∪ L(Y).
● X . Y is a Regular Expression corresponding to the language L(X) .
L(Y) where L(X.Y) = L(X) . L(Y)
● R* is a Regular Expression corresponding to the language L(R*)
Where L(R*) = (L(R))*
● If we apply any of the rules several times from 1 to 5, they are Regular
Expressions.
Unix Operator Extensions
Regular expressions are used frequently in Unix:
● In the command line
● Within text editors
● In the context of pattern matching programs such as grep and egrep
Additional operators are recognized by unix. These operators are used for convenience only.
● character classes: ‘[‘ <list of chars> ‘]’
● start of a line: ‘^’
● end of a line: ‘$’
● wildcard matching any character except newline: ‘.’
● optional instance: R? = epsilon | R
● one or more instances: R+ == RR*
Key takeaway:
Regular languages are referred to as the languages recognised by certain regular expressions.
A regular expression may also be defined as a pattern sequence that defines a series.
Given L, M, N as regular expressions, the following identities hold −
- L + M = M + L
- (L + M) + N = L + (M + N)
- (LM)N = L(MN)
- ∅ + L = L + ∅ = L
- L = L = L
- ∅L = L∅ = ∅
- L(M + N) = LM + LN
- (M + N)L = ML + NL
- L + L = L
- (L ∗ ) ∗ = L ∗
- ∅ ∗ =
- ∗ =
- (xy) ∗x = x(yx) ∗
- The following are all equivalent:
(a) (x + y) ∗
(b) (x ∗ + y) ∗
(c) x ∗ (x + y) ∗
(d) (x + yx∗ ) ∗
(e) (x ∗ y ∗ ) ∗
(f) x ∗ (yx∗ ) ∗
(g) (x ∗ y) ∗x ∗
Associativity law
Let's look at the Regular Expression Associativity Laws.
A + (B + C) = (A + B) + C and A.(B.C) = (A.B).C.
Commutativity for regular expression
Let's look at the Regular Expression Commutativity Laws.
A + B = B + A. However, A.B 6= B.A in general.
Identity for regular expression
Let's look at the Regular Expression Identity.
∅ + A = A + ∅ = A and ε.A = A.ε = A
Distributivity
Let's look at the Regular Expression Distributivity.
Left distributivity: A.(B + C) = A.B + A.C.
Right distributivity: (B + C).A = B.A + C.A.
Idempotent A + A = A.
Closure laws
Let's look at the Regular Expression Closure laws.
(A*)* = A*, ∅* = ε, ε* = ε, A+ = AA* = A*A, and A* = A + + ε.
DeMorgan Type law
Let's look at the Regular Expression DeMorgan laws.
(L + B)* = (L*B*)*
Union - R1 | R2 (sometimes written as R1 U R2 or R1 + R2) is a regular expression if R1 and R2 are regular expressions.
L(R1|R2) = L(R1) U L(R2).
Concatenation - R1R2 (sometimes written as R1.R2) is a regular expression if R1 and R2 are regular expressions.
L(R1R2) = L(R1) concatenated with L(R2).
Kleene closure - R1* (the Kleene closure of R1) is a regular expression if R1 is a regular expression.
L(R1*) = epsilon U L(R1) U L(R1R1) U L(R1R1R1) U ...
Closure takes precedence over concatenation, which takes precedence over union.
Example
Over the set ∑ = {a}, write the regular expression for the language that accepts all combinations of a's.
A can be zero, single, double, and so on in any combination of a's. If the letter an appears zero times, the string is null. That is, the set of {ε, a, aa, aaa, ....}. As a result, we can write this as a regular expression:
R = a*
That's how a Kleen closure works.
Theorem -
Let L be a regular language. Then a constant c' exists such that for every string w in L
|w| ≥ c
We are able to split w into three strings, w=xyz, so that
● |y| > 0
● |xy| ≤ c
● For all k ≥ 0, the string xyKz is also in L
Application of Pumping Lemma
It is important to apply Pumping Lemma to show that certain languages are not normal. It can never be used to illustrate the regularity of a language.
● If L is regular, it satisfies Pumping Lemma.
● If L does not satisfy Pumping Lemma, it is non-regular.
Method for demonstrating that a language L is not regular
● We have to assume that L is regular.
● The pumping lemma should hold for L.
● Use the pumping lemma to obtain a contradiction −
● Select w such that |w| ≥ c
● Select y such that |y| ≥ 1
● Select x such that |xy| ≤ c
● Assign the remaining string to z.
● Select k such that the resulting string is not in L.
Therefore, L is not regular.
Example:
Prove that L = {aibi | i ≥ 0} is not regular.
Sol:
● At first, we assume that L is regular and n is the number of states.
● Let w = anbn. Thus |w| = 2n ≥ n.
● By pumping lemma, let w = xyz, where |xy| ≤ n.
● Let x = ap , y = aq , and z = arbn , where p + q + r = n, p ≠ 0, q ≠ 0, r ≠ 0. Thus |y| ≠ 0.
● Let k = 2. Then xy2z = apa2qarbn.
● Number of as = (p + 2q + r) = (p + q + r) + q = n + q
● Hence, xy2z = an+q bn . Since q ≠ 0, xy2z is not of the form anbn .
● Thus, xy2z is not in L.
Hence L is not regular.
Regular sets contain the following characteristics:
Property 1: A regular set is formed by the union of two regular sets.
Proof −
Take a look at two regular expressions.
RE1 = a(aa)* and RE2 = (aa)*
So, L1 = {a, aaa, aaaaa,.....} (Strings of odd length excluding Null)
And L2 ={ ε, aa, aaaa, aaaaaa,.......} (Strings of even length including Null)
L1 ∪ L2 = { ε, a, aa, aaa, aaaa, aaaaa, aaaaaa,.......}
(Strings of all possible lengths including Null)
RE (L1 ∪ L2) = a* (which is a regular expression itself)
Hence proved.
Property 2: It's regular when two regular sets intersect.
Proof -
Take a look at two regular expressions.
RE1 = a(a*) and RE2 = (aa)*
So, L1 = { a,aa, aaa, aaaa, ....} (Strings of all possible lengths excluding Null)
L2 = { ε, aa, aaaa, aaaaaa,.......} (Strings of even length including Null)
L1 ∩ L2 = { aa, aaaa, aaaaaa,.......} (Strings of even length excluding Null)
RE (L1 ∩ L2) = aa(aa)* which is a regular expression itself.
Hence proved.
Property 3: A regular set's complement is also regular.
Proof -
Let's look at an example of a regular expression:
RE = (aa)*
So, L = {ε, aa, aaaa, aaaaaa, .......} (Strings of even length including Null)
L's complement is made up of all strings that aren't in L.
So, L’ = {a, aaa, aaaaa, .....} (Strings of odd length excluding Null)
RE (L’) = a(aa)* which is a regular expression itself.
Hence proved.
Property 4: The difference between two regular sets is regular.
Proof -
Take a look at two regular expressions.
RE1 = a (a*) and RE2 = (aa)*
So, L1 = {a, aa, aaa, aaaa, ....} (Strings of all possible lengths excluding Null)
L2 = { ε, aa, aaaa, aaaaaa,.......} (Strings of even length including Null)
L1 – L2 = {a, aaa, aaaaa, aaaaaaa, ....}
(Strings of all odd lengths excluding Null)
RE (L1 – L2) = a (aa)* which is a regular expression.
Hence proved.
Property 5: A regular set's reversal is also regular.
Proof -
If L is a regular set, we must show that LR is also regular.
Let, L = {01, 10, 11, 10}
RE (L) = 01 + 10 + 11 + 10
LR = {10, 01, 11, 01}
RE (LR) = 01 + 10 + 11 + 10 which is regular
Hence proved.
Property 6: The closure of a regular set is regular.
Proof -
If L = {a, aaa, aaaaa, .......} (Strings of odd length excluding Null)
i.e., RE (L) = a (aa)*
L* = {a, aa, aaa, aaaa , aaaaa,……………} (Strings of all lengths excluding Null)
RE (L*) = a (a)*
Hence proved.
Property 7: The concatenation of two regular sets is regular.
Proof -
Let RE1 = (0+1)*0 and RE2 = 01(0+1)*
Here, L1 = {0, 00, 10, 000, 010, ......} (Set of strings ending in 0)
And L2 = {01, 010,011,.....} (Set of strings beginning with 01)
Then, L1 L2 = {001,0010,0011,0001,00010,00011,1001,10010,.............}
Set of strings containing 001 as a substring which can be represented by an RE − (0 + 1)*001(0 + 1)*
Hence, proved.
The Chomsky Hierarchy describes the class of languages that the various machines embrace. The language group in Chomsky's Hierarchy is as follows:
- Type 0 known as Unrestricted Grammar.
- Type 1 known as Context Sensitive Grammar.
- Type 2 known as Context Free Grammar.
- Type 3 Regular Grammar.
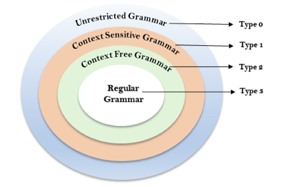
Fig: Chomsky hierarchy
The above diagram shows the hierarchy of chomsky. Each language of type 3 is therefore also of type 2, 1 and 0 respectively. Similarly, every language of type 2 is also of type 1 and type 0 likewise.
● Type 0 grammar -
Type 0 grammar is known as Unrestricted grammar.The grammar rules of these types of languages are unregulated. Turing machines can model these languages efficiently.
Example:
- BAa → aa
- P → p
● Type 1 grammar -
Type 1 grammar is known as Context Sensitive Grammar.Context-sensitive grammar is used to describe language that is sensitive to context. The context-sensitive grammar follows the rules below:
● There may be more than one symbol on the left side of their development rules for context-sensitive grammar.
● The number of left-hand symbols does not surpass the number of right-hand symbols.
● The A → ε type rule is not permitted unless A is a beginning symbol. It does not occur on the right-hand side of any rule.
● The Type 1 grammar should be Type 0. Production is in the form of V →T in type1
Key takeaway:
● Where the number of symbols in V is equal to or less than T
Example:
- S → AT
- T → xy
- A → a
● Type 2 grammar -
Type 2 Grammar is called Context Free Grammar. Context free languages are the languages which can be represented by the CNF (context free grammar) Type 2 should be type 1. The production rule is:
A → α
Key takeaway:
● Where A is any single non-terminal and is any combination of terminals and non-terminals.
Example:
- A → aBb
- A → b
- B → a
● Type 3 grammar -
Type 3 Grammar is called Regular Grammar. Those languages that can be represented using regular expressions are regular languages. These languages may be NFA or DFA-modeled.
Type3 has to be in the form of -
V → T*V / T*
Example:
A → xy
Key takeaway:
● The most limited form of grammar is Type3. Type2 and Type1 should be the grammar of Type3.
If it has rules of form A -> an or A -> aB or A -> ⁇ where ⁇ is a special symbol called NULL, grammar is natural. Standard grammar is formal grammar, i.e. regular right or regular left. Regular language is defined in every periodic grammar
Right linear grammar
Right linear grammar is also called right regular grammar is a formal grammar N, Σ, P, S such that all the production rules in P are of one of the following forms:
- A → a, where A is a non-terminal in N and a is a terminal in Σ.
- A → aB, where A and B are non-terminals in N and a is in Σ
- A → ε, where A is in N and ε denotes the empty string, i.e. the string of length 0.
Left linear grammar
Left linear grammar is also called left regular grammar. There are some rules to follow:
- A → a, where A in N is a non-terminal and an in Σ is a terminal.
- A → Ba, where A and B in N are non-terminals and an in Σ is
- A → ε, where A is N and ε denotes the empty string, i.e. the longitudinal string 0.
Key takeaway
Right linear grammar, also called right regular grammar, is a formal grammar.
Left linear grammar is also called left regular grammar.
The equivalence of regular grammar and finite automata is the subject of the following theorems.
Theorem 1: There is one finite automaton M for each right linear grammar GR (or left linear grammar GL), where
L (M) = L (GR) (or L (M) = G (GL))
Here is the proof of correctness and the construction algorithm from regular grammar to finite automata. It has two cases, one from right linear grammar to finite automata and the other from left linear grammar to finite automata.
Construction Algorithm 1.
For a given linear grammar, 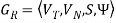 there is a corresponding NFA.
there is a corresponding NFA.
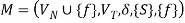
The transition function δ is specified by the following rules, where f is a newly added final state with 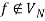 holding.
holding.
1) For any 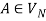 and
and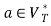 , if
, if 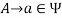 holds, then let
holds, then let 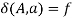 hold; or 2) For any
hold; or 2) For any 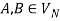 and
and 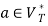 , if
, if 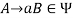 holds, then let
holds, then let 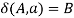 hold.
hold.
Proof. Using A→aB once in the leftmost derivation of S =>*ω (ω ∈ ∑*) for a right linear grammar GR is equivalent to the scenario that the current state A meeting with a will be transited to the subsequent state B in M. Using A→a once in the last derivation is equivalent to the current state A meeting with a being transited to f, the final state in M. Here we let 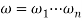 where
where 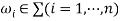 , then S =>*ω if and only if
, then S =>*ω if and only if
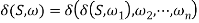
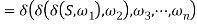
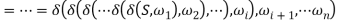
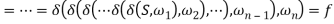
Holds.
The sufficient and necessary criteria of S =>*ω for GR are that there is only one path from S, the initial state, to f, the conclusion state in M. During the transition, all of the conditions that are met one by one are simply equivalent to ω, viz., 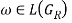 if and only if
if and only if 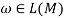 Therefore, it is evident that
Therefore, it is evident that 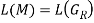 holds.
holds.
Construction Algorithm 2
For a given linear grammar, 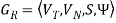 there is a corresponding NFA.
there is a corresponding NFA.
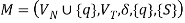
The transition function δ is described by the following rules, where q is a newly inserted start state with 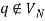 holding.
holding.
1) For any 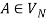 and
and 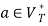 , if
, if 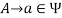 holds, then let
holds, then let 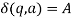 hold; or 2) for any
hold; or 2) for any 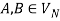 and
and 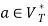 , if
, if 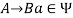 holds, then let
holds, then let 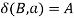 hold.
hold.
The proof of construction Algorithm 2 is the same as the proof of construction Algorithm 1, and we get the same result.
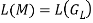
Theorem 2: There is a right linear grammar GR or a left linear grammar GL for each finite automaton M, where
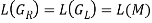
References:
- Harry R. Lewis and Christos H. Papadimitriou, Elements of the Theory of Computation, Pearson Education Asia.
- Dexter C. Kozen, Automata and Computability, Undergraduate Texts in Computer Science, Springer.
- Michael Sipser, Introduction to the Theory of Computation, PWS Publishing.
- John Martin, “Introduction to Languages and The Theory of Computation”, 2nd Edition, McGraw Hill Education, ISBN-13: 978-1-25-900558-9, ISBN-10: 1-25-900558-5
- J.Carroll & D Long, “Theory of Finite Automata”, Prentice Hall, ISBN 0-13-913708-45