Unit - 3
Context Free Grammar
Context-free grammar (CFG) is a collection of rules (or productions) for recursive rewriting used to produce string patterns.
It consists of:
● a set of terminal symbols,
● a set of non terminal symbols,
● a set of productions,
● a start symbol.
Context-free grammar G can be defined as:
G = (V, T, P, S)
Where
G - grammar, used to generate string,
V - final set of non terminal symbols, which are denoted by capital letters,
T - final set of terminal symbols, which are denoted by small letters,
P - set of production rules, it is used for replacing the non terminal symbol of a string on both sides (left or right)
S - start symbol, which is used to derive the string
A CFG for Arithmetic Expressions -
An example grammar that generates strings representing arithmetic expressions with the four operators +, -, *, /, and numbers as operands is:
1. <expression> --> number
2. <expression> --> (<expression>)
3.<expression> --> <expression> +<expression>
4. <expression> --> <expression> - <expression>
5. <expression> --> <expression> * <expression>
6. <expression> --> <expression> / <expression>
The only non terminal symbol in this grammar is <expression>, which is also the start symbol. The terminal symbols are {+,-,*,/ , (,),number}
● The first rule states that an <expression> can be rewritten as a number.
● The second rule says that an <expression> enclosed in parentheses is also an <expression>
● The remaining rules say that the sum, difference, product, or division of two <expression> is also an expression.
Example 1:
Construct a CFG for a language with any number of a's in the set ∑= {a}.
Solution:
The regular expression for the above language is, as we know:
r.e. = a*
The following is the Regular expression's production rule:
S → aS rule 1
S → ε rule 2
We may now start with start symbols to derive the string “aaaaaa” :
S
AS
AaS rule 1
AaaS rule 1
AaaaS rule 1
AaaaaS rule 1
AaaaaaS rule 1
Aaaaaaε rule 2
Aaaaaa
The r.e. = a* can generate a set of string {ε, a, aa, aaa,.....}. We can have a null string because S is a start symbol and rule 2 gives S → ε.
Key takeaway
Context-free grammar (CFG) is a collection of rules (or productions) for recursive rewriting used to produce string patterns.
Suppose we have a context free grammar G with production rules:
S->aSb|bSa|SS|ɛ
Left most derivation (LMD) and Derivation Tree:
Leftmost derivation of a string from staring symbol S is done by replacing leftmost
Non-terminal symbol by RHS of corresponding production rule.
For example:
The leftmost derivation of string abab from grammar G above is done as:
S =>aSb =>abSab =>abab
The symbols in bold are replaced using production rules.
Example:
● Produle rule -
P = P + P
P = P - P
P = a | b
● Input -
a - b + a
● Leftmost derivation is:
P = P + P
P = P - P + P
P = a - P + P
P = a - b + P
P = a - b + a
Derivation tree: It explains how string is derived using production rules from S and is shown in Figure.
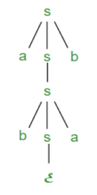
Fig 2: Derivation tree
Right most derivation (RMD):
It is done by replacing rightmost non-terminal symbol S by RHS of corresponding production rule.
For Example: The rightmost derivation of string abab from grammar G above
Is done as:
S =>SS =>SaSb =>Sab =>aSbab =>abab
The symbols in bold are replaced using production rules.
The derivation tree for abab using rightmost derivation is shown in Figure.
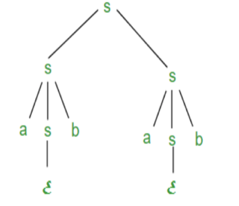
Fig 3: Right most derivation
A derivation can be either LMD or RMD or both or none.
For Example:
S =>aSb =>abSab =>abab is LMD as well as RMD But
S => SS =>SaSb =>Sab =>aSbab =>abab is RMD but not LMD.
Example:
● Produle rule -
P = P + P
P = P - P
P = a | b
● Input -
a - b + a
● Rightmost Derivation is -
P = P - P
P = P - P + P
P = P - P + a
P = P - b + a
P = a - b + a
● We can receive the same string when we use the leftmost derivation or rightmost derivation.
Parse Trees and Derivations
A derivation is a sequence of strings in V * which starts with a non-terminal in V-Σ and ends with a string in Σ * .
Let’s consider the sample grammar
E → E+E | a
We write:
E ⇒ E+E ⇒ E+E+E ⇒a+E+E⇒a+a+E⇒a+a+a
But this is incomplete, because it doesn’t tell us where the replacement rules are applied.
We actually need "marked" strings which indicate which non-terminal is replaced in all but the first and last step:
E ⇒ Ě+E ⇒ Ě+E+E ⇒a+Ě+E ⇒a+a+Ě ⇒a+a+a
In this case, the marking is only necessary in the second step; however it is crucial, because we want to distinguish between this derivation and the following one:
E ⇒ E+Ě ⇒ Ě+E+E ⇒a+Ě+E ⇒a+a+Ě ⇒a+a+a
We want to characterize two derivations as “coming from the same parse tree.”
The first step is to define the relation among derivations as being “more left-oriented at one step”. Assume we have two equal length derivations of length n > 2:
D: x 1 ⇒ x 2 ⇒ ... ⇒x n
D′: x 1 ′ ⇒ x 2 ′ ⇒ ... ⇒x n ′
Where x 1 = x 1 ′ is a non-terminal and
x n = x n ′ ∈ Σ *
Namely they start with the same non-terminal and end at the same terminal string and have at least two intermediate steps.
Let’s say D < D′ if the two derivations differ in only one step in which there are 2 non-terminals, A and B, such that D replaces the left one before the right one and D′ does the opposite. Formally:
D < D′ if there exists k, 1 < k < n such that
x i = x i ′ for all i ≠ k (equal strings, same marked position)
x k-1 = uǍvBw, for u, v, w ∈ V*
x k-1 ′ = uAvB̌w, for u, v, w ∈ V*
x k =uyvB̌w, for production A → y
x k ′ = uǍvzw, for production B → z
x k+1 = x k+1 ′ = uyvzw (marking not shown)
Two derivations are said to be similar if they belong to the reflexive, symmetric, transitive closure of <.
Chomsky normal form
A context free grammar (CFG) is in Chomsky Normal Form (CNF) if all production rules satisfy one of the following conditions:
A non-terminal generating a terminal (e.g.; X->x)
A non-terminal generating two non-terminals (e.g.; X->YZ)
Start symbol generating ε. (e.g.; S->ε)
Consider the following grammars,
G1 = {S->a, S->AZ, A->a, Z->z}
G2 = {S->a, S->aZ, Z->a}
The grammar G1 is in CNF as production rules satisfy the rules specified for CNF. However, the grammar G2 is not in CNF as the production rule S->aZ contains terminal followed by non-terminal which does not satisfy the rules specified for CNF.
Greibach normal forms
A CFG is in Greibach Normal Form if the Productions are in the following forms −
A → b
A → bD 1 …D n
S → ε
Where A, D 1 ,....,D n are non-terminals and b is a terminal.
Algorithm to Convert a CFG into Greibach Normal Form
Step 1 − If the start symbol S occurs on some right side, create a new start
Symbol S’ and a new production S’ → S.
Step 2 − Remove Null productions.
Step 3 − Remove unit productions.
Step 4 − Remove all direct and indirect left-recursion.
Step 5 − Do proper substitutions of productions to convert it into the proper form of
GNF.
Problem
Convert the following CFG into CNF
S → XY | Xn | p
X → mX | m
Y → Xn | o
Solution
Here, S does not appear on the right side of any production and there are no unit or
Null productions in the production rule set. So, we can skip Step 1 to Step 3.
Step 4
Now after replacing
X in S → XY | Xo | p
With
MX | m
We obtain
S → mXY | mY | mXo | mo | p.
And after replacing
X in Y → X n | o
With the right side of
X → mX | m
We obtain
Y → mXn | mn | o.
Two new productions O → o and P → p are added to the production set and then we came to the final GNF as the following −
S → mXY | mY | mXC | mC | p
X → mX | m
Y → mXD | mD | o
O → o
P → p
Key takeaway:
- CNF is a pre-processing step used in various algorithms.
- For generation of string x of length ‘m’, it requires ‘2m-1’ production or steps in CNF.
It is a way to implement a context-free grammar as we design DFA for a regular grammar. A DFA can remember a finite amount of information, but a PDA can remember an infinite amount of information.
Basically a pushdown automaton is -
“Finite state machine” + “a stack”
A pushdown automaton has three components −
● an input tape,
● a control unit, and
● a stack with infinite size.
The stack head scans the top symbol of the stack.
A stack does two operations −
● Push − a new symbol is added at the top.
● Pop − the top symbol is read and removed.
A PDA may or may not read an input symbol, but it has to read the top of the stack in every transition.
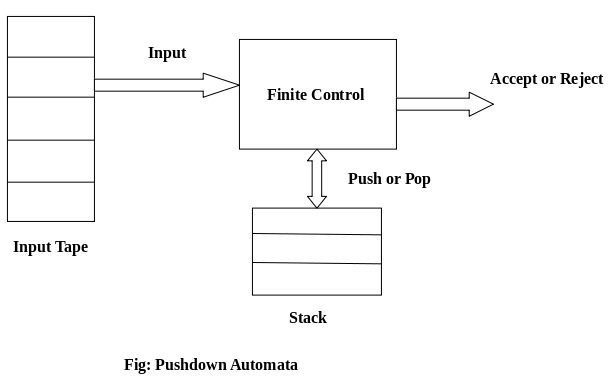
Fig1: Basic structure of PDA
A PDA can be formally described as a 7-tuple (Q, ∑, S, δ, q 0 , I, F) −
Where,
● Q is the finite number of states
● ∑ is input alphabet
● S is stack symbols
● δ is the transition function: Q × (∑ ∪ {ε}) × S × Q × S* )
● q 0 is the initial state (q 0 ∈ Q)
● I is the initial stack top symbol (I ∈ S)
● F is a set of accepting states (F ∈ Q)
The following diagram shows a transition in a PDA from a state q 1 to state q 2 , labeled as a,b → c −
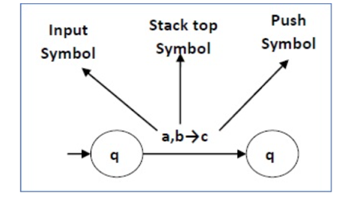
Fig 2: Example
This means at state q1, if we encounter an input string ‘a’ and the top symbol of the stack is ‘b’, then we pop ‘b’, push ‘c’ on top of the stack and move to state q2 .
Key takeaway
It is a way to implement a context-free grammar as we design DFA for a regular grammar. A DFA can remember a finite amount of information, but a PDA can remember an infinite amount of information.
When a PDA accepts a string in final state acceptability, the PDA is in a final state after reading the full string. We can make moves from the starting state to a final state with any stack values. As long as we end up in a final state, the stack values don't matter.
If the PDA enters any final state in zero or more moves after receiving the complete input, it is said to accept it by the final state.
Let P =(Q, ∑, Γ, δ, q0, Z, F) be a PDA. The language acceptable by the final state can be defined as:
L(PDA) = {w | (q0, w, Z) ⊢* (p, ε, ε), q ∈ F}
Equivalence of Acceptance by Final State and Empty Stack
There is a PDA P2 such that L = L (P2) if L = N(P1) for some PDA P1. That is, the language supported by the empty stack PDA will be supported by the end state PDA as well.
Empty stack
If a language L = L (P1) exists for a PDA P1, then L = N (P2) exists for a PDA P2. That is, language supported by the end state PDA is also supported by the empty stack PDA.
The stack of PDAs becomes empty after reading the input string from the initial setup for some PDA.
When a PDA has exhausted its stack after reading the entire string, it accepts a string.
Let P =(Q, ∑, Γ, δ, q0, Z, F) be a PDA. The language acceptable by empty stack can be defined as:
N(PDA) = {w | (q0, w, Z) ⊢* (p, ε, ε), q ∈ Q}
Example
Construct a PDA that accepts L = {0n 1n | n ≥ 0}
Solution:
This language accepts L = {ε, 01, 0011, 000111, ............................. }
The number of ‘a' and ‘b' in this example must be the same.
● We began by inserting the special symbol ‘$' into the empty stack.
● If we encounter input 0 and top is Null at state q2, we push 0 into the stack. It's possible that this will happen again. We pop this 0 if we meet input 1 and top is 0.
● If we encounter input 1 at state q3 and the top is 0, we pop this 0. It's possible that this will continue to iterate. We pop the top element if we meet input 1 and top is 0.
● If the special symbol '$' appears at the top of the stack, it is popped out, and the stack eventually moves to the accepting state q4.
Equivalence of PDA and CFL
● We can design a similar nondeterministic PDA that accepts the language produced by the context-free grammar G if it is context-free. For the grammar G, a parser can be created.
● In addition, if P is a pushdown automaton, an analogous context-free grammar G can be built.
L(G) = L(P)
Application
Because of this equivalence, a CFG can be used to specify a programming language, and the PDA can be used to construct the language's compiler.
Theorem
Theorem: If a pushdown automaton recognises a language, it is context-free. It's worth noting that this means:
1. If a language L is context-free, it is recognised by a PDA ML.
2. If a PDA ML recognises a language L, a CFG GL that generates L exists.
CFG to PDA Conversion
On R.H.S. Manufacturing, the initial symbol must be a terminal symbol. The steps for obtaining PDA from CFG are as follows:
Step 1: Convert the CFG outputs into GNF outputs.
Step 2: There will be only one state q on the PDA.
Step 3: The CFG's initial symbol will be the PDA's initial symbol.
Step 4: Add the following rule to non-terminal symbols:
δ(q, ε, A) = (q, α)
Where the production rule is A → α
Step 5: Add the following rule to each terminal symbol:
δ(q, a, a) = (q, ε) for every terminal symbol
They are closed under −
● Union
● Concatenation
● Kleene Star operation
Union of the languages A1 and A2 , A = A1 A2 = { anbncmdm }
The additional development would have the corresponding grammar G, P: S → S1 S2
Union
Let A1 and A2 be two context free languages. Then A1 ∪ A2 is also context free.
Example
Let A1 = { xn yn , n ≥ 0}. Corresponding grammar G 1 will have P: S1 → aAb|ab
Let A2 = { cm dm , m ≥ 0}. Corresponding grammar G 2 will have P: S2 → cBb| ε
Union of A1 and A2 , A = A1 ∪ A2 = { xn yn } ∪ { cm dm }
The corresponding grammar G will have the additional production S → S1 | S2
Note - So under Union, CFLs are closed.
Concatenation
If A1 and A2 are context free languages, then A1 A2 is also context free.
Example
Union of the languages A 1 and A 2 , A = A 1 A 2 = { an bn cm dm }
The corresponding grammar G will have the additional production S → S1 S2
Note - So under Concatenation, CFL are locked.
Kleene Star
If A is a context free language, so that A* is context free as well .
Example
Let A = { xn yn , n ≥ 0}. G will have corresponding grammar P: S → aAb| ε
Kleene Star L 1 = { xn yn }*
The corresponding grammar G 1 will have additional productions S1 → SS 1 | ε
Note - So under Kleene Closure, CFL's are closed.
Context-free languages are not closed under −
● Intersection − If A1 and A2 are context free languages, then A1 ∩ A2 is not necessarily context free.
● Intersection with Regular Language − If A1 is a regular language and A2 is a context free language, then A1 ∩ A2 is a context free language.
● Complement − If A1 is a context free language, then A1’ may not be context free.
Lemma:
The language L = {anbncn | n ≥ 1} is not context free.
Proof (By contradiction)
Assuming that this language is context-free; hence it will have a context-free Grammar.
Let K be the constant of the Pumping Lemma.
Considering the string akbkck , where L is length greater than K .
By the Pumping Lemma this is represented as uvxyz , such that all uvixyiz are also in L, which is not possible, as: either v or y cannot contain many letters from {a,b,c}; else they are in the wrong order.
If v or y consists of a’s, b’s or c’s, then uv2xy2z cannot maintain the balance amongst the three letters.
Lemma:
The language L = {aibjck | i < j and i < k } is not context free.
Proof (By contradiction)
Assuming that this language is context-free; hence it will have a context-free grammar.
Let K be the constant of the Pumping Lemma.
Considering the string akbk+1ck+1 , which is L > K.
By the Pumping Lemma this must be represented as uvxyz , such that all are also In L.
-As mentioned previously neither v nor y may contain a mixture of symbols.
-Suppose consists of a’s.
Then there is no way y cannot have b’s and c’s. It generate enough letters to keep them more than that of the a’s (it can do it for one or the other of them, not both)
Similarly y cannot consist of just a’s.
-So suppose then that v or y contains only b’s or only c’s.
Consider the string uv0xy0z which must be in L . Since we have dropped both v and y, we must have at least one b’ or one c’ less than we had in uvxyz , which was akbk+1ck+1. Consequently, this string no longer has enough of either b’s or c’s to be a member of L.
References:
- John E. Hopcroft, Rajeev Motwani, Jeffrey D.Ullman, “Introduction to Automata Theory Languages and Computation”, Addison-Wesley,ISBN 0-201-44124-1
- Sanjeev Arora and Boaz Barak, “Computational Complexity: A Modern Approach”,
- Cambridge University Press, ISBN: 0521424267 97805214242643
- John Martin, “Introduction to Languages and The Theory of Computation”, 2nd Edition, McGraw Hill Education, ISBN-13: 978-1-25-900558-9, ISBN-10: 1-25-900558-5
- J.Carroll & D Long, “Theory of Finite Automata”, Prentice Hall, ISBN 0-13-913708-45
Unit - 3
Context Free Grammar
Context-free grammar (CFG) is a collection of rules (or productions) for recursive rewriting used to produce string patterns.
It consists of:
● a set of terminal symbols,
● a set of non terminal symbols,
● a set of productions,
● a start symbol.
Context-free grammar G can be defined as:
G = (V, T, P, S)
Where
G - grammar, used to generate string,
V - final set of non terminal symbols, which are denoted by capital letters,
T - final set of terminal symbols, which are denoted by small letters,
P - set of production rules, it is used for replacing the non terminal symbol of a string on both sides (left or right)
S - start symbol, which is used to derive the string
A CFG for Arithmetic Expressions -
An example grammar that generates strings representing arithmetic expressions with the four operators +, -, *, /, and numbers as operands is:
1. <expression> --> number
2. <expression> --> (<expression>)
3.<expression> --> <expression> +<expression>
4. <expression> --> <expression> - <expression>
5. <expression> --> <expression> * <expression>
6. <expression> --> <expression> / <expression>
The only non terminal symbol in this grammar is <expression>, which is also the start symbol. The terminal symbols are {+,-,*,/ , (,),number}
● The first rule states that an <expression> can be rewritten as a number.
● The second rule says that an <expression> enclosed in parentheses is also an <expression>
● The remaining rules say that the sum, difference, product, or division of two <expression> is also an expression.
Example 1:
Construct a CFG for a language with any number of a's in the set ∑= {a}.
Solution:
The regular expression for the above language is, as we know:
r.e. = a*
The following is the Regular expression's production rule:
S → aS rule 1
S → ε rule 2
We may now start with start symbols to derive the string “aaaaaa” :
S
AS
AaS rule 1
AaaS rule 1
AaaaS rule 1
AaaaaS rule 1
AaaaaaS rule 1
Aaaaaaε rule 2
Aaaaaa
The r.e. = a* can generate a set of string {ε, a, aa, aaa,.....}. We can have a null string because S is a start symbol and rule 2 gives S → ε.
Key takeaway
Context-free grammar (CFG) is a collection of rules (or productions) for recursive rewriting used to produce string patterns.
Suppose we have a context free grammar G with production rules:
S->aSb|bSa|SS|ɛ
Left most derivation (LMD) and Derivation Tree:
Leftmost derivation of a string from staring symbol S is done by replacing leftmost
Non-terminal symbol by RHS of corresponding production rule.
For example:
The leftmost derivation of string abab from grammar G above is done as:
S =>aSb =>abSab =>abab
The symbols in bold are replaced using production rules.
Example:
● Produle rule -
P = P + P
P = P - P
P = a | b
● Input -
a - b + a
● Leftmost derivation is:
P = P + P
P = P - P + P
P = a - P + P
P = a - b + P
P = a - b + a
Derivation tree: It explains how string is derived using production rules from S and is shown in Figure.
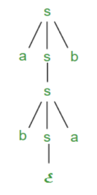
Fig 2: Derivation tree
Right most derivation (RMD):
It is done by replacing rightmost non-terminal symbol S by RHS of corresponding production rule.
For Example: The rightmost derivation of string abab from grammar G above
Is done as:
S =>SS =>SaSb =>Sab =>aSbab =>abab
The symbols in bold are replaced using production rules.
The derivation tree for abab using rightmost derivation is shown in Figure.
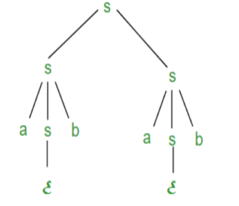
Fig 3: Right most derivation
A derivation can be either LMD or RMD or both or none.
For Example:
S =>aSb =>abSab =>abab is LMD as well as RMD But
S => SS =>SaSb =>Sab =>aSbab =>abab is RMD but not LMD.
Example:
● Produle rule -
P = P + P
P = P - P
P = a | b
● Input -
a - b + a
● Rightmost Derivation is -
P = P - P
P = P - P + P
P = P - P + a
P = P - b + a
P = a - b + a
● We can receive the same string when we use the leftmost derivation or rightmost derivation.
Parse Trees and Derivations
A derivation is a sequence of strings in V * which starts with a non-terminal in V-Σ and ends with a string in Σ * .
Let’s consider the sample grammar
E → E+E | a
We write:
E ⇒ E+E ⇒ E+E+E ⇒a+E+E⇒a+a+E⇒a+a+a
But this is incomplete, because it doesn’t tell us where the replacement rules are applied.
We actually need "marked" strings which indicate which non-terminal is replaced in all but the first and last step:
E ⇒ Ě+E ⇒ Ě+E+E ⇒a+Ě+E ⇒a+a+Ě ⇒a+a+a
In this case, the marking is only necessary in the second step; however it is crucial, because we want to distinguish between this derivation and the following one:
E ⇒ E+Ě ⇒ Ě+E+E ⇒a+Ě+E ⇒a+a+Ě ⇒a+a+a
We want to characterize two derivations as “coming from the same parse tree.”
The first step is to define the relation among derivations as being “more left-oriented at one step”. Assume we have two equal length derivations of length n > 2:
D: x 1 ⇒ x 2 ⇒ ... ⇒x n
D′: x 1 ′ ⇒ x 2 ′ ⇒ ... ⇒x n ′
Where x 1 = x 1 ′ is a non-terminal and
x n = x n ′ ∈ Σ *
Namely they start with the same non-terminal and end at the same terminal string and have at least two intermediate steps.
Let’s say D < D′ if the two derivations differ in only one step in which there are 2 non-terminals, A and B, such that D replaces the left one before the right one and D′ does the opposite. Formally:
D < D′ if there exists k, 1 < k < n such that
x i = x i ′ for all i ≠ k (equal strings, same marked position)
x k-1 = uǍvBw, for u, v, w ∈ V*
x k-1 ′ = uAvB̌w, for u, v, w ∈ V*
x k =uyvB̌w, for production A → y
x k ′ = uǍvzw, for production B → z
x k+1 = x k+1 ′ = uyvzw (marking not shown)
Two derivations are said to be similar if they belong to the reflexive, symmetric, transitive closure of <.
Chomsky normal form
A context free grammar (CFG) is in Chomsky Normal Form (CNF) if all production rules satisfy one of the following conditions:
A non-terminal generating a terminal (e.g.; X->x)
A non-terminal generating two non-terminals (e.g.; X->YZ)
Start symbol generating ε. (e.g.; S->ε)
Consider the following grammars,
G1 = {S->a, S->AZ, A->a, Z->z}
G2 = {S->a, S->aZ, Z->a}
The grammar G1 is in CNF as production rules satisfy the rules specified for CNF. However, the grammar G2 is not in CNF as the production rule S->aZ contains terminal followed by non-terminal which does not satisfy the rules specified for CNF.
Greibach normal forms
A CFG is in Greibach Normal Form if the Productions are in the following forms −
A → b
A → bD 1 …D n
S → ε
Where A, D 1 ,....,D n are non-terminals and b is a terminal.
Algorithm to Convert a CFG into Greibach Normal Form
Step 1 − If the start symbol S occurs on some right side, create a new start
Symbol S’ and a new production S’ → S.
Step 2 − Remove Null productions.
Step 3 − Remove unit productions.
Step 4 − Remove all direct and indirect left-recursion.
Step 5 − Do proper substitutions of productions to convert it into the proper form of
GNF.
Problem
Convert the following CFG into CNF
S → XY | Xn | p
X → mX | m
Y → Xn | o
Solution
Here, S does not appear on the right side of any production and there are no unit or
Null productions in the production rule set. So, we can skip Step 1 to Step 3.
Step 4
Now after replacing
X in S → XY | Xo | p
With
MX | m
We obtain
S → mXY | mY | mXo | mo | p.
And after replacing
X in Y → X n | o
With the right side of
X → mX | m
We obtain
Y → mXn | mn | o.
Two new productions O → o and P → p are added to the production set and then we came to the final GNF as the following −
S → mXY | mY | mXC | mC | p
X → mX | m
Y → mXD | mD | o
O → o
P → p
Key takeaway:
- CNF is a pre-processing step used in various algorithms.
- For generation of string x of length ‘m’, it requires ‘2m-1’ production or steps in CNF.
It is a way to implement a context-free grammar as we design DFA for a regular grammar. A DFA can remember a finite amount of information, but a PDA can remember an infinite amount of information.
Basically a pushdown automaton is -
“Finite state machine” + “a stack”
A pushdown automaton has three components −
● an input tape,
● a control unit, and
● a stack with infinite size.
The stack head scans the top symbol of the stack.
A stack does two operations −
● Push − a new symbol is added at the top.
● Pop − the top symbol is read and removed.
A PDA may or may not read an input symbol, but it has to read the top of the stack in every transition.
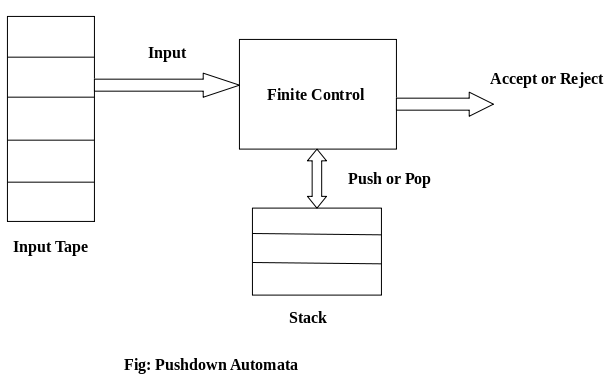
Fig1: Basic structure of PDA
A PDA can be formally described as a 7-tuple (Q, ∑, S, δ, q 0 , I, F) −
Where,
● Q is the finite number of states
● ∑ is input alphabet
● S is stack symbols
● δ is the transition function: Q × (∑ ∪ {ε}) × S × Q × S* )
● q 0 is the initial state (q 0 ∈ Q)
● I is the initial stack top symbol (I ∈ S)
● F is a set of accepting states (F ∈ Q)
The following diagram shows a transition in a PDA from a state q 1 to state q 2 , labeled as a,b → c −
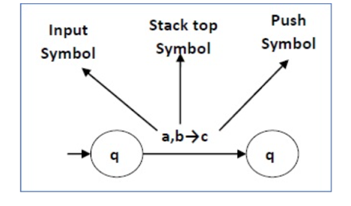
Fig 2: Example
This means at state q1, if we encounter an input string ‘a’ and the top symbol of the stack is ‘b’, then we pop ‘b’, push ‘c’ on top of the stack and move to state q2 .
Key takeaway
It is a way to implement a context-free grammar as we design DFA for a regular grammar. A DFA can remember a finite amount of information, but a PDA can remember an infinite amount of information.
When a PDA accepts a string in final state acceptability, the PDA is in a final state after reading the full string. We can make moves from the starting state to a final state with any stack values. As long as we end up in a final state, the stack values don't matter.
If the PDA enters any final state in zero or more moves after receiving the complete input, it is said to accept it by the final state.
Let P =(Q, ∑, Γ, δ, q0, Z, F) be a PDA. The language acceptable by the final state can be defined as:
L(PDA) = {w | (q0, w, Z) ⊢* (p, ε, ε), q ∈ F}
Equivalence of Acceptance by Final State and Empty Stack
There is a PDA P2 such that L = L (P2) if L = N(P1) for some PDA P1. That is, the language supported by the empty stack PDA will be supported by the end state PDA as well.
Empty stack
If a language L = L (P1) exists for a PDA P1, then L = N (P2) exists for a PDA P2. That is, language supported by the end state PDA is also supported by the empty stack PDA.
The stack of PDAs becomes empty after reading the input string from the initial setup for some PDA.
When a PDA has exhausted its stack after reading the entire string, it accepts a string.
Let P =(Q, ∑, Γ, δ, q0, Z, F) be a PDA. The language acceptable by empty stack can be defined as:
N(PDA) = {w | (q0, w, Z) ⊢* (p, ε, ε), q ∈ Q}
Example
Construct a PDA that accepts L = {0n 1n | n ≥ 0}
Solution:
This language accepts L = {ε, 01, 0011, 000111, ............................. }
The number of ‘a' and ‘b' in this example must be the same.
● We began by inserting the special symbol ‘$' into the empty stack.
● If we encounter input 0 and top is Null at state q2, we push 0 into the stack. It's possible that this will happen again. We pop this 0 if we meet input 1 and top is 0.
● If we encounter input 1 at state q3 and the top is 0, we pop this 0. It's possible that this will continue to iterate. We pop the top element if we meet input 1 and top is 0.
● If the special symbol '$' appears at the top of the stack, it is popped out, and the stack eventually moves to the accepting state q4.
Equivalence of PDA and CFL
● We can design a similar nondeterministic PDA that accepts the language produced by the context-free grammar G if it is context-free. For the grammar G, a parser can be created.
● In addition, if P is a pushdown automaton, an analogous context-free grammar G can be built.
L(G) = L(P)
Application
Because of this equivalence, a CFG can be used to specify a programming language, and the PDA can be used to construct the language's compiler.
Theorem
Theorem: If a pushdown automaton recognises a language, it is context-free. It's worth noting that this means:
1. If a language L is context-free, it is recognised by a PDA ML.
2. If a PDA ML recognises a language L, a CFG GL that generates L exists.
CFG to PDA Conversion
On R.H.S. Manufacturing, the initial symbol must be a terminal symbol. The steps for obtaining PDA from CFG are as follows:
Step 1: Convert the CFG outputs into GNF outputs.
Step 2: There will be only one state q on the PDA.
Step 3: The CFG's initial symbol will be the PDA's initial symbol.
Step 4: Add the following rule to non-terminal symbols:
δ(q, ε, A) = (q, α)
Where the production rule is A → α
Step 5: Add the following rule to each terminal symbol:
δ(q, a, a) = (q, ε) for every terminal symbol
They are closed under −
● Union
● Concatenation
● Kleene Star operation
Union of the languages A1 and A2 , A = A1 A2 = { anbncmdm }
The additional development would have the corresponding grammar G, P: S → S1 S2
Union
Let A1 and A2 be two context free languages. Then A1 ∪ A2 is also context free.
Example
Let A1 = { xn yn , n ≥ 0}. Corresponding grammar G 1 will have P: S1 → aAb|ab
Let A2 = { cm dm , m ≥ 0}. Corresponding grammar G 2 will have P: S2 → cBb| ε
Union of A1 and A2 , A = A1 ∪ A2 = { xn yn } ∪ { cm dm }
The corresponding grammar G will have the additional production S → S1 | S2
Note - So under Union, CFLs are closed.
Concatenation
If A1 and A2 are context free languages, then A1 A2 is also context free.
Example
Union of the languages A 1 and A 2 , A = A 1 A 2 = { an bn cm dm }
The corresponding grammar G will have the additional production S → S1 S2
Note - So under Concatenation, CFL are locked.
Kleene Star
If A is a context free language, so that A* is context free as well .
Example
Let A = { xn yn , n ≥ 0}. G will have corresponding grammar P: S → aAb| ε
Kleene Star L 1 = { xn yn }*
The corresponding grammar G 1 will have additional productions S1 → SS 1 | ε
Note - So under Kleene Closure, CFL's are closed.
Context-free languages are not closed under −
● Intersection − If A1 and A2 are context free languages, then A1 ∩ A2 is not necessarily context free.
● Intersection with Regular Language − If A1 is a regular language and A2 is a context free language, then A1 ∩ A2 is a context free language.
● Complement − If A1 is a context free language, then A1’ may not be context free.
Lemma:
The language L = {anbncn | n ≥ 1} is not context free.
Proof (By contradiction)
Assuming that this language is context-free; hence it will have a context-free Grammar.
Let K be the constant of the Pumping Lemma.
Considering the string akbkck , where L is length greater than K .
By the Pumping Lemma this is represented as uvxyz , such that all uvixyiz are also in L, which is not possible, as: either v or y cannot contain many letters from {a,b,c}; else they are in the wrong order.
If v or y consists of a’s, b’s or c’s, then uv2xy2z cannot maintain the balance amongst the three letters.
Lemma:
The language L = {aibjck | i < j and i < k } is not context free.
Proof (By contradiction)
Assuming that this language is context-free; hence it will have a context-free grammar.
Let K be the constant of the Pumping Lemma.
Considering the string akbk+1ck+1 , which is L > K.
By the Pumping Lemma this must be represented as uvxyz , such that all are also In L.
-As mentioned previously neither v nor y may contain a mixture of symbols.
-Suppose consists of a’s.
Then there is no way y cannot have b’s and c’s. It generate enough letters to keep them more than that of the a’s (it can do it for one or the other of them, not both)
Similarly y cannot consist of just a’s.
-So suppose then that v or y contains only b’s or only c’s.
Consider the string uv0xy0z which must be in L . Since we have dropped both v and y, we must have at least one b’ or one c’ less than we had in uvxyz , which was akbk+1ck+1. Consequently, this string no longer has enough of either b’s or c’s to be a member of L.
References:
- John E. Hopcroft, Rajeev Motwani, Jeffrey D.Ullman, “Introduction to Automata Theory Languages and Computation”, Addison-Wesley,ISBN 0-201-44124-1
- Sanjeev Arora and Boaz Barak, “Computational Complexity: A Modern Approach”,
- Cambridge University Press, ISBN: 0521424267 97805214242643
- John Martin, “Introduction to Languages and The Theory of Computation”, 2nd Edition, McGraw Hill Education, ISBN-13: 978-1-25-900558-9, ISBN-10: 1-25-900558-5
- J.Carroll & D Long, “Theory of Finite Automata”, Prentice Hall, ISBN 0-13-913708-45