Unit - 5
Decidability and Undecidability of problems
If we can always create a comparable algorithm that can correctly answer the problem, the problem is said to be Decidable. By considering a basic example, we may immediately comprehend Decidable problems. Let's say we're asked to find all the prime numbers between 1000 and 2000. We can easily build an algorithm to enumerate all the prime numbers in this range in order to solve this challenge.
In terms of a Turing machine, a problem is said to be Decidable if there is a matching Turing machine that halts on every input with a yes or no answer. It's also worth noting that these issues are referred to as Turing Decidable since a Turing machine always comes to a halt on every input, accepting or rejecting it.
Example
We'll take a look at a couple key Decidable issues now:
● Is it possible to compare two regular languages, L and M?
Using the Set Difference technique, we can quickly verify this.
L-M =Null and M-L =Null.
Hence (L-M) U (M-L) = Null, then L,M are equivalent.
● Are you a CFL member?
Using a dynamic programming approach, we can always determine whether a string occurs in a particular CFL.
● A CFL's emptiness
By examining the CFL's production rules, we can quickly determine whether or not the language generates any strings.
Undecidable problem
Undecidable Problems are those for which we can't come up with an algorithm that can solve the problem correctly in a finite amount of time. These issues may be partially solvable, but they will never be completely solved. That is to say, there will always be a condition that causes the Turing Machine to go into an infinite loop without giving a response.
Consider Fermat's Theorem, a well-known Undecidable Problem that claims that no three positive numbers a, b, and c for any n>2 can ever meet the equation: a^n + b^n = c^n.
If we submit this problem to a Turing machine to discover a solution that produces a contradiction, the Turing machine could run indefinitely to find the appropriate values for n, a, b, and c. However, we are never clear whether a contradiction occurs, hence we call this problem an Undecidable Problem.
Example
Here are a few significant Undecided Issues:
● Is it true that a CFG generates all of the strings?
We can never reach the last string because a CFG generates infinite strings, hence it is undecidable.
● Is there a difference between two CFG L and M?
We can forecast if two CFGs are equal or not since we cannot determine all of the strings of any CFG.
● CFG's ambiguity?
There is no algorithm that can determine whether a CFL is ambiguous. We can only determine whether the CFL is ambiguous if any given string yields two separate parse trees.
● Is it possible to convert an ambiguous CFG into its non-ambiguous counterpart?
It's also an Insolvable Problem because there's no solution for converting ambiguous CFLs to non-ambiguous CFLs.
● Is it possible to learn a language that is a CFL on a regular basis?
This is an undecidable problem since we can't tell whether the CFL is regular or not from the production rules.
Key takeaway
- If there is no Turing machine that will always cease in a finite amount of time to deliver a yes or no answer, the problem is undecidable.
- There is no technique for determining the answer to an undecidable problem for a given input.
● Union and Intersection
Recursive
L1 x L2 and L1 x L2 are both recursive if L1 is recursive and L2 is recursive.
Using a multitape TM:
● Copy to Tape 2 and Tape 3 inputs
● Run M1 to tape 2 and M2 to tape 3 (neither will run forever; i.e.we get a result)
● They will determine whether x is in L1 and/or L2
● Test if approved by both M1 and M2 (intersection)
● Test if one is approved by M1 and M2 (union)
If L1 and L2 are recursive, the difference between L1 - L2=L1 and L2 is recursive.
Recursively Enumerable
If L1 and L2 are enumerated recursively, then L1 ∪ L2 and L1 ∩ L2 are recursively enumerated .
● Similar to the recursive case, but the case where M1 and M2 will run constantly
● Simulate simultaneously running M1 and M2-alternate one move from each machine.
A union, for reference,
● If any computer ever accepts it, accept it.
● If any machine ever refuses or fails, then the other machine continues to run.
If L is enumerated recursively and L is enumerated recursively, L is enumerated recursively.
● Let M and M be TMs, respectively, that accept L and L.
● Simultaneously, Run M and M'
● It must be agreed for any term x by any one of M or M'
● Therefore, either M or M 'will stop and agree
● If M stops and agrees, then stop and embrace.
● If M' stops and embraces, then stop and deny.
The TM that runs M and M at the same time always stops and accepts or refuses so that L and L are recursive.
If L is enumerable recursively, and L is not recursive, then L is not enumerable recursively.
● Concatenation
If L1 and L2 are two recursive languages, the L1.L2 concatenation would also be recursive. For instance:
L1 = {anbncn|n>=0}
L2 = {dmemfm|m>=0}
L3 = L1.L2
= {anbncndn emfm|m>=0 and n>=0} is also recursive.
L1 states that n no. Of a's is followed by n no. Of b's, and n no. Of c's. L2 says that m no. Of d's is followed by m no. Of e's, m no. Of f's. First, their concatenation matches no. Of a's, b's, and c's, then no. Of d's, e's, and f's. It can therefore be determined by TM.
● Kleene Closure
If L1 is recursive, its L1* smaller closure would also be recursive. For instance:
L1 = {anbncn|n>=0}
L1*= { anbncn||n>=0}* is also recursive.
Typically, programs are made up of loops that are either limited or infinite in length.
The program's overall output is entirely dependent on the input it receives.
The program may contain numerous different numbers of loops, which can be linear or nested.
The Halting Challenge is the problem of determining whether a given arbitrary computer program will stop operating or run in an infinite loop for the given input dependent on its input.
The Halting Problem states that it is difficult to develop a computer program that can decide if a program should halt for an input in a limited amount of time.
Furthermore, the Halting Problem never claims that determining whether a given random program will halt is impossible (stop).
In general, it asks, "Specify a random program and an input, determine whether the given random program will halt when that input is provided."
Writing Halting Problem
Input: A turing machine and an input string T.
Problem - Does the Turing machine complete the T-string computation in a finite number of steps? Either yes or no must be the answer.
Sol: We will first assume that there is such a Turing machine to solve this problem, and then we will demonstrate that it contradicts itself. This Turing machine would be called a Halting machine that produces in a finite amount of time a 'yes' or no'. The performance comes as 'yes' if the stopping machine finishes in a finite amount of time, otherwise as no'.
The following is a Halting Computer block diagram -
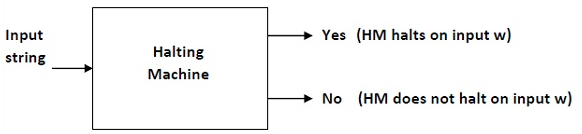
Fig 1: Halting machine
Now we will design an inverted halting machine (HM)’ as -
● If H returns YES, then loop forever.
● If H returns NO, then halt.
Below is the block diagram of inverted halting machine -
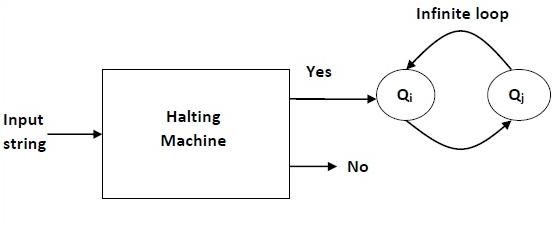
Fig 2: Inverted halting machine
In addition, as follows, a machine (HM)2 whose input itself is constructed -
● If - (HM)2 halts on input, loop forever
● Else - halt
Now, we have a contradiction. So, the halting problem is undecidable.
It was introduced by Emil Post and is an undecidable decision problem. The PCP problem over an alphabet ∑ is stated as follows −
Given the following two lists, M and N of non-empty strings over ∑ −
M = (x 1, x 2, x 3 ,………, x n )
N = (y 1, y 2, y 3 ,………, y n )
We can say that there is a Post Correspondence Solution, if for some i 1, i 2……… i k,
Where 1 ≤ i j ≤ n, the condition x i1 …….x ik = y i1 ……. y ik satisfies.
Example 1
Find whether the lists
M = (abb, aa, aaa) and N = (bba, aaa, aa)
Have a Post Correspondence Solution?
Sol:
| X1 | X2 | X3 |
M | Abb | Aa | Aaa |
N | Bba | Aaa | Aa |
Here,
x2 x1 x3 = ‘aaabbaaa’
And y2 y1 y3 = ‘aaabbaaa’
We can see that
x2 x1 x3 = y2 y1 y3
Hence, the solution is i = 2, j = 1, and k = 3.
Example 3
Find whether the lists M = (ab, bab, bbaaa) and N = (a, ba, bab) have a Post
Correspondence Solution?
Sol:
| X1 | X2 | X3 |
M | Ab | Bab | Bbaaa |
N | a | Ba | Bab |
In this case, there is no solution because −
| x 2 x 1 x 3 | ≠ | y 2 y 1 y 3 | (Lengths are not same)
Hence, it can be said that this Post Correspondence Problem is undecidable.
The Ackermann function, named after Wilhelm Ackermann, is one of the simplest and earliest examples of a complete computable function that is not basic recursive in computability theory. All primitive recursive functions are total and computable, however not all total computable functions are primitive recursive, as the Ackermann function demonstrates.
It's a function having two arguments, each of which can take any non-negative number as an argument.
Ackermann function is defined as:
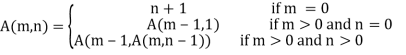
Where m and n are non-negative integers
Ackermann algorithm:
Ackermann(m, n)
{next and goal are arrays indexed from 0 to m, initialized so that next[O]
through next[m] are 0, goal[O] through goal[m - l] are 1, and goal[m] is -1}
Repeat
value <-- next[O] + 1
transferring <-- true
current <-- O
while transferring do begin
if next[current] = goal[current] then goal[current] <-- value
else transferring <-- false
next[current] <-- next[current]+l
current <-- current + 1
end while
Until next[m] = n + 1
Return value {the value of A(m, n)}
End Ackermann
Here's how the given Algorithm is explained:
Let's look at an example of the algorithm, A(1, 2), where m = 1 and n = 2.
The initial values of next, goal, value, and current, according to the algorithm, are:
Because next[current]!= goal[current], the else statement will be executed, resulting in the transfer being false.
As a result, the following are the values of next, aim, value, and current:
Similarly, tracing the procedure until next[m] = 3 changes the value of next, target, value, and current. The following is an explanation of how the values are changing:
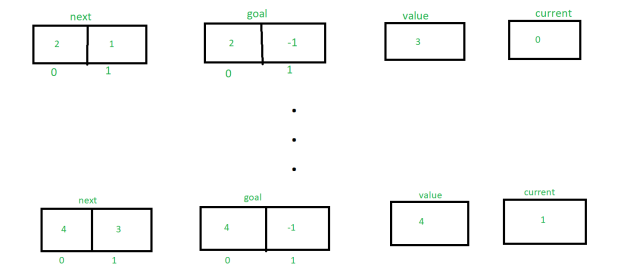
Finally returning the value e.g 4
Analysis of this algorithm:
The time complexity of this algorithm is: O(mA(m, n)) to compute A(m, n).
The space complexity of this algorithm is: O(m) to compute A(m, n).
Key takeaway
The Ackermann function, named after Wilhelm Ackermann, is one of the simplest and earliest examples of a complete computable function that is not basic recursive in computability theory.
In 1936, a technique named as lambda-calculus was created by Alonzo Church within which the Church numerals area unit well outlined, i.e. the encryption of natural numbers. Additionally in 1936, mathematician machines (earlier known as theoretical model for machines) was created by mathematician, that’s used for manipulating the symbols of string with the assistance of tape.
Church - Turing Thesis:
Turing machine is outlined as associate degree abstract illustration of a computer like hardware in computers. Mathematician planned Logical Computing Machines (LCMs), i.e. mathematician’s expressions for Turing Machines. This was done to outline algorithms properly. So, Church created a mechanical methodology named as ‘M’ for manipulation of strings by mistreatment logic and arithmetic.
This methodology M should pass the subsequent statements:
• Number of directions in M should be finite.
• Output ought to be made when playing a finite variety of steps.
• It mustn’t be imagined, i.e. is created in the world.
• It doesn't need any complicated understanding.
Using these statements Church planned a hypothesis known as Church’s mathematician thesis that may be expressed as: “The assumption that the intuitive the notion of estimable functions is known with partial algorithmic functions.”
In 1930, this statement was initially developed by Alonzo Church and is typically brought up as Church’s thesis, or the Church-Turing thesis. However, this hypothesis cannot be proved.
The algorithmic functions are estimable when taking the following assumptions:
1. Every and each operate should be estimable.
2. Let ‘F’ be the estimable operation and when playing some elementary operations to ‘F’, it’ll rework a replacement operation ‘G’ then this operate ‘G’ mechanically becomes the estimable operation.
3. If any operates that follow on top of 2 assumptions should be states as estimable function.
What Justifies the Church-Turing Thesis?
Stephen Kleene who coined the term “Church-Turing thesis” catalogued four sorts of argument for CTT-O: initial, the argument from non-refutation points out the thesis has ne’er been refuted, despite sustained (and ongoing) makes an attempt to search out a disproof (such because the makes an attempt by László Kalmár and, additional recently, by Doukas Kapantais).
Second, the argument from confluence points to the very fact that the assorted characterizations of computability, whereas differing in their approaches and formal details, end up to comprehend the exact same category of estimable functions. Four such characterizations were bestowed (independently) in 1936 and like a shot proved to be extensionally equivalent: mathematician computability, Church’s -definability, Kleene’s algorithmic functions, and Post’s finitary combinatory processes.
Third is associate degree argument typically brought up today as “Turing’s analysis.” mathematician known as it merely argument “I”; stating 5 terribly general and intuitive constraints or axioms the human pc is also assumed to satisfy: “The behavior of the pc at any moment is set by the symbols that he’s perceptive, associate degreed his “state of mind” at that moment”.
The second part of mathematician’s argument I may be a demonstration that every operate computed by any human pc subject to those constraints is additionally estimable by a computing machine; it’s not tough to visualize that every of the computer’s steps are mimicked by the Turing machine, either during a single step or by means of a series of steps.
Fourth during this catalog of issues supporting CTT-O area unit arguments from first- order logic. They’re typified by a 1936 argument of Church’s and by Turing’s
Argument II, from Section nine of Turing’s 1936 paper. In 2013, Saul Kripke bestowed a reconstruction of Turing’s argument II, which works as follows:
Computation may be a special variety of mathematical deduction; each|and each} mathematical deduction and thus every computation can be formalized as a legitimate deduction within the language of first-order predicate logic with identity (a step Kripke brought up as “Hilbert’s thesis”); following Gödel’s completeness theorem, every computation is so formalized by a obvious formula of first-order logic; and each computation will thus be disbursed by the universal computing machine. This last step concerning the universal computing machine is secured by a theorem proved by Turing: each obvious formula of first-order logic is proved by the universal computing machine.
The third and fourth of those arguments offer justification for CTT-O however not for CTT-A. As Robin Gandy found out, the third argument Turing’s Icontains “crucial steps ... Wherever he [Turing] appeals to the very fact that the calculation is being disbursed by a person’s being.” as an example, mathematician assumed “a soul will solely write one image at a time,” associate degreed Gandy noted this assumption cannot be carried over to a parallel machine that “prints an discretionary variety of symbols at the same time.” In Conway’s Game of Life, for example, there’s no edge on the amount of cells that conjure the grid, nevertheless the symbols altogether the cells area unit updated at the same time. Likewise, the fourth argument (Turing’s II) involves the claim that computation may be a special variety of formal proof, however the notion of proof is in and of itself associated with what a person’s mathematicians and not some oracle can prove.
It is thus perhaps not too surprising that the third and fourth arguments in this catalog seldom if ever appear in logic and computer science textbooks. The two arguments that are always given for the Church-Turing thesis (in, for example, Lewis and Papadimitriou are confluence and non-refutation. Yet both those arguments are merely inductive, whereas the third and fourth arguments are deductive in nature.
However, a number of attempts have sought to extend Turing’s axiomatic analysis to machine computation; for example, Gandy broadened Turing’s analysis in such a way that parallel computation is included, while Dershowitz and Gurevich gave a more general analysis in terms of abstract state machines. We return to the topic of extending the analysis to machine computation later in this article but first address the important question of whether CTT-O is mathematically provable.
Key takeaway:
- Turing machine is outlined as associate degree abstract illustration of a computer like hardware in computers.
- A common one is that a Turing machine can perform any good computation.
- The Church-Turing thesis is often misunderstood, especially in the philosophy of mind in recent writing.
Total recursive function -
If f(a1, a2, ...an) is defined for all its arguments, a recursive function is called the complete recursive function. Let f(a1, a2, ...an) be a function defined for function g(b1, b2, ...bn). If each element of f is assigned to a unique element of function g, then f is a total function.
● A complete function is called recursive or primitive recursive if and only if it is an initial over-n function, or if it is obtained by applying a finite number of times composition or recursion to an initial over-n function.
● A complete recursive function or primitive recursive function is the multiplication of two positive integers.
● Not all complete recursive functions are recursive primitive functions.
● The function of Ackerman is a complete function.
● Both primitive recursive features are complete functions.
Partial recursive function -
A function f(a1, a2,....an) determined by a TM is referred to as a partial recursive function. If f is defined for some but not all values of a1, a2,....an. Let f(a1, a2,...an) be a function defined by function g(b1, b2,....bn), then f is a partial function if almost one element of function g is assigned to some element of f.
If it is an initial function over N, a partial function is recursive, or if it is obtained by applying recursion or composition or minimization to an initial function over N.
● The partial recursive function is the subtraction of two positive integers.
● The partial function composition yields a partial(total) function.
● A partial recursive function is the minimization of a complete recursive function.
Primitive Functions
Three types of beginning functions (which are elementary primitive functions) plus three structural principles for generating more sophisticated functions from already produced functions yield the set of primitive recursive functions.
A simple form of recursion is primitive recursion, which is defined as follows:
Definition: If primitive recursion is used, definition f is derived from g and h.
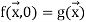
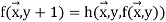
We allow n = 0 so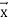 
could be missing.
As an example, f+(x, y) = x + y can be defined by primitive recursion as follows:
x + 0 = x
x + (y + 1) = (x + y) + 1
In this case, g(x) = x, and h(x, y, z) = z + 1
If f is defined by primitive recursion from g and h, the following high-level programme can compute f from g and h:
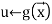
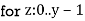
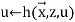
End for
The final value of u is f(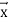
, y)
Initial functions
Z 0-ary function equal to 0
S S(x) = x + 1
In,i(x1 · · · xn) = xi 1 ≤ i ≤ n infinite class of projection functions
Definition: If f can be derived from the initial functions by a finite number of applications of primitive recursion and composition, then it is primitive recursive.
For an (n + 1)-place predicate P, the bounded minimization of P is the function mP : Nn+1 → N defined by
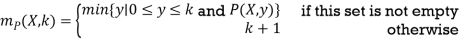
The minimization operator is frequently denoted by μ, and we sometimes write
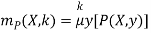
The scenario in which P (X, y) equals (f (X, y) = 0 for some f: Nn+1 → N is an interesting specific case. mP is written as mf and is referred to as the bounded minimization of f in this situation.
Theorem: If P is a primitive recursive (n + 1)-place predicate, its bounded minimization mP is a primitive recursive function.
Proof:
The operation of primitive recursion is used to obtain mP from primitive recursive functions. MP (X, 0) is 0 if P (X, 0) is true and 1 otherwise for X ∈ N n. We explore three scenarios in order to estimate mP (X, k + 1). First, if there exists y ≤ k for which P (X, y) is true, then mP (X, k + 1) = mP (X, k). Second, if there is no such y but P (X, k + 1) is true, then mP (X, k + 1) = k + 1. Third, if neither of these conditions
Holds, then mP (X, k + 1) = k + 2. It follows that the function mp can be obtained by primitive recursive from the function g and h, where
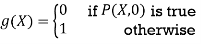
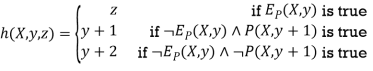
The functions g and h are both primitive recursive because P and EP are primitive recursive predicates.
Definition: Unbounded Minimization
For a certain function,
g : Nk+1 N
We define a function
f: Nk N such that
For x = (x1, x2, ...,xk) Nk and for some y N,
f( x ) equals y
If (and only if) the following conditions are satisfied:
(i) g( x , y) = 0 and
(ii) if g( x , z) = 0 then y z
(i.e., y is the smallest among all the values z N for which g( x , z) = 0)
(iii) g(x,u) is defined for all u y,with u N
Furthermore, if such a y does not exist for some x NK, then f(x) = undefined. Unbounded minimization is used to obtain such a function f, which is denoted as
f(x)= y[g(x,y) =0]
Example: Let g : N N N be defined by the following table.
g(0,0)=5 g(l,0)=5g(2, 0) = 8g(3, 0) = l
g(0,1)=4g(l,1)=6g (2,3) = 0g(3, 1) = 2
g(0,2)=6 g(l,2)=0g(2, l) = 5g(3, 2) = 0
g(0,3)=0 g(l,3)=3g(2, 2) = undefinedg(3, 3) = 4
g(0, 4) = lg(l,4)=0g(2, 4) = 7g(3, 4) = undefined
Then
f(0) = 3
f(1)=2 (but g(1,4)=0 as well, but 2 is the smallest k that allows f(1,2)=0).
f(2) = is not defined, Because g (2,3) =0, and g (2,n) is undefined for n = 2, which is less than 3.
f(3) = 2 (but g(3, 4) is undefined for y = 4, but 4 > 2 and g(3, 2)=0).
Minimisation can be defined for functions that are undefined for some domain values, as seen in the example above. Minimisation may also result in functions that are undefined for specific domain values.
Unbounded minimization can also lead to partial functions from total functions g: Nk+1 N. f: Nk N.
References:
- John E. Hopcroft, Rajeev Motwani, Jeffrey D.Ullman, “Introduction to Automata Theory Languages Sanjeev Arora and Boaz Barak, “Computational Complexity: A Modern Approach”,
- Cambridge University Press, ISBN: 0521424267 97805214242643
- John Martin, “Introduction to Languages and The Theory of Computation”, 2nd Edition, McGrawHill Education, ISBN-13: 978-1-25-900558-9, ISBN-10: 1-25-900558-5
- J.Carroll & D Long, “Theory of Finite Automata”, Prentice Hall, ISBN 0-13-913708-45 and Computation”, Addison-Wesley,ISBN
- Daniel Cohen, “Introduction to Computer Theory”, Wiley & Sons, ISBN 97881265133454
Unit - 5
Decidability and Undecidability of problems
If we can always create a comparable algorithm that can correctly answer the problem, the problem is said to be Decidable. By considering a basic example, we may immediately comprehend Decidable problems. Let's say we're asked to find all the prime numbers between 1000 and 2000. We can easily build an algorithm to enumerate all the prime numbers in this range in order to solve this challenge.
In terms of a Turing machine, a problem is said to be Decidable if there is a matching Turing machine that halts on every input with a yes or no answer. It's also worth noting that these issues are referred to as Turing Decidable since a Turing machine always comes to a halt on every input, accepting or rejecting it.
Example
We'll take a look at a couple key Decidable issues now:
● Is it possible to compare two regular languages, L and M?
Using the Set Difference technique, we can quickly verify this.
L-M =Null and M-L =Null.
Hence (L-M) U (M-L) = Null, then L,M are equivalent.
● Are you a CFL member?
Using a dynamic programming approach, we can always determine whether a string occurs in a particular CFL.
● A CFL's emptiness
By examining the CFL's production rules, we can quickly determine whether or not the language generates any strings.
Undecidable problem
Undecidable Problems are those for which we can't come up with an algorithm that can solve the problem correctly in a finite amount of time. These issues may be partially solvable, but they will never be completely solved. That is to say, there will always be a condition that causes the Turing Machine to go into an infinite loop without giving a response.
Consider Fermat's Theorem, a well-known Undecidable Problem that claims that no three positive numbers a, b, and c for any n>2 can ever meet the equation: a^n + b^n = c^n.
If we submit this problem to a Turing machine to discover a solution that produces a contradiction, the Turing machine could run indefinitely to find the appropriate values for n, a, b, and c. However, we are never clear whether a contradiction occurs, hence we call this problem an Undecidable Problem.
Example
Here are a few significant Undecided Issues:
● Is it true that a CFG generates all of the strings?
We can never reach the last string because a CFG generates infinite strings, hence it is undecidable.
● Is there a difference between two CFG L and M?
We can forecast if two CFGs are equal or not since we cannot determine all of the strings of any CFG.
● CFG's ambiguity?
There is no algorithm that can determine whether a CFL is ambiguous. We can only determine whether the CFL is ambiguous if any given string yields two separate parse trees.
● Is it possible to convert an ambiguous CFG into its non-ambiguous counterpart?
It's also an Insolvable Problem because there's no solution for converting ambiguous CFLs to non-ambiguous CFLs.
● Is it possible to learn a language that is a CFL on a regular basis?
This is an undecidable problem since we can't tell whether the CFL is regular or not from the production rules.
Key takeaway
- If there is no Turing machine that will always cease in a finite amount of time to deliver a yes or no answer, the problem is undecidable.
- There is no technique for determining the answer to an undecidable problem for a given input.
● Union and Intersection
Recursive
L1 x L2 and L1 x L2 are both recursive if L1 is recursive and L2 is recursive.
Using a multitape TM:
● Copy to Tape 2 and Tape 3 inputs
● Run M1 to tape 2 and M2 to tape 3 (neither will run forever; i.e.we get a result)
● They will determine whether x is in L1 and/or L2
● Test if approved by both M1 and M2 (intersection)
● Test if one is approved by M1 and M2 (union)
If L1 and L2 are recursive, the difference between L1 - L2=L1 and L2 is recursive.
Recursively Enumerable
If L1 and L2 are enumerated recursively, then L1 ∪ L2 and L1 ∩ L2 are recursively enumerated .
● Similar to the recursive case, but the case where M1 and M2 will run constantly
● Simulate simultaneously running M1 and M2-alternate one move from each machine.
A union, for reference,
● If any computer ever accepts it, accept it.
● If any machine ever refuses or fails, then the other machine continues to run.
If L is enumerated recursively and L is enumerated recursively, L is enumerated recursively.
● Let M and M be TMs, respectively, that accept L and L.
● Simultaneously, Run M and M'
● It must be agreed for any term x by any one of M or M'
● Therefore, either M or M 'will stop and agree
● If M stops and agrees, then stop and embrace.
● If M' stops and embraces, then stop and deny.
The TM that runs M and M at the same time always stops and accepts or refuses so that L and L are recursive.
If L is enumerable recursively, and L is not recursive, then L is not enumerable recursively.
● Concatenation
If L1 and L2 are two recursive languages, the L1.L2 concatenation would also be recursive. For instance:
L1 = {anbncn|n>=0}
L2 = {dmemfm|m>=0}
L3 = L1.L2
= {anbncndn emfm|m>=0 and n>=0} is also recursive.
L1 states that n no. Of a's is followed by n no. Of b's, and n no. Of c's. L2 says that m no. Of d's is followed by m no. Of e's, m no. Of f's. First, their concatenation matches no. Of a's, b's, and c's, then no. Of d's, e's, and f's. It can therefore be determined by TM.
● Kleene Closure
If L1 is recursive, its L1* smaller closure would also be recursive. For instance:
L1 = {anbncn|n>=0}
L1*= { anbncn||n>=0}* is also recursive.
Typically, programs are made up of loops that are either limited or infinite in length.
The program's overall output is entirely dependent on the input it receives.
The program may contain numerous different numbers of loops, which can be linear or nested.
The Halting Challenge is the problem of determining whether a given arbitrary computer program will stop operating or run in an infinite loop for the given input dependent on its input.
The Halting Problem states that it is difficult to develop a computer program that can decide if a program should halt for an input in a limited amount of time.
Furthermore, the Halting Problem never claims that determining whether a given random program will halt is impossible (stop).
In general, it asks, "Specify a random program and an input, determine whether the given random program will halt when that input is provided."
Writing Halting Problem
Input: A turing machine and an input string T.
Problem - Does the Turing machine complete the T-string computation in a finite number of steps? Either yes or no must be the answer.
Sol: We will first assume that there is such a Turing machine to solve this problem, and then we will demonstrate that it contradicts itself. This Turing machine would be called a Halting machine that produces in a finite amount of time a 'yes' or no'. The performance comes as 'yes' if the stopping machine finishes in a finite amount of time, otherwise as no'.
The following is a Halting Computer block diagram -
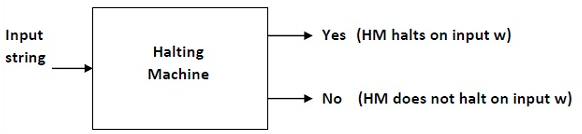
Fig 1: Halting machine
Now we will design an inverted halting machine (HM)’ as -
● If H returns YES, then loop forever.
● If H returns NO, then halt.
Below is the block diagram of inverted halting machine -
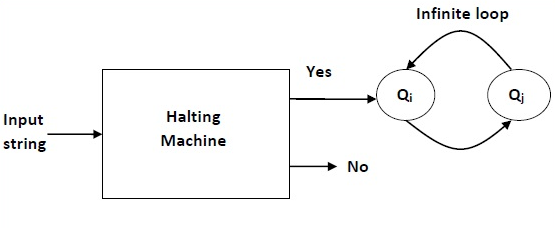
Fig 2: Inverted halting machine
In addition, as follows, a machine (HM)2 whose input itself is constructed -
● If - (HM)2 halts on input, loop forever
● Else - halt
Now, we have a contradiction. So, the halting problem is undecidable.
It was introduced by Emil Post and is an undecidable decision problem. The PCP problem over an alphabet ∑ is stated as follows −
Given the following two lists, M and N of non-empty strings over ∑ −
M = (x 1, x 2, x 3 ,………, x n )
N = (y 1, y 2, y 3 ,………, y n )
We can say that there is a Post Correspondence Solution, if for some i 1, i 2……… i k,
Where 1 ≤ i j ≤ n, the condition x i1 …….x ik = y i1 ……. y ik satisfies.
Example 1
Find whether the lists
M = (abb, aa, aaa) and N = (bba, aaa, aa)
Have a Post Correspondence Solution?
Sol:
| X1 | X2 | X3 |
M | Abb | Aa | Aaa |
N | Bba | Aaa | Aa |
Here,
x2 x1 x3 = ‘aaabbaaa’
And y2 y1 y3 = ‘aaabbaaa’
We can see that
x2 x1 x3 = y2 y1 y3
Hence, the solution is i = 2, j = 1, and k = 3.
Example 3
Find whether the lists M = (ab, bab, bbaaa) and N = (a, ba, bab) have a Post
Correspondence Solution?
Sol:
| X1 | X2 | X3 |
M | Ab | Bab | Bbaaa |
N | a | Ba | Bab |
In this case, there is no solution because −
| x 2 x 1 x 3 | ≠ | y 2 y 1 y 3 | (Lengths are not same)
Hence, it can be said that this Post Correspondence Problem is undecidable.
The Ackermann function, named after Wilhelm Ackermann, is one of the simplest and earliest examples of a complete computable function that is not basic recursive in computability theory. All primitive recursive functions are total and computable, however not all total computable functions are primitive recursive, as the Ackermann function demonstrates.
It's a function having two arguments, each of which can take any non-negative number as an argument.
Ackermann function is defined as:
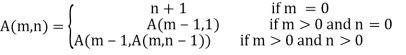
Where m and n are non-negative integers
Ackermann algorithm:
Ackermann(m, n)
{next and goal are arrays indexed from 0 to m, initialized so that next[O]
through next[m] are 0, goal[O] through goal[m - l] are 1, and goal[m] is -1}
Repeat
value <-- next[O] + 1
transferring <-- true
current <-- O
while transferring do begin
if next[current] = goal[current] then goal[current] <-- value
else transferring <-- false
next[current] <-- next[current]+l
current <-- current + 1
end while
Until next[m] = n + 1
Return value {the value of A(m, n)}
End Ackermann
Here's how the given Algorithm is explained:
Let's look at an example of the algorithm, A(1, 2), where m = 1 and n = 2.
The initial values of next, goal, value, and current, according to the algorithm, are:
Because next[current]!= goal[current], the else statement will be executed, resulting in the transfer being false.
As a result, the following are the values of next, aim, value, and current:
Similarly, tracing the procedure until next[m] = 3 changes the value of next, target, value, and current. The following is an explanation of how the values are changing:
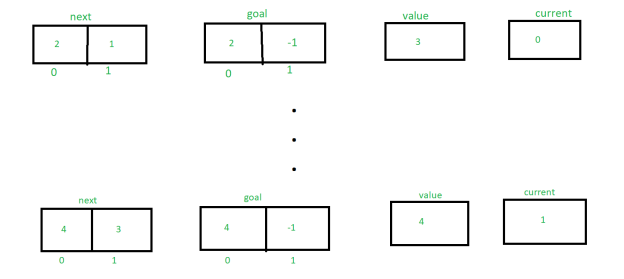
Finally returning the value e.g 4
Analysis of this algorithm:
The time complexity of this algorithm is: O(mA(m, n)) to compute A(m, n).
The space complexity of this algorithm is: O(m) to compute A(m, n).
Key takeaway
The Ackermann function, named after Wilhelm Ackermann, is one of the simplest and earliest examples of a complete computable function that is not basic recursive in computability theory.
In 1936, a technique named as lambda-calculus was created by Alonzo Church within which the Church numerals area unit well outlined, i.e. the encryption of natural numbers. Additionally in 1936, mathematician machines (earlier known as theoretical model for machines) was created by mathematician, that’s used for manipulating the symbols of string with the assistance of tape.
Church - Turing Thesis:
Turing machine is outlined as associate degree abstract illustration of a computer like hardware in computers. Mathematician planned Logical Computing Machines (LCMs), i.e. mathematician’s expressions for Turing Machines. This was done to outline algorithms properly. So, Church created a mechanical methodology named as ‘M’ for manipulation of strings by mistreatment logic and arithmetic.
This methodology M should pass the subsequent statements:
• Number of directions in M should be finite.
• Output ought to be made when playing a finite variety of steps.
• It mustn’t be imagined, i.e. is created in the world.
• It doesn't need any complicated understanding.
Using these statements Church planned a hypothesis known as Church’s mathematician thesis that may be expressed as: “The assumption that the intuitive the notion of estimable functions is known with partial algorithmic functions.”
In 1930, this statement was initially developed by Alonzo Church and is typically brought up as Church’s thesis, or the Church-Turing thesis. However, this hypothesis cannot be proved.
The algorithmic functions are estimable when taking the following assumptions:
1. Every and each operate should be estimable.
2. Let ‘F’ be the estimable operation and when playing some elementary operations to ‘F’, it’ll rework a replacement operation ‘G’ then this operate ‘G’ mechanically becomes the estimable operation.
3. If any operates that follow on top of 2 assumptions should be states as estimable function.
What Justifies the Church-Turing Thesis?
Stephen Kleene who coined the term “Church-Turing thesis” catalogued four sorts of argument for CTT-O: initial, the argument from non-refutation points out the thesis has ne’er been refuted, despite sustained (and ongoing) makes an attempt to search out a disproof (such because the makes an attempt by László Kalmár and, additional recently, by Doukas Kapantais).
Second, the argument from confluence points to the very fact that the assorted characterizations of computability, whereas differing in their approaches and formal details, end up to comprehend the exact same category of estimable functions. Four such characterizations were bestowed (independently) in 1936 and like a shot proved to be extensionally equivalent: mathematician computability, Church’s -definability, Kleene’s algorithmic functions, and Post’s finitary combinatory processes.
Third is associate degree argument typically brought up today as “Turing’s analysis.” mathematician known as it merely argument “I”; stating 5 terribly general and intuitive constraints or axioms the human pc is also assumed to satisfy: “The behavior of the pc at any moment is set by the symbols that he’s perceptive, associate degreed his “state of mind” at that moment”.
The second part of mathematician’s argument I may be a demonstration that every operate computed by any human pc subject to those constraints is additionally estimable by a computing machine; it’s not tough to visualize that every of the computer’s steps are mimicked by the Turing machine, either during a single step or by means of a series of steps.
Fourth during this catalog of issues supporting CTT-O area unit arguments from first- order logic. They’re typified by a 1936 argument of Church’s and by Turing’s
Argument II, from Section nine of Turing’s 1936 paper. In 2013, Saul Kripke bestowed a reconstruction of Turing’s argument II, which works as follows:
Computation may be a special variety of mathematical deduction; each|and each} mathematical deduction and thus every computation can be formalized as a legitimate deduction within the language of first-order predicate logic with identity (a step Kripke brought up as “Hilbert’s thesis”); following Gödel’s completeness theorem, every computation is so formalized by a obvious formula of first-order logic; and each computation will thus be disbursed by the universal computing machine. This last step concerning the universal computing machine is secured by a theorem proved by Turing: each obvious formula of first-order logic is proved by the universal computing machine.
The third and fourth of those arguments offer justification for CTT-O however not for CTT-A. As Robin Gandy found out, the third argument Turing’s Icontains “crucial steps ... Wherever he [Turing] appeals to the very fact that the calculation is being disbursed by a person’s being.” as an example, mathematician assumed “a soul will solely write one image at a time,” associate degreed Gandy noted this assumption cannot be carried over to a parallel machine that “prints an discretionary variety of symbols at the same time.” In Conway’s Game of Life, for example, there’s no edge on the amount of cells that conjure the grid, nevertheless the symbols altogether the cells area unit updated at the same time. Likewise, the fourth argument (Turing’s II) involves the claim that computation may be a special variety of formal proof, however the notion of proof is in and of itself associated with what a person’s mathematicians and not some oracle can prove.
It is thus perhaps not too surprising that the third and fourth arguments in this catalog seldom if ever appear in logic and computer science textbooks. The two arguments that are always given for the Church-Turing thesis (in, for example, Lewis and Papadimitriou are confluence and non-refutation. Yet both those arguments are merely inductive, whereas the third and fourth arguments are deductive in nature.
However, a number of attempts have sought to extend Turing’s axiomatic analysis to machine computation; for example, Gandy broadened Turing’s analysis in such a way that parallel computation is included, while Dershowitz and Gurevich gave a more general analysis in terms of abstract state machines. We return to the topic of extending the analysis to machine computation later in this article but first address the important question of whether CTT-O is mathematically provable.
Key takeaway:
- Turing machine is outlined as associate degree abstract illustration of a computer like hardware in computers.
- A common one is that a Turing machine can perform any good computation.
- The Church-Turing thesis is often misunderstood, especially in the philosophy of mind in recent writing.
Total recursive function -
If f(a1, a2, ...an) is defined for all its arguments, a recursive function is called the complete recursive function. Let f(a1, a2, ...an) be a function defined for function g(b1, b2, ...bn). If each element of f is assigned to a unique element of function g, then f is a total function.
● A complete function is called recursive or primitive recursive if and only if it is an initial over-n function, or if it is obtained by applying a finite number of times composition or recursion to an initial over-n function.
● A complete recursive function or primitive recursive function is the multiplication of two positive integers.
● Not all complete recursive functions are recursive primitive functions.
● The function of Ackerman is a complete function.
● Both primitive recursive features are complete functions.
Partial recursive function -
A function f(a1, a2,....an) determined by a TM is referred to as a partial recursive function. If f is defined for some but not all values of a1, a2,....an. Let f(a1, a2,...an) be a function defined by function g(b1, b2,....bn), then f is a partial function if almost one element of function g is assigned to some element of f.
If it is an initial function over N, a partial function is recursive, or if it is obtained by applying recursion or composition or minimization to an initial function over N.
● The partial recursive function is the subtraction of two positive integers.
● The partial function composition yields a partial(total) function.
● A partial recursive function is the minimization of a complete recursive function.
Primitive Functions
Three types of beginning functions (which are elementary primitive functions) plus three structural principles for generating more sophisticated functions from already produced functions yield the set of primitive recursive functions.
A simple form of recursion is primitive recursion, which is defined as follows:
Definition: If primitive recursion is used, definition f is derived from g and h.
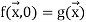
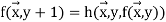
We allow n = 0 so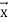 
could be missing.
As an example, f+(x, y) = x + y can be defined by primitive recursion as follows:
x + 0 = x
x + (y + 1) = (x + y) + 1
In this case, g(x) = x, and h(x, y, z) = z + 1
If f is defined by primitive recursion from g and h, the following high-level programme can compute f from g and h:
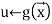
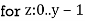
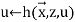
End for
The final value of u is f(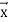
, y)
Initial functions
Z 0-ary function equal to 0
S S(x) = x + 1
In,i(x1 · · · xn) = xi 1 ≤ i ≤ n infinite class of projection functions
Definition: If f can be derived from the initial functions by a finite number of applications of primitive recursion and composition, then it is primitive recursive.
For an (n + 1)-place predicate P, the bounded minimization of P is the function mP : Nn+1 → N defined by
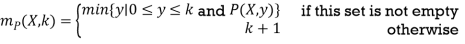
The minimization operator is frequently denoted by μ, and we sometimes write
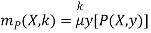
The scenario in which P (X, y) equals (f (X, y) = 0 for some f: Nn+1 → N is an interesting specific case. mP is written as mf and is referred to as the bounded minimization of f in this situation.
Theorem: If P is a primitive recursive (n + 1)-place predicate, its bounded minimization mP is a primitive recursive function.
Proof:
The operation of primitive recursion is used to obtain mP from primitive recursive functions. MP (X, 0) is 0 if P (X, 0) is true and 1 otherwise for X ∈ N n. We explore three scenarios in order to estimate mP (X, k + 1). First, if there exists y ≤ k for which P (X, y) is true, then mP (X, k + 1) = mP (X, k). Second, if there is no such y but P (X, k + 1) is true, then mP (X, k + 1) = k + 1. Third, if neither of these conditions
Holds, then mP (X, k + 1) = k + 2. It follows that the function mp can be obtained by primitive recursive from the function g and h, where
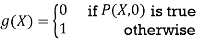
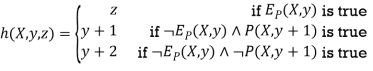
The functions g and h are both primitive recursive because P and EP are primitive recursive predicates.
Definition: Unbounded Minimization
For a certain function,
g : Nk+1 N
We define a function
f: Nk N such that
For x = (x1, x2, ...,xk) Nk and for some y N,
f( x ) equals y
If (and only if) the following conditions are satisfied:
(i) g( x , y) = 0 and
(ii) if g( x , z) = 0 then y z
(i.e., y is the smallest among all the values z N for which g( x , z) = 0)
(iii) g(x,u) is defined for all u y,with u N
Furthermore, if such a y does not exist for some x NK, then f(x) = undefined. Unbounded minimization is used to obtain such a function f, which is denoted as
f(x)= y[g(x,y) =0]
Example: Let g : N N N be defined by the following table.
g(0,0)=5 g(l,0)=5g(2, 0) = 8g(3, 0) = l
g(0,1)=4g(l,1)=6g (2,3) = 0g(3, 1) = 2
g(0,2)=6 g(l,2)=0g(2, l) = 5g(3, 2) = 0
g(0,3)=0 g(l,3)=3g(2, 2) = undefinedg(3, 3) = 4
g(0, 4) = lg(l,4)=0g(2, 4) = 7g(3, 4) = undefined
Then
f(0) = 3
f(1)=2 (but g(1,4)=0 as well, but 2 is the smallest k that allows f(1,2)=0).
f(2) = is not defined, Because g (2,3) =0, and g (2,n) is undefined for n = 2, which is less than 3.
f(3) = 2 (but g(3, 4) is undefined for y = 4, but 4 > 2 and g(3, 2)=0).
Minimisation can be defined for functions that are undefined for some domain values, as seen in the example above. Minimisation may also result in functions that are undefined for specific domain values.
Unbounded minimization can also lead to partial functions from total functions g: Nk+1 N. f: Nk N.
References:
- John E. Hopcroft, Rajeev Motwani, Jeffrey D.Ullman, “Introduction to Automata Theory Languages Sanjeev Arora and Boaz Barak, “Computational Complexity: A Modern Approach”,
- Cambridge University Press, ISBN: 0521424267 97805214242643
- John Martin, “Introduction to Languages and The Theory of Computation”, 2nd Edition, McGrawHill Education, ISBN-13: 978-1-25-900558-9, ISBN-10: 1-25-900558-5
- J.Carroll & D Long, “Theory of Finite Automata”, Prentice Hall, ISBN 0-13-913708-45 and Computation”, Addison-Wesley,ISBN
- Daniel Cohen, “Introduction to Computer Theory”, Wiley & Sons, ISBN 97881265133454
