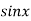UNIT 1
Differential Calculus
It is the process of differentiating the given function simultaneously many times and the result obtained are called successive derivative.
Let 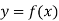 be a differentiable function.
be a differentiable function.
First derivative is denoted by 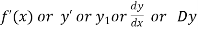
Second derivative is 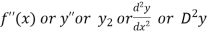
Third derivative is 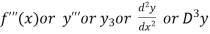
Similarly the nth derivative is 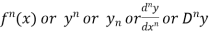
Example:
Function | Derivaties |
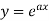 | 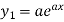 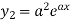 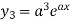 …………..  |
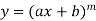 | 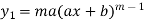  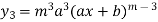 ……….. 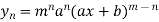 |
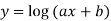 | 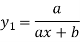 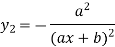 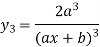 ………… 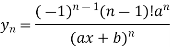 |
Example1: Find the nth derivative of 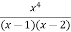
Since 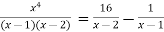
Differentiating both side with respect to x
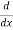 [
[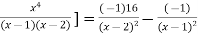
Again differentiating with respect to x

Again differentiating with respect to x
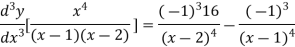
Similarly the nth derivative is
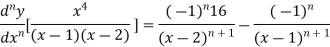
Example2: Find the nth derivative of 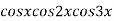
Let 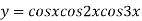
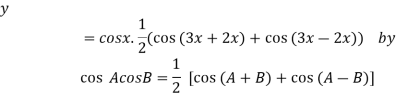
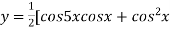 ]
]
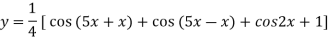
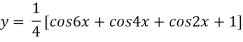
Differentiating with respect to x we get
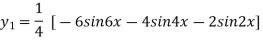

Again differentiating with respect to x we get
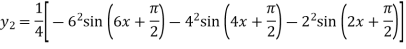
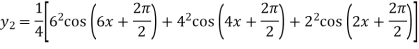
Again differentiating with respect to x we get
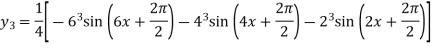
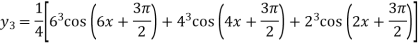
Similarly Again differentiating with respect to x we get
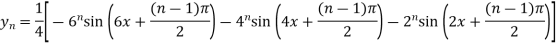
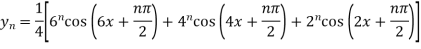
Example3: Find the nth derivative
Let 
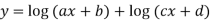
Differentiating with respect to x.
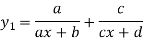
Again differentiating with respect to x.
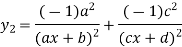
Again differentiating with respect to x.
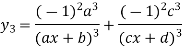
Again differentiating with respect to x.
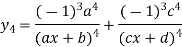
Again differentiating with respect to x.
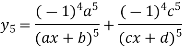
Similarly the nth derivative with respect to x.
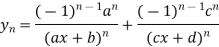
TAYLOR’S
If 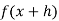 can be expanded as an infinite series, then
can be expanded as an infinite series, then
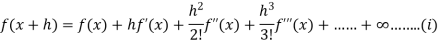
If 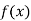 possesses derivative of all orders and the remainder
possesses derivative of all orders and the remainder 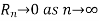 .
.
Corollary: Taking 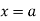 and
and 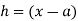 in equation (i) we get
in equation (i) we get

Taking  in above we get Maclaurin’s series.
in above we get Maclaurin’s series.
Example1: Expand the polynomial 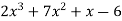 in power of
in power of 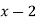 , by Taylor’s theorem.
, by Taylor’s theorem.
Let 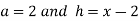 .
.
Also 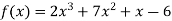
Then 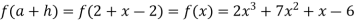
Differentiating with respect to x.
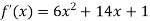
Again differentiating with respect to x the above function.
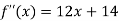
Again differentiating with respect to x the above function.
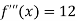
Also the value of above functions at x=2 will be
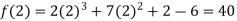
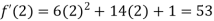
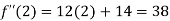
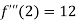
By Taylor’s theorem
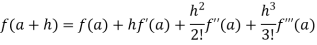
On substituting above values we get

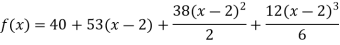
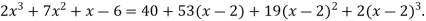
Example2: Expand 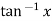 in power of
in power of 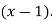
Let 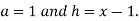
Also 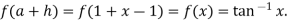
Differentiating f(x) with respect to x.

Again differentiating f(x) with respect to x.

Again differentiating f(x) with respect to x.
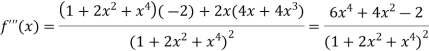
Also the value of above functions at x=1 will be
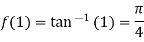
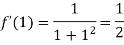
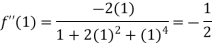

By Taylor’s theorem
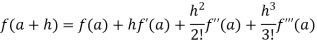
On substituting above values we get
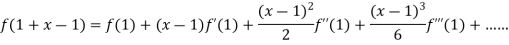

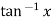 =
= 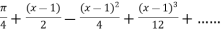
Example3:Expand 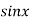 in power of
in power of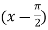 . Hence find the value of
. Hence find the value of 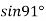 correct to four decimal places.
correct to four decimal places.
Let 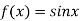
And 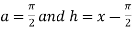 .
.
Differentiating 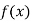 with respect to x.
with respect to x.
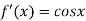
Again differentiating 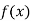 with respect to x.
with respect to x.
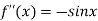
Again differentiating 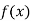 with respect to x.
with respect to x.
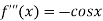
Again differentiating 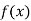 with respect to x.
with respect to x.
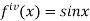
Also the value of above functions at 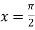 will be
will be
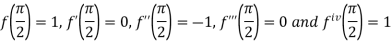
By Taylor’s theorem
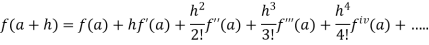
On substituting above values we get
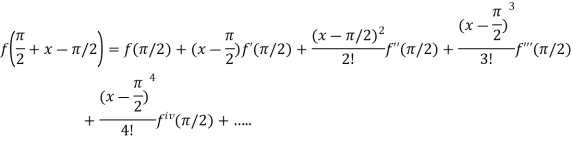
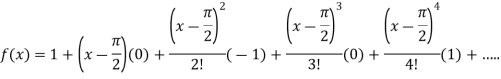

At 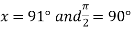
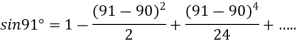
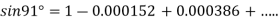
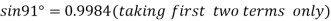 .
.
Maclaurin’s theorem:
This is a particular case of Taylor’s theorem in which a=0 and h=x in Taylor’s theorem.
If f(x) can be expanded as an infinite series, then
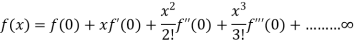
Where the remainder is 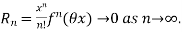
Example1:If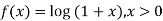 using Taylor’s theorem, show that for
using Taylor’s theorem, show that for 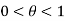 .
.

Deduce that 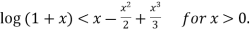
Let 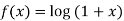 then
then 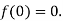
Differentiating with respect to x.
 .Then
.Then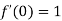
Again differentiating with respect to x.
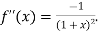 Then
Then 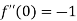
Again differentiating with respect to x.
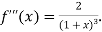 Then
Then 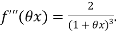
By Maclaurin’s theorem
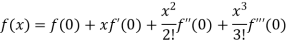
Substituting the above values we get
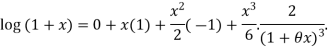
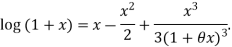
Since 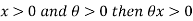
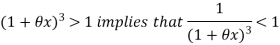
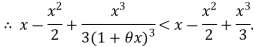
Hence 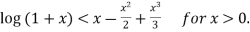
Example2: Prove that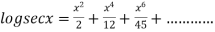
Let 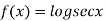
Differentiating 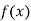 with respect to x.
with respect to x.
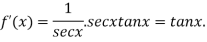
Again differentiating 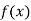 with respect to x.
with respect to x.
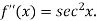
Again differentiating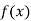 with respect to x.
with respect to x.
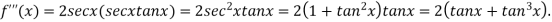
Again differentiating 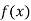 with respect to x.
with respect to x.
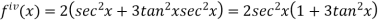 and so on.
and so on.
Putting 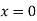 , in above derivatives we get
, in above derivatives we get
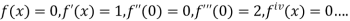 so on.
so on.
By Maclaurin’s theorem
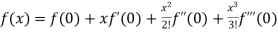 +………
+………
Substituting the above values we get
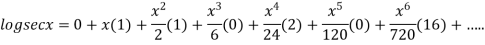
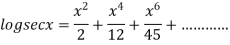
Example3:Prove that
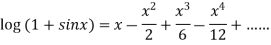
Let 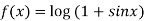
Differentiating above function with respect to x.
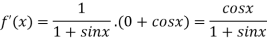
Again differentiating above function with respect to x.
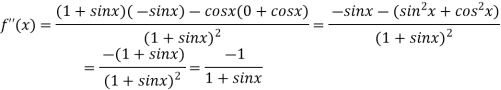
Again differentiating above function with respect to x.
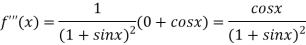
Again differentiating above function with respect to x.
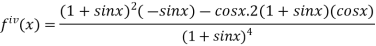
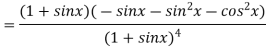

Putting 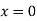 , in above derivatives we get
, in above derivatives we get
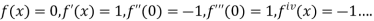 so on.
so on.
By Maclaurin’s theorem
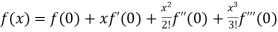 +………
+………
Substituting the above values we get
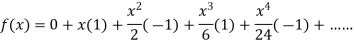
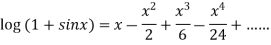
Example: Expansion of Some standard series
Let 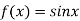 and
and 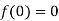
Differentiating above function with respect to x.

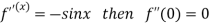
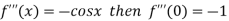
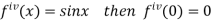

By Maclaurin’s theorem
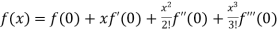 +………
+………
Substituting the above values we get

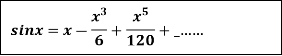
2. 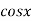
Let 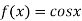 and
and 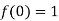
Differentiating above function with respect to x.
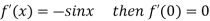
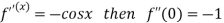
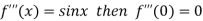

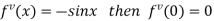
By Maclaurin’s theorem
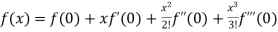 +………
+………
Substituting the above values we get
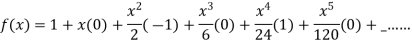


3.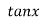
Let  and
and 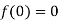
Differentiating above function with respect to x.
 .
.

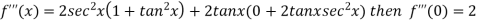
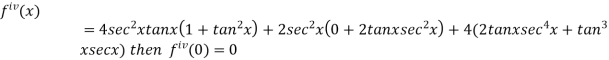
By Maclaurin’s theorem
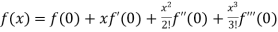 +………
+………
Substituting the above values we get
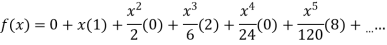
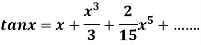
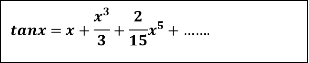
4.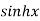
Let 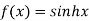 and also
and also 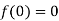
Differentiating above function with respect to x.
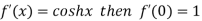

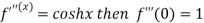
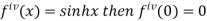

By Maclaurin’s theorem
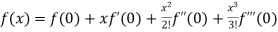 +………
+………
Substituting the above values we get

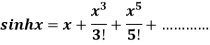

5. 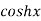
Let 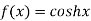 and also
and also 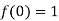
Differentiating above function with respect to x.
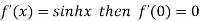
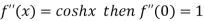
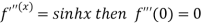
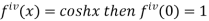
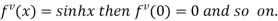
By Maclaurin’s theorem
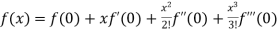 +………
+………
Substituting the above values we get
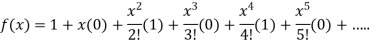
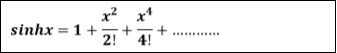
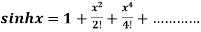
6. 
Let 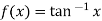 and also
and also 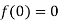
Differentiating above function with respect to x.
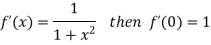
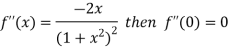


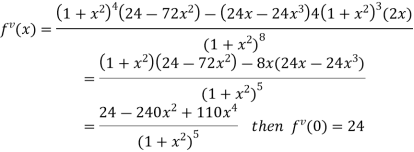
By Maclaurin’s theorem
 +………
+………
Substituting the above values we get
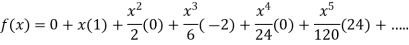
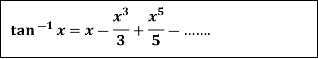
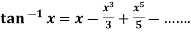
7. 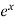
Let 
Differentiating above function with respect to x.
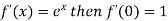
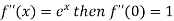
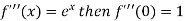
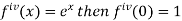
By Maclaurin’s theorem
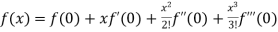 +………
+………
Substituting the above values we get
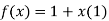 +
+ +………
+………
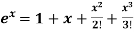 +………
+………

8. 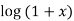
Let 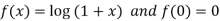
Differentiating above function with respect to x.
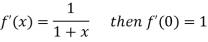
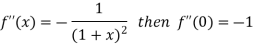

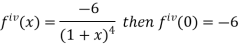

By Maclaurin’s theorem
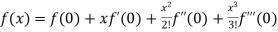 +………
+………
Substituting the above values we get
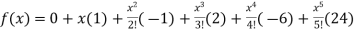 +………
+………
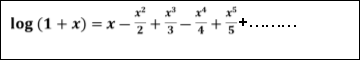
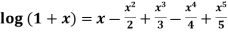 +………
+………
9. 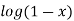
Let 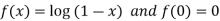
Differentiating above function with respect to x.
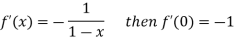
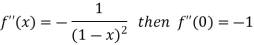
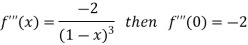
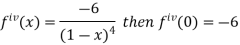
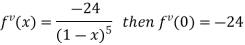
By Maclaurin’s theorem
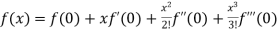 +………
+………
Substituting the above values we get
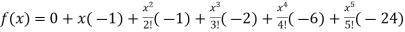 +………
+………
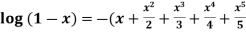 +………)
+………)

10. 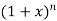
Let 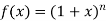
Differentiating the above function with respect to x.
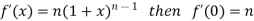
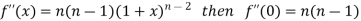
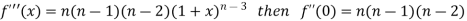
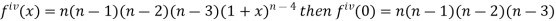
By Maclaurin’s theorem
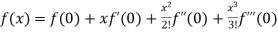 +………
+………
Substituting the above values we get
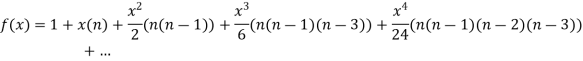

In calculus and other branches of mathematical analysis, limits involving an algebraic combination of functions in an independent variable may often be evaluated by replacing these functions by their limits; if the expression obtained after this substitution does not provide sufficient information to determine the original limit, then it is said to assume an indeterminate form. More specifically, an indeterminate form is a mathematical expression involving 0,1 and  , obtained by applying the algebraic limit theorem in the process of attempting to determine a limit, which fails to restrict that limit to one specific value and thus does not yet determine the limit being sought. The term was originally introduced by Cauchy's student Moigno in the middle of the 19th century.
, obtained by applying the algebraic limit theorem in the process of attempting to determine a limit, which fails to restrict that limit to one specific value and thus does not yet determine the limit being sought. The term was originally introduced by Cauchy's student Moigno in the middle of the 19th century.
There are seven indeterminate forms which are typically considered in the literature:
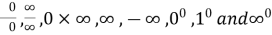
The most common example of an indeterminate form occurs when determining the limit of the ratio of two functions, in which both of these functions tend to zero in the limit, and is referred to as "the indeterminate form 0/0". For example, as x approaches 0, the ratios , (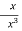 ,
, and
and 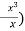 go to
go to 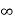 , 1, and 0 respectively. In each case, if the limits of the numerator and denominator are substituted, the resulting expression is (
, 1, and 0 respectively. In each case, if the limits of the numerator and denominator are substituted, the resulting expression is (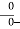 , which is undefined. In a loose manner of speaking,(
, which is undefined. In a loose manner of speaking,( 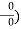 can take on the values 0,1 , or
can take on the values 0,1 , or 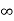 , and it is easy to construct similar examples for which the limit is any particular value.
, and it is easy to construct similar examples for which the limit is any particular value.
So, given that two functions f(x) and g(x) both approaching 0 as x approaches some limit point c, that fact alone does not give enough information for evaluating the limit
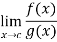

Not every undefined algebraic expression corresponds to an indeterminate form. For example, the expression (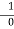 ) is undefined as a real number but does not correspond to an indeterminate form, because any limit that gives rise to this form will diverge to infinity.
) is undefined as a real number but does not correspond to an indeterminate form, because any limit that gives rise to this form will diverge to infinity.
Expressions that arise in other ways than by applying the algebraic limit theorem may assume the same form as one of the indeterminate forms. It is not appropriate, however, to call these expressions "indeterminate forms" outside the context of determining limits. The most common case is 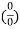 , which may, for example, arise from substituting 0 for x in the equation f(x)=
, which may, for example, arise from substituting 0 for x in the equation f(x)= 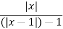 . This expression is undefined, as is division by zero in general. The other case is the expression
. This expression is undefined, as is division by zero in general. The other case is the expression 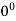 . Whether this expression is left undefined, or is defined to equal 1, depends on the field of application and may vary between authors. For more, see the article Zero to the power of zero. Note that
. Whether this expression is left undefined, or is defined to equal 1, depends on the field of application and may vary between authors. For more, see the article Zero to the power of zero. Note that  and other expressions involving infinity are not indeterminate forms.
and other expressions involving infinity are not indeterminate forms.
Example 1:
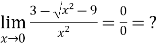
Solution:
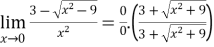

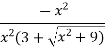
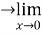
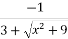 =
= 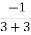 = 0
= 0
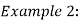
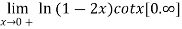 =?
=?
Solution:
=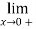
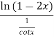

=
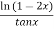
=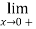
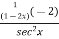
=-2
Curvature of a given curve:
In mathematics, curvature is any of several strongly related concepts in geometry. Intuitively, the curvature is the amount by which a curve deviates from being a straight line, or a surface deviates from being a plane.
For curves, the canonical example is that of a circle, which has a curvature equal to the reciprocal of its radius. Smaller circles bend more sharply, and hence have higher curvature. The curvature at a point of a differentiable curve is the curvature of its osculating circle, that is the circle that best approximates the curve near this point. The curvature of a straight line is zero. The curvature of a curve at a point is normally a scalar quantity, that is, it is expressed by a single real number.
For surfaces (and, more generally for higher-dimensional manifolds), that are embedded in a Euclidean space, the concept of curvature is more complex, as depending on the choice of a direction on the surface or manifold. This leads to the concepts of maximal curvature, minimal curvature, and mean curvature.
Radius of curvature:
We can draw a circle that closely fits nearby points on a local section of a curve, as follows.

We say the curve and the circle osculate (which means "to kiss"), since the 2 curves have the same tangent and curvature at the point where they meet.
The radius of curvature of the curve at a particular point is defined as the radius of the approximating circle. This radius changes as we move along the curve.
How do we find this changing radius of curvature?
The formula for the radius of curvature at any point x for the curve y = f(x) is given by:
Radius of curvature =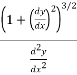
Example 1:
Find the radius of curvature for the following
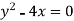
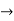 2y’’-4=0
2y’’-4=0
Y’=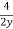 =
=
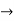 y’’=
y’’=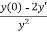 = -
= -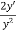
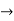 y’’.y2 = -2
y’’.y2 = -2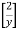
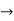 y’’=-
y’’=-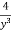
Substitute y=4, consider y’ and y’’ to solve for R:
We know that,
Radius of convergence (R) = 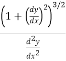 …..(1)
…..(1)
Now substituting the values y’ and y’’ in (1)
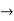
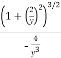 =
= 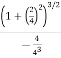 = 22.36
= 22.36
 Radius of convergence (R) =22.36
Radius of convergence (R) =22.36
Curvature of a given circle:
The curvature of a given curve at a particular point is the curvature of the approximating circle at that point. The curvature depends on the radius - the smaller the radius, the greater the curvature (approaching a point at the extreme) and the larger the radius, the smaller the curvature.
Let Cr be a circle of radius r centred at the origin.
A canonical parameterization of the curve is (counter clockwise)
g(s) =r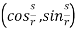
For s∈ (0,2πr) (actually this leaves out the point (r,0) but this could be treated via another parameterization taking s∈(−πr,πr)
Differentiating the parameterization we get
T = g’(s)= 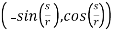 |
|
|
And this results in the normal
N=j.T = -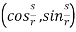 = -
= -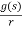
Differentiating g a second time we can calculate the curvature
T’= - -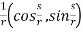 =
=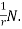
And by definition
T’=kN
 k=
k=
And thus the curvature of a circle of radius r is 1r provided that the positive direction on the circle is anticlockwise; otherwise it is −1r.