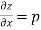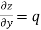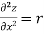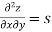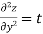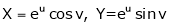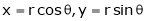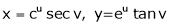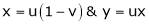UNIT 2
Partial Differentiation
There are two types of quantities whose value depend on a single variable and another whose value depend on more than a single variable.
In other words : A symbol z which has a definite value for each pair of values of x and y is called a function of two independent variables x and y, denoted by
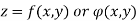
Example: velocity depends on distance and time.
Volume of cylinder depends on height and radius of cylinder.
Consider a function z which has a definite value for the independent variables 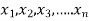
Then it is called as function of several variables and is denoted by
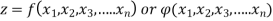
A function whose value dependent on several independent variables is called as function of several variables.
Let 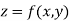
Then partial derivative of z with respect to x is obtained by differentiating z with respect to x treating y as constant and is denoted as
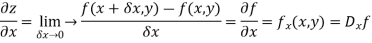
Then partial derivative of z with respect to y is obtained by differentiating z with respect to y treating x as constant and is denoted as
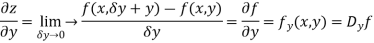
Partial derivative of higher order:
When we differentiate a function depend on more than one independent variable, we differentiate it with respect to one variable keeping other as constant.
A second order partial derivative means differentiating twice
In general 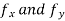 are also function of x and y and so these can be further partially differentiated with respect to x and y.
are also function of x and y and so these can be further partially differentiated with respect to x and y.
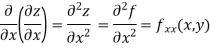
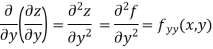

In general 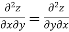
Notation:
Generalization: If 
Then the partial derivative of z with respect to 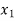 is obtained by differentiating z with respect to
is obtained by differentiating z with respect to 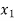 treating all the other variables as constant and is denoted by
treating all the other variables as constant and is denoted by

Example1: If  . Then prove that
. Then prove that
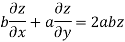
Given 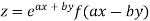
Partially differentiating z with respect to x keeping y as constant
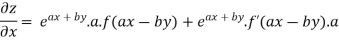
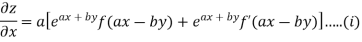
Again partially differentiating given z with respect to y keeping x as constant
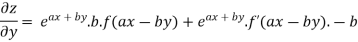

On b.eq(i) +a.eq(ii) we get
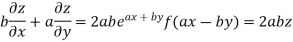
Hence proved.
Example2: If 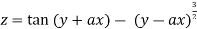
Show that 
Given 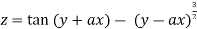
Partially differentiating z with respect to x keeping y as constant
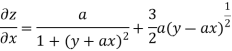
Again partially differentiating z with respect to x keeping y as constant
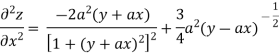

Partially differentiating z with respect to y keeping x as constant
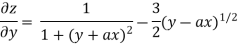
Again partially differentiating z with respect to y keeping x as constant
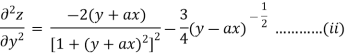
From eq(i) and eq(ii) we conclude that
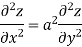
Example3 : Find the value of n so that the equation
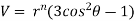
Satisfies the relation 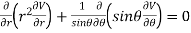
Given 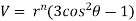
Partially differentiating V with respect to r keeping 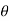 as constant
as constant
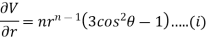
Again partially differentiating given V with respect to 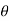 keeping r as constant
keeping r as constant
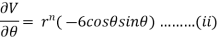
Now, we are taking the given relation
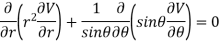
Substituting values using eq(i) and eq(ii)
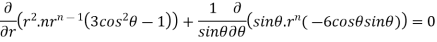
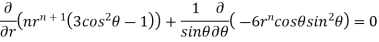
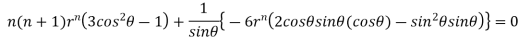
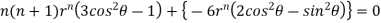
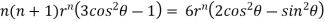
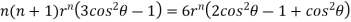
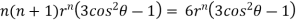
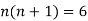
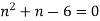
On solving we get 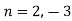
Example 4: If 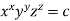 then show that when
then show that when 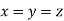
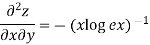
Given 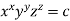
Taking log on both side we get
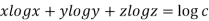
Partially differentiating with respect to x we get
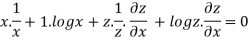
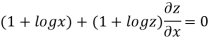
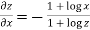 …..(i)
…..(i)
Similarly partially differentiating with respect y we get
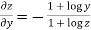 ……(ii)
……(ii)
LHS 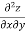
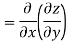
Substituting value from (ii)

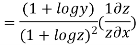
Again substituting value from (i) we get
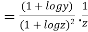 .(
.(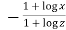 )
)
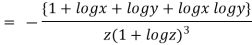
When 
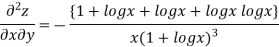
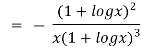
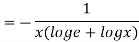

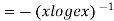
=RHS
Hence proved
Example5:If 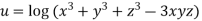
Then show that 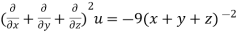
Given 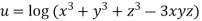
Partially differentiating u with respect to x keeping y and z as constant
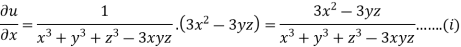
Similarly paritially differentiating u with respect to y keeping x and z as constant
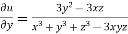 …….(ii)
…….(ii)
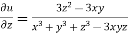 ……..(iii)
……..(iii)
LHS: 
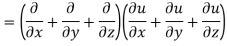
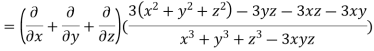


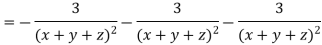
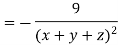
Hence proved
A polynomial in x & y is said to be Homogeneous expression in x & y of degree n. If the degree of each term in the expression is same & equal to n.
e.g.
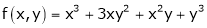 is a homogeneous function of degree 3.
is a homogeneous function of degree 3.
To find the degree of homogeneous expression f(x, y).
- Consider
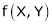
- Put
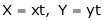 . Then if we get
. Then if we get 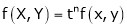 .
.
Then the degree of 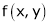 is n.
is n.
Ex.
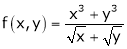
Consider 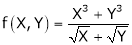
Put 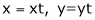
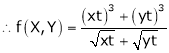
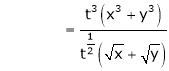
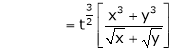
 .
.
Thus degree of f(x, y) is 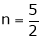
Note that
If 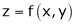 be a homogeneous function of degree n then z can be written as
be a homogeneous function of degree n then z can be written as
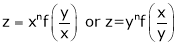
Differentiation of Implicit function
Suppose that we cannot find y explicitly as a function of x. But only implicitly through the relation f(x, y) = 0.
Then we find 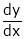
Since 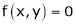
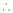 diff. P. w.r.t. x we get
diff. P. w.r.t. x we get
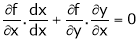
i.e. 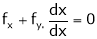
Similarly,
It f (x, y, z) = 0 then z is called implicit function of x, y. Then in this case we get
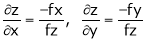
Ex.
Find  if
if 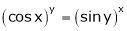
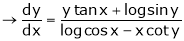
Ex. Find 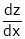 . If
. If 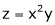 , &
, &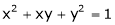
Ex. If 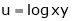 , where
, where 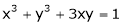
Find 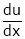
Ex. If 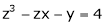
Then find 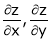
Eulers Theorem on Homogeneous functions:
Statement:
If 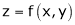 be a homogeneous function of degree n in x & y then,
be a homogeneous function of degree n in x & y then,
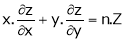
Deductions from Eulers theorem
- If
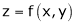 be a homogeneous function of degree n in x & y then,
be a homogeneous function of degree n in x & y then,
 .
.
2. If  be a homogeneous functions of degree n in x & y and also
be a homogeneous functions of degree n in x & y and also 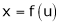 then,
then,
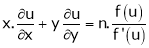
And
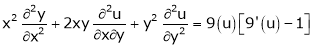
Where 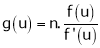
Ex.
If  , find the value of
, find the value of

Ex.
If  then find the value of
then find the value of 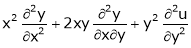
Ex. If 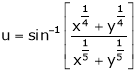 then prove
then prove
That 
Ex. If 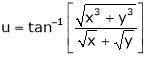 the prove that
the prove that

Ex. If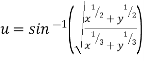 then show
then show
That 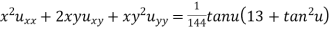
In calculus, the general Leibniz rule named after Gottfried Wilhelm Leibniz, generalizes the product rule (which is also known as "Leibniz's rule"). It states that if f and g are n-times differentiable functions, then the product fg is also n-times differentiable and its nth derivative is given by
(fg)n = 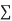 k=0n (nk) f(n-k).g(k)
k=0n (nk) f(n-k).g(k)
Alternatively, by letting F = f ∘ g (equiv., F(x) = f(g(x)) for all x), one can also write the chain rule in Lagrange's notation, as follows:
F’(X)= f’(g(x)).g’(x)
The chain rule may also be rewritten in Leibniz's notation in the following way. If a variable z depends on the variable y, which itself depends on the variable x (i.e., y and z are dependent variables), then z, via the intermediate variable of y, depends on x as well. In which case, the chain rule states that:

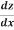 =
= 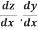
The Chain Rule Formula is as follows –
 =
=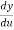 .
.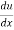
Solved Examples
Example 1: Differentiate y = cos x2
Solution:
Given,
y = cos x2
Let u = x2, so that y = cos u
Therefore: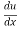 =2x
=2x
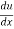 = -sin u
= -sin u
And so, the chain rule says:
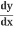 =
=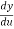 .
.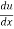
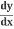 = -sin u × 2x
= -sin u × 2x
= -2x sin x2
Example 2:
Differentiate f(x)=(1+x2)5.
Solution:
Using the Chain rule,
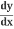 =
= 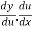
Let us take y = u5 and u = 1+x2
Then 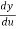 =
= 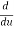 (u5) = 5u4
(u5) = 5u4
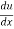 =
= 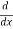 (1 + x2 )= 2x.
(1 + x2 )= 2x.
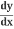 = 5u4⋅2x = 5(1+x2)4⋅2x
= 5u4⋅2x = 5(1+x2)4⋅2x
= 10x(1+x4)
3. Implicit differentiation
Implicit differentiation:
A function can be explicit or implicit:
Explicit: "y = some function of x". When we know x we can calculate y directly.
Implicit: "some function of y and x equals something else". Knowing x does not lead directly to y.
How to do Implicit Differentiation
- Differentiate with respect to x
- Collect all the
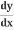 on one side
on one side - Solve for
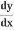
Example 1: x2 + y2 = r2
Differentiate with respect to x:
 (x2) +
(x2) +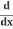 (y2) =
(y2) =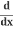 (r2)
(r2)
Let's solve each term:
Use the Power Rule: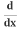 (x2) = 2x
(x2) = 2x
Use the Chain Rule (explained below):  (y2) = 2y
(y2) = 2y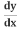
r2 is a constant, so its derivative is 0:d/dx(r2) = 0
Which gives us:
2x + 2y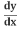 = 0
= 0
Collect all the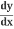 on one side
on one side
Y 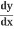 = −x
= −x
Solve for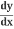 :
:
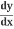 =-
=- 
The Chain Rule Using 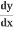 :
:
Let's look more closely at how 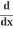 (y2) becomes 2y
(y2) becomes 2y 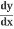
The Chain Rule says:
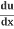 =
=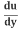 .
.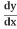
Substitute in u = y2:
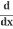 (y2) =
(y2) =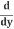 (y2) .
(y2) .
And then:
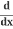 (y2) = 2y
(y2) = 2y
Basically, all we did was differentiate with respect to y and multiply by dy/dx
Example 2:
The following problems require the use of implicit differentiation. Implicit differentiation is nothing more than a special case of the well-known chain rule for derivatives. The majority of differentiation problems in first-year calculus involve functions y written EXPLICITLY as functions of x. For example, if
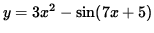 ,
,
Then the derivative of y is
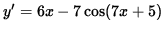 .
.
However, some functions y is written IMPLICITLY as functions of x. A familiar example of this is the equation
x2 + y2 = 25,
Which represents a circle of radius five cantered at the origin. Suppose that we wish to find the slope of the line tangent to the graph of this equation at the point (3, -4) .
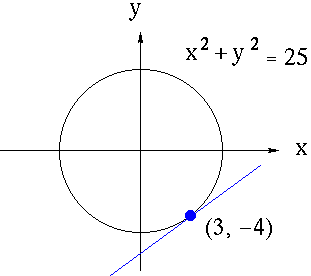
How could we find the derivative of y in this instance? One way is to first write y explicitly as a function of x. Thus,
x2 + y2 = 25,
y2 = 25 - x2,
And
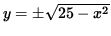 ,
,
Where the positive square root represents the top semi-circle and the negative square root represents the bottom semi-circle. Since the point
(3, -4) lies on the bottom semi-circle given by
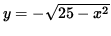 ,
,
The derivative of y is
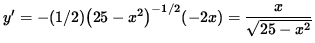 ,
,
i.e.,
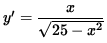 .
.
Thus, the slope of the line tangent to the graph at the point (3, -4) is
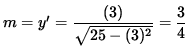 .
.
Unfortunately, not every equation involving x and y can be solved explicitly for y . For the sake of illustration we will find the derivative of y WITHOUT writing y explicitly as a function of x . Recall that the derivative (D) of a function of x squared, (f(x))2 , can be found using the chain rule :
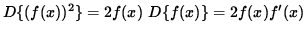 .
.
Since y symbolically represents a function of x, the derivative of y2 can be found in the same fashion :
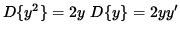 .
.
Now begin with
x2 + y2 = 25 .
Differentiate both sides of the equation, getting
D ( x2 + y2 ) = D ( 25 ) ,
D ( x2 ) + D ( y2 ) = D ( 25 ) ,
And
2x + 2 y y' = 0 ,
So that
2 y y' = - 2x ,
And
 ,
,
i.e.,
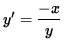 .
.
Thus, the slope of the line tangent to the graph at the point (3, -4) is
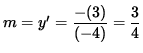 .
.
Jacobians, Errors and Approximations, maxima and minima
Jacobians
If u and v be continuous and differentiable functions of two other independent variables x and y such as
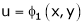 ,
, 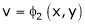 then we define the determine
then we define the determine
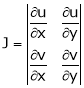 as Jacobian of u, v with respect to x, y
as Jacobian of u, v with respect to x, y
Similarly ,
JJ’ = 1
Actually Jacobins are functional determines
Ex.
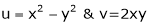 Calculate
Calculate 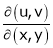
- If
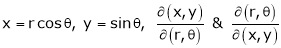
- If
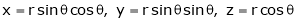
ST 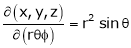
4.  find
find 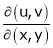
5. If 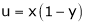 and
and 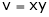 , find
, find 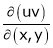
6. 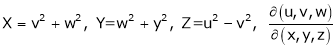
7. If 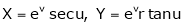
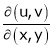
8. If 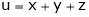 ,
, 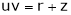 ,
, 
JJ1 = 1
If 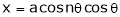 ,
, 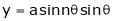
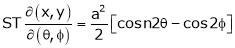
JJ1=1
Jacobian of composite function (chain rule)
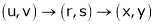
Then 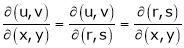
Ex.
- If
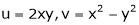
Where 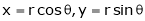
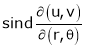
2. If 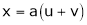
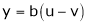 and
and 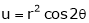
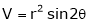
Find 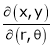
3. If 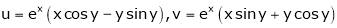

Find 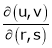
Jacobian of Implicit function
Let u1, u2 be implicit functions of x1, x2 connected by f1, f2 such there
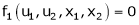 ,
, 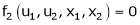
Then 
Similarly,
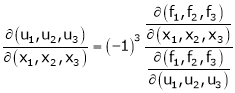
Ex.
If 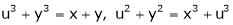
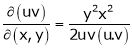
If 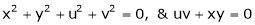
Find 
Partial derivative of implicit functions
Consider four variables u, v, x, y related by implicit function.
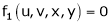 ,
, 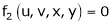
Then

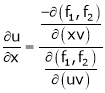
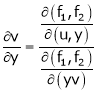
Ex.
If  and
and 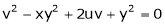
Find 
If 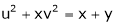 and
and 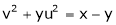
Find 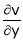
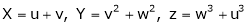
Find 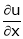
If 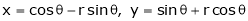
Find 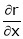
Taylor series:
The taylor’s series can be represented as the following
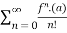 (x-a)n
(x-a)n
Example 1:
Find the taylor series for the following:

 =
= 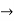
 <1
<1
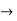 (x/10)<1 and (x/10) > -1
(x/10)<1 and (x/10) > -1
Therefore radius of convergence is (-10,10)
 ROC =10
ROC =10
Example 2:
f(n)5 = 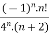
Here the ROC is 4
Maclaurian series:
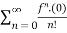 (x)n
(x)n
Example:
f(x)=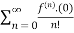
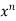
= f(0)+f’(0)x+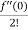 x2 +
x2 + 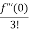 x3 +......
x3 +......
= 1+x+x2 +x3 + .....
= 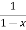
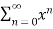
As we know that the value of a function at maximum point is called maximum value of a function. Similarly, the value of a function at minimum point is called minimum value of a function.
The maxima and minima of a function is an extreme biggest and extreme smallest point of a function in a given range (interval) or entire region. Pierre de Fermat was the first mathematician to discover general method for calculating maxima and minima of a function. The maxima and minima are complementing of each other.
Maxima and Minima of a function of one variables
If f(x) is a single valued function defined in a region R then
Maxima is a maximum point 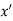 if and only if
if and only if 
Minima is a minimum point  if and only if
if and only if 


Maxima and Minima of a function of two independent variables
Let 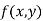 be a defined function of two independent variables.
be a defined function of two independent variables.
Then the point 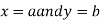 is said to be a maximum point of
is said to be a maximum point of  if
if

Or 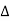 =
= 
For all positive and negative values of h and k.
Similarly the point 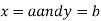 is said to be a minimum point of
is said to be a minimum point of  if
if
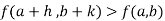
Or 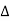 =
= 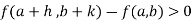
For all positive and negative values of h and k.
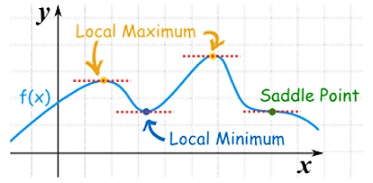
Saddle point: Critical points of a function of two variables are those points at which both partial derivatives of the function are zero. A critical point of a function of a single variable is either a local maximum, a local minimum, or neither. With functions of two variables there is a fourth possibility - a saddle point.
A point is a saddle point of a function of two variables if
![2 2 [ 2 ] 2
@f-= 0, @f--= 0, and @-f- @-f-- -@-f- < 0
@x @y @x2 @y2 @x @y](https://glossaread-contain.s3.ap-south-1.amazonaws.com/epub/1643166672_495797.png)
At the point.
Stationary Value
The value 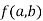 is said to be a stationary value of
is said to be a stationary value of 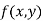 if
if
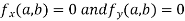
i.e. the function is a stationary at (a , b).
Rule to find the maximum and minimum values of 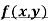
- Calculate
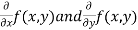 .
. - Form and solve
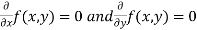 , we get the value of x and y let it be pairs of values
, we get the value of x and y let it be pairs of values 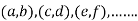
- Calculate the following values :
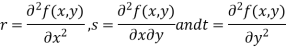
4. (a) If 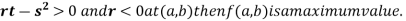
(b) If 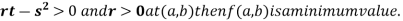
(c) If 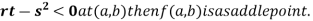
(d) If 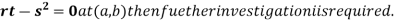
Example1 Find out the maxima and minima of the function
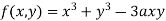
Given 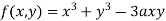 …(i)
…(i)
Partially differentiating (i) with respect to x we get
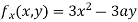 ….(ii)
….(ii)
Partially differentiating (i) with respect to y we get
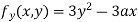 ….(iii)
….(iii)
Now, form the equations 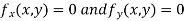
Using (ii) and (iii) we get
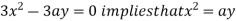
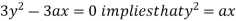
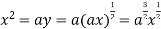 using above two equations
using above two equations
Squaring both side we get
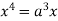
Or 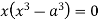
This show that 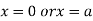
Also we get 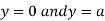
Thus we get the pair of value as 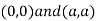
Now, we calculate


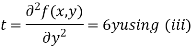
Putting above values in
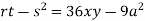
At point (0,0) we get

So, the point (0,0) is a saddle point.
At point 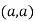 we get
we get
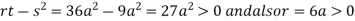
So the point 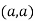 is the minimum point where
is the minimum point where 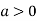
In case 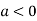
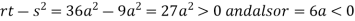
So the point 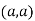 is the maximum point where
is the maximum point where 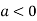
Example2 Find the maximum and minimum point of the function
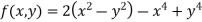
Partially differentiating given equation with respect to and x and y then equate them to zero

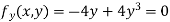
On solving above we get 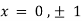
Also 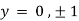
Thus we get the pair of values (0,0), (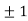 ,0) and (0,
,0) and (0,
Now, we calculate
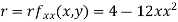
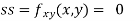
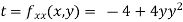
At the point (0,0)
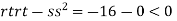
So function has saddle point at (0,0).
At the point (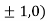

So the function has maxima at this point (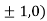 .
.
At the point (0,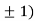
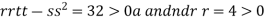
So the function has minima at this point (0,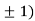 .
.
At the point (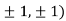
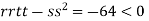
So the function has an saddle point at (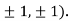
Example3 Find the maximum and minimum value of 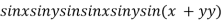
Let 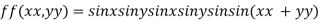
Partially differentiating given function with respect to x and y and equate it to zero
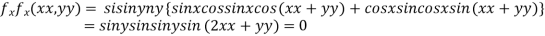 ..(i)
..(i)
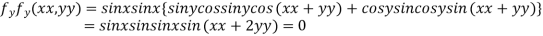 ..(ii)
..(ii)
On solving (i) and (ii) we get
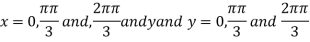
Thus pair of values are 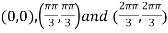
Now, we calculate
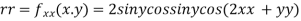

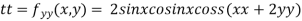
At the point (0,0)

So further investigation is required
On the x axis y = 0 , f(x,0)=0
On the line y=x, 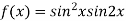
At the point 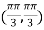
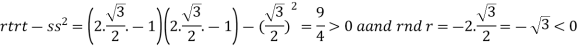
So that the given function has maximum value at 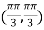
Therefore maximum value of given function
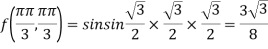
At the point 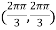
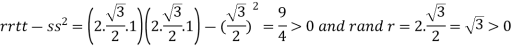
So that the given function has minimum value at 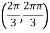
Therefore minimum value of the given function
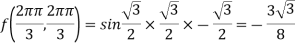
Generally to calculate the stationary value of a function with some relation by converting the given function into the least possible independent variables and then solve them. When this method fail we use Lagrange’s method.
This method is used to calculate the stationary value of a function of several variables which are all not independent but are connected by some relation.
Let 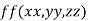 be the function in the variable x, y and z which is connected by the relation
be the function in the variable x, y and z which is connected by the relation 
Rule: a) Form the equation
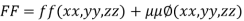
Where 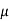 is a parameter.
is a parameter.
b) Form the equation using partial differentiation is

(We always try to eliminate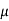 )
)
c) Solve the all above equation with the given relation 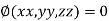
These give the value of 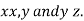
These value obtained when substituted in the given function will give the stationary value of the function.
Example1 Divide 24 into three parts such that the continued product of the first, square of second and cube of third may be maximum.
Let first number be x, second be y and third be z.
According to the question
Let the given function be f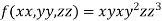
And the relation 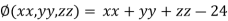
By Lagrange’s Method
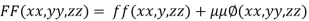
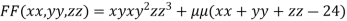 ….(i)
….(i)
Partially differentiating (i) with respect to x,y and z and equate them to zero
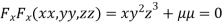 ….(ii)
….(ii)
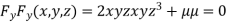 ….(iii)
….(iii)
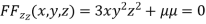 ….(iv)
….(iv)
From (ii),(iii) and (iv) we get
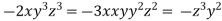
On solving
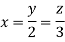
Putting it in given relation we get
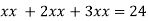
Or 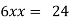
Or 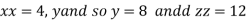
Thus the first number is 4 second is 8 and third is 12
Example2 The temperature T at any point 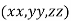 in space is
in space is  .Find the highest temperature on the surface of the unit sphere.
.Find the highest temperature on the surface of the unit sphere.
Given function is 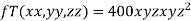
On the surface of unit sphere given 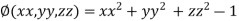 [
[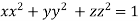 is an equation of unit sphere in 3 dimensional space]
is an equation of unit sphere in 3 dimensional space]
By Lagrange’s Method
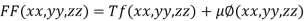
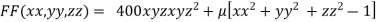 ….(i)
….(i)
Partially differentiating (i) with respect to x, y and z and equate them to zero
 or
or 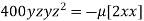 …(ii)
…(ii)
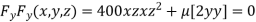 or
or 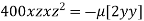 …(iii)
…(iii)
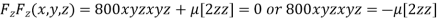 …(iv)
…(iv)
Dividing (ii) and (ii) by (iv) we get
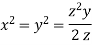
Using given relation 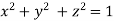
Or 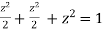
Or 
So that 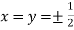
Or 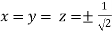
Thus points are 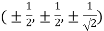
The maximum temperature is 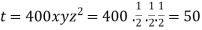
Example3 If 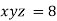 ,Find the value of x and y for which
,Find the value of x and y for which 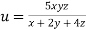 is maximum.
is maximum.
Given function is 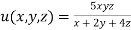
And relation is 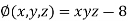
By Lagrange’s Method
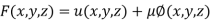
 [
[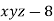 ] ..(i)
] ..(i)
Partially differentiating (i) with respect to x, y and z and equate them to zero
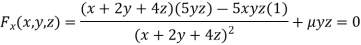
Or 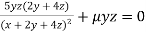 …(ii)
…(ii)
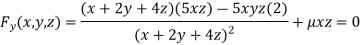
Or 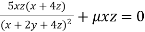 …(iii)
…(iii)
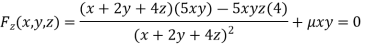
Or 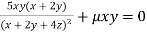 …(iv)
…(iv)
On solving (ii),(iii) and (iv) we get
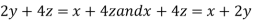
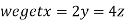
Using the given relation we get 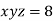
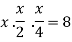
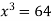
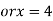
So that 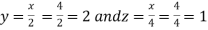
Thus the point for the maximum value of the given function is 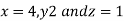
Example4 Find the points on the surface 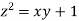 nearest to the origin.
nearest to the origin.
Let  be any point on the surface, then its distance from the origin
be any point on the surface, then its distance from the origin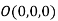 is
is
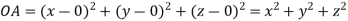
Thus the given equation will be

And relation is 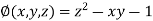
By Lagrange’s Method
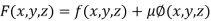
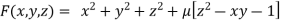 ….(i)
….(i)
Partially differentiating (i) with respect to x, y and z and equate them to zero
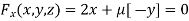
Or 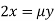 …(ii)
…(ii)
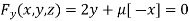
Or 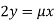 …(iii)
…(iii)
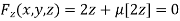
Or 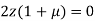
Or 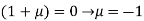
On solving equation (ii) by (iii) we get
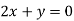
And 
On subtracting we get 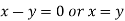
Putting in above 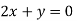
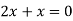
Or 
Thus 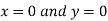
Using the given relation we get
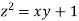 = 0.0 +1=1
= 0.0 +1=1
Or 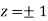
Thus point on the surface nearest to the origin is