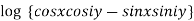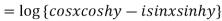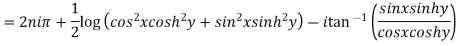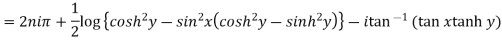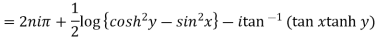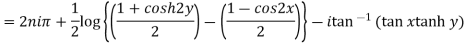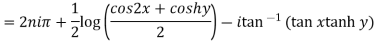UNIT 6

Complex Numbers

6.1 Cartesian & Polar forms of Complex Numbers

Basic of Complex Numbers

There is no real number x that satisfies the polynomial equation 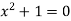. To permit the solution of this and similar equation, the set of complex number is introduced.

a)     Complex Numbers: A complex number is an ordered pair of real numbers and is of the form , where x and y are real numbers and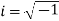

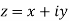
Also x is real part of z denoted by R(z) and y is the imaginary part of z denoted by I(z).

b)    Equal complex numbers: Two complex numbers are equal when there real and imaginary parts are equal i.e.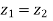if and only if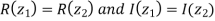

i.e. 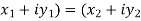 () if and only if 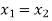and .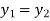

Algebra of Complex numbers

1) Addition: 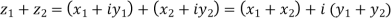i.e adding real and imaginary parts and result is again a complex number.

2) Subtraction: i.e subtracting real and imaginary parts and the result is again a complex number.

3) Multiplication: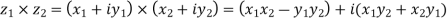

4) Quotient: 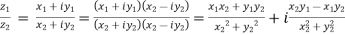The sum, difference, product and the quotient of a complex numbers are itself a complex number.

Different forms of a complex numbers:

Cartesian form of z: A complex number is an ordered pair of real numbers and is of the form , where x and y are real numbers and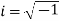

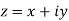
Also x is real part of z denoted by R(z) and y is the imaginary part of z denoted by I(z)

Polar form of a complex number: Every complex number z can be written in the form

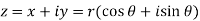
Where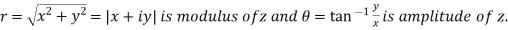

Also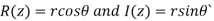

Exponential form of z: The exponential form of 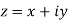is given by

Modulus of complex number: The number 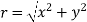 is called the modulus of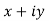denoted by 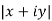or |z| or mod z .

Ex: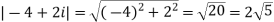

Argument of complex number: The angle is called the amplitude or argument of.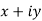

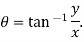
The amplitude 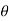has infinite number of values. For any non zero complex number z, there is only one and one value of in 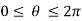The value of 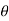which lies between 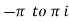s called the principle value of the amplitude.

c)     Conjugate numbers: A pair of complex numbers and 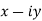are said to be conjugate to each other denoted by z and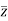

If two complex numbers are equal then so its conjugate.

Important points: If conjugate of z is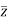  n then

1)

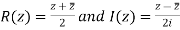
2)

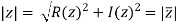
3)

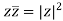
4)

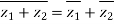
5)

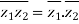
6)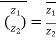where

7)

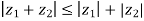
8)

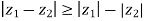
Dot and Cross Product

Let 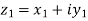and 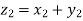be two complex numbers.

The dot product of

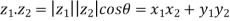
The cross product of 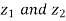is given by

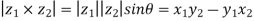
Example1: Express in the form of a + ib :

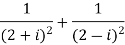
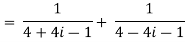
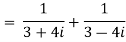
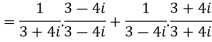
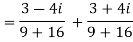
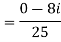
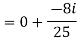
Example2: find the modulus of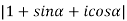

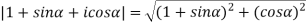
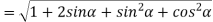
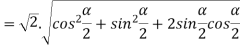
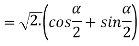
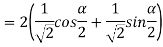
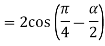
Example3: If 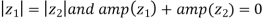then show that 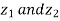are   conjugate complex numbers?

Let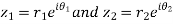

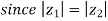
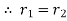
Also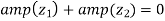

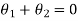
Again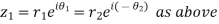

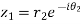
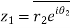
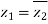
Hence both of them are conjugate to each other.

Example4: If 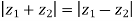, then show that the difference of the amplitude of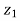and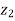

Is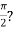

Let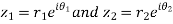

|

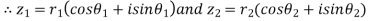
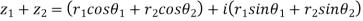
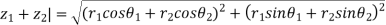
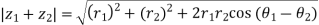
Similarly

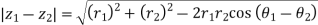
So,

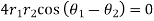
So,

Therefore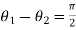

Try: If 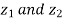be two complex numbers. Show that

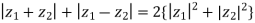
Example5:  If 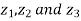be the vertices of an isosceles triangle, right angled at 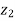, prove that

 The triangle ABC is isosceles A

BC when rotated with 90 degree coincide

With BA.

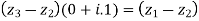
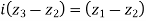
Squaring on both sides

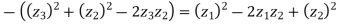
So,

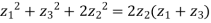
Equation of a circle in the complex plane:

The equation of the circle in the complex plane is given by

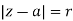
Where the center of the circle is point “a” and radius of circle is “r”.

6.2 Geometrical representation of fundamental operations on complex numbers

Geometric representation of complex numbers

With complex numbers, operations can also be represented geometrically. With the geometric representation of the complex numbers we can recognize new connections, which make it possible to solve further questions.

The complex plane (Gaussian plane)

Complex numbers are defined as numbers in the form z=a+ib or z=a+bi, where i is the imaginary part and a and b are real numbers. A complex number z is thus uniquely determined by the numbers (a,b)(a,b).

The geometric representation of complex numbers is defined as follows

A complex number z=a+ib z=a+ib is assigned the point (a,b)(a,b) in the complex plane. The complex plane is similar to the Cartesian coordinate system, it differs from that in the name of the axes.

The x-axis represents the real part of the complex number. This axis is called real axis and is labelled as Rℝ or Re

The y-axis represents the imaginary part of the complex number. This axis is called imaginary axis and is labelled with iR or Im

The origin of the coordinates is called zero point.

On the complex plane, the number 1 is a unit to the right of the zero point on the real axis and the Number ii is a unit above the zero point on the imaginary axis.

The complex numbers can be represented by points on a two-dimensional Cartesian coordinate system called the complex plane. In this way we establish a one to one correspondence between the set of all complex numbers and the set of all points in the plane. The set of all real numbers corresponds to the real axis x and the set of all purely imaginary numbers corresponds to the imaginary axis y 

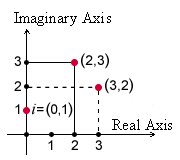
The Cartesian representation of the complex numbers specifies a unique point on the complex plane, and a given point has a unique Cartesian representation of the complex numbers.

Algebraic Operations on Complex Numbers

There can be four types of algebraic operation on complex numbers which are mentioned below. Visit the linked article to know more about these algebraic operations along with solved examples. The four operations on the complex numbers include:

• Addition
• Subtraction
• Multiplication
• Division

Roots of Complex Numbers

When we solve a quadratic equation in the form of ax2 +bx+c = 0, the roots of the equations can be determined in three forms;

• Two Distinct Real Roots
• Similar Root
• No Real roots (Complex Roots)

Complex Number Formulas

While performing the arithmetic operations of complex numbers such as addition and subtraction, combine similar terms. It means that combine the real number with the real number and imaginary number with the imaginary number.

Addition

(a + ib) + (c + id) = (a + c) + i(b + d)

Subtraction

(a + ib) – (c + id) = (a – c) + i(b – d)

Multiplication

When two complexes are multiplied by each other, the multiplication process should be similar to the multiplication of two binomials. It means that FOIL method (Distributive multiplication process) is used.

(a + ib). (c + id) = (ac – bd) + i(ad + bc)

Division

The division of two complex number can be performed by multiplying the numerator and denominator by its conjugate value of the denominator, and then applies the FOIL Method.

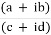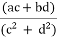=  +i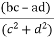

Complex Numbers Identities

Let us see some of the identities:

1. (z1 + z2)2 = (z1)2 + (z2)2 + 2 z1 × z2
2. (z1 – z2)2 = (z1)2 + (z2)2 – 2 z1 × z2
3. (z1)2 – (z2)2 =  (z1 + z2)(z1 – z2)
4. (z1 + z2)3 = (z1)3 + 3(z1)2 z2  +3(z2)2 z1 + (z2 )3
5. (z1 – z2)3 = (z1)3 – 3(z1)2 z2  +3(z2)2 z1 – (z2 )3 a

Properties of Complex Numbers

The properties of complex numbers are listed below:

• The addition of two conjugate complex numbers will result in a real number
• The multiplication of two conjugate complex number will also result in a real number
• If x and y are the real numbers and x+yi =0, then x =0 and y =0
• If p, q, r, and s are the real numbers and p+qi = r+si, then p = r, and q=s
• The complex number obeys the commutative law of addition and multiplication.

z1+z2 = z2+z1

z1. z2 = z2. z1

• The complex number obeys the associative law of addition and multiplication.

(z1+z2) +z3 = z1 + (z2+z3)

(z1.z2).z3 = z1. (z2. z3)

• The complex number obeys the distributive law

z1. (z2+z3) = z1.z2 + z1.z3

• If the sum of two complex number is real, and also the product of two complex number is also real, then these complex numbers are conjugate to each other.
• For any two complex numbers, say z1 and z2, then |z1+z2| ≤ |z1|+|z2|
• The result of the multiplication of two complex numbers and its conjugate value should result in a complex number and it should be a positive value.

Modulus and Conjugate:

Let z = a+ib be a complex number.

The Modulus of z is represented by |z|.

Mathematically, |z|=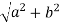

The conjugate of “z” is denoted by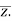 

Mathematically,

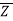= a – ib
 

Argand Plane and Polar Representation:

Similar to the XY plane, the Argand(or complex) plane is a system of rectangular coordinates in which the complex number a+ib is represented by the point whose coordinates are a and b.

We find the real and complex components in terms of r and θ, where r is the length of the vector and θ is the angle made with the real axis. Check out the detailed argand plane and polar representation of complex numbers in this article and understand this concept in a detailed way along with solved examples.

Example 1:

Problem: simplify 16 i+10i (3-i)

Solution:

Given,

16i +10i (3-i)

=16i+10i(3i)+10i(-i)

=16i+30i-10i2

=46i-10(-1)

=46i+10

Here real part is 10 and imaginary part is 46

Example 2:

Problem: express the following into a+ib form

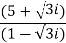
Solution:

Given.,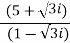  

z   =  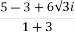    = = + i

Modulus , = = =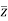 

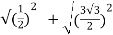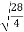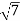
Conjugate = (  -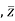 

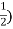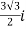
6.3 De Moivre’s theorem

If n be

(i)                A positive or negative integer then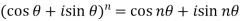

(ii)              A positive or negative fraction then one of the value of

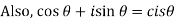
Note:

1)

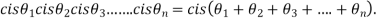
2)

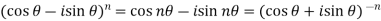
3)

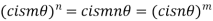
Some example based on above theorem:

1. Find the value of

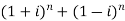
Sol:

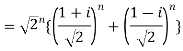
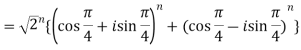
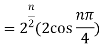
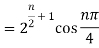
2.   Find the value of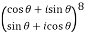

Sol: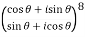  

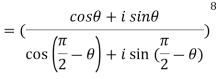
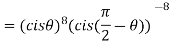
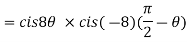
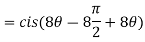
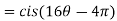
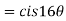
3. If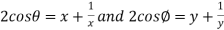

Then find out the values of : a)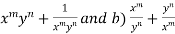

Sol: Let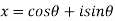

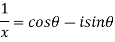
By Demoviers theorem

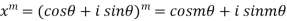
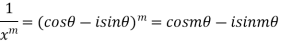
Similarly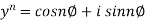

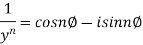
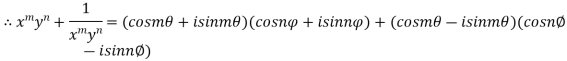
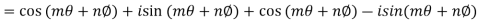
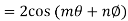
Second part is left for exercise.

4. If 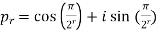,then find out the limiting value of the product series

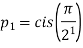
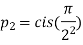
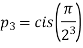
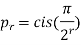
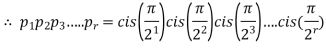
Sol: Given can be written 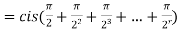as

……………….

as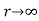

by geometric progression

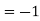
5. If p=cisx and q =cisy then show that

a)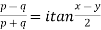

b)

a)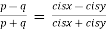   

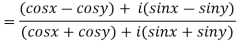
After rationalizing we get

=

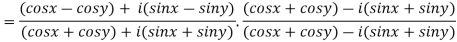
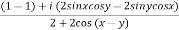
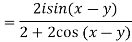
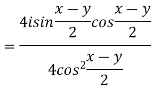
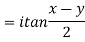
Second part is for exercise.

6. If 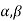are the roots of the equation .prove that

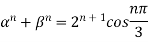
Sol: If 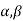are the roots of the equation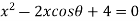

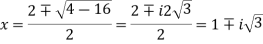
Therefore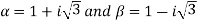

So,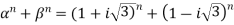

}

=

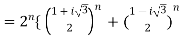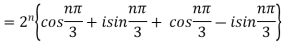
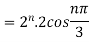
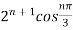
6.4 Hyperbolic functions and their inverse

If z is any real and complex numbers:

i)                   is defined as hyperbolic sine of z and is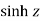

Ii) 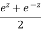                is defined as hyperbolic cosine of z and is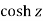

Iii) 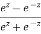             is hyperbolic tan of z and is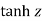

Relation between circular and hyperbolic function:

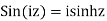
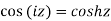
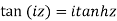
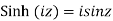
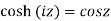
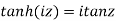
Fundamental formula of hyperbolic functions:

x =1

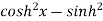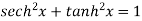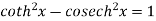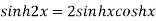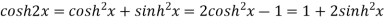
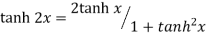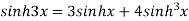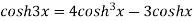Example 1: Prove that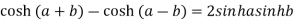

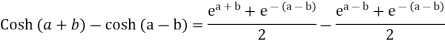
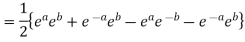
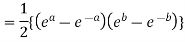
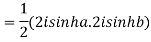
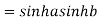
Example 2: If 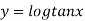,show that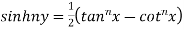

Given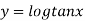

Taking exponential on both side

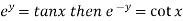
Taking nth power on both sides

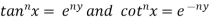
RHS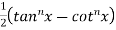  

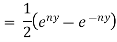
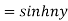
Example 3: If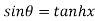 then prove that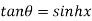

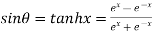……(i)

Squaring both sides

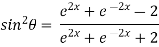
Now,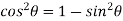

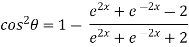
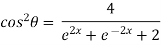
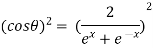
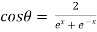……(ii)

Dividing (i) by (ii)

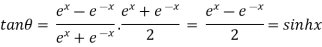
Inverse Circular functions-

If 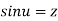,then u is called the inverse circular function of z as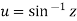 

Similarly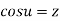 then u is inverse circular function of z as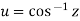

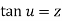then u is inverse circular function of z as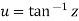

Inverse Hyperbolic functions-

If 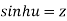, then u is called the h-yperbolic sine inverse of z as

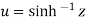
Similarly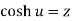 then hyperbolic cosine inverse of z is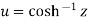

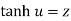then hyperbolic tan inverse of z is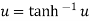

The above functions are multi valued but we consider only principal value.     

Example1 : Find the value of ?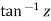

Let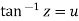

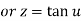
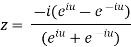
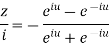
By componendo and dividendo we get

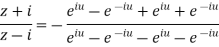
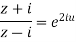
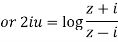
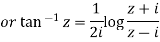
Example 2: Prove that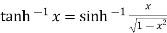

Let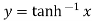

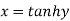
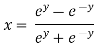
Squaring on both sides

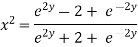
Again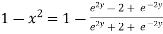   

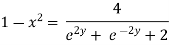
Taking square root on both side

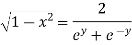
Now,

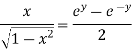
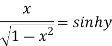
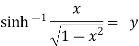
Hence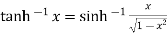 

Example 3:Prove that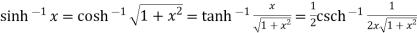

Let ….(i)

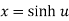
Squaring both side

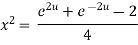
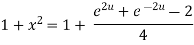
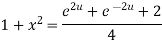
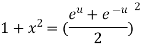
Taking square root on both side

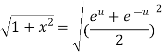
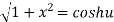
  …….(ii)

Again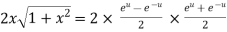  

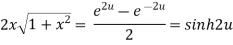
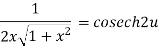
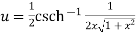……(iii)

Now,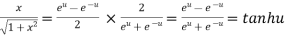 

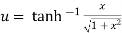   ……(iv)

From all above equation we get

6.5 Logarithm of complex number

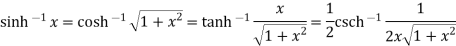
Let a + i b be a complex number whose logarithm is to be found.
Step 1: Convert the given complex number, into polar form.
Where amplitude and argument is given.
Step 2: Use Euler’s Theorem to rewrite complex number in polar form to exponential form.
There r (cos θ + isinθ) is written as rei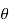. This means that
a+ib= rei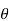
Step 3: Take logarithm of both sides we get.

Example 1:

Prove that sinlog (i-1) = 1

Solution:

Let i-1 =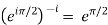

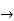log (i-1) = log (eπ/2) =

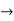Sin log (i-1) = sin (π/2) =1

Example 2:

Prove that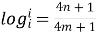

=

=

=   

=   

=   

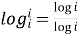
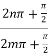
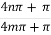
=R.H.S

6.6 Separation of real and imaginary parts

We will expand the given function in form of complex number (x+iy) and compare the real and imaginary parts of both side will give the required answer.

Example1:

Separate the real and imaginary parts of 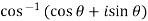and also show that the angle 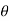is positive and acute angle?

Sol: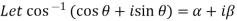  

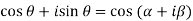
Equating real and imaginary parts we get

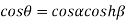…..(1)

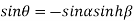….(2)

Squaring and adding (1) and (2) we get

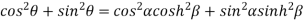
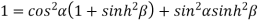
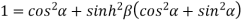
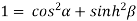
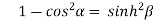
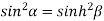…..(3)

From equation(2)

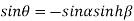
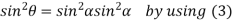
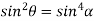
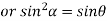
Hence is positive and acute angle.

Example 2: Separate the real and imaginary part of

Let 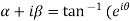)….(1)

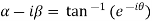…..(2)

On adding (1) and (2) we get

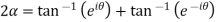
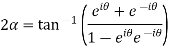
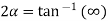
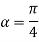
Subtracting (1) and(2) we get

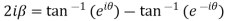
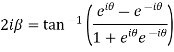
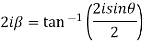
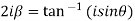
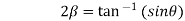
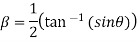
Which are the required real and imaginary parts.

Example 3:  Prove that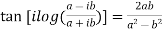

LHS :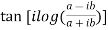

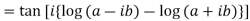
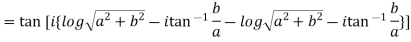
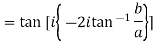
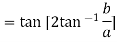
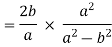
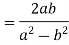
Logarithmic Function of a Complex Variable:

If 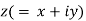and 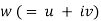be so related that 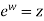, then w is said to be a logarithm of z to the base e and is written as   ….(i)

Also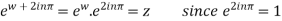   

…..(ii)

i.e. the logarithm of a complex number has an infinite number of values and is, therefore,

a multi-valued function.

The general value of the logarithm of z is written as

Thus from (i) and (ii)

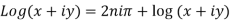
Note 1. If , then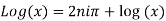

The logarithm of a real quantity is also multi-valued. Its  principal value is real while all other values are imaginary

Note 2. We know that the logarithm of a negative quantity has no real value.

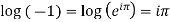
Example 1:  Find the general value of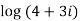

The general value is

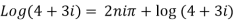
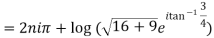
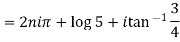
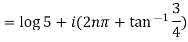
Example 2: Find the general value of 

The general value is

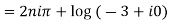
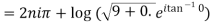
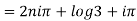
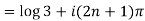
Example 3: Find the general value of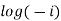

The general value is

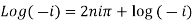
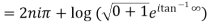
Separation of real and imaginary parts of a logarithmic function                  

1. Real and imaginary part of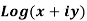

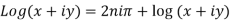
where

]

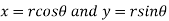
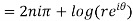
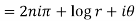
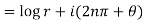
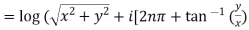Example 1: Separate the real and imaginary part of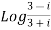

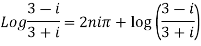
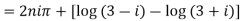
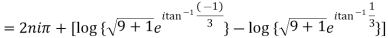
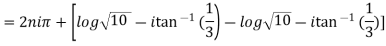
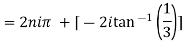
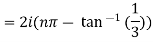
Example 2: If 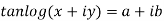where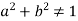 

Then Show that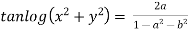

Given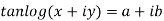

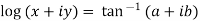
Similarly conjugate of above

On adding above two we get

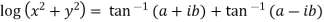
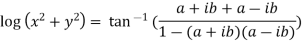
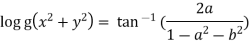
Or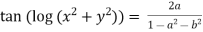   

Example 3: If 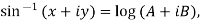show that

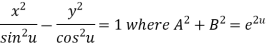
Given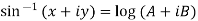  

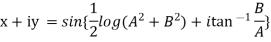
Its conjugate will be

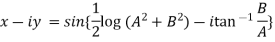
On adding above

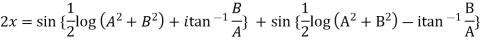
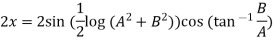
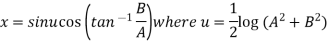
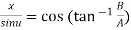     ……(i)

Similarly on Subtracting on above we get

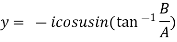
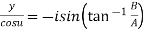     ……(ii)

Now, LHS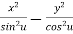  

=

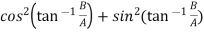
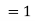
Hence proved

2.Real and Imaginary parts of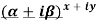

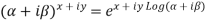
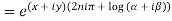
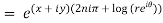  where

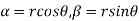
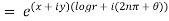
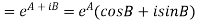
Where

Example 1:  Find the modulus and argument of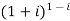

{}

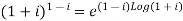
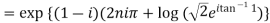
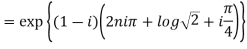
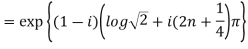
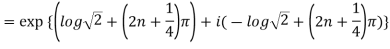
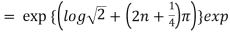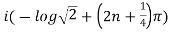Therefore modulus of 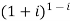 is 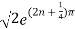  and argument is

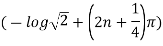
Example 3: Find all the roots of the equation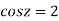

Given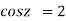

Or       

Or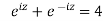

Or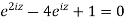  

Using formula of quadratic equation

Taking natural logarithm on both side

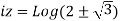
Or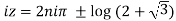

Or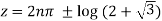 

Example 3: Separate the real and imaginary parts of

Given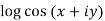

=