Unit - 2
Electron Ballistics
It is the force exerted on the charged particle q moving with velocity v through an electric field E and magnetic field B. The entire electromagnetic force F on the charged particle is called Lorentz force which is given by
F = qE + qv x B ---------------------(1)
The first term indicates electric field. The second term indicates magnetic force which has direction perpendicular to both velocity and magnetic field.
The magnetic force is proportional to q and to the magnitude of the vector cross product v × B. In terms of the angle ϕ between v and B, the magnitude of the force equals qvB sin ϕ.
If v is perpendicular to B the particle will follow circular trajectory with radius of r = mv/qB. If the angle ϕ is less than 90°, the particle orbit will be a helix with an axis parallel to the field lines.
If ϕ is zero, there will be no magnetic force on the particle, which will continue to move undeflected along the field lines.
When a conductor is placed with B field perpendicular to current, the magnetic force on both types of charge carriers is in the same direction. This force gives rise to small potential difference between the sides of the conductor.
If a wire with a current i is placed in an external magnetic field B, Since, current represents movement of charges in the wire, the Lorentz force acts on the moving charges. Because these charges are bound to the conductor, the magnetic forces on the moving charges are transferred to the wire.
The force on a small length dl of the wire depends on the orientation of the wire with respect to the field. The magnitude of the force is given by I dlB sin ϕ, where ϕ is the angle between B and dl. There is no force when ϕ = 0 or 180°, both of which correspond to a current along a direction parallel to the field. The force is at a maximum when the current and field are perpendicular to each other. The force is given by dF= idl × B.
Motion of a charged particle in the simultaneous presence of both electric and magnetic fields has variety of manifestations ranging from straight line motion to the cycloid and other complex motion. Both electric and magnetic fields impart acceleration to the charged particle. But, there is a qualification for magnetic field as acceleration due to magnetic field relates only to the change of direction of motion.
Magnetic force being always normal to the velocity of the particle tends to move the particle about a circular trajectory. On the other hand, electric force is along electric field and is capable to bring about change in both direction and magnitude depending upon the initial direction of velocity of the charged particle with respect to electric field. If velocity and electric vectors are at an angle then the particle follows a parabolic path.
One of the important orientations of electric and magnetic fields is referred as “crossed fields”. We use the term “crossed fields” to mean simultaneous presence of electric and magnetic fields at right angle. The behaviour of charged particles such as electrons under crossed fields has important significance in the study of electromagnetic measurement and application (determination of specific charge of electron, cyclotron etc.).
Before we proceed, we should understand that elementary charged particles have mass of the order of 10−28 kg or less. Therefore, even small electric or magnetic force is capable to generate very high acceleration of the order of 1012 m/s2 or more.
Charged particle is moving along parallel electric and magnetic field
The velocity, electric and magnetic vectors are in in the same direction. Let they are aligned along x-axis. Since magnetic field and velocity vectors are parallel, there is no magnetic force.
FM=v0qBsin0°=0
Where v0 is initial speed of the particle. The charged particle is, however, acted upon by electric field. It is accelerated or decelerated depending on the polarity of charge and direction of electric field.
Considering positive charge, the electric force on the charge is given as
FE=qE
The acceleration of particle carrying charge in x-direction is:
⇒ay=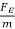 
The displacement along x-axis after time “t” is given by:
x=v0t+
ayt2
x=v0t+
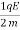t2
Charge is moving perpendicular to parallel electric and magnetic fields
Let electric and magnetic fields align along y-direction and velocity vector is aligned along positive x-direction. Let the charge be positive and initial velocity be v0.
In this case, velocity and magnetic field vectors are perpendicular to each other. Applying Right hand vector cross product rule, we determine that magnetic force is acting in positive z-direction. If electric field is not present, then the particle revolves along a circle in xz plane as shown in the figure below.
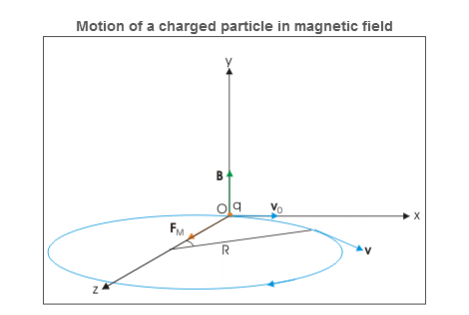
However, electric field in y-direction imparts acceleration in that direction. The particle, therefore, acquires velocity in y-direction and resulting motion is a helical motion. But since particle is accelerated in y –direction, the linear distance between consecutive circular elements of helix increases. In other words, the resulting motion is a helical motion with increasing pitch.
The radius of each of the circular element and other periodic attributes like time period, frequency and angular frequency are same as for the case of circular motion of charged particle in perpendicular to magnetic field.
R =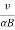 
T =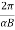 
ν=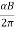 
ω=αB
Velocity of the charged particle
The velocity of the particle in xz is:
v=vxi + vzj=v0cosωt i+ vosinωt k
⇒v= v0cosωt i+ vosinωt k
= v0cos(αBt)i+v0sin(αBt)k
Where α is specific charge.
We know that magnetic force does not change the magnitude of velocity. It follows then that magnitude of velocity is xy plane is a constant given as:
v2x+v2z=vxy2
But, there is electric field in y-direction. This imparts linear acceleration to the charged particle. As such, the particle which was initially having no component in y direction gains velocity with time as electric field imparts acceleration to the particle in y direction. The velocity components in xz plane, however, remain same. The acceleration in y-direction due to electric field is:
⇒ay= 
= 
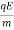=αE
Since initial velocity in y-direction is zero, the velocity after time t is:
⇒vy=ayt=αEt
The velocity of the particle at a time t, therefore, is given in terms of component velocities as :
v=vxi+ vyj+ vjk
⇒v=v0cos(αBt) i+αEt j+v0sin(αBt) k
Displacement of the charged particle
Component of displacement of the charged particle in xz plane is given as
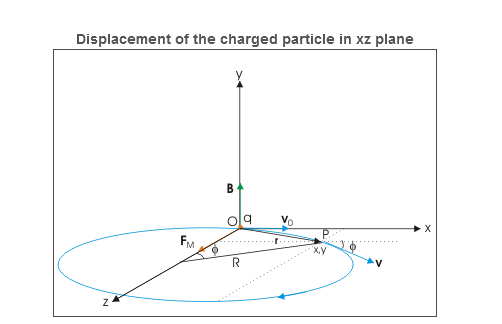
x=R sin(αBt)=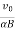 
sin(αBt)
z=R[1−cos(αBt)]=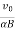 
[1−cos(αBt)]
The motion in y-direction is due to electric force. Let the displacement in this direction be y after time t. Then:
y= 
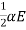ayt2 = 
t2
The position vector of the particle after time t is :
r=xi+yj+zk
⇒r=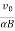
sin(αBt)i+
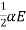t2j+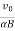
[1−cos(αBt)]k
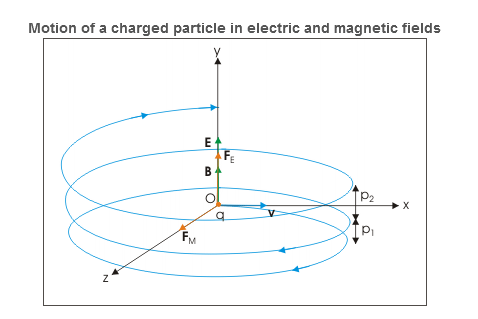
Charge is placed at rest in crossed electric and magnetic fields
Let electric and magnetic fields are aligned along z and x directions and charge is placed at the origin of coordinate system. Initially, there is no magnetic force as charge is at rest. However, there is electric force, which accelerates the charge in z-direction. As the particle acquires velocity in z-direction, the magnetic force comes into play and tries to rotate the particle in xz plane about a center on x-axis.
However, z-component of velocity keeps increasing with time due to electric force in that direction. The magnetic force though draws the charged particle away from z-axis along a curved path. This action of magnetic force is countered by electric force in z-direction. The velocity of charged particle ultimately reduces to zero at x-axis. This cycle repeats itself forming cycloid motion. The cycloid path is generated by a point on the circumference of a rolling wheel.
Motion of a charged particle in the simultaneous presence of both electric and magnetic fields has variety of manifestations ranging from straight line motion to the cycloid and other complex motion. Both electric and magnetic fields impart acceleration to the charged particle. But, there is a qualification for magnetic field as acceleration due to magnetic field relates only to the change of direction of motion. Magnetic force being always normal to the velocity of the particle tends to move the particle about a circular trajectory. On the other hand, electric force is along electric field and is capable to bring about change in both direction and magnitude depending upon the initial direction of velocity of the charged particle with respect to electric field. If velocity and electric vectors are at an angle then the particle follows a parabolic path.
One of the important orientations of electric and magnetic fields is referred as “crossed fields”. We use the term “crossed fields” to mean simultaneous presence of electric and magnetic fields at right angle. The behavior of charged particles such as electrons under crossed fields has important significance in the study of electromagnetic measurement and application (determination of specific charge of electron, cyclotron etc.).
Before we proceed, we should understand that elementary charged particles have mass of the order of 10−2810-28 kg or less. Therefore, even small electric or magnetic force is capable to generate very high acceleration of the order of 10121012 m/s2m/s2 or more. Under proper set up, these particles achieve velocity comparable to speed of light. In order to keep our discussion in the simple classical context, however, we shall confine our discussion limited to the cases which are less complicated and which neglect relativistic effects.
Some of the important applications or phenomena associated with simultaneous presence of two fields include:
- Motion of a charged particle in electric and magnetic fields
- Measurement of specific charge of an electron (J.J.Thomson experiment)
- Acceleration of charged particles (cyclotron)
In this module, we shall study first two of the listed application or phenomena. The third one i.e. cyclotron will be discussed in a separate module.
Motion of a charged particle in electric and magnetic fields
We have already studied motion of charged particle in individual fields. Here, we shall combine the effects of two fields. Few of the interesting cases are discussed here.
Charged particle is moving along parallel electric and magnetic field
The velocity, electric and magnetic vectors are in in the same direction. Let they are aligned along x-axis. Since magnetic field and velocity vectors are parallel, there is no magnetic force.
FM=v0qBsin0°=0
Where v0v0 is initial speed of the particle. The charged particle is, however, acted upon by electric field. It is accelerated or decelerated depending on the polarity of charge and direction of electric field. Considering positive charge, the electric force on the charge is given as:
FE=qEFE=qE
The acceleration of particle carrying charge in x-direction is :
⇒ay=FEm=qEm
The displacement along x-axis after time “t” is given by :
x=v0t+12ayt2
⇒x=v0t+qEt22m
Charge is moving perpendicular to parallel electric and magnetic fields
Let electric and magnetic fields align along y-direction and velocity vector is aligned along positive x-direction. Let the charge be positive and initial velocity be v0v0 .In this case, velocity and magnetic field vectors are perpendicular to each other. Applying Right hand vector cross product rule, we determine that magnetic force is acting in positive z-direction. If electric field is not present, then the particle revolves along a circle in xz plane as shown in the figure below.
Motion of a charged particle in magnetic field
Motion of a charged particle in magnetic field
However, electric field in y-direction imparts acceleration in that direction. The particle, therefore, acquires velocity in y-direction and resulting motion is a helical motion. But since particle is accelerated in y –direction, the linear distance between consecutive circular elements of helix increases. In other words, the resulting motion is a helical motion with increasing pitch.
Motion of a charged particle in electric and magnetic fields
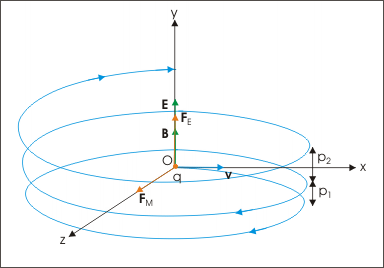
Resulting motion is a helical motion with increasing pitch.
The radius of each of the circular element and other periodic attributes like time period, frequency and angular frequency are same as for the case of circular motion of charged particle in perpendicular to magnetic field.
R=vαB;T=2παB;ν=αB/2π;ω=Αb
Velocity of the charged particle
The velocity of the particle in xz plane is :
v=vxi+vzj=v0cosωti+vosinωtk
⇒v=v0cos(αBt)i+v0sin(αBt)k
Where α is specific charge. We know that magnetic force does not change the magnitude of velocity. It follows then that magnitude of velocity is xy plane is a constant given as :
v2x+v2z=vxy2vx2+vz2=vxy2
But, there is electric field in y-direction. This imparts linear acceleration to the charged particle. As such, the particle which was initially having no component in y direction gains velocity with time as electric field imparts acceleration to the particle in y direction. The velocity components in xz plane, however, remain same. The acceleration in y-direction due to electric field is :
⇒ay=FEm=qEm=αE
Since initial velocity in y-direction is zero, the velocity after time t is :
⇒vy=ayt=αEt
The velocity of the particle at a time t, therefore, is given in terms of component velocities as
v=vxi+vyj+vjk
⇒v=v0cos(αBt)i+αEtj+v0sin(αBt)k
Displacement of the charged particle
Component of displacement of the charged particle in xz plane is given as:
Displacement of the charged particle in xz plane
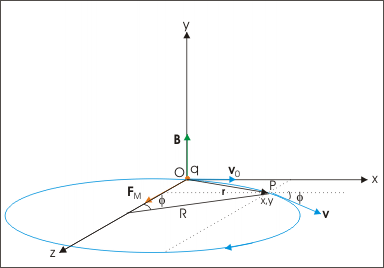
Fig. Displacement of the charged particle in xz plane
x=Rsin(αBt)=v0αBsin(αBt)
z=R[1−cos(αBt)]=v0αB[1−cos(αBt)]
The motion in y-direction is due to electric force. Let the displacement in this direction be y after time t. Then :
y=12ayt2=12αEt2
The position vector of the particle after time t is :
r=xi+yj+zk
⇒r=v0αBsin(αBt)i+12αEt2j+v0αB[1−cos(αBt)]k
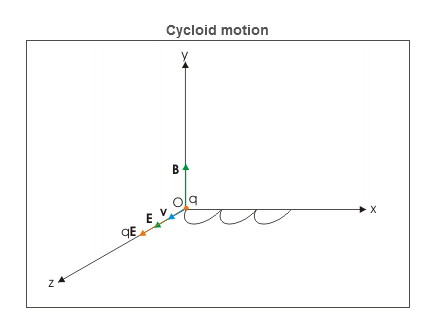
Charge is placed at rest in crossed electric and magnetic fields
Let electric and magnetic fields are aligned along z and x directions and charge is placed at the origin of coordinate system. Initially, there is no magnetic force as charge is at rest. However, there is electric force, which accelerates the charge in z-direction. As the particle acquires velocity in z-direction, the magnetic force comes into play and tries to rotate the particle in xz plane about a center on x-axis.
Cycloid motion
Fig. Cycloid motion
However, z-component of velocity keeps increasing with time due to electric force in that direction. The magnetic force though draws the charged particle away from z-axis along a curved path. This action of magnetic force is countered by electric force in z-direction. The velocity of charged particle ultimately reduces to zero at x-axis. This cycle repeats itself forming cycloid motion. The cycloid path is generated by a point on the circumference of a rolling wheel. Here, we shall skip the mathematical derivation and limit ourselves to a descriptive analysis only.
Electric field and magnetic field which are uniform and are perpendicular to each other which is called crossed electric and magnetic field. Perpendicular arrangement of both the fields are also called velocity selector. Magnetic force is countered by electric force in z-direction. Initially charge is at rest in crossed fields. Particle which is in the electric and magnetic field and the force which is acted on it is the Lorentz force. The formula for Lorentz force is:
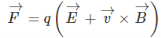
Where
F=force, q=charge, E=electric field, v=velocity, B=magnetic field, F=force
The Hall Effect further explains that when the magnetic field is perpendicular to the electric field it will result in the deflection and separation of ions in the area around us. Moving charges produce a magnetic field. If the direction of a charged particle is either parallel or anti-parallel to the field then the force is zero, and the force is maximum when charge moves perpendicular to the field. A Charged particle will get undeflected when an electric field is switched off in a region of crossed electric and magnetic field but if the magnetic field is switched off instead of electric field the particle will have initial acceleration.
Torque is the measure of how much force is acted on an object and which makes an object rotate about an axis. It is also known as pulling power and is also called moment of force about an axis. When a particle is travelling in a straight line then electric and magnetic force gets balanced. A particle will be undeflected, if it will travel with a velocity which is equals to
V=E/B.
Frequency domain multichannel filters F1(k), F2(k), ..., FN(k) can be applied to the data to produce one single output trace of the form
Y(k) = 
FN(k)Xn(k) ___(1)
In matrix form, the above expression can be written as:
Y(k) = X'(k)F(k) = S'(k) A'(k) F(k) + N'(k) F(k) ___(2)
Where F(k) is an N x 1 vector whose elements are the individual channel filters. That is,
F(k) = [F1(k), F2(k), ..., FN(k)] ___(3)
By following the procedure, an optimum filter vector F(k) can be designed to attenuate, in the least square sense, the undesired coherent interferences S1(k),S2(k),...,SM(k) while preserving the desired signal S0(k) in Y(k). This filter can be shown [1],[2] to be of the form:
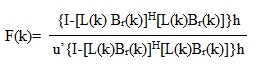
Where h is an arbitrary N x 1 nonzero vector, u = [1,0,...,0], I is the unit matrix, Br(k) is a submatrix of the matrix obtained by dropping all linearly dependent rows, and L(k) is a lower triangular matrix satisfying:
[L(k) Br(k)] [L(k) Br(k)]H = I
The multichannel processing scheme produces one dimensional output trace. A velocity filter, on the other hand, is a two-dimensional filter which produces a two-dimensional output record.
A two-dimensional record can be generated by a procedure which involves repeatedly applying multichannel optimum filters to a small number of overlapping subarrays of the input data.
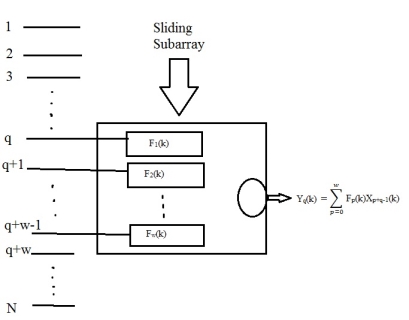
Fig. A sliding subarray of multichannel filters
More specifically, consider a subarray of W channels, where W<<N, which slides over the input data as shown in Fig. For every subarray position an optimum multichannel filter can be designed so that the undesired interferences are suppressed from its corresponding output trace. In designing this filter we use W instead of N in expression. Thus traces 1,2,...,W of the input record produce the first trace of the output record, traces K,K+1,...K+W-1 of the input record produce the Kth trace of the output record, and traces N-W+1,N-W+2,...,N of the input record produce the (N-W+1)st trace, which is the last trace, of the output record. For a large N and small W, as is typically the case in geophysical data, the output record can be viewed as comparable in dimensions to the input record. Clearly for such a scheme to work effectively W must be as small as possible; while at the same time it must be large enough to provide the necessary attenuation of the undesired signals. Note that a maximum of W-1 undesired interferences can be totally suppressed by such a scheme
Electrostatic deflection | Magnetic deflection |
1. Beam deflection angle is less. | Beam deflection angle is wider. |
2. Deflection sensitivity is independent of deflection voltage ED. | Deflection sensitivity is independent of magnetic field intensity B. |
3. Deflection sensitivity S is inversely proportional to accelerating voltage Ea. | Deflection sensitivity is inversely proportional to square root of accelerating voltage Va. |
4. S is independent of electron's parameters. | S is dependent on (elm) ratio. |
5. Deflection D (in metres) on the screen is directly proportional to the voltage applied and can be used to measure voltage. | Deflection D is directly proportional to B and is not useful for measurement purposes. |
6. For full scan display being electrostatic, less current is required from the amplifier. | Being inductive, large currents are required for full scan display. Consequently, power consumption is more, more power dissipation rendering the whole unit bulky. |
7. Speed of deflection is faster.
| Speed of deflection is slow. |
8. Minimum deflection factor (greatest sensitivity) means long plates, minimum separation, long tube, and low beam potential. | Deflection sensitivity is not so sensitive to Va, being '/. Hence magnetic tubes can provide greater brightness and resolution since higher beam energy can be attained without losing much sensitivity. |
9. Tubes become long as the deflection plates have to be long. | Shorter tubes can be built for the same display area. |
10. Deflection plates limit the scan angle. To overcome this, plates are bent or curved. | Absence of plates makes the scan angle very wide. Aberrations also are fewer with magnetic deflection. |
11. Very large bandwidths up to 350 MHz are possible, the limit being the capacitance between plates. Segmented plates are used for large bandwidth. | Bandwidth is small which is of the order of 10 kHz, on account of limitation by the inductance of the coils. TV bandwidth is less than 20 kHz. |
12. Widely used in laboratories for display, measurement, and analysis. | Mostly used as TV picture tubes, monitors, and low bandwidth applications. |
References:
- LASERS: Theory and Applications: Thyagarajan K and Ghatak A.K.
- Nanomaterials & Nanotechnologies and Design: M.F.Ashby, Paulo Ferreira and Daniel L.Schodek, Elsevier Publications.
- University Physics: Young and Freedman (Pearson Education).
- Optics: Jenkins and White (Tata Mcgraw Hill)
