Unit - 1

Laplace Transform

1.1 Definition

Let f(t) be any function of t defined for all positive values of t. Then the Laplace transform of the function f(t) is defined as-

Provided that the integral exists, here ‘s’ is the parameter that could be real or complex.

The inverse of the Laplace transform can be defined as below-

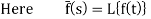
f(t) is called the inverse Laplace transform of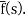

L is called the Laplace transformation operator.

Conditions for the existence of Laplace transform-

The Laplace transform of f(t) exists for s>a, if

1. f(t) is a continuous function.

2. 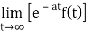is finite.

Important formulae-

1.

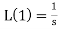
2.

3.

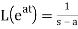
4.

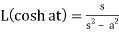
5.

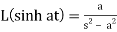
6.

7.

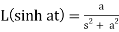
Example-1: Find the Laplace transform of the following functions-

1. Cos2 2t                           2. Sin32t

Sol. 1.

Here cos2 2t

So that we can write it as-

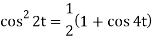
Now-

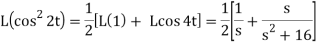
2.  Since  sin 6t = 3 sin 2t - 4 sin3 2t

Or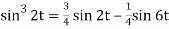      

Now-

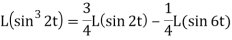
Example-2: Find the Laplace transform of (1 + cos 2t)

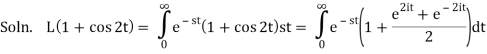
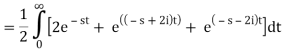
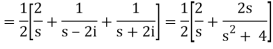
So that-

1.2 Properties (Statement only)

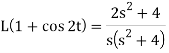
Properties and theorems of LT

1. Linearity property-

Let a and b be any two constants and f1 ,f2 any two functions of t, then-

L[a f1(t) + bf2(t)] = a L [af1(t)] + b L[af2(t)]

Proof: L[a f1(t) + bf2(t)] =

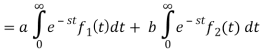
= a L [a f1(t)] + b L [ af2(t)]

Hence proved.

2. First shifting property (Theorem)- If Lf(t) = then

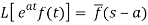
Proof: By definition-

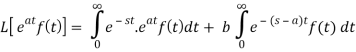
Let (s – a) = r

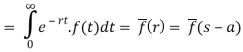
Hence proved.

We can find the following results with the help of the above theorem-

1.        

2.

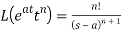
4.                  

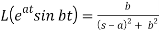
5.                           

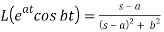
6.               

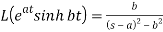
7.

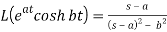
Here s>a in each case.

Example-1: Find the Laplace transform of t sin at.

Sol. Here-

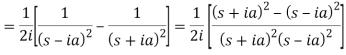
Example-2: Find the Laplace transform of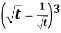        

Sol. Here-

So that-

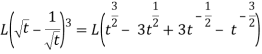
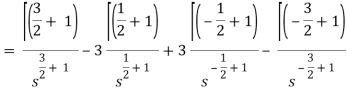
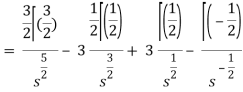
As we know that-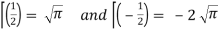   

So that-

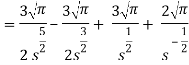
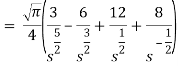
Hence-

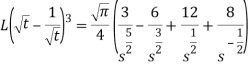
Example-3: Find the Laplace transform of the following function-

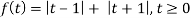
Sol. The given function f(t) can be written as-

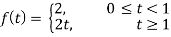
So, by definition,

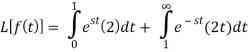
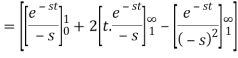
Existence theorem

The Laplace transform of f(t) exists for s>a if –

1. F(t) is continuous
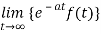2. is finite.

The above conditions are not necessary but sufficient.

Key Takeaways:

1. 
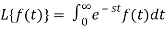
2. The inverse of the Laplace transform can be defined as below-
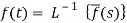
3. If 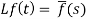then

1.3 Inverse Laplace transform using partial fraction method and properties of Laplace transform

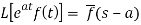
We can find the inverse Laplace transform by using partial fractions method described below-

Example: Find the Laplace inverse of-

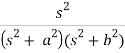
Sol.

We will convert the function into partial fractions-

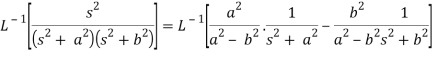
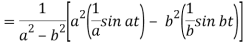
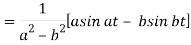
Example: Find the inverse transform of-

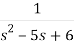
Sol.

First we will convert it into partial fractions-

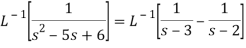
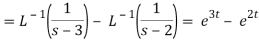
Inverse Laplace transform by convolution theorem-

According to the convolution theorem-

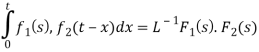
Example: Find

Sol.

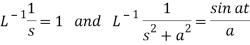
Therefore by the convolution theorem-

1.4 Convolution theorem (Statement only)

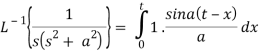
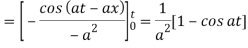
If L[f1(t)] = F1(s)   and  L[f2(t)] = F2(s)        

Then

Proof:

We have

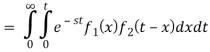
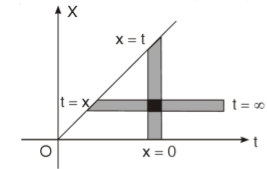
Where the double integral is taken over the infinite region in the first quadrant lying between the lines x = 0 and x = t.

If we change the order of integration, the above integrals changes to-

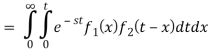
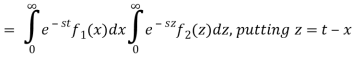
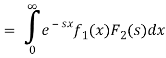
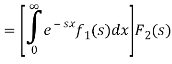
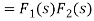
Hence proved.

Example: Apply convolution theorem to evaluate-

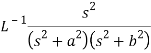
Sol.

Since

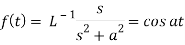
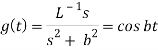
By convolution theorem, we get-

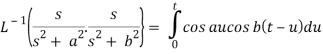
Because- f(u) = cos au, g(t-u) = cos b(t – u)

1.5 Laplace transform of periodic functions (Statement only)

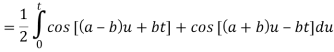
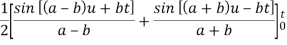
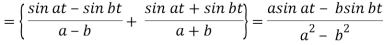
Laplace Transform of Periodic Function

If function f(t) is:

Periodic with period p > 0, so that f(t + p) = f(t), and

f1(t) is one period (i.e. one cycle) of the function, written using Unit Step functions,

Then

ℒ{f(t)} = ℒ{f1 (t)} e-sp

The Laplace Transform of the periodic function f(t) with period p, equals the Laplace Transform of one cycle of the function, divided by (1−e−sp).

Examples

Find the Laplace transforms of the periodic functions shown below:

(a)

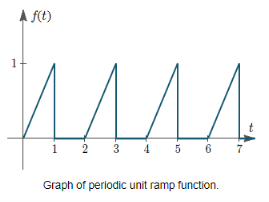
From the graph, we see that the first period is given by:

f1(t) = t . [u(t) – u(t – 1)]

And that the period is p=2.

ℒ{f1(t)}

=ℒ{t . [(u(t) – u(t – 1)]}

= ℒ {t . u(t)} - ℒ{ t . u(t – 1)}

Now

t .u(t – 1) = ( t – 1) . u(t – 1) + u(t – 1)

So

ℒ{t . u(t)} - ℒ{t . u(t – 1)}

= ℒ{t . u(t)} - ℒ{(t-1) . u(t-1) + u(t-1)}

= ℒ{t . u(t)} - ℒ{(t – 1) . u(t – 1)} - ℒ{u(t-1)}

= 1/s2 – e-s/s2 – e-s/s

= 1 – e-s – se-s/s2

Hence, the Laplace transform of the periodic function, f(t) is given by:

ℒ{f(t)} = (1 – e-s – se-s/s2)  1/1-e-2s

= 1-e-s – se-s/s2(1 – e-2s)

NUMERICALS:

1)     Let f(x) be a function and “k” be a positive real number such that:

f(x+k) + f(x) = 0                          for all x ∈ R

Prove that f(x) is periodic. Also determine its period.

Solution:

The given equation can be re-written as:

f(x+k) = - f(x) for all x ∈ R

Here, our objective is to convert RHS of the equation as f(x). For this, we need to substitute "x" such that RHS function acquires RHS function form. Replacing “x” by “x+k”, we have:

 f(x+2k) = -f(x+k)                        for all x∈R

Combining two equations,

  f(x+2k) = - 1X – f(x) = f(x)                 for all x∈R

It means that f(x) is a periodic function and its period is “2k”

2)     What is the period of function:

f(x) = 3+2 sin {(πx+2)/3}

Solution:

Rearranging, we have:

f(x) = 3+2 sin (π/3 x + 2/3)

The period of sine function is “2π”. Comparing with function form "af(bx+c)+d, magnitude of b i.e. |b| is π/3. Hence, period of the given function is:

 T’ = T/ |b| = 2π/ π/3 = 6

1.6 Unit step function and unit impulse function (Statement only)

To use the Laplace transform on a periodic function, we must first change the domain from time to Laplace. To find the Laplace transform, we must first evaluate the integral. Let's have a look at the Laplace transform of several important elementary functions.

The Unit Step Function:

We know how to write the unit step function:

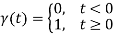
It's depicted graphically as:

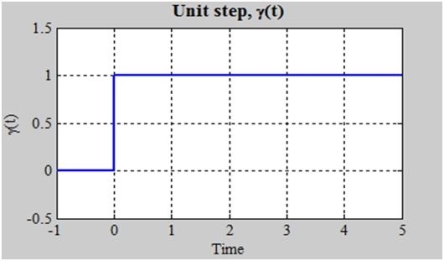
The definition of step is sometimes altered so that the bottom inequality becomes a strict inequality (t>0), leaving (0) undefined. There is also a discontinuity at t=0, but we have drawn a vertical line to make it easier to grasp and to demonstrate that the blue line represents a single function.

We'll now use the definition to obtain the Laplace transform.

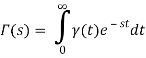
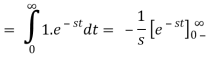
Thus,

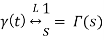
The Unit Impulse Function:

To give you a quick overview of the impulse function, it exists everywhere except at t=0, when it is infinitely huge. One is the impulse function area. On a graph, it can be represented by an arrow with a height equal to its area.

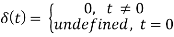
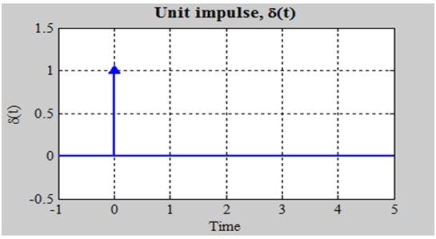
Now we'll use the following formula to find the Laplace transform:

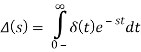
We'll apply the impulse property, which states that the impulse is 0 everywhere except at t=0, when the upper limit of the integral is 0+.

We can argue that e-st is constant from t=0– to t=0+ because it is continuous at t=0. We can now place the value of e-st at t=0.

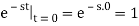
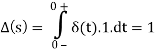
By this derivation, we get to know that Laplace transform is just one of unit impulse. This shows that the impulse is very easy to deal with in Laplace domain unlike in time domain. Unit impulse will be significant in what we do.

References:

(1) Advanced Engineering Mathematics (Wiley), Erwin Kreyzig.

(2) Higher Engineering Mathematics (Khanna Publishers), B. S. Grewal.

(3) Advanced Engineering Mathematics (S. Chand), H. K. Dass.

(4) Applied Mathematics for Engineers and Physicists, L. A. Pipes and L. R. Harville.

(5) Advanced Mathematics for Engineers, Chandrika Prasad.

(6) A text book of Engineering Mathematics (Laxmi Publication), N. P. Bali & M. Goyal.