Unit - 3
Functions of Complex Variables
A function f(x) is said to be analytic at a point Z0 if f is differentiable not only at Z0 but every point of some neighborhood at Z0.
Note-
1. A point at which the function is not differentiable is called singular point.
2. A function which is analytic everywhere is called an entire function.
3. An entire function is always analytic, differentiable and continuous function. (converse is not true)
4. Analytic function is always differentiable and continuous but converse is not true.
5. A differentiable function is always continuous but converse is not true.
The necessary condition for f(z) to be analytic-
f(z) = u + i(v) is to be analytic at all the points in a region R are-
1. 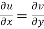 …………. (1)
…………. (1)
2. 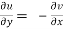 ……...…. (2)
……...…. (2)
Provided 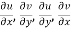 exists
exists
Equation (1) and (2) are known as Cauchy-Riemann equations.
The sufficient condition for f(z) to be analytic-
f(z) = u + i(v) is to be analytic at all the points in a region R are-
1. 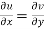 …………. (1)
…………. (1)
2. 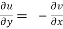 ……...…. (2)
……...…. (2)
 are continuous function of x and y in region R.
are continuous function of x and y in region R.
Important note-
1. If a function is analytic in a domain D, then u and v will satisfy Cauchy-Riemann conditions.
2. C-R conditions are necessary but not sufficient for analytic function.
3. C-R conditions are sufficient if the partial derivative are continuous.
State and prove sufficient condition for analytic functions
Statement – The sufficient condition for a function f(z) = u + iv to be analytic at all points in a region R are
1. 
2. 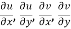 are continuous function of x and y in region R.
are continuous function of x and y in region R.
Proof:- Let f(z) be a simple valued function having  at each point in the region R. Then Cauchy-Reimann equation are satisfied by Taylor’s Theorem
at each point in the region R. Then Cauchy-Reimann equation are satisfied by Taylor’s Theorem
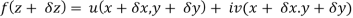
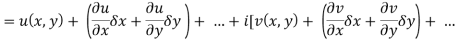
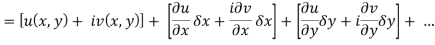
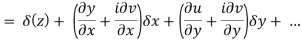
Ignoring the terms of second power and higher power
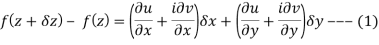
We know C-R equation
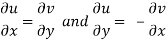
Replacing 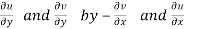
Respectively in (1) we get
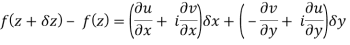
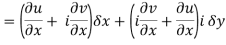
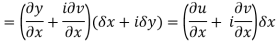
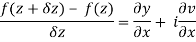
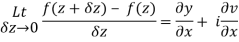
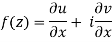
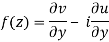
Q. Show that 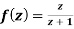 is analytic at z = ∞
is analytic at z = ∞
Ans. The function f(z) is analytic at z = ∞ if the function 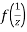 is analytic at z=0
is analytic at z=0
Since 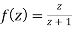
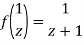
Now 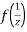 is differentiable at z=0 and at all points in its neighbourhood Hence the function
is differentiable at z=0 and at all points in its neighbourhood Hence the function  is analytic at z=0 and in turn f(z) is analytic at z = ∞
is analytic at z=0 and in turn f(z) is analytic at z = ∞
Example: If w = log z, then find 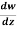 . Also determine where w is non-analytic.
. Also determine where w is non-analytic.
Sol. Here we have 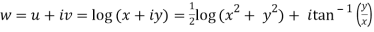
Therefore-
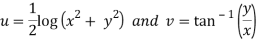
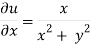
And
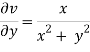 Again-
Again-
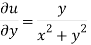
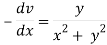
Hence the C-R conditions are satisfied also the partial derivatives are continuous except at (0 , 0).
So that w is analytic everywhere but not at z = 0
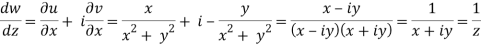
Example: Prove that the function ey(cos y + i sin y) is an analytical function.
Sol.
Let ey (cos y + i sin y) = u + iv
Let ey cos y = u and ey isin y = v
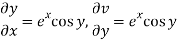
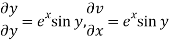
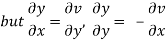
Hence C-R-Equation satisfied.
Example: Prove that 
Sol. Given that
z = f(u, v) u = x2 - y2 v = 2xy
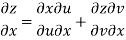
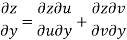
Since u = x2 - y2
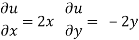
V = 2xy
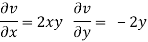
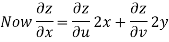
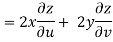
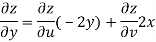
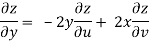
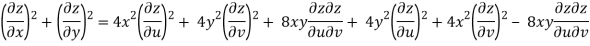
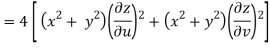
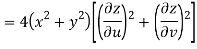
But u2 + v2 = x4 + y4 - 2x2y2 + 4x2y2
= x4 + y4 + 2x2y2
= (x2 + y2)2
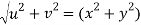
Hence 
Example: Show that polar form of C-R equations are-
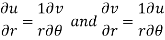
Sol. z = x + iy = reiθ
u + iv = f(z) = reiθ
U and v are expressed in terms of r and θ.
Differentiate it partially w.r.t. r and θ, we get-
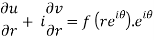
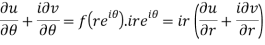
By equating real and imaginary parts, we get-
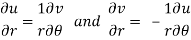
Key takeaways-
- A function f(z) is said to be analytic at a point Z0 if f is differentiable not only at Z0 but a every point of some neighborhood at Z0.
- A point at which the function is not differentiable is called singular point.
- A function which is analytic everywhere is called an entire function.
- If a function is analytic in a domain D, then u and v will satisfy Cauchy-Riemann conditions.
- C-R conditions are necessary but not sufficient for analytic function.
- C-R conditions are sufficient if the partial derivative are continuous
In Cartesian form-
Theorem; The necessary condition for a function f(z) = u +iv to be analytic at all the points in a region R are
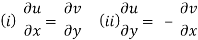
Provided,  exist
exist
Proof:
Let f(z) be an analytic function in region R.
f(z) = u + iv
f(z+δz) = (u + δu) + i(v+δv)
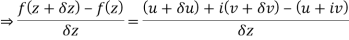
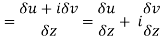
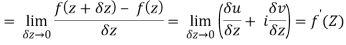
Along real axis
z = x + iy but on x - axis, y = 0
z = x δz = δx, δy = 0
Then f’(z), becomes-
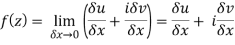
………… (1)
Along imaginary axis
z = x+iy but on y axis, x= 0
z = +iy ⇒ δx = 0, δz = i δy
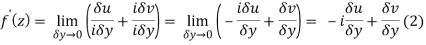
From equation (1) and (2)
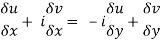
Equating real and imaginary parts
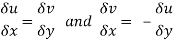
Therefore-
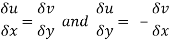
These are called Cauchy Riemann Equations.
C-R equations in polar form are-
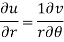
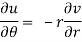
Proof:
As we know that-
x = r cosθ and u is the function of x and y
z = x + iy = r ( cos θ + i sin θ ) = reiθ
u + iv =f(z) = f(reiθ) . . . (1)
Differentiate (1) partially with respect to r, we get-
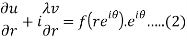
Now differentiate (1) with respect to θ, we get-
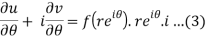
Substitute the value of  , we get-
, we get-
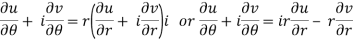
Equating real and imaginary parts, we get-
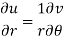
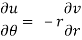
Proved
Key takeaways-
- The necessary condition for a function f(z) = u + iv to be analytic at all the points in a region R are
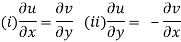
2. C-R equations in polar form are-
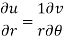
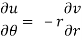
A function which satisfies the Laplace equation is known as a harmonic function.
Theorem- if f(z) = u + iv is an analytic function, then u and v are both harmonic functions.
Proof:
Suppose f(z) = u + iv, be an analytic function, then we have
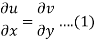
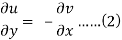
Differentiate (1) with respect to x, we get
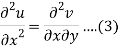
Differentiate (2) with respect to y, we get
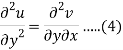
Add 3 and 4-
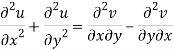
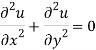
Similarly-
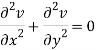
So that u and v are harmonic functions.
Example: Prove that u = x2 - y2and 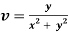 are harmonic functions of (x, y).
are harmonic functions of (x, y).
Sol.
We have u = x2 - y2
Now
u/x = 2x, 2u/x2 = 2, u/y = -2y, 2u/y2 = -2
2u/x2 +2u/y2 = 2 – 2 = 0
Here it satisfies Laplace equation so that u (x, y) is harmonic.
Now-
v = y/(x2 + y2), v/x = - 2xy/(x2 + y2)2
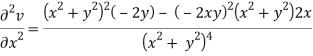
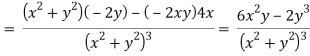
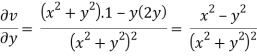
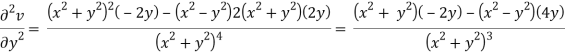
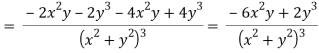
On adding the above results-
We get-
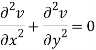
So that v(x, y) is also a harmonic function.
Example: Find the harmonic conjugate function of the function U (x, y) = 2x (1 – y).
Sol.
We have,
U(x, y) = 2x (1 – y)
Let V is the harmonic conjugate of U.
So that by total differentiation,
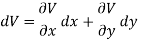
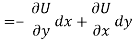
= (-2x)dx + (2-2y)dy + C
= 2xdx + (2dy - 2ydy) + C
V = x2 + 2y - y2 + C
Hence the harmonic conjugate of U is x2 + 2y - y2 + C
Milne-Thomson method is used to construct an analytic function without finding v,
The method is given below-
Since,
z = x+iy and z = x - iy
So that-
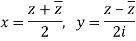
f(z) = u(x, y) + iv(x, y)
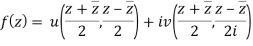
The relation above can be regarded as a formal identity in two independent variables z and 
Replacing 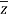 by z we get-
by z we get-
f(z) = u(z, 0) + iv(z, 0)
Condition-1 if u is given-
We have-
f(z) = u + iv
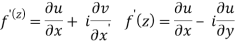
If we write -
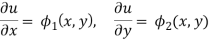
f'(z) = 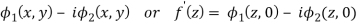
On integrating-
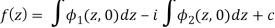
Condition-2: If v is given-
f(z) = u + iv
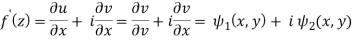
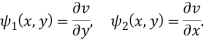
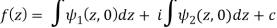
Example: If
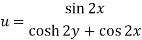
Then find f(z)
Sol.
Here-
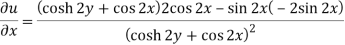
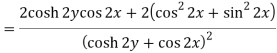
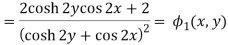
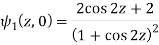
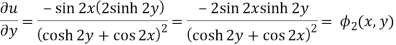
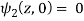
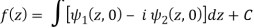
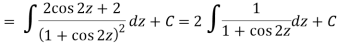
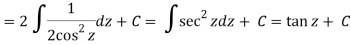
Which is the required answer.
Cauchy’s integral theorem
If a function f(z) is analytic and its derivative f’(z) continuous at all points inside and on a closed curve c, then 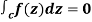
Proof: Suppose the region is R which is closed by curve c and let-
f(z) = u + iv, z= x+ iy, and dz = dx + i dy
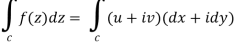
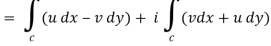
By using Green’s theorem-
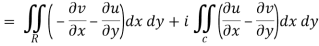
Replace 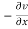 by
by 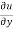 and
and  by
by 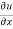
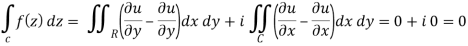
So that-
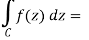
Example-1: Evaluate 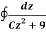 where C is |z + 3i| = 2
where C is |z + 3i| = 2
Sol.
Here we have-
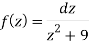
Hence the poles of f(z),
z2 + 9 = 0
Note- put determine equal to zero to find the poles.
z = ± 3i
Here pole z = -3i lies in the given circle C.
So that-
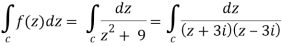
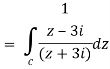
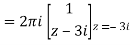
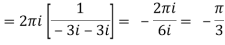
Example 2:
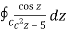 where C = |z - 3 | = 2
where C = |z - 3 | = 2
Sol.
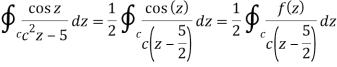
Where f(z) = cosz
 by cauchy’s integral formula
by cauchy’s integral formula
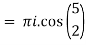
Example 3:
Solve the following by cauchy’s integral method:
Solution:
Given,
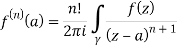
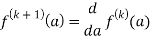
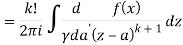
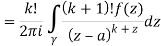
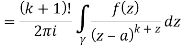
Cauchy’s integral formula-
Cauchy’s integral formula can be defined as-
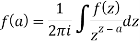
Where f(z) is analytic function within and on closed curve C, a is any point within C.
Example-1: Evaluate  by using Cauchy’s integral formula.
by using Cauchy’s integral formula.
Here c is the circle |z - 2| = 1/2
Sol. It is given that-
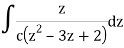
Find its poles by equating denominator equals to zero.
z2 - 3z + 2 = 0
(z - 1)(z - 2) = 0
z = 1, 2
There is one pole inside the circle, z = 2,
So that-
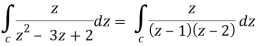
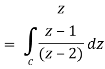
Now by using Cauchy’s integral formula, we get-
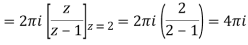
Example-2: Evaluate the integral given below by using Cauchy’s integral formula-
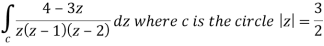
Sol. Here we have-
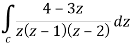
Find its poles by equating denominator equals to zero.
z(z-1)(z-2) = 0
We get-
z = 0, 1, 2
There are two poles in the circle-
Z = 0 and z = 1
So that-
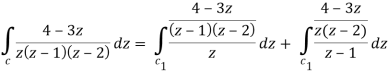
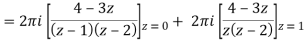
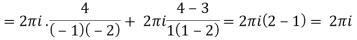
Example-3: Evaluate 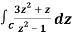 if c is circle |z - 1| = 1.
if c is circle |z - 1| = 1.
Sol. Here we have-
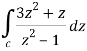
Find its poles by equating denominator equals to zero.
z2 - 1 = 0 or z2 = 1 or z = ± 1
The given circle encloses a simple pole at z = 1.
So that-
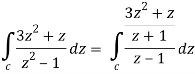
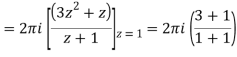
= 4πi
Taylor’s series
If f(z) is analytic inside a circle C with centre ‘a’ then for z inside C,
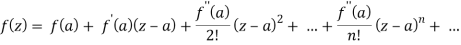
Laurent’s series-
If f(z) is analytic in the ring shaped region R bounded by two concentric circles C and C1 of radii ‘r’ and r1 where r is greater and with centre at’a’, then for all z in R
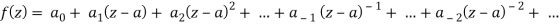
Where
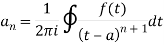
Example: using Taylor's series
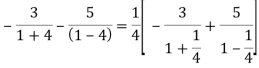
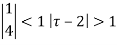
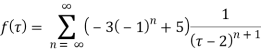
Example: Obtain the Taylor’s and Laurent’s series which represents the function 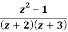 in the regions
in the regions
1) |z|<2
2) 2<|z|<3
3) |z|>3
Solution We have
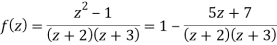
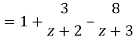
1) For |z|<2 we have
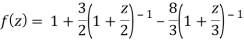
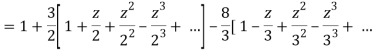
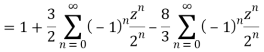
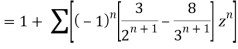
Which is Taylor’s series valid for |z|<2
2) For 2<|z|<3 we have
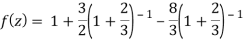
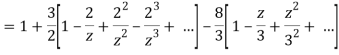
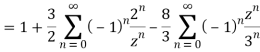
3) For |z|<3
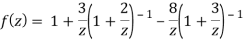
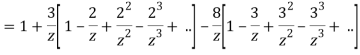
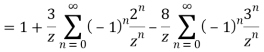
Example: Expand sin z in a Taylor’s series about z = 0.
Sol.
It is given that-
f(z) = sin z, f'(z) = cos z, f'''(z) = - sin z and so on . . .
Now-
f(0) = sin 0 = 0
f'(0) = 1
f''(0) = 0
f'''(0) = 1
We know that, Taylor’s series-
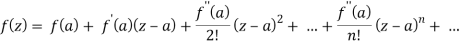
So that
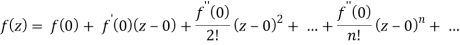
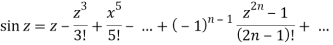
Hence
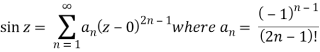
Example: Expand
f(z) = 1/ [(z - 1) (z - 2)]
In the region |z| < 1.
Sol.
By using partial fractions-
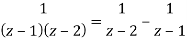
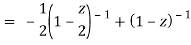
Now for |z|<1, both |z/2| and |z| are < 1,
Hence we get from second equation-
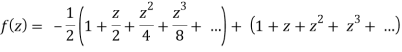
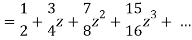
Which is a Taylor’s series.
Example: Find the Laurent’s expansion of-
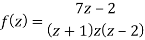
In the region 1 < z + 1< 3.
Sol.
Let z + 1 = u, we get-
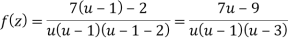
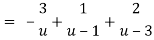
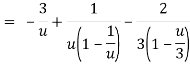
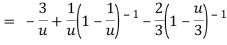
Here since 1 < u < 3 or 1/u < 1 and u/3 < 1,
Now expanding by Binomial theorem-
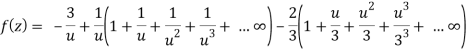
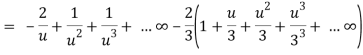
Hence
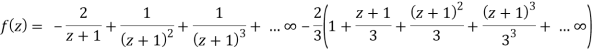
Which is valid in the region 1 < z + 1 < 3
Key takeaways-
- Taylor’s series-
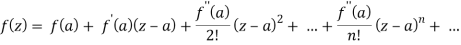
2. Laurent’s series-
f(z) = a0 + a1(z-a) + a2(z-a)2 + . . . + a-1(z-a)-1+ . . .+ a-2(z-a)-2+ . . .
Where
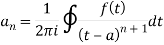
A point at which a function f(z) is not analytic is known as a singular point or singularity of the function.
Isolated singular point- If z = a is a singularity of f(z) and if there is no other singularity within a small circle surrounding the point z = a, then z = a is said to be an isolated singularity of the function f (z); otherwise it is called non-isolated.
Pole of order m- Suppose a function f(z) have an isolated singular point z = a, f(z) can be expanded in a Laurent’s series around z = a, giving
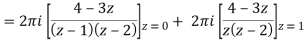
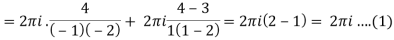
In some cases it may happen that the coefficient bm+1 = bm+2 = bm+3 = 0, then equation (1) becomes-
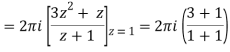
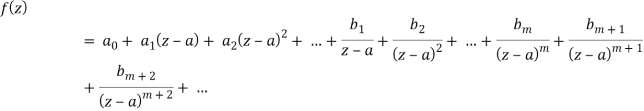
Then z = a is said to be a pole of order m of the function f(z).
Note- The pole is said to be simple pole when m = 1.
In this case-
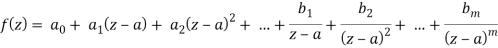
Working steps to find singularity-
Step-1: If 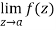 exists and it is finite then z = a is a removable singular point.
exists and it is finite then z = a is a removable singular point.
Step-2: If 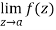 does not exists then z = a is an essential singular point.
does not exists then z = a is an essential singular point.
Step-3: If 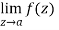 is infinite then f(z) has a pole at z = a. The order of the pole is same as the number of negative power terms in the series expansion of f(z).
is infinite then f(z) has a pole at z = a. The order of the pole is same as the number of negative power terms in the series expansion of f(z).
Example: Find the singularity of the function-
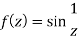
Sol.
As we know that-
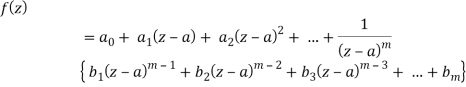
So that there is a number of singularity.
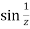 is not analytic at z = a
is not analytic at z = a
(1/z = ∞ at z = 0)
Example: Find the singularity of 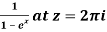
Sol.
Here we have-
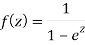
We find the poles by putting the denominator equals to zero.
That means-
1 - ez = 0
ez = 0 = (cos 2nπ + isin 2nπ) = e2nπi
z = 2nπi(n = 0, ±1, ±2 . . . )
z = 2nπi is a simple pole
Example: Determine the poles of the function-
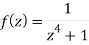
Sol.
Here we have-
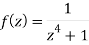
We find the poles by putting the denominator of the function equals to zero-
We get-
z4 + 1 = 0 and z4=-1
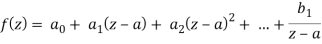
By De Moivre’s theorem-
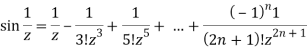
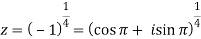
If n = 0, then pole-
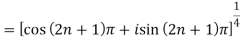
If n = 1, then pole-
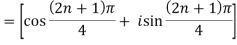
If n = 2, then pole-
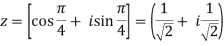
If n = 3, then pole-
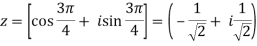
Zero of an analytic function-
The value of z is said to be zero of the analytic function f(z) when f(z) = 0.
If f(z) is analytic in the neighbourhood of z = a, then by Taylor’s theorem-
f(z) = a0 + a1(z-a) + a2(z-a)2 + a3(z-a)3 + . . . + an(z-a)n + . . . ∞
If a0= a1 = a2 . . . = an-1 = 0 but an is non-zero, then f(z) is said to have a zero of order n at z = a.
The zero is said to be simple if n = 1.
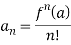
For a zero of order m at z = a,
f(a) = f'(a) = f''(a) = fn-1(a) = 0 but fn(a) ≠ 0
Thus in the neighbourhood of the zero at z = a of order n
f(z) = an (z-a)n + an+1(z-a)n+1 = (z-a)n[an+an+1(z-a)+ . . . ] = (z-a)n∅(z)
Where ∅(z) = an + an+1(z-a) + . . . Is analytic and non-zero at and in the neighbourhood of z = a.
Example: Find out the zero of the following-
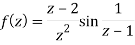
Sol. Zeroes of the function-
f(z) = 0
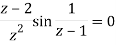
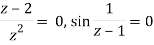
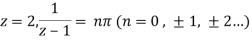
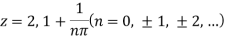
Key takeaways-
- The pole is said to be simple pole when m = 1.
- Cauchy’s residue theorem-
If f(z) is analytic in a closed curve C, except at a finite number of poles within C, then-
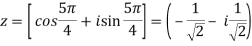
Cauchy’s residue theorem-
If f(z) is analytic in a closed curve C, except at a finite number of poles within C, then-
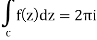
Example: Find the poles of the following functions and residue at each pole:
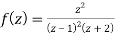 and hence evaluate-
and hence evaluate-
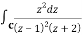 where c: |z| = 3.
where c: |z| = 3.
Sol.
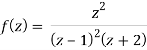
The poles of the function are-
(z-1)2(z+2) = 0 which means z = 1, 1 -2
The pole at z = 1 is of second order and the pole at z = -2 is simple-
Residue of f(z) (at z = 1)
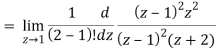
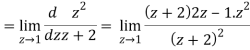
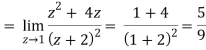
Residue of f(z) ( at z = -2)
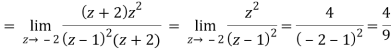
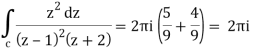
Example: Evaluate-
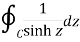
Where C is the circle |z| = 4.
Sol.
Here we have,
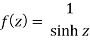
Poles are given by-
Sinh z = 0
Sin iz = 0
z = nπi where n is an integer
Out of these, the poles z = -πi , 0 and πi lie inside the circle |z| = 4.
The given function 1/sinh z is of the form 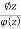
Its poles at z = a is 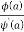
Residue (at z = -πi)
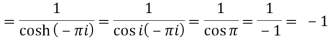
Residue (at z = 0)
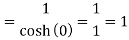
Residue (at z = πi)
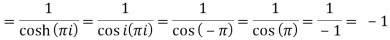
Hence the required integral is = 2πi (-1 + 1-1) = - 2πi
References:
(1) Advanced Engineering Mathematics (Wiley), Erwin Kreyzig.
(2) Higher Engineering Mathematics (Khanna Publishers), B. S. Grewal.
(3) Advanced Engineering Mathematics (S. Chand), H. K. Dass.
(4) Applied Mathematics for Engineers and Physicists, L. A. Pipes and L. R. Harville.
(5) Advanced Mathematics for Engineers, Chandrika Prasad.
(6) A text book of Engineering Mathematics (Laxmi Publication), N. P. Bali & M. Goyal.