Unit - 4

Partial Differential Equations

4.1 Partial differential equations of first order first degree i.e. Lagrange’s form

A partial differential equation (PDE) is an equation involving one or more partial derivatives of an (unknown) function, call it u, that depends on two or more variables, often time t and one or several variables in space. The order of the highest derivative is called the order of the PDE. Just as was the case for ODEs, second-order PDEs will be the most important ones in applications.

Just as for ordinary differential equations (ODEs) we say that a PDE is linear if it is of the first degree in the unknown function u and its partial derivatives. Otherwise, we call it nonlinear.

The standard methods of solving the differential equations of the following

Types:

1. Equations solvable by separation of the variables.
2. Homogeneous equations.
3. Linear equations of the first order.
4. Exact differential equations.

The differential equation of first order and first degree is namely:

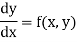
And

M(x, y)dx + N(x, y) dy = 0

Example 1. Solve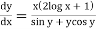

Solution. We have,

Separating the variables, we get

(sin y + y cos y) dy = {x (2 log x +1} dx

Integrating both the sides we get

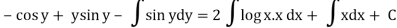
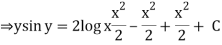
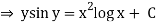
Example 2. Solve the differential equation

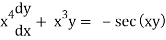
Solution.

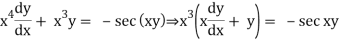
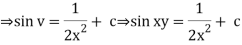
Solutions of first order linear PDEs 

Linear Equations of the First Order

A linear partial differential equation of the first order, commonly known as Lagrange’s Linear equation is of the for4m

Pp + Qq = R              (1)

Where, P, Q and R are functions of x, y, z. This equation is called a quast linear equation. When P, Q and R are independent of z it is known as linear equation.

Such asn equation is obtained by eliminating an arbitrary function ϕ from ϕ  (u, v) = 0 ....(2)

Where u,v are are some functions of x, y, z.

Differentiating (2) partially with respect to x and y

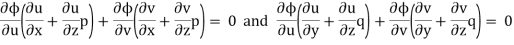
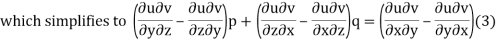
This is of the same form as (1)

Now suppose u = a and v=b, where a, b are constants, so that

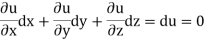
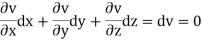
By cross multiplication we have,

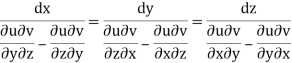
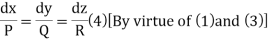
The solution of these equations are u = a and v = b

Therefore, ϕ(u, v) = 0 is the required solution of (1).

Thus, to solve the equation Pp + Qq =R.

(i) Form the subsidiary equations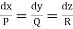                

(ii) Solve these simultaneous equations

(iii) Write the complete solution as ϕ(u, v) = 0 or u = f(v)

Example. Solve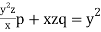

Solution. Rewriting the given equation as

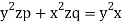
The subsidiary equations are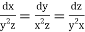               

The first two fractions give

Integrating we get 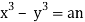(i)

Again, the first and third fraction give xdx = zdz

Integrating, we get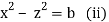

Hence from (i) and (ii), the complete solution is

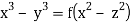
Example. Solve

Solution. Here the subsidiary equations are

Using multipliers x, y and z we get each fraction =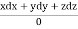

Xdx + ydy + zdz = 0 which on integration gives x2 + y2 + z2 = a    (i)

Again, using multipliers l, m and n we get each fraction

which on integration gives lx +my +nz = b (ii)

Hence from (i) and (ii) the required solution is x2 + y2 + z2 = f(lx + my + nz)

Example. Solve (x2 - y2 - z2)p + 2xyq = 2xz

Solution. Here the subsidiary equations are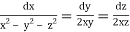

From the last two fractions, we have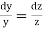

Which on integration gives log y = log z + log a or y/z=a (i)

Using multipliers x, y and z we have

Each fraction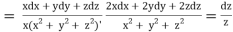

Which on integration gives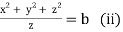

Hence from (i) and (ii) the required solution is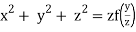

4.2 Method of separations of variables

Method of separation of variables

In this method, we assume that the dependent variable is the product of two functions, each of which involves only one of the independent variables. So to ordinary differential equations are formed.

Example 1. Using the method of separation of variables, solve

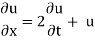
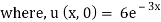
Solution.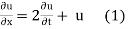 

Let, u = X(x). T (t).                     (2)

Where X is a function of x only and T is a function of t only.

Putting the value of u in (1), we get

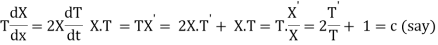
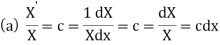
On integration log X = cx + log a = log

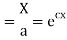
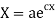
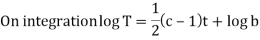
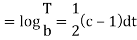
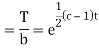
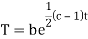
Putting the value of X and T in (2) we have

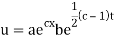
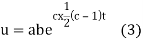
u(x, 0) = abecx

But,   u(x, 0) = 6e-3x

i.e.abecx = 6e-3x

= ab = 6 and c = - 3

Putting the value of a b and c in (3) we have

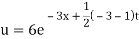
Which is the required solution.

Example 2. Use the method of separation of variables to solve the equation

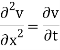
Given that v = 0 when t→∞  as well as v =0 at x = 0 and x = 1.

Solution.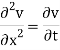
 

Let us assume that v = XT where X is a function of x only and T that of t only

Substituting these values in (1), we get

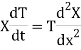
Let each side of (2) equal to a constant (-p2)

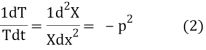
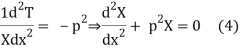
Solving (3) and (4) we have

X = C2cospx + C3 sinpx      (5)

v = C1 (C2 cospx + C3 sin px)

Putting x = 0, v = 0 in (5) we get

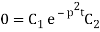
C2 = 0, since C1 ≠ 0

On putting the value of C2 in (5) we get

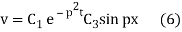
Again putting x = l, v= 0 in (6) we get

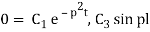
Since C3 cannot be zero.

Sinpl = 0 = sinnπ

Inputting the value of p in (6) it becomes

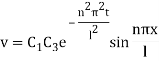
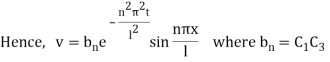
This equation satisfies the given condition for all integral values of n. Hence taking n = 1, 2, 3,… the most general solution is

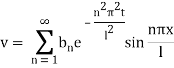
Example 3. Using the method of separation of variables, solve Where

Solution. Assume the given solution u(x, t) = X(x)T(t)

Substituting in the given equation, we have

XT = 2XT' + XT or (X' - X)T = wXT'

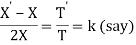
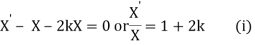
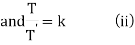
Solving (i) log X = (1+2k)x + logc or X = ce(1+2k)x

From (ii) log T = kt + log c' or T = c'ekt

Thus u(x, t) = XT = cc'e(1+2k)xekt      (iii)

Now, 6e-3x = u(x, 0) = cc'e(1+2k)x

Cc' = 6  and  1+2k = -3 or k = -2

Substituting these values in (iii) we get

u = 6e-3x e-2t i.e. u = 6e-(3x+2t)

Which is the required solution

References:

(1) Advanced Engineering Mathematics (Wiley), Erwin Kreyzig.

(2) Higher Engineering Mathematics (Khanna Publishers), B. S. Grewal.

(3) Advanced Engineering Mathematics (S. Chand), H. K. Dass.

(4) Applied Mathematics for Engineers and Physicists, L. A. Pipes and L. R. Harville.

(5) Advanced Mathematics for Engineers, Chandrika Prasad.

(6) A text book of Engineering Mathematics (Laxmi Publication), N. P. Bali & M. Goyal.