Unit - 6
Introduction to flexibility method upto two DOF
Flexibility Method or Method of Consistent Deformation:
- Flexibility method is also called as method of consistent deformation. Convert the indeterminate shape to a determinate one through disposing of a few unknown forces / assist reactions and changing them with (assumed) known / unit forces
- Using superposition, calculate the pressure that might be required to reap compatibility with the unique shape.
- This approach is relevant for any type of shape: beam, frame or truss. It is to be cited that beam and frames systems are predominantly bending (flexure) systems whilst trusses are predominantly direct pressure systems (compression) in nature. The truss individuals aren't subjected to bending. In different words, all masses are axial.
- Unknowns to be solved for are generally redundant pressure.
- The outcomes received through fixing the hassle the use of the pressure approach, are all of the unknown forces (along with reactions on the supports).
- Coefficients of the unknowns in equations to be solved are "flexibility" coefficients.
- It could be very conceptual in nature. The pressure approach turns into bulky while the Static Indeterminacy of a shape is large.
- The pressure approach (that is additionally referred to as the power approach or the approach of steady deformations) makes use of the idea of structural Static Indeterminacy (SI).
- If one is inquisitive about locating rotational or translational displacements of an indeterminate shape, they ought to be receive done by one the use of any techniques of locating displacements (Example: unit load approach, second region approach or conjugate beam approach).
Flexibility Coefficient:
The flexibility approach is primarily based totally upon the answer of "equilibrium equations and compatibility equations". There will continually be as many compatibility equations as redundant. It is referred to as the flexibility approach due to the fact flexibilities seem within side the equations of compatibility. Another call for the approach is the pressure approach due to the fact forces is the unknown portions in equations of compatibility.
Q= [DQL]+[F][Q]-compatibility equation
DQ=External displacement at redundant position
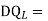Displacement at the redundant position because of applied loading
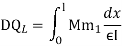
F=flexibility matrix
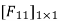
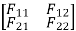
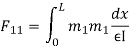
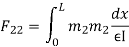
- Redundant reaction
It is also called as Force Method
In this method, horizontal displacement is neglected
Degree of indeterminacy=R-E
R=Reaction
E=Equilibrium equation
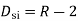
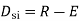
=4-2
=2
The redundant structure is 2.
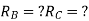
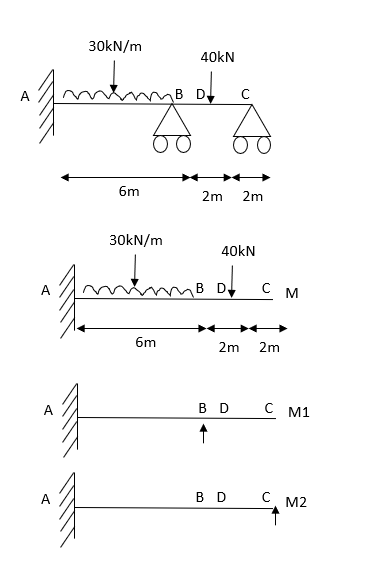
1) Use flexibility Matrix Method
Step 1)
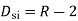
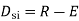
=4-2
=2
Redundant structure is 2.
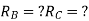
Zone | Limit | Origin | M |  |  |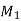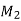
CD | 0-2 | C | 0 | 0 | x |
DB | 0-2 | D | -40 | 0 | x+2 |
BA | 0-6 | B |  | X | x+4 |
=
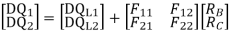
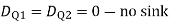
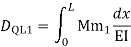
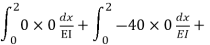
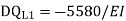
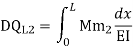
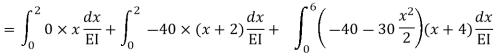
= - 11100 /EI
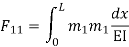
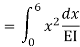
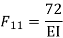
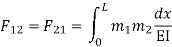
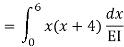
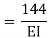
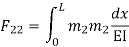
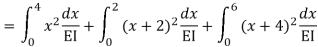
=333.33/
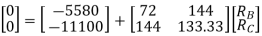
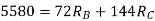
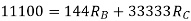
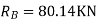
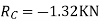
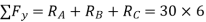
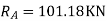
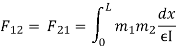
Key takeaways
1. Find degree of indeterminacy
2. Find reactions (RA, RB, & RC)
3. Flexibility method (Find F11, F12, F21& F22)
The approach is precisely relevant to a most of third degree of indeterminacy. This approach is basically an oblique software of the steady deformation approach.
This approach is primarily based totally on a mathematical similarity (i.e. analogy) among the stresses developed on a column phase subjected to eccentric load and the moments imposed on a member due to fixity of its supports.*(We have already used an analogy with inside the shape of approach of second and shear in which it became assumed that parallel chord trusses behave as a deep beam).
In the evaluation of actual engineering systems of present day times, such a lot of analogies are used like slab analogy, shell analogy &girder analogy etc. In these kinds of methods, calculations aren't made without delay at the real shape but, infect it's far usually assumed that the real shape has been changed via way of means of its mathematical version and the calculations are made at the version.
The very last consequences are associated with the real shape thru same logical engineering interpretation.
In the approach of column analogy, the real shape is taken into consideration below the movement of applied hundreds and the redundant performing simultaneously.
The load at the pinnacle of the analogous column is usually the B.M.D. Because of implemented hundreds on easy spans and consequently the response to this implemented load is the B.M.D. Because of redundant on easy spans.
Cross, has been a perennial. But the column analogy has been lost.
It merits recycling. The column analogy is largely a theorem for locating indeterminate moments in a one-span restricted beam. What is critical and beneficial approximately its miles that it applies to immediately and curved beams. It may be a completely beneficial device for figuring out flexural stiffness homes of no prismatic beams.
To recognize Cross’s soar of imagination, allow us to study the best column-analogy application. Consider a prismatic beam with constant ends over a span L. It is loaded at mid-span through a focused load P.
To remedy the problem, Cross takes us to an imagined world. In that world, the beam is represented through a segment (segment of an imagined or analogous column) with intensity L and thickness 1/EI in which E is the Young’s modulus for the fabric of the beam and I is its second of inertia.
This imaginary segment responds linearly to an imagined load represented through the angle-alternate diagram, M/EI, dispensed over the segment simply because the second, M, is dispensed over the span of a simply-supported beam.
The unit stresses on the ends, with inside the imagined world, are the moments sought:
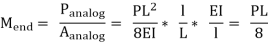
Panalog : Total load on the analogous section or (1/2)(PL/4)(L)
Aanaog : Area of analogus section or L/EI
If the load on the beam is uniform,
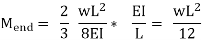
The operation is so easy that the correctness of the effects seems to be coincidence, however it is not. Plates I via V gift examples. Plate I includes the column-analogy answer for a focused load at any distance αL from one give up of a prismatic beam with constant ends. The extension of this version to a comparable beam with uniform load is defined in Plate II.
It is to be referred to that the stresses with inside the imagined international are calculated from the acquainted expression
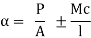
Hence the term “column analogy.” The column analogy has its best use in determining fixed end moments and stiffness’s for no prismatic beams. An application is demonstrated in Plate III.
The solution, given in Plate IV, for a focused load on a prismatic beam with one end constant and the alternative free, takes us down the rabbit-hollow to the Queen of Hearts.
Cross needs us to assume a segment which has a countless width over an infinitesimal length. The most effective thing that the observer can say is that she has visible the impossible and it works.
The utility is likewise a witness to Cross’s uncommon capacity to partner images. Beyond this it does now no longer appear smart or worthwhile to attract conclusions, though others are reputedly indicated through the data.
The vital reality is that any wide departure from the anticipated values of the moments and thrusts in a concrete arch isn't feasible until the version with inside the residences of concrete is much more than is normally supposed.
Within a slender area of uncertainty, then, the most moments and thrusts because of hundreds in a concrete arch are given without feasible query through the “geometrical” (elastic) evaluation.
The area of such uncertainty appears to have a width of about "10 consistent with cent; the area of possibly uncertainty appears to have a width of about "five consistent with cent.
The terms “real value” and “actual value,” however, are meaningless besides as carried out to a given arch beneath a given situation of loading and a given atmospheric situation; in any other case the reactions are a remember of chance.
The geometrical concept of evaluation for arch reactions seems greater reliable than the concept of flexure used to compute the fiber stresses produced through these reactions, and plenty greater reliable than the concrete itself. It isn't genuine or precise, however it's far a secure and handy manual in design.
Key Takeaways:
- The approach is precisely relevant to a most of third degree of indeterminacy. This approach is basically an oblique software of the steady deformation approach.
- The very last consequences are associated with the real shape thru same logical engineering interpretation.
- This imaginary segment responds linearly to an imagined load represented through the angle-alternate diagram, M/EI, dispensed over the segment simply because the second, M, is dispensed over the span of a simply-supported beam.
References:
1. Structural Analysis by C.S. Reddy Mc. Graw Hill
2. Structural Analysis by R.C. Hibbler Pearson Education
Unit - 6
Introduction to flexibility method upto two DOF
Unit - 6
Introduction to flexibility method upto two DOF
Flexibility Method or Method of Consistent Deformation:
- Flexibility method is also called as method of consistent deformation. Convert the indeterminate shape to a determinate one through disposing of a few unknown forces / assist reactions and changing them with (assumed) known / unit forces
- Using superposition, calculate the pressure that might be required to reap compatibility with the unique shape.
- This approach is relevant for any type of shape: beam, frame or truss. It is to be cited that beam and frames systems are predominantly bending (flexure) systems whilst trusses are predominantly direct pressure systems (compression) in nature. The truss individuals aren't subjected to bending. In different words, all masses are axial.
- Unknowns to be solved for are generally redundant pressure.
- The outcomes received through fixing the hassle the use of the pressure approach, are all of the unknown forces (along with reactions on the supports).
- Coefficients of the unknowns in equations to be solved are "flexibility" coefficients.
- It could be very conceptual in nature. The pressure approach turns into bulky while the Static Indeterminacy of a shape is large.
- The pressure approach (that is additionally referred to as the power approach or the approach of steady deformations) makes use of the idea of structural Static Indeterminacy (SI).
- If one is inquisitive about locating rotational or translational displacements of an indeterminate shape, they ought to be receive done by one the use of any techniques of locating displacements (Example: unit load approach, second region approach or conjugate beam approach).
Flexibility Coefficient:
The flexibility approach is primarily based totally upon the answer of "equilibrium equations and compatibility equations". There will continually be as many compatibility equations as redundant. It is referred to as the flexibility approach due to the fact flexibilities seem within side the equations of compatibility. Another call for the approach is the pressure approach due to the fact forces is the unknown portions in equations of compatibility.
Q= [DQL]+[F][Q]-compatibility equation
DQ=External displacement at redundant position
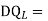Displacement at the redundant position because of applied loading
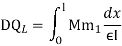
F=flexibility matrix
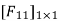
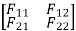
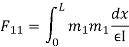
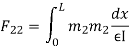
- Redundant reaction
It is also called as Force Method
In this method, horizontal displacement is neglected
Degree of indeterminacy=R-E
R=Reaction
E=Equilibrium equation
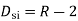
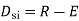
=4-2
=2
The redundant structure is 2.
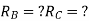
1) Use flexibility Matrix Method
Step 1)
=4-2
=2
Redundant structure is 2.
Zone | Limit | Origin | M |  |  |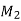
CD | 0-2 | C | 0 | 0 | x |
DB | 0-2 | D | -40 | 0 | x+2 |
BA | 0-6 | B | 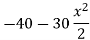 | X | x+4 |
=
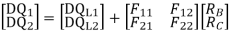
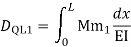
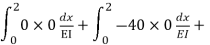
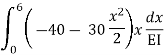
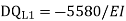
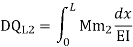
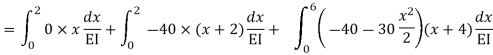
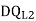= - 11100 /EI
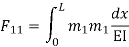
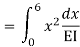
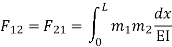
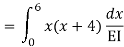
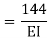
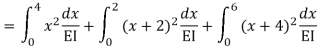
=333.33/
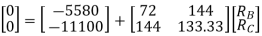
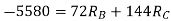
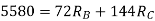
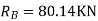
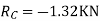
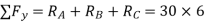
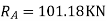
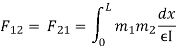
Key takeaways
1. Find degree of indeterminacy
2. Find reactions (RA, RB, & RC)
3. Flexibility method (Find F11, F12, F21& F22)
The approach is precisely relevant to a most of third degree of indeterminacy. This approach is basically an oblique software of the steady deformation approach.
This approach is primarily based totally on a mathematical similarity (i.e. analogy) among the stresses developed on a column phase subjected to eccentric load and the moments imposed on a member due to fixity of its supports.*(We have already used an analogy with inside the shape of approach of second and shear in which it became assumed that parallel chord trusses behave as a deep beam).
In the evaluation of actual engineering systems of present day times, such a lot of analogies are used like slab analogy, shell analogy &girder analogy etc. In these kinds of methods, calculations aren't made without delay at the real shape but, infect it's far usually assumed that the real shape has been changed via way of means of its mathematical version and the calculations are made at the version.
The very last consequences are associated with the real shape thru same logical engineering interpretation.
In the approach of column analogy, the real shape is taken into consideration below the movement of applied hundreds and the redundant performing simultaneously.
The load at the pinnacle of the analogous column is usually the B.M.D. Because of implemented hundreds on easy spans and consequently the response to this implemented load is the B.M.D. Because of redundant on easy spans.
Cross, has been a perennial. But the column analogy has been lost.
It merits recycling. The column analogy is largely a theorem for locating indeterminate moments in a one-span restricted beam. What is critical and beneficial approximately its miles that it applies to immediately and curved beams. It may be a completely beneficial device for figuring out flexural stiffness homes of no prismatic beams.
To recognize Cross’s soar of imagination, allow us to study the best column-analogy application. Consider a prismatic beam with constant ends over a span L. It is loaded at mid-span through a focused load P.
To remedy the problem, Cross takes us to an imagined world. In that world, the beam is represented through a segment (segment of an imagined or analogous column) with intensity L and thickness 1/EI in which E is the Young’s modulus for the fabric of the beam and I is its second of inertia.
This imaginary segment responds linearly to an imagined load represented through the angle-alternate diagram, M/EI, dispensed over the segment simply because the second, M, is dispensed over the span of a simply-supported beam.
The unit stresses on the ends, with inside the imagined world, are the moments sought:
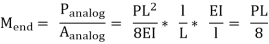
Panalog : Total load on the analogous section or (1/2)(PL/4)(L)
Aanaog : Area of analogus section or L/EI
If the load on the beam is uniform,
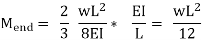
The operation is so easy that the correctness of the effects seems to be coincidence, however it is not. Plates I via V gift examples. Plate I includes the column-analogy answer for a focused load at any distance αL from one give up of a prismatic beam with constant ends. The extension of this version to a comparable beam with uniform load is defined in Plate II.
It is to be referred to that the stresses with inside the imagined international are calculated from the acquainted expression
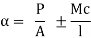
Hence the term “column analogy.” The column analogy has its best use in determining fixed end moments and stiffness’s for no prismatic beams. An application is demonstrated in Plate III.
The solution, given in Plate IV, for a focused load on a prismatic beam with one end constant and the alternative free, takes us down the rabbit-hollow to the Queen of Hearts.
Cross needs us to assume a segment which has a countless width over an infinitesimal length. The most effective thing that the observer can say is that she has visible the impossible and it works.
The utility is likewise a witness to Cross’s uncommon capacity to partner images. Beyond this it does now no longer appear smart or worthwhile to attract conclusions, though others are reputedly indicated through the data.
The vital reality is that any wide departure from the anticipated values of the moments and thrusts in a concrete arch isn't feasible until the version with inside the residences of concrete is much more than is normally supposed.
Within a slender area of uncertainty, then, the most moments and thrusts because of hundreds in a concrete arch are given without feasible query through the “geometrical” (elastic) evaluation.
The area of such uncertainty appears to have a width of about "10 consistent with cent; the area of possibly uncertainty appears to have a width of about "five consistent with cent.
The terms “real value” and “actual value,” however, are meaningless besides as carried out to a given arch beneath a given situation of loading and a given atmospheric situation; in any other case the reactions are a remember of chance.
The geometrical concept of evaluation for arch reactions seems greater reliable than the concept of flexure used to compute the fiber stresses produced through these reactions, and plenty greater reliable than the concrete itself. It isn't genuine or precise, however it's far a secure and handy manual in design.
Key Takeaways:
- The approach is precisely relevant to a most of third degree of indeterminacy. This approach is basically an oblique software of the steady deformation approach.
- The very last consequences are associated with the real shape thru same logical engineering interpretation.
- This imaginary segment responds linearly to an imagined load represented through the angle-alternate diagram, M/EI, dispensed over the segment simply because the second, M, is dispensed over the span of a simply-supported beam.
References:
1. Structural Analysis by C.S. Reddy Mc. Graw Hill
2. Structural Analysis by R.C. Hibbler Pearson Education
