Unit - 1
Laminar Flow
Laminar Flow
In laminar waft, every so often called streamline waft, the velocity, pressure, and distinct waft houses at each aspect with inside the fluid live steady. Laminar waft over a horizontal ground may be concept of as consisting of thin layers, or lamina, all parallel to each distinct. The fluid in contact with the horizontal ground is stationary, but all the distinct layers slide over each distinct.
Laminar waft in a without delay pipe may be considered due to the fact the relative motion of a set of concentric cylinders of fluid, the outside one steady at the pipe wall and the others moving at developing speeds due to the fact the center of the pipe is approached.
Laminar waft isn't unusual place simplest in times in which the waft channel is fantastically small, the fluid is moving slowly, and its viscosity is fantastically high.
Most distinct styles of fluid waft are turbulent except near strong boundaries, wherein the waft is regularly laminar, mainly in a thin layer really adjacent to the ground. See fluid mechanics.
In fluid dynamics, laminar float is characterized through fluid debris following clean paths in layers, with every layer transferring easily beyond the adjoining layers with very little mixing. At low velocities, the fluid has a tendency to float without lateral mixing, and adjoining layers slide beyond each other like gambling cards.
There aren't any cross-currents perpendicular to the path of float, nor eddies or swirls of fluids. In laminar float, the movement of the debris of the fluid could be very orderly with debris near a stable floor transferring in immediately traces parallel to that floor.
Laminar float is a float regime characterized through excessive momentum diffusion and coffee momentum convection.
When a fluid is flowing via a closed channel which include a pipe or among flat plates, both of kinds of float can also additionally arise relying on the rate and viscosity of the fluid: laminar float or turbulent float.
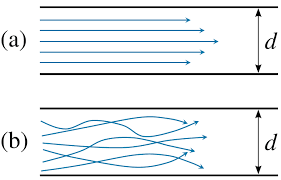
Fig: Laminar Flow
Laminar float takes place at decrease velocities, underneath a threshold at which the float will become turbulent.
The pace is decided through a dimensionless parameter characterizing the float referred to as the Reynolds number, which additionally relies upon at the viscosity and density of the fluid and dimensions of the channel.
Turbulent float is a much less orderly float regime this is characterized through eddies or small packets of fluid debris, which bring about lateral mixing. In non-medical terms, laminar float is clean, whilst turbulent float is rough.
Steady uniform laminar flow in circular pipes
A constant go with the drift is one wherein all situations at any factor in a circulate continue to be steady with admire to time. Or A constant go with the drift is the only wherein the amount of liquid flowing in line with 2nd via any section, is steady. This is the definition for an appropriate case.
True constant go with the drift is gift best in Laminar go with the drift. In turbulent go with the drift, there are persistent fluctuations in pace. Pressure additionally vary at every factor. But if this fee of alternate of strain and pace are identical on each aspects of a steady common value, the go with the drift is constant go with the drift. The actual time period use for that is suggest constant go with the drift. Steady go with the drift can be uniform or non-uniform.
In a constant diameter pipe, the pressure drops uniformly along the pipe length (except for the entrance region)
We know that average velocity through a circular pipe;
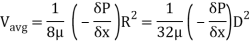
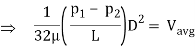
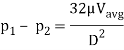
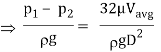
From the above expression, it is clear that hydraulic gradient is inversely proportional to D2
Velocity and shear stress distribution
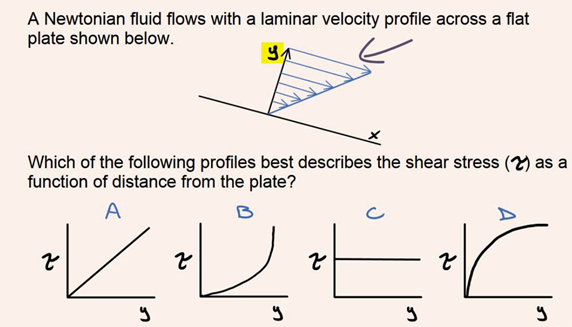
Shear strain, frequently denoted through τ (Greek: tau), is the aspect of strain coplanar with a cloth go phase. It arises from the shear pressure, the aspect of pressure vector parallel to the cloth go phase. Normal strain, on the opposite hand, arises from the pressure vector aspect perpendicular to the cloth go phase on which it acts. This dating may be exploited to degree the wall shear strain. If a sensor ought to at once degree the gradient of the speed profile on the wall, then multiplying through the dynamic viscosity could yield the shear strain.
Separation of the shear stresses at the 2 partitions for float in annular channels has been studied through numerous investigators, whose main item have been to correlate warmth switch and friction in clean annuli. The trouble has received new hobby for the reason that benefits connected with floor roughening of gas factors in nuclear reactors have been realized.
Heat switch and stress drop experiments with hard surfaces are very with no trouble made in annular geometry with a hard take a look at rod in a clean shroud. The software of such facts to hard rod clusters calls for a technique for separation of the consequences of the 2 surfaces.
A idea for this separation has been submitted through Hall, However, for software of the idea the location of the floor via which the net (time average) switch of momentum is 0 ought to be known. Hall, in addition to in advance investigators, assumed that this occurs wherein the speed gradient is 0.
The interference sample generated through sending a beam of mild via parallel slits bureaucracy a community of linearly diverging fringes that appear to originate from the aircraft of the 2 slits (see double-slit experiment). As a particle in a fluid passes via the fringes, a receiver detects the mirrored image of the perimeter sample. The sign may be processed, and understanding the perimeter angle, the peak and speed of the particle may be extrapolated.
The measured cost of wall speed gradient is impartial of the fluid houses and as a end result does now no longer require calibration. Recent improvements with inside the micro-optic fabrication technology have made it viable to apply included diffractive optical detail to manufacture diverging fringe shear strain sensors usable each in air and liquid.
Hagen Poiseuille equation
For velocities and pipe diameters above a threshold, real fluid waft isn't always laminar however turbulent, main to large stress drops than calculated with the aid of using the Hagen–Poiseuille equation.
Poiseuille's equation describes the stress drop because of the viscosity of the fluid; Other varieties of stress drops may also nonetheless arise in a fluid (see an illustration here). For instance, the stress had to force a viscous fluid up in opposition to gravity could include each that as wished in Poiseuille's regulation plus that as wished in Bernoulli's equation, such that any factor withinside the waft could have a stress more than zero (in any other case no waft could happen).
Another instance is while blood flows right into a narrower constriction, its pace might be more than in a bigger diameter (because of continuity of volumetric waft rate), and its stress might be decrease than in a bigger diameter (because of Bernoulli's equation). However, the viscosity of blood will motive extra stress drop alongside the course of waft, that's proportional to period traveled (as in step with Poiseuille's regulation). Both results make a contribution to the real stress drop.
In standard fluid-kinetics notation:
Where:
Δp is the pressure difference between the two ends,
L is the length of pipe,
μ is the dynamic viscosity,
Q is the volumetric flow rate,
R is the pipe radius,
A is the cross section of pipe.
The equation does not hold close to the pipe entrance.
Boundary Layer Theory
Laminar boundary layers may be loosely labeled consistent with their shape and the instances beneath which they're created. The skinny shear layer which develops on an oscillating frame is an instance of a Stokes boundary layer, even as the Blasius boundary layer refers back to the famous similarity answer close to an connected flat plate held in an oncoming unidirectional glide and Falkner–Skan boundary layer, a generalization of Blasius profile.
When a fluid rotates and viscous forces are balanced via way of means of the Coriolis effect (in preference to convective inertia), an Ekman layer forms. In the principle of warmth transfer, a thermal boundary layer occurs. A floor will have a couple of sorts of boundary layer simultaneously. The viscous nature of airflow reduces the nearby velocities on a floor and is chargeable for pores and skin friction. The layer of air over the wing's floor this is bogged down or stopped via way of means of viscosity, is the boundary layer. There are specific sorts of boundary layer glide: laminar and turbulent.
Laminar boundary layer glide
The laminar boundary is a totally easy glide, even as the turbulent boundary layer carries swirls or "eddies. The laminar glide creates much less pores and skin friction drag than the turbulent glide, however is much less stable. Boundary layer glide over a wing floor starts off evolved as a easy laminar glide. As the glide maintains again from the main edge, the laminar boundary layer will increase in thickness.
Turbulent boundary layer glide
At a ways again from the main edge, the easy laminar glide breaks down and transitions to a turbulent glide. From a drag standpoint, it's far recommended to have the transition from laminar to turbulent glide as a long way aft at the wing as possible, or have a big quantity of the wing floor inside the laminar part of the boundary layer. The low power laminar glide, however, has a tendency to interrupt down greater all at once than the turbulent layer.
Nominal thickness, displacement thickness
Nominal Thickness
Nominal thickness of the boundary layer is described because the thickness of sector extending from stable boundary to a degree wherein pace is 99% of the loose circulation pace (U). This is arbitrary, especially due to the fact transition from zero pace at boundary to the U outdoor the boundary takes region asymptotically. It is primarily based totally at the truth that past this boundary, impact of viscous stresses may be neglected. Many different definitions of boundary layer thickness has been delivered at distinct instances and offer vital ideas primarily based totally on mathematical calculations and logic
These definitions are
Displacement Thickness (d*)
Momentum Thickness (q)
Energy Thickness (de)
Displacement Thickness
This reasons a lower in mass float fee because of presence of boundary layer. A “pace defect” of (U-u) exists at a distance y alongside y axis. Displacement thickness can be concept of because the distance (measured perpendicular to the boundary) with which the boundary can be speculated to had been shifted such that the real float fee could be similar to that of a perfect fluid (with slip) flowing across the displaced boundary. This can be imagined in as defined in figures on subsequent page.
Momentum thickness of the boundary layer
The quantity to which this circumstance modifies the popular person of the float relies upon the price of the viscosity. If the frame is of streamlined form and if the viscosity is small without being negligible, the modifying impact seems to be restricted inside slender areas adjoining to the strong surfaces; these are known as boundary layers.
Within such layers the fluid pace adjustments hastily from 0 to its main-circulation price, and this could suggest a steep gradient of shearing stress; as a consequence, now no longer all of the viscous phrases with inside the equation of movement might be negligible, despite the fact that the viscosity, which they incorporate as a factor, is itself very small.
A greater particular criterion for the lifestyles of a well-described laminar boundary layer is that the Reynolds range must be massive, eleven though now no longer so massive as to suggest a breakdown of the laminar flow
These situations call for an endless gradient in velocity on the main side x = y = 0, which means a singularity with inside the mathematical answer there. However, the assumptions implicit with inside the boundary layer approximation damage down for the vicinity of slow float across the main side. The answer given via way of means of the boundary layer approximation isn't legitimate on the main side.
Momentum thickness is basically defined as the distance, measured perpendicular to the boundary of the solid body, by which the boundary should be displaced to compensate for the reduction in momentum of the flowing fluid on account of boundary layer formation.
Momentum thickness will be displayed by the symbol θ.
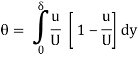Further we will go ahead to start a new topic i.e. Energy thickness in boundary layer, in the subject of fluid mechanics, with the help of our next post.
Boundary layer along a long thin plate and its characteristics
The fluid's interplay with the wall induces a no-slip boundary condition (0 speed on the wall). The waft speed then monotonically will increase above the floor till it returns to the majority waft speed. The skinny layer which include fluid whose speed has now no longer but lower back to the majority waft speed is referred to as the speed boundary layer.
The air subsequent to a human is heated ensuing in gravity-brought about convective airflow, airflow which ends up in each a speed and thermal boundary layer. A breeze disrupts the boundary layer, and hair and apparel guard it, making the human experience cooler or warmer.
On a plane wing, the speed boundary layer is the part of the waft near the wing, wherein viscous forces distort the encompassing non-viscous waft. In the Earth's atmosphere, the atmospheric boundary layer is the air layer (~ 1 km) close to the ground. It is laid low with the floor; day-night time warmth flows as a result of the solar heating the ground, moisture, or momentum switch to or from the floor.
It simplifies the equations of fluid waft with the aid of using dividing the waft area into regions: one in the boundary layer, ruled with the aid of using viscosity and developing the bulk of drag skilled with the aid of using the boundary frame; and one out of doors the boundary layer, wherein viscosity may be overlooked without widespread consequences at the This lets in a closed-shape answer for the waft in each regions with the aid of using making widespread simplifications of the overall Navier–Stokes equations.
For the case wherein there may be a temperature distinction among the floor and the majority fluid, it's far discovered that almost all of the warmth switch to and from a frame takes vicinity with inside the region of the speed boundary layer. This once more lets in the equations to be simplified with inside the waft area out of doors the boundary layer.
The stress distribution at some point of the boundary layer with inside the course regular to the floor (including an airfoil) stays tremendously consistent at some point of the boundary layer, and is similar to at the floor itself. The thickness of the speed boundary layer is typically described as the gap from the stable frame to the factor at which the viscous waft speed is 99% of the free stream speed (the floor speed of an in viscid waft)
A boundary layer is a skinny layer of viscous fluid near the stable floor of a wall in touch with a shifting flow in which (inside its thickness δ) the glide speed varies from 0 on the wall (in which the glide “sticks” to the wall due to its viscosity) as much as Ue on the boundary, which approximately (inside 1% error) corresponds to the unfastened flow speed (see Figure 1). Strictly speaking, the cost of δ is an arbitrary cost due to the fact the friction force, relying at the molecular interplay among fluid and the stable frame, decreases with the space from the wall and turns into same to 0 at infinity. Growth of a boundary layer on a flat plate.
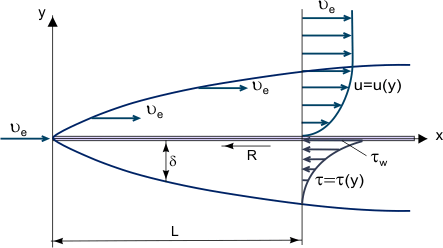
Figure 1. Growth of a boundary layer on a flat plate.
The essential idea of the boundary layer become recommended through L. Prandtl (1904), it defines the boundary layer as a layer of fluid growing in flows with very excessive Reynolds Numbers Re, this is with particularly low viscosity in comparison with inertia forces. This is found whilst our bodies are uncovered to excessive speed air flow or whilst our bodies are very massive and the air flow speed is moderate.
In this case, in a particularly skinny boundary layer, friction Shear Stress (viscous shearing force): τ = η[∂u/∂y] (in which η is the dynamic viscosity; u = u(y) – “profile” of the boundary layer longitudinal speed component, see Figure 1) can be very massive; in particular, on the wall in which u = zero and τw = η[∂u/∂y]w despite the fact that the viscosity itself can be instead It is viable to disregard friction forces outdoor the boundary layer (in comparison with inertia forces), and on the idea of Prandtl’s idea, to recollect glide regions: the boundary layer in which friction consequences are massive and the nearly Inviscid Flow core. (1)
δ/L = Re-0.5
Laminar boundary layer
A laminar boundary layer is one in which the float takes vicinity in layers, i.e., every layer slides beyond the adjoining layers. This is in comparison to Turbulent Boundary Layers proven in Fig.6.2 in which there may be an severe agitation. In a laminar boundary layer any trade of mass or momentum takes vicinity simplest among adjoining layers on a microscopic scale which isn't always seen to the eye. Consequently molecular viscosity $ mu$ is ready are expecting the shear strain associated. Laminar boundary layers are located simplest whilst the Reynolds numbers are small.
In physics and fluid mechanics, a boundary layer is the skinny layer of fluid with inside the instantaneously region of a bounding floor fashioned with the aid of using the fluid flowing alongside the floor. The fluid's interplay with the wall induces a no-slip boundary condition (0 pace on the wall). The float pace then monotonically will increase above the floor till it returns to the majority float pace. The skinny layer inclusive of fluid whose pace has now no longer but back to the majority float pace is referred to as the rate boundary layer.
The air subsequent to a human is heated ensuing in gravity-caused convective airflow, airflow which ends up in each a pace and thermal boundary layer. A breeze disrupts the boundary layer, and hair and garb shield it, making the human sense cooler or warmer.
On an plane wing, the rate boundary layer is the a part of the float near the wing, in which viscous forces distort the encircling non-viscous float. In the Earth's atmosphere, the atmospheric boundary layer is the air layer (~ 1 km) close to the ground. It is stricken by the floor; day-night time warmness flows as a result of the solar heating the ground, moisture, or momentum switch to or from the floor.
Fig: Laminar Boundary layer & Turbulent boundary layer
Turbulent boundary layer
The Earth's turbulent boundary layer, inclusive of the decrease surroundings and the top ocean, is the maximum crucial medium for human activities. The manager of optical alerts propagating in those environments is critical for meteorology, faraway sensing, free-area communications, and direct electricity applications.
Optical turbulence, i.e., the spatiotemporal fluctuations with inside the index of refraction, resulting from fluctuations with inside the thermodynamically parameters and attention of chemical substances of the medium, introduces extreme boundaries to the first-rate of those systems.
The idea of boundary layers is of significance in all of viscous fluid dynamics, aerodynamics, and additionally with inside the concept of warmth transfer. Basic traits of all laminar and turbulent boundary layers are proven with inside the growing glide over a flat plate.
Boundary layers can be both laminar, or turbulent relying at the price of the Reynolds quantity. Also right here the Reynolds quantity represents the ratio of inertia forces to viscous forces and is a handy parameter for predicting if a glide situation can be laminar or turbulent.
For decrease Reynolds numbers, the boundary layer is laminar and the stream wise speed modifications uniformly as one actions far from the wall, as proven at the left aspect of the parent. As the Reynolds quantity increases (with x) the glide will become volatile and eventually for better Reynolds numbers, the boundary layer is turbulent and the stream wise speed is characterized with the aid of using unsteady (converting with time) swirling flows in the boundary layer.
Transition might also additionally arise earlier, however it's far based specifically at the floor roughness. The turbulent boundary layer thickens greater hastily than the laminar boundary layer due to elevated shear pressure on the frame floor.
Laminar sub-layer
The laminar sub layer, additionally known as the viscous sub layer, is the location of a mainly-turbulent go with the drift this is close to a no-slip boundary and wherein the go with the drift is laminar. As such, it's miles a sort of boundary layer. The life of the laminar sub layer may be understood in that the go with the drift pace decreases in the direction of the no-slip boundary. Because of this, the Reynolds variety decreases till sooner or later the go with the drift crosses the edge from turbulent to laminar.
The laminar sub layer is vital for river-mattress ecology: underneath the laminar-turbulent interface, the go with the drift is stratified, however above it, it hastily will become well-mixed. This threshold may be vital in imparting houses and feeding grounds for benthic organisms. Whether the roughness because of the mattress sediment or different elements are smaller or large than this sub layer has a vital bearing in hydraulics and sediment transport.
Flow is described as hydraulically hard if the roughness factors are large than the laminar sub layer (thereby perturbing the go with the drift), and as hydraulically easy if they may be smaller than the laminar sub layer (and consequently ignorable via way of means of the principle frame of the go with the drift).
- Laminar sub layer is the region in the region in the turbulent boundary layer zone, adjacent to the solid surface of the plate.
- The velocity variation in this region is assumed linear as it’s a very thin layer and so that velocity gradient (du / dy) can be considered constant.
- Shear stress in laminar sub-layer
τ0 = μ (du / dy)y = 0 For linear variation du / dy = u / y
τ0 = μ (u/y)
For more help in Laminar Sub-Layer click the button below to submit your homework assignment τ μ
Separation of boundary layer on plane and curved surfaces
Boundary layers may be both laminar and turbulent. A affordable evaluation of whether or not the boundary layer might be laminar or turbulent may be made through calculating the Reynolds variety of the neighborhood glide conditions. Flow separation or boundary layer separation is the detachment of a boundary layer from a floor right into a wake.
Separation takes place in glide this is slowing down, with stress growing, after passing the thickest a part of a streamline frame or passing through a widening passage, for example. Flowing towards an growing stress is referred to as flowing in an damaging stress gradient.
The boundary layer separates while it has travelled a ways sufficient in an damaging stress gradient that the velocity of the boundary layer relative to the floor has stopped and reversed direction. The glide turns into indifferent from the floor, and as an alternative takes the types of eddies and vortices.
The fluid exerts a steady stress at the floor as soon as it has separated in place of a always growing stress if nevertheless connected. In aerodynamics, glide separation consequences in decreased elevate and expanded stress drag, due to the stress differential among the front and rear surfaces of the object. It reasons buffeting of plane systems and manipulate surfaces.
In inner passages separation reasons stalling and vibrations in equipment blading and expanded losses(decrease efficiency) in inlets and compressors.
Much attempt and studies has long past into the layout of aerodynamic and hydrodynamic floor contours and brought functions which postpone glide separation and preserve the glide connected for so long as possible. Examples consist of the fur on a tennis ball, dimples on a golfing ball, tabulators on a glider, which result in an early transition to turbulent glide; vortex mills on plane.
At the begin of the nineteenth century, after reading the notably cambered skinny wings of many one of a kind birds, Sir George Cayley designed and constructed the primary contemporary-day aerofoil, later used on a hand-released glider.
This biomimetic, notably cambered and skinny-walled layout remained the foremost aerofoil form for nearly a hundred years, especially because of the truth that the real mechanisms of elevate and drag had been now no longer understood scientifically however had been explored in an empirical fashion. One of the primary issues with those early aerofoil designs become that they skilled a phenomenon now called boundary layer separation at very low angles of attack.
This extensively restrained the quantity of elevate that would be created through the wings and supposed that larger and larger wings had been had to permit for any development in phrases of plane size. Lacking the analytical gear to take a look at this trouble, aerodynamicists persisted to propose skinny aerofoil sections, as there has been lots of proof in nature to indicate their efficacy.
The trouble become taken into consideration to be greater certainly considered one among degree, i.e. incrementally iterating the aerofoil shapes determined in nature, instead of of type, this is designing a completely new form of aerofoil in accord with essential physics.
During the pre-WWI era, the erroneous notions of designers become compounded through the ever-growing use of wind-tunnel tests. The wind tunnels used on the time had been quite small and ran at very low glide speeds. This supposed that the overall performance of the aerofoils become being examined below the situations of laminar glide (clean glide in layers, no blending perpendicular to glide direction) instead of the turbulent glide (blending of glide through small vortices) gift over the wing surfaces.
Under laminar glide situations, growing the thickness of an aerofoil will increase the quantity of skin-friction drag (as proven in final month’s post), and consequently thinner aerofoils had been taken into consideration to be superior.
Key Takeaways:
- Further we will go ahead to start a new topic i.e. Energy thickness in boundary layer, in the subject of fluid mechanics, with the help of our next post.
- The manager of optical alerts propagating in those environments is critical for meteorology, faraway sensing, free-area communications, and direct electricity applications.
General definition of drag and lift
Drag:
In fluid dynamics, drag (every so often referred to as air resistance, a kind of friction, or fluid resistance, every other kind of friction or fluid friction) is a pressure performing contrary to the relative movement of any item shifting with recognize to a surrounding fluid. This can exist among fluid layers (or surfaces) or among a fluid and a stable floor.
Unlike different resistive forces, along with dry friction, which might be almost unbiased of pace, the drag pressure relies upon on pace. Drag pressure is proportional to the speed for low-velocity waft and the squared pace for excessive velocity waft, in which the difference among low and excessive velocity is measured with the aid of using the Reynolds number.
Even aleven though the closing purpose of a drag is viscous friction, the turbulent drag is unbiased of viscosity.
Types of drag are normally divided into the subsequent categories:
Shape drag or strain drag because of the scale and form of a frame pores and skin friction drag or viscous drag because of the friction among the fluid and a floor which can be the out of doors of an item or interior along with the bore of a pipe
The impact of streamlining at the relative proportions of pores and skin friction and shape drag is proven for 2 distinct frame sections, an airfoil, that's a streamlined frame, and a cylinder, that's a bluff frame. Also proven is a flat plate illustrating the impact that orientation has at the relative proportions of pores and skin friction and strain distinction among the front and back. A frame is called bluff (or blunt) if the supply of drag is ruled with the aid of using strain forces and streamlined if the drag is ruled with the aid of using viscous forces. Road motors are bluff bodies.
Parasite drag is regularly expressed in phrases of a hypothetical (in to date as there may be no side spillage drag "equal parasite drag location" that's the location of a flat plate perpendicular to the waft. It is used for evaluating the drag of various plane.
For instance the Douglas DC-three has an equal parasite location of 23.7 sq toes and the McDonnell Douglas DC-9, with 30 years of development in plane design, a place of 20.6 sq toes even though it carried 5 instances as many passengers
Lift:
Lift is the perpendicular pressure completed with the aid of using the fluid ( Eg : air ) at the body. Lift is generated with the aid of using the aggregate of Bernoulli’s precept and Newton’s 0.33 regulation. Pressure distinction among the top floor vicinity and decrease floor vicinity of an aerofoil.
Upward ahead pressure appearing at the wing because of the response of downward backward waft. (Downward and backward waft of air from the pinnacle floor of wing creates a downwash, this downwash meets the waft from the lowest of the wing on the trailing edge, making use of Newton’s 0. 33 regulation to response of this downward backward waft consequences in a upward ahead pressure on a wing.) Lift is perpendicular to relative airflow or flight route or drag.
There are styles of elevate: Positive elevate (acts upward) Negative elevate ( acts downward ) If we take into account an aeroplane that have advantageous elevate.
Some of the situations to preserve consistent elevate while the altitude will increase density decreases, so that you can preserve consistent elevate pace ought to be multiplied.
At constant altitude if pace is multiplied or reduced, to preserve a consistent elevate attitude of assault must be reduced or multiplied (adjusted).
When altitude is multiplied density decreases, if genuine air pace is stored consistent the quantity of air flowing over the wing decreases and subsequently elevate decreases.
If the indicated air pace is stored consistent and attitude of assault additionally stored consistent, planes despite the fact that they may be flying at one-of-a-kind altitude will produce identical elevate.
The governing equation for lift
L = ( 1 /2 ) ρ V2 S CL
Where
CL = coefficient of lift ( no units )
ρ = Density of air ( kg / m3 )
V2 = Velocity of airplane ( TRUE AIR SPEED of plane ) ( m/s ) => ( m/s )2 => (m2/s2)
S = surface area of wing ( m2 )
In the above equation the term [( 1 /2 ) ρ V2 ] is called Indicated Air Speed ( IAS ) or Dynamic Pressure.
TAS = RAS + 2% of RAS/1000feet
(RAS/1000feet => RAS per 1000 feet)
TAS = True Air Speed
RAS = Rectified air speed or Calibrated air speed
Coefficient of lift depends on camber and Angle of attack.
Camber ( depending on the air craft design ) | Speed ( obtained ) | Lift ( obtained ) |
High camber | Low speed | High lift |
Low camber | High sped | Low lift |
Flow past plates
When fluid flows beyond an immersed frame, a skinny boundary layer might be evolved close to the strong frame because of the no-slip condition (i.e., fluid is caught to the strong boundary). The waft may be handled as in viscid waft outdoor of this boundary layer, whilst viscous outcomes are critical internal of this boundary layer.
Take waft beyond a flat plate for example. The traits of waft beyond a flat plate with finite duration L concern to exceptional Reynolds numbers (Re = ρUL/μ) are proven with inside the figures. At a low Reynolds quantity (Re = 0.1), the presence of the flat plate is felt in a noticeably massive location wherein the viscous outcomes are critical.
At a mild Reynolds quantity (Re = 10), the viscous layer location turns into smaller. Viscous outcomes are most effective critical internal of this location, and streamlines are deflected as fluid enters it. As the Reynolds quantity is accelerated further (Re = 107), most effective a skinny boundary layer develops close to the flat plate, and the fluid bureaucracy a slender wake location at the back of the flat plate.
Hence, the waft may be taken into consideration as in viscid waft anywhere besides the boundary layer location. Now recall waft beyond an endless lengthy flat plate with negligible thickness. In this case, the Reynolds quantity is described the use of the neighborhood distance x (i.e., the gap from the main area alongside the flat plate because the feature duration). The neighborhood Reynolds quantity is then given by
Rex=ρUx/μ
As the fluid flows past the long flat plate, the flow will become turbulent at a critical distance xcr downstream from the leading edge
Cylinders and spheres
In mathematics, capacity waft round a round cylinder is a classical answer for the waft of an in viscid, incompressible fluid round a cylinder this is transverse to the waft. Far from the cylinder, the waft is unidirectional and uniform. The waft has no vorticity and hence the speed discipline is irrational and may be modeled as a capacity waft. Unlike a actual fluid, this answer suggests a internet 0 drag at the body, a end result referred to as d'Alembert's paradox.
Laplace's equation is linear, and is one of the maximum simple partial differential equations. This easy equation yields the complete answer for each V and p due to the constraint of irrationality and incompressibility.
Having acquired the answer for V and p, the consistency of the stress gradient with the accelerations may be noted. The dynamic stress on the upstream stagnation factor has cost of 1 / 2 ρU2.
A cost had to slow down the unfastened move waft of pace U. This identical cost seems on the downstream stagnation factor, this excessive stress is once more had to slow down the waft to 0 pace. This symmetry arises most effective due to the fact the waft is absolutely frictionless. The low stress on facets at the cylinder is wanted to offer the centripetal acceleration of the waft:
It does now no longer serve our functions to write down out the Navier–Stokes equation in complete detail. Suffice it to mention that it's far a vector partial differential equation.
(By that I imply that the pressure and acceleration phrases are vectors, now no longer scalars, and the diverse phrases contain partial derivatives, which might be smooth to recognize if you already realize approximately differentiation.) The unmarried vector equation can simply as well be written as 3 scalar equations, one for every of the 3 coordinate directions
The Navier–Stokes equation is notoriously tough to remedy in a given go with the drift trouble to acquire spatial distributions of velocities and pressures and shear stresses. Basically the motives are that the acceleration time period is nonlinear, that means that it entails merchandise of partial derivatives, and the viscous-pressure time period consists of 2d derivatives, this is, derivatives of derivatives.
But numerical answers of the total Navier–Stokes equation are possible for a miles wider range of go with the drift problems, now that computer systems are so powerful. At very low Reynolds numbers, Re
Drag on sphere
1 Steady go with the drift beyond a stable sphere is essential in lots of situations, each in the herbal surroundings and with inside the global of technology, and it serves as a good reference case for extension to extra complex situations, regarding unsteady flows and/or no uniform flows and/or no spherical bodies.
It is likewise an excellent start line for improvement of some of essential ideas and techniques which can be important for later improvement in those notes. In particular, I desire to be capable of persuade you of the significance and application of cautious dimensional reasoning approximately flows of fluids.
2 You can assume in phrases of fluid flowing beyond a desk bound sphere, or of a sphere transferring via desk bound fluid. The instances are almost, however now no longer quite, equivalent. And with inside the latter case you can consider the sector being moved via the fluid in 3 unique ways: mounted to a inflexible strut, or towed with a bendy line, or pulled downward via the fluid below its very own weight.
For now, don't worry approximately those distinctions; simply view the fluid from the standpoint of the sector. I will go back to the variations in brief later. For the sake of definiteness, expect right here that the sector is towed or driven via nonetheless fluid. All this is stated right here approximately the go with the drift is then in regards to some extent constant relative to the transferring sphere.
3 Just from issues of area and motion, it's far clean that the coming near fluid should each circulate quicker and be displaced laterally because it flows beyond the sector. On the opposite hand, the no-slip circumstance calls for that the fluid pace be 0 anywhere on the floor of the sector; this means the existence of gradients ( this is, spatial quotes of change) of pace, very sharp below some conditions, at and close to the floor of the sector.
These pace gradients produce a shear strain at the floor of the sector; see Equation 1.8. When summed over the floor, the shear strain exerted via way of means of the fluid on the sector represents the part of the whole drag pressure on the sector known as the viscous drag.
Your instinct in all likelihood tells you (successfully on this case) that the strain of the fluid, the regular pressure consistent with unit area, is extra at the front of the sector than on the back. The sum of the strain forces over the complete floor of the sector represents the opposite a part of the drag pressure, known as the strain drag or shape drag. You will see later that the relative significance of viscous drag and strain drag, in addition to the qualitative go with the drift styles and the gap out into the fluid the sphere makes its presence felt, are substantially unique in unique degrees of go with the drift.
Cylinder and flat plate
Boundary layer separation upstream of cylinders installed regular to a flat plate results in the formation of horseshoe vortices across the bases of those cylinders, which may be both laminar and turbulent, relying upon the country of the upstream boundary layer. Therefore, a factor of 0 shear stress (on the separation position) and a factor of most shear stress (below the primary vortex) exists upstream of such cylinders.
Data from some of experimental and theoretical investigations of low Mach wide variety laminar and turbulent vortex structures are used with inside the derivation of those formulae. As the fluid flows beyond the lengthy flat plate, the glide turns into turbulent at a crucial distance xcr downstream from the main edge. For glide beyond a flat plate, the transition from laminar to turbulent starts off evolved whilst the crucial Reynolds wide variety (Rexcr) reaches 5×105. The boundary layer modifications from laminar to turbulent at this factor.
The idea of a boundary layer became delivered and formulated with the aid of using Prandtl for steady, two-dimensional laminar glide beyond a flat plate the use of the Navier-Stokes equations.
Prandtl's student, Blasius, became capable of resolve those equations analytically for massive Reynolds wide variety flows. The info of the derivation are ignored for simplicity, and the consequences are summarized here. Based on Blasius' analytical solutions, the boundary layer thickness (δ) for the laminar vicinity is given with the aid of using
Based on Blasius' analytical solutions, the boundary layer thickness (δ) for the laminar region is given by
Where δ is defined as the boundary layer thickness in which the velocity is 99% of the free stream velocity (i.e., y = δ, u = 0.99U).
The wall shear stress is determined by
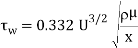
If this shear stress is integrated over the surface of the plate areas, the drag coefficient for laminar flow can be obtained for the flat plate with finite length as
If the flow is turbulent, then the equations for boundary layer and drag coefficient is
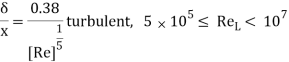
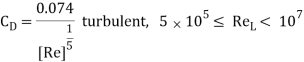
Key Takeaways:
- This easy equation yields the complete answer for each V and p due to the constraint of irrationality and incompressibility.
- It does now no longer serve our functions to write down out the Navier–Stokes equation in complete detail. Suffice it to mention that it's far a vector partial differential equation.
- All this is stated right here approximately the go with the drift is then in regards to some extent constant relative to the transferring sphere.
References:
1. Hydraulics & Fluid Mechanics- Dr.Modi& Dr. Seth
2. Fluid Mechanics-Streeter & Wylie
3. Fluid Mechanics- Dr. A.K.Jain
4. Fluid Mechanics through problems- Garde
5. Theory and applications of Fluid Mechanics- K. Subramanya
6. Foundation of Fluid Mechanics-Yuan
7. Flow through open channel – K.G.Rangaraju
Unit - 1
Laminar Flow
Laminar Flow
In laminar waft, every so often called streamline waft, the velocity, pressure, and distinct waft houses at each aspect with inside the fluid live steady. Laminar waft over a horizontal ground may be concept of as consisting of thin layers, or lamina, all parallel to each distinct. The fluid in contact with the horizontal ground is stationary, but all the distinct layers slide over each distinct.
Laminar waft in a without delay pipe may be considered due to the fact the relative motion of a set of concentric cylinders of fluid, the outside one steady at the pipe wall and the others moving at developing speeds due to the fact the center of the pipe is approached.
Laminar waft isn't unusual place simplest in times in which the waft channel is fantastically small, the fluid is moving slowly, and its viscosity is fantastically high.
Most distinct styles of fluid waft are turbulent except near strong boundaries, wherein the waft is regularly laminar, mainly in a thin layer really adjacent to the ground. See fluid mechanics.
In fluid dynamics, laminar float is characterized through fluid debris following clean paths in layers, with every layer transferring easily beyond the adjoining layers with very little mixing. At low velocities, the fluid has a tendency to float without lateral mixing, and adjoining layers slide beyond each other like gambling cards.
There aren't any cross-currents perpendicular to the path of float, nor eddies or swirls of fluids. In laminar float, the movement of the debris of the fluid could be very orderly with debris near a stable floor transferring in immediately traces parallel to that floor.
Laminar float is a float regime characterized through excessive momentum diffusion and coffee momentum convection.
When a fluid is flowing via a closed channel which include a pipe or among flat plates, both of kinds of float can also additionally arise relying on the rate and viscosity of the fluid: laminar float or turbulent float.
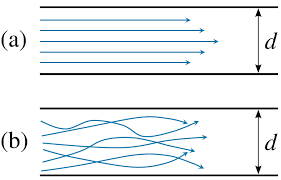
Fig: Laminar Flow
Laminar float takes place at decrease velocities, underneath a threshold at which the float will become turbulent.
The pace is decided through a dimensionless parameter characterizing the float referred to as the Reynolds number, which additionally relies upon at the viscosity and density of the fluid and dimensions of the channel.
Turbulent float is a much less orderly float regime this is characterized through eddies or small packets of fluid debris, which bring about lateral mixing. In non-medical terms, laminar float is clean, whilst turbulent float is rough.
Steady uniform laminar flow in circular pipes
A constant go with the drift is one wherein all situations at any factor in a circulate continue to be steady with admire to time. Or A constant go with the drift is the only wherein the amount of liquid flowing in line with 2nd via any section, is steady. This is the definition for an appropriate case.
True constant go with the drift is gift best in Laminar go with the drift. In turbulent go with the drift, there are persistent fluctuations in pace. Pressure additionally vary at every factor. But if this fee of alternate of strain and pace are identical on each aspects of a steady common value, the go with the drift is constant go with the drift. The actual time period use for that is suggest constant go with the drift. Steady go with the drift can be uniform or non-uniform.
In a constant diameter pipe, the pressure drops uniformly along the pipe length (except for the entrance region)
We know that average velocity through a circular pipe;
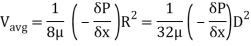
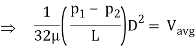
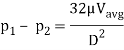
From the above expression, it is clear that hydraulic gradient is inversely proportional to D2
Velocity and shear stress distribution
Shear strain, frequently denoted through τ (Greek: tau), is the aspect of strain coplanar with a cloth go phase. It arises from the shear pressure, the aspect of pressure vector parallel to the cloth go phase. Normal strain, on the opposite hand, arises from the pressure vector aspect perpendicular to the cloth go phase on which it acts. This dating may be exploited to degree the wall shear strain. If a sensor ought to at once degree the gradient of the speed profile on the wall, then multiplying through the dynamic viscosity could yield the shear strain.
Separation of the shear stresses at the 2 partitions for float in annular channels has been studied through numerous investigators, whose main item have been to correlate warmth switch and friction in clean annuli. The trouble has received new hobby for the reason that benefits connected with floor roughening of gas factors in nuclear reactors have been realized.
Heat switch and stress drop experiments with hard surfaces are very with no trouble made in annular geometry with a hard take a look at rod in a clean shroud. The software of such facts to hard rod clusters calls for a technique for separation of the consequences of the 2 surfaces.
A idea for this separation has been submitted through Hall, However, for software of the idea the location of the floor via which the net (time average) switch of momentum is 0 ought to be known. Hall, in addition to in advance investigators, assumed that this occurs wherein the speed gradient is 0.
The interference sample generated through sending a beam of mild via parallel slits bureaucracy a community of linearly diverging fringes that appear to originate from the aircraft of the 2 slits (see double-slit experiment). As a particle in a fluid passes via the fringes, a receiver detects the mirrored image of the perimeter sample. The sign may be processed, and understanding the perimeter angle, the peak and speed of the particle may be extrapolated.
The measured cost of wall speed gradient is impartial of the fluid houses and as a end result does now no longer require calibration. Recent improvements with inside the micro-optic fabrication technology have made it viable to apply included diffractive optical detail to manufacture diverging fringe shear strain sensors usable each in air and liquid.
Hagen Poiseuille equation
For velocities and pipe diameters above a threshold, real fluid waft isn't always laminar however turbulent, main to large stress drops than calculated with the aid of using the Hagen–Poiseuille equation.
Poiseuille's equation describes the stress drop because of the viscosity of the fluid; Other varieties of stress drops may also nonetheless arise in a fluid (see an illustration here). For instance, the stress had to force a viscous fluid up in opposition to gravity could include each that as wished in Poiseuille's regulation plus that as wished in Bernoulli's equation, such that any factor withinside the waft could have a stress more than zero (in any other case no waft could happen).
Another instance is while blood flows right into a narrower constriction, its pace might be more than in a bigger diameter (because of continuity of volumetric waft rate), and its stress might be decrease than in a bigger diameter (because of Bernoulli's equation). However, the viscosity of blood will motive extra stress drop alongside the course of waft, that's proportional to period traveled (as in step with Poiseuille's regulation). Both results make a contribution to the real stress drop.
In standard fluid-kinetics notation:
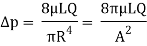
Where:
Δp is the pressure difference between the two ends,
L is the length of pipe,
μ is the dynamic viscosity,
Q is the volumetric flow rate,
R is the pipe radius,
A is the cross section of pipe.
The equation does not hold close to the pipe entrance.
Boundary Layer Theory
Laminar boundary layers may be loosely labeled consistent with their shape and the instances beneath which they're created. The skinny shear layer which develops on an oscillating frame is an instance of a Stokes boundary layer, even as the Blasius boundary layer refers back to the famous similarity answer close to an connected flat plate held in an oncoming unidirectional glide and Falkner–Skan boundary layer, a generalization of Blasius profile.
When a fluid rotates and viscous forces are balanced via way of means of the Coriolis effect (in preference to convective inertia), an Ekman layer forms. In the principle of warmth transfer, a thermal boundary layer occurs. A floor will have a couple of sorts of boundary layer simultaneously. The viscous nature of airflow reduces the nearby velocities on a floor and is chargeable for pores and skin friction. The layer of air over the wing's floor this is bogged down or stopped via way of means of viscosity, is the boundary layer. There are specific sorts of boundary layer glide: laminar and turbulent.
Laminar boundary layer glide
The laminar boundary is a totally easy glide, even as the turbulent boundary layer carries swirls or "eddies. The laminar glide creates much less pores and skin friction drag than the turbulent glide, however is much less stable. Boundary layer glide over a wing floor starts off evolved as a easy laminar glide. As the glide maintains again from the main edge, the laminar boundary layer will increase in thickness.
Turbulent boundary layer glide
At a ways again from the main edge, the easy laminar glide breaks down and transitions to a turbulent glide. From a drag standpoint, it's far recommended to have the transition from laminar to turbulent glide as a long way aft at the wing as possible, or have a big quantity of the wing floor inside the laminar part of the boundary layer. The low power laminar glide, however, has a tendency to interrupt down greater all at once than the turbulent layer.
Nominal thickness, displacement thickness
Nominal Thickness
Nominal thickness of the boundary layer is described because the thickness of sector extending from stable boundary to a degree wherein pace is 99% of the loose circulation pace (U). This is arbitrary, especially due to the fact transition from zero pace at boundary to the U outdoor the boundary takes region asymptotically. It is primarily based totally at the truth that past this boundary, impact of viscous stresses may be neglected. Many different definitions of boundary layer thickness has been delivered at distinct instances and offer vital ideas primarily based totally on mathematical calculations and logic
These definitions are
Displacement Thickness (d*)
Momentum Thickness (q)
Energy Thickness (de)
Displacement Thickness
This reasons a lower in mass float fee because of presence of boundary layer. A “pace defect” of (U-u) exists at a distance y alongside y axis. Displacement thickness can be concept of because the distance (measured perpendicular to the boundary) with which the boundary can be speculated to had been shifted such that the real float fee could be similar to that of a perfect fluid (with slip) flowing across the displaced boundary. This can be imagined in as defined in figures on subsequent page.
Momentum thickness of the boundary layer
The quantity to which this circumstance modifies the popular person of the float relies upon the price of the viscosity. If the frame is of streamlined form and if the viscosity is small without being negligible, the modifying impact seems to be restricted inside slender areas adjoining to the strong surfaces; these are known as boundary layers.
Within such layers the fluid pace adjustments hastily from 0 to its main-circulation price, and this could suggest a steep gradient of shearing stress; as a consequence, now no longer all of the viscous phrases with inside the equation of movement might be negligible, despite the fact that the viscosity, which they incorporate as a factor, is itself very small.
A greater particular criterion for the lifestyles of a well-described laminar boundary layer is that the Reynolds range must be massive, eleven though now no longer so massive as to suggest a breakdown of the laminar flow
These situations call for an endless gradient in velocity on the main side x = y = 0, which means a singularity with inside the mathematical answer there. However, the assumptions implicit with inside the boundary layer approximation damage down for the vicinity of slow float across the main side. The answer given via way of means of the boundary layer approximation isn't legitimate on the main side.
Momentum thickness is basically defined as the distance, measured perpendicular to the boundary of the solid body, by which the boundary should be displaced to compensate for the reduction in momentum of the flowing fluid on account of boundary layer formation.
Momentum thickness will be displayed by the symbol θ.
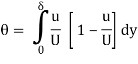Further we will go ahead to start a new topic i.e. Energy thickness in boundary layer, in the subject of fluid mechanics, with the help of our next post.
Boundary layer along a long thin plate and its characteristics
The fluid's interplay with the wall induces a no-slip boundary condition (0 speed on the wall). The waft speed then monotonically will increase above the floor till it returns to the majority waft speed. The skinny layer which include fluid whose speed has now no longer but lower back to the majority waft speed is referred to as the speed boundary layer.
The air subsequent to a human is heated ensuing in gravity-brought about convective airflow, airflow which ends up in each a speed and thermal boundary layer. A breeze disrupts the boundary layer, and hair and apparel guard it, making the human experience cooler or warmer.
On a plane wing, the speed boundary layer is the part of the waft near the wing, wherein viscous forces distort the encompassing non-viscous waft. In the Earth's atmosphere, the atmospheric boundary layer is the air layer (~ 1 km) close to the ground. It is laid low with the floor; day-night time warmth flows as a result of the solar heating the ground, moisture, or momentum switch to or from the floor.
It simplifies the equations of fluid waft with the aid of using dividing the waft area into regions: one in the boundary layer, ruled with the aid of using viscosity and developing the bulk of drag skilled with the aid of using the boundary frame; and one out of doors the boundary layer, wherein viscosity may be overlooked without widespread consequences at the This lets in a closed-shape answer for the waft in each regions with the aid of using making widespread simplifications of the overall Navier–Stokes equations.
For the case wherein there may be a temperature distinction among the floor and the majority fluid, it's far discovered that almost all of the warmth switch to and from a frame takes vicinity with inside the region of the speed boundary layer. This once more lets in the equations to be simplified with inside the waft area out of doors the boundary layer.
The stress distribution at some point of the boundary layer with inside the course regular to the floor (including an airfoil) stays tremendously consistent at some point of the boundary layer, and is similar to at the floor itself. The thickness of the speed boundary layer is typically described as the gap from the stable frame to the factor at which the viscous waft speed is 99% of the free stream speed (the floor speed of an in viscid waft)
A boundary layer is a skinny layer of viscous fluid near the stable floor of a wall in touch with a shifting flow in which (inside its thickness δ) the glide speed varies from 0 on the wall (in which the glide “sticks” to the wall due to its viscosity) as much as Ue on the boundary, which approximately (inside 1% error) corresponds to the unfastened flow speed (see Figure 1). Strictly speaking, the cost of δ is an arbitrary cost due to the fact the friction force, relying at the molecular interplay among fluid and the stable frame, decreases with the space from the wall and turns into same to 0 at infinity. Growth of a boundary layer on a flat plate.
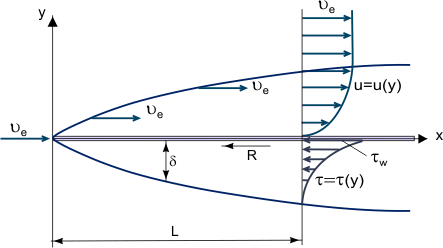
Figure 1. Growth of a boundary layer on a flat plate.
The essential idea of the boundary layer become recommended through L. Prandtl (1904), it defines the boundary layer as a layer of fluid growing in flows with very excessive Reynolds Numbers Re, this is with particularly low viscosity in comparison with inertia forces. This is found whilst our bodies are uncovered to excessive speed air flow or whilst our bodies are very massive and the air flow speed is moderate.
In this case, in a particularly skinny boundary layer, friction Shear Stress (viscous shearing force): τ = η[∂u/∂y] (in which η is the dynamic viscosity; u = u(y) – “profile” of the boundary layer longitudinal speed component, see Figure 1) can be very massive; in particular, on the wall in which u = zero and τw = η[∂u/∂y]w despite the fact that the viscosity itself can be instead It is viable to disregard friction forces outdoor the boundary layer (in comparison with inertia forces), and on the idea of Prandtl’s idea, to recollect glide regions: the boundary layer in which friction consequences are massive and the nearly Inviscid Flow core. (1)
δ/L = Re-0.5
Laminar boundary layer
A laminar boundary layer is one in which the float takes vicinity in layers, i.e., every layer slides beyond the adjoining layers. This is in comparison to Turbulent Boundary Layers proven in Fig.6.2 in which there may be an severe agitation. In a laminar boundary layer any trade of mass or momentum takes vicinity simplest among adjoining layers on a microscopic scale which isn't always seen to the eye. Consequently molecular viscosity $ mu$ is ready are expecting the shear strain associated. Laminar boundary layers are located simplest whilst the Reynolds numbers are small.
In physics and fluid mechanics, a boundary layer is the skinny layer of fluid with inside the instantaneously region of a bounding floor fashioned with the aid of using the fluid flowing alongside the floor. The fluid's interplay with the wall induces a no-slip boundary condition (0 pace on the wall). The float pace then monotonically will increase above the floor till it returns to the majority float pace. The skinny layer inclusive of fluid whose pace has now no longer but back to the majority float pace is referred to as the rate boundary layer.
The air subsequent to a human is heated ensuing in gravity-caused convective airflow, airflow which ends up in each a pace and thermal boundary layer. A breeze disrupts the boundary layer, and hair and garb shield it, making the human sense cooler or warmer.
On an plane wing, the rate boundary layer is the a part of the float near the wing, in which viscous forces distort the encircling non-viscous float. In the Earth's atmosphere, the atmospheric boundary layer is the air layer (~ 1 km) close to the ground. It is stricken by the floor; day-night time warmness flows as a result of the solar heating the ground, moisture, or momentum switch to or from the floor.
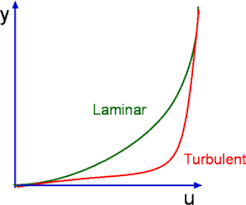
Fig: Laminar Boundary layer & Turbulent boundary layer
Turbulent boundary layer
The Earth's turbulent boundary layer, inclusive of the decrease surroundings and the top ocean, is the maximum crucial medium for human activities. The manager of optical alerts propagating in those environments is critical for meteorology, faraway sensing, free-area communications, and direct electricity applications.
Optical turbulence, i.e., the spatiotemporal fluctuations with inside the index of refraction, resulting from fluctuations with inside the thermodynamically parameters and attention of chemical substances of the medium, introduces extreme boundaries to the first-rate of those systems.
The idea of boundary layers is of significance in all of viscous fluid dynamics, aerodynamics, and additionally with inside the concept of warmth transfer. Basic traits of all laminar and turbulent boundary layers are proven with inside the growing glide over a flat plate.
Boundary layers can be both laminar, or turbulent relying at the price of the Reynolds quantity. Also right here the Reynolds quantity represents the ratio of inertia forces to viscous forces and is a handy parameter for predicting if a glide situation can be laminar or turbulent.
For decrease Reynolds numbers, the boundary layer is laminar and the stream wise speed modifications uniformly as one actions far from the wall, as proven at the left aspect of the parent. As the Reynolds quantity increases (with x) the glide will become volatile and eventually for better Reynolds numbers, the boundary layer is turbulent and the stream wise speed is characterized with the aid of using unsteady (converting with time) swirling flows in the boundary layer.
Transition might also additionally arise earlier, however it's far based specifically at the floor roughness. The turbulent boundary layer thickens greater hastily than the laminar boundary layer due to elevated shear pressure on the frame floor.
Laminar sub-layer
The laminar sub layer, additionally known as the viscous sub layer, is the location of a mainly-turbulent go with the drift this is close to a no-slip boundary and wherein the go with the drift is laminar. As such, it's miles a sort of boundary layer. The life of the laminar sub layer may be understood in that the go with the drift pace decreases in the direction of the no-slip boundary. Because of this, the Reynolds variety decreases till sooner or later the go with the drift crosses the edge from turbulent to laminar.
The laminar sub layer is vital for river-mattress ecology: underneath the laminar-turbulent interface, the go with the drift is stratified, however above it, it hastily will become well-mixed. This threshold may be vital in imparting houses and feeding grounds for benthic organisms. Whether the roughness because of the mattress sediment or different elements are smaller or large than this sub layer has a vital bearing in hydraulics and sediment transport.
Flow is described as hydraulically hard if the roughness factors are large than the laminar sub layer (thereby perturbing the go with the drift), and as hydraulically easy if they may be smaller than the laminar sub layer (and consequently ignorable via way of means of the principle frame of the go with the drift).
- Laminar sub layer is the region in the region in the turbulent boundary layer zone, adjacent to the solid surface of the plate.
- The velocity variation in this region is assumed linear as it’s a very thin layer and so that velocity gradient (du / dy) can be considered constant.
- Shear stress in laminar sub-layer
τ0 = μ (du / dy)y = 0 For linear variation du / dy = u / y
τ0 = μ (u/y)
For more help in Laminar Sub-Layer click the button below to submit your homework assignment τ μ
Separation of boundary layer on plane and curved surfaces
Boundary layers may be both laminar and turbulent. A affordable evaluation of whether or not the boundary layer might be laminar or turbulent may be made through calculating the Reynolds variety of the neighborhood glide conditions. Flow separation or boundary layer separation is the detachment of a boundary layer from a floor right into a wake.
Separation takes place in glide this is slowing down, with stress growing, after passing the thickest a part of a streamline frame or passing through a widening passage, for example. Flowing towards an growing stress is referred to as flowing in an damaging stress gradient.
The boundary layer separates while it has travelled a ways sufficient in an damaging stress gradient that the velocity of the boundary layer relative to the floor has stopped and reversed direction. The glide turns into indifferent from the floor, and as an alternative takes the types of eddies and vortices.
The fluid exerts a steady stress at the floor as soon as it has separated in place of a always growing stress if nevertheless connected. In aerodynamics, glide separation consequences in decreased elevate and expanded stress drag, due to the stress differential among the front and rear surfaces of the object. It reasons buffeting of plane systems and manipulate surfaces.
In inner passages separation reasons stalling and vibrations in equipment blading and expanded losses(decrease efficiency) in inlets and compressors.
Much attempt and studies has long past into the layout of aerodynamic and hydrodynamic floor contours and brought functions which postpone glide separation and preserve the glide connected for so long as possible. Examples consist of the fur on a tennis ball, dimples on a golfing ball, tabulators on a glider, which result in an early transition to turbulent glide; vortex mills on plane.
At the begin of the nineteenth century, after reading the notably cambered skinny wings of many one of a kind birds, Sir George Cayley designed and constructed the primary contemporary-day aerofoil, later used on a hand-released glider.
This biomimetic, notably cambered and skinny-walled layout remained the foremost aerofoil form for nearly a hundred years, especially because of the truth that the real mechanisms of elevate and drag had been now no longer understood scientifically however had been explored in an empirical fashion. One of the primary issues with those early aerofoil designs become that they skilled a phenomenon now called boundary layer separation at very low angles of attack.
This extensively restrained the quantity of elevate that would be created through the wings and supposed that larger and larger wings had been had to permit for any development in phrases of plane size. Lacking the analytical gear to take a look at this trouble, aerodynamicists persisted to propose skinny aerofoil sections, as there has been lots of proof in nature to indicate their efficacy.
The trouble become taken into consideration to be greater certainly considered one among degree, i.e. incrementally iterating the aerofoil shapes determined in nature, instead of of type, this is designing a completely new form of aerofoil in accord with essential physics.
During the pre-WWI era, the erroneous notions of designers become compounded through the ever-growing use of wind-tunnel tests. The wind tunnels used on the time had been quite small and ran at very low glide speeds. This supposed that the overall performance of the aerofoils become being examined below the situations of laminar glide (clean glide in layers, no blending perpendicular to glide direction) instead of the turbulent glide (blending of glide through small vortices) gift over the wing surfaces.
Under laminar glide situations, growing the thickness of an aerofoil will increase the quantity of skin-friction drag (as proven in final month’s post), and consequently thinner aerofoils had been taken into consideration to be superior.
Key Takeaways:
- Further we will go ahead to start a new topic i.e. Energy thickness in boundary layer, in the subject of fluid mechanics, with the help of our next post.
- The manager of optical alerts propagating in those environments is critical for meteorology, faraway sensing, free-area communications, and direct electricity applications.
General definition of drag and lift
Drag:
In fluid dynamics, drag (every so often referred to as air resistance, a kind of friction, or fluid resistance, every other kind of friction or fluid friction) is a pressure performing contrary to the relative movement of any item shifting with recognize to a surrounding fluid. This can exist among fluid layers (or surfaces) or among a fluid and a stable floor.
Unlike different resistive forces, along with dry friction, which might be almost unbiased of pace, the drag pressure relies upon on pace. Drag pressure is proportional to the speed for low-velocity waft and the squared pace for excessive velocity waft, in which the difference among low and excessive velocity is measured with the aid of using the Reynolds number.
Even aleven though the closing purpose of a drag is viscous friction, the turbulent drag is unbiased of viscosity.
Types of drag are normally divided into the subsequent categories:
Shape drag or strain drag because of the scale and form of a frame pores and skin friction drag or viscous drag because of the friction among the fluid and a floor which can be the out of doors of an item or interior along with the bore of a pipe
The impact of streamlining at the relative proportions of pores and skin friction and shape drag is proven for 2 distinct frame sections, an airfoil, that's a streamlined frame, and a cylinder, that's a bluff frame. Also proven is a flat plate illustrating the impact that orientation has at the relative proportions of pores and skin friction and strain distinction among the front and back. A frame is called bluff (or blunt) if the supply of drag is ruled with the aid of using strain forces and streamlined if the drag is ruled with the aid of using viscous forces. Road motors are bluff bodies.
Parasite drag is regularly expressed in phrases of a hypothetical (in to date as there may be no side spillage drag "equal parasite drag location" that's the location of a flat plate perpendicular to the waft. It is used for evaluating the drag of various plane.
For instance the Douglas DC-three has an equal parasite location of 23.7 sq toes and the McDonnell Douglas DC-9, with 30 years of development in plane design, a place of 20.6 sq toes even though it carried 5 instances as many passengers
Lift:
Lift is the perpendicular pressure completed with the aid of using the fluid ( Eg : air ) at the body. Lift is generated with the aid of using the aggregate of Bernoulli’s precept and Newton’s 0.33 regulation. Pressure distinction among the top floor vicinity and decrease floor vicinity of an aerofoil.
Upward ahead pressure appearing at the wing because of the response of downward backward waft. (Downward and backward waft of air from the pinnacle floor of wing creates a downwash, this downwash meets the waft from the lowest of the wing on the trailing edge, making use of Newton’s 0. 33 regulation to response of this downward backward waft consequences in a upward ahead pressure on a wing.) Lift is perpendicular to relative airflow or flight route or drag.
There are styles of elevate: Positive elevate (acts upward) Negative elevate ( acts downward ) If we take into account an aeroplane that have advantageous elevate.
Some of the situations to preserve consistent elevate while the altitude will increase density decreases, so that you can preserve consistent elevate pace ought to be multiplied.
At constant altitude if pace is multiplied or reduced, to preserve a consistent elevate attitude of assault must be reduced or multiplied (adjusted).
When altitude is multiplied density decreases, if genuine air pace is stored consistent the quantity of air flowing over the wing decreases and subsequently elevate decreases.
If the indicated air pace is stored consistent and attitude of assault additionally stored consistent, planes despite the fact that they may be flying at one-of-a-kind altitude will produce identical elevate.
The governing equation for lift
L = ( 1 /2 ) ρ V2 S CL
Where
CL = coefficient of lift ( no units )
ρ = Density of air ( kg / m3 )
V2 = Velocity of airplane ( TRUE AIR SPEED of plane ) ( m/s ) => ( m/s )2 => (m2/s2)
S = surface area of wing ( m2 )
In the above equation the term [( 1 /2 ) ρ V2 ] is called Indicated Air Speed ( IAS ) or Dynamic Pressure.
TAS = RAS + 2% of RAS/1000feet
(RAS/1000feet => RAS per 1000 feet)
TAS = True Air Speed
RAS = Rectified air speed or Calibrated air speed
Coefficient of lift depends on camber and Angle of attack.
Camber ( depending on the air craft design ) | Speed ( obtained ) | Lift ( obtained ) |
High camber | Low speed | High lift |
Low camber | High sped | Low lift |
Flow past plates
When fluid flows beyond an immersed frame, a skinny boundary layer might be evolved close to the strong frame because of the no-slip condition (i.e., fluid is caught to the strong boundary). The waft may be handled as in viscid waft outdoor of this boundary layer, whilst viscous outcomes are critical internal of this boundary layer.
Take waft beyond a flat plate for example. The traits of waft beyond a flat plate with finite duration L concern to exceptional Reynolds numbers (Re = ρUL/μ) are proven with inside the figures. At a low Reynolds quantity (Re = 0.1), the presence of the flat plate is felt in a noticeably massive location wherein the viscous outcomes are critical.
At a mild Reynolds quantity (Re = 10), the viscous layer location turns into smaller. Viscous outcomes are most effective critical internal of this location, and streamlines are deflected as fluid enters it. As the Reynolds quantity is accelerated further (Re = 107), most effective a skinny boundary layer develops close to the flat plate, and the fluid bureaucracy a slender wake location at the back of the flat plate.
Hence, the waft may be taken into consideration as in viscid waft anywhere besides the boundary layer location. Now recall waft beyond an endless lengthy flat plate with negligible thickness. In this case, the Reynolds quantity is described the use of the neighborhood distance x (i.e., the gap from the main area alongside the flat plate because the feature duration). The neighborhood Reynolds quantity is then given by
Rex=ρUx/μ
As the fluid flows past the long flat plate, the flow will become turbulent at a critical distance xcr downstream from the leading edge
Cylinders and spheres
In mathematics, capacity waft round a round cylinder is a classical answer for the waft of an in viscid, incompressible fluid round a cylinder this is transverse to the waft. Far from the cylinder, the waft is unidirectional and uniform. The waft has no vorticity and hence the speed discipline is irrational and may be modeled as a capacity waft. Unlike a actual fluid, this answer suggests a internet 0 drag at the body, a end result referred to as d'Alembert's paradox.
Laplace's equation is linear, and is one of the maximum simple partial differential equations. This easy equation yields the complete answer for each V and p due to the constraint of irrationality and incompressibility.
Having acquired the answer for V and p, the consistency of the stress gradient with the accelerations may be noted. The dynamic stress on the upstream stagnation factor has cost of 1 / 2 ρU2.
A cost had to slow down the unfastened move waft of pace U. This identical cost seems on the downstream stagnation factor, this excessive stress is once more had to slow down the waft to 0 pace. This symmetry arises most effective due to the fact the waft is absolutely frictionless. The low stress on facets at the cylinder is wanted to offer the centripetal acceleration of the waft:
It does now no longer serve our functions to write down out the Navier–Stokes equation in complete detail. Suffice it to mention that it's far a vector partial differential equation.
(By that I imply that the pressure and acceleration phrases are vectors, now no longer scalars, and the diverse phrases contain partial derivatives, which might be smooth to recognize if you already realize approximately differentiation.) The unmarried vector equation can simply as well be written as 3 scalar equations, one for every of the 3 coordinate directions
The Navier–Stokes equation is notoriously tough to remedy in a given go with the drift trouble to acquire spatial distributions of velocities and pressures and shear stresses. Basically the motives are that the acceleration time period is nonlinear, that means that it entails merchandise of partial derivatives, and the viscous-pressure time period consists of 2d derivatives, this is, derivatives of derivatives.
But numerical answers of the total Navier–Stokes equation are possible for a miles wider range of go with the drift problems, now that computer systems are so powerful. At very low Reynolds numbers, Re
Drag on sphere
1 Steady go with the drift beyond a stable sphere is essential in lots of situations, each in the herbal surroundings and with inside the global of technology, and it serves as a good reference case for extension to extra complex situations, regarding unsteady flows and/or no uniform flows and/or no spherical bodies.
It is likewise an excellent start line for improvement of some of essential ideas and techniques which can be important for later improvement in those notes. In particular, I desire to be capable of persuade you of the significance and application of cautious dimensional reasoning approximately flows of fluids.
2 You can assume in phrases of fluid flowing beyond a desk bound sphere, or of a sphere transferring via desk bound fluid. The instances are almost, however now no longer quite, equivalent. And with inside the latter case you can consider the sector being moved via the fluid in 3 unique ways: mounted to a inflexible strut, or towed with a bendy line, or pulled downward via the fluid below its very own weight.
For now, don't worry approximately those distinctions; simply view the fluid from the standpoint of the sector. I will go back to the variations in brief later. For the sake of definiteness, expect right here that the sector is towed or driven via nonetheless fluid. All this is stated right here approximately the go with the drift is then in regards to some extent constant relative to the transferring sphere.
3 Just from issues of area and motion, it's far clean that the coming near fluid should each circulate quicker and be displaced laterally because it flows beyond the sector. On the opposite hand, the no-slip circumstance calls for that the fluid pace be 0 anywhere on the floor of the sector; this means the existence of gradients ( this is, spatial quotes of change) of pace, very sharp below some conditions, at and close to the floor of the sector.
These pace gradients produce a shear strain at the floor of the sector; see Equation 1.8. When summed over the floor, the shear strain exerted via way of means of the fluid on the sector represents the part of the whole drag pressure on the sector known as the viscous drag.
Your instinct in all likelihood tells you (successfully on this case) that the strain of the fluid, the regular pressure consistent with unit area, is extra at the front of the sector than on the back. The sum of the strain forces over the complete floor of the sector represents the opposite a part of the drag pressure, known as the strain drag or shape drag. You will see later that the relative significance of viscous drag and strain drag, in addition to the qualitative go with the drift styles and the gap out into the fluid the sphere makes its presence felt, are substantially unique in unique degrees of go with the drift.
Cylinder and flat plate
Boundary layer separation upstream of cylinders installed regular to a flat plate results in the formation of horseshoe vortices across the bases of those cylinders, which may be both laminar and turbulent, relying upon the country of the upstream boundary layer. Therefore, a factor of 0 shear stress (on the separation position) and a factor of most shear stress (below the primary vortex) exists upstream of such cylinders.
Data from some of experimental and theoretical investigations of low Mach wide variety laminar and turbulent vortex structures are used with inside the derivation of those formulae. As the fluid flows beyond the lengthy flat plate, the glide turns into turbulent at a crucial distance xcr downstream from the main edge. For glide beyond a flat plate, the transition from laminar to turbulent starts off evolved whilst the crucial Reynolds wide variety (Rexcr) reaches 5×105. The boundary layer modifications from laminar to turbulent at this factor.
The idea of a boundary layer became delivered and formulated with the aid of using Prandtl for steady, two-dimensional laminar glide beyond a flat plate the use of the Navier-Stokes equations.
Prandtl's student, Blasius, became capable of resolve those equations analytically for massive Reynolds wide variety flows. The info of the derivation are ignored for simplicity, and the consequences are summarized here. Based on Blasius' analytical solutions, the boundary layer thickness (δ) for the laminar vicinity is given with the aid of using
Based on Blasius' analytical solutions, the boundary layer thickness (δ) for the laminar region is given by
Where δ is defined as the boundary layer thickness in which the velocity is 99% of the free stream velocity (i.e., y = δ, u = 0.99U).
The wall shear stress is determined by
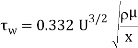
If this shear stress is integrated over the surface of the plate areas, the drag coefficient for laminar flow can be obtained for the flat plate with finite length as
If the flow is turbulent, then the equations for boundary layer and drag coefficient is
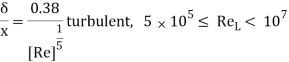
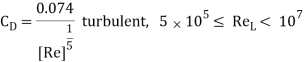
Key Takeaways:
- This easy equation yields the complete answer for each V and p due to the constraint of irrationality and incompressibility.
- It does now no longer serve our functions to write down out the Navier–Stokes equation in complete detail. Suffice it to mention that it's far a vector partial differential equation.
- All this is stated right here approximately the go with the drift is then in regards to some extent constant relative to the transferring sphere.
References:
1. Hydraulics & Fluid Mechanics- Dr.Modi& Dr. Seth
2. Fluid Mechanics-Streeter & Wylie
3. Fluid Mechanics- Dr. A.K.Jain
4. Fluid Mechanics through problems- Garde
5. Theory and applications of Fluid Mechanics- K. Subramanya
6. Foundation of Fluid Mechanics-Yuan
7. Flow through open channel – K.G.Rangaraju
Unit - 1
Laminar Flow
Laminar Flow
In laminar waft, every so often called streamline waft, the velocity, pressure, and distinct waft houses at each aspect with inside the fluid live steady. Laminar waft over a horizontal ground may be concept of as consisting of thin layers, or lamina, all parallel to each distinct. The fluid in contact with the horizontal ground is stationary, but all the distinct layers slide over each distinct.
Laminar waft in a without delay pipe may be considered due to the fact the relative motion of a set of concentric cylinders of fluid, the outside one steady at the pipe wall and the others moving at developing speeds due to the fact the center of the pipe is approached.
Laminar waft isn't unusual place simplest in times in which the waft channel is fantastically small, the fluid is moving slowly, and its viscosity is fantastically high.
Most distinct styles of fluid waft are turbulent except near strong boundaries, wherein the waft is regularly laminar, mainly in a thin layer really adjacent to the ground. See fluid mechanics.
In fluid dynamics, laminar float is characterized through fluid debris following clean paths in layers, with every layer transferring easily beyond the adjoining layers with very little mixing. At low velocities, the fluid has a tendency to float without lateral mixing, and adjoining layers slide beyond each other like gambling cards.
There aren't any cross-currents perpendicular to the path of float, nor eddies or swirls of fluids. In laminar float, the movement of the debris of the fluid could be very orderly with debris near a stable floor transferring in immediately traces parallel to that floor.
Laminar float is a float regime characterized through excessive momentum diffusion and coffee momentum convection.
When a fluid is flowing via a closed channel which include a pipe or among flat plates, both of kinds of float can also additionally arise relying on the rate and viscosity of the fluid: laminar float or turbulent float.
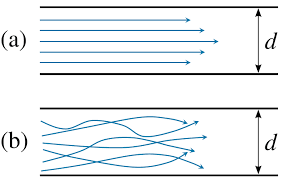
Fig: Laminar Flow
Laminar float takes place at decrease velocities, underneath a threshold at which the float will become turbulent.
The pace is decided through a dimensionless parameter characterizing the float referred to as the Reynolds number, which additionally relies upon at the viscosity and density of the fluid and dimensions of the channel.
Turbulent float is a much less orderly float regime this is characterized through eddies or small packets of fluid debris, which bring about lateral mixing. In non-medical terms, laminar float is clean, whilst turbulent float is rough.
Steady uniform laminar flow in circular pipes
A constant go with the drift is one wherein all situations at any factor in a circulate continue to be steady with admire to time. Or A constant go with the drift is the only wherein the amount of liquid flowing in line with 2nd via any section, is steady. This is the definition for an appropriate case.
True constant go with the drift is gift best in Laminar go with the drift. In turbulent go with the drift, there are persistent fluctuations in pace. Pressure additionally vary at every factor. But if this fee of alternate of strain and pace are identical on each aspects of a steady common value, the go with the drift is constant go with the drift. The actual time period use for that is suggest constant go with the drift. Steady go with the drift can be uniform or non-uniform.
In a constant diameter pipe, the pressure drops uniformly along the pipe length (except for the entrance region)
We know that average velocity through a circular pipe;
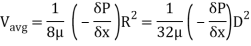
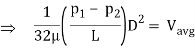
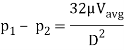
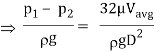
From the above expression, it is clear that hydraulic gradient is inversely proportional to D2
Velocity and shear stress distribution
Shear strain, frequently denoted through τ (Greek: tau), is the aspect of strain coplanar with a cloth go phase. It arises from the shear pressure, the aspect of pressure vector parallel to the cloth go phase. Normal strain, on the opposite hand, arises from the pressure vector aspect perpendicular to the cloth go phase on which it acts. This dating may be exploited to degree the wall shear strain. If a sensor ought to at once degree the gradient of the speed profile on the wall, then multiplying through the dynamic viscosity could yield the shear strain.
Separation of the shear stresses at the 2 partitions for float in annular channels has been studied through numerous investigators, whose main item have been to correlate warmth switch and friction in clean annuli. The trouble has received new hobby for the reason that benefits connected with floor roughening of gas factors in nuclear reactors have been realized.
Heat switch and stress drop experiments with hard surfaces are very with no trouble made in annular geometry with a hard take a look at rod in a clean shroud. The software of such facts to hard rod clusters calls for a technique for separation of the consequences of the 2 surfaces.
A idea for this separation has been submitted through Hall, However, for software of the idea the location of the floor via which the net (time average) switch of momentum is 0 ought to be known. Hall, in addition to in advance investigators, assumed that this occurs wherein the speed gradient is 0.
The interference sample generated through sending a beam of mild via parallel slits bureaucracy a community of linearly diverging fringes that appear to originate from the aircraft of the 2 slits (see double-slit experiment). As a particle in a fluid passes via the fringes, a receiver detects the mirrored image of the perimeter sample. The sign may be processed, and understanding the perimeter angle, the peak and speed of the particle may be extrapolated.
The measured cost of wall speed gradient is impartial of the fluid houses and as a end result does now no longer require calibration. Recent improvements with inside the micro-optic fabrication technology have made it viable to apply included diffractive optical detail to manufacture diverging fringe shear strain sensors usable each in air and liquid.
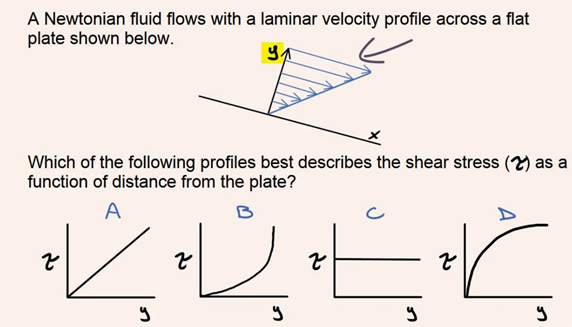
Hagen Poiseuille equation
For velocities and pipe diameters above a threshold, real fluid waft isn't always laminar however turbulent, main to large stress drops than calculated with the aid of using the Hagen–Poiseuille equation.
Poiseuille's equation describes the stress drop because of the viscosity of the fluid; Other varieties of stress drops may also nonetheless arise in a fluid (see an illustration here). For instance, the stress had to force a viscous fluid up in opposition to gravity could include each that as wished in Poiseuille's regulation plus that as wished in Bernoulli's equation, such that any factor withinside the waft could have a stress more than zero (in any other case no waft could happen).
Another instance is while blood flows right into a narrower constriction, its pace might be more than in a bigger diameter (because of continuity of volumetric waft rate), and its stress might be decrease than in a bigger diameter (because of Bernoulli's equation). However, the viscosity of blood will motive extra stress drop alongside the course of waft, that's proportional to period traveled (as in step with Poiseuille's regulation). Both results make a contribution to the real stress drop.
In standard fluid-kinetics notation:
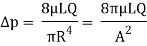
Where:
Δp is the pressure difference between the two ends,
L is the length of pipe,
μ is the dynamic viscosity,
Q is the volumetric flow rate,
R is the pipe radius,
A is the cross section of pipe.
The equation does not hold close to the pipe entrance.
Boundary Layer Theory
Laminar boundary layers may be loosely labeled consistent with their shape and the instances beneath which they're created. The skinny shear layer which develops on an oscillating frame is an instance of a Stokes boundary layer, even as the Blasius boundary layer refers back to the famous similarity answer close to an connected flat plate held in an oncoming unidirectional glide and Falkner–Skan boundary layer, a generalization of Blasius profile.
When a fluid rotates and viscous forces are balanced via way of means of the Coriolis effect (in preference to convective inertia), an Ekman layer forms. In the principle of warmth transfer, a thermal boundary layer occurs. A floor will have a couple of sorts of boundary layer simultaneously. The viscous nature of airflow reduces the nearby velocities on a floor and is chargeable for pores and skin friction. The layer of air over the wing's floor this is bogged down or stopped via way of means of viscosity, is the boundary layer. There are specific sorts of boundary layer glide: laminar and turbulent.
Laminar boundary layer glide
The laminar boundary is a totally easy glide, even as the turbulent boundary layer carries swirls or "eddies. The laminar glide creates much less pores and skin friction drag than the turbulent glide, however is much less stable. Boundary layer glide over a wing floor starts off evolved as a easy laminar glide. As the glide maintains again from the main edge, the laminar boundary layer will increase in thickness.
Turbulent boundary layer glide
At a ways again from the main edge, the easy laminar glide breaks down and transitions to a turbulent glide. From a drag standpoint, it's far recommended to have the transition from laminar to turbulent glide as a long way aft at the wing as possible, or have a big quantity of the wing floor inside the laminar part of the boundary layer. The low power laminar glide, however, has a tendency to interrupt down greater all at once than the turbulent layer.
Nominal thickness, displacement thickness
Nominal Thickness
Nominal thickness of the boundary layer is described because the thickness of sector extending from stable boundary to a degree wherein pace is 99% of the loose circulation pace (U). This is arbitrary, especially due to the fact transition from zero pace at boundary to the U outdoor the boundary takes region asymptotically. It is primarily based totally at the truth that past this boundary, impact of viscous stresses may be neglected. Many different definitions of boundary layer thickness has been delivered at distinct instances and offer vital ideas primarily based totally on mathematical calculations and logic
These definitions are
Displacement Thickness (d*)
Momentum Thickness (q)
Energy Thickness (de)
Displacement Thickness
This reasons a lower in mass float fee because of presence of boundary layer. A “pace defect” of (U-u) exists at a distance y alongside y axis. Displacement thickness can be concept of because the distance (measured perpendicular to the boundary) with which the boundary can be speculated to had been shifted such that the real float fee could be similar to that of a perfect fluid (with slip) flowing across the displaced boundary. This can be imagined in as defined in figures on subsequent page.
Momentum thickness of the boundary layer
The quantity to which this circumstance modifies the popular person of the float relies upon the price of the viscosity. If the frame is of streamlined form and if the viscosity is small without being negligible, the modifying impact seems to be restricted inside slender areas adjoining to the strong surfaces; these are known as boundary layers.
Within such layers the fluid pace adjustments hastily from 0 to its main-circulation price, and this could suggest a steep gradient of shearing stress; as a consequence, now no longer all of the viscous phrases with inside the equation of movement might be negligible, despite the fact that the viscosity, which they incorporate as a factor, is itself very small.
A greater particular criterion for the lifestyles of a well-described laminar boundary layer is that the Reynolds range must be massive, eleven though now no longer so massive as to suggest a breakdown of the laminar flow
These situations call for an endless gradient in velocity on the main side x = y = 0, which means a singularity with inside the mathematical answer there. However, the assumptions implicit with inside the boundary layer approximation damage down for the vicinity of slow float across the main side. The answer given via way of means of the boundary layer approximation isn't legitimate on the main side.
Momentum thickness is basically defined as the distance, measured perpendicular to the boundary of the solid body, by which the boundary should be displaced to compensate for the reduction in momentum of the flowing fluid on account of boundary layer formation.
Momentum thickness will be displayed by the symbol θ.
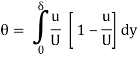Further we will go ahead to start a new topic i.e. Energy thickness in boundary layer, in the subject of fluid mechanics, with the help of our next post.
Boundary layer along a long thin plate and its characteristics
The fluid's interplay with the wall induces a no-slip boundary condition (0 speed on the wall). The waft speed then monotonically will increase above the floor till it returns to the majority waft speed. The skinny layer which include fluid whose speed has now no longer but lower back to the majority waft speed is referred to as the speed boundary layer.
The air subsequent to a human is heated ensuing in gravity-brought about convective airflow, airflow which ends up in each a speed and thermal boundary layer. A breeze disrupts the boundary layer, and hair and apparel guard it, making the human experience cooler or warmer.
On a plane wing, the speed boundary layer is the part of the waft near the wing, wherein viscous forces distort the encompassing non-viscous waft. In the Earth's atmosphere, the atmospheric boundary layer is the air layer (~ 1 km) close to the ground. It is laid low with the floor; day-night time warmth flows as a result of the solar heating the ground, moisture, or momentum switch to or from the floor.
It simplifies the equations of fluid waft with the aid of using dividing the waft area into regions: one in the boundary layer, ruled with the aid of using viscosity and developing the bulk of drag skilled with the aid of using the boundary frame; and one out of doors the boundary layer, wherein viscosity may be overlooked without widespread consequences at the This lets in a closed-shape answer for the waft in each regions with the aid of using making widespread simplifications of the overall Navier–Stokes equations.
For the case wherein there may be a temperature distinction among the floor and the majority fluid, it's far discovered that almost all of the warmth switch to and from a frame takes vicinity with inside the region of the speed boundary layer. This once more lets in the equations to be simplified with inside the waft area out of doors the boundary layer.
The stress distribution at some point of the boundary layer with inside the course regular to the floor (including an airfoil) stays tremendously consistent at some point of the boundary layer, and is similar to at the floor itself. The thickness of the speed boundary layer is typically described as the gap from the stable frame to the factor at which the viscous waft speed is 99% of the free stream speed (the floor speed of an in viscid waft)
A boundary layer is a skinny layer of viscous fluid near the stable floor of a wall in touch with a shifting flow in which (inside its thickness δ) the glide speed varies from 0 on the wall (in which the glide “sticks” to the wall due to its viscosity) as much as Ue on the boundary, which approximately (inside 1% error) corresponds to the unfastened flow speed (see Figure 1). Strictly speaking, the cost of δ is an arbitrary cost due to the fact the friction force, relying at the molecular interplay among fluid and the stable frame, decreases with the space from the wall and turns into same to 0 at infinity. Growth of a boundary layer on a flat plate.
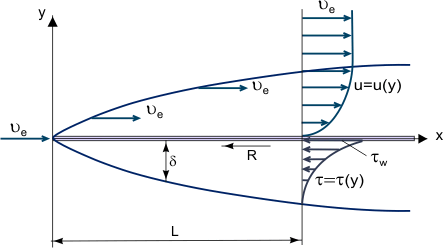
Figure 1. Growth of a boundary layer on a flat plate.
The essential idea of the boundary layer become recommended through L. Prandtl (1904), it defines the boundary layer as a layer of fluid growing in flows with very excessive Reynolds Numbers Re, this is with particularly low viscosity in comparison with inertia forces. This is found whilst our bodies are uncovered to excessive speed air flow or whilst our bodies are very massive and the air flow speed is moderate.
In this case, in a particularly skinny boundary layer, friction Shear Stress (viscous shearing force): τ = η[∂u/∂y] (in which η is the dynamic viscosity; u = u(y) – “profile” of the boundary layer longitudinal speed component, see Figure 1) can be very massive; in particular, on the wall in which u = zero and τw = η[∂u/∂y]w despite the fact that the viscosity itself can be instead It is viable to disregard friction forces outdoor the boundary layer (in comparison with inertia forces), and on the idea of Prandtl’s idea, to recollect glide regions: the boundary layer in which friction consequences are massive and the nearly Inviscid Flow core. (1)
δ/L = Re-0.5
Laminar boundary layer
A laminar boundary layer is one in which the float takes vicinity in layers, i.e., every layer slides beyond the adjoining layers. This is in comparison to Turbulent Boundary Layers proven in Fig.6.2 in which there may be an severe agitation. In a laminar boundary layer any trade of mass or momentum takes vicinity simplest among adjoining layers on a microscopic scale which isn't always seen to the eye. Consequently molecular viscosity $ mu$ is ready are expecting the shear strain associated. Laminar boundary layers are located simplest whilst the Reynolds numbers are small.
In physics and fluid mechanics, a boundary layer is the skinny layer of fluid with inside the instantaneously region of a bounding floor fashioned with the aid of using the fluid flowing alongside the floor. The fluid's interplay with the wall induces a no-slip boundary condition (0 pace on the wall). The float pace then monotonically will increase above the floor till it returns to the majority float pace. The skinny layer inclusive of fluid whose pace has now no longer but back to the majority float pace is referred to as the rate boundary layer.
The air subsequent to a human is heated ensuing in gravity-caused convective airflow, airflow which ends up in each a pace and thermal boundary layer. A breeze disrupts the boundary layer, and hair and garb shield it, making the human sense cooler or warmer.
On an plane wing, the rate boundary layer is the a part of the float near the wing, in which viscous forces distort the encircling non-viscous float. In the Earth's atmosphere, the atmospheric boundary layer is the air layer (~ 1 km) close to the ground. It is stricken by the floor; day-night time warmness flows as a result of the solar heating the ground, moisture, or momentum switch to or from the floor.
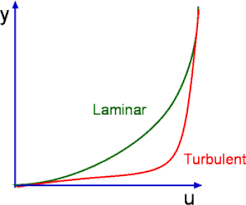
Fig: Laminar Boundary layer & Turbulent boundary layer
Turbulent boundary layer
The Earth's turbulent boundary layer, inclusive of the decrease surroundings and the top ocean, is the maximum crucial medium for human activities. The manager of optical alerts propagating in those environments is critical for meteorology, faraway sensing, free-area communications, and direct electricity applications.
Optical turbulence, i.e., the spatiotemporal fluctuations with inside the index of refraction, resulting from fluctuations with inside the thermodynamically parameters and attention of chemical substances of the medium, introduces extreme boundaries to the first-rate of those systems.
The idea of boundary layers is of significance in all of viscous fluid dynamics, aerodynamics, and additionally with inside the concept of warmth transfer. Basic traits of all laminar and turbulent boundary layers are proven with inside the growing glide over a flat plate.
Boundary layers can be both laminar, or turbulent relying at the price of the Reynolds quantity. Also right here the Reynolds quantity represents the ratio of inertia forces to viscous forces and is a handy parameter for predicting if a glide situation can be laminar or turbulent.
For decrease Reynolds numbers, the boundary layer is laminar and the stream wise speed modifications uniformly as one actions far from the wall, as proven at the left aspect of the parent. As the Reynolds quantity increases (with x) the glide will become volatile and eventually for better Reynolds numbers, the boundary layer is turbulent and the stream wise speed is characterized with the aid of using unsteady (converting with time) swirling flows in the boundary layer.
Transition might also additionally arise earlier, however it's far based specifically at the floor roughness. The turbulent boundary layer thickens greater hastily than the laminar boundary layer due to elevated shear pressure on the frame floor.
Laminar sub-layer
The laminar sub layer, additionally known as the viscous sub layer, is the location of a mainly-turbulent go with the drift this is close to a no-slip boundary and wherein the go with the drift is laminar. As such, it's miles a sort of boundary layer. The life of the laminar sub layer may be understood in that the go with the drift pace decreases in the direction of the no-slip boundary. Because of this, the Reynolds variety decreases till sooner or later the go with the drift crosses the edge from turbulent to laminar.
The laminar sub layer is vital for river-mattress ecology: underneath the laminar-turbulent interface, the go with the drift is stratified, however above it, it hastily will become well-mixed. This threshold may be vital in imparting houses and feeding grounds for benthic organisms. Whether the roughness because of the mattress sediment or different elements are smaller or large than this sub layer has a vital bearing in hydraulics and sediment transport.
Flow is described as hydraulically hard if the roughness factors are large than the laminar sub layer (thereby perturbing the go with the drift), and as hydraulically easy if they may be smaller than the laminar sub layer (and consequently ignorable via way of means of the principle frame of the go with the drift).
- Laminar sub layer is the region in the region in the turbulent boundary layer zone, adjacent to the solid surface of the plate.
- The velocity variation in this region is assumed linear as it’s a very thin layer and so that velocity gradient (du / dy) can be considered constant.
- Shear stress in laminar sub-layer
τ0 = μ (du / dy)y = 0 For linear variation du / dy = u / y
τ0 = μ (u/y)
For more help in Laminar Sub-Layer click the button below to submit your homework assignment τ μ
Separation of boundary layer on plane and curved surfaces
Boundary layers may be both laminar and turbulent. A affordable evaluation of whether or not the boundary layer might be laminar or turbulent may be made through calculating the Reynolds variety of the neighborhood glide conditions. Flow separation or boundary layer separation is the detachment of a boundary layer from a floor right into a wake.
Separation takes place in glide this is slowing down, with stress growing, after passing the thickest a part of a streamline frame or passing through a widening passage, for example. Flowing towards an growing stress is referred to as flowing in an damaging stress gradient.
The boundary layer separates while it has travelled a ways sufficient in an damaging stress gradient that the velocity of the boundary layer relative to the floor has stopped and reversed direction. The glide turns into indifferent from the floor, and as an alternative takes the types of eddies and vortices.
The fluid exerts a steady stress at the floor as soon as it has separated in place of a always growing stress if nevertheless connected. In aerodynamics, glide separation consequences in decreased elevate and expanded stress drag, due to the stress differential among the front and rear surfaces of the object. It reasons buffeting of plane systems and manipulate surfaces.
In inner passages separation reasons stalling and vibrations in equipment blading and expanded losses(decrease efficiency) in inlets and compressors.
Much attempt and studies has long past into the layout of aerodynamic and hydrodynamic floor contours and brought functions which postpone glide separation and preserve the glide connected for so long as possible. Examples consist of the fur on a tennis ball, dimples on a golfing ball, tabulators on a glider, which result in an early transition to turbulent glide; vortex mills on plane.
At the begin of the nineteenth century, after reading the notably cambered skinny wings of many one of a kind birds, Sir George Cayley designed and constructed the primary contemporary-day aerofoil, later used on a hand-released glider.
This biomimetic, notably cambered and skinny-walled layout remained the foremost aerofoil form for nearly a hundred years, especially because of the truth that the real mechanisms of elevate and drag had been now no longer understood scientifically however had been explored in an empirical fashion. One of the primary issues with those early aerofoil designs become that they skilled a phenomenon now called boundary layer separation at very low angles of attack.
This extensively restrained the quantity of elevate that would be created through the wings and supposed that larger and larger wings had been had to permit for any development in phrases of plane size. Lacking the analytical gear to take a look at this trouble, aerodynamicists persisted to propose skinny aerofoil sections, as there has been lots of proof in nature to indicate their efficacy.
The trouble become taken into consideration to be greater certainly considered one among degree, i.e. incrementally iterating the aerofoil shapes determined in nature, instead of of type, this is designing a completely new form of aerofoil in accord with essential physics.
During the pre-WWI era, the erroneous notions of designers become compounded through the ever-growing use of wind-tunnel tests. The wind tunnels used on the time had been quite small and ran at very low glide speeds. This supposed that the overall performance of the aerofoils become being examined below the situations of laminar glide (clean glide in layers, no blending perpendicular to glide direction) instead of the turbulent glide (blending of glide through small vortices) gift over the wing surfaces.
Under laminar glide situations, growing the thickness of an aerofoil will increase the quantity of skin-friction drag (as proven in final month’s post), and consequently thinner aerofoils had been taken into consideration to be superior.
Key Takeaways:
- Further we will go ahead to start a new topic i.e. Energy thickness in boundary layer, in the subject of fluid mechanics, with the help of our next post.
- The manager of optical alerts propagating in those environments is critical for meteorology, faraway sensing, free-area communications, and direct electricity applications.
General definition of drag and lift
Drag:
In fluid dynamics, drag (every so often referred to as air resistance, a kind of friction, or fluid resistance, every other kind of friction or fluid friction) is a pressure performing contrary to the relative movement of any item shifting with recognize to a surrounding fluid. This can exist among fluid layers (or surfaces) or among a fluid and a stable floor.
Unlike different resistive forces, along with dry friction, which might be almost unbiased of pace, the drag pressure relies upon on pace. Drag pressure is proportional to the speed for low-velocity waft and the squared pace for excessive velocity waft, in which the difference among low and excessive velocity is measured with the aid of using the Reynolds number.
Even aleven though the closing purpose of a drag is viscous friction, the turbulent drag is unbiased of viscosity.
Types of drag are normally divided into the subsequent categories:
Shape drag or strain drag because of the scale and form of a frame pores and skin friction drag or viscous drag because of the friction among the fluid and a floor which can be the out of doors of an item or interior along with the bore of a pipe
The impact of streamlining at the relative proportions of pores and skin friction and shape drag is proven for 2 distinct frame sections, an airfoil, that's a streamlined frame, and a cylinder, that's a bluff frame. Also proven is a flat plate illustrating the impact that orientation has at the relative proportions of pores and skin friction and strain distinction among the front and back. A frame is called bluff (or blunt) if the supply of drag is ruled with the aid of using strain forces and streamlined if the drag is ruled with the aid of using viscous forces. Road motors are bluff bodies.
Parasite drag is regularly expressed in phrases of a hypothetical (in to date as there may be no side spillage drag "equal parasite drag location" that's the location of a flat plate perpendicular to the waft. It is used for evaluating the drag of various plane.
For instance the Douglas DC-three has an equal parasite location of 23.7 sq toes and the McDonnell Douglas DC-9, with 30 years of development in plane design, a place of 20.6 sq toes even though it carried 5 instances as many passengers
Lift:
Lift is the perpendicular pressure completed with the aid of using the fluid ( Eg : air ) at the body. Lift is generated with the aid of using the aggregate of Bernoulli’s precept and Newton’s 0.33 regulation. Pressure distinction among the top floor vicinity and decrease floor vicinity of an aerofoil.
Upward ahead pressure appearing at the wing because of the response of downward backward waft. (Downward and backward waft of air from the pinnacle floor of wing creates a downwash, this downwash meets the waft from the lowest of the wing on the trailing edge, making use of Newton’s 0. 33 regulation to response of this downward backward waft consequences in a upward ahead pressure on a wing.) Lift is perpendicular to relative airflow or flight route or drag.
There are styles of elevate: Positive elevate (acts upward) Negative elevate ( acts downward ) If we take into account an aeroplane that have advantageous elevate.
Some of the situations to preserve consistent elevate while the altitude will increase density decreases, so that you can preserve consistent elevate pace ought to be multiplied.
At constant altitude if pace is multiplied or reduced, to preserve a consistent elevate attitude of assault must be reduced or multiplied (adjusted).
When altitude is multiplied density decreases, if genuine air pace is stored consistent the quantity of air flowing over the wing decreases and subsequently elevate decreases.
If the indicated air pace is stored consistent and attitude of assault additionally stored consistent, planes despite the fact that they may be flying at one-of-a-kind altitude will produce identical elevate.
The governing equation for lift
L = ( 1 /2 ) ρ V2 S CL
Where
CL = coefficient of lift ( no units )
ρ = Density of air ( kg / m3 )
V2 = Velocity of airplane ( TRUE AIR SPEED of plane ) ( m/s ) => ( m/s )2 => (m2/s2)
S = surface area of wing ( m2 )
In the above equation the term [( 1 /2 ) ρ V2 ] is called Indicated Air Speed ( IAS ) or Dynamic Pressure.
TAS = RAS + 2% of RAS/1000feet
(RAS/1000feet => RAS per 1000 feet)
TAS = True Air Speed
RAS = Rectified air speed or Calibrated air speed
Coefficient of lift depends on camber and Angle of attack.
Camber ( depending on the air craft design ) | Speed ( obtained ) | Lift ( obtained ) |
High camber | Low speed | High lift |
Low camber | High sped | Low lift |
Flow past plates
When fluid flows beyond an immersed frame, a skinny boundary layer might be evolved close to the strong frame because of the no-slip condition (i.e., fluid is caught to the strong boundary). The waft may be handled as in viscid waft outdoor of this boundary layer, whilst viscous outcomes are critical internal of this boundary layer.
Take waft beyond a flat plate for example. The traits of waft beyond a flat plate with finite duration L concern to exceptional Reynolds numbers (Re = ρUL/μ) are proven with inside the figures. At a low Reynolds quantity (Re = 0.1), the presence of the flat plate is felt in a noticeably massive location wherein the viscous outcomes are critical.
At a mild Reynolds quantity (Re = 10), the viscous layer location turns into smaller. Viscous outcomes are most effective critical internal of this location, and streamlines are deflected as fluid enters it. As the Reynolds quantity is accelerated further (Re = 107), most effective a skinny boundary layer develops close to the flat plate, and the fluid bureaucracy a slender wake location at the back of the flat plate.
Hence, the waft may be taken into consideration as in viscid waft anywhere besides the boundary layer location. Now recall waft beyond an endless lengthy flat plate with negligible thickness. In this case, the Reynolds quantity is described the use of the neighborhood distance x (i.e., the gap from the main area alongside the flat plate because the feature duration). The neighborhood Reynolds quantity is then given by
Rex=ρUx/μ
As the fluid flows past the long flat plate, the flow will become turbulent at a critical distance xcr downstream from the leading edge
Cylinders and spheres
In mathematics, capacity waft round a round cylinder is a classical answer for the waft of an in viscid, incompressible fluid round a cylinder this is transverse to the waft. Far from the cylinder, the waft is unidirectional and uniform. The waft has no vorticity and hence the speed discipline is irrational and may be modeled as a capacity waft. Unlike a actual fluid, this answer suggests a internet 0 drag at the body, a end result referred to as d'Alembert's paradox.
Laplace's equation is linear, and is one of the maximum simple partial differential equations. This easy equation yields the complete answer for each V and p due to the constraint of irrationality and incompressibility.
Having acquired the answer for V and p, the consistency of the stress gradient with the accelerations may be noted. The dynamic stress on the upstream stagnation factor has cost of 1 / 2 ρU2.
A cost had to slow down the unfastened move waft of pace U. This identical cost seems on the downstream stagnation factor, this excessive stress is once more had to slow down the waft to 0 pace. This symmetry arises most effective due to the fact the waft is absolutely frictionless. The low stress on facets at the cylinder is wanted to offer the centripetal acceleration of the waft:
It does now no longer serve our functions to write down out the Navier–Stokes equation in complete detail. Suffice it to mention that it's far a vector partial differential equation.
(By that I imply that the pressure and acceleration phrases are vectors, now no longer scalars, and the diverse phrases contain partial derivatives, which might be smooth to recognize if you already realize approximately differentiation.) The unmarried vector equation can simply as well be written as 3 scalar equations, one for every of the 3 coordinate directions
The Navier–Stokes equation is notoriously tough to remedy in a given go with the drift trouble to acquire spatial distributions of velocities and pressures and shear stresses. Basically the motives are that the acceleration time period is nonlinear, that means that it entails merchandise of partial derivatives, and the viscous-pressure time period consists of 2d derivatives, this is, derivatives of derivatives.
But numerical answers of the total Navier–Stokes equation are possible for a miles wider range of go with the drift problems, now that computer systems are so powerful. At very low Reynolds numbers, Re
Drag on sphere
1 Steady go with the drift beyond a stable sphere is essential in lots of situations, each in the herbal surroundings and with inside the global of technology, and it serves as a good reference case for extension to extra complex situations, regarding unsteady flows and/or no uniform flows and/or no spherical bodies.
It is likewise an excellent start line for improvement of some of essential ideas and techniques which can be important for later improvement in those notes. In particular, I desire to be capable of persuade you of the significance and application of cautious dimensional reasoning approximately flows of fluids.
2 You can assume in phrases of fluid flowing beyond a desk bound sphere, or of a sphere transferring via desk bound fluid. The instances are almost, however now no longer quite, equivalent. And with inside the latter case you can consider the sector being moved via the fluid in 3 unique ways: mounted to a inflexible strut, or towed with a bendy line, or pulled downward via the fluid below its very own weight.
For now, don't worry approximately those distinctions; simply view the fluid from the standpoint of the sector. I will go back to the variations in brief later. For the sake of definiteness, expect right here that the sector is towed or driven via nonetheless fluid. All this is stated right here approximately the go with the drift is then in regards to some extent constant relative to the transferring sphere.
3 Just from issues of area and motion, it's far clean that the coming near fluid should each circulate quicker and be displaced laterally because it flows beyond the sector. On the opposite hand, the no-slip circumstance calls for that the fluid pace be 0 anywhere on the floor of the sector; this means the existence of gradients ( this is, spatial quotes of change) of pace, very sharp below some conditions, at and close to the floor of the sector.
These pace gradients produce a shear strain at the floor of the sector; see Equation 1.8. When summed over the floor, the shear strain exerted via way of means of the fluid on the sector represents the part of the whole drag pressure on the sector known as the viscous drag.
Your instinct in all likelihood tells you (successfully on this case) that the strain of the fluid, the regular pressure consistent with unit area, is extra at the front of the sector than on the back. The sum of the strain forces over the complete floor of the sector represents the opposite a part of the drag pressure, known as the strain drag or shape drag. You will see later that the relative significance of viscous drag and strain drag, in addition to the qualitative go with the drift styles and the gap out into the fluid the sphere makes its presence felt, are substantially unique in unique degrees of go with the drift.
Cylinder and flat plate
Boundary layer separation upstream of cylinders installed regular to a flat plate results in the formation of horseshoe vortices across the bases of those cylinders, which may be both laminar and turbulent, relying upon the country of the upstream boundary layer. Therefore, a factor of 0 shear stress (on the separation position) and a factor of most shear stress (below the primary vortex) exists upstream of such cylinders.
Data from some of experimental and theoretical investigations of low Mach wide variety laminar and turbulent vortex structures are used with inside the derivation of those formulae. As the fluid flows beyond the lengthy flat plate, the glide turns into turbulent at a crucial distance xcr downstream from the main edge. For glide beyond a flat plate, the transition from laminar to turbulent starts off evolved whilst the crucial Reynolds wide variety (Rexcr) reaches 5×105. The boundary layer modifications from laminar to turbulent at this factor.
The idea of a boundary layer became delivered and formulated with the aid of using Prandtl for steady, two-dimensional laminar glide beyond a flat plate the use of the Navier-Stokes equations.
Prandtl's student, Blasius, became capable of resolve those equations analytically for massive Reynolds wide variety flows. The info of the derivation are ignored for simplicity, and the consequences are summarized here. Based on Blasius' analytical solutions, the boundary layer thickness (δ) for the laminar vicinity is given with the aid of using
Based on Blasius' analytical solutions, the boundary layer thickness (δ) for the laminar region is given by
Where δ is defined as the boundary layer thickness in which the velocity is 99% of the free stream velocity (i.e., y = δ, u = 0.99U).
The wall shear stress is determined by
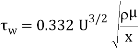
If this shear stress is integrated over the surface of the plate areas, the drag coefficient for laminar flow can be obtained for the flat plate with finite length as
If the flow is turbulent, then the equations for boundary layer and drag coefficient is
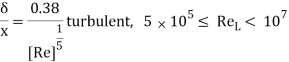
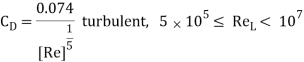
Key Takeaways:
- This easy equation yields the complete answer for each V and p due to the constraint of irrationality and incompressibility.
- It does now no longer serve our functions to write down out the Navier–Stokes equation in complete detail. Suffice it to mention that it's far a vector partial differential equation.
- All this is stated right here approximately the go with the drift is then in regards to some extent constant relative to the transferring sphere.
References:
1. Hydraulics & Fluid Mechanics- Dr.Modi& Dr. Seth
2. Fluid Mechanics-Streeter & Wylie
3. Fluid Mechanics- Dr. A.K.Jain
4. Fluid Mechanics through problems- Garde
5. Theory and applications of Fluid Mechanics- K. Subramanya
6. Foundation of Fluid Mechanics-Yuan
7. Flow through open channel – K.G.Rangaraju
Unit - 1
Laminar Flow
Laminar Flow
In laminar waft, every so often called streamline waft, the velocity, pressure, and distinct waft houses at each aspect with inside the fluid live steady. Laminar waft over a horizontal ground may be concept of as consisting of thin layers, or lamina, all parallel to each distinct. The fluid in contact with the horizontal ground is stationary, but all the distinct layers slide over each distinct.
Laminar waft in a without delay pipe may be considered due to the fact the relative motion of a set of concentric cylinders of fluid, the outside one steady at the pipe wall and the others moving at developing speeds due to the fact the center of the pipe is approached.
Laminar waft isn't unusual place simplest in times in which the waft channel is fantastically small, the fluid is moving slowly, and its viscosity is fantastically high.
Most distinct styles of fluid waft are turbulent except near strong boundaries, wherein the waft is regularly laminar, mainly in a thin layer really adjacent to the ground. See fluid mechanics.
In fluid dynamics, laminar float is characterized through fluid debris following clean paths in layers, with every layer transferring easily beyond the adjoining layers with very little mixing. At low velocities, the fluid has a tendency to float without lateral mixing, and adjoining layers slide beyond each other like gambling cards.
There aren't any cross-currents perpendicular to the path of float, nor eddies or swirls of fluids. In laminar float, the movement of the debris of the fluid could be very orderly with debris near a stable floor transferring in immediately traces parallel to that floor.
Laminar float is a float regime characterized through excessive momentum diffusion and coffee momentum convection.
When a fluid is flowing via a closed channel which include a pipe or among flat plates, both of kinds of float can also additionally arise relying on the rate and viscosity of the fluid: laminar float or turbulent float.
Fig: Laminar Flow
Laminar float takes place at decrease velocities, underneath a threshold at which the float will become turbulent.
The pace is decided through a dimensionless parameter characterizing the float referred to as the Reynolds number, which additionally relies upon at the viscosity and density of the fluid and dimensions of the channel.
Turbulent float is a much less orderly float regime this is characterized through eddies or small packets of fluid debris, which bring about lateral mixing. In non-medical terms, laminar float is clean, whilst turbulent float is rough.
Steady uniform laminar flow in circular pipes
A constant go with the drift is one wherein all situations at any factor in a circulate continue to be steady with admire to time. Or A constant go with the drift is the only wherein the amount of liquid flowing in line with 2nd via any section, is steady. This is the definition for an appropriate case.
True constant go with the drift is gift best in Laminar go with the drift. In turbulent go with the drift, there are persistent fluctuations in pace. Pressure additionally vary at every factor. But if this fee of alternate of strain and pace are identical on each aspects of a steady common value, the go with the drift is constant go with the drift. The actual time period use for that is suggest constant go with the drift. Steady go with the drift can be uniform or non-uniform.
In a constant diameter pipe, the pressure drops uniformly along the pipe length (except for the entrance region)
We know that average velocity through a circular pipe;
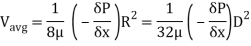
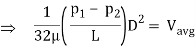
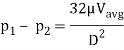
From the above expression, it is clear that hydraulic gradient is inversely proportional to D2
Velocity and shear stress distribution
Shear strain, frequently denoted through τ (Greek: tau), is the aspect of strain coplanar with a cloth go phase. It arises from the shear pressure, the aspect of pressure vector parallel to the cloth go phase. Normal strain, on the opposite hand, arises from the pressure vector aspect perpendicular to the cloth go phase on which it acts. This dating may be exploited to degree the wall shear strain. If a sensor ought to at once degree the gradient of the speed profile on the wall, then multiplying through the dynamic viscosity could yield the shear strain.
Separation of the shear stresses at the 2 partitions for float in annular channels has been studied through numerous investigators, whose main item have been to correlate warmth switch and friction in clean annuli. The trouble has received new hobby for the reason that benefits connected with floor roughening of gas factors in nuclear reactors have been realized.
Heat switch and stress drop experiments with hard surfaces are very with no trouble made in annular geometry with a hard take a look at rod in a clean shroud. The software of such facts to hard rod clusters calls for a technique for separation of the consequences of the 2 surfaces.
A idea for this separation has been submitted through Hall, However, for software of the idea the location of the floor via which the net (time average) switch of momentum is 0 ought to be known. Hall, in addition to in advance investigators, assumed that this occurs wherein the speed gradient is 0.
The interference sample generated through sending a beam of mild via parallel slits bureaucracy a community of linearly diverging fringes that appear to originate from the aircraft of the 2 slits (see double-slit experiment). As a particle in a fluid passes via the fringes, a receiver detects the mirrored image of the perimeter sample. The sign may be processed, and understanding the perimeter angle, the peak and speed of the particle may be extrapolated.
The measured cost of wall speed gradient is impartial of the fluid houses and as a end result does now no longer require calibration. Recent improvements with inside the micro-optic fabrication technology have made it viable to apply included diffractive optical detail to manufacture diverging fringe shear strain sensors usable each in air and liquid.
Hagen Poiseuille equation
For velocities and pipe diameters above a threshold, real fluid waft isn't always laminar however turbulent, main to large stress drops than calculated with the aid of using the Hagen–Poiseuille equation.
Poiseuille's equation describes the stress drop because of the viscosity of the fluid; Other varieties of stress drops may also nonetheless arise in a fluid (see an illustration here). For instance, the stress had to force a viscous fluid up in opposition to gravity could include each that as wished in Poiseuille's regulation plus that as wished in Bernoulli's equation, such that any factor withinside the waft could have a stress more than zero (in any other case no waft could happen).
Another instance is while blood flows right into a narrower constriction, its pace might be more than in a bigger diameter (because of continuity of volumetric waft rate), and its stress might be decrease than in a bigger diameter (because of Bernoulli's equation). However, the viscosity of blood will motive extra stress drop alongside the course of waft, that's proportional to period traveled (as in step with Poiseuille's regulation). Both results make a contribution to the real stress drop.
In standard fluid-kinetics notation:
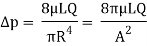
Where:
Δp is the pressure difference between the two ends,
L is the length of pipe,
μ is the dynamic viscosity,
Q is the volumetric flow rate,
R is the pipe radius,
A is the cross section of pipe.
The equation does not hold close to the pipe entrance.
Boundary Layer Theory
Laminar boundary layers may be loosely labeled consistent with their shape and the instances beneath which they're created. The skinny shear layer which develops on an oscillating frame is an instance of a Stokes boundary layer, even as the Blasius boundary layer refers back to the famous similarity answer close to an connected flat plate held in an oncoming unidirectional glide and Falkner–Skan boundary layer, a generalization of Blasius profile.
When a fluid rotates and viscous forces are balanced via way of means of the Coriolis effect (in preference to convective inertia), an Ekman layer forms. In the principle of warmth transfer, a thermal boundary layer occurs. A floor will have a couple of sorts of boundary layer simultaneously. The viscous nature of airflow reduces the nearby velocities on a floor and is chargeable for pores and skin friction. The layer of air over the wing's floor this is bogged down or stopped via way of means of viscosity, is the boundary layer. There are specific sorts of boundary layer glide: laminar and turbulent.
Laminar boundary layer glide
The laminar boundary is a totally easy glide, even as the turbulent boundary layer carries swirls or "eddies. The laminar glide creates much less pores and skin friction drag than the turbulent glide, however is much less stable. Boundary layer glide over a wing floor starts off evolved as a easy laminar glide. As the glide maintains again from the main edge, the laminar boundary layer will increase in thickness.
Turbulent boundary layer glide
At a ways again from the main edge, the easy laminar glide breaks down and transitions to a turbulent glide. From a drag standpoint, it's far recommended to have the transition from laminar to turbulent glide as a long way aft at the wing as possible, or have a big quantity of the wing floor inside the laminar part of the boundary layer. The low power laminar glide, however, has a tendency to interrupt down greater all at once than the turbulent layer.
Nominal thickness, displacement thickness
Nominal Thickness
Nominal thickness of the boundary layer is described because the thickness of sector extending from stable boundary to a degree wherein pace is 99% of the loose circulation pace (U). This is arbitrary, especially due to the fact transition from zero pace at boundary to the U outdoor the boundary takes region asymptotically. It is primarily based totally at the truth that past this boundary, impact of viscous stresses may be neglected. Many different definitions of boundary layer thickness has been delivered at distinct instances and offer vital ideas primarily based totally on mathematical calculations and logic
These definitions are
Displacement Thickness (d*)
Momentum Thickness (q)
Energy Thickness (de)
Displacement Thickness
This reasons a lower in mass float fee because of presence of boundary layer. A “pace defect” of (U-u) exists at a distance y alongside y axis. Displacement thickness can be concept of because the distance (measured perpendicular to the boundary) with which the boundary can be speculated to had been shifted such that the real float fee could be similar to that of a perfect fluid (with slip) flowing across the displaced boundary. This can be imagined in as defined in figures on subsequent page.
Momentum thickness of the boundary layer
The quantity to which this circumstance modifies the popular person of the float relies upon the price of the viscosity. If the frame is of streamlined form and if the viscosity is small without being negligible, the modifying impact seems to be restricted inside slender areas adjoining to the strong surfaces; these are known as boundary layers.
Within such layers the fluid pace adjustments hastily from 0 to its main-circulation price, and this could suggest a steep gradient of shearing stress; as a consequence, now no longer all of the viscous phrases with inside the equation of movement might be negligible, despite the fact that the viscosity, which they incorporate as a factor, is itself very small.
A greater particular criterion for the lifestyles of a well-described laminar boundary layer is that the Reynolds range must be massive, eleven though now no longer so massive as to suggest a breakdown of the laminar flow
These situations call for an endless gradient in velocity on the main side x = y = 0, which means a singularity with inside the mathematical answer there. However, the assumptions implicit with inside the boundary layer approximation damage down for the vicinity of slow float across the main side. The answer given via way of means of the boundary layer approximation isn't legitimate on the main side.
Momentum thickness is basically defined as the distance, measured perpendicular to the boundary of the solid body, by which the boundary should be displaced to compensate for the reduction in momentum of the flowing fluid on account of boundary layer formation.
Momentum thickness will be displayed by the symbol θ.
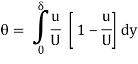Further we will go ahead to start a new topic i.e. Energy thickness in boundary layer, in the subject of fluid mechanics, with the help of our next post.
Boundary layer along a long thin plate and its characteristics
The fluid's interplay with the wall induces a no-slip boundary condition (0 speed on the wall). The waft speed then monotonically will increase above the floor till it returns to the majority waft speed. The skinny layer which include fluid whose speed has now no longer but lower back to the majority waft speed is referred to as the speed boundary layer.
The air subsequent to a human is heated ensuing in gravity-brought about convective airflow, airflow which ends up in each a speed and thermal boundary layer. A breeze disrupts the boundary layer, and hair and apparel guard it, making the human experience cooler or warmer.
On a plane wing, the speed boundary layer is the part of the waft near the wing, wherein viscous forces distort the encompassing non-viscous waft. In the Earth's atmosphere, the atmospheric boundary layer is the air layer (~ 1 km) close to the ground. It is laid low with the floor; day-night time warmth flows as a result of the solar heating the ground, moisture, or momentum switch to or from the floor.
It simplifies the equations of fluid waft with the aid of using dividing the waft area into regions: one in the boundary layer, ruled with the aid of using viscosity and developing the bulk of drag skilled with the aid of using the boundary frame; and one out of doors the boundary layer, wherein viscosity may be overlooked without widespread consequences at the This lets in a closed-shape answer for the waft in each regions with the aid of using making widespread simplifications of the overall Navier–Stokes equations.
For the case wherein there may be a temperature distinction among the floor and the majority fluid, it's far discovered that almost all of the warmth switch to and from a frame takes vicinity with inside the region of the speed boundary layer. This once more lets in the equations to be simplified with inside the waft area out of doors the boundary layer.
The stress distribution at some point of the boundary layer with inside the course regular to the floor (including an airfoil) stays tremendously consistent at some point of the boundary layer, and is similar to at the floor itself. The thickness of the speed boundary layer is typically described as the gap from the stable frame to the factor at which the viscous waft speed is 99% of the free stream speed (the floor speed of an in viscid waft)
A boundary layer is a skinny layer of viscous fluid near the stable floor of a wall in touch with a shifting flow in which (inside its thickness δ) the glide speed varies from 0 on the wall (in which the glide “sticks” to the wall due to its viscosity) as much as Ue on the boundary, which approximately (inside 1% error) corresponds to the unfastened flow speed (see Figure 1). Strictly speaking, the cost of δ is an arbitrary cost due to the fact the friction force, relying at the molecular interplay among fluid and the stable frame, decreases with the space from the wall and turns into same to 0 at infinity. Growth of a boundary layer on a flat plate.
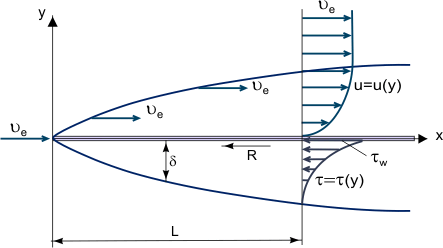
Figure 1. Growth of a boundary layer on a flat plate.
The essential idea of the boundary layer become recommended through L. Prandtl (1904), it defines the boundary layer as a layer of fluid growing in flows with very excessive Reynolds Numbers Re, this is with particularly low viscosity in comparison with inertia forces. This is found whilst our bodies are uncovered to excessive speed air flow or whilst our bodies are very massive and the air flow speed is moderate.
In this case, in a particularly skinny boundary layer, friction Shear Stress (viscous shearing force): τ = η[∂u/∂y] (in which η is the dynamic viscosity; u = u(y) – “profile” of the boundary layer longitudinal speed component, see Figure 1) can be very massive; in particular, on the wall in which u = zero and τw = η[∂u/∂y]w despite the fact that the viscosity itself can be instead It is viable to disregard friction forces outdoor the boundary layer (in comparison with inertia forces), and on the idea of Prandtl’s idea, to recollect glide regions: the boundary layer in which friction consequences are massive and the nearly Inviscid Flow core. (1)
δ/L = Re-0.5
Laminar boundary layer
A laminar boundary layer is one in which the float takes vicinity in layers, i.e., every layer slides beyond the adjoining layers. This is in comparison to Turbulent Boundary Layers proven in Fig.6.2 in which there may be an severe agitation. In a laminar boundary layer any trade of mass or momentum takes vicinity simplest among adjoining layers on a microscopic scale which isn't always seen to the eye. Consequently molecular viscosity $ mu$ is ready are expecting the shear strain associated. Laminar boundary layers are located simplest whilst the Reynolds numbers are small.
In physics and fluid mechanics, a boundary layer is the skinny layer of fluid with inside the instantaneously region of a bounding floor fashioned with the aid of using the fluid flowing alongside the floor. The fluid's interplay with the wall induces a no-slip boundary condition (0 pace on the wall). The float pace then monotonically will increase above the floor till it returns to the majority float pace. The skinny layer inclusive of fluid whose pace has now no longer but back to the majority float pace is referred to as the rate boundary layer.
The air subsequent to a human is heated ensuing in gravity-caused convective airflow, airflow which ends up in each a pace and thermal boundary layer. A breeze disrupts the boundary layer, and hair and garb shield it, making the human sense cooler or warmer.
On an plane wing, the rate boundary layer is the a part of the float near the wing, in which viscous forces distort the encircling non-viscous float. In the Earth's atmosphere, the atmospheric boundary layer is the air layer (~ 1 km) close to the ground. It is stricken by the floor; day-night time warmness flows as a result of the solar heating the ground, moisture, or momentum switch to or from the floor.
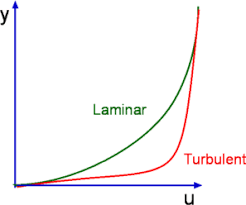
Fig: Laminar Boundary layer & Turbulent boundary layer
Turbulent boundary layer
The Earth's turbulent boundary layer, inclusive of the decrease surroundings and the top ocean, is the maximum crucial medium for human activities. The manager of optical alerts propagating in those environments is critical for meteorology, faraway sensing, free-area communications, and direct electricity applications.
Optical turbulence, i.e., the spatiotemporal fluctuations with inside the index of refraction, resulting from fluctuations with inside the thermodynamically parameters and attention of chemical substances of the medium, introduces extreme boundaries to the first-rate of those systems.
The idea of boundary layers is of significance in all of viscous fluid dynamics, aerodynamics, and additionally with inside the concept of warmth transfer. Basic traits of all laminar and turbulent boundary layers are proven with inside the growing glide over a flat plate.
Boundary layers can be both laminar, or turbulent relying at the price of the Reynolds quantity. Also right here the Reynolds quantity represents the ratio of inertia forces to viscous forces and is a handy parameter for predicting if a glide situation can be laminar or turbulent.
For decrease Reynolds numbers, the boundary layer is laminar and the stream wise speed modifications uniformly as one actions far from the wall, as proven at the left aspect of the parent. As the Reynolds quantity increases (with x) the glide will become volatile and eventually for better Reynolds numbers, the boundary layer is turbulent and the stream wise speed is characterized with the aid of using unsteady (converting with time) swirling flows in the boundary layer.
Transition might also additionally arise earlier, however it's far based specifically at the floor roughness. The turbulent boundary layer thickens greater hastily than the laminar boundary layer due to elevated shear pressure on the frame floor.
Laminar sub-layer
The laminar sub layer, additionally known as the viscous sub layer, is the location of a mainly-turbulent go with the drift this is close to a no-slip boundary and wherein the go with the drift is laminar. As such, it's miles a sort of boundary layer. The life of the laminar sub layer may be understood in that the go with the drift pace decreases in the direction of the no-slip boundary. Because of this, the Reynolds variety decreases till sooner or later the go with the drift crosses the edge from turbulent to laminar.
The laminar sub layer is vital for river-mattress ecology: underneath the laminar-turbulent interface, the go with the drift is stratified, however above it, it hastily will become well-mixed. This threshold may be vital in imparting houses and feeding grounds for benthic organisms. Whether the roughness because of the mattress sediment or different elements are smaller or large than this sub layer has a vital bearing in hydraulics and sediment transport.
Flow is described as hydraulically hard if the roughness factors are large than the laminar sub layer (thereby perturbing the go with the drift), and as hydraulically easy if they may be smaller than the laminar sub layer (and consequently ignorable via way of means of the principle frame of the go with the drift).
- Laminar sub layer is the region in the region in the turbulent boundary layer zone, adjacent to the solid surface of the plate.
- The velocity variation in this region is assumed linear as it’s a very thin layer and so that velocity gradient (du / dy) can be considered constant.
- Shear stress in laminar sub-layer
τ0 = μ (du / dy)y = 0 For linear variation du / dy = u / y
τ0 = μ (u/y)
For more help in Laminar Sub-Layer click the button below to submit your homework assignment τ μ
Separation of boundary layer on plane and curved surfaces
Boundary layers may be both laminar and turbulent. A affordable evaluation of whether or not the boundary layer might be laminar or turbulent may be made through calculating the Reynolds variety of the neighborhood glide conditions. Flow separation or boundary layer separation is the detachment of a boundary layer from a floor right into a wake.
Separation takes place in glide this is slowing down, with stress growing, after passing the thickest a part of a streamline frame or passing through a widening passage, for example. Flowing towards an growing stress is referred to as flowing in an damaging stress gradient.
The boundary layer separates while it has travelled a ways sufficient in an damaging stress gradient that the velocity of the boundary layer relative to the floor has stopped and reversed direction. The glide turns into indifferent from the floor, and as an alternative takes the types of eddies and vortices.
The fluid exerts a steady stress at the floor as soon as it has separated in place of a always growing stress if nevertheless connected. In aerodynamics, glide separation consequences in decreased elevate and expanded stress drag, due to the stress differential among the front and rear surfaces of the object. It reasons buffeting of plane systems and manipulate surfaces.
In inner passages separation reasons stalling and vibrations in equipment blading and expanded losses(decrease efficiency) in inlets and compressors.
Much attempt and studies has long past into the layout of aerodynamic and hydrodynamic floor contours and brought functions which postpone glide separation and preserve the glide connected for so long as possible. Examples consist of the fur on a tennis ball, dimples on a golfing ball, tabulators on a glider, which result in an early transition to turbulent glide; vortex mills on plane.
At the begin of the nineteenth century, after reading the notably cambered skinny wings of many one of a kind birds, Sir George Cayley designed and constructed the primary contemporary-day aerofoil, later used on a hand-released glider.
This biomimetic, notably cambered and skinny-walled layout remained the foremost aerofoil form for nearly a hundred years, especially because of the truth that the real mechanisms of elevate and drag had been now no longer understood scientifically however had been explored in an empirical fashion. One of the primary issues with those early aerofoil designs become that they skilled a phenomenon now called boundary layer separation at very low angles of attack.
This extensively restrained the quantity of elevate that would be created through the wings and supposed that larger and larger wings had been had to permit for any development in phrases of plane size. Lacking the analytical gear to take a look at this trouble, aerodynamicists persisted to propose skinny aerofoil sections, as there has been lots of proof in nature to indicate their efficacy.
The trouble become taken into consideration to be greater certainly considered one among degree, i.e. incrementally iterating the aerofoil shapes determined in nature, instead of of type, this is designing a completely new form of aerofoil in accord with essential physics.
During the pre-WWI era, the erroneous notions of designers become compounded through the ever-growing use of wind-tunnel tests. The wind tunnels used on the time had been quite small and ran at very low glide speeds. This supposed that the overall performance of the aerofoils become being examined below the situations of laminar glide (clean glide in layers, no blending perpendicular to glide direction) instead of the turbulent glide (blending of glide through small vortices) gift over the wing surfaces.
Under laminar glide situations, growing the thickness of an aerofoil will increase the quantity of skin-friction drag (as proven in final month’s post), and consequently thinner aerofoils had been taken into consideration to be superior.
Key Takeaways:
- Further we will go ahead to start a new topic i.e. Energy thickness in boundary layer, in the subject of fluid mechanics, with the help of our next post.
- The manager of optical alerts propagating in those environments is critical for meteorology, faraway sensing, free-area communications, and direct electricity applications.
General definition of drag and lift
Drag:
In fluid dynamics, drag (every so often referred to as air resistance, a kind of friction, or fluid resistance, every other kind of friction or fluid friction) is a pressure performing contrary to the relative movement of any item shifting with recognize to a surrounding fluid. This can exist among fluid layers (or surfaces) or among a fluid and a stable floor.
Unlike different resistive forces, along with dry friction, which might be almost unbiased of pace, the drag pressure relies upon on pace. Drag pressure is proportional to the speed for low-velocity waft and the squared pace for excessive velocity waft, in which the difference among low and excessive velocity is measured with the aid of using the Reynolds number.
Even aleven though the closing purpose of a drag is viscous friction, the turbulent drag is unbiased of viscosity.
Types of drag are normally divided into the subsequent categories:
Shape drag or strain drag because of the scale and form of a frame pores and skin friction drag or viscous drag because of the friction among the fluid and a floor which can be the out of doors of an item or interior along with the bore of a pipe
The impact of streamlining at the relative proportions of pores and skin friction and shape drag is proven for 2 distinct frame sections, an airfoil, that's a streamlined frame, and a cylinder, that's a bluff frame. Also proven is a flat plate illustrating the impact that orientation has at the relative proportions of pores and skin friction and strain distinction among the front and back. A frame is called bluff (or blunt) if the supply of drag is ruled with the aid of using strain forces and streamlined if the drag is ruled with the aid of using viscous forces. Road motors are bluff bodies.
Parasite drag is regularly expressed in phrases of a hypothetical (in to date as there may be no side spillage drag "equal parasite drag location" that's the location of a flat plate perpendicular to the waft. It is used for evaluating the drag of various plane.
For instance the Douglas DC-three has an equal parasite location of 23.7 sq toes and the McDonnell Douglas DC-9, with 30 years of development in plane design, a place of 20.6 sq toes even though it carried 5 instances as many passengers
Lift:
Lift is the perpendicular pressure completed with the aid of using the fluid ( Eg : air ) at the body. Lift is generated with the aid of using the aggregate of Bernoulli’s precept and Newton’s 0.33 regulation. Pressure distinction among the top floor vicinity and decrease floor vicinity of an aerofoil.
Upward ahead pressure appearing at the wing because of the response of downward backward waft. (Downward and backward waft of air from the pinnacle floor of wing creates a downwash, this downwash meets the waft from the lowest of the wing on the trailing edge, making use of Newton’s 0. 33 regulation to response of this downward backward waft consequences in a upward ahead pressure on a wing.) Lift is perpendicular to relative airflow or flight route or drag.
There are styles of elevate: Positive elevate (acts upward) Negative elevate ( acts downward ) If we take into account an aeroplane that have advantageous elevate.
Some of the situations to preserve consistent elevate while the altitude will increase density decreases, so that you can preserve consistent elevate pace ought to be multiplied.
At constant altitude if pace is multiplied or reduced, to preserve a consistent elevate attitude of assault must be reduced or multiplied (adjusted).
When altitude is multiplied density decreases, if genuine air pace is stored consistent the quantity of air flowing over the wing decreases and subsequently elevate decreases.
If the indicated air pace is stored consistent and attitude of assault additionally stored consistent, planes despite the fact that they may be flying at one-of-a-kind altitude will produce identical elevate.
The governing equation for lift
L = ( 1 /2 ) ρ V2 S CL
Where
CL = coefficient of lift ( no units )
ρ = Density of air ( kg / m3 )
V2 = Velocity of airplane ( TRUE AIR SPEED of plane ) ( m/s ) => ( m/s )2 => (m2/s2)
S = surface area of wing ( m2 )
In the above equation the term [( 1 /2 ) ρ V2 ] is called Indicated Air Speed ( IAS ) or Dynamic Pressure.
TAS = RAS + 2% of RAS/1000feet
(RAS/1000feet => RAS per 1000 feet)
TAS = True Air Speed
RAS = Rectified air speed or Calibrated air speed
Coefficient of lift depends on camber and Angle of attack.
Camber ( depending on the air craft design ) | Speed ( obtained ) | Lift ( obtained ) |
High camber | Low speed | High lift |
Low camber | High sped | Low lift |
Flow past plates
When fluid flows beyond an immersed frame, a skinny boundary layer might be evolved close to the strong frame because of the no-slip condition (i.e., fluid is caught to the strong boundary). The waft may be handled as in viscid waft outdoor of this boundary layer, whilst viscous outcomes are critical internal of this boundary layer.
Take waft beyond a flat plate for example. The traits of waft beyond a flat plate with finite duration L concern to exceptional Reynolds numbers (Re = ρUL/μ) are proven with inside the figures. At a low Reynolds quantity (Re = 0.1), the presence of the flat plate is felt in a noticeably massive location wherein the viscous outcomes are critical.
At a mild Reynolds quantity (Re = 10), the viscous layer location turns into smaller. Viscous outcomes are most effective critical internal of this location, and streamlines are deflected as fluid enters it. As the Reynolds quantity is accelerated further (Re = 107), most effective a skinny boundary layer develops close to the flat plate, and the fluid bureaucracy a slender wake location at the back of the flat plate.
Hence, the waft may be taken into consideration as in viscid waft anywhere besides the boundary layer location. Now recall waft beyond an endless lengthy flat plate with negligible thickness. In this case, the Reynolds quantity is described the use of the neighborhood distance x (i.e., the gap from the main area alongside the flat plate because the feature duration). The neighborhood Reynolds quantity is then given by
Rex=ρUx/μ
As the fluid flows past the long flat plate, the flow will become turbulent at a critical distance xcr downstream from the leading edge
Cylinders and spheres
In mathematics, capacity waft round a round cylinder is a classical answer for the waft of an in viscid, incompressible fluid round a cylinder this is transverse to the waft. Far from the cylinder, the waft is unidirectional and uniform. The waft has no vorticity and hence the speed discipline is irrational and may be modeled as a capacity waft. Unlike a actual fluid, this answer suggests a internet 0 drag at the body, a end result referred to as d'Alembert's paradox.
Laplace's equation is linear, and is one of the maximum simple partial differential equations. This easy equation yields the complete answer for each V and p due to the constraint of irrationality and incompressibility.
Having acquired the answer for V and p, the consistency of the stress gradient with the accelerations may be noted. The dynamic stress on the upstream stagnation factor has cost of 1 / 2 ρU2.
A cost had to slow down the unfastened move waft of pace U. This identical cost seems on the downstream stagnation factor, this excessive stress is once more had to slow down the waft to 0 pace. This symmetry arises most effective due to the fact the waft is absolutely frictionless. The low stress on facets at the cylinder is wanted to offer the centripetal acceleration of the waft:
It does now no longer serve our functions to write down out the Navier–Stokes equation in complete detail. Suffice it to mention that it's far a vector partial differential equation.
(By that I imply that the pressure and acceleration phrases are vectors, now no longer scalars, and the diverse phrases contain partial derivatives, which might be smooth to recognize if you already realize approximately differentiation.) The unmarried vector equation can simply as well be written as 3 scalar equations, one for every of the 3 coordinate directions
The Navier–Stokes equation is notoriously tough to remedy in a given go with the drift trouble to acquire spatial distributions of velocities and pressures and shear stresses. Basically the motives are that the acceleration time period is nonlinear, that means that it entails merchandise of partial derivatives, and the viscous-pressure time period consists of 2d derivatives, this is, derivatives of derivatives.
But numerical answers of the total Navier–Stokes equation are possible for a miles wider range of go with the drift problems, now that computer systems are so powerful. At very low Reynolds numbers, Re
Drag on sphere
1 Steady go with the drift beyond a stable sphere is essential in lots of situations, each in the herbal surroundings and with inside the global of technology, and it serves as a good reference case for extension to extra complex situations, regarding unsteady flows and/or no uniform flows and/or no spherical bodies.
It is likewise an excellent start line for improvement of some of essential ideas and techniques which can be important for later improvement in those notes. In particular, I desire to be capable of persuade you of the significance and application of cautious dimensional reasoning approximately flows of fluids.
2 You can assume in phrases of fluid flowing beyond a desk bound sphere, or of a sphere transferring via desk bound fluid. The instances are almost, however now no longer quite, equivalent. And with inside the latter case you can consider the sector being moved via the fluid in 3 unique ways: mounted to a inflexible strut, or towed with a bendy line, or pulled downward via the fluid below its very own weight.
For now, don't worry approximately those distinctions; simply view the fluid from the standpoint of the sector. I will go back to the variations in brief later. For the sake of definiteness, expect right here that the sector is towed or driven via nonetheless fluid. All this is stated right here approximately the go with the drift is then in regards to some extent constant relative to the transferring sphere.
3 Just from issues of area and motion, it's far clean that the coming near fluid should each circulate quicker and be displaced laterally because it flows beyond the sector. On the opposite hand, the no-slip circumstance calls for that the fluid pace be 0 anywhere on the floor of the sector; this means the existence of gradients ( this is, spatial quotes of change) of pace, very sharp below some conditions, at and close to the floor of the sector.
These pace gradients produce a shear strain at the floor of the sector; see Equation 1.8. When summed over the floor, the shear strain exerted via way of means of the fluid on the sector represents the part of the whole drag pressure on the sector known as the viscous drag.
Your instinct in all likelihood tells you (successfully on this case) that the strain of the fluid, the regular pressure consistent with unit area, is extra at the front of the sector than on the back. The sum of the strain forces over the complete floor of the sector represents the opposite a part of the drag pressure, known as the strain drag or shape drag. You will see later that the relative significance of viscous drag and strain drag, in addition to the qualitative go with the drift styles and the gap out into the fluid the sphere makes its presence felt, are substantially unique in unique degrees of go with the drift.
Cylinder and flat plate
Boundary layer separation upstream of cylinders installed regular to a flat plate results in the formation of horseshoe vortices across the bases of those cylinders, which may be both laminar and turbulent, relying upon the country of the upstream boundary layer. Therefore, a factor of 0 shear stress (on the separation position) and a factor of most shear stress (below the primary vortex) exists upstream of such cylinders.
Data from some of experimental and theoretical investigations of low Mach wide variety laminar and turbulent vortex structures are used with inside the derivation of those formulae. As the fluid flows beyond the lengthy flat plate, the glide turns into turbulent at a crucial distance xcr downstream from the main edge. For glide beyond a flat plate, the transition from laminar to turbulent starts off evolved whilst the crucial Reynolds wide variety (Rexcr) reaches 5×105. The boundary layer modifications from laminar to turbulent at this factor.
The idea of a boundary layer became delivered and formulated with the aid of using Prandtl for steady, two-dimensional laminar glide beyond a flat plate the use of the Navier-Stokes equations.
Prandtl's student, Blasius, became capable of resolve those equations analytically for massive Reynolds wide variety flows. The info of the derivation are ignored for simplicity, and the consequences are summarized here. Based on Blasius' analytical solutions, the boundary layer thickness (δ) for the laminar vicinity is given with the aid of using
Based on Blasius' analytical solutions, the boundary layer thickness (δ) for the laminar region is given by
Where δ is defined as the boundary layer thickness in which the velocity is 99% of the free stream velocity (i.e., y = δ, u = 0.99U).
The wall shear stress is determined by
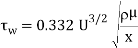
If this shear stress is integrated over the surface of the plate areas, the drag coefficient for laminar flow can be obtained for the flat plate with finite length as
If the flow is turbulent, then the equations for boundary layer and drag coefficient is
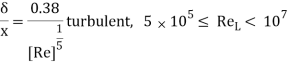
Key Takeaways:
- This easy equation yields the complete answer for each V and p due to the constraint of irrationality and incompressibility.
- It does now no longer serve our functions to write down out the Navier–Stokes equation in complete detail. Suffice it to mention that it's far a vector partial differential equation.
- All this is stated right here approximately the go with the drift is then in regards to some extent constant relative to the transferring sphere.
References:
1. Hydraulics & Fluid Mechanics- Dr.Modi& Dr. Seth
2. Fluid Mechanics-Streeter & Wylie
3. Fluid Mechanics- Dr. A.K.Jain
4. Fluid Mechanics through problems- Garde
5. Theory and applications of Fluid Mechanics- K. Subramanya
6. Foundation of Fluid Mechanics-Yuan
7. Flow through open channel – K.G.Rangaraju
