Unit - 4
Applications of Specific Energy
Applications of specific energy
The preceding packages of precise strength to drilling operations have centered in particular on drilling optimization and identity of inefficient drilling conditions.
Recent advances in precise strength make bigger its packages to overpressure detection and pore strain prediction. In this paper, a try is made to in addition make bigger the software of precise strength to real-time identity of subsurface lithology.
The idea is primarily based totally at the precept that the entire strength required to interrupt and cast off a unit extent of rock is a characteristic of lithology. The proposed technique is examined the use of a lately drilled exploratory fuel line properly with inside the tertiary deltaic gadget of the Niger Delta basin.
In general, an amazing settlement is found in fashion among the conventional lithology identifiers (gamma ray and sonic pace ratio) and the entire strength fed on in breaking and disposing of the penetrated rocks.
The proposed technique can offer a dependable way of choosing formation tops and figuring out subsurface lithology on the bit without a greater fee due to the fact drilling parameters are robotically recorded on the well site in the course of the drilling of a properly.
The proposed technique will help the drilling engineers and geologists in figuring out the casing putting depths and coring factors while not having to drill too deep into the formation of interest.
Application of precise strength and momentum characteristic Discussion With the underlying downstream and corresponding discharge, the upstream intensity this is y2 and y3 are taken because the extrude depths owning comparable precise strength. As the sluice gate is raised, y2 processes the corresponding y3 and E is minimized arise beneath the most discharge for the given strength (Chiseled, Fomin&. Vorozhtsov, 1999).
Moreover, short, clean step with an upward push alternate in y in the channel (∆y), y2 used the extrude intensity viable given the upstream and the discharge. When short, clean step with the most upward push with inside the alternate of y (∆y) in the channel and the step is escalated in addition y2 increases.
Conversely, the increase, in short, clean step with the alternate in y in the channel and with the given upstream intensity and corresponding discharge, y3 is accelerated. Y3 is accelerated because of the enlargement and strength loss.
A hydraulic bounce is applied for strength dissipation that takes place while the flows transitions from the supercritical to corresponding subcritical in particular because of the spillway and the steep slope to the moderate slope. The intensity of water downstream from the bounce and the region of the bounce are computed the use of the conservation of strength equation (Kiselev, Fomin&. Vorozhtsov, 1999). It is predicted from y1 that the intensity of water to amplify because the precise strength of the triumphing reduces slowly.
Moreover, the extrude depths at which the precise energies must be identical. Nevertheless, the values amassed does now no longer depict that because the underlying values have been now no longer ok to provide the right and predicted graph for that reason the affiliation became now no longer represented as anticipated.
The triumphing graphs derived from the depths of the flow, and corresponding precise strength on the phase depicts that the intensity escalates because the time elapses linearly with the precise strength indicating that the 2 underlying variables are linearly associated.
Gradual transitions of channels
No uniform flows for which the modifications intensive and pace are so abrupt that radial accelerations distort the vertical distribution of fluid strain from the hydrostatic situation are referred to as hastily various flows.
Such flows are hard to address analytically, and I will now no longer pursue them here, even though they're vital in lots of engineering applications.
No uniform open-channel flows for which the modifications intensive and pace are sluggish sufficient with inside the downstream path that the vertical distribution of fluid strain from the unfastened floor to the lowest isn't always an awful lot extraordinary from hydrostatic are referred to as progressively various flows. An instance is the waft transition over a mild step, delivered at the start of this bankruptcy
It is finished in a sufficiently quick distance that lack of waft power through friction may be neglected, however the fluid accelerations are nonetheless small enough that the vertical distribution of fluid strain is near being hydrostatic. In maximum progressively various flows, however, the alternate takes location over a distance sufficiently extraordinary that we cannot expect 0 power loss because of backside friction.
The 2nd channel-transition instance posed at the start of this bankruptcy falls into that category. To see what occurs to the elevation of the water floor through a transition over this sort of lengthy distance that backside friction cannot be neglected, we want to begin with the equation for the overall head at a go segment of the waft and differentiate every time period with appreciate to distance with inside the waft (In what follows, I am going to write γ alternatively of d for the waft depth.)
The time period at the left facet of Equation 5.7.2 is the charge of alternate in general power with inside the downstream path. This is usually negative, due to the fact power is unavoidably misplaced through friction. Think in phrases of the downward slope of the road fashioned through plotting Ew as a feature of downstream distance. This slope, denoted through Se, is what changed into referred to as the power slope, or the power gradient, or the slope of the power line in advance on this bankruptcy.
Ew = U2/2g + y + ho
A subject have a look at changed into performed to decide the results of a channel transition on turbulence traits. Detailed three-dimensional (three-D) waft measurements have been accumulated at a move phase this is positioned downstream of a slow channel growth.
These measurements have been acquired through an acoustic Dopplervelocimeter and encompass the three-D pace subject, the suggest nearby velocities, the turbulent intensities, the frictional traits of the waft, the secondary pace alongside the transverse aircraft, and the immediate shear pressure additives with inside the stream wise and transverse instructions.
Analysis of the three-D waft statistics suggests that the turbulent waft at the outer financial institution of the channel is anisotropic.
Turbulent intensities boom in the direction of the unfastened floor indicating the switch of a higher-momentum flux from the channel mattress to the unfastened floor, which contradicts not unusual place wisdom. Results for the normalized pressure additives with inside the stream wise and transverse path display comparable conduct to the intensities.
Key Takeaways:
- The preceding packages of precise strength to drilling operations have centered in particular on drilling optimization and identity of inefficient drilling conditions.
- The proposed technique will help the drilling engineers and geologists in figuring out the casing putting depths and coring factors while not having to drill too deep into the formation of interest.
GRADUALLY VARIED FLOW
The definition of those go with the drift sorts move something like this- Rapidly Varied Flow (RVF) is a sizable extrude in water intensity or pace of go with the drift over a brief distance. This distance may be some instances the water intensity.
Gradually Varied Flow (GVF) is the go with the drift in which the water intensity adjustments step by step over a big distance. In an extra formal and technical way, gradually numerous go with the drift is the no uniform, consistent open-channel flows
Vertical distribution of fluid stress from the loose floor to the lowest isn't always plenty extraordinary from hydrostatic. I actually have already blanketed the kinds of fluid go with the drift which includes consistent and unsteady go with the drift, uniform and non-uniform go with the drift here.
Assumptions of Gradually Varied Flow
Some of the critical assumptions below which the step by step numerous go with the drift (GVF) holds best are:
- The slope of the channel/canal may be very small.
- The vertical intensity is taken into consideration from the lowest.
- The stress distribution is hydrostatic due to the fact the curvature of streamlines is small.
- Manning's and Chery’s system is legitimate for the computation of pace.
- Channel mattress slope is small, HGL will lie on the loose floor.
- The go with the drift channel is prismatic.
- The channel has consistent form and alignment.
- The pace distribution coefficients are consistent.
- This is all approximately the fundamentals of Gradually Varied Flow.
Dynamic Equation of GVF
The general form of gradually varied flow(GVF) equation is:
(dy/dx)=(So-Sf)/(1-Fr^2)
In this equation, So = Bottom slope, positive in the downward direction
Sf = Friction slope. It is positive in the downward direction.
y = Water depth, measured from culvert bottom to water surface
x = Longitudinal distance, measured along the culvert bottom
Fr = Froude number
The friction slope is approximated as the below equation(Manning's equation),
Sf = (nv)^2/R^(4/3)
Where: Sf = Friction slope, positive in the downward direction
n = Manning's roughness coefficient
v = Average cross section velocity
R = Hydraulic radius, (Wetted Area / Wetted Perimeter)
Bottom Slope and Friction Slope Correlation
From the above mentioned Dynamic Equation, the following inferences can be drawn.
- If Sf = So, then dy/dx = 0, the surface profile of flow is parallel to the bottom of the channel.
- If Sf< So, then dy/dx is positive which means the flow profile is rising gradually.
- If Sf>So, then dy/dx is negative which means the flow profile is lowering gradually.
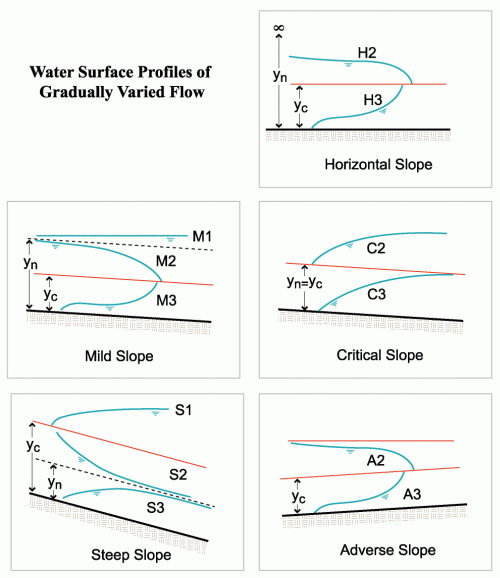
Classification and characteristics of surface profiles
The water surface profile within a culvert can be classified two different ways:
1. Hydraulic Slope, which is based on the slope of the culvert bottom and
2. Hydraulic Curve, which is based on the relationship of the water depth relative to critical depth and normal depth.
Hydraulic Slope Classifications
The Hydraulic Slope of a culvert at a specific flow classifies the hydraulic regime and defines the type of solution generated from the Gradually Varied Flow calculations.
Hydraulic Slope is determined from:
1. The culvert bottom slope (So) and
2. The relationship between critical depth (yc) and normal depth (yn) at a specific flow.
There are five slope classifications:
Adverse (A) if So <0 (slope is positive in the downstream direction)
Horizontal (H) if So = 0
Critical (C) if Yo = yc
Mild (M) if So> 0 and yn > yc
Steep (S) if So> 0 and yn < yc
Hydraulic Curve Classifications
Hydraulic Curve classifications are used to describe the shape of the water surface profile at a specific flow. The curves are based on the Hydraulic Slope (A, H, C, M, or S) and the relative position of the actual flow depth to normal and critical depth as designated by the numbers 1, 2, and 3.
- Type 1 curve: Depth is greater than yc and yn, flow is subcritical
- Type 2 curve: Depth is between ycand yn, flow can be either subcritical or supercritical
- Type 3 curve: Depth is less than both ycand yn, flow is supercritical.
Direct Step method of computing profile length.
The float is assessed as regularly various float whilst the extrude of the fluid intensity alongside the channel dy/dx is a good deal much less than one. For regularly various float, the channel may be divided into exceptional sections referred to as reaches, and the uniform float equations, which include the Chezy and Manning equations, are relevant for calculating head losses in such reaches.
Gradually Varied Flow For consistent and one-dimensional float, the equation for regularly various float, primarily based totally at the power equation, may be written as
DE/dx = So - Sf [1]
Where E is the specific energy, So is the slope of the channel bed, and Sf is the slope of the energy grade line (EGL).
The equation above can also be rewritten in terms of the change of the water surface elevation and Froude number (Fr) as follows:
Dy/dx = (S0 – Sf)/(1 – Fr2) [2]
Note that equations 1 and a couple of are nonlinear differential equations, and analytical answers are viable handiest for some problems. Hence numerical strategies are essential to approximate the answers. One of the only numerical strategies is the finite distinction technique. Eqn. 1 may be discretized as follows:
E/x = S0 -  [4]
[4]
Where  is the average slope of the energy grade line between the end points of a given reach?
is the average slope of the energy grade line between the end points of a given reach?
The direct step technique begins off evolved from a boundary circumstance or manage factor (i.e., a factor in which the water floor elevation is given), and proceeds via way of means of assuming a floor elevation (y) and computing the gap Δx to the assumed elevation:
x = E/( S0 -  ) [5]
) [5]
The computations then keep on to the subsequent reach, and prevent whilst a predetermined restriction or criterion is reached. The case have a look at gives particular approaches for the usage of the direct step technique in figuring out the water floor elevation.
Key Takeaways:
- The definition of those go with the drift sorts move something like this- Rapidly Varied Flow (RVF) is a sizable extrude in water intensity or pace of go with the drift over a brief distance. This distance may be some instances the water intensity.
RAPIDLY VARIED FLOW
Rapidly numerous waft is every other kind of no uniform open-channel waft in which the fluid intensity adjustments swiftly over a small attain of the channel. The phenomenon of a hydraulic bounce, one kind of swiftly numerous waft, might be supplied first, accompanied through a dialogue of the precise force. A quick dialogue of a sharp-crested weir is given on the quilt of this section.
Hydraulic jumps arise whilst the waft adjustments unexpectedly from supercritical to subcritical waft. This procedure is frequently observed through intense turbulence and excessive power losses. Hydraulic jumps frequently arise whilst there may be a war among the upstream and downstream controls. It is the water equal of a sonic boom.
The shear pressure at the lowest of the channel is thought to be negligible. It is likewise similarly assumed that the 2 ends of the manipulate quantity (indicated through crimson dashed lines) are some distance far from the bounce such that the waft is uniform, consistent and one-dimensional.
Applying the momentum equation to the manipulate quantity with inside the waft route yields
Definition of hydraulic jump; Equation of hydraulic jump in horizontal, rectangular channel
Hydraulic jumps arise while the go with the drift modifications all of sudden from supercritical to subcritical go with the drift. This method is regularly followed with the aid of using severe turbulence and excessive strength losses. Hydraulic jumps regularly arise while there's a warfare among the upstream and downstream controls.
It is the water equal of a sonic boom. The shear pressure at the lowest of the channel is believed to be negligible. It is likewise in addition assumed that the 2 ends of the manipulate quantity (indicated with the aid of using crimson dashed lines) are a ways far from the bounce such that the go with the drift is uniform, consistent and one-dimensional. Applying the momentum equation to the manipulate quantity with inside the go with the drift course yields:
-ρV12A1 + ρV22A2 = p1A1 - p2A2 [1]
Where V and A denote the average velocity and cross sectional area, respectively. The pressures at both sections are hydrostatic, the net force due to these is simply the pressure at the centroid times the cross-sectional area. That is,
p1 = ρgz1 and p2 = ρgz2 [2]
Where z is the distance from the water surface to the centroid of the cross-sectional area.
The average velocity can be expressed in terms of the volumetric flow rate as
V1 = Q/A1 and V2 = Q/A2 [3]
Combining Eqns. [1] through [3], and rearranging terms yields
Q2/gA1 + z1A1 = Q2/gA2 + z2A2 [4]
For a rectangular channel with a width of b (A = by, Q = Vby and z = y/2), the momentum equation (Eqn. 4) becomes
V12/gy1 y12 + y12/2 = V22/gy2 y22 + y22/2 [5]
From the continuity equation
Q = V1by1 = V2by2
Which gives V2 = V1 (y1/y2). Then, eliminating V2 from Eqn. 5, and rearranging terms yields
[(y2/y1)2 + y2/y – 2Fr12] [ y2/y1 – 1] = 0 [6]
Where Fr1 is the upstream Froude number, and is given by
Fr1 = V12/gy1 [7]
The root y1 = y2 represents the trivial case where no hydraulic jump occurs. The remaining two roots are
y2/y1 = ½ (-1 ± 1+ 8Fr12)
The solution with the minus sign yields a negative water depth ratio y1/y2, hence this solution is not physically possible.
Thus,
y2/y1 = ½ (-1 ± 1+ 8Fr12) [8]
Is the relation to describe the upstream and downstream water depths of a hydraulic jump in a rectangular channel?
Length & height of jump
Height of the Standing Wave or Hydraulic Jump:
This is the difference of water levels between two sections before and after the hydraulic jump.
Height of standing wave = (d2 – d1)
Length of Hydraulic Jump:
This cannot be calculated analytically. The exact point of commencement of the jump and the exact point where it ends are not well defined. For purposes of analysis we may assume the length of the hydraulic jump to be 5 to 7 times the height of the jump.
A hydraulic jump occurs in site in the following conditions:
(i) When water moving in shooting flow impacts with water having a larger depth with streaming flow.
(ii) On the downstream sides of sluices.
(iii) At the foot of spillways.
(iv) Where the gradient suddenly changes from a steep slope to a flat slope.
Relation between Pre Jump and Post Jump Froude Numbers:
Let Fr1 and Fr2 be the Froude numbers before and after the hydraulic jump.
We know, Fr1 = v1/gd1 and Fr2 = v2/gd2
v1 = Fr1 gd1 and v2 = Fr2 gd2
By continuity condition,
d1v1 = d2v2
d1Fr1gd1 = d2Fr2 gd2
(d1/d2)3/2 = Fr2/Fr1
d1/d2 = (Fr2/Fr1)2/3
We also know,
d2 = d1/2 ((1+8Fr12) -1)
d1/d2 = 2/ ((1+8Fr12) -1)
From the above relations for d1/d2
(Fr2/Fr1)2/3 = 2/((1+8Fr12) -1)
Fr2/Fr1 = [2/((1+8Fr12) -1)]3/2
Fr2 = Fr1 [2/((1+8Fr12) -1)]3/2
For a hydraulic jump to occur, the pre jump Froude number Fr1 should be greater than 1. The post jump Froude number Fr2 will be less than 1.
The table below shows the values of the post jump Froude number Fr2 for various values of pre jump Froude number Fr1.
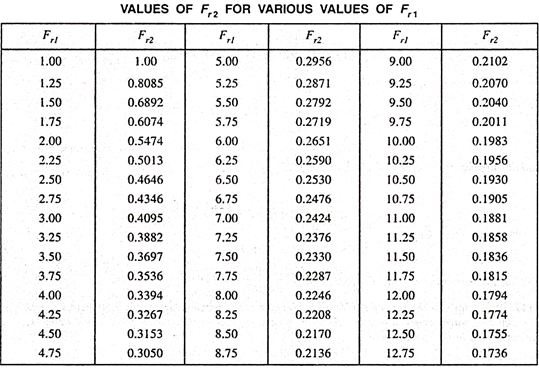
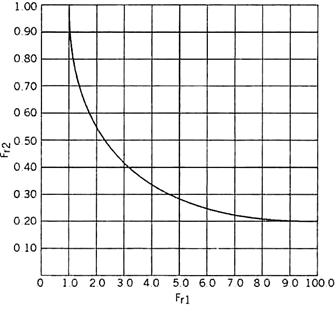
A hydraulic soar is a phenomenon with inside the technological know-how of hydraulics that is regularly found in open channel float which includes rivers and spillways. When liquid at excessive pace discharges right into a sector of decrease pace, a instead abrupt upward push takes place with inside the liquid floor.
The unexpectedly flowing liquid is all of sudden slowed and will increase in height, changing a number of the float's preliminary kinetic strength into an growth in ability strength, with a few strength irreversibly misplaced via turbulence to heat. In an open channel float, this manifests as the short float unexpectedly slowing and piling up on pinnacle of itself just like how a shockwave forms.
As the preliminary float velocity will increase further, the transition turns into extra abrupt, till at excessive sufficient speeds, the transition the front will wreck and curl lower back upon itself.
However, the mechanisms at the back of them are comparable due to the fact they're truly versions of every different visible from special frames of reference, and so the physics and evaluation strategies may be used for each types.
Energy loss in jump
Hydraulic leap in a square channel, additionally referred to as classical leap, is a herbal phenomenon that takes place on every occasion glide adjustments from supercritical to subcritical glide. In this transition, the water floor rises abruptly, floor rollers are formed, extreme blending takes place, air is entrained, and frequently a big quantity of electricity is dissipated.
In different words, a hydraulic leap occurs whilst a better velocity, v1, supercritical glide upstream is met through a subcritical downstream glide with a reduced velocity, v2, and enough depth. Numeric fashions created the usage of the same old step technique or HEC-RAS are used to tune supercritical and subcritical flows to decide in which in a selected attain a hydraulic leap will form.
There also are man-made hydraulic jumps created through gadgets like weirs or sluice gates. In popular, a hydraulic leap can be used to deplete electricity, to combine chemicals, or to behave as an aeration device. To produce equations describing the leap, seeing that there may be an unknown electricity loss, there may be a want to use conservation of momentum.
To broaden this equation, a popular scenario wherein there may also or might not be an electricity loss among upstream and downstream, and there may also or might not be a few impediment on which there may be a drag pressure Pf is considered. However, for a easy or traditional hydraulic leap the pressure in step with unit width(Pf) equals 0. From there the momentum equation, and the conjugate depths equation may be derived.
Although momentum is conserved throughout the hydraulic jump, the energy is not. There is an initial loss of energy when the flow jumps from supercritical to subcritical depths. The resulting loss of energy is equal to the change in specific energy across the jump and is given by the equation for ΔE below. The equation below is based on the condition that y1 and y2 are conjugate depths.
E = E1 – E2 = (y1 + q2/2gy12) – (y2 + q2/2gy22) = (y2 – y1)3/4y1y2
When searching on the vital factors at the M-y diagram and what their places inform us approximately the character of the hydraulic bounce, we referred to that a growth in q could have an effect on the electricity misplaced with inside the bounce.
From Figure 7 we see that growing the glide fee decreases the distinction with inside the upstream and downstream intensity of the bounce (y2 – y1). From this we are able to infer that if the momentum is held to be constant, there may be a lower with inside the electricity misplaced with inside the bounce if the glide fee is increased.
The performance of the bounce is decided through the dimensionless parameter E2/E1 which tells us how a whole lot of the authentic electricity is ultimate after the bounce is complete.
The equation for the electricity performance is given underneath and indicates the heavy dependence that the performance has at the Froude wide variety of the upstream glide. Example 2 indicates a pattern calculation for electricity loss and performance.
E2/E1 = 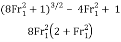
Classifications of jump
Basically a hydraulic soar takes place in lots of kinds relying on topographical capabilities and mattress floor roughness and plenty of different herbal interface relations. This hydraulic soar kinds may be possibly expressed primarily based totally on Froude’s variety:
1. Undular Hydraulic Jump – Froude Number (1 to three):
Undular Jump is irregular, now no longer well fashioned and there are positive turbulences in water debris.
2. Weak Jump –
Froude Number (three to 6) Weak soar takes location while the speed in water may be very much less and the water debris can't be strong and flows in numerous ways.
3. Oscillating Hydraulic Jump – Froude Number (6-20)
Oscillating soar paperwork while an oscillating jet input into amazing crucial nation and there the variety of debris begins off evolved oscillating in clockwise or both anticlockwise path, forming slighter tides or waves to the pinnacle floor. Also the go with the drift is depending on heavy blow of air in a single path.
4. Steady Hydraulic Jump – Froude Number (20 to 80)
In consistent soar, the mattress floor is pretty difficult so the debris begin to generally tend in a single path with heavy speed and turbulence, frictional losses are extra on this form of soar.
5. Strong Hydraulic Jump – Froude Number (more than 80)
Strong soar is an excellent soar fashioned while frictional losses are extra, air stress department is identical and speed may be very excessive that losses take location. The water modifications its nation from amazing crucial to subcritical in very shorter period while as compared to all different varieties of hydraulic jumps, so this soar is rather favored in dam structures.
Key Takeaways:
- Hydraulic jumps regularly arise while there's a warfare among the upstream and downstream controls.
- This cannot be calculated analytically. The exact point of commencement of the jump and the exact point where it ends are not well defined.
References:
1. Hydraulics & Fluid Mechanics- Dr.Modi & Dr. Seth
2. Fluid Mechanics-Streeter & Wylie
3. Fluid Mechanics- Dr. A.K.Jain
4. Fluid Mechanics through problems- Garde
5. Theory and applications of Fluid Mechanics- K. Subramanya
6. Foundation of Fluid Mechanics-Yuan
7. Flow through open channel – K.G.Rangaraju
Unit - 4
Applications of Specific Energy
Applications of specific energy
The preceding packages of precise strength to drilling operations have centered in particular on drilling optimization and identity of inefficient drilling conditions.
Recent advances in precise strength make bigger its packages to overpressure detection and pore strain prediction. In this paper, a try is made to in addition make bigger the software of precise strength to real-time identity of subsurface lithology.
The idea is primarily based totally at the precept that the entire strength required to interrupt and cast off a unit extent of rock is a characteristic of lithology. The proposed technique is examined the use of a lately drilled exploratory fuel line properly with inside the tertiary deltaic gadget of the Niger Delta basin.
In general, an amazing settlement is found in fashion among the conventional lithology identifiers (gamma ray and sonic pace ratio) and the entire strength fed on in breaking and disposing of the penetrated rocks.
The proposed technique can offer a dependable way of choosing formation tops and figuring out subsurface lithology on the bit without a greater fee due to the fact drilling parameters are robotically recorded on the well site in the course of the drilling of a properly.
The proposed technique will help the drilling engineers and geologists in figuring out the casing putting depths and coring factors while not having to drill too deep into the formation of interest.
Application of precise strength and momentum characteristic Discussion With the underlying downstream and corresponding discharge, the upstream intensity this is y2 and y3 are taken because the extrude depths owning comparable precise strength. As the sluice gate is raised, y2 processes the corresponding y3 and E is minimized arise beneath the most discharge for the given strength (Chiseled, Fomin&. Vorozhtsov, 1999).
Moreover, short, clean step with an upward push alternate in y in the channel (∆y), y2 used the extrude intensity viable given the upstream and the discharge. When short, clean step with the most upward push with inside the alternate of y (∆y) in the channel and the step is escalated in addition y2 increases.
Conversely, the increase, in short, clean step with the alternate in y in the channel and with the given upstream intensity and corresponding discharge, y3 is accelerated. Y3 is accelerated because of the enlargement and strength loss.
A hydraulic bounce is applied for strength dissipation that takes place while the flows transitions from the supercritical to corresponding subcritical in particular because of the spillway and the steep slope to the moderate slope. The intensity of water downstream from the bounce and the region of the bounce are computed the use of the conservation of strength equation (Kiselev, Fomin&. Vorozhtsov, 1999). It is predicted from y1 that the intensity of water to amplify because the precise strength of the triumphing reduces slowly.
Moreover, the extrude depths at which the precise energies must be identical. Nevertheless, the values amassed does now no longer depict that because the underlying values have been now no longer ok to provide the right and predicted graph for that reason the affiliation became now no longer represented as anticipated.
The triumphing graphs derived from the depths of the flow, and corresponding precise strength on the phase depicts that the intensity escalates because the time elapses linearly with the precise strength indicating that the 2 underlying variables are linearly associated.
Gradual transitions of channels
No uniform flows for which the modifications intensive and pace are so abrupt that radial accelerations distort the vertical distribution of fluid strain from the hydrostatic situation are referred to as hastily various flows.
Such flows are hard to address analytically, and I will now no longer pursue them here, even though they're vital in lots of engineering applications.
No uniform open-channel flows for which the modifications intensive and pace are sluggish sufficient with inside the downstream path that the vertical distribution of fluid strain from the unfastened floor to the lowest isn't always an awful lot extraordinary from hydrostatic are referred to as progressively various flows. An instance is the waft transition over a mild step, delivered at the start of this bankruptcy
It is finished in a sufficiently quick distance that lack of waft power through friction may be neglected, however the fluid accelerations are nonetheless small enough that the vertical distribution of fluid strain is near being hydrostatic. In maximum progressively various flows, however, the alternate takes location over a distance sufficiently extraordinary that we cannot expect 0 power loss because of backside friction.
The 2nd channel-transition instance posed at the start of this bankruptcy falls into that category. To see what occurs to the elevation of the water floor through a transition over this sort of lengthy distance that backside friction cannot be neglected, we want to begin with the equation for the overall head at a go segment of the waft and differentiate every time period with appreciate to distance with inside the waft (In what follows, I am going to write γ alternatively of d for the waft depth.)
The time period at the left facet of Equation 5.7.2 is the charge of alternate in general power with inside the downstream path. This is usually negative, due to the fact power is unavoidably misplaced through friction. Think in phrases of the downward slope of the road fashioned through plotting Ew as a feature of downstream distance. This slope, denoted through Se, is what changed into referred to as the power slope, or the power gradient, or the slope of the power line in advance on this bankruptcy.
Ew = U2/2g + y + ho
A subject have a look at changed into performed to decide the results of a channel transition on turbulence traits. Detailed three-dimensional (three-D) waft measurements have been accumulated at a move phase this is positioned downstream of a slow channel growth.
These measurements have been acquired through an acoustic Dopplervelocimeter and encompass the three-D pace subject, the suggest nearby velocities, the turbulent intensities, the frictional traits of the waft, the secondary pace alongside the transverse aircraft, and the immediate shear pressure additives with inside the stream wise and transverse instructions.
Analysis of the three-D waft statistics suggests that the turbulent waft at the outer financial institution of the channel is anisotropic.
Turbulent intensities boom in the direction of the unfastened floor indicating the switch of a higher-momentum flux from the channel mattress to the unfastened floor, which contradicts not unusual place wisdom. Results for the normalized pressure additives with inside the stream wise and transverse path display comparable conduct to the intensities.
Key Takeaways:
- The preceding packages of precise strength to drilling operations have centered in particular on drilling optimization and identity of inefficient drilling conditions.
- The proposed technique will help the drilling engineers and geologists in figuring out the casing putting depths and coring factors while not having to drill too deep into the formation of interest.
GRADUALLY VARIED FLOW
The definition of those go with the drift sorts move something like this- Rapidly Varied Flow (RVF) is a sizable extrude in water intensity or pace of go with the drift over a brief distance. This distance may be some instances the water intensity.
Gradually Varied Flow (GVF) is the go with the drift in which the water intensity adjustments step by step over a big distance. In an extra formal and technical way, gradually numerous go with the drift is the no uniform, consistent open-channel flows
Vertical distribution of fluid stress from the loose floor to the lowest isn't always plenty extraordinary from hydrostatic. I actually have already blanketed the kinds of fluid go with the drift which includes consistent and unsteady go with the drift, uniform and non-uniform go with the drift here.
Assumptions of Gradually Varied Flow
Some of the critical assumptions below which the step by step numerous go with the drift (GVF) holds best are:
- The slope of the channel/canal may be very small.
- The vertical intensity is taken into consideration from the lowest.
- The stress distribution is hydrostatic due to the fact the curvature of streamlines is small.
- Manning's and Chery’s system is legitimate for the computation of pace.
- Channel mattress slope is small, HGL will lie on the loose floor.
- The go with the drift channel is prismatic.
- The channel has consistent form and alignment.
- The pace distribution coefficients are consistent.
- This is all approximately the fundamentals of Gradually Varied Flow.
Dynamic Equation of GVF
The general form of gradually varied flow(GVF) equation is:
(dy/dx)=(So-Sf)/(1-Fr^2)
In this equation, So = Bottom slope, positive in the downward direction
Sf = Friction slope. It is positive in the downward direction.
y = Water depth, measured from culvert bottom to water surface
x = Longitudinal distance, measured along the culvert bottom
Fr = Froude number
The friction slope is approximated as the below equation(Manning's equation),
Sf = (nv)^2/R^(4/3)
Where: Sf = Friction slope, positive in the downward direction
n = Manning's roughness coefficient
v = Average cross section velocity
R = Hydraulic radius, (Wetted Area / Wetted Perimeter)
Bottom Slope and Friction Slope Correlation
From the above mentioned Dynamic Equation, the following inferences can be drawn.
- If Sf = So, then dy/dx = 0, the surface profile of flow is parallel to the bottom of the channel.
- If Sf< So, then dy/dx is positive which means the flow profile is rising gradually.
- If Sf>So, then dy/dx is negative which means the flow profile is lowering gradually.
Classification and characteristics of surface profiles
The water surface profile within a culvert can be classified two different ways:
1. Hydraulic Slope, which is based on the slope of the culvert bottom and
2. Hydraulic Curve, which is based on the relationship of the water depth relative to critical depth and normal depth.
Hydraulic Slope Classifications
The Hydraulic Slope of a culvert at a specific flow classifies the hydraulic regime and defines the type of solution generated from the Gradually Varied Flow calculations.
Hydraulic Slope is determined from:
1. The culvert bottom slope (So) and
2. The relationship between critical depth (yc) and normal depth (yn) at a specific flow.
There are five slope classifications:
Adverse (A) if So <0 (slope is positive in the downstream direction)
Horizontal (H) if So = 0
Critical (C) if Yo = yc
Mild (M) if So> 0 and yn > yc
Steep (S) if So> 0 and yn < yc
Hydraulic Curve Classifications
Hydraulic Curve classifications are used to describe the shape of the water surface profile at a specific flow. The curves are based on the Hydraulic Slope (A, H, C, M, or S) and the relative position of the actual flow depth to normal and critical depth as designated by the numbers 1, 2, and 3.
- Type 1 curve: Depth is greater than yc and yn, flow is subcritical
- Type 2 curve: Depth is between ycand yn, flow can be either subcritical or supercritical
- Type 3 curve: Depth is less than both ycand yn, flow is supercritical.
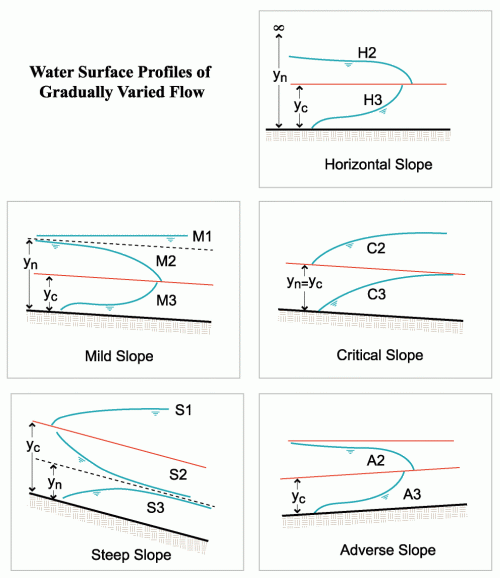
Direct Step method of computing profile length.
The float is assessed as regularly various float whilst the extrude of the fluid intensity alongside the channel dy/dx is a good deal much less than one. For regularly various float, the channel may be divided into exceptional sections referred to as reaches, and the uniform float equations, which include the Chezy and Manning equations, are relevant for calculating head losses in such reaches.
Gradually Varied Flow For consistent and one-dimensional float, the equation for regularly various float, primarily based totally at the power equation, may be written as
DE/dx = So - Sf [1]
Where E is the specific energy, So is the slope of the channel bed, and Sf is the slope of the energy grade line (EGL).
The equation above can also be rewritten in terms of the change of the water surface elevation and Froude number (Fr) as follows:
Dy/dx = (S0 – Sf)/(1 – Fr2) [2]
Note that equations 1 and a couple of are nonlinear differential equations, and analytical answers are viable handiest for some problems. Hence numerical strategies are essential to approximate the answers. One of the only numerical strategies is the finite distinction technique. Eqn. 1 may be discretized as follows:
E/x = S0 - 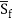 [4]
[4]
Where 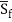 is the average slope of the energy grade line between the end points of a given reach?
is the average slope of the energy grade line between the end points of a given reach?
The direct step technique begins off evolved from a boundary circumstance or manage factor (i.e., a factor in which the water floor elevation is given), and proceeds via way of means of assuming a floor elevation (y) and computing the gap Δx to the assumed elevation:
x = E/( S0 - 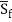 ) [5]
) [5]
The computations then keep on to the subsequent reach, and prevent whilst a predetermined restriction or criterion is reached. The case have a look at gives particular approaches for the usage of the direct step technique in figuring out the water floor elevation.
Key Takeaways:
- The definition of those go with the drift sorts move something like this- Rapidly Varied Flow (RVF) is a sizable extrude in water intensity or pace of go with the drift over a brief distance. This distance may be some instances the water intensity.
RAPIDLY VARIED FLOW
Rapidly numerous waft is every other kind of no uniform open-channel waft in which the fluid intensity adjustments swiftly over a small attain of the channel. The phenomenon of a hydraulic bounce, one kind of swiftly numerous waft, might be supplied first, accompanied through a dialogue of the precise force. A quick dialogue of a sharp-crested weir is given on the quilt of this section.
Hydraulic jumps arise whilst the waft adjustments unexpectedly from supercritical to subcritical waft. This procedure is frequently observed through intense turbulence and excessive power losses. Hydraulic jumps frequently arise whilst there may be a war among the upstream and downstream controls. It is the water equal of a sonic boom.
The shear pressure at the lowest of the channel is thought to be negligible. It is likewise similarly assumed that the 2 ends of the manipulate quantity (indicated through crimson dashed lines) are some distance far from the bounce such that the waft is uniform, consistent and one-dimensional.
Applying the momentum equation to the manipulate quantity with inside the waft route yields
Definition of hydraulic jump; Equation of hydraulic jump in horizontal, rectangular channel
Hydraulic jumps arise while the go with the drift modifications all of sudden from supercritical to subcritical go with the drift. This method is regularly followed with the aid of using severe turbulence and excessive strength losses. Hydraulic jumps regularly arise while there's a warfare among the upstream and downstream controls.
It is the water equal of a sonic boom. The shear pressure at the lowest of the channel is believed to be negligible. It is likewise in addition assumed that the 2 ends of the manipulate quantity (indicated with the aid of using crimson dashed lines) are a ways far from the bounce such that the go with the drift is uniform, consistent and one-dimensional. Applying the momentum equation to the manipulate quantity with inside the go with the drift course yields:
-ρV12A1 + ρV22A2 = p1A1 - p2A2 [1]
Where V and A denote the average velocity and cross sectional area, respectively. The pressures at both sections are hydrostatic, the net force due to these is simply the pressure at the centroid times the cross-sectional area. That is,
p1 = ρgz1 and p2 = ρgz2 [2]
Where z is the distance from the water surface to the centroid of the cross-sectional area.
The average velocity can be expressed in terms of the volumetric flow rate as
V1 = Q/A1 and V2 = Q/A2 [3]
Combining Eqns. [1] through [3], and rearranging terms yields
Q2/gA1 + z1A1 = Q2/gA2 + z2A2 [4]
For a rectangular channel with a width of b (A = by, Q = Vby and z = y/2), the momentum equation (Eqn. 4) becomes
V12/gy1 y12 + y12/2 = V22/gy2 y22 + y22/2 [5]
From the continuity equation
Q = V1by1 = V2by2
Which gives V2 = V1 (y1/y2). Then, eliminating V2 from Eqn. 5, and rearranging terms yields
[(y2/y1)2 + y2/y – 2Fr12] [ y2/y1 – 1] = 0 [6]
Where Fr1 is the upstream Froude number, and is given by
Fr1 = V12/gy1 [7]
The root y1 = y2 represents the trivial case where no hydraulic jump occurs. The remaining two roots are
y2/y1 = ½ (-1 ± 1+ 8Fr12)
The solution with the minus sign yields a negative water depth ratio y1/y2, hence this solution is not physically possible.
Thus,
y2/y1 = ½ (-1 ± 1+ 8Fr12) [8]
Is the relation to describe the upstream and downstream water depths of a hydraulic jump in a rectangular channel?
Length & height of jump
Height of the Standing Wave or Hydraulic Jump:
This is the difference of water levels between two sections before and after the hydraulic jump.
Height of standing wave = (d2 – d1)
Length of Hydraulic Jump:
This cannot be calculated analytically. The exact point of commencement of the jump and the exact point where it ends are not well defined. For purposes of analysis we may assume the length of the hydraulic jump to be 5 to 7 times the height of the jump.
A hydraulic jump occurs in site in the following conditions:
(i) When water moving in shooting flow impacts with water having a larger depth with streaming flow.
(ii) On the downstream sides of sluices.
(iii) At the foot of spillways.
(iv) Where the gradient suddenly changes from a steep slope to a flat slope.
Relation between Pre Jump and Post Jump Froude Numbers:
Let Fr1 and Fr2 be the Froude numbers before and after the hydraulic jump.
We know, Fr1 = v1/gd1 and Fr2 = v2/gd2
v1 = Fr1 gd1 and v2 = Fr2 gd2
By continuity condition,
d1v1 = d2v2
d1Fr1gd1 = d2Fr2 gd2
(d1/d2)3/2 = Fr2/Fr1
d1/d2 = (Fr2/Fr1)2/3
We also know,
d2 = d1/2 ((1+8Fr12) -1)
d1/d2 = 2/ ((1+8Fr12) -1)
From the above relations for d1/d2
(Fr2/Fr1)2/3 = 2/((1+8Fr12) -1)
Fr2/Fr1 = [2/((1+8Fr12) -1)]3/2
Fr2 = Fr1 [2/((1+8Fr12) -1)]3/2
For a hydraulic jump to occur, the pre jump Froude number Fr1 should be greater than 1. The post jump Froude number Fr2 will be less than 1.
The table below shows the values of the post jump Froude number Fr2 for various values of pre jump Froude number Fr1.
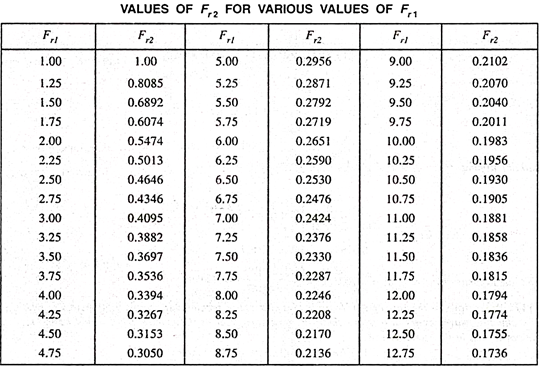
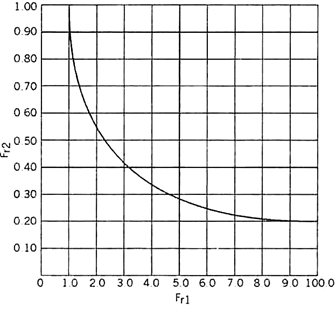
A hydraulic soar is a phenomenon with inside the technological know-how of hydraulics that is regularly found in open channel float which includes rivers and spillways. When liquid at excessive pace discharges right into a sector of decrease pace, a instead abrupt upward push takes place with inside the liquid floor.
The unexpectedly flowing liquid is all of sudden slowed and will increase in height, changing a number of the float's preliminary kinetic strength into an growth in ability strength, with a few strength irreversibly misplaced via turbulence to heat. In an open channel float, this manifests as the short float unexpectedly slowing and piling up on pinnacle of itself just like how a shockwave forms.
As the preliminary float velocity will increase further, the transition turns into extra abrupt, till at excessive sufficient speeds, the transition the front will wreck and curl lower back upon itself.
However, the mechanisms at the back of them are comparable due to the fact they're truly versions of every different visible from special frames of reference, and so the physics and evaluation strategies may be used for each types.
Energy loss in jump
Hydraulic leap in a square channel, additionally referred to as classical leap, is a herbal phenomenon that takes place on every occasion glide adjustments from supercritical to subcritical glide. In this transition, the water floor rises abruptly, floor rollers are formed, extreme blending takes place, air is entrained, and frequently a big quantity of electricity is dissipated.
In different words, a hydraulic leap occurs whilst a better velocity, v1, supercritical glide upstream is met through a subcritical downstream glide with a reduced velocity, v2, and enough depth. Numeric fashions created the usage of the same old step technique or HEC-RAS are used to tune supercritical and subcritical flows to decide in which in a selected attain a hydraulic leap will form.
There also are man-made hydraulic jumps created through gadgets like weirs or sluice gates. In popular, a hydraulic leap can be used to deplete electricity, to combine chemicals, or to behave as an aeration device. To produce equations describing the leap, seeing that there may be an unknown electricity loss, there may be a want to use conservation of momentum.
To broaden this equation, a popular scenario wherein there may also or might not be an electricity loss among upstream and downstream, and there may also or might not be a few impediment on which there may be a drag pressure Pf is considered. However, for a easy or traditional hydraulic leap the pressure in step with unit width(Pf) equals 0. From there the momentum equation, and the conjugate depths equation may be derived.
Although momentum is conserved throughout the hydraulic jump, the energy is not. There is an initial loss of energy when the flow jumps from supercritical to subcritical depths. The resulting loss of energy is equal to the change in specific energy across the jump and is given by the equation for ΔE below. The equation below is based on the condition that y1 and y2 are conjugate depths.
E = E1 – E2 = (y1 + q2/2gy12) – (y2 + q2/2gy22) = (y2 – y1)3/4y1y2
When searching on the vital factors at the M-y diagram and what their places inform us approximately the character of the hydraulic bounce, we referred to that a growth in q could have an effect on the electricity misplaced with inside the bounce.
From Figure 7 we see that growing the glide fee decreases the distinction with inside the upstream and downstream intensity of the bounce (y2 – y1). From this we are able to infer that if the momentum is held to be constant, there may be a lower with inside the electricity misplaced with inside the bounce if the glide fee is increased.
The performance of the bounce is decided through the dimensionless parameter E2/E1 which tells us how a whole lot of the authentic electricity is ultimate after the bounce is complete.
The equation for the electricity performance is given underneath and indicates the heavy dependence that the performance has at the Froude wide variety of the upstream glide. Example 2 indicates a pattern calculation for electricity loss and performance.
E2/E1 = 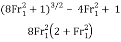
Classifications of jump
Basically a hydraulic soar takes place in lots of kinds relying on topographical capabilities and mattress floor roughness and plenty of different herbal interface relations. This hydraulic soar kinds may be possibly expressed primarily based totally on Froude’s variety:
1. Undular Hydraulic Jump – Froude Number (1 to three):
Undular Jump is irregular, now no longer well fashioned and there are positive turbulences in water debris.
2. Weak Jump –
Froude Number (three to 6) Weak soar takes location while the speed in water may be very much less and the water debris can't be strong and flows in numerous ways.
3. Oscillating Hydraulic Jump – Froude Number (6-20)
Oscillating soar paperwork while an oscillating jet input into amazing crucial nation and there the variety of debris begins off evolved oscillating in clockwise or both anticlockwise path, forming slighter tides or waves to the pinnacle floor. Also the go with the drift is depending on heavy blow of air in a single path.
4. Steady Hydraulic Jump – Froude Number (20 to 80)
In consistent soar, the mattress floor is pretty difficult so the debris begin to generally tend in a single path with heavy speed and turbulence, frictional losses are extra on this form of soar.
5. Strong Hydraulic Jump – Froude Number (more than 80)
Strong soar is an excellent soar fashioned while frictional losses are extra, air stress department is identical and speed may be very excessive that losses take location. The water modifications its nation from amazing crucial to subcritical in very shorter period while as compared to all different varieties of hydraulic jumps, so this soar is rather favored in dam structures.
Key Takeaways:
- Hydraulic jumps regularly arise while there's a warfare among the upstream and downstream controls.
- This cannot be calculated analytically. The exact point of commencement of the jump and the exact point where it ends are not well defined.
References:
1. Hydraulics & Fluid Mechanics- Dr.Modi & Dr. Seth
2. Fluid Mechanics-Streeter & Wylie
3. Fluid Mechanics- Dr. A.K.Jain
4. Fluid Mechanics through problems- Garde
5. Theory and applications of Fluid Mechanics- K. Subramanya
6. Foundation of Fluid Mechanics-Yuan
7. Flow through open channel – K.G.Rangaraju
Unit - 4
Applications of Specific Energy
Applications of specific energy
The preceding packages of precise strength to drilling operations have centered in particular on drilling optimization and identity of inefficient drilling conditions.
Recent advances in precise strength make bigger its packages to overpressure detection and pore strain prediction. In this paper, a try is made to in addition make bigger the software of precise strength to real-time identity of subsurface lithology.
The idea is primarily based totally at the precept that the entire strength required to interrupt and cast off a unit extent of rock is a characteristic of lithology. The proposed technique is examined the use of a lately drilled exploratory fuel line properly with inside the tertiary deltaic gadget of the Niger Delta basin.
In general, an amazing settlement is found in fashion among the conventional lithology identifiers (gamma ray and sonic pace ratio) and the entire strength fed on in breaking and disposing of the penetrated rocks.
The proposed technique can offer a dependable way of choosing formation tops and figuring out subsurface lithology on the bit without a greater fee due to the fact drilling parameters are robotically recorded on the well site in the course of the drilling of a properly.
The proposed technique will help the drilling engineers and geologists in figuring out the casing putting depths and coring factors while not having to drill too deep into the formation of interest.
Application of precise strength and momentum characteristic Discussion With the underlying downstream and corresponding discharge, the upstream intensity this is y2 and y3 are taken because the extrude depths owning comparable precise strength. As the sluice gate is raised, y2 processes the corresponding y3 and E is minimized arise beneath the most discharge for the given strength (Chiseled, Fomin&. Vorozhtsov, 1999).
Moreover, short, clean step with an upward push alternate in y in the channel (∆y), y2 used the extrude intensity viable given the upstream and the discharge. When short, clean step with the most upward push with inside the alternate of y (∆y) in the channel and the step is escalated in addition y2 increases.
Conversely, the increase, in short, clean step with the alternate in y in the channel and with the given upstream intensity and corresponding discharge, y3 is accelerated. Y3 is accelerated because of the enlargement and strength loss.
A hydraulic bounce is applied for strength dissipation that takes place while the flows transitions from the supercritical to corresponding subcritical in particular because of the spillway and the steep slope to the moderate slope. The intensity of water downstream from the bounce and the region of the bounce are computed the use of the conservation of strength equation (Kiselev, Fomin&. Vorozhtsov, 1999). It is predicted from y1 that the intensity of water to amplify because the precise strength of the triumphing reduces slowly.
Moreover, the extrude depths at which the precise energies must be identical. Nevertheless, the values amassed does now no longer depict that because the underlying values have been now no longer ok to provide the right and predicted graph for that reason the affiliation became now no longer represented as anticipated.
The triumphing graphs derived from the depths of the flow, and corresponding precise strength on the phase depicts that the intensity escalates because the time elapses linearly with the precise strength indicating that the 2 underlying variables are linearly associated.
Gradual transitions of channels
No uniform flows for which the modifications intensive and pace are so abrupt that radial accelerations distort the vertical distribution of fluid strain from the hydrostatic situation are referred to as hastily various flows.
Such flows are hard to address analytically, and I will now no longer pursue them here, even though they're vital in lots of engineering applications.
No uniform open-channel flows for which the modifications intensive and pace are sluggish sufficient with inside the downstream path that the vertical distribution of fluid strain from the unfastened floor to the lowest isn't always an awful lot extraordinary from hydrostatic are referred to as progressively various flows. An instance is the waft transition over a mild step, delivered at the start of this bankruptcy
It is finished in a sufficiently quick distance that lack of waft power through friction may be neglected, however the fluid accelerations are nonetheless small enough that the vertical distribution of fluid strain is near being hydrostatic. In maximum progressively various flows, however, the alternate takes location over a distance sufficiently extraordinary that we cannot expect 0 power loss because of backside friction.
The 2nd channel-transition instance posed at the start of this bankruptcy falls into that category. To see what occurs to the elevation of the water floor through a transition over this sort of lengthy distance that backside friction cannot be neglected, we want to begin with the equation for the overall head at a go segment of the waft and differentiate every time period with appreciate to distance with inside the waft (In what follows, I am going to write γ alternatively of d for the waft depth.)
The time period at the left facet of Equation 5.7.2 is the charge of alternate in general power with inside the downstream path. This is usually negative, due to the fact power is unavoidably misplaced through friction. Think in phrases of the downward slope of the road fashioned through plotting Ew as a feature of downstream distance. This slope, denoted through Se, is what changed into referred to as the power slope, or the power gradient, or the slope of the power line in advance on this bankruptcy.
Ew = U2/2g + y + ho
A subject have a look at changed into performed to decide the results of a channel transition on turbulence traits. Detailed three-dimensional (three-D) waft measurements have been accumulated at a move phase this is positioned downstream of a slow channel growth.
These measurements have been acquired through an acoustic Dopplervelocimeter and encompass the three-D pace subject, the suggest nearby velocities, the turbulent intensities, the frictional traits of the waft, the secondary pace alongside the transverse aircraft, and the immediate shear pressure additives with inside the stream wise and transverse instructions.
Analysis of the three-D waft statistics suggests that the turbulent waft at the outer financial institution of the channel is anisotropic.
Turbulent intensities boom in the direction of the unfastened floor indicating the switch of a higher-momentum flux from the channel mattress to the unfastened floor, which contradicts not unusual place wisdom. Results for the normalized pressure additives with inside the stream wise and transverse path display comparable conduct to the intensities.
Key Takeaways:
- The preceding packages of precise strength to drilling operations have centered in particular on drilling optimization and identity of inefficient drilling conditions.
- The proposed technique will help the drilling engineers and geologists in figuring out the casing putting depths and coring factors while not having to drill too deep into the formation of interest.
GRADUALLY VARIED FLOW
The definition of those go with the drift sorts move something like this- Rapidly Varied Flow (RVF) is a sizable extrude in water intensity or pace of go with the drift over a brief distance. This distance may be some instances the water intensity.
Gradually Varied Flow (GVF) is the go with the drift in which the water intensity adjustments step by step over a big distance. In an extra formal and technical way, gradually numerous go with the drift is the no uniform, consistent open-channel flows
Vertical distribution of fluid stress from the loose floor to the lowest isn't always plenty extraordinary from hydrostatic. I actually have already blanketed the kinds of fluid go with the drift which includes consistent and unsteady go with the drift, uniform and non-uniform go with the drift here.
Assumptions of Gradually Varied Flow
Some of the critical assumptions below which the step by step numerous go with the drift (GVF) holds best are:
- The slope of the channel/canal may be very small.
- The vertical intensity is taken into consideration from the lowest.
- The stress distribution is hydrostatic due to the fact the curvature of streamlines is small.
- Manning's and Chery’s system is legitimate for the computation of pace.
- Channel mattress slope is small, HGL will lie on the loose floor.
- The go with the drift channel is prismatic.
- The channel has consistent form and alignment.
- The pace distribution coefficients are consistent.
- This is all approximately the fundamentals of Gradually Varied Flow.
Dynamic Equation of GVF
The general form of gradually varied flow(GVF) equation is:
(dy/dx)=(So-Sf)/(1-Fr^2)
In this equation, So = Bottom slope, positive in the downward direction
Sf = Friction slope. It is positive in the downward direction.
y = Water depth, measured from culvert bottom to water surface
x = Longitudinal distance, measured along the culvert bottom
Fr = Froude number
The friction slope is approximated as the below equation(Manning's equation),
Sf = (nv)^2/R^(4/3)
Where: Sf = Friction slope, positive in the downward direction
n = Manning's roughness coefficient
v = Average cross section velocity
R = Hydraulic radius, (Wetted Area / Wetted Perimeter)
Bottom Slope and Friction Slope Correlation
From the above mentioned Dynamic Equation, the following inferences can be drawn.
- If Sf = So, then dy/dx = 0, the surface profile of flow is parallel to the bottom of the channel.
- If Sf< So, then dy/dx is positive which means the flow profile is rising gradually.
- If Sf>So, then dy/dx is negative which means the flow profile is lowering gradually.
Classification and characteristics of surface profiles
The water surface profile within a culvert can be classified two different ways:
1. Hydraulic Slope, which is based on the slope of the culvert bottom and
2. Hydraulic Curve, which is based on the relationship of the water depth relative to critical depth and normal depth.
Hydraulic Slope Classifications
The Hydraulic Slope of a culvert at a specific flow classifies the hydraulic regime and defines the type of solution generated from the Gradually Varied Flow calculations.
Hydraulic Slope is determined from:
1. The culvert bottom slope (So) and
2. The relationship between critical depth (yc) and normal depth (yn) at a specific flow.
There are five slope classifications:
Adverse (A) if So <0 (slope is positive in the downstream direction)
Horizontal (H) if So = 0
Critical (C) if Yo = yc
Mild (M) if So> 0 and yn > yc
Steep (S) if So> 0 and yn < yc
Hydraulic Curve Classifications
Hydraulic Curve classifications are used to describe the shape of the water surface profile at a specific flow. The curves are based on the Hydraulic Slope (A, H, C, M, or S) and the relative position of the actual flow depth to normal and critical depth as designated by the numbers 1, 2, and 3.
- Type 1 curve: Depth is greater than yc and yn, flow is subcritical
- Type 2 curve: Depth is between ycand yn, flow can be either subcritical or supercritical
- Type 3 curve: Depth is less than both ycand yn, flow is supercritical.
Direct Step method of computing profile length.
The float is assessed as regularly various float whilst the extrude of the fluid intensity alongside the channel dy/dx is a good deal much less than one. For regularly various float, the channel may be divided into exceptional sections referred to as reaches, and the uniform float equations, which include the Chezy and Manning equations, are relevant for calculating head losses in such reaches.
Gradually Varied Flow For consistent and one-dimensional float, the equation for regularly various float, primarily based totally at the power equation, may be written as
DE/dx = So - Sf [1]
Where E is the specific energy, So is the slope of the channel bed, and Sf is the slope of the energy grade line (EGL).
The equation above can also be rewritten in terms of the change of the water surface elevation and Froude number (Fr) as follows:
Dy/dx = (S0 – Sf)/(1 – Fr2) [2]
Note that equations 1 and a couple of are nonlinear differential equations, and analytical answers are viable handiest for some problems. Hence numerical strategies are essential to approximate the answers. One of the only numerical strategies is the finite distinction technique. Eqn. 1 may be discretized as follows:
E/x = S0 - 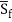 [4]
[4]
Where 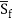 is the average slope of the energy grade line between the end points of a given reach?
is the average slope of the energy grade line between the end points of a given reach?
The direct step technique begins off evolved from a boundary circumstance or manage factor (i.e., a factor in which the water floor elevation is given), and proceeds via way of means of assuming a floor elevation (y) and computing the gap Δx to the assumed elevation:
x = E/( S0 -  ) [5]
) [5]
The computations then keep on to the subsequent reach, and prevent whilst a predetermined restriction or criterion is reached. The case have a look at gives particular approaches for the usage of the direct step technique in figuring out the water floor elevation.
Key Takeaways:
- The definition of those go with the drift sorts move something like this- Rapidly Varied Flow (RVF) is a sizable extrude in water intensity or pace of go with the drift over a brief distance. This distance may be some instances the water intensity.
RAPIDLY VARIED FLOW
Rapidly numerous waft is every other kind of no uniform open-channel waft in which the fluid intensity adjustments swiftly over a small attain of the channel. The phenomenon of a hydraulic bounce, one kind of swiftly numerous waft, might be supplied first, accompanied through a dialogue of the precise force. A quick dialogue of a sharp-crested weir is given on the quilt of this section.
Hydraulic jumps arise whilst the waft adjustments unexpectedly from supercritical to subcritical waft. This procedure is frequently observed through intense turbulence and excessive power losses. Hydraulic jumps frequently arise whilst there may be a war among the upstream and downstream controls. It is the water equal of a sonic boom.
The shear pressure at the lowest of the channel is thought to be negligible. It is likewise similarly assumed that the 2 ends of the manipulate quantity (indicated through crimson dashed lines) are some distance far from the bounce such that the waft is uniform, consistent and one-dimensional.
Applying the momentum equation to the manipulate quantity with inside the waft route yields
Definition of hydraulic jump; Equation of hydraulic jump in horizontal, rectangular channel
Hydraulic jumps arise while the go with the drift modifications all of sudden from supercritical to subcritical go with the drift. This method is regularly followed with the aid of using severe turbulence and excessive strength losses. Hydraulic jumps regularly arise while there's a warfare among the upstream and downstream controls.
It is the water equal of a sonic boom. The shear pressure at the lowest of the channel is believed to be negligible. It is likewise in addition assumed that the 2 ends of the manipulate quantity (indicated with the aid of using crimson dashed lines) are a ways far from the bounce such that the go with the drift is uniform, consistent and one-dimensional. Applying the momentum equation to the manipulate quantity with inside the go with the drift course yields:
-ρV12A1 + ρV22A2 = p1A1 - p2A2 [1]
Where V and A denote the average velocity and cross sectional area, respectively. The pressures at both sections are hydrostatic, the net force due to these is simply the pressure at the centroid times the cross-sectional area. That is,
p1 = ρgz1 and p2 = ρgz2 [2]
Where z is the distance from the water surface to the centroid of the cross-sectional area.
The average velocity can be expressed in terms of the volumetric flow rate as
V1 = Q/A1 and V2 = Q/A2 [3]
Combining Eqns. [1] through [3], and rearranging terms yields
Q2/gA1 + z1A1 = Q2/gA2 + z2A2 [4]
For a rectangular channel with a width of b (A = by, Q = Vby and z = y/2), the momentum equation (Eqn. 4) becomes
V12/gy1 y12 + y12/2 = V22/gy2 y22 + y22/2 [5]
From the continuity equation
Q = V1by1 = V2by2
Which gives V2 = V1 (y1/y2). Then, eliminating V2 from Eqn. 5, and rearranging terms yields
[(y2/y1)2 + y2/y – 2Fr12] [ y2/y1 – 1] = 0 [6]
Where Fr1 is the upstream Froude number, and is given by
Fr1 = V12/gy1 [7]
The root y1 = y2 represents the trivial case where no hydraulic jump occurs. The remaining two roots are
y2/y1 = ½ (-1 ± 1+ 8Fr12)
The solution with the minus sign yields a negative water depth ratio y1/y2, hence this solution is not physically possible.
Thus,
y2/y1 = ½ (-1 ± 1+ 8Fr12) [8]
Is the relation to describe the upstream and downstream water depths of a hydraulic jump in a rectangular channel?
Length & height of jump
Height of the Standing Wave or Hydraulic Jump:
This is the difference of water levels between two sections before and after the hydraulic jump.
Height of standing wave = (d2 – d1)
Length of Hydraulic Jump:
This cannot be calculated analytically. The exact point of commencement of the jump and the exact point where it ends are not well defined. For purposes of analysis we may assume the length of the hydraulic jump to be 5 to 7 times the height of the jump.
A hydraulic jump occurs in site in the following conditions:
(i) When water moving in shooting flow impacts with water having a larger depth with streaming flow.
(ii) On the downstream sides of sluices.
(iii) At the foot of spillways.
(iv) Where the gradient suddenly changes from a steep slope to a flat slope.
Relation between Pre Jump and Post Jump Froude Numbers:
Let Fr1 and Fr2 be the Froude numbers before and after the hydraulic jump.
We know, Fr1 = v1/gd1 and Fr2 = v2/gd2
v1 = Fr1 gd1 and v2 = Fr2 gd2
By continuity condition,
d1v1 = d2v2
d1Fr1gd1 = d2Fr2 gd2
(d1/d2)3/2 = Fr2/Fr1
d1/d2 = (Fr2/Fr1)2/3
We also know,
d2 = d1/2 ((1+8Fr12) -1)
d1/d2 = 2/ ((1+8Fr12) -1)
From the above relations for d1/d2
(Fr2/Fr1)2/3 = 2/((1+8Fr12) -1)
Fr2/Fr1 = [2/((1+8Fr12) -1)]3/2
Fr2 = Fr1 [2/((1+8Fr12) -1)]3/2
For a hydraulic jump to occur, the pre jump Froude number Fr1 should be greater than 1. The post jump Froude number Fr2 will be less than 1.
The table below shows the values of the post jump Froude number Fr2 for various values of pre jump Froude number Fr1.
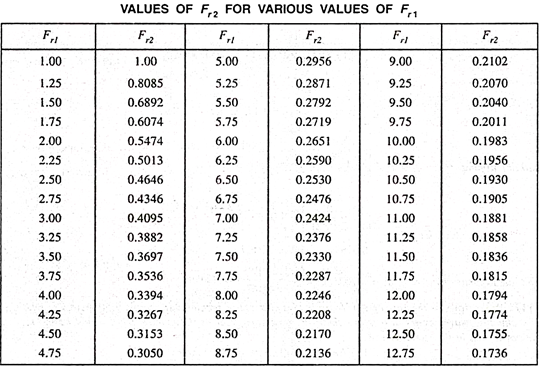
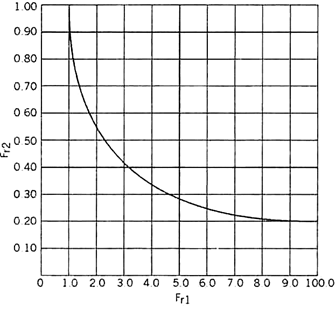
A hydraulic soar is a phenomenon with inside the technological know-how of hydraulics that is regularly found in open channel float which includes rivers and spillways. When liquid at excessive pace discharges right into a sector of decrease pace, a instead abrupt upward push takes place with inside the liquid floor.
The unexpectedly flowing liquid is all of sudden slowed and will increase in height, changing a number of the float's preliminary kinetic strength into an growth in ability strength, with a few strength irreversibly misplaced via turbulence to heat. In an open channel float, this manifests as the short float unexpectedly slowing and piling up on pinnacle of itself just like how a shockwave forms.
As the preliminary float velocity will increase further, the transition turns into extra abrupt, till at excessive sufficient speeds, the transition the front will wreck and curl lower back upon itself.
However, the mechanisms at the back of them are comparable due to the fact they're truly versions of every different visible from special frames of reference, and so the physics and evaluation strategies may be used for each types.
Energy loss in jump
Hydraulic leap in a square channel, additionally referred to as classical leap, is a herbal phenomenon that takes place on every occasion glide adjustments from supercritical to subcritical glide. In this transition, the water floor rises abruptly, floor rollers are formed, extreme blending takes place, air is entrained, and frequently a big quantity of electricity is dissipated.
In different words, a hydraulic leap occurs whilst a better velocity, v1, supercritical glide upstream is met through a subcritical downstream glide with a reduced velocity, v2, and enough depth. Numeric fashions created the usage of the same old step technique or HEC-RAS are used to tune supercritical and subcritical flows to decide in which in a selected attain a hydraulic leap will form.
There also are man-made hydraulic jumps created through gadgets like weirs or sluice gates. In popular, a hydraulic leap can be used to deplete electricity, to combine chemicals, or to behave as an aeration device. To produce equations describing the leap, seeing that there may be an unknown electricity loss, there may be a want to use conservation of momentum.
To broaden this equation, a popular scenario wherein there may also or might not be an electricity loss among upstream and downstream, and there may also or might not be a few impediment on which there may be a drag pressure Pf is considered. However, for a easy or traditional hydraulic leap the pressure in step with unit width(Pf) equals 0. From there the momentum equation, and the conjugate depths equation may be derived.
Although momentum is conserved throughout the hydraulic jump, the energy is not. There is an initial loss of energy when the flow jumps from supercritical to subcritical depths. The resulting loss of energy is equal to the change in specific energy across the jump and is given by the equation for ΔE below. The equation below is based on the condition that y1 and y2 are conjugate depths.
E = E1 – E2 = (y1 + q2/2gy12) – (y2 + q2/2gy22) = (y2 – y1)3/4y1y2
When searching on the vital factors at the M-y diagram and what their places inform us approximately the character of the hydraulic bounce, we referred to that a growth in q could have an effect on the electricity misplaced with inside the bounce.
From Figure 7 we see that growing the glide fee decreases the distinction with inside the upstream and downstream intensity of the bounce (y2 – y1). From this we are able to infer that if the momentum is held to be constant, there may be a lower with inside the electricity misplaced with inside the bounce if the glide fee is increased.
The performance of the bounce is decided through the dimensionless parameter E2/E1 which tells us how a whole lot of the authentic electricity is ultimate after the bounce is complete.
The equation for the electricity performance is given underneath and indicates the heavy dependence that the performance has at the Froude wide variety of the upstream glide. Example 2 indicates a pattern calculation for electricity loss and performance.
E2/E1 = 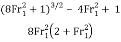
Classifications of jump
Basically a hydraulic soar takes place in lots of kinds relying on topographical capabilities and mattress floor roughness and plenty of different herbal interface relations. This hydraulic soar kinds may be possibly expressed primarily based totally on Froude’s variety:
1. Undular Hydraulic Jump – Froude Number (1 to three):
Undular Jump is irregular, now no longer well fashioned and there are positive turbulences in water debris.
2. Weak Jump –
Froude Number (three to 6) Weak soar takes location while the speed in water may be very much less and the water debris can't be strong and flows in numerous ways.
3. Oscillating Hydraulic Jump – Froude Number (6-20)
Oscillating soar paperwork while an oscillating jet input into amazing crucial nation and there the variety of debris begins off evolved oscillating in clockwise or both anticlockwise path, forming slighter tides or waves to the pinnacle floor. Also the go with the drift is depending on heavy blow of air in a single path.
4. Steady Hydraulic Jump – Froude Number (20 to 80)
In consistent soar, the mattress floor is pretty difficult so the debris begin to generally tend in a single path with heavy speed and turbulence, frictional losses are extra on this form of soar.
5. Strong Hydraulic Jump – Froude Number (more than 80)
Strong soar is an excellent soar fashioned while frictional losses are extra, air stress department is identical and speed may be very excessive that losses take location. The water modifications its nation from amazing crucial to subcritical in very shorter period while as compared to all different varieties of hydraulic jumps, so this soar is rather favored in dam structures.
Key Takeaways:
- Hydraulic jumps regularly arise while there's a warfare among the upstream and downstream controls.
- This cannot be calculated analytically. The exact point of commencement of the jump and the exact point where it ends are not well defined.
References:
1. Hydraulics & Fluid Mechanics- Dr.Modi & Dr. Seth
2. Fluid Mechanics-Streeter & Wylie
3. Fluid Mechanics- Dr. A.K.Jain
4. Fluid Mechanics through problems- Garde
5. Theory and applications of Fluid Mechanics- K. Subramanya
6. Foundation of Fluid Mechanics-Yuan
7. Flow through open channel – K.G.Rangaraju
Unit - 4
Applications of Specific Energy
Applications of specific energy
The preceding packages of precise strength to drilling operations have centered in particular on drilling optimization and identity of inefficient drilling conditions.
Recent advances in precise strength make bigger its packages to overpressure detection and pore strain prediction. In this paper, a try is made to in addition make bigger the software of precise strength to real-time identity of subsurface lithology.
The idea is primarily based totally at the precept that the entire strength required to interrupt and cast off a unit extent of rock is a characteristic of lithology. The proposed technique is examined the use of a lately drilled exploratory fuel line properly with inside the tertiary deltaic gadget of the Niger Delta basin.
In general, an amazing settlement is found in fashion among the conventional lithology identifiers (gamma ray and sonic pace ratio) and the entire strength fed on in breaking and disposing of the penetrated rocks.
The proposed technique can offer a dependable way of choosing formation tops and figuring out subsurface lithology on the bit without a greater fee due to the fact drilling parameters are robotically recorded on the well site in the course of the drilling of a properly.
The proposed technique will help the drilling engineers and geologists in figuring out the casing putting depths and coring factors while not having to drill too deep into the formation of interest.
Application of precise strength and momentum characteristic Discussion With the underlying downstream and corresponding discharge, the upstream intensity this is y2 and y3 are taken because the extrude depths owning comparable precise strength. As the sluice gate is raised, y2 processes the corresponding y3 and E is minimized arise beneath the most discharge for the given strength (Chiseled, Fomin&. Vorozhtsov, 1999).
Moreover, short, clean step with an upward push alternate in y in the channel (∆y), y2 used the extrude intensity viable given the upstream and the discharge. When short, clean step with the most upward push with inside the alternate of y (∆y) in the channel and the step is escalated in addition y2 increases.
Conversely, the increase, in short, clean step with the alternate in y in the channel and with the given upstream intensity and corresponding discharge, y3 is accelerated. Y3 is accelerated because of the enlargement and strength loss.
A hydraulic bounce is applied for strength dissipation that takes place while the flows transitions from the supercritical to corresponding subcritical in particular because of the spillway and the steep slope to the moderate slope. The intensity of water downstream from the bounce and the region of the bounce are computed the use of the conservation of strength equation (Kiselev, Fomin&. Vorozhtsov, 1999). It is predicted from y1 that the intensity of water to amplify because the precise strength of the triumphing reduces slowly.
Moreover, the extrude depths at which the precise energies must be identical. Nevertheless, the values amassed does now no longer depict that because the underlying values have been now no longer ok to provide the right and predicted graph for that reason the affiliation became now no longer represented as anticipated.
The triumphing graphs derived from the depths of the flow, and corresponding precise strength on the phase depicts that the intensity escalates because the time elapses linearly with the precise strength indicating that the 2 underlying variables are linearly associated.
Gradual transitions of channels
No uniform flows for which the modifications intensive and pace are so abrupt that radial accelerations distort the vertical distribution of fluid strain from the hydrostatic situation are referred to as hastily various flows.
Such flows are hard to address analytically, and I will now no longer pursue them here, even though they're vital in lots of engineering applications.
No uniform open-channel flows for which the modifications intensive and pace are sluggish sufficient with inside the downstream path that the vertical distribution of fluid strain from the unfastened floor to the lowest isn't always an awful lot extraordinary from hydrostatic are referred to as progressively various flows. An instance is the waft transition over a mild step, delivered at the start of this bankruptcy
It is finished in a sufficiently quick distance that lack of waft power through friction may be neglected, however the fluid accelerations are nonetheless small enough that the vertical distribution of fluid strain is near being hydrostatic. In maximum progressively various flows, however, the alternate takes location over a distance sufficiently extraordinary that we cannot expect 0 power loss because of backside friction.
The 2nd channel-transition instance posed at the start of this bankruptcy falls into that category. To see what occurs to the elevation of the water floor through a transition over this sort of lengthy distance that backside friction cannot be neglected, we want to begin with the equation for the overall head at a go segment of the waft and differentiate every time period with appreciate to distance with inside the waft (In what follows, I am going to write γ alternatively of d for the waft depth.)
The time period at the left facet of Equation 5.7.2 is the charge of alternate in general power with inside the downstream path. This is usually negative, due to the fact power is unavoidably misplaced through friction. Think in phrases of the downward slope of the road fashioned through plotting Ew as a feature of downstream distance. This slope, denoted through Se, is what changed into referred to as the power slope, or the power gradient, or the slope of the power line in advance on this bankruptcy.
Ew = U2/2g + y + ho
A subject have a look at changed into performed to decide the results of a channel transition on turbulence traits. Detailed three-dimensional (three-D) waft measurements have been accumulated at a move phase this is positioned downstream of a slow channel growth.
These measurements have been acquired through an acoustic Dopplervelocimeter and encompass the three-D pace subject, the suggest nearby velocities, the turbulent intensities, the frictional traits of the waft, the secondary pace alongside the transverse aircraft, and the immediate shear pressure additives with inside the stream wise and transverse instructions.
Analysis of the three-D waft statistics suggests that the turbulent waft at the outer financial institution of the channel is anisotropic.
Turbulent intensities boom in the direction of the unfastened floor indicating the switch of a higher-momentum flux from the channel mattress to the unfastened floor, which contradicts not unusual place wisdom. Results for the normalized pressure additives with inside the stream wise and transverse path display comparable conduct to the intensities.
Key Takeaways:
- The preceding packages of precise strength to drilling operations have centered in particular on drilling optimization and identity of inefficient drilling conditions.
- The proposed technique will help the drilling engineers and geologists in figuring out the casing putting depths and coring factors while not having to drill too deep into the formation of interest.
GRADUALLY VARIED FLOW
The definition of those go with the drift sorts move something like this- Rapidly Varied Flow (RVF) is a sizable extrude in water intensity or pace of go with the drift over a brief distance. This distance may be some instances the water intensity.
Gradually Varied Flow (GVF) is the go with the drift in which the water intensity adjustments step by step over a big distance. In an extra formal and technical way, gradually numerous go with the drift is the no uniform, consistent open-channel flows
Vertical distribution of fluid stress from the loose floor to the lowest isn't always plenty extraordinary from hydrostatic. I actually have already blanketed the kinds of fluid go with the drift which includes consistent and unsteady go with the drift, uniform and non-uniform go with the drift here.
Assumptions of Gradually Varied Flow
Some of the critical assumptions below which the step by step numerous go with the drift (GVF) holds best are:
- The slope of the channel/canal may be very small.
- The vertical intensity is taken into consideration from the lowest.
- The stress distribution is hydrostatic due to the fact the curvature of streamlines is small.
- Manning's and Chery’s system is legitimate for the computation of pace.
- Channel mattress slope is small, HGL will lie on the loose floor.
- The go with the drift channel is prismatic.
- The channel has consistent form and alignment.
- The pace distribution coefficients are consistent.
- This is all approximately the fundamentals of Gradually Varied Flow.
Dynamic Equation of GVF
The general form of gradually varied flow(GVF) equation is:
(dy/dx)=(So-Sf)/(1-Fr^2)
In this equation, So = Bottom slope, positive in the downward direction
Sf = Friction slope. It is positive in the downward direction.
y = Water depth, measured from culvert bottom to water surface
x = Longitudinal distance, measured along the culvert bottom
Fr = Froude number
The friction slope is approximated as the below equation(Manning's equation),
Sf = (nv)^2/R^(4/3)
Where: Sf = Friction slope, positive in the downward direction
n = Manning's roughness coefficient
v = Average cross section velocity
R = Hydraulic radius, (Wetted Area / Wetted Perimeter)
Bottom Slope and Friction Slope Correlation
From the above mentioned Dynamic Equation, the following inferences can be drawn.
- If Sf = So, then dy/dx = 0, the surface profile of flow is parallel to the bottom of the channel.
- If Sf< So, then dy/dx is positive which means the flow profile is rising gradually.
- If Sf>So, then dy/dx is negative which means the flow profile is lowering gradually.
Classification and characteristics of surface profiles
The water surface profile within a culvert can be classified two different ways:
1. Hydraulic Slope, which is based on the slope of the culvert bottom and
2. Hydraulic Curve, which is based on the relationship of the water depth relative to critical depth and normal depth.
Hydraulic Slope Classifications
The Hydraulic Slope of a culvert at a specific flow classifies the hydraulic regime and defines the type of solution generated from the Gradually Varied Flow calculations.
Hydraulic Slope is determined from:
1. The culvert bottom slope (So) and
2. The relationship between critical depth (yc) and normal depth (yn) at a specific flow.
There are five slope classifications:
Adverse (A) if So <0 (slope is positive in the downstream direction)
Horizontal (H) if So = 0
Critical (C) if Yo = yc
Mild (M) if So> 0 and yn > yc
Steep (S) if So> 0 and yn < yc
Hydraulic Curve Classifications
Hydraulic Curve classifications are used to describe the shape of the water surface profile at a specific flow. The curves are based on the Hydraulic Slope (A, H, C, M, or S) and the relative position of the actual flow depth to normal and critical depth as designated by the numbers 1, 2, and 3.
- Type 1 curve: Depth is greater than yc and yn, flow is subcritical
- Type 2 curve: Depth is between ycand yn, flow can be either subcritical or supercritical
- Type 3 curve: Depth is less than both ycand yn, flow is supercritical.
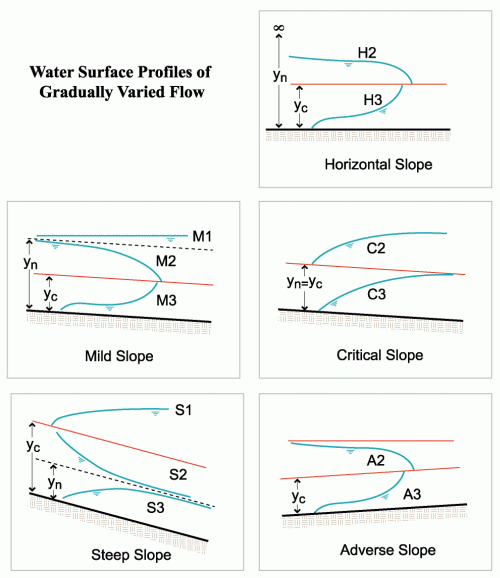
Direct Step method of computing profile length.
The float is assessed as regularly various float whilst the extrude of the fluid intensity alongside the channel dy/dx is a good deal much less than one. For regularly various float, the channel may be divided into exceptional sections referred to as reaches, and the uniform float equations, which include the Chezy and Manning equations, are relevant for calculating head losses in such reaches.
Gradually Varied Flow For consistent and one-dimensional float, the equation for regularly various float, primarily based totally at the power equation, may be written as
DE/dx = So - Sf [1]
Where E is the specific energy, So is the slope of the channel bed, and Sf is the slope of the energy grade line (EGL).
The equation above can also be rewritten in terms of the change of the water surface elevation and Froude number (Fr) as follows:
Dy/dx = (S0 – Sf)/(1 – Fr2) [2]
Note that equations 1 and a couple of are nonlinear differential equations, and analytical answers are viable handiest for some problems. Hence numerical strategies are essential to approximate the answers. One of the only numerical strategies is the finite distinction technique. Eqn. 1 may be discretized as follows:
E/x = S0 - 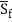 [4]
[4]
Where 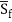 is the average slope of the energy grade line between the end points of a given reach?
is the average slope of the energy grade line between the end points of a given reach?
The direct step technique begins off evolved from a boundary circumstance or manage factor (i.e., a factor in which the water floor elevation is given), and proceeds via way of means of assuming a floor elevation (y) and computing the gap Δx to the assumed elevation:
x = E/( S0 - 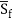 ) [5]
) [5]
The computations then keep on to the subsequent reach, and prevent whilst a predetermined restriction or criterion is reached. The case have a look at gives particular approaches for the usage of the direct step technique in figuring out the water floor elevation.
Key Takeaways:
- The definition of those go with the drift sorts move something like this- Rapidly Varied Flow (RVF) is a sizable extrude in water intensity or pace of go with the drift over a brief distance. This distance may be some instances the water intensity.
RAPIDLY VARIED FLOW
Rapidly numerous waft is every other kind of no uniform open-channel waft in which the fluid intensity adjustments swiftly over a small attain of the channel. The phenomenon of a hydraulic bounce, one kind of swiftly numerous waft, might be supplied first, accompanied through a dialogue of the precise force. A quick dialogue of a sharp-crested weir is given on the quilt of this section.
Hydraulic jumps arise whilst the waft adjustments unexpectedly from supercritical to subcritical waft. This procedure is frequently observed through intense turbulence and excessive power losses. Hydraulic jumps frequently arise whilst there may be a war among the upstream and downstream controls. It is the water equal of a sonic boom.
The shear pressure at the lowest of the channel is thought to be negligible. It is likewise similarly assumed that the 2 ends of the manipulate quantity (indicated through crimson dashed lines) are some distance far from the bounce such that the waft is uniform, consistent and one-dimensional.
Applying the momentum equation to the manipulate quantity with inside the waft route yields
Definition of hydraulic jump; Equation of hydraulic jump in horizontal, rectangular channel
Hydraulic jumps arise while the go with the drift modifications all of sudden from supercritical to subcritical go with the drift. This method is regularly followed with the aid of using severe turbulence and excessive strength losses. Hydraulic jumps regularly arise while there's a warfare among the upstream and downstream controls.
It is the water equal of a sonic boom. The shear pressure at the lowest of the channel is believed to be negligible. It is likewise in addition assumed that the 2 ends of the manipulate quantity (indicated with the aid of using crimson dashed lines) are a ways far from the bounce such that the go with the drift is uniform, consistent and one-dimensional. Applying the momentum equation to the manipulate quantity with inside the go with the drift course yields:
-ρV12A1 + ρV22A2 = p1A1 - p2A2 [1]
Where V and A denote the average velocity and cross sectional area, respectively. The pressures at both sections are hydrostatic, the net force due to these is simply the pressure at the centroid times the cross-sectional area. That is,
p1 = ρgz1 and p2 = ρgz2 [2]
Where z is the distance from the water surface to the centroid of the cross-sectional area.
The average velocity can be expressed in terms of the volumetric flow rate as
V1 = Q/A1 and V2 = Q/A2 [3]
Combining Eqns. [1] through [3], and rearranging terms yields
Q2/gA1 + z1A1 = Q2/gA2 + z2A2 [4]
For a rectangular channel with a width of b (A = by, Q = Vby and z = y/2), the momentum equation (Eqn. 4) becomes
V12/gy1 y12 + y12/2 = V22/gy2 y22 + y22/2 [5]
From the continuity equation
Q = V1by1 = V2by2
Which gives V2 = V1 (y1/y2). Then, eliminating V2 from Eqn. 5, and rearranging terms yields
[(y2/y1)2 + y2/y – 2Fr12] [ y2/y1 – 1] = 0 [6]
Where Fr1 is the upstream Froude number, and is given by
Fr1 = V12/gy1 [7]
The root y1 = y2 represents the trivial case where no hydraulic jump occurs. The remaining two roots are
y2/y1 = ½ (-1 ± 1+ 8Fr12)
The solution with the minus sign yields a negative water depth ratio y1/y2, hence this solution is not physically possible.
Thus,
y2/y1 = ½ (-1 ± 1+ 8Fr12) [8]
Is the relation to describe the upstream and downstream water depths of a hydraulic jump in a rectangular channel?
Length & height of jump
Height of the Standing Wave or Hydraulic Jump:
This is the difference of water levels between two sections before and after the hydraulic jump.
Height of standing wave = (d2 – d1)
Length of Hydraulic Jump:
This cannot be calculated analytically. The exact point of commencement of the jump and the exact point where it ends are not well defined. For purposes of analysis we may assume the length of the hydraulic jump to be 5 to 7 times the height of the jump.
A hydraulic jump occurs in site in the following conditions:
(i) When water moving in shooting flow impacts with water having a larger depth with streaming flow.
(ii) On the downstream sides of sluices.
(iii) At the foot of spillways.
(iv) Where the gradient suddenly changes from a steep slope to a flat slope.
Relation between Pre Jump and Post Jump Froude Numbers:
Let Fr1 and Fr2 be the Froude numbers before and after the hydraulic jump.
We know, Fr1 = v1/gd1 and Fr2 = v2/gd2
v1 = Fr1 gd1 and v2 = Fr2 gd2
By continuity condition,
d1v1 = d2v2
d1Fr1gd1 = d2Fr2 gd2
(d1/d2)3/2 = Fr2/Fr1
d1/d2 = (Fr2/Fr1)2/3
We also know,
d2 = d1/2 ((1+8Fr12) -1)
d1/d2 = 2/ ((1+8Fr12) -1)
From the above relations for d1/d2
(Fr2/Fr1)2/3 = 2/((1+8Fr12) -1)
Fr2/Fr1 = [2/((1+8Fr12) -1)]3/2
Fr2 = Fr1 [2/((1+8Fr12) -1)]3/2
For a hydraulic jump to occur, the pre jump Froude number Fr1 should be greater than 1. The post jump Froude number Fr2 will be less than 1.
The table below shows the values of the post jump Froude number Fr2 for various values of pre jump Froude number Fr1.
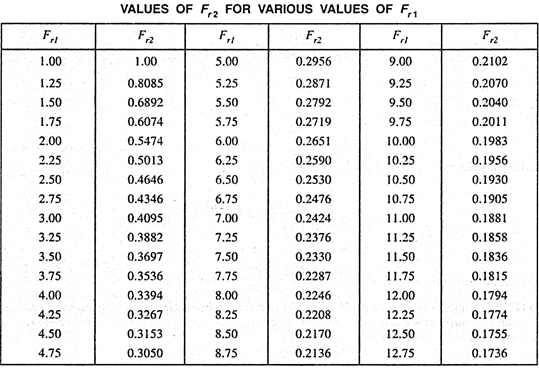

A hydraulic soar is a phenomenon with inside the technological know-how of hydraulics that is regularly found in open channel float which includes rivers and spillways. When liquid at excessive pace discharges right into a sector of decrease pace, a instead abrupt upward push takes place with inside the liquid floor.
The unexpectedly flowing liquid is all of sudden slowed and will increase in height, changing a number of the float's preliminary kinetic strength into an growth in ability strength, with a few strength irreversibly misplaced via turbulence to heat. In an open channel float, this manifests as the short float unexpectedly slowing and piling up on pinnacle of itself just like how a shockwave forms.
As the preliminary float velocity will increase further, the transition turns into extra abrupt, till at excessive sufficient speeds, the transition the front will wreck and curl lower back upon itself.
However, the mechanisms at the back of them are comparable due to the fact they're truly versions of every different visible from special frames of reference, and so the physics and evaluation strategies may be used for each types.
Energy loss in jump
Hydraulic leap in a square channel, additionally referred to as classical leap, is a herbal phenomenon that takes place on every occasion glide adjustments from supercritical to subcritical glide. In this transition, the water floor rises abruptly, floor rollers are formed, extreme blending takes place, air is entrained, and frequently a big quantity of electricity is dissipated.
In different words, a hydraulic leap occurs whilst a better velocity, v1, supercritical glide upstream is met through a subcritical downstream glide with a reduced velocity, v2, and enough depth. Numeric fashions created the usage of the same old step technique or HEC-RAS are used to tune supercritical and subcritical flows to decide in which in a selected attain a hydraulic leap will form.
There also are man-made hydraulic jumps created through gadgets like weirs or sluice gates. In popular, a hydraulic leap can be used to deplete electricity, to combine chemicals, or to behave as an aeration device. To produce equations describing the leap, seeing that there may be an unknown electricity loss, there may be a want to use conservation of momentum.
To broaden this equation, a popular scenario wherein there may also or might not be an electricity loss among upstream and downstream, and there may also or might not be a few impediment on which there may be a drag pressure Pf is considered. However, for a easy or traditional hydraulic leap the pressure in step with unit width(Pf) equals 0. From there the momentum equation, and the conjugate depths equation may be derived.
Although momentum is conserved throughout the hydraulic jump, the energy is not. There is an initial loss of energy when the flow jumps from supercritical to subcritical depths. The resulting loss of energy is equal to the change in specific energy across the jump and is given by the equation for ΔE below. The equation below is based on the condition that y1 and y2 are conjugate depths.
E = E1 – E2 = (y1 + q2/2gy12) – (y2 + q2/2gy22) = (y2 – y1)3/4y1y2
When searching on the vital factors at the M-y diagram and what their places inform us approximately the character of the hydraulic bounce, we referred to that a growth in q could have an effect on the electricity misplaced with inside the bounce.
From Figure 7 we see that growing the glide fee decreases the distinction with inside the upstream and downstream intensity of the bounce (y2 – y1). From this we are able to infer that if the momentum is held to be constant, there may be a lower with inside the electricity misplaced with inside the bounce if the glide fee is increased.
The performance of the bounce is decided through the dimensionless parameter E2/E1 which tells us how a whole lot of the authentic electricity is ultimate after the bounce is complete.
The equation for the electricity performance is given underneath and indicates the heavy dependence that the performance has at the Froude wide variety of the upstream glide. Example 2 indicates a pattern calculation for electricity loss and performance.
E2/E1 = 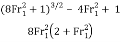
Classifications of jump
Basically a hydraulic soar takes place in lots of kinds relying on topographical capabilities and mattress floor roughness and plenty of different herbal interface relations. This hydraulic soar kinds may be possibly expressed primarily based totally on Froude’s variety:
1. Undular Hydraulic Jump – Froude Number (1 to three):
Undular Jump is irregular, now no longer well fashioned and there are positive turbulences in water debris.
2. Weak Jump –
Froude Number (three to 6) Weak soar takes location while the speed in water may be very much less and the water debris can't be strong and flows in numerous ways.
3. Oscillating Hydraulic Jump – Froude Number (6-20)
Oscillating soar paperwork while an oscillating jet input into amazing crucial nation and there the variety of debris begins off evolved oscillating in clockwise or both anticlockwise path, forming slighter tides or waves to the pinnacle floor. Also the go with the drift is depending on heavy blow of air in a single path.
4. Steady Hydraulic Jump – Froude Number (20 to 80)
In consistent soar, the mattress floor is pretty difficult so the debris begin to generally tend in a single path with heavy speed and turbulence, frictional losses are extra on this form of soar.
5. Strong Hydraulic Jump – Froude Number (more than 80)
Strong soar is an excellent soar fashioned while frictional losses are extra, air stress department is identical and speed may be very excessive that losses take location. The water modifications its nation from amazing crucial to subcritical in very shorter period while as compared to all different varieties of hydraulic jumps, so this soar is rather favored in dam structures.
Key Takeaways:
- Hydraulic jumps regularly arise while there's a warfare among the upstream and downstream controls.
- This cannot be calculated analytically. The exact point of commencement of the jump and the exact point where it ends are not well defined.
References:
1. Hydraulics & Fluid Mechanics- Dr.Modi & Dr. Seth
2. Fluid Mechanics-Streeter & Wylie
3. Fluid Mechanics- Dr. A.K.Jain
4. Fluid Mechanics through problems- Garde
5. Theory and applications of Fluid Mechanics- K. Subramanya
6. Foundation of Fluid Mechanics-Yuan
7. Flow through open channel – K.G.Rangaraju