Unit 3
Crystal Structure
If the atoms or molecules are uniquely arranged in crystalline solid or liquid, we call it as a crystal structure. A crystal possesses long range order and symmetry. The main property of crystal structure is its periodicity. This periodicity is due to the arrangement of atoms/molecules in the lattice points
Some common crystal structures you should know
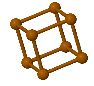 Simple Cubic | 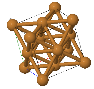 Face Cantered Cubic | 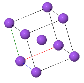 Body Centered Cubic |  Hexagonal Close Packed | 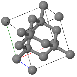 Diamond |
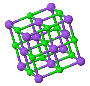 NaCl | 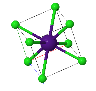 CsCl | 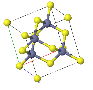 Zincblende |  Wurtzite | 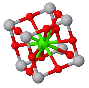 Perovskite |
Lattice:
A lattice is in general defined as a discrete but infinite regular arrangement of points (lattice sites) in a vector space
Bravais Lattice
In solid state physics one usually encounters lattices which exhibit a discrete translational symmetry. If one considers for instance the vector space R3 this means that a translation of the whole lattice by any translation vector given by.
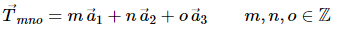
A lattice that can be characterised in this way is referred to as a Bravais lattice. All lattice points are equivalent, However, if there are lattice points with different environments they cannot form a Bravais lattice.
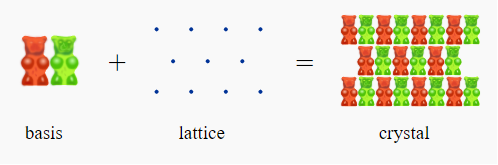
Basis:
A basis is a collection of atoms in particular fixed arrangement in space. We could have a basis of a single atom as well as a basis of a complicated but fixed arrangement of hundreds of atoms.
The structure of a crystal can be seen to be composed of a repeated element in three dimensions. This repeated element is known as the unit cell. It is the building block of the crystal structure. We define the unit cell in terms of the lattice (set of identical points). In three dimensions the unit cell is any parallelepiped whose vertices are lattice points, in two dimensions it is any parallelogram whose vertices are lattice points.
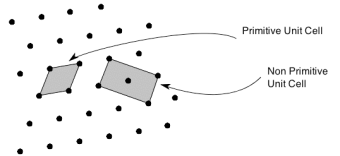
So, in general, the unit cell is chosen such that it is the smallest unit cell that reflects the symmetry of the structure. There are two distinct types of unit cell: primitive and non-primitive.
Primitive unit cells contain only one lattice point, which is made up from the lattice points at each of the corners. Non-primitive unit cells contain additional lattice points, either on a face of the unit cell or within the unit cell, and so have more than one lattice point per unit cell.
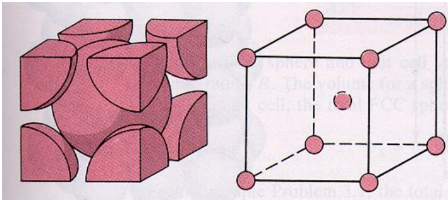
FCC (face centered cubic):
Atoms are arranged at the corners and center of each cube face of the cell. 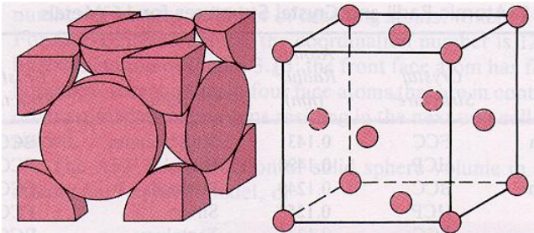
In fcc
Close packed Plane: On each face of the cube Atoms are assumed to touch along face diagonals.
And atoms in one-unit cell.
a 2R√2 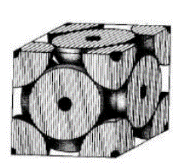
BCC(Body Centric Cubic Cell):
• Atoms are arranged at the corners of the cube with another atom at the cube center.
• Close Packed Plane cuts the unit cube in half diagonally
•2 atoms in one-unit cell 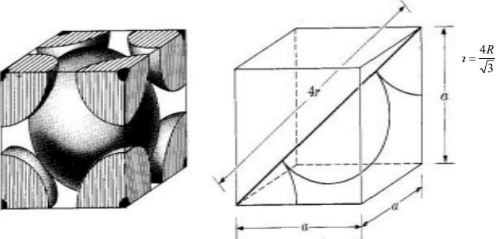
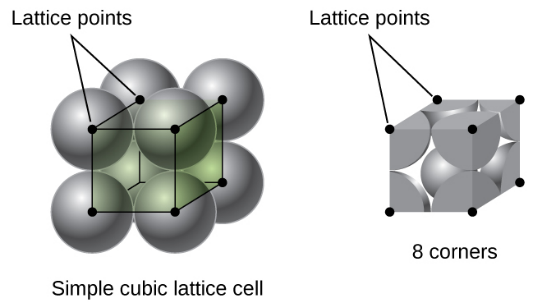
SC(Simple Cubic)
In a simple cubic lattice, the unit cell that repeats in all directions is a cube defined by the centers of eight atoms
A cubic unit cell contains only the parts of these atoms that are within it. Since an atom at a corner of a simple cubic unit cell is contained by a total of eight unit cells, only one-eighth of that atom is within a specific unit cell.
- No. Of atom in per unit cell
Primitive or simple cubic unit cell: A unit cell in which all the eight corners of the cube occupied by the particles.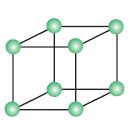
No of atoms present in this unit cell = 8 x 1/8 = 1
Each Corner atom contributes 1/8th portion to the unit cell
Body-cantered cubic unit cell (B.C.C): A unit cell contains one constituent particle present at the centre of each face, along with eight particles at its corners.
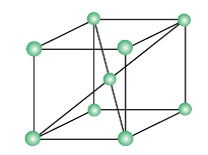
No of atoms present in this unit cell = (8 x 1/8) + 1 = 2
(Each Corner atom contributes 1/8th portion to the unit cell)
(Body cantered atom is 1)
Face-centred cubic unit cell (F.C.C): A unit cell contains one constituent particle present at the centre of each face, along with eight particles at its corners.
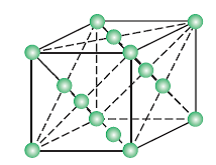
No. Of atoms present in this unit cell = (8 x 1/8) + (6 x ½) = 1 + 3 = 4
(Each Corner atom contributes 1/8th portion to the unit cell)
(Each face cantered atom contributes ½ portion to the unit cell)
Atomic radii
The radius of an atom is determined from the unit cell edge length (a), which is determined from the location of the atoms, and the assumption that the atoms touch
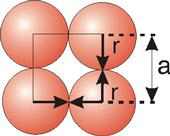
2r=a
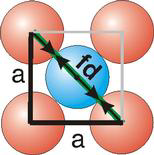
Fd | = | 4r |
|
|
|
|
|
|
Fd2 | = | a2 + a2 |
|
|
|
|
|
|
(4r)2 | = | 2a2 |
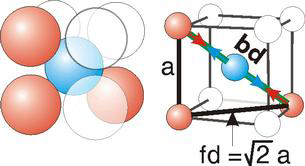
Bd | = | 4r |
|
|
|
|
|
|
Bd2 | = | Fd2 + a2 |
|
|
|
|
|
|
(4r)2 | = | 2a2 + a2 = 3a2 |
|
|
|
Coordination no.
The coordination number (CN) is the number of nearest neighbors of a given particle in the crystal lattice. It determines the nature of the bonding in a crystal. The most common coordination numbers are 4, 6, 8, and 12.
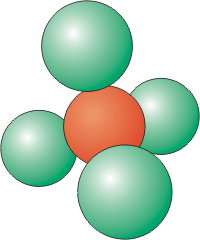
Coordination Number of 4
Four atoms around a central atom are located at the corners of a tetrahedron.
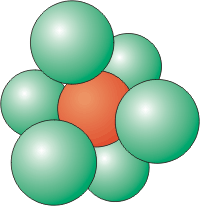
Coordination Number of 6
Six atoms around a central atom are located at the corners of an octahedron. An atom on the corner of a simple cubic unit cell has a coordination number of six.
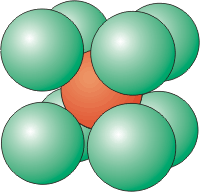
Coordination Number of 8
Eight atoms around a central atom are located at the corners of a cube. The atom in the center of a body-centered unit cell has a coordination number of eight.
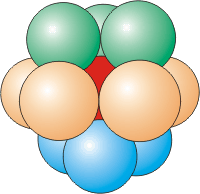
Coordination Number of 12
Each atom in a face-centered cubic unit cell has a coordination number of 12. The 12 particles, which make up the coordination sphere of the red particle lie in three planes.
Packing Efficiency or atomic packing fraction
Packing efficiency is the fraction of the unit cell that is occupied by particles. Closest packed spheres pack with a packing efficiency of 74%.
Spheres cannot be packed without creating some void space, but the amount of void space depends upon how well they are packed. Packing efficiency (PE) is that fraction of the unit cell volume that is actually occupied by particles, not void space., the packing efficiency of a unit cell is
Packing Efficiency | = |
× 100% | ||
|
|
| ||
|
|
| ||
PE | = |
× 100% |
a = the length of a side of the unit cell, so a3 is the volume of the unit cell.
r = the radius of the atoms that occupy the unit cell, so (4/3) πr3 is the volume of a single atom in the unit cell.
N = the number of atoms in the unit cell, so N (4/3) πr3 is the volume occupied by all of the atoms in the unit cell.
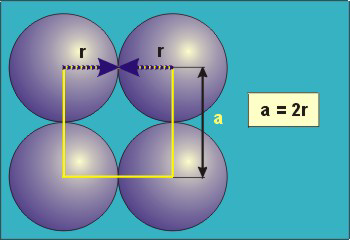
In the simple cubic unit cell, the spheres touch along the cell edge. Consequently, the edge length is two atomic radii
(a = 2r).
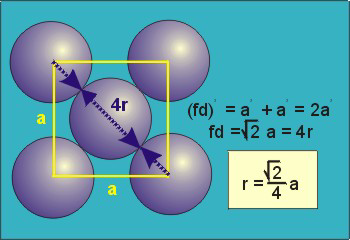
Particle contact in the face-centered cubic unit cell is along the face diagonal (fd). The face diagonal is four atomic radii
(fd = 4r)
Nearest neighbour distance
The distance between the centres of the nuclei of two adjacent atoms is equal to the edge length of the cell which is a.
Hence, the nearest neighbour distance in a simple cubic lattice is a
0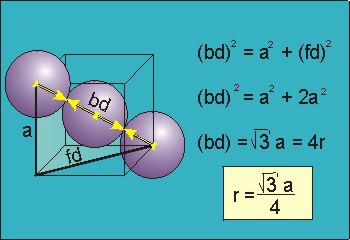
Bd = 4r.
The body diagonal is related to the face diagonal (fd) and the cell edge (a) by the Pythagorean theorem. The relationship between the cell edge and the face diagonal was derived in the discussion of the fcc unit cell.
Void space and density
It is impossible to pack spheres without introducing some void space (space that is not occupied). How well the atoms pack a unit cell depends upon the unit cell type and is given by the packing efficiency of the unit cell. Solids with tightly packed unit cells are more dense than those with low packing efficiencies. In this section, we examine the packing efficiencies of the cubic unit cells and show how to determine the density of a solid from its crystal structure.
Mass of substance |
Volume of substance |
Density is the mass-to-volume ratio of a substance
D=
Densities of metals range from 0.53 g/cm3 for lithium to 22.65 g/cm3 for iridium.
Crystal planes is an important concept used in powder diffraction and crystallography in general. One can imagine a crystal being sub-divided into smaller component units; crystallographers use, depending on context, two alternative sub-divisions: one is the unit cell, the crystal building block, which we will return to later, and the other components are sets of planes invariably known as diffracting planes, reflecting planes, Bragg planes, crystal planes or hkl planes. A set of such planes consists of parallel evenly spaced planes which are extended to exactly fill the entire crystal; each plane is an equal distance, d (the inter-planar spacing), from its neighbouring plane. There are however an infinite number of such types of planes that can be devised and, between them all, they cover every region of space, and indeed every atom, within the crystal: this is one of the properties that makes their concept useful.
It is necessary to have some method of identifying and visualising the most useful planes. Crystallographers use an identification system referred to as Miller, or hkl, indices (a sort of zip-code for the planes).
Miller indices are simply a set of three numbers, hkl, which can take on any combination of three integer values between +∞ and −∞, e.g. (111), (-501) and (7-2-2). Each combination of hkl describes a unique set of planes filling the crystal and so hkl is often presented as a subscript to a property: e.g. dhkl which therefore means the d spacing between the planes defined by hkl. The Miller indices, hkl, also provide a useful means for visualising the planes. The convention is that if you have three axis, x, y, z, with three unit spacings, a, b, c, on each then one of these hkl planes can be visualised as the plane which intersects the x, y, z-axes at distances of a/h, b/k, c/l respectively
The next such plane parallel to this would pass through the origin. The illustration below shows an example of such a set of planes for the case of hkl = (222)
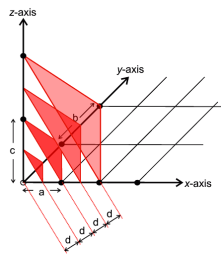
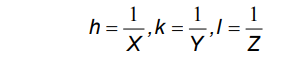
The inter-planar spacing (dhkl) between crystallographic planes belonging to the same family (h,k,l) is denoted (dhkl) Distances between planes defined by the same set of Miller indices are unique for each material dhkl Inter-planar spacings can be measured by x-ray diffraction (Bragg’s Law) The lattice parameters a, b, c of a unit cell can then be calculated The relationship between d and the lattice parameters can be determined geometrically and depends on the crystal system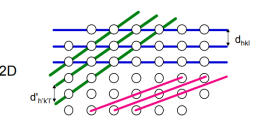
Bragg’s Law can be derived using simple geometry by considering the distances traveled by two parallel X-rays reflecting from adjacent planes. The X-ray hitting the lower plane must travel the extra distance AB and BC. To remain in phase with the first X-ray, this distance must be a multiple of the wavelength thus:
nλ = AB+BC = 2AB(since the two triangles are identical)
The distance AB can be expressed in terms of the interplanar spacing (d) and incident angle (θ) because d is the hypotenuse of right triangle ZAB shown at right.
Sin(θ) = AB/d
Thus AB = d sin(θ)
Therefore:
nλ = 2 d sin(θ)
Reflection (signal) only occurs when conditions for constructive interference between the beams are met
These conditions are met when the difference in path length equals an integral number of wavelengths, n. The final equation is the
BRAGG’S LAW n λ = 2 d sin θ
The vacant space in a closed packed arrangement are called voids. There are two types of Voids (i) Tetrahedral voids (ii)octahedral voids.
Tetrahedral void
A void Surrounded by four spheres in tetrahedral positions are called tetrahedral voids.
(i) It is a triangular void
(ii) It is surrounded by 4 spheres
(iii) Can be observed in the edges of the unit cell.
(iv) Coordination number is four.
(v) Number of tetrahedral voids is 2n or twice the number of octahedral voids.
Octahedral voids
A void surrounded by 6 spheres in octahedral positions are called octahedral voids.
(i) It is surrounded by 6 spheres
(ii) Can be observed in the centre of the unit cells
(iii) Coordination number is six.
(iv) Number of octahedral voids is n or half the number of tetrahedral voids.