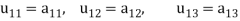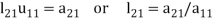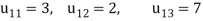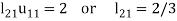Unit - 1
Numerical Methods
Introduction of numerical analysis-
Numerical analysis is a branch of mathematics that deal with solving the difficult mathematical problems by using efficient methods
Sometime the mathematical problems are very hard then an approximation to a difficult Mathematical problem is very important to make it more easy to solve numerical approximation has become more popular and a modern tool there are three parts of numerical analysis. The first part of the subject is about the development of a method to a problem. The second part deals with the analysis of the method, which includes the error analysis and the efficiency analysis. Error analysis gives us the understanding of how accurate the result will be if we use the method and the efficiency analysis tells us how fast we can compute the result
The third part of the subject is the development of an efficient algorithm to implement the method as a computer code.
Concept of roots of an equation-
There are two types of equations Linear and Non linear equations. Linear equations are those in which dependent variable y is directly proportional to independent variable x and is of degree one. On the other hand non linear equation are those in which y does not directly proportional to x and of degree more than one.
Ex: 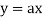 +b, where a and b are constant is a linear equation.
+b, where a and b are constant is a linear equation.
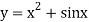 is a non linear equation.
is a non linear equation.
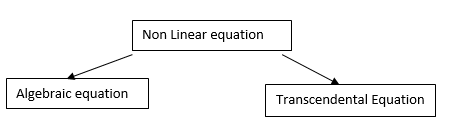
Algebraic Equation: If f(x) is a pure polynomial, then the equation 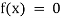 is called an algebraic equation in x.
is called an algebraic equation in x.
Ex: 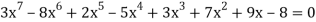
Transcendental Equation: If f(x) is an expression contain function as trigonometric, exponential and logarithmic etc. Then 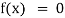 is called transcendental equation.
is called transcendental equation.
Ex 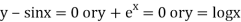
Non –linear equation can be solved by using various analytical methods. The transcendental equations and higher order algebraic equations are difficult to solve even sometime are impossible. Finding solution of equation means just to calculate its roots.
Numerical methods are often repetitive in nature. They consist of repetitive calculation of the same process where in each step the result of preceding values are used (substitute). This is known as iteration process and is repeated till the result is obtained to desired accuracy.
The analytical methods used to solve equation; exact value of the root is obtained whereas in numerical method approximate value is obtained.
Newton-Raphson Method:
Let 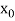 be the approximate root of the equation
be the approximate root of the equation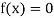 .
.
By Newton Raphson formula 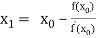
In general,
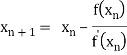
Where n=1, 2, 3…… we keep on calculating until we get desired root to the correct decimal places.
Example1Using Newton-Raphson method, find a root of the following equation correct to 3 decimal places: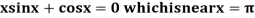 .
.
Given 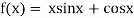
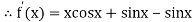
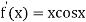
By Newton Raphson Method
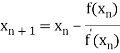
= 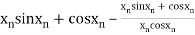
=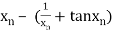
The initial approximation is 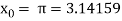 in radian.
in radian.
For n =0, the first approximation 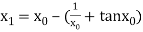
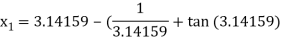
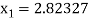
For n =1, the second approximation 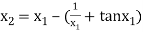
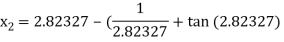
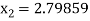
For n =2, the third approximation 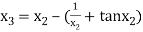
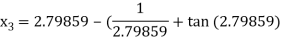
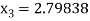
For n =3, the fourth approximation 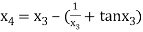
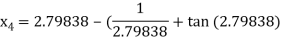
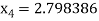
Hence the root of the given equation correct to five decimal place 2.79838.
Example2 Using Newton-Raphson method, find a root of the following equation correct to 3 decimal places: 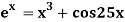 near to 4.5
near to 4.5
Let
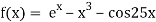
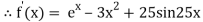
The initial approximation 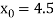
By Newton Raphson Method
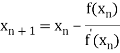
For n =0, the first approximation 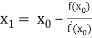
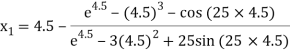
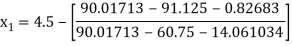
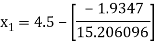
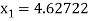
For n =1, the second approximation 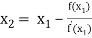

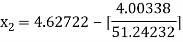
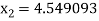
For n =2, the third approximation 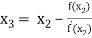

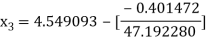
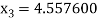
For n =3, the fourth approximation 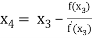

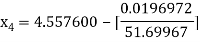
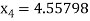
Hence the root of the equation correct to three decimal places is 4.5579
Example 3: Using Newton-Raphson method, find a root of the following equation correct to 4 decimal places: 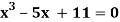
Let 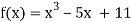
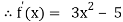
By Newton Raphson Method
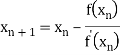
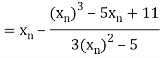
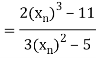
Let the initial approximation be 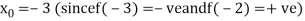
For n=0, the first approximation 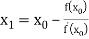
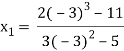
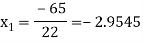
For n=1, the second approximation 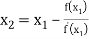
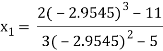
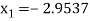
For n=2, the third approximation 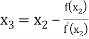
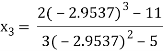
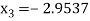
Since 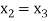 therefore the root of the given equation correct to four decimal places is -2.9537
therefore the root of the given equation correct to four decimal places is -2.9537
Key takeaways-
- Newton-Raphson Method-
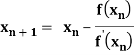
Regula - Falsi Method (Method of false position)
This is the oldest method of finding the approximate numerical value of a real root of an equation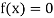 .
.
In this method we suppose that 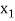 and
and 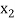 are two points where
are two points where 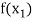 and
and 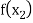 are of opposite sign .Let
are of opposite sign .Let 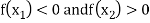
Hence the root of the equation 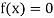 lies between
lies between 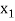 and
and 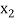 and so,
and so, 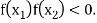
The Regula Falsi formula
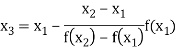
Find 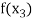 is positive or negative. If
is positive or negative. If 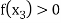 then root lies between
then root lies between 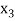 and
and 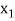 or if
or if 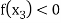 then root lies between
then root lies between 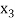 and
and 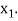 similarly we calculate
similarly we calculate 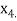
Proceed in this manner until the desired accurate root is found.
Example 1: Find a real root of the equation 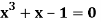 near
near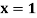 , correct to three decimal place by the Regula Falsi method.
, correct to three decimal place by the Regula Falsi method.
Let 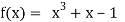
Now, 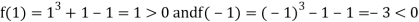
And also 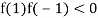
Hence the root of the equation 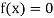 lies between
lies between 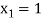 and
and 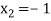 and so,
and so, 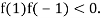
By Regula Falsi Mehtod
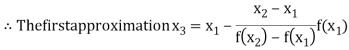
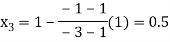
Now, 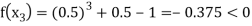
So the root of the equation 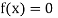 lies between 1 and 0.5 and so
lies between 1 and 0.5 and so 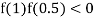
By Regula Fasli Method
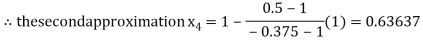
Now, 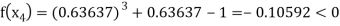
So the root of the equation 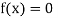 lies between 1 and 0.63637 and so
lies between 1 and 0.63637 and so 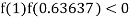
By Regula Fasli Method
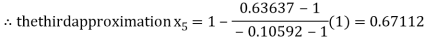
Now, 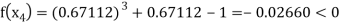
So the root of the equation 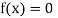 lies between 1 and 0.67112 and so
lies between 1 and 0.67112 and so 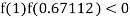
By Regula Fasli Method
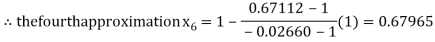
Now, 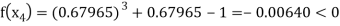
So the root of the equation 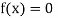 lies between 1 and 0.63636 and so
lies between 1 and 0.63636 and so 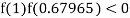
By Regula Fasli Method
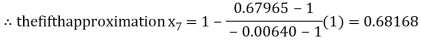
Now, 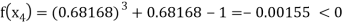
So the root of the equation 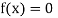 lies between 1 and 0.68168 and so
lies between 1 and 0.68168 and so 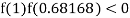
By Regula Fasli Method
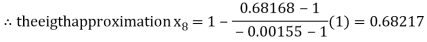
Now, 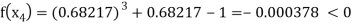
Hence the approximate root of the given equation near to 1 is 0.68217
Example 2: Find the real root of the equation
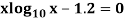
By the method of false position correct to four decimal places
Let 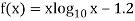
By hit and trail method
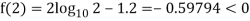
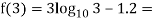 0.23136 > 0
0.23136 > 0
So, the root of the equation 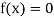 lies between
lies between 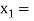 2 and
2 and 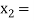 3 and also
3 and also 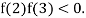
By Regula Falsi Mehtod
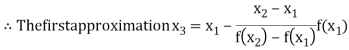
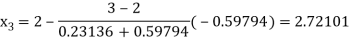
Now, 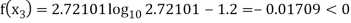
So, root of the equation 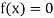 lies between 2.72101 and 3 and also
lies between 2.72101 and 3 and also 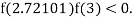
By Regula Falsi Mehtod
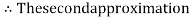
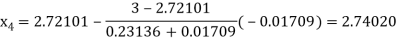
Now, 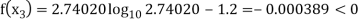
So, root of the equation 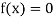 lies between 2.74020 and 3 and also
lies between 2.74020 and 3 and also 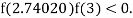
By Regula Falsi Mehtod
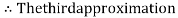
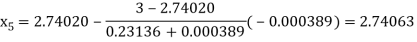
Now, 
So, root of the equation 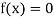 lies between 2.74063 and 3 and also
lies between 2.74063 and 3 and also 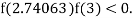
By Regula Falsi Mehtod
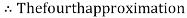
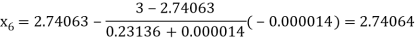
Hence the root of the given equation correct to four decimal places is 2.7406
Example 3: Apply Regula Falsi Method to solve the equation
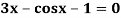
Let 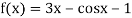
By hit and trail
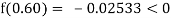
And 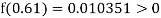
So the root of the equation lies between 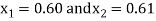 and also
and also 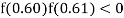
By Regula Falsi Mehtod
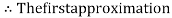
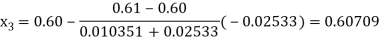
Now, 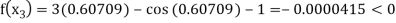
So, root of the equation 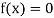 lies between 0.60709 and 0.61 and also
lies between 0.60709 and 0.61 and also 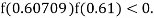
By Regula Falsi Mehtod
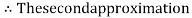

Now, 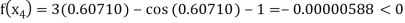
So, root of the equation 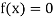 lies between 0.60710 and 0.61 and also
lies between 0.60710 and 0.61 and also 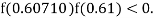
By Regula Falsi Mehtod
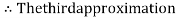

Hence the root of the given equation correct to five decimal place is 0.60710.
Key takeaways-
- Algebraic Equation: If f(x) is a pure polynomial, then the equation
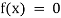 is called an algebraic equation in x.
is called an algebraic equation in x. - Transcendental Equation: If f(x) is an expression contain function as trigonometric, exponential and logarithmic etc. Then
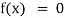 is called transcendental equation.
is called transcendental equation. - Root of an equation lies between its positive and negative values and we take average of them to come closer to its accurate root.
- The Regula Falsi formula
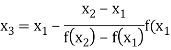
Jacobi’s Iteration method and Gauss-Seidal method:
Let us consider the system of simultaneous linear equation
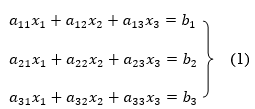
The coefficients of the diagonal elements are larger than the all other coefficients and are non zero. Rewrite the above equation we get
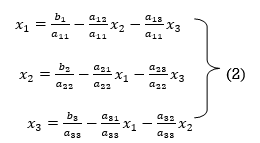
Take the initial approximation 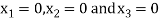 we get the values of the first approximation of
we get the values of the first approximation of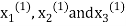 .
.
By the successive iteration we will get the desired the result.
Example 1 Use Jacobi’s method to solve the system of equations:
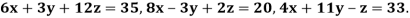
Since 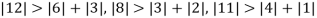
So, we express the unknown with large coefficient in terms of other coefficients.
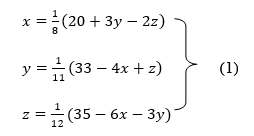
Let the initial approximation be 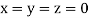
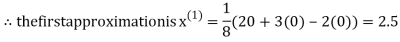
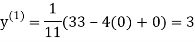
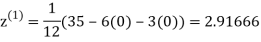
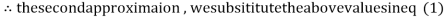
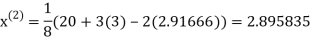
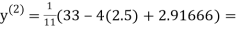 2.35606
2.35606
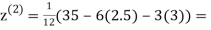 0.91666
0.91666
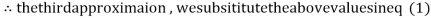
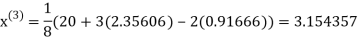
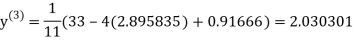
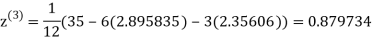

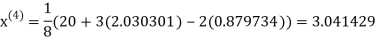
 1.932936
1.932936
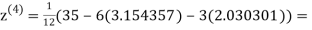 0.831912
0.831912
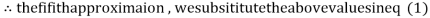
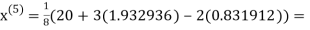 3.016873
3.016873
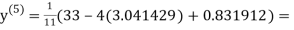 1.969654
1.969654
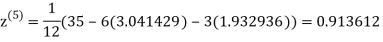
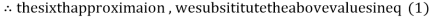
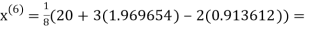 3.010217
3.010217
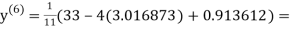 1.986010
1.986010
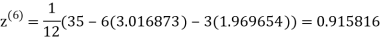

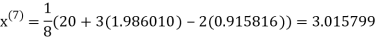
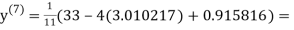 1.988631
1.988631
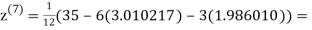 0.915055
0.915055
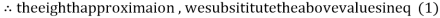
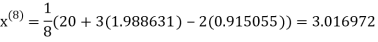
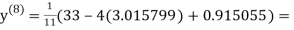 1.986532
1.986532
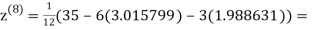 0.911609
0.911609
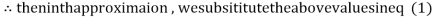
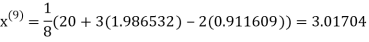
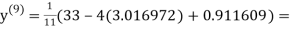 1.985792
1.985792
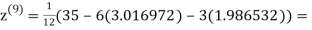 0.911547
0.911547
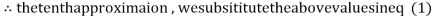
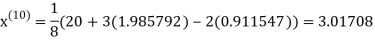
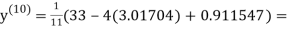 1.98576
1.98576
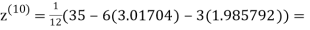 0.911698
0.911698
Since the approximation in ninth and tenth iteration is same up to three decimal places, hence the solution of the given equations is 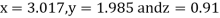
Example 2 Solve by Jacobi’s Method, the equations
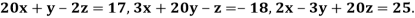
Given equation can be rewrite in the form
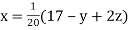 … (i)
… (i)
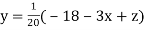 ..(ii)
..(ii)
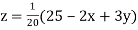 ..(iii)
..(iii)
Let the initial approximation be 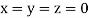
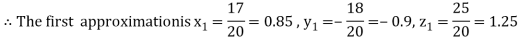
Putting these values on the right of the equation (i), (ii) and (iii) and so we get
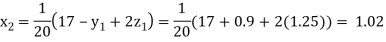
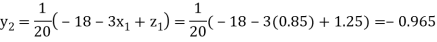
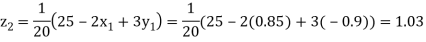
Putting these values on the right of the equation (i), (ii) and (iii) and so we get
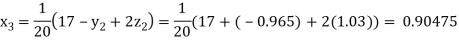
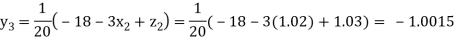
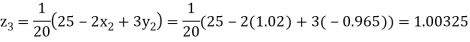
Putting these values on the right of the equation (i), (ii) and (iii) and so we get
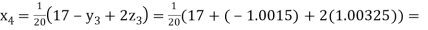 0.90025
0.90025
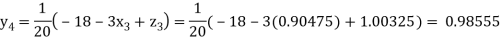
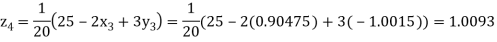
Putting these values on the right of the equation (i), (ii) and (iii) and so we get
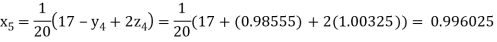
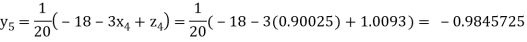
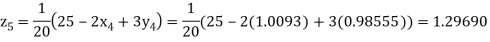
Putting these values on the right of the equation (i), (ii) and (iii) and so we get
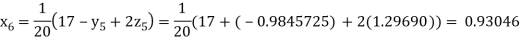
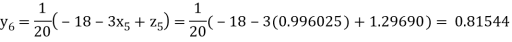
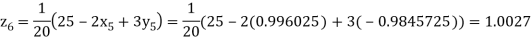
Hence solution approximately is 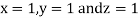
Example 3 Use Jacobi’s method to solve the system of the equations
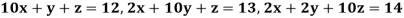
Rewrite the given equations
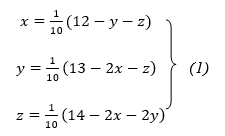
Let the initial approximation be 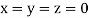
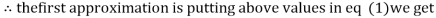
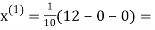 1.2
1.2
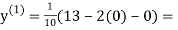 1.3
1.3
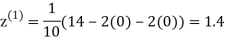

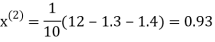
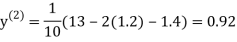
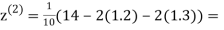 0.9
0.9
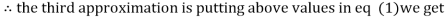
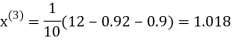
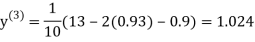
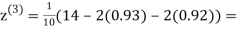 1.03
1.03
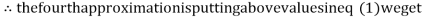
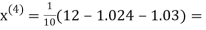 0.9946
0.9946
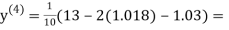 0.9934
0.9934
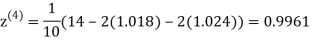
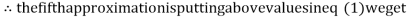
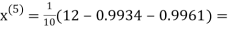 1.0015
1.0015
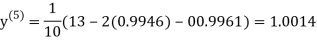
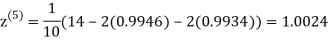
Hence the solution of the above equation correct to two decimal places is
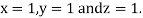
Gauss Seidel method:
This is the modification of the Jacobi’s Iteration. As above in Jacobi’s Iteration, we take first approximation as 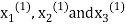 and put in the right hand side of the first equation of (2) and let the result be
and put in the right hand side of the first equation of (2) and let the result be 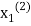 . Now we put
. Now we put 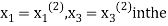 right hand side of second equation of (2) and suppose the result is
right hand side of second equation of (2) and suppose the result is 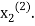 now put
now put 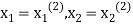 in the RHS of third equation of (2) and suppose the result be
in the RHS of third equation of (2) and suppose the result be 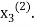 the above method is repeated till the values of all the unknown are found up to desired accuracy.
the above method is repeated till the values of all the unknown are found up to desired accuracy.
Example 1 Use Gauss –Seidel Iteration method to solve the system of equations
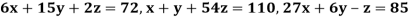
Since 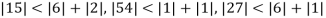
So, we express the unknown of larger coefficient in terms of the unknowns with smaller coefficients.
Rewrite the above system of equations
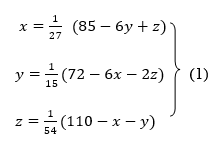
Let the initial approximation be 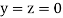
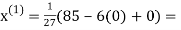 3.14814
3.14814
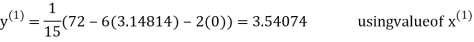
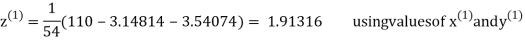
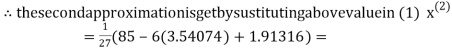 2.43217
2.43217
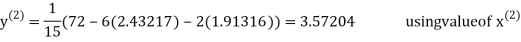
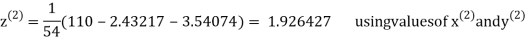
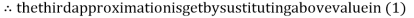
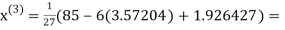 2.42571
2.42571
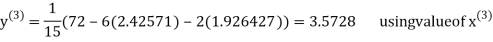
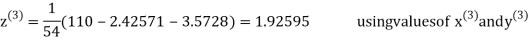
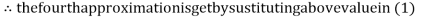
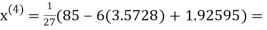 2.4260
2.4260
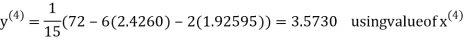
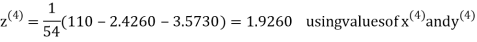
Hence the solution correct to three decimal places is
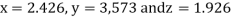
Example 2 Solve the following system of equations
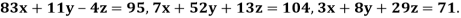 By Gauss-Seidel method.
By Gauss-Seidel method.
Rewrite the given system of equations as
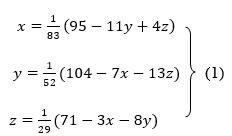
Let the initial approximation be 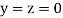
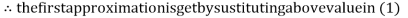
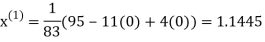
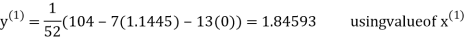
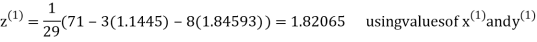
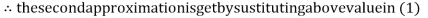
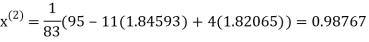
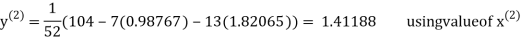
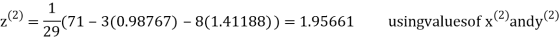
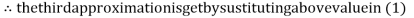
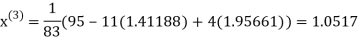
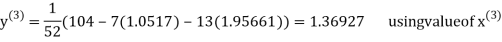
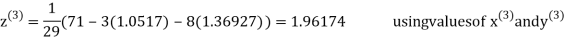
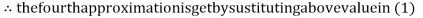
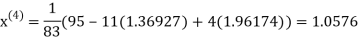
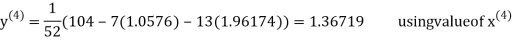
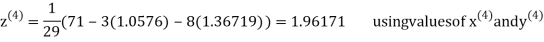
Thus the required solution is 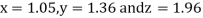
Example 3 Solve the following equations by Gauss-Seidel Method
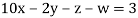
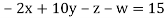
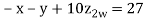
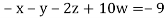
Rewrite the above system of equations
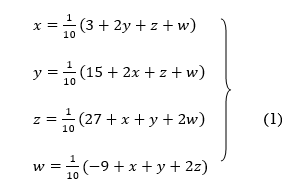
Let the initial approximation be 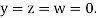

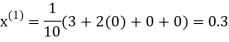
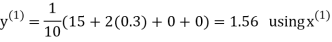
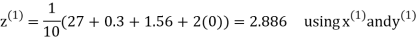
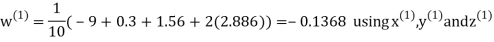

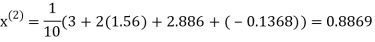
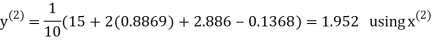
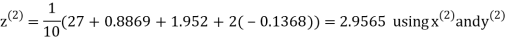
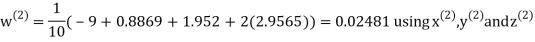

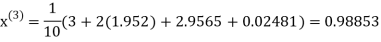
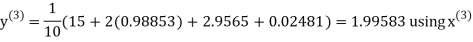
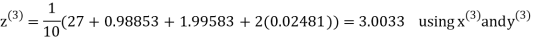
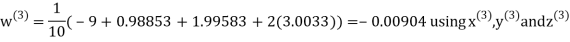
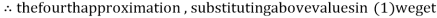
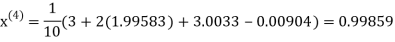
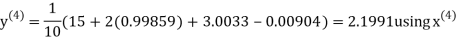
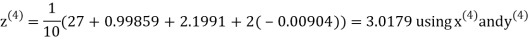
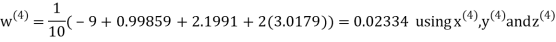

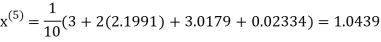
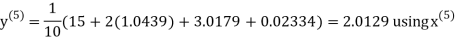
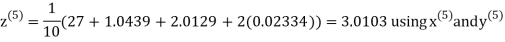
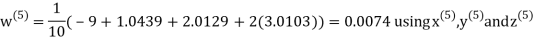
Hence the required solution is 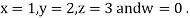
Crout’s method (LU decomposition)
The method is based on the fact that every matrix A can be expressed as the product of a lower triangular matrix and an upper triangular matrix , provided all the principal minors of A are non-singular.
Which means-
If 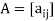 , then-
, then-
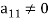

Now consider the equations-
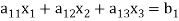
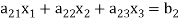
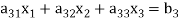
We can write it as-
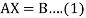
Where-
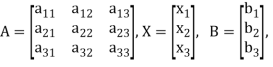
Let
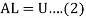
Where-
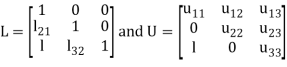
Equation (1) becomes-
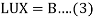
Writing-
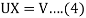
Equation (3) becomes-
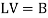 which is equivalent to the equations-
which is equivalent to the equations-
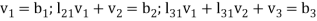
Solving these for 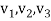 we know V. Then equation (4) becomes-
we know V. Then equation (4) becomes-
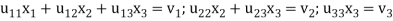
From which 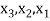 can be found by back substitution.
can be found by back substitution.
We write (2) as to find the matrix L and U-
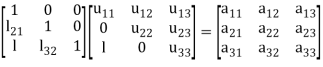
Multiplying the matrix on the left and equating corresponding elements from both sides, we get-
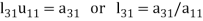
3. 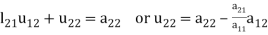
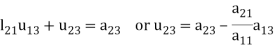
4. 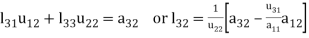
5. 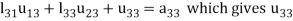
We compute the elements of L and U in the following manner-
- First row of U
- First column of L
- Second row of U
- Second column of L
- Third row of U
Example: Solve the equations-
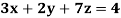
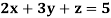
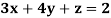
Sol.
Let
So that-
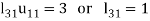
3. 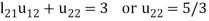
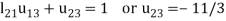
4. 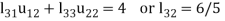
5. 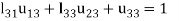
So
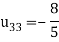
Thus-
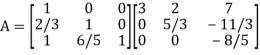
Writing UX = V,
The system of given equations become-
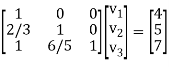
By solving this-
We get-
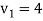
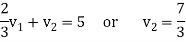
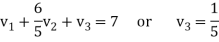
Therefore the given system becomes-
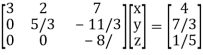
Which means-
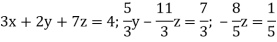
By back substitution, we have-
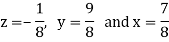
Taylor’s Series Method:
The general first order differential equation
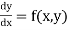 ….(1)
….(1)
With the initial condition 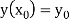 …(2)
…(2)
Let 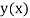 be the exact solution of equation (1), then the Taylor’s series for
be the exact solution of equation (1), then the Taylor’s series for 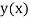 around
around 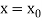 is given by
is given by
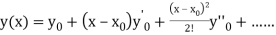 (3)
(3)
If the values of 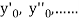 are known, then equation (3) gives apowwer series for y. By total derivatives we have
are known, then equation (3) gives apowwer series for y. By total derivatives we have
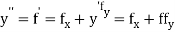 ,
,
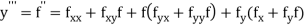

And other higher derivatives of y. The method can easily be extended to simultaneous and higher –order differential equations. In general,
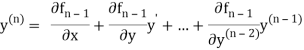
Putting 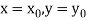 in these above results, we can obtain the values of
in these above results, we can obtain the values of 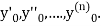 finally, we substitute these values of
finally, we substitute these values of 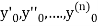 in equation (2) and obtain the approximate value of y; i.e. the solutions of (1).
in equation (2) and obtain the approximate value of y; i.e. the solutions of (1).
Example 1: Solve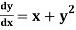 ,
, 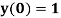 using Taylor’s series method and compute
using Taylor’s series method and compute 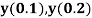 .
.
Here 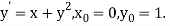 This implies that
This implies that 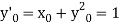 .
.
Differentiating, we get
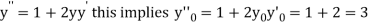 .
.
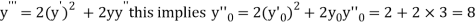 .
.
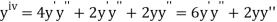
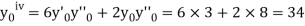 .
.
The Taylor’s series at 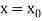 ,
,
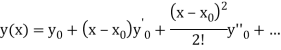
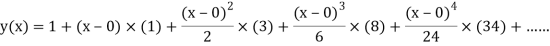
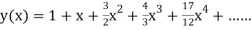 (1)
(1)
At 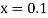 in equation (1) we get
in equation (1) we get
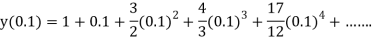
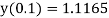
At 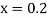 in equation (1) we get
in equation (1) we get
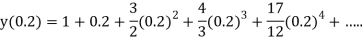
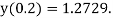
Example 2: Using Taylor’s series method, find the solution of
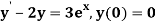
At 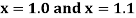 ?
?
Here 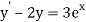
At 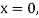 implies that
implies that 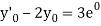 or
or 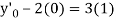 or
or 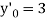
Differentiating, we get
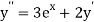 implies that
implies that 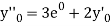 or
or 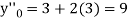 .
.
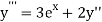 implies that
implies that 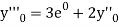 or
or 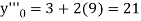
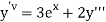 implies that
implies that 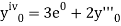 or
or 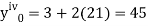
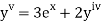 implies that
implies that 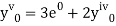 or
or 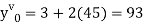
The Taylor’s series at 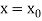 ,
,
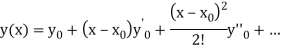
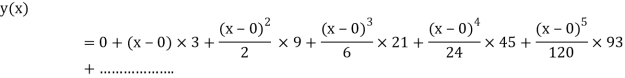
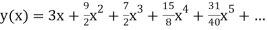 (1)
(1)
At 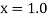 in equation (1) we get
in equation (1) we get
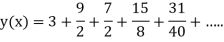
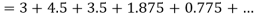
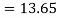
At 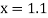 in equation (1) we get
in equation (1) we get
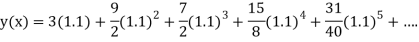
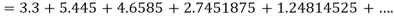
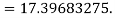
Example 3: Solve 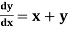 numerically, start from
numerically, start from 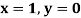 and carry to
and carry to 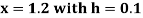 using Taylor’s series method.
using Taylor’s series method.
Here 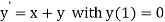 .
.
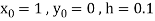
We have 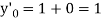
Differentiating, we get
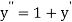 implies that
implies that 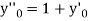 or
or 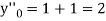
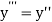 implies that
implies that 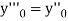 or
or 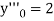 .
.
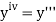 implies that
implies that 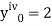
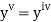 implies that
implies that 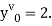
The Taylor’s series at 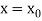 ,
,
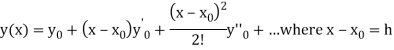
Or 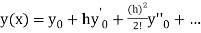
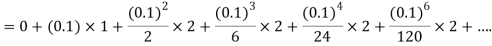
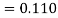
Here 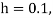
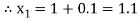
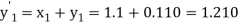
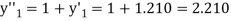
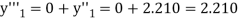
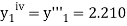
The Taylor’s series
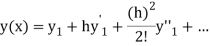
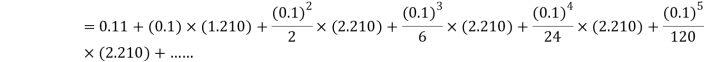
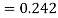 .
.
Euler’s method:
In this method the solution is in the form of a tabulated values
Integrating both side of the equation (i) we get
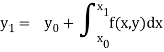
Assuming that 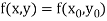 in
in 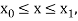 this gives Euler’s formula
this gives Euler’s formula
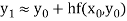
In general formula
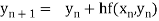 , n=0,1,2,…..
, n=0,1,2,…..
Error estimate for the Euler’s method
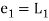
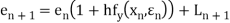
Example 1: Use Euler’s method to find y(0.4) from the differential equation
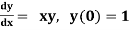 with h=0.1
with h=0.1
Given equation 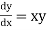
Here 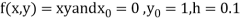
We break the interval in four steps.
So that 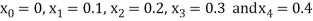
By Euler’s formula
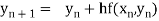 , n=0,1,2,3 ……(i)
, n=0,1,2,3 ……(i)
For n=0 in equation (i) we get
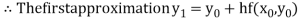
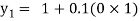
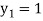
For n=1 in equation (i) we get
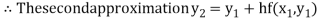
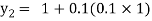
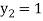 .01
.01
For n=2 in equation (i) we get
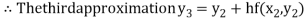
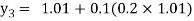
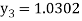
For n=3 in equation (i) we get
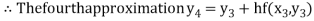
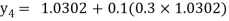
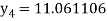
Hence y(0.4) =1.061106.
Example 2: Using Euler’s method solve the differential equation for y at x=1 in five steps
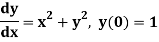
Given equation 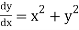
Here 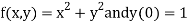
No. Of steps n=5 and so that 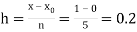
So that 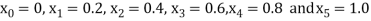
Also 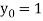
By Euler’s formula
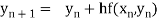 , n=0,1,2,3,4 ……(i)
, n=0,1,2,3,4 ……(i)
For n=0 in equation (i) we get
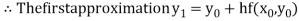
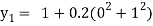
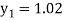
For n=1 in equation (i) we get
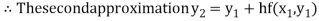
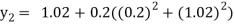
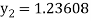
For n=2 in equation (i) we get
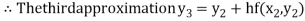
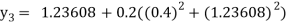
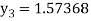
For n=3 in equation (i) we get
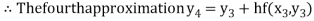
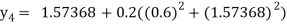
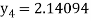
For n=4 in equation (i) we get
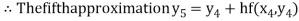
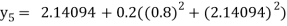
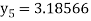
Hence 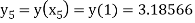
Example 3: Given 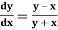 with the initial condition y=1 at x=0.Find y for x=0.1 by Euler’s method(five steps).
with the initial condition y=1 at x=0.Find y for x=0.1 by Euler’s method(five steps).
Given equation is 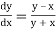
Here 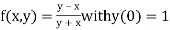
No. Of steps n=5 and so that 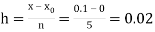
So that 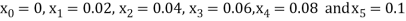
Also 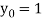
By Euler’s formula
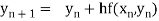 , n=0,1,2,3,4 ……(i)
, n=0,1,2,3,4 ……(i)
For n=0 in equation (i) we get
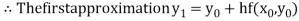
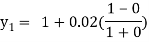
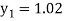
For n=1 in equation (i) we get
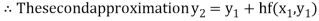
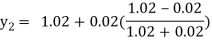
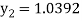
For n=2 in equation (i) we get
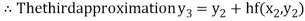
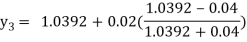
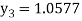
For n=3 in equation (i) we get
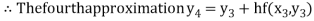
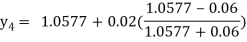
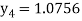
For n=4 in equation (i) we get
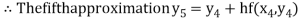
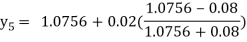
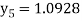
Hence 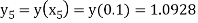
Modified Euler’s Method:
Instead of approximating 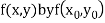 as in Euler’s method. In the modified Euler’s method we have the iteration formula
as in Euler’s method. In the modified Euler’s method we have the iteration formula
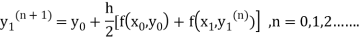
Where 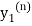 is the nth approximation to
is the nth approximation to 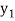 .The iteration started with the Euler’s formula
.The iteration started with the Euler’s formula
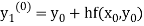
Example1: Use modified Euler’s method to compute y for x=0.05. Given that
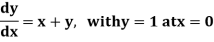
Result correct to three decimal places.
Given equation 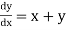
Here 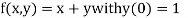
Take h = 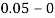 = 0.05
= 0.05
By modified Euler’s formula the initial iteration is
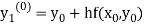
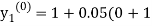 )
)
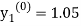
The iteration formula by modified Euler’s method is
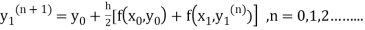 -----(i)
-----(i)
For n=0 in equation (i) we get
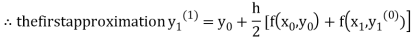
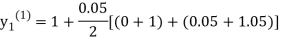
Where 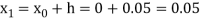 and
and 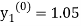 as above
as above

For n=1 in equation (i) we get
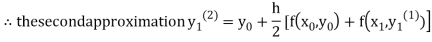
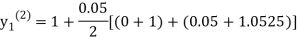
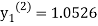
For n=3 in equation (i) we get
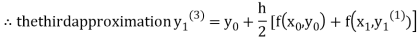
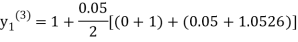
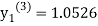
Since third and fourth approximation are equal .
Hence y=1.0526 at x = 0.05 correct to three decimal places.
Example 2: Using modified Euler’s method, obtain a solution of the equation
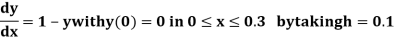
Given equation 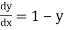
Here 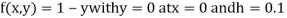
By modified Euler’s formula the initial iteration is
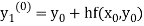
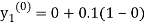
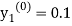
The iteration formula by modified Euler’s method is
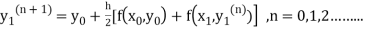 -----(i)
-----(i)
For n=0 in equation (i) we get
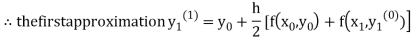
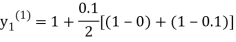
Where 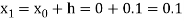 and
and 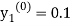 as above
as above
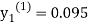
For n=1 in equation (i) we get
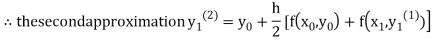
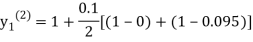
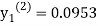
For n=2 in equation (i) we get
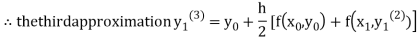
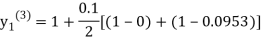
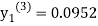
For n=3 in equation (i) we get
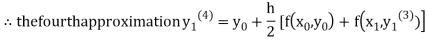
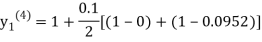
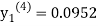
Since third and fourth approximation are equal.
Hence y=0.0952 at x=0.1
To calculate the value of  at x=0.2
at x=0.2
By modified Euler’s formula the initial iteration is
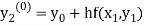
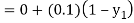
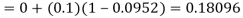
The iteration formula by modified Euler’s method is
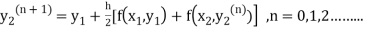 -----(ii)
-----(ii)
For n=0 in equation (ii) we get
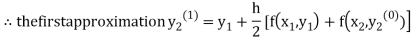
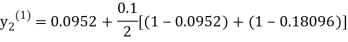
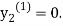 1814
1814
For n=1 in equation (ii) we get
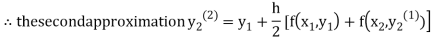
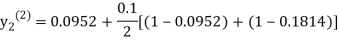
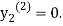 1814
1814
Since first and second approximation are equal .
Hence y = 0.1814 at x=0.2
To calculate the value of 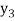 at x=0.3
at x=0.3
By modified Euler’s formula the initial iteration is
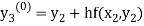
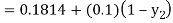
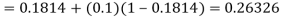
The iteration formula by modified Euler’s method is
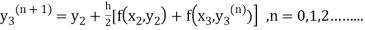 -----(iii)
-----(iii)
For n=0 in equation (iii) we get
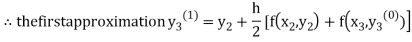
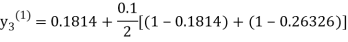
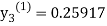
For n=1 in equation (iii) we get
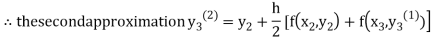
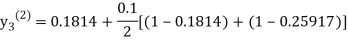
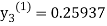
For n=2 in equation (iii) we get
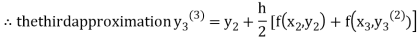
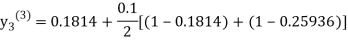
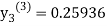
For n=3 in equation (iii) we get
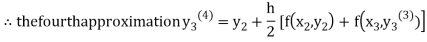
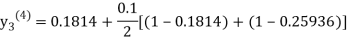
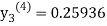
Since third and fourth approximation are same.
Hence y = 0.25936 at x = 0.3
Key takeaways-
1. Euler’s method:
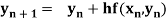 , n=0,1,2,…..
, n=0,1,2,…..
2. Modified Euler’s Method:
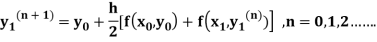
Runge-kutta methods-
This method is more accurate than Euler’s method.
Consider the differential equation of first order
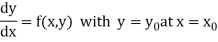
Let 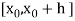 be the first interval.
be the first interval.
A second order Runge Kutta formula
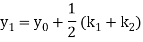
Where 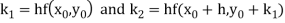
Rewrite as
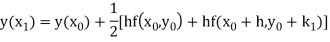
A fourth order Runge Kutta formula:
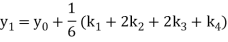
Where 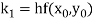
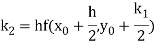
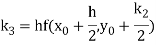
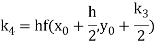
Example 1: Use Runge Kutta method to find y when x=1.2 in step of h=0.1 given that
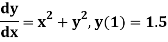
Given equation 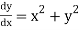
Here 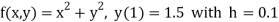
Also 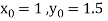
By Runge Kutta formula for first interval
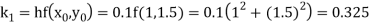
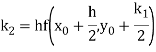
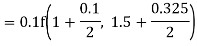
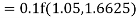
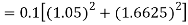
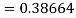
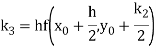
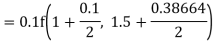
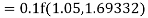
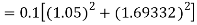
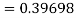
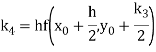
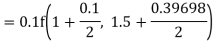
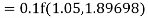
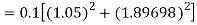
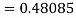
Again 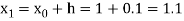
A fourth order Runge Kutta formula:
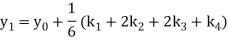

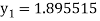
To find y at 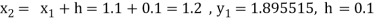
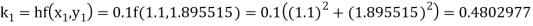
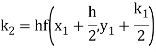
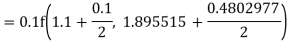
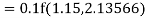
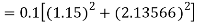
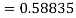
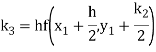
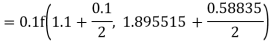
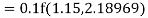
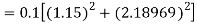
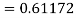
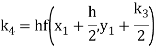
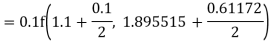
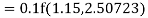
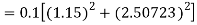
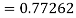
A fourth order Runge Kutta formula:
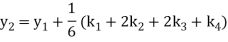
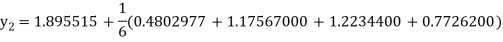
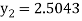
Example 2: Apply Runge Kutta fourth order method to find an approximate value of y for x=0.2 in step of 0.1, if
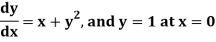
Given equation 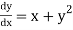
Here 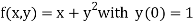
Also 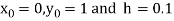
By Runge Kutta formula for first interval
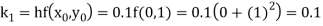
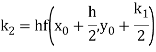
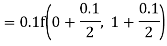
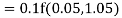
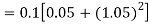
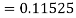
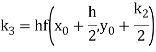
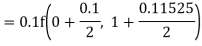
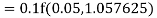
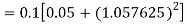
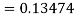
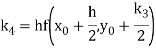
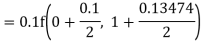
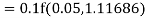
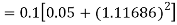
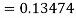
A fourth order Runge Kutta formula:
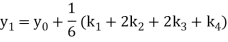
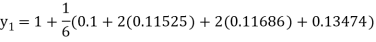
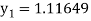
Again 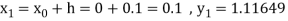
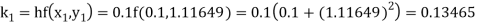
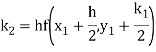
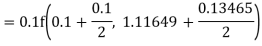
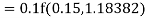
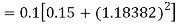
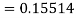
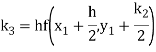
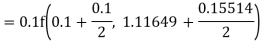
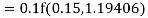
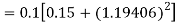
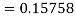
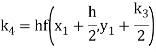
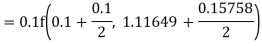
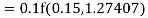
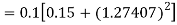
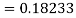
A fourth order Runge Kutta formula:
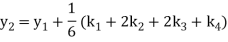
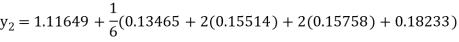
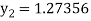
Example 3: Using Runge Kutta method of fourth order, solve
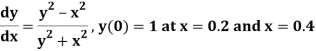
Given equation 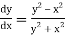
Here 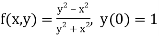
Also 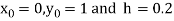
By Runge Kutta formula for first interval
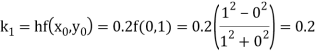
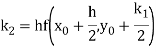
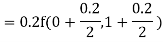
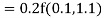
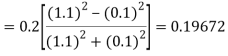
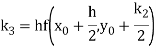
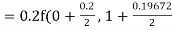 )
)
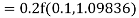
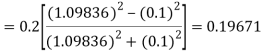
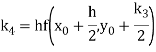
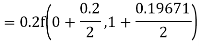
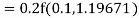
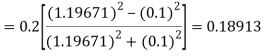
A fourth order Runge Kutta formula:
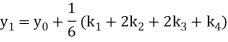
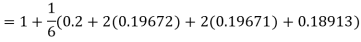
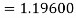
Hence at x = 0.2 then y = 1.196
To find the value of y at x=0.4. In this case 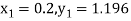
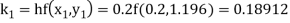
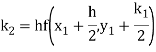
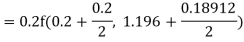
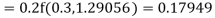
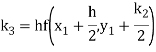
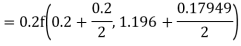
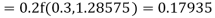
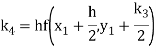
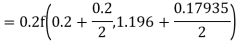
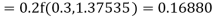
A fourth order Runge Kutta formula:
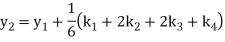
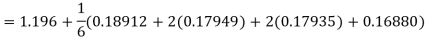
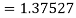
Hence at x = 0.4 then y=1.37527
Simultaneous equation using Runge Kutta method of 2 orders:
The second order differential equation
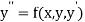
Let 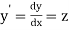 then the above equation reduces to first order simultaneous differential equation
then the above equation reduces to first order simultaneous differential equation
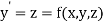
Then 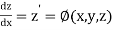
This can be solved as we discuss above by Runge Kutta Method. Here 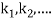 for
for 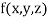 and
and 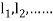 for
for 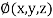 .
.
A fourth order Runge Kutta formula:
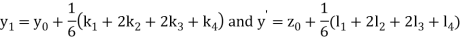
Where 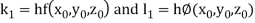
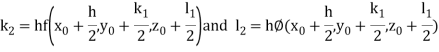
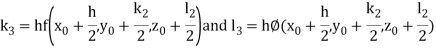
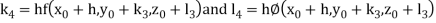
Example 1: Using Runge Kutta method of order four , solve 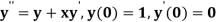 to find
to find 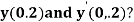
Given second order differential equation is
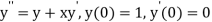
Let 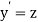 then above equation reduces to
then above equation reduces to
Or 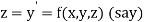
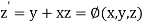 (say)
(say)
Or 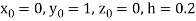 .
.
By Runge Kutta Method we have
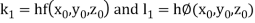
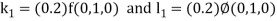
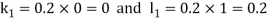
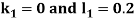
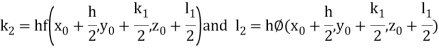
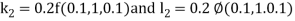
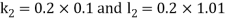
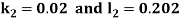
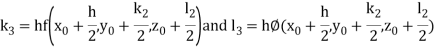
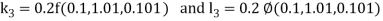
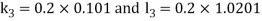
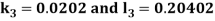
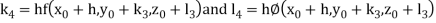
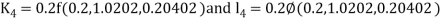
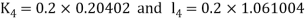
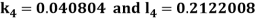
A fourth order Runge Kutta formula:
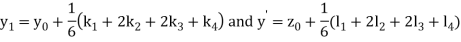
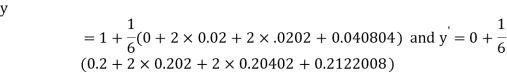
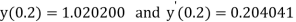
Example 2: Using Runge Kutta method, solve
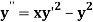 for
for 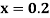 correct to four decimal places with initial condition
correct to four decimal places with initial condition 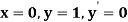 .
.
Given second order differential equation is
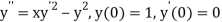
Let 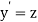 then above equation reduces to
then above equation reduces to
Or 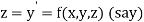
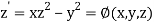 (say)
(say)
Or 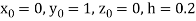 .
.
By Runge Kutta Method we have
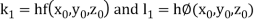
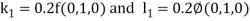
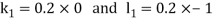
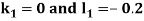
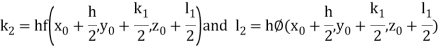
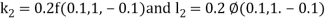
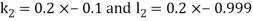
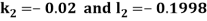
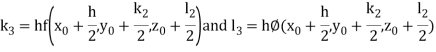
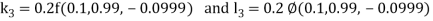
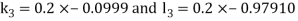
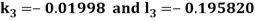
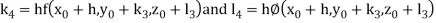
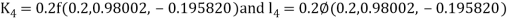

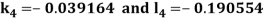
A fourth order Runge Kutta formula:
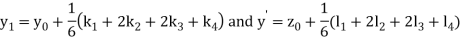
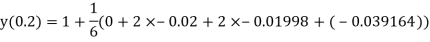
And
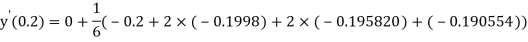
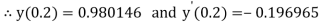 .
.
Example 3: Solve the differential equations
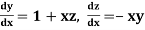 for
for 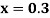
Using four order Runge Kutta method with initial conditions 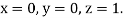
Given differential equation are
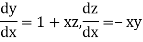
Let 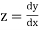
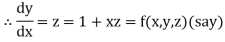
And 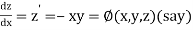
Also 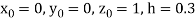
By Runge Kutta Method we have
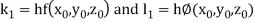
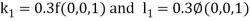
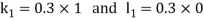

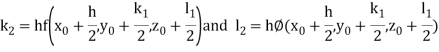
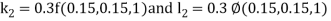
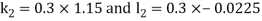
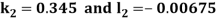
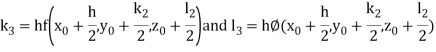
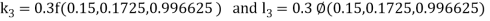
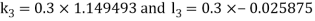
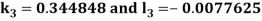
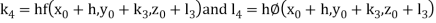
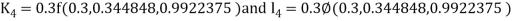
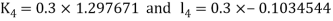
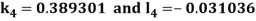
A fourth order Runge Kutta formula:
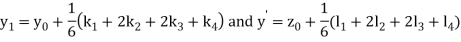
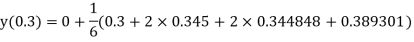
And 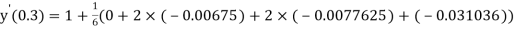
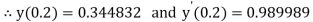 .
.
Key takeaways-
Runge-kutta methods-
- A second order Runge Kutta formula
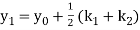
Where 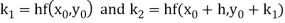
- A fourth order Runge Kutta formula:
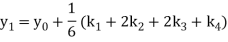
Where 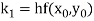
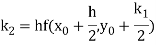
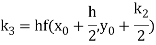
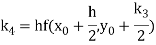
For given dy/dx = f(x,y) and y = 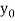 and x =
and x = 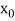 , to find the value of y for x =
, to find the value of y for x = 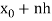 , by using Milne’s method,
, by using Milne’s method,
We follow the steps given below-
The value 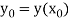 being given, here we calculate-
being given, here we calculate-
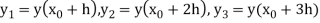
By Taylor’s series or Picard’s method.
Now we calculate-
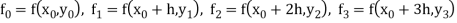
Then to find
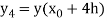
We substitute Newton’s forward interpolation formula-
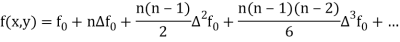
In the relation-
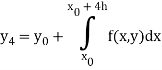
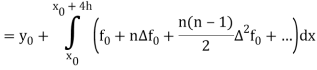
By putting x = 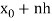 , dx = h dn
, dx = h dn
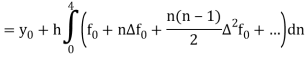
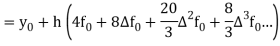
Neglecting fourth and higher order differences and expressing 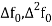 in terms of the function values, we get-
in terms of the function values, we get-
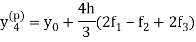
This is called a predictor.
Now having found 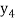 we obtain a first approaximation to
we obtain a first approaximation to 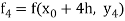
Then the better value of 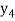 is found by simpson’s rule as-
is found by simpson’s rule as-
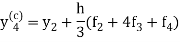
Which is called corrector.
Then an improved value of 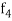 is computed and again corrector is applied to find a better value of
is computed and again corrector is applied to find a better value of 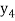 .
.
We continues this step until 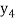 remains unchanged.
remains unchanged.
Once 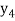 and
and 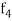 are obtained to desired degree of accuracy,
are obtained to desired degree of accuracy,
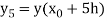 is found from the predictor as-
is found from the predictor as-
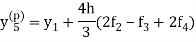
And
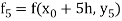 is calculated.
is calculated.
Then the better approximation to the value of 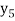 we get from the corrector as-
we get from the corrector as-
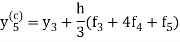
We repeat until 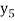 becomes stationary and we proceed to calculate
becomes stationary and we proceed to calculate 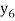 .
.
This is called the Milne’s predictor-corrector method.
Adams - Bashforth predictor and corrector formula-
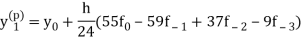
This is called Adams - Bashforth predictor formula.
And
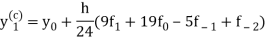
This is called Adams - Bashforth corrector formula.
Example: Find the solution of the differential equation 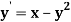 in the range
in the range 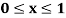 for the boundary conditions y = 0 and x = 0 by using Milne’s method.
for the boundary conditions y = 0 and x = 0 by using Milne’s method.
Sol.
By using Picards method-
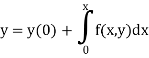
Where
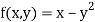
To get the first approximation-
We put y = 0 in f(x, y),
Giving-
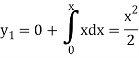
In order to find the second approximation, we put y = 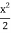 in f(x,y)
in f(x,y)
Giving-
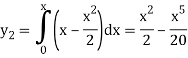
And the third approximation-
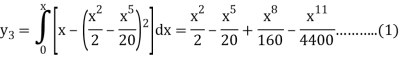
Now determine the starting values of the Milne’s method from equation (1), by choosing h = 0.2
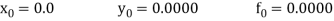
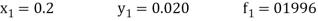
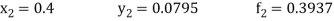
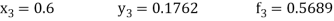
Now using the predictor-
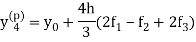
X = 0.8
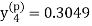 ,
, 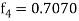
And the corrector-
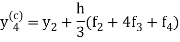
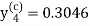 ,
, 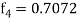 ................(2)
................(2)
Now again using corrector-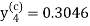
Using predictor-
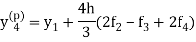
X = 1.0,
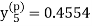 ,
, 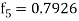
And the corrector-
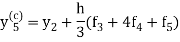
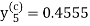 ,
, 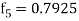
Again using corrector-
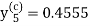 , which is same as before
, which is same as before
Hence
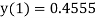
Example: Solve the initial value problem 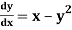 , y(0) = 1 to find y(0.4) by using Adams-Bashforth method.
, y(0) = 1 to find y(0.4) by using Adams-Bashforth method.
Starting solutions required are to be obtained using Runge-Kutta method of order 4 using step value h = 0.1
Sol.
Here we have-
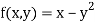
Here 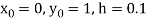
So that-
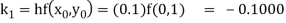
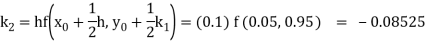
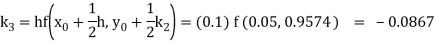
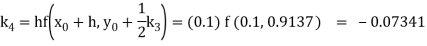
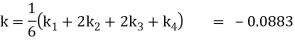
Thus
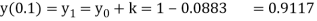
To find y(0.2)-
Here 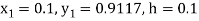
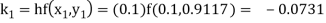
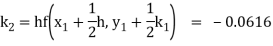
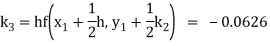
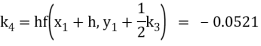
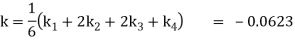
Thus,
Y(0.2) = 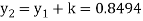
To find y(0.3)-
Here 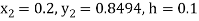
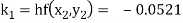
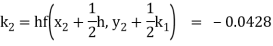
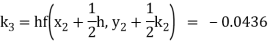
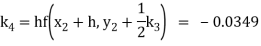
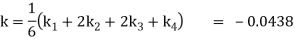
Thus,
Y(0.3) = 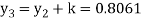
Now the starting values of Adam’s method with h = 0.1-
x = 0.0 y-3 = 1.0000 f-3 = 0.0 – (1.0)2 = - 1.0000
x = 0.1 y-2 = 0.9117 f-2 = 0.1 – (0.9117)2 = - 1.7312
x = 0.2 y-1 = 0.8494 f-1 = 0.2 – (0.8494)2 = - 0.5215
x = 0.3 y0 = 0.8061 f0 = 0.3 – (0.8061)2 = - 0.3498
Using predictor-
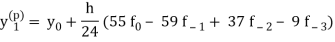

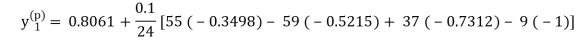
= 0.7789 f1 = - 0.2067
Using corrector-
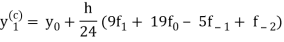
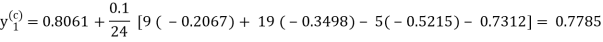
Hence
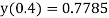
Key takeaways-
1. Predictor- 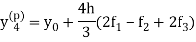
2. Corrector- 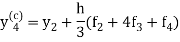
3. Adams - Bashforth predictor formula-
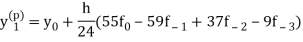
4. Adams - Bashforth corrector formula.
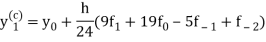
References:
- E. Kreyszig, “Advanced Engineering Mathematics”, John Wiley & Sons, 2006.
- P. G. Hoel, S. C. Port And C. J. Stone, “Introduction To Probability Theory”, Universal Book Stall, 2003.
- S. Ross, “A First Course in Probability”, Pearson Education India, 2002.
- W. Feller, “An Introduction To Probability Theory and Its Applications”, Vol. 1, Wiley, 1968.
- N.P. Bali and M. Goyal, “A Text Book of Engineering Mathematics”, Laxmi Publications, 2010.
- B.S. Grewal, “Higher Engineering Mathematics”, Khanna Publishers, 2000.