Unit - 3
Linked list
To use the sorted list, keep in mind that the items' relative places are determined by some underlying attribute. The linked structure illustrated below can represent the ordered list of integers given above (17, 26, 31, 54, 77, and 93). The node and link structure is perfect for displaying relative item location once again.

Fig: An ordered linked list
We'll use the same strategy as we did with unordered lists to create the OrderedList class. We'll subclass UnorderedList and keep the __init__ method because an empty list will be signified by a head reference to None once again.
From unordered_list import Node, UnorderedList
Class OrderedList(UnorderedList):
When considering the operations for the ordered list, it's worth noting that the is empty and size methods can be used in the same way they are for unordered lists because they only care about the number of nodes in the list, not the actual item values. Similarly, since we still need to find the item and then link around the node to remove it, the remove method will suffice. The remaining two methods, search and add, will need to be tweaked.
In order to discover an item in an unordered linked list, we must explore the nodes one by one until we either find it or run out of nodes (None). The same strategy appears to work with the ordered list, and in fact, in the case where we discover the item, it is exactly what we require. In the event that the item is not on the list, we can use the ordering to quickly end the search.
The ordered linked list in the picture below, for example, is being searched for the number 45. Starting from the top of the list and working our way down, we compare to 17. We go on to the next node, in this case 26, because 17 isn't the thing we're seeking for. We move on to 31 and then 54 because this isn't what we want. Something is different at this point. Because 54 isn't the thing we're looking for, our previous strategy was to keep moving forward. This isn't essential, though, because this is an ordered list. When the node's value exceeds the value of the item we're looking for, the search can come to a halt and return False. The item could not possibly exist farther down the linked list.
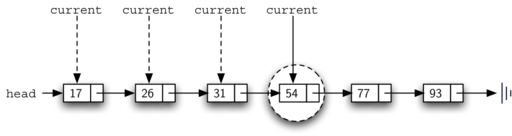
Fig: Searching an ordered linked list
To take use of this improvement, we present a modification of the search method from our Unordered List class below.
Def search(self, item):
Current = self.head
While current is not None:
If current.value == item:
Return True
If current.value > item:
Return False
Current = current.next
Return False
In add, the most significant procedure change will take place. Remember that the add method for unordered lists might just put a new node at the top of the list. It was the most convenient access point. With ordered lists, however, this will no longer operate. It's now up to us to figure out exactly where a new item should go in the existing ordered list.
Let's pretend we have an ordered list with the values 17, 26, 54, 77, and 93, and we wish to add the value 31 to it. The add method must determine whether the new item belongs in the 26-54 range. The setup that we require is shown below. As previously said, we must traverse the linked list in search of the location where the new node will be added. When we run out of nodes (current becomes None) or the value of the current node exceeds the value of the item we want to add, we know we've found it. In our case, seeing the number 54 prompts us to come to a halt.
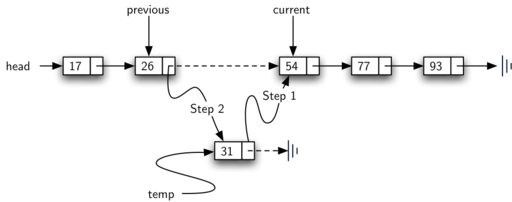
Fig: Adding an item to an ordered linked list
Analysis of Linked Lists
To assess the difficulty of linked list operations, we must first determine whether they necessitate traversal. Consider the case of an n-node linked list. Because it only takes one step to verify the head reference for None, the is empty method is O(1)O(1). Because there is no way to know how many nodes are in the linked list without travelling from head to end, size will always need nn steps. As a result, length is O(n)O. (n). Because we just set the new node at the top of the linked list, adding an item to an unordered list is always O(1)O(1). However, the traversal process is required for searching, removing, and adding items to an ordered list. Despite the fact that they may only need to traverse half of the nodes on average, these methods are all O(n)O(n), because in the worst case, they will each process every node in the list.
A linked list is a data structure that consists of a succession of linked nodes. A linked list is a collection of nodes that are kept in memory at random. A node in a linked list has two pieces, the first of which is the data and the second of which is the address. A pointer to the null is contained in the list's last node. The linked list is the second most popular data structure after the array. Every link in a linked list is connected to another link.
Representation
The connection of nodes in a linked list can be represented as each node pointing to the next node in the list. The linked list's representation is shown below -
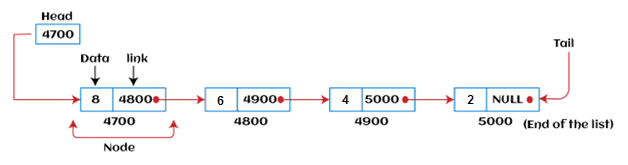
Array data structures have been used to organise groups of elements that must be stored independently in memory until now. Array, on the other hand, has a number of pros and disadvantages that must be considered when deciding on the data structure to be utilised throughout the programme.
Operations on linked list
- Insert
- Insert initially position
- Insert eventually position
- Insert into ordered list
- Delete
- Traverse list (Print list)
- Copy linked list
Application
The following are some of the applications of the linked list:
● Polynomials can be represented and operations on polynomials can be performed with the help of a linked list.
● The sparse matrix can be represented using a linked list.
● The linked list can be used to implement many processes such as student details, employee details, or product details since it employs the structural data type, which can carry a variety of data types.
● Stack, queue, tree, and other data structures can all be implemented using linked lists.
● The graph is made up of edges and vertices, and it can be represented as an adjacency matrix or a list of adjacencies. The graph can be implemented as an array if we want to express it as an adjacency matrix. The graph can be represented as a linked list if we want to express it as an adjacency list.
● To implement dynamic memory allocation, a linked list can be utilised. The memory allocation done at run-time is known as dynamic memory allocation.
Advantages
The following are some of the benefits of using a linked list:
● Dynamic data structure - The linked list's size can vary depending on the requirements. The size of a linked list is not fixed.
● Insertion and deletion - In contrast to arrays, insertion and deletion are much easier in linked lists. The items of an array are stored in a sequential order, whereas the elements of a linked list are stored in a random order. To add or remove an element from an array, we must first shift the elements to make room. Instead of shifting, we only need to update the address of the node's pointer in a linked list.
● Memory efficient - Because the size of a linked list can be adjusted to meet the needs, memory consumption in linked lists is low.
● Implementation - We can implement both stacks and queues using linked list.
Disadvantages
The following are some of the drawbacks of utilising a linked list:
● Memory usage - Node takes up more memory than array in a linked list. Each node in the linked list has two sorts of variables, one of which is a simple variable and the other of which is a pointer variable.
● Traversal - The linked list makes traversal difficult. If we need to access an element in a linked list, we can't do so randomly, but an array can be accessed randomly by index. For example, if we want to go to the third node, we must first go through all of the nodes that come before it. As a result, accessing a certain node takes a long time.
● Reverse traversing - In a linked list, backtracking or reverse traversing is tough. The back pointer is easier to keep in a doubly-linked list, but it takes up more memory.
Key takeaway
A linked list is a data structure that consists of a succession of linked nodes. A linked list is a collection of nodes that are kept in memory at random. A node in a linked list has two pieces, the first of which is the data and the second of which is the address.
In programming, it is the most widely used linked list. When we talk about a linked list, we're talking about a singly linked list. The singly linked list is a data structure that is divided into two parts: the data portion and the address part, which contains the address of the next or successor node. A pointer is another name for the address component of a node.
Assume we have three nodes with addresses of 100, 200, and 300, respectively. The following diagram depicts the representation of three nodes as a linked list:
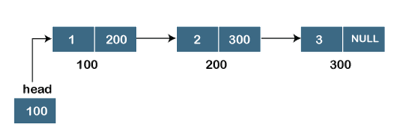
Fig: Singly linked list
In the diagram above, we can see three separate nodes with addresses of 100, 200, and 300, respectively. The first node has the address of the next node, which is 200, the second has the address of the last node, which is 300, and the third has the NULL value in its address portion because it does not point to any node. A head pointer is a pointer that stores the address of the first node.
Because there is just one link in the linked list depicted in the figure, it is referred to as a singly linked list. Just forward traversal is permitted in this list; we can't go backwards because there is only one link in the list.
Representation of the node in a singly linked list
Struct node
{
Int data;
Struct node *next;
}
In the above diagram, we've constructed a user-made structure called a node, which has two members: one is data of integer type, and the other is the node type's pointer (next).
Key takeaway
The singly linked list is a data structure that is divided into two parts: the data portion and the address part, which contains the address of the next or successor node.
Allocation of Memory Memory is allocated at compile time in static memory allocation. If we declare a stack with a 100-element array (all integers), the statement will be as follows:
Int stk[100];
If 100 records are to be saved in memory, this declaration would be used. When we make this declaration, 200 bytes in memory are set aside for storing 100 integers. However, it is possible that when we run the programme, we will only be interested in keeping 60 integers; in this case, 200 bytes will be reserved in memory, resulting in memory waste. In some circumstances, we may need to hold more than 100 records; the array would be too small.
These issues can be solved by allocating memory at run time (rather than compile time), which is known as Dynamic Memory Allocation. It's done with the help of the malloc () and calloc () methods from the Standard Library ().
Syntax for Allocating memory through malloc:
p = (data type*) malloc (n*size of ());
Example 1
p = (int *) malloc (n * 2);
The expression (int *) is used to typecast the returned address as an integer address. The calloc() function is identical to malloc() except that it requires two parameters instead of the one required by malloc() ().
Example 2
Int *p p = (int *) calloc (100, 2);
Since an integer is a 2 byte item, 2 implies that we want to allocate memory for storing integers, and 100 indicates that we want to reserve space for storing 100 integers. Another distinction between malloc() and colloc() is that malloc() allocates memory with garbage values by default, whereas calloc() allocates memory with all zeros.
Pointers
A pointer is a variable that has the address (or link or reference) to another variable. Pointer, like other variables, cannot be utilised before declaration. The pointer variable can be declared as:
Datatype *p;
This declares that p is a pointer variable that will be used to store the address of a variable of a specific datatype. 'Value saved at address' is denoted by a '*'. If we declare int *p, we are indicating that the value at the location p is an integer.
Static and Dynamic Variables
While writing the programme, static variables are declared and named. (As long as the programme in which they are declared is running, there remains space for them.) Static variables cannot be created or removed while the programme in which they are defined is being executed.
Because dynamic variables do not exist when the programme is being written, but only when it is run, they must be generated (and may be destroyed) during programme execution. They cannot be given names while the programme is being written. Pointers are the sole way to access dynamic variables. A dynamic variable, on the other hand, does contain data once it is formed and, like any other variable, must have a type. If a dynamic variable is created in a function, then it can continue to exist even after the function terminates.
Insertion
When placing a node into a linked list, there are three possible scenarios:
● Insertion at the beginning
● Insertion at the end. (Append)
● Insertion after a given node
Insertion at the beginning
There's no need to look for the end of the list. If the list is empty, the new node becomes the list's head. Otherwise, we must connect the new node to the existing list's head and make the new node the list's head.
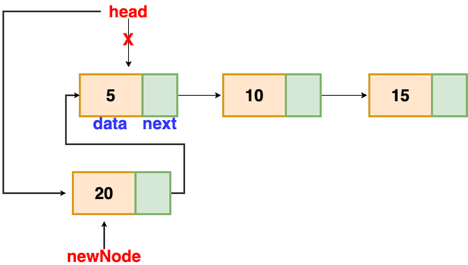
Fig: Insertion at beginning
// function is returning the head of the singly linked-list
Node insertAtBegin(Node head, int val)
{
NewNode = new Node(val) // creating new node of linked list
If(head == NULL) // check if linked list is empty
Return newNode
Else // inserting the node at the beginning
{
NewNode.next = head
Return newNode
}
}
Insertion at the end
We'll go through the list till we reach the last node. The new node is then appended to the end of the list. It's worth noting that there are some exceptions, such as when the list is empty.
We will return the updated head of the linked list if the list is empty, because the inserted node is both the first and end node of the linked list in this case.
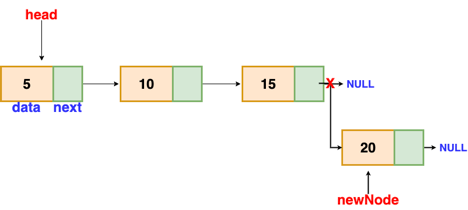
Fig: Insertion at end
// the function is returning the head of the singly linked list
Node insertAtEnd(Node head, int val)
{
If( head == NULL ) // handing the special case
{
NewNode = new Node(val)
Head = newNode
Return head
}
Node temp = head
// traversing the list to get the last node
While( temp.next != NULL )
{
Temp = temp.next
}
NewNode = new Node(val)
Temp.next = newNode
Return head
}
Insertion after a given node
The reference to a node is passed to us, and the new node is put after it.
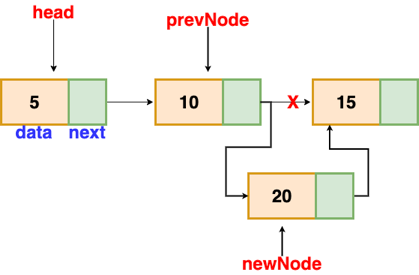
Fig: Insertion after given node
Void insertAfter(Node prevNode, int val)
{
NewNode = new Node(val)
NewNode.next = prevNode.next
PrevNode.next = newNode
}
Deletion
These are the procedures to delete a node from a linked list.
● Find the previous node of the node to be deleted.
● Change the next pointer of the previous node
● Free the memory of the deleted node.
There is a specific circumstance in which the first node is removed upon deletion. We must update the connected list's head in this case.
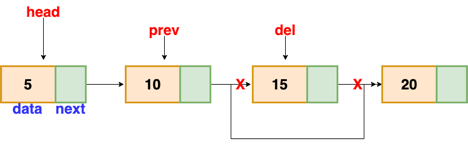
Fig: Deleting a node in linked list
// this function will return the head of the linked list
Node deleteLL(Node head, Node del)
{
If(head == del) // if the node to be deleted is the head node
{
Return head.next // special case for the first Node
}
Node temp = head
While( temp.next != NULL )
{
If(temp.next == del) // finding the node to be deleted
{
Temp.next = temp.next.next
Delete del // free the memory of that Node
Return head
}
Temp = temp.next
}
Return head // if no node matches in the Linked List
}
Traversal
The goal is to work your way through the list from start to finish. We might want to print the list or search for a certain node in it, for example.
The traversal algorithm for a list
● Start with the head of the list. Access the content of the head node if it is not null.
● Then go to the next node(if exists) and access the node information
● Continue until no more nodes (that is, you have reached the null node)
Void traverseLL(Node head) {
While(head != NULL)
{
Print(head.data)
Head = head.next
}
}
Update
● This is a type of linked list operation in C/C++ in which the data section of the needed node is replaced with the given value.
● We'll do this by traversing the linked list until we identify a node that corresponds to the node that needs to be modified.
Void updateNode(Node* head, int value, int newValue)
{
// temp is the traversing node
Node* temp = head;
While(temp != NULL)
{
// If the node matches the given node to be updated.
If( temp->data == val)
{
// Updating the data part of the node with the new value.
Temp->data = newVal;
Return;
}
Temp = temp->next;
}
}
Key takeaway
There's no need to look for the end of the list. If the list is empty, the new node becomes the list's head.
The goal is to work your way through the list from start to finish. We might want to print the list or search for a certain node in it.
Polynomials can be represented in a number of different ways. These are the following:
● By the use of arrays
● By the use of Linked List
Representation of polynomial using Arrays
There may be times when you need to evaluate a large number of polynomial expressions and execute fundamental arithmetic operations on them, such as addition and subtraction. You'll need a mechanism to express the polynomials for this. The simplest method is to express a polynomial of degree 'n' and store the coefficient of the polynomial's n+1 terms in an array. As a result, each array element will have two values:
● Coefficient and
● Exponent
Polynomial of representation using linked lists
An ordered list of non-zero terms can be thought of as a polynomial. Each non-zero word is a two-tuple, containing two pieces of data:
● The exponent part
● The coefficient part
The term "polynomial" refers to a mathematical expression made up of variables and coefficients. For example x^2 - 4x + 7
The coefficients and exponents of the polynomial are defined as the list's data node in the Polynomial linked list.
When two polynomials are stored as a linked list, add them together. The coefficients of variables with the same power must be added. Each node in a linked list has three members, with the coefficient value linking to the next node.
A linked list for storing Polynomial looks like this:
Polynomial: 4x7 + 12x2 + 45
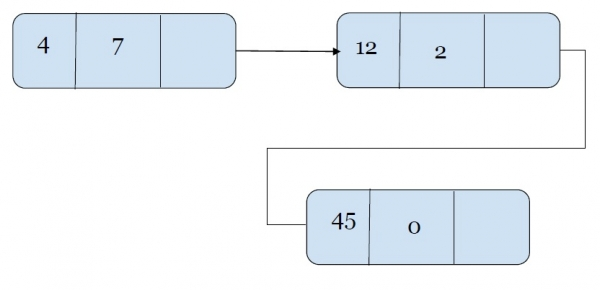
This is how a polynomial represented by a linked list looks.
Adding two polynomials with linked lists as representations. We examine values at the node's exponent value. We'll add the coefficients for the same exponent values.
Example
Input:
p1= 13x8 + 7x5 + 32x2 + 54
p2= 3x12 + 17x5 + 3x3 + 98
Output: 3x12 + 13x8 + 24x5 + 3x3 + 32x2 + 152
For all powers, we'll add the coefficients of the exponents with the same exponent value. The final polynomial is returned.
Algorithm
Input − Linked list representation of polynomials p1 and p2.
Step 1: loop through all of the linked list's values, then on to steps 2 and 3.
Step 2: if the exponent of a node is greater, copy it to the result node and move on to the next node.
Step 3: add the coefficients if the values of both node's exponents are the same, and then copy the additional value with node to the result.
Step 4: Print the node that results.
Key takeaway
There may be times when you need to evaluate a large number of polynomial expressions and execute fundamental arithmetic operations on them, such as addition and subtraction.
To multiply two polynomials, multiply the terms of one polynomial by the terms of the other polynomial.
A singly linked list is a type of circular linked list. The sole difference between a singly linked list and a circular linked list is that the last node in a singly linked list does not point to any other node, therefore its link portion is NULL. The circular linked list, on the other hand, is a list in which the last node connects to the first node, and the address of the first node is stored in the link section of the last node.
There are no nodes at the beginning or finish of the circular linked list. We can travel in either way, backwards or forwards. The following is a diagrammatic illustration of the circular linked list:
Struct node
{
Int data;
Struct node *next;
}
A circular linked list is a collection of elements in which each node is linked to the next and the last node is linked to the first. The circular linked list will be represented similarly to the singly linked list, as demonstrated below:
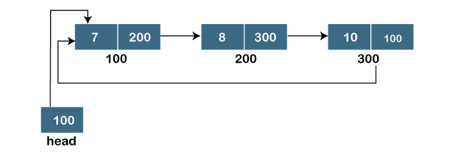
Fig: Circular linked list
Operations On Circular Linked List
1. Insertion of a node
2. Deletion of a node
3. Traversing
Insertion of a node
Node can be inserted at 3 positions i.e., at the beginning, in the middle and at the end of circular linked list.
Insertion at the beginning:
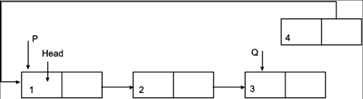
Assume node to be inserted is pointed by P. Insertion can be done in following steps.
1. Position pointer Q to the last node of CLL. For this traverse the list to the end of list.
Q=Head
While(Q->next! =NULL)
Q=Q->next
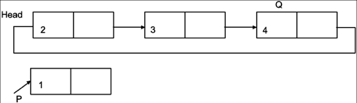
2. Set next link of Q to P and next link of P to Head of CLL.
Q->next=P
P->next=Head
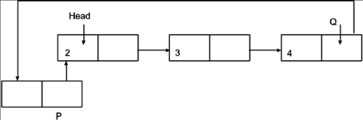
3. Make P as Head of CLL
Head=P
Insertion in the middle
Insertion of node in the middle of CLL is same as that of Singly linked List.
Insertion at the end
1. Position pointer Q to the last node of CLL. For this traverse the list to the end of list.
Q= Head
While(Q->next! =Head)
Q=Q->next

2. Set next link of Q to P and next link of P to Head.
P= Q->next
Head= P->next

Deletion Of Node from CLL
Node can be deleted at the beginning, from the middle and end of CLL.
Deletion at the beginning
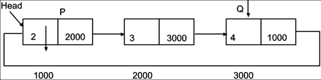
Assume node to be deleted is pointed by P. Deletion can be done in following steps.
1. Position pointer P to point to Head Node and Q to the last node.
P=Q= Head
While(Q->next! =Head)
Q=Q->next
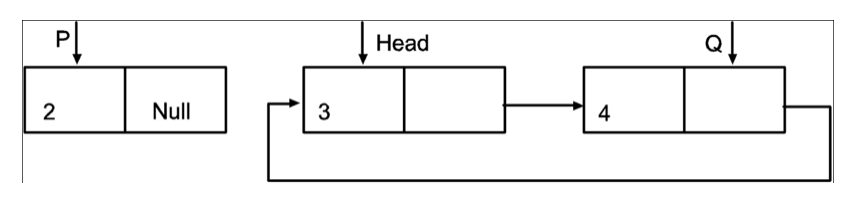
2. Position pointer Head to the next of P. Set next link of Q to point to new Head.
Head=Head->next
Head= Q->next
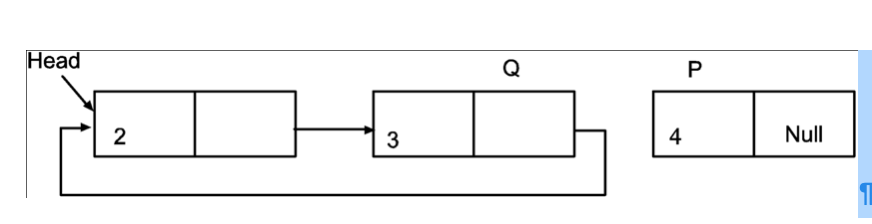
3. Dispose P.
Free(P)
Deletion in the middle of CLL
Deletion of node in middle of CLL is same as that of Singly linked list.
Deletion at the end of CLL
1. Position pointer Q to last but one node of CLL.
Q=Head
While(Q->next->next! =Head)
Q=Q->next

2. Set next link of Q to Head and P to NULL. Dispose P.
Q->next=Head
Free(P)
3. Set next link of Q to Head and P to NULL. Dispose P.
Q->next=Head
Free(P)
Program to create add remove & display element from circular linked list
#include<stdio.h>
#include<alloc.h>
#include<conio.h>
Struct node
{
Int data;
Struct node *next;
};
Struct node *head=NULL;
Struct node *tail=NULL;
Void main()
{
Void addrecord();
Void deleterecord();
Void disrecord();
Int ch;
Clrscr();
Do
{
Printf("\n 1. To add records\n");
Printf("\n 2. To delete a records\n");
Printf("\n 3. To view the records\n");
Printf("\n 4. To exit\n");
Printf("\n Enter your choice\n");
Scanf("%d",&ch);
Fflush(stdin);
switch(ch)
{
Case 1:addrecord();
Break;
Case 2:deleterecord();
Break;
Case 3: disrecord();
Break;
Case 4:exit(0);
}
} while (ch!=4);
}
Void addrecord()
{
Int new_data;
Char ans='y';
Struct node *ptr,*prev,*temp;
Clrscr();
While (ans=='y')
{
Temp=(struct node*)malloc(sizeof(struct node));
Printf("\n Enter the new element:\n");
Scanf("%d",&new_data);
Fflush(stdin);
Temp->data=new_data;
Temp->next=NULL;
If (head==NULL)
{
Head=tail=temp;
Temp->next=head;
}
Else
{
Tail->next=temp;
Tail=temp;
}
Printf("\n Would you like to enter another data(y\\n): \n");
Ans = getchar();
Fflush(stdin);
}
}
Void deleterecord()
{
Struct node *ptr,*prev,*delnode;
Int elt;
Printf("\n Enter the enrollment number to be deleted \n");
Scanf("%d",&elt);
Fflush(stdin);
If (head==NULL)
{
Printf("\n No elements in the list \n");
Return;
}
Else
{
If (head->data==elt)
{
Delnode=head;
If (head==tail)
Head=tail=NULL;
Else
{
Head=head->next;
Tail->next=head;
}
}
Else if (tail->data==elt)
{
For(ptr=head;(ptr!=tail);prev=ptr,ptr=ptr->next);
Delnode=tail;
Tail=prev;
Tail->next=head;
}
Else
{
For(prev=ptr=head;(ptr->data!=elt)&&(ptr!=tail);
Prev=ptr,ptr=ptr->next);
If(ptr->data==elt)
{
Delnode=ptr;
Prev->next=ptr->next;
Printf("yes...");
}
Else
{
Printf("Given element not found in the list");
Getch();
Return;
}
}
}
Free(delnode);
}
Void disrecord()
{
Struct node *ptr,*prev=NULL;
If (head==NULL)
{
Printf("\n No records to view\n");
Return;
}
Printf("\n The elements in the circular list are\n");
For (ptr=head;prev!=tail;prev=ptr,ptr=ptr->next)
Printf("\n\n %d",ptr->data);
Printf(" NULL\n\n ");
Getch();
}
The doubly linked list, as its name implies, has two pointers. The doubly linked list can be described as a three-part linear data structure: the data component, the address part, and the other two address parts. A doubly linked list, in other terms, is a list with three parts in each node: one data portion, a pointer to the previous node, and a pointer to the next node.
Let's pretend we have three nodes with addresses of 100, 200, and 300, respectively. The representation of these nodes in a doubly-linked list is shown below:
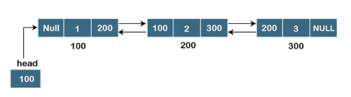
Fig: Doubly linked list
The node in a doubly-linked list contains two address portions, as shown in the diagram above; one part keeps the address of the next node, while the other half stores the address of the previous node. The address component of the first node in the doubly linked list is NULL, indicating that the prior node's address is NULL.
Representation of the node in a doubly linked list
Struct node
{
Int data;
Struct node *next;
Struct node *prev;
}
In the above representation, we've constructed a user-defined structure called a node, which has three members: one is data of integer type, and the other two are pointers of the node type, i.e. next and prev. The address of the next node is stored in the next pointer variable, whereas the address of the previous node is stored in the prev pointer variable. The type of both the pointers, i.e., next and prev is struct node as both the pointers are storing the address of the node of the struct node type.
Operations On Doubly Linked List
1. Insertion of Node
2. Deletion of Node
3. Traversing
Insertion of Node
Node can be inserted in doubly linked list at 3 positions.
(A) At the beginning
(B) In the middle
(C) At the end
Algorithms:
Assume node to be inserted is pointed by P.
(A) Insertion of node at the beginning of Doubly Linked List
Suppose our DLL consists of 3 nodes.
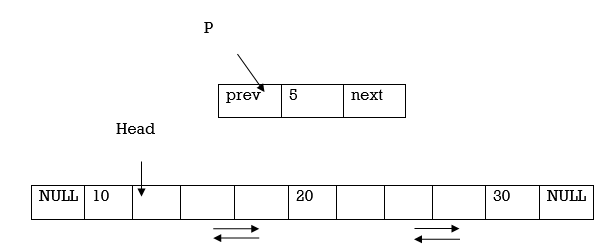
Insertion can be done in following steps
1. Allocate memory to node pointed by P
P= (node*) malloc(sizeof(node))
2. Update the next pointer of the node P to the Head node and make prev pointer as
NULL
P->next=Head
P->prev= NULL

3. Now update Head node’s prev pointer to point to node P and make node P as head node.
Head->prev=P
P = Head

Insertion of node in the middle of Doubly Linked List
To insert a node in the middle of DLL we must know the data value of node after which node is to be inserted. Once we get the data value of node, traverse to that node.
Let us represent data value in a node by variable ‘data’ and value of node after which new node is to be inserted is ‘val’. Suppose we want to insert new node after 2nd node.
2. Initially Q points to first node.
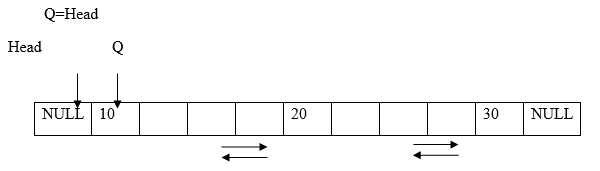
Traverse to the node after which node is to be inserted.
While (Q! =NULL)
{
If(Q->data==val)
Break;
Q=Q->next
}
Now Q points to 2nd node.
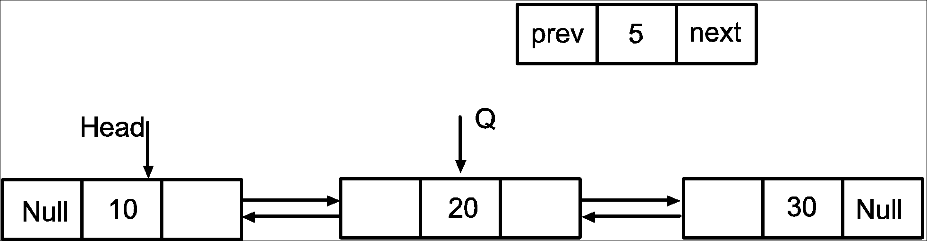 P
P
Make the next pointer of node P to point to node next to Q. Also make the prev point of node P to point to node 2nd node.
P->next=Q->next
P->prev=Q
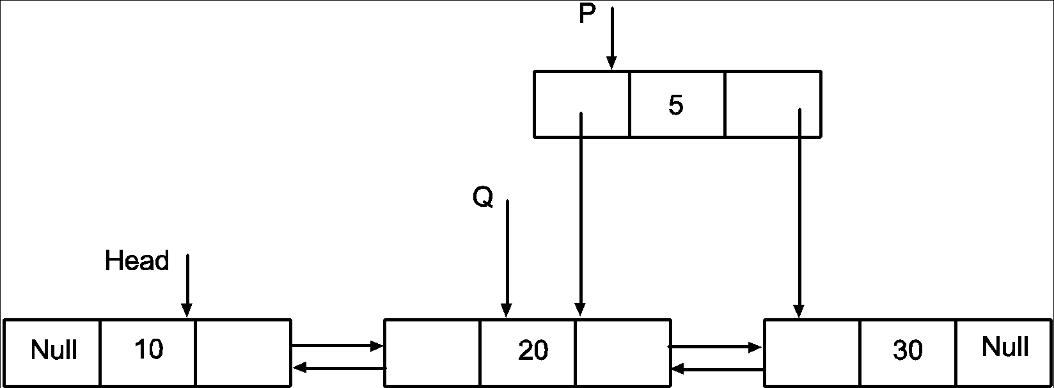
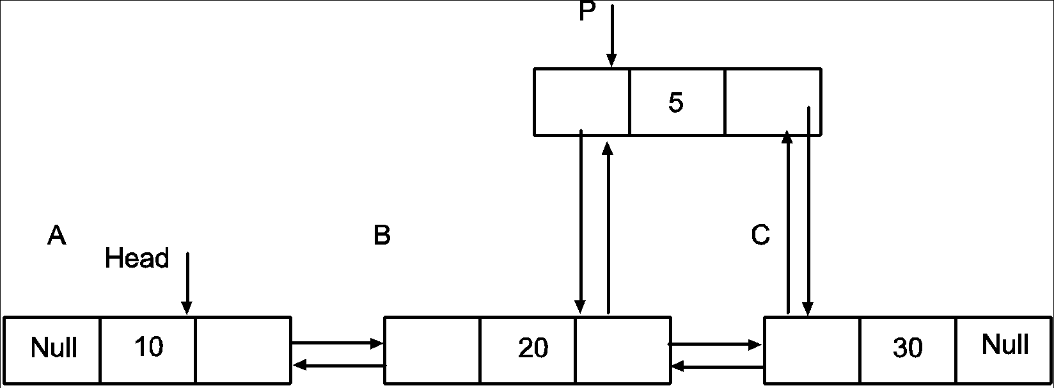
Now point Q’s next to P
Q->next=P
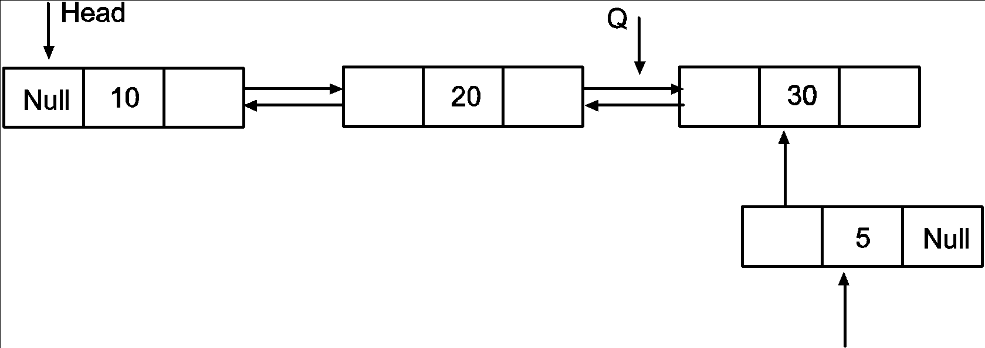
Insertion of node at the last of Doubly Linked List
1. Traverse the list to end.

Q=Head
While(Q->next! =Null)
Q=Q->next
2. Update next pointer of Q to point to P.
Q->next=P

3. Make next pointer of P to point to NULL and prev pointer to point to Q
P->prev=Q
P->next=NULL
Deletion Of Node from Dll
Node can be deleted from doubly linked list at 3 positions
(A) At the beginning
(B) In the middle
(C) At the end
Algorithms:
(A) Deletion of node from the beginning of Doubly Linked List
Assume P points to node to be deleted.
1. P and Head points to the first node in DLL.
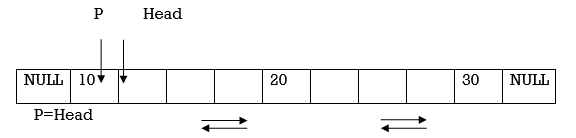
2. Now move the Head pointer to point to the next node. Also change the Head’s prev and P’s next to NULL. Then dispose the node pointed by P.
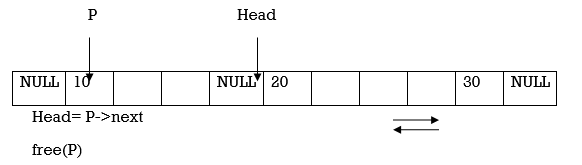
(B) Deletion of node from the middle of Doubly Linked List
To delete a node in the middle of DLL we must know the data value of node after which node is to be deleted. Once we get the data value of node, traverse to that node.
Let us represent data value in a node by variable ‘data’ and value of node after which new node is to be inserted is ‘val’. Suppose we want to delete 3rd node
1. Initially P and Head points to first node.

2. Traverse to the node after which node is to be deleted.
While (P! =NULL)
{
If(P->data==val)
Break;
Q=P;
P=P->next
}
Now Q points to 2nd node and P points to 3rd node i.e., node to be deleted.

3. Set next of Q to next of P and prev of next of P to Q.
P->next=Q->next
P->next->prev=Q

Dispose P.
Free(P)
(c) Deletion of node from the end of Doubly Linked List
1. Position pointer Q to the node previous to P. In order to find this position, list should be traversed first, beginning from the head.
Q=Head
While(Q->next->next! =NuLL)
Q=Q->next
P=Q->next

2. Set next link of the Q and prev link of P to NULL.
Q->next=NuLL

3. Dispose of the Last Node.
Free(P)
Program to perform following operations on doubly linked list
(A) Create a doubly linked list
(B) Insertion of a node
1. At the beginning of doubly Linked List
2. In the middle of doubly Linked List
3. At the end of doubly Linked List
(C) Deletion of a node
1. Beginning of doubly Linked List
2. The middle of doubly Linked List
3. End of doubly Linked List
(D) Display doubly Linked List
#include <stdio.h>
#include<conio.h>
#include<stdlib.h>
Typedef struct node
{
Char data;
Struct node *next, *prev;
}node;
Node *create();
Node *insert_s(node *head, char x)
Node *insert_b(node *head, char x)
Node *insert_e(node *head, char x);
Node *delete_s(node *head );
Node *delete_b(node *head );
Node *delete_e(node *head );
Void display(node*);
Void main()
{
Int c,op;
Char x;
Node *head=NULL;
Do
{
Printf(“1.create\n2.insert\n3.delete\n4.display\n5.Quit”);
Printf(“Enter your choice”);
Scanf(“%d”, &c);
Switch(c)
{
Case 1:head=create();
Break;
Case 2:printf(“\n 1.Beginning\n2. Middle\n3.end”);
Printf(“Enter your choice”);
Scanf(“%d”,&op);
Printf(“Enter data to be inserted”);
Flushall();
x=getchar();
Switch(op)
{
Case 1:head=insert_s(head,x);
Break;
Case 2:head=insert_m(head,x);
Break;
Case 3:head=insert_e(head,x);
Break;
}
Break;
Case 3:printf(“\n 1.Beginning\n2. Middle\n3.end”);
Printf(“Enter your choice”);
Scanf(“%d”,&op);
Switch(op)
{
Case 1:head=delete_s(head);
Break;
Case 2:head=delete_m(head);
Break;
Case 3:head=delete_e(head);
Break;
}
Break;
Case 4:display(head);
Break;
}
}while(op!=5);
}
Node *create()
{
Node *head,*p;
Char x;
Head=NULL;
Printf(“Enter string”);
Flushall();
While(x=getchar()!=’\n’)
{
If(head==NULL)
{
Head=p=(node *)malloc(sizeof(node));
Head->next=head->prev=NULL;
}
Else
{
p->next=(node*)malloc(sizeof(node));
p->next->prev=p;
p=p->next;
p->next=NULL;
}
p->data=x;
}
Return(head);
}
Node *insert_s(node *head, char x)
{
Node *p;
p= (node*)malloc(sizeof(node));
p->data=x;
If(head==NULL)
{
Head=p;
Head->next=head->prev=NULL;
}
Else
{
p->next=head;
Head->prev=p;
p->prev=NULL;
Head=p;
}
Return(head);
}
Node *insert_m(node *head, char x)
{
Node *p,*q;
Char y;
p= (node*)malloc(sizeof(node));
p->data=x;
Printf(“Insert after which character”);
Flushall();
y=getchar();
For(q=head;q!=NULL && q->data!=y;q=q->next)
{
If(q->data==y)
{
p->next=q->next;
p->prev=q;
p->next->prev=p;
p->prev->next=p;
}
Else
Printf(“data not found”);
Return(head);
}
}
Node *insert_e(node *head, char x)
{
Node *p,*q;
p= (node*)malloc(sizeof(node));
p->data=x;
If(head==NULL)
{
Head=p;
Head->next=head->prev=NULL;
}
Else
{
For(q=head;q->next!=NULL;q=q->next)
{
q->next=p;
p->prev=q;
p->next=NULL;
}
Return(head);
}
Node *delete_s(node *head)
{
Node *p,*q;
If(head==NULL)
{
Printf(“Linked list is empty”);
Return(head);
}
If(head->next==NULL)
{
p=head;
Free(p);
Head=NULL;
}
Else
{
P=head;
Head=head->next;
Head->prev=NULL;
Free(p);
}
Return(head);
}
Node *delete_m(node *head)
{
Node *p,*q;
Char x;
If(head==NULL)
{
Printf(“List is empty”);
Return(head);
}
Printf(“Enter data to be deleted”);
Flushall();
x=getchar();
For(p=head;p!=NULL && p->data!=x;p=p->next)
{
If(p->data!=x)
{
Printf(“data not found”);
Return(head);
}
If(p==head)
{
Head=head->next;
If(head!=NULL)
Head->prev=NULL;
Free(p);
}
Else
{
p->prev->next=p->next;
p->next->prev=p->prev;
Free(p);
}
Return(head);
}
}
Void display(node *head)
{
Node *p;
If(head!=NULL)
{
For(p=head;p!=NULL;p=p->next)
Printf(“%c”, p->data);
}
}
Output:
Create
Insert
Delete
Display
Quit
Enter choice: 1
Enter a string: abcde
1. Create
2. Insert
3. Delete
4. Display
5. Quit
Enter choice: 2
Beginning
Middle
End
Enter choice: 2
Enter data to be inserted: f
Insert after which character: c
1. Create
2. Insert
3. Delete
4. Display
5. Quit
Enter choice: 4
Abcfde
1. Create
2. Insert
3. Delete
4. Display
5. Quit
Enter choice:3
Beginning
Middle
End
Enter choice: 1
1. Create
2. Insert
3. Delete
4. Display
5. Quit
Enter choice:4
Bcfde
Key takeaway
The doubly linked list, as its name implies, has two pointers. The doubly linked list can be described as a three-part linear data structure: the data component, the address part, and the other two address parts.
References:
- Data Structures and Algorithms in C, M.T. Goodrich, R. Tamassia and D. Mount, Wiley India.
- Data Structures Using C – A.M. Tenenbaum (PHI)
- Data Structures and Algorithm Analysis in C, 3rd Edition, M.A. Weiss, Pearson.
- Classic Data Structures, D. Samanta, 2nd Edition, PHI.
- Data Structure Using C by Pankaj Kumar Pandey.