Unit - 2
Fuzzy set and fuzzy logic
Fuzzy sets:
The symbols used in this unit are defined as below:
Z = f..., -2, -1, 0, 1, 2, ...} (the set of all integers),
N = (1, 2, 3,...) (the set of all positive integers or natural numbers),
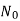 = {0, 1, 2, ...} (the set of all nonnegative integers),
= {0, 1, 2, ...} (the set of all nonnegative integers),
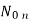 = {0, 1, , n},
= {0, 1, , n},
IR: the set of all real numbers,
R+: the set of all nonnegative real numbers,
[a, b], (a, b], [a, b), (a, b): closed, left-open, right-open, open interval of real numbers
Between a and b, respectively,
(x1, x2, ... , xn): ordered n-tuple of elements x1, x2, ... , xn.
In addition, we use "iff" as a shorthand expression of "if and only if," and the standard symbols 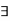 and
and 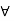 are used for the existential quantifier anti the universal quantifier, respectively. The characteristic function of a crisp set assigns a value of either 1 or 0 to each individual in the universal set, thereby discriminating between members and nonmembers of the crisp set under consideration. This function can be generalized such that the values assigned to the elements of the universal set fall within a specified range and indicate the membership grade of these elements in the set in question. Larger values denote higher degrees of set membership. Such a function is called a membership function, and the set defined by it a fuzzy set.
are used for the existential quantifier anti the universal quantifier, respectively. The characteristic function of a crisp set assigns a value of either 1 or 0 to each individual in the universal set, thereby discriminating between members and nonmembers of the crisp set under consideration. This function can be generalized such that the values assigned to the elements of the universal set fall within a specified range and indicate the membership grade of these elements in the set in question. Larger values denote higher degrees of set membership. Such a function is called a membership function, and the set defined by it a fuzzy set.
The most commonly used range of values of membership functions is the unit interval [0, 1]. In this case, each membership function maps elements of a given universal set X, which is always a crisp set, into real numbers in [0, 1].
Two distinct notations are most commonly employed in the literature to denote membership functions. In one of them, the membership function of a fuzzy set A is denoted by 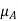 , that is
, that is
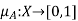
I n In the other one, the function is denoted by A and has, of course, the same form:
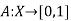
According to the first notation, the symbol (label, identifier, name) of the fuzzy set (A) is distinguished from the symbol of its membership function (AA). According to the second notation, this distinction is not made, but no ambiguity results from this double use of the same symbol. Each fuzzy set is completely and uniquely defined by one particular membership function; consequently, symbols of membership functions may also be used as labels of the associated fuzzy sets.
In this text, we use the second notation. That is, each fuzzy set and the associated membership function are denoted by the same capital letter. Since crisp sets and the associated characteristic functions may be viewed, respectively, as special fuzzy sets and membership functions, the same notation is used for crisp sets as well. Fuzzy sets allow us to represent vague concepts expressed in natural language. The representation depends not only on the concept, but also on the context in which it is used. For example, applying the concept of high temperature in one context to weather and in another context to a nuclear reactor would necessarily be represented by very different fuzzy sets. That would also be the case, although to a lesser degree, if the concept were applied to weather in different seasons, at least in some climates.
Even for similar contexts, fuzzy sets representing the same concept may vary considerably.
In this case, however, they also have to be similar in some key features. As an example, let us consider four fuzzy sets whose membership functions are shown in Fig. 1.2. Each of these fuzzy sets expresses, in a particular form, the general conception of a class of real numbers that are close to 2. In spite of their differences, the four fuzzy sets are similar in the sense that the following properties are possessed by each 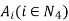
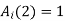 and
and 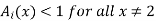
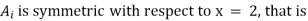
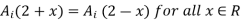
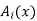 decreases monotonically from 1 to 0 with the increasing difference 12 - x1.
decreases monotonically from 1 to 0 with the increasing difference 12 - x1.
These properties are necessary in order to properly represent the given conception. Any additional fuzzy sets attempting to represent the same conception would have to possess them as well.
Fig: Examples of membership functions that may be used in different contexts for characterizing fuzzy sets of real numbers close to 2.
The four membership functions in Fig. Above are also similar in the sense that numbers outside the interval [1, 3] are virtually excluded from the associated fuzzy sets, since their membership grades are either equal to 0 or negligible. This similarity does not reflect the conception itself, but rather the context in which it is used. The functions are manifested by very different shapes of their graphs. Whether a particular shape is suitable or not can be determined only in the context of a particular application. It turns out, however, that many applications are not overly sensitive to variations in the shape. In such cases, it is convenient to use a simple shape, such as the triangular shape of 
The following are general formulas describing the four families of membership functions, where r denotes the real number for which the membership grade is required to be one (r = 2 for all functions in Fig.above), and  (i belongs to
(i belongs to 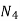 ) is a parameter that determines the rate at which, for each x, the function decreases with the increasing difference |r – x|:
) is a parameter that determines the rate at which, for each x, the function decreases with the increasing difference |r – x|:
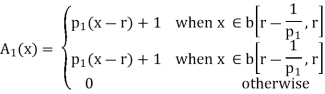
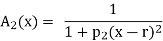
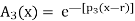
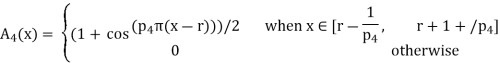
For each i 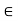
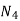 , when p; increases, the graph of A; becomes narrower. Functions in Fig. Exemplify these classes of functions for
, when p; increases, the graph of A; becomes narrower. Functions in Fig. Exemplify these classes of functions for 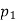 = 1,
= 1, 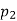 = 10,
= 10, 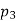 = 5,
= 5, 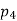 = 2, and r = 2.
= 2, and r = 2.
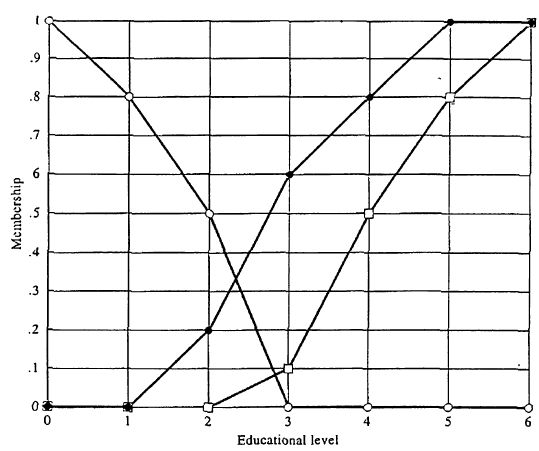
Fuzzy sets in Fig. Are defined within the set of real numbers. Let us consider now, as a simple example, three fuzzy' sets defined within a finite universal set that consists of seven levels of education:
0 - no education
1 - elementary school
2 - high school
3 - two-year college degree
4 - bachelor's degree
5 - master's degree
6 - doctoral degree
Membership functions of the three fuzzy- sets, which attempt to capture the concepts of little-educated, highly educated, and very highly educated people are defined in Fig. Below by the symbols o, , and , respectively. Thus, for example, a person who has a bachelor's degree but no higher degree is viewed, according to these definitions, as highly educated to the degree of 0.8 and very highly educated to the degree of 0.5.
Several fuzzy sets representing linguistic concepts such as low, medium, high, and so on are often employed to define states of a variable. Such a variable is usually called a fuzzy variable.
The significance of fuzzy variables is that they facilitate gradual transitions between states and, consequently, possess a natural capability to express and deal with observation and measurement uncertainties. Traditional variables, which we may refer to as crisp variables, do not have this capability. Although the definition of states by crisp sets is mathematically correct, it is unrealistic in the face of unavoidable measurement errors. A measurement that falls into a close neighborhood of each precisely defined border between states of a crisp variable is taken as evidential support for only one of the states, in spite of the inevitable uncertainty involved in this decision. The uncertainty reaches its maximum at each border, where any measurement should be regarded as equal evidence for the two states on either side of the border. When dealing with crisp -variables, however, the uncertainty is ignored even in this extreme case; the measurement is regarded as evidence for one of the states, the one that includes the border point by virtue of an arbitrary mathematical definition.
Since fuzzy variables capture measurement uncertainties as part of experimental data, they are more attuned to reality than crisp variables. It is an interesting paradox that data based on fuzzy variables provide us, in fact, with more accurate evidence about real phenomena than data based upon crisp variables. This important point can hardly be expressed better than by the following statement made by Albert Einstein in 1921: So far as laws of mathematics refer to reality, they are not certain. And so far as they are certain, they do not refer to reality.
Although mathematics based on fuzzy sets has far greater expressive power than classical mathematics based on crisp sets, its usefulness depends critically on our capability to construct appropriate membership functions for various given concepts is various contexts.
This capability, which was rather weak at the early stages of fuzzy set theory, is now well developed for many application areas. However, the problem of constructing meaningful membership functions is a difficult one, and a lot of additional research work will have to be done on it to achieve full satisfaction.
Thus far, we introduced only one type of fuzzy set. Given a relevant universal set X, any arbitrary fuzzy set of this type (say, set A) is defined by a function of the form
A : X 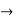 [0, 1]. ……..(1)
[0, 1]. ……..(1)
Fuzzy sets of this type are by far the most common in the literature as well as in the various successful applications of fuzzy set theory. However, several more general types of fuzzy sets have also been proposed in the literature. Let fuzzy sets of the type thus far discussed be called ordinary fuzzy sets to distinguish them from fuzzy sets of the various generalized types.
The primary reason for generalizing ordinary fuzzy sets is that their membership functions are often overly precise. They require that each element of the universal set be assigned a particular real number. However, for some concepts and contexts in which they are applied, we may be able to identify appropriate membership functions only approximately.
For example, we may only be able to identify meaningful lower and upper bounds of membership grades for each element of the universal set. In such cases, we may basically take one of two possible approaches. We may either suppress the identification uncertainty by choosing reasonable values between the lower and upper bounds (e.g., the middle values), or we may accept the uncertainty and include it in the definition of the membership function. A membership function based on the latter approach does not assign to each element of the universal set one real number, but a closed interval of real numbers between the identified lower and upper bounds. Fuzzy sets defined by membership functions of this type are called interval-valued fuzzy sets. These sets are defined formally by functions of the.
Form
A : X 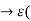 [0, 1]). ……….. (2)
[0, 1]). ……….. (2)
Where 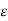 ([0, 1]) denotes the family of all closed intervals of real numbers in [0, 1]; clearly,
([0, 1]) denotes the family of all closed intervals of real numbers in [0, 1]; clearly,
ε([0, 1]) ⊂ ℘([0, 1])
The primary disadvantage of interval-valued fuzzy sets is that this processing, when compared with ordinary fuzzy sets, is computationally more demanding. Since most current applications of fuzzy set theory do not seem to be overly sensitive to minor changes in relevant membership functions, this disadvantage of interval-valued fuzzy sets usually outweighs their advantages.
Interval-valued fuzzy sets can further be generalized by allowing their intervals to be fuzzy. Each interval now becomes an ordinary fuzzy set defined within the universal set [0, 1]. Since membership grades assigned to elements of the universal set by these generalized fuzzy sets are ordinary fuzzy sets, these sets are referred to as fuzzy sets of type 2. Their membership functions have the form
A: X → ℱ ([0, 1])
Where 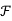 ([O, 1]) denotes the set of all ordinary fuzzy sets that can be defined within the universal set [0, 1];
([O, 1]) denotes the set of all ordinary fuzzy sets that can be defined within the universal set [0, 1]; 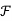 ([0,1]) is also called a fuzzy power set of [0, 1].
([0,1]) is also called a fuzzy power set of [0, 1].
Fuzzy sets: basic concept:
In this section, we introduce some basic concepts and terminology of fuzzy sets. To illustrate the concepts, we consider three fuzzy sets that represent the concepts of a young,. Middle-aged, and old person. A reasonable expression of these concepts by trapezoidal membership functions 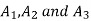
These functions are defined on the interval [0, 80] as follows:
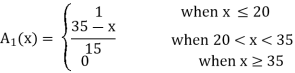


One of the most important concepts of fuzzy sets is the concept of an a-cut and its variant, a strong 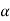 -cut. Given a fuzzy set A defined on X and any number a belongs to [0, 1], the
-cut. Given a fuzzy set A defined on X and any number a belongs to [0, 1], the 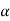 cut,
cut, 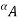 , and the strong
, and the strong 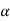 -cut,
-cut, 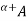 , are the crisp sets
, are the crisp sets
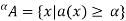
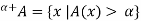
That is, the a-cut (or the strong a-cut) of a fuzzy set A is the crisp set 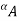 (or the crisp set
(or the crisp set
, 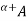 ) that contains all the elements of the universal set X whose membership grades in A are greater than or equal to (or only greater than) the specified value of
) that contains all the elements of the universal set X whose membership grades in A are greater than or equal to (or only greater than) the specified value of 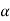 .
.
As an example, the following is a complete characterization of all a-cuts' and all strong acuts for the fuzzy sets A2, A2, A3 given in fig below
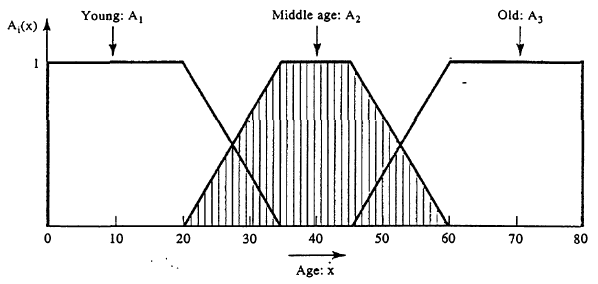
The set of all levels  [0, 1] that represent distinct
[0, 1] that represent distinct  -cuts of a given fuzzy set A is called a level set of A. Formally,
-cuts of a given fuzzy set A is called a level set of A. Formally,
⋀ (A) = { α | A(x) = α for some x ∈ X},
Where A denotes the level set of fuzzy set A defined on X. For our examples, we have:
⋀ (A1) = ⋀ (A2) =⋀ (A3) =[0,1], and
⋀ (D2) = { 0, 0.13, 0.27, 0.4, 0.53, 0.67, 0.8, 0.93, 1}
An important property of both a-cuts and strong 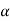 - cuts, which follows immediately from their definitions, is that the total ordering of values of a in [0, 1] is inversely preserved by set inclusion of the corresponding a-cuts as well as strong a-cuts. That is, for any fuzzy set A and pair
- cuts, which follows immediately from their definitions, is that the total ordering of values of a in [0, 1] is inversely preserved by set inclusion of the corresponding a-cuts as well as strong a-cuts. That is, for any fuzzy set A and pair 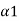 ,
, 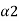
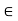 [0, 1] of distinct values such that
[0, 1] of distinct values such that 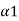 <
< 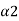 , we have
, we have
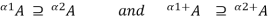
This property can also be expressed by the equations
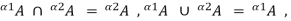
And
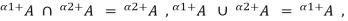
An obvious consequence of this property is that all a-cuts and all strong a-cuts of any fuzzy set form two distinct families of nested crisp sets.
The following special operations of fuzzy complement, intersection, and union are introduced as
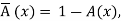
(A ∩ B)(x) = min [A(x), B(x)],
(A ∪ B)(x) = max [A(x), B(x)]
For all x  X. These operations are called the standard fuzzy operations.
X. These operations are called the standard fuzzy operations.
As the reader can easily see, the standard fuzzy operations perform precisely as the corresponding operations for crisp sets when the range of membership grades is restricted to the set {0, 1}. That is, the standard fuzzy operations are generalizations of the corresponding classical set operations. It is now well understood, however, that they are not the only possible generalizations. For each of the three operations, there exists a broad class of functions whose members qualify as fuzzy generalizations of the classical operations as well.
Functions that qualify as fuzzy intersections and fuzzy unions are usually referred to in the literature as t-norms and tconornns, respectively.
Since the fuzzy complement, intersection, and union are not unique operations, contrary to their crisp counterparts, different functions may be appropriate to represent these operations in different contexts. That is, not only membership functions of fuzzy sets but also operations on fuzzy sets are context-dependent. The capability to determine appropriate membership functions and meaningful fuzzy operations in the context of each particular application is crucial for making fuzzy set theory practically useful.
A desirable feature of the standard fuzzy operations is their inherent prevention of the compounding of errors of the operands. If any error e is associated with the membership grades A(x) and B(x), then the maximum error associated with the membership grade of x in  remains e. Most of the alternative fuzzy set operations lack this characteristic.
remains e. Most of the alternative fuzzy set operations lack this characteristic.
Fuzzy intersections (t-norms) and fuzzy unions (t-conorms) do not cover all operations by which fuzzy sets can be aggregated, but they cover all aggregating operations that are associative. Due to the lack of associativity, the remaining aggregating operations must be defined as functions of n arguments for each n > 2. Aggregation operations that, for any given membership grades al, a2, ..., a., produce a membership grade that lies between min(ai, a2.... , and max(al, a2, ... , a,,) are called averaging operations. For any given fuzzy sets, each of the averaging operations produces a fuzzy set that is larger than any fuzzy intersection and smaller than any fuzzy union.
FUZZY COMPLEMENTS:
Let A be a fuzzy set on X. Then, by definition, A(x) is interpreted as the degree to which x belongs to A. Let cA denote a fuzzy complement of A of type c. Then, cA (x) may be interpreted not only as the degree to which x belongs to cA, but also as the degree to which x does not belong to A. Similarly, A (x) may.'also be interpreted as the degree to which x does not belong to cA.
As a notational convention, let a complement cA be defined by a function
c : [0, 1] → [0, 1],
Which assigns a value c(A(x)) to each membership grade A(x) of any given fuzzy set A. The
Value c(A(x)) is interpreted as the value of cA(x). That is,
c(A(x)) = cA(x)
For all x E X by definition. Given a fuzzy set A, we obtain cA by applying function c to values A(x) for all x E X.
Observe that function c is totally independent of elements x to which values A(x) are assigned; it depends only on the values themselves. In the following investigation of its formal properties, we may thus ignore x and assume that the argument of c is an arbitrary number a E [0, 1].
It is obvious that function c must possess certain properties to produce fuzzy sets that qualify, on intuitive grounds, as meaningful complements of given fuzzy sets. To characterize functions c that produce meaningful fuzzy complements, we may state any intuitively justifiable properties in terms of axiomatic requirements, and then examine the class of functions that satisfy these requirements.
To produce meaningful fuzzy complements, function c must satisfy at least the following two axiomatic requirements:
Axiom cl. c(O) = 1 and c(1) = 0 (boundary conditions).
Axiom c2. For all a, b belongs to [0, 1], if a 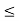 b, then c(a)
b, then c(a) 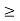 c(b) (monotonicity).
c(b) (monotonicity).
According to Axiom c1, function c is required to produce correct complements for crisp sets. According to Axiom c2, it is required to be monotonic decreasing: when a membership grade in A increases (by changing x), the corresponding membership grade in cA must not increase as well; it may decrease or, at least, remain the same.
There are many functions that satisfy both Axioms ci and c2. For any particular fuzzy set A, different fuzzy sets cA can be said to constitute its complement, each being produced by a distinct function c. All functions that satisfy the axioms form the most general class of fuzzy complements. It is rather obvious that the exclusion or weakening of either of these axioms would add to this class some functions totally unacceptable as complements.
Indeed, a violation of Axiom ci would include functions that do not conform to the ordinary complement for crisp sets. Axiom c2 is essential since we intuitively expect that an increase in the degree of membership in a fuzzy set must result in either a decrease or, in the extreme case, no change in the degree of membership in its complement. Let Axioms cl and c2 be called the axiomatic skeleton for fuzzy complements.
In most cases of practical significance, it is desirable to consider various additional requirements for fuzzy complements. Each of them reduces the general class of fuzzy
Complements to a special subclass. Two of the most desirable requirements, which are usually listed in the literature among axioms of fuzzy complements, are the following:
Axiom c3. c is a continuous function.
Axiom c4. c is involutive, which means that c(c(a)) = a for each a belongs to [0, 1].
Theorem:
Let a function c : [0, 1] [0, 1] satisfy Axioms c2 and c4. Then, c also satisfies Axioms cl and c3, Moreover, c must be a bijective function.
A crisp relation represents the presence or absence of association, interaction or interconnectedness between the elements of two or more sets. This concept can be generalized to allow for various degrees or strengths of association or interaction between elements. Degrees of association can be represented by membership grades in a fuzzy relation in the same way as degrees of set membership are represented in the fuzzy set. In fact, just as the crisp set can be viewed as a restricted case of the more general fuzzy set concept, the crisp relation can be considered to be a restricted case of the fuzzy relation
A relation among crisp sets X1, X2, ... , X, is a subset of the Cartesian product
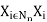
It is denoted either by R(XI, X2, ... , or by the abbreviated form R(Xi\i ∈ ℕn). Thus,
R(X1, X2, …, Xn) ⊆ X1× X2 × . . . × Xn
So that for relations among sets X1, X2, ... , X,,, the Cartesian product X1 x X2 x ... x X represents the universal set. Because a relation is itself a set, the basic set concepts such as containment or subset, union, intersection, and complement can be applied without modification to relations.
Each crisp relation R can be defined by a characteristic function which assigns a value of 1 to every tuple of the universal set belonging to the relation and a 0 to every tuple not belonging to it. Denoting a relation and its characteristic function by the same symbol R, we have
R(x1, x2, …, xn) = 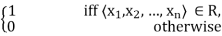
The membership of a tuple in a relation signifies that the elements of the tuple are related to or associated with one another. For instance, let R represent the relation of marriage between the set of all men and the set of all women. Of all the possible pairings of men and women, then, only those pairs who are married to each other will be assigned a value of 1 indicating that they belong to this relation. A relation between two sets is called binary; if three, four, or five sets are involved, the relation is called ternary, quaternary, or quinary, respectively. In general, a relation defined on n sets is called n-ary or n-dimensional. .
A relation can be written as a set of ordered tuples. Another convenient way of representing a relation R(X1, X2, ..., involves an n-dimensional membership array:
R =[ri1, i2, . . . , in]. Each element of the first dimension ii of this array corresponds to exactly one member of X1 and each element of dimension i2 to exactly one member of X2, and so on. If the n-tuple (x1, x2, ... , x X corresponds to the element r,,,,2,.,,,;, of R, then
ri1, i2, … in = 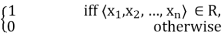
Example:
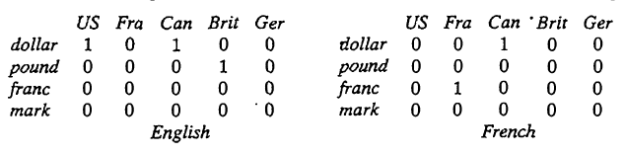
Let R be a relation among the three sets X = (English, French), Y = (dollar, pound, franc, mark) and Z = {US, France, Canada, Britain, Germany), which associates a country with a currency and language as follows:
R(X, Y, Z) = {(English, dollar, US), (French, Franc, France), (English, dollar,
Canada), (French, dollar, Canada), (English, pound, Britain)).
This relation can also be represented with the following three-dimensional membership array:
To illustrate the convenience of representing n-ary relations by n-dimensional arrays (especially important for computer processing), a possible structure for a five-dimensional array based on sets X, (i belongs to N5) is shown in Fig.. The full array (five-dimensional) can be viewed as a "library" that consists of ]XiI "books" (four-dimensional arrays) distinguished from each other by elements of X1. Each "book" consists of 1X21 "pages" (three-dimensional arrays) distinguished from each other by elements of X2. Each "page" consists of X31 matrices (two-dimensional arrays) distinguished from each other by elements of X3. Each matrix consists of IX41 rows (one-dimensional arrays) distinguished from each other by elements of X4. Each row consists of IX5 1 individual entries distinguished from each other by elements of X5. Just as the characteristic function of a crisp set can be generalized to allow for degrees of set membership, the characteristic function of a crisp relation can be generalized to allow tuples to have degrees of membership within the relation. Thus, a fuzzy relation is a fuzzy set defined on the Cartesian product of crisp sets X1, X2, ..., X,,, where tuples (x1, x2, ..., may have varying degrees of membership within the relation. The membership grade indicates the strength of the relation present between the elements of the tuple.
A fuzzy relation can also be conveniently represented by an n-dimensional membership
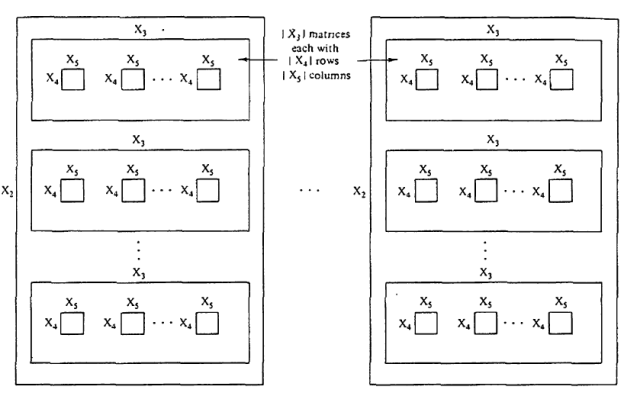
Array whose entries correspond to n-tuples in the universal set. These entries take values representing the membership grades of the corresponding n-tuples.
Example: Let R be a fuzzy relation between the two sets X = (New York City, Paris) and Y = {Beijing, New York City, London), which represents the relational concept "very far." This relation can be written in list notation as R(X, Y) = 1/NYC, Beijing +0/NYC, NYC+.6/NYC, London + .9/Paris, Beijing + .7/Paris, NYC + .3/Paris, London.
This relation can also be represented by the following two-dimensional membership array (matrix):

Ordinary fuzzy relations (with the valuation set [0, 1]) can obviously be extended to
L-fuzzy relations (with an arbitrary ordered valuation set L) in the same way as fuzzy sets are extended to L-fuzzy sets. Similarly, type t, level k, and interval-valued fuzzy relations can be defined.
Binary fuzzy relation:
Binary relations have a special significance among n-dimensional relations since they are, in some sense, generalized mathematical functions. Contrary to functions from X to Y, binary relations R (X, Y) may assign to each element of X two or more elements of Y. Some basic operations on functions, such as the inverse and composition, are applicable to binary relations as well.
Given a fuzzy relation R(X, Y), its domain is a fuzzy set on X, dom R, whose membership function is defined by
Dom R(x) = 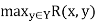
For each x belongs to X. That is, each element of set X belongs to the domain of R to the degree equal to the strength of its strongest relation to any member of set Y. The range of R(X, Y) is a fuzzy relation on Y, ran R, whose membership function is defined by
Ran R(y) = 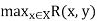
For each y belongs to Y. That is, the strength of the strongest relation that each element of Y has to an element of X is equal to the degree of that element's membership in the range of R. In addition, the height of a fuzzy relation R(X, .Y) is a number, h(R), defined by
h(R) = 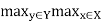 R(x, y)
R(x, y)
That is, h(R) is the largest membership grade attained by any pair (x, y) in R.
A convenient representation of binary relation R(X, Y) are membership matrices
R = [rxy], where r.,y = R(x, y). Another useful representation of binary relations is a
Sagittal diagram. Each of the sets X, Y is represented by a set of nodes in the diagram; nodes corresponding to one set are clearly distinguished from nodes representing the other set. Elements of X x Y with nonzero membership grades in R(X, Y) are represented in the diagram by lines connecting the respective nodes. These lines are labelled with the values of the membership grades.
The inverse of a fuzzy relation R(X, Y), which is denoted by R-1 (Y, X) is a relation on Y x X defined by
R-1(y, x) = R(x, y)
Consider now two binary fuzzy relations P(X, Y) and Q(Y, Z) with a common set
Y. The standard composition of these relations, which is denoted by P (X, Y) o Q (Y, Z), produces a binary relation R(X, Z) on X x Z defined by
R(x, z) = [P o Q](x, z) = 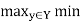 [P(x, y), Q(y, z)]
[P(x, y), Q(y, z)]
BINARY RELATIONS ON A SINGLE SET:
In addition to defining a binary relation that exists between two different sets, it is also possible to define a crisp or fuzzy binary relation among the elements of a single set X.
A binary relation of this type can be denoted by R(X, X) or R(X2) and is a subset of
X x X = X2. These relations are often referred to as directed graphs or digraphs.
Binary relations R (X, X) can be expressed by the same forms as general binary relations (matrices, sagittal diagrams, tables). In addition, however, they can be conveniently expressed in terms of simple diagrams with the following properties: (1) each element of the set X is represented by a single node in the diagram; (2) directed connections between nodes indicate pairs of elements of X for which the grade of membership in R is nonzero; and (3) each connection in the diagram is labeled by the actual membership grade of the corresponding pair in R. An example of this diagram for a relation R(X, X) defined on X = {1, 2, 3, 4) is shown in Fig. 5.4, where it can be compared with the other forms of representation of binary relations.
Various significant types of relations R(X, X) are distinguished on the basis of three different characteristic properties: reflexivity, symmetry, and transitivity. First, let us consider crisp relations.
A crisp relation R(X, X) is reflexive if (x, x) 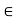 R for each x
R for each x 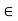 X, that is, if every element of X is related to itself. Otherwise, R(X, X) is called irreflexive. If (x, x) ¢ R for every x
X, that is, if every element of X is related to itself. Otherwise, R(X, X) is called irreflexive. If (x, x) ¢ R for every x 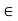 X, the relation is called antireflexive.
X, the relation is called antireflexive.
A crisp relation R(X, X) is symmetric if for every (x, y) 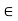 R, it is also the case that (y, x) E R, where x, y,
R, it is also the case that (y, x) E R, where x, y, 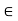 X. Thus, whenever an element x is related to an element y through a symmetric relation, y is also related to x. If this is not the case for some x, y, then the relation is called asymmetric. If both (x, y)
X. Thus, whenever an element x is related to an element y through a symmetric relation, y is also related to x. If this is not the case for some x, y, then the relation is called asymmetric. If both (x, y) 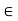 R and (y, x)
R and (y, x) 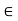 R implies x = y, then the relation is called antisymmetric. If either (x, y)
R implies x = y, then the relation is called antisymmetric. If either (x, y) 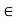 R or (y, x)
R or (y, x) 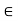 R, whenever x
R, whenever x 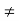 y, then the relation is called strictly antisymmetric.
y, then the relation is called strictly antisymmetric.
A crisp relation R(X, X) is called transitive iff (x, z) 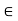 R whenever both (x, y) E R and (y, z)
R whenever both (x, y) E R and (y, z) 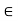 R for at least one y
R for at least one y 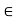 X. In other words, the relation of x to y and of y to z implies the relation of x to z in a transitive relation. A relation that does not satisfy this property is called nontransitive. If (x, z) does not belongs to R whenever both (x, y)
X. In other words, the relation of x to y and of y to z implies the relation of x to z in a transitive relation. A relation that does not satisfy this property is called nontransitive. If (x, z) does not belongs to R whenever both (x, y) 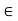 R and (y, z)
R and (y, z) 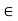 R, then the relation is called antitransitive.
R, then the relation is called antitransitive.
Example: Let R be a crisp relation defined on X x X, where X is the set of all university courses and R represents the relation "is a prerequisite of." R is antireflexive because a course is never a prerequisite of itself. Further, if one course is a prerequisite of another, the reverse will never be true. Therefore, R is antisymmetric. Finally, if a course is a prerequisite for a second course that
Is itself a prerequisite for a third, then the first course is also a prerequisite for the third course.
Thus, the relation R is transitive. These three properties can be extended for fuzzy relations R(X, X), by defining them in terms of the membership function of the relation. Thus, R(X, X) is reflexive iff
R(x, x) = 1 for all x E X. If this is not the case for some x E X, the relation is called irreflexive; if it is not satisfied for all x E X, the relation is called antireflexive. A weaker form of reflexivity, referred to as s-reflexivity, is sometimes defined by requiring that
R(x, x) 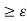 ,
,
Where 0 < s < 1.
A fuzzy relation is symmetric iff
R(x, y) = R(y, x)
For all x, y 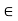 X. Whenever this equality is not satisfied for some x, y
X. Whenever this equality is not satisfied for some x, y 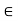 X, the relation is called asymmetric. Furthermore, when R(x, y) > 0 and R(y, x) > 0 implies that x = y for all x, y
X, the relation is called asymmetric. Furthermore, when R(x, y) > 0 and R(y, x) > 0 implies that x = y for all x, y 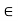 X, the relation R is called antisymmetric.
X, the relation R is called antisymmetric.
A fuzzy relation R (X, X) is transitive (or, more specifically, max-min transitive) if
R(x, z) ≥ 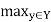 min [R(x, y), R(y, z)]
min [R(x, y), R(y, z)]
Is satisfied for each pair (x, z) 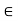 X2: A relation failing to satisfy this inequality for some members of X is called nontransitive, and if
X2: A relation failing to satisfy this inequality for some members of X is called nontransitive, and if
R(x, z) < 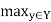 min [R(x, y), R(y, z)],
min [R(x, y), R(y, z)],
For all (x, z) 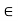 X2, then the relation is called antitransitive.
X2, then the relation is called antitransitive.
Fuzzy logic:
Logic is the study of the methods and principles of reasoning in all its possible forms.
Classical logic deals with propositions that are required to be either true or false. Each proposition has its opposite, which is usually called a negation of the proposition. A proposition and its negation are required to assume opposite truth values.
One area of logic, referred to as propositional logic, deals with combinations of variables that stand for arbitrary propositions. These variables are usually called logic variables (or propositional variables). As each variable stands for a hypothetical proposition, it may assume either of the two truth values; the variable is not committed to either truth value unless a particular proposition is substituted for it.
One of the main concerns of propositional logic is the study of rules by which new logic variables can be produced as functions of some given logic variables. It is not concerned with the internal structure of the propositions that the logic variables represent.
Assume that n logic variables v1, v2, ... , V. Are given. A new logic variable can then be defined by a function that assigns a particular truth value to the new variable for each combination of truth values of the given variables. This function is usually called a logic function. Since n logic variables may assume 2" prospective truth values, there are 22" possible logic functions of these variables. For example, all the logic functions of two variables are listed in Table 8.1, where falsity and truth are denoted by 0 and 1, respectively, and the resulting 16 logic variables are denoted by w1, W2, ... , w16. Logic functions of one
Or two variables are usually called logic operations.
The key issue of propositional logic is the expression of all the logic functions of n variables (n E Nl), the number of which grows extremely rapidly with increasing values of n, with the aid of a small number of simple logic functions. These simple functions are preferably logic operations of one or two variables, which are called logic primitives. It is known that this can be accomplished only with some sets of logic primitives. We say that a set of primitives is complete if any logic function of variables v1, v2, ... , v (for any finite n) can be composed by a finite number of these primitives.
Two of the many complete sets of primitives have been predominant in propositional logic: (i) negation, conjunction, and disjunction; and (ii) negation and implication. By combining, for example, negations, conjunctions, and disjunctions (employed as primitives) in appropriate algebraic expressions, referred to as logic formulas, we can form any other logic function. Logic formulas are then defined recursively as follows:
1. If v denotes a logic variable, then v and v are logic formulas;
2. If a and b denote logic formulas, then a A b and a V b are also logic formulas;
3. The only logic formulas are those defined by the previous two rules.
Every logic formula of this type defines a logic function by composing it from the three primary functions. To define a unique function, the order in which the individual compositions are to be performed must be specified in some way. There are various ways in which this order can be specified. The most common is the usual use of parentheses as in any other algebraic expressions.
Other types of logic formulas can be defined by replacing some of the three operations in this definition with other operations or by including some additional operations. We may replace, for example, a A b and a v bin the definition with a = b, or we' may simply add a b to the definition.
While each proper logic formula represents a single logic function and the associated logic variable, different formulas may represent the same function and variable. If they do, we consider them equivalent. When logic formulas a and b are equivalent, we write a = b.
For example,
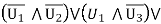
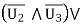
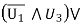
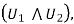
As can be easily verified by evaluating each of the formulas for all eight combinations of truth values of the logic variables v1, v2, v3.
When the variable represented by a logic formula is always true regardless of the truth values assigned to the variables participating in the formula, it is called a tautology; when it is always false, it is called a contradiction. For example, when two logic formulas a and b are equivalent, then a 4 b is a tautology, while the formula a A b is a contradiction. Tautologies are important for deductive reasoning because they represent logic formulas that, due to their form, are true on logical. Grounds alone. Various forms of tautologies can be used for making deductive inferences. They are referred to as inference rules. Examples of some tautologies frequently used as inference rules are
(a ⋀ (a ⟹ b)) ⟹ b ( modus ponens),
(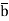 ⋀ (a ⟹ b)) ⟹
⋀ (a ⟹ b)) ⟹ 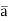 (modus tollens),
(modus tollens),
((a ⟹ b) ⋀ ( b ⟹ c )) ⟹ (a ⟹ c) ( hypothetical syllogism).
Modus ponens, for instance, states that given two true propositions, "a" and "a = b" (the premises), the truth of the proposition "b" (the conclusion) may be inferred.
Every tautology remains a tautology when any of its variables is replaced with any arbitrary logic formula. This property is another example of a powerful rule of inference, referred to as a rule of substitution.
It is well established that propositional logic based on a finite set of logic variables is isomorphic to finite set -theory under a particular correspondence between components of these two mathematical systems. Furthermore, both of these systems are isomorphic to a finite Boolean algebra, which is a mathematical system defined by abstract (interpretationfree) entities and their axiomatic properties.
A Boolean algebra on a set B is defined as the quadruple
ℬ = 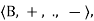
Where the set B has at least two elements (bounds) 0 and 1; + and are binary operations on B, and - is a unary operation on B for which the properties listed in Table 8.2 are satisfied.
Not all of these properties are necessary for an axiomatic characterization of Boolean algebras; we present this larger set of properties in order to emphasize the relationship between Boolean algebras, set theory, and propositional logic.
Properties (B1)-(B4) are common to all lattices. Boolean algebras are therefore lattices that are distributive (B5), bounded (B6), and complemented (B7)-{B9). This means that each Boolean algebra can also be characterized in terms of a partial ordering on a set, which is defined as follows: a < b if a b = a or, alternatively, if a + b = b.
The isomorphisms between finite Boolean algebra, set theory, and propositional logic guarantee that every theorem in any one of these theories has a counterpart in each of the
PROPERTIES OF BOOLEAN ALGEBRAS
(B1) Idempotence a+a = a
a.a =a
(B2) Commutativity a+b = b+a
a.b = b.a
(B3) Associativity (a+b)+c = a+(b+c)
(a.b).c = a.(b.c)
(B4) Absorption a ÷ (a. b) = a
a . (a+b) = a
(B5) Distributivity a . (b+c) = (a . b)+(a . c)
a ÷ (b . c) = (a + b) . (a+c)
(B6) Universal bounds a+ 0 = a, a + a = 1
a . 1 = a, a . 0 = 0
(B7) Complementarity a + 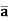 =1
=1
a . 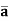 = 0
= 0
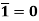
(B8) Involution 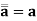
(B9) Dualization 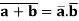
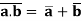
References:
1. “Discrete Mathematics and its Applications” by Kenneth H Rosen
2. “Discrete Mathematics” by Norman L Biggs
3. “Discrete Mathematics for Computer Science” by Kenneth Bogart and Robert L Drysdale