Unit - 3
Group theory and ring theory
Binary operations-
A binary operation * is a set A is a function from A × A to A.
If * is a binary operation in a set A then than for the * image of the ordered pair (a, b) ∈ A×A, we write a*b.
For example:
Addition + is a binary operation in the set of natural number N, integer Z and real number R.
Multiplication is a binary operation in N, Q, Z, R and C.
General properties-
Propery-1: Let A be any set. A binary operation * A × A →A is said to be commutative if for every a, a, b ∈A.
a* b = b * a
Property-2: Let A be a non-empty set. A binary operation *; A × A →A is said to be associative if
a* b) * c = a * (b * c) for every a, b, c ∈A.
Property-3: Let * be a binary operation on a non-empty set A. If there exists an element e ∈A such that e * a = a * e = a for every a ∈A, then the element e is called identity with respect to * in A.
Property-4: Let * be a binary operation on a non-empty set A and e be the identity element in A with respect the operation *. An element a ∈A is said to be invertible if there exists an element b ∈A such that
a* b = b * a = e
In which case a and b are inverses of each other. For the operation * if b is the inverses of a ∈A then we can write b = 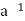
Cancellation laws-
A binary operation denoted by * in a set A, is said to satisfy.
(i) Left cancellation law if for all a, b, c ∈A,
a* b = a * c ⇒b = c
(ii) Right cancellation law if for all a, b, c ∈A
b* a = c * a ⇒b = c
Algebraic system-
If A is a set and * is a binary operation on A, then (A, *) is called an algebraic structure.
Example: Let R be the set of real numbers, then (R, +) is an algebraic structure.
Example: If N denotes the set of natural numbers then (N, +) is an algebraic structure.
Groups and subgroups
A group is an algebraic structure (G, *) in which the binary operation * on G satisfies the following conditions:
Condition-1: For all a, b, c, ∈ G
a* (b * c) = (a * b) * c (associativity)
Condition-2: There exists an elements e ∈G such that for any a ∈G
a* e= e * a = a (existence of identity)
Condition-3: For every a ∈G, there exists an element denoted by 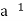 in G such that
in G such that
a* 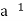 =
=  * a = e
* a = e
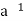 is called the inverse of a in G.
is called the inverse of a in G.
Example: (Z, +) is a group where Z denote the set of integers.
Example: (R, +) is a group where R denote the set of real numbers.
Abelian group-
Let (G, *) be a group. If * is commutative that is
a* b = b * a for all a, b ∈G then (G, *) is called an Abelian group.
Finite group-
A group G is said to be a finite group if the set G is a finite set.
Infinite group-
A group G, which is not finite is called an infinite group.
Order of a finite group-
The order of a finite group (G, *) is the number of distinct element in G. The order of
G is denoted by O (G) or by |G|.
Example: If G = {1, -1, i, -i} where i = 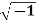 , then show that G is an abelian group with respect to multiplication as a binary operation.
, then show that G is an abelian group with respect to multiplication as a binary operation.
Sol.
First we will construct a composition table-
. | 1 | -1 | I | -i |
1 | 1 | -1 | I | -i |
-1 | -1 | 1 | -i | i |
i | i | -i | -1 | 1 |
-i | -i | I | 1 | -1 |
It is clear from the above table that algebraic structure (G, .) is closed and satisfies the following conditions.
Associativity- For any three elements a, b, c ∈G (a ⋅b) ⋅c = a ⋅(b ⋅c)
Since
1 ⋅(−1 ⋅i) = 1 ⋅−i= −i
(1 ⋅−1) ⋅i= −1 ⋅i= −i
⇒1 ⋅(−1 ⋅i) = (1 ⋅−1) i
Similarly with any other three elements of G the properties holds.
∴ Associative law holds in (G, ⋅)
Existence of identity: 1 is the identity element (G, ⋅) such that 1 ⋅a = a = a ⋅1 ∀a ∈G
Existence of inverse: 1 ⋅1 = 1 = 1 ⋅1 ⇒1 is inverse of 1
(−1) ⋅(−1) = 1 = (−1) ⋅(−1) ⇒–1 is the inverse of (–1)
i⋅(−i) = 1 = −i⋅i⇒–iis the inverse of iin G.
−i⋅i= 1 = i⋅(−i) ⇒iis the inverse of –iin G.
Hence inverse of every element in G exists.
Thus all the axioms of a group are satisfied.
Commutativity: a ⋅b = b ⋅a ∀a, b ∈G hold in G
1 ⋅1 = 1 = 1 ⋅1, −1 ⋅1 = −1 = 1 ⋅−1
i⋅1 = i= 1 ⋅i; i⋅−i= −i⋅i= 1 = 1 etc.
Commutative law is satisfied.
Hence (G, ⋅) is an abelian group.
Example-
Prove that the set Z of all integers with binary operation * defined by a * b = a + b + 1 ∀a, b ∈G is an abelian group.
Sol: Sum of two integers is again an integer; therefore a +b ∈Z ∀a, b ∈Z
⇒a +b + 1 ⋅∈Z ∀a, b ∈Z
⇒Z is called with respect to *
Associative law for all a, b, a, b ∈G we have (a * b) * c = a * (b * c) as
(a* b) * c = (a + b + 1) * c
= a + b + 1 + c + 1
= a + b + c + 2
Also
a* (b * c) = a * (b + c + 1)
= a + b + c + 1 + 1
= a + b + c + 2
Hence (a * b) * c = a * (b * c) ∈a, b ∈Z.
Key takeaways-
- Let (G, *) be a group. If * is commutative that is
a* b = b * a for all a, b ∈G then (G, *) is called an Abelian group.
2. A group G is said to be a finite group if the set G is a finite set.
3. The order of a finite group (G, *) is the number of distinct element in G. The order of
G is denoted by O (G) or by |G|.
Subgroup
Let (G, *) be a group and H, be a non-empty subset of G. If (H, *) is itself is a group, then (H, *) is called sub-group of (G, *).
Example-Let a = {1, –1, i, –i} and H = {1, –1}
G and H are groups with respect to the binary operation, multiplication.
H is a subset of G, therefore (H, X) is a sub-group (G, X).
Theorem-
If (G, *) is a group and H ≤G, then (H, *) is a sub-group of (G, *) if and only if
(i) a, b ∈H ⇒a * b ∈H;
(ii) a ∈ H ⇒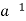 ∈H
∈H
Proof:
If (H, *) is a sub-group of (G, *), then both the conditions are obviously satisfied.
We, therefore prove now that if conditions (i) and (ii) are satisfied then (H, *) is a sub-group of (G, *).
To prove that (H, *) is a sub-group of (G, *) all that we are required to prove is : * is associative in H and identity e ∈ H.
That * is associative in H follows from the fact that * is associative in G.
Also,
A ∈ H ⇒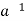 ∈H by (ii) and e ∈H and
∈H by (ii) and e ∈H and 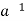 ∈H ⇒a *
∈H ⇒a * 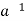 = e ∈H by (i)
= e ∈H by (i)
Hence, H is a sub-group of G.
Cosets-
Let (H, *) be a sub-group (G, *) and a ∈G
Then the sub-set:
a* H = {a * h: h ∈H }is called a left coset of H in G, and the subset
H * G = {h * a: h ∈H}is called a right coset of H in G.
Theorem: If (H, *) is a sub-group (G, *), then a * H = H if and only if a ∈H.
Proof: Let a * H = H
Since e ∈H then a = a * e ∈a * H
Hence a ∈H
Conversely
Let a ∈H then a * H ⊆H
(H, *) is a sub-group.
∴a ∈ H, h ∈ H ⇒ 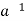 * h ∈ H.
* h ∈ H.
Now h ∈H
⇒h = a * (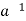 * h) ∈a * H
* h) ∈a * H
∴h ∈ H ⇒h ∈a * H
⇒H ⊆ a * H
Hence a * H = H
Homomorphism-
Let (G, *) and (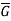 ,
,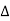 ) be any two groups. A mapping f: G →
) be any two groups. A mapping f: G →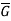 is called a homomorphism of G to
is called a homomorphism of G to 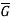 if.
if.
f(a * b) = f (a) 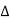 f (b) ∀a, b ∈G
f (b) ∀a, b ∈G
Example: Let G = R, the set of real numbers and 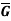 = R – {u)
= R – {u)
(G, +) and (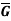 , ⋅) are groups. Define a mapping f: G →G by
, ⋅) are groups. Define a mapping f: G →G by
f(a) = 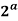 ∀a ∈G
∀a ∈G
Clearly f (a + b) = 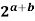 =
= 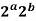 = f (a) ⋅f (b)
= f (a) ⋅f (b)
⇒fis a homomorphism of G into G.
Monoid:
Let S be a nonempty set with an operation. Then S is called a semigroup if the operation is associative. If the operation also has an identity element, then S is called a monoid.
(a) Consider the positive integers N. Then (N, +) and (N, ×) are semigroups since addition and multiplication on N are associative. In particular, (N, ×) is a monoid since it has the identity element 1. However, (N, +) is not a monoid since addition in N has no zero element.
(b) Let S be a finite set, and let F(S) be the collection of all functions f : S → S under the operation of composition of functions. Since the composition of functions is associative, F(S) is a semigroup. In fact,
F(S) is a monoid since the identity function is an identity element for F(S).
(c) Let S = {a, b, c, d}. The multiplication tables in Fig. B-1 define operations ∗ and ・ on S. Note that ∗ can be defined by the formula x ∗ y = x for any x and y in S. Hence
(x ∗ y) ∗ z = x ∗ z = x and x ∗ (y ∗ z) = x ∗ y = x
Therefore, ∗ is associative and hence (S, ∗) is a semigroup. On the other hand, ・ is not associative since,
For example,
(b ・ c) ・ c = a ・ c = c but b ・ (c ・ c) = b ・ a = b
Thus (S, ・) is not a semigroup.
SUBGROUPS, NORMAL SUBGROUPS, AND HOMOMORPHISMS:
Let H be a subset of a group G. Then H is called a subgroup of G if H itself is a group under the operation of G. Simple criteria to determine subgroups follow.
Proposition B.5: A subset H of a group G is a subgroup of G if:
(i) The identity element e ∈ H.
(ii) H is closed under the operation of G, i.e. if a, b ∈ H, then ab ∈ H.
(iii) H is closed under inverses, that is, if a ∈ H, then 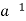 ∈ H.
∈ H.
Every group G has the subgroups {e} and G itself. Any other subgroup of G is called a nontrivial subgroup.
Cosets
Suppose H is a subgroup of G and a ∈ G. Then the set
Ha = {ha | h ∈ H}
Is called a right coset of H. (Analogously, aH is called a left coset of H.).
Theorem: Let H be a subgroup of a group G. Then the right cosets Ha form a partition of G.
Theorem (Lagrange): Let H be a subgroup of a finite group G. Then the order of H divides the order of G.
The number of right cosets of H in G, called the index of H in G, is equal to the number of left cosets of H in G; and both numbers are equal to |G| divided by |H|.
Normal Subgroups:
Definition: A subgroup H of G is a normal subgroup if 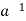 Ha ⊆ H, for every a ∈ G, or, equivalently, if aH = Ha, i.e., if the right and left cosets coincide.
Ha ⊆ H, for every a ∈ G, or, equivalently, if aH = Ha, i.e., if the right and left cosets coincide.
Note that every subgroup of an abelian group is normal.
Theorem:
Let H be a normal subgroup of a group G. Then the cosets of H form a group under coset multiplication:
(aH)(bH) = abH
This group is called the quotient group and is denoted by G/H.
Suppose the operation in G is addition or, in other words, G is written additively. Then the cosets of a subgroup H of G are of the form a +H. Moreover, if H is a normal subgroup of G, then the cosets form a group under coset addition, that is,
(a + H) + (b + H) = (a + b) + H
Kernel of homomorphism-
Let G and G be any two groups and f: G →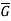 be a homomorphism. Then Kernel of f denoted by Ker f the set K = (a ∈G: f (a) =
be a homomorphism. Then Kernel of f denoted by Ker f the set K = (a ∈G: f (a) = 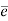 ).
).
Where e is the identity of 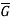 .
.
Example: Let G be (Z, +) i.e., the group of integers under addition and let f: G → G defined by
∅(x) = 3x ∀x ∈G. Prove that f is homomorphism, determine its Kernel.
Solution: We have ∅(x) = 3x ∀x ∈G
∀x, y ∈G ⇒x + y ∈G (∴G is a group under addition)
Now
f(x + y) = 3 (x + y)
= 3x + 3y
= f (x) + f (y)
Hence f is homomorphism.
Kernel of homomorphism consists of half of zero i.e., the integers whose double is zero.
Thus K = {0}
Key takeaways
- Let (G, *) be a group and H, be a non-empty subset of G. If (H, *) is itself is a group, then (H, *) is called sub-group of (G, *).
- Let (H, *) be a sub-group (G, *) and a ∈G
Then the sub-set:
a* H = {a * h: h ∈H}is called a left coset of H in G, and the subset
H * G = {h * a: h ∈H}is called a right coset of H in G.
3. Let G and G be any two groups and f: G →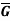 be a homomorphism. Then Kernel of f denoted by Ker f the set K = (a ∈G: f (a) =
be a homomorphism. Then Kernel of f denoted by Ker f the set K = (a ∈G: f (a) = 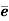 ).
).
Where e is the identity of 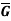 .
.
Ring:
A non-empty set R, equipped with two binary operations, called addition (+) and multiplication (.) is called a ring if the following postulates are satisfied.
(1) R is an additive Abelian group,
(2) R is an multiplicative semigroup
(3) The two distributive laws hold good, viz
a. (b + c) =a.b + a.c. (left distributive law)
(a + b). c = a.c + b.c, (right distributive law) for all a, b, c 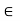 R
R
Note: 1. In order to be a ring, there must be a non-empty set equipped with two binary operations, viz, + and . , satisfying the postulates mentioned above. Later on we will simply write ‘‘Let R be a ring’’. It should be borne in mind that there are two binary operations, viz, + and , on R.
2. It should also be borne in mind that the binary operations + and . May not be own usual addition and multiplication.
3. Since R is an additive Abelian group, the additive identity, denoted by 0, belongs to R. It is called the zero element of R. Here 0 is a symbol.
It should not be confused with the real number zero.
4. If a , b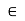 R, then – b
R, then – b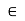 R ( R is an additive group). a+ (– b) is, generally, denoted by a – b.
R ( R is an additive group). a+ (– b) is, generally, denoted by a – b.
5. a.b is, generally, written as ab.
Commutative Ring: A ring R is said to be commutative if ab = ba, for all a, b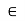 R.
R.
Ring with unity: A ring R is said to be a ring with unity (or identity) if there exists an element e 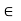 R such that
R such that
Ae = a = ea, for all a 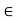 R.
R.
Note: A ring may or may not have a unity.
2. If R is a ring with unity, unity may be same as the zero element. For example, {0} is a commutative ring with unity. Here 0 is the additive as well as the multiplicative identity. It is known as the zero ring.
Theorem: If R is a ring with unity, then unity is unique.
Proof Let R be a ring with unity. If possible, let e and f be two identities of R.
Ef = e = fe [ f is unity]
f is unity]
Ef = f = fe [ e is unity]
e is unity]
 e = f
e = f
Example: Suppose
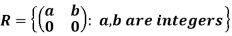
- Let
 and
and 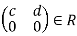
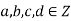
Now
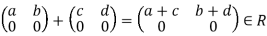
Hence Matrix addition is a binary operation on R.
2. We know that matrix addition is associative.
3. We have 
And
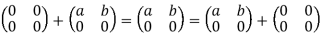
4. For every  we have
we have 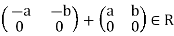 such that
such that

Such that
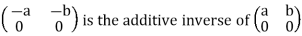
5. We know that matrix additive is commutative.
R is an Abelian group under matrix addition.
- We have

Matrix multiplication is a binary operation on R
We know that matrix multiplication is associative.
R is a semigroup under matrix multiplication.
We know that matrix multiplication is distributive over matrix addition.
The two distributive laws are satisfied.
R is a ring under matrix addition and matrix multiplication.
We have
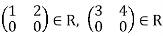
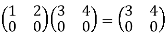
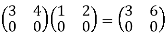
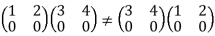
Hence R is a non- commutative ring.
Again, there does not exist any element X 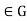 such that
such that

R is a ring without unity.
Theorem: Let R be a ring. Then
- a0 = 0a = 0; for all a
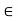 R
R - a (–b) = (–a)b = –(ab); for all a, b
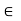 R
R - (–a) (–b) = ab; for all a , b
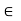 R
R - a (b – c) = ab – ac; for all a, b, c
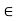 R
R
Proof
(i) we have
a0 = a (0 + 0)
= a0 + a0, by left distributive law
So that a0 + 0 = a0 + a0
0 = a0, by left cancellation law in the additive group R
i. e a0 = 0
Similarly 0a = 0
(ii) We have a0 = 0
This a ((–b) + b) = 0, [ (–b) + b = 0]
a (–b) + ab = 0, by left distributive law
a (–b) is the additive inverse of ab
i.e., a(–b) = –(ab)
Similarly (–a)b = – (ab)
(iii) We have (–a) (–b) = l (– b), taking l = –a
= – (lb), using (ii)
= – ((– a) b)
= – (– (ab)), using (ii)
= ab
(iv) a (b – c) = a (b + (–c))
= ab + a (– c), by left distributive law
= ab – ac, by (ii)
Definition: An element a ( 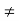 0) in a ring R is called a zero divisor if there exists an element b (
0) in a ring R is called a zero divisor if there exists an element b (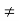 0) in R such that ab = 0 or ba = 0.
0) in R such that ab = 0 or ba = 0.
We see that the ring R of all 2 x 2 matrices over integers has zero divisors whereas the ring Z of integers has no zero divisors, for if a 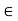 Z, b
Z, b 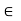 Z, a
Z, a 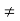 0, b
0, b 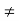 0, then ab
0, then ab 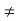 0, ba
0, ba 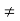 0.
0.
Cancellation Laws: Let R be a ring. The additive cancellation laws hold good in R, since R is an additive Abelian group.
So, by cancellation laws in a ring, we mean multiplication laws (cancellation of non zero elements).
The cancellation laws hold good in R if ab = ac 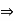 b = c, ba = ca
b = c, ba = ca 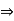 b = c; where a, b, c
b = c; where a, b, c R, a
R, a 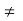 0.
0.
Theorem: The cancellation laws hold good in a ring R if and only if R has no zero divisors.
Proof:
Let the cancellation laws hold good
Let a, b 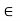 R such that ab = 0
R such that ab = 0
If a 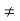 0, ab = 0 ,ab = a0
0, ab = 0 ,ab = a0 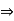 b = 0, by cancellation law.
b = 0, by cancellation law.
Similarly, if b 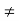 0, ab = 0
0, ab = 0 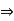 ab = 0b
ab = 0b 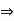 a = 0.
a = 0.
So there can be no zero divisor.
Conversely, let there be no zero divisors in R.
Let a, b, c 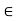 R and ab = ac, a
R and ab = ac, a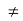 0
0
Ab – ac = 0
a (b – c) = 0
a 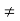 0 and R is without zero divisors
0 and R is without zero divisors
b – c = 0  b = c
b = c
Thus, if a 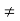 0, ab = ac
0, ab = ac 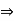 b = c
b = c
Similarly, if a 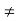 0, ba = ca
0, ba = ca 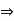 b = c
b = c
Thus, the cancellation laws hold good in R.
Definition, A commutative ring with unity e 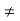 0 and containing no zero divisors is called an Integral Domain.
0 and containing no zero divisors is called an Integral Domain.
The simplest example of an integral domain in the ring Z of integers, It is a commutative ring, has unity and is without zero divisors.
Or in other words,
A commutative ring R is an integral domain if R has no zero divisors, that is, if ab = 0 implies
a = 0 or b = 0.
A commutative ring R with an identity element 1 (not equal to 0) is a field if every nonzero a ∈ R is a unit, that is, has a multiplicative inverse.
A field is necessarily an integral domain; for if ab = 0 and a 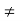 0, then
0, then
b = 1 . b = a = 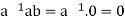
We remark that a field may also be viewed as a commutative ring in which the nonzero elements form a group under multiplication.
Note: An integral domain may be considered as a generalisation of Z.
Example:
(a) The set Z of integers with the usual operations of addition and multiplication is the classical example of an integral domain (with an identity element). The units in Z are only 1 and −1, that is, no other element in Z has a multiplicative inverse.
(b) The rational numbers Q and the real numbers R each form a field with respect to the usual operations of addition and multiplication.
(c) Let M denote the set of 2×2 matrices with integer or real entries. ThenM is a noncommutative ring with zero divisors under the operations of matrix addition and matrix multiplication. M does have an identity element, the identity matrix.
(d) Let R be any ring. Then the set R[x] of all polynomials over R is a ring with respect to the usual operations of addition and multiplication of polynomials. Moreover, if R is an integral domain then R[x] is also an integral domain.
Divisibility in Integral Domains:
Now let D be an integral domain. We say that b divides a in D if a = bc for some c ∈ D. An element u ∈ D is called a unit if u divides 1, i.e., if u has a multiplicative inverse. An element b ∈ D is called an associate of a ∈ D if b = ua for some unit u ∈ D. A non unit p ∈ D is said to be irreducible if p = ab implies a or b is a unit. An integral domain D is called a unique factorization domain (UFD), if every non unit a ∈ D can be written uniquely (up to associates and order) as a product of irreducible elements.
References:
1. “Discrete Mathematics and its Applications” by Kenneth H Rosen
2. “Discrete Mathematics” by Norman L Biggs
3. “Discrete Mathematics for Computer Science” by Kenneth Bogart and Robert L Drysdale