Unit - 4
Graph theory
Overview:
Graph theory is intimately related to many branches of mathematics. It is widely applied in subjects like, Computer Technology, Communication Science, Electrical Engineering, Physics, Architecture, Operations Research, Economics, Sociology, Genetics, etc. In the earlier stages it was called slum Topology. It also has uses in social sciences, chemical sciences, information retrieval systems, linguistics even in economics also.
Graphs are discrete structures consisting of vertices and edges that connects these vertices. There are several different types of graphs that differ with respect to the kind and number of edges that can a connect a pair of vertices. Problems in almost every conceivable discipline can be solved using graph models.
Basic terminology-
Graph theory is a relatively new area of mathematics
Graph is the form of representing of descriptive data in the terms of verticals and edges.
Graph theory is used in various fields like computer science, information technology, genetics, telecommunication etc.
A graph is a collection of vertices and edges in which each edge is assigned to pair of points called terminal.
We can say that a graph is a network of dots connected by lines.
Mathematically we can define a graph as-
A graph is a pair of set (V, E) where-
1. V is a non-empty set whose elements are called vertices.
2. E is collection of two-element subset of V called edges.
Terminology: A graph G is an ordered pair (V, E) where V is a non-empty set and E is the set of edges in which each element of E is assigned to a unique unordered pair of elements of V.
An element of a set E is generally denoted as- e = (v,u) where u, v ∈ V.
U and v are called the end vertices of edge e.
Note- In any graph the number of vertices with odd degree must be even.
Loop: If both the end vertices of an edge are same then the edge is called a loop.
Parallel edge: If two or more edges have same terminal vertices, then these edges are called parallel edges.
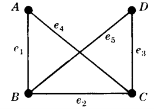
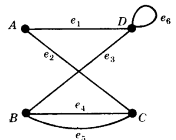
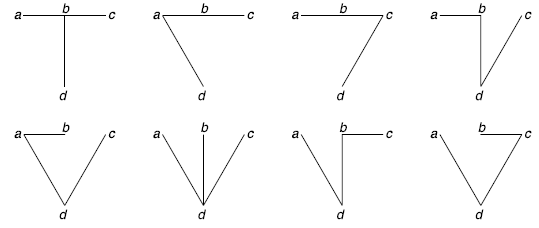
Example: Consider the graphs given below-
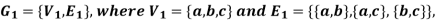
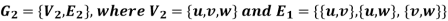
Check whether these graphs are same or not?
Sol.
As we can see that these graphs are not same because here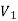 
and 
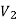are not same since 
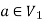but a does not belongs to 
.
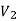These two graphs look same but not equal.
We can draw these graphs as below-
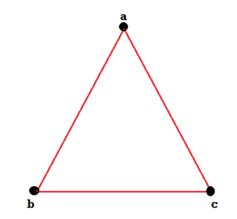
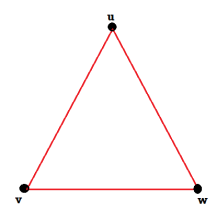
These types of graphs are known as isomorphic graph when they are same except for the name of vertices.
Simple graph: A graph which has no loops and parallel edges is known as simple graph.
Compound graph: A graph which contains loops or parallel edges is called compound or multi-graph.
Degree of vertex: The number of edges incident on a vertex v is called degree of vertex v, with loop being counted twice.
We can denote it as-
Degree of v = d(v)
Examples of graph and multi-graph are-
Graph-
Multi-graph-
Weighted Graphs
A graph G is said to be a weighted graph if each edge e of G is assigned a non-negative number w(e) called the weight of v.
The weighted graph is given below-
Sub Graphs-
We can say that 
is a sub-graph of G = (V, E), and write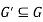 
provided 
.
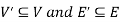We can say that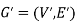 
is an induced sub-graph of G = (V, E), provided 
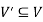and every edge in E whose vertices are still in 
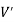is also an edge in 
.
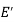Isomorphic graphs-
Let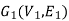 
and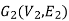 
be two graphs. The graph 
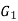and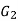 
are said to be isomorphic if there is a bijective function 
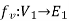such that if u and v are end vertices of some edge e ∈ 
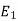then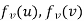 
end vertices of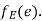 
Complete Graphs-
A simple graph G is called a complete graph, if there is an edge between each pair of vertices.
Regular Graphs-
If all vertices of a graph G have same degree, then G is called as a regular graph.
Bipartite Graphs-
A graph G(V, E) is said to be bipartite, if the vertex set V can be partitioned in to two non-empty disjoint subset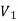 
and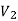 
such that each edge is G had end vertex is 
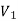and other end vertex in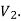 
There is no edge between two vertices of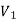 
as well as there is no edge between two vertices of 
.
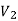Here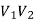 
bipartition of V.
Applications of graph theory-
Applications in computer Science
In computer science graph theory is used for the study of algorithms like:
Dijkstra's Algorithm
Prims's Algorithm
Kruskal's Algorithm
1. Graphs are used to define the flow of computation.
2. Graphs are used to represent networks of communication.
3. Graphs are used to represent data organization.
4. Graph transformation systems work on rule-based in-memory manipulation of graphs. Graph databases ensure transaction-safe, persistent storing and querying of graph structured data.
5. Graph theory is used to find shortest path in road or a network.
6. In Google Maps, various locations are represented as vertices or nodes and the roads are represented as edges and graph theory is used to find the shortest path between two nodes.
We can represent a graph in matrix form in two ways-
1. Adjacent matrix
2. Incidence matrix
Adjacency matrix of a non-directed graph-
Let G be a graph with n vertices and no parallel edges. The adjacency matrix of G in a n × n. Symmetric binary matrix A (G)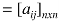 
Where
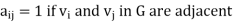
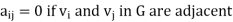
Where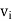 
and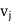 
are vertices of G.
The following is a example of the adjacency matrix of the simple graph G.
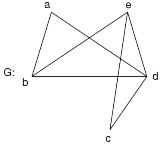
Adjacency matrix x; A (G)-
Adjacency matrix of a Digraph-
Let G be a digraph with n vertices, containing non-parallel edges. The adjacency matrix A(G) of the digraph G is an n × n matrix defined by
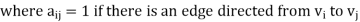
= 0 otherwise
Example: Find the adjacency matrix of the graph-
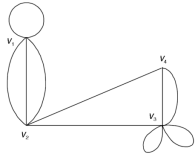
Sol. The adjacency matrix of the above graph will be-
Incidence matrix of a non-directed graph-
Let G be a graph with n vertices and m edges. The incidence matrix denoted by X (G) is defined as the matrix X (G) is defined as the matrix
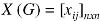
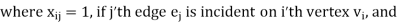
= 0, otherwise
X (G) is an n by m matrix whose n rows correspond to the n vertices, and mcolumns correspond to m edges.
Graph and its incidence matrix-
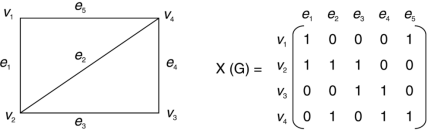
Sub-graphs:
Def:
Let G and H be two graphs. H is called a subgraph of G if V (H) is a subset of V (G)
And E (H) is a subset of E (G).
If H is a subgraph of G then
(i) All the vertices of H are in G.
(ii) All the edges of H are in G.
(iii) Each edge of H has the same end points in H as in G.
For example:
In Fig. Given below H is a subgraph of G.
Isomorphism of graphs: Two graphs are said to be isomorphic it they have identical behaviour in terms of graph-theoretic properties. More precisely:
Let G1 (V1, E1) and G2 (V2, E2) be two simple undirected graphs. A function f: V1 
V2 is called a graph isomorphism if i) f is one-one and onto, i.e there exists a one-to-one correspondence between their vertices as well as edges (both the graphs have equal number of vertices and edges, however, vertices may have different levels.)
Ii) for all u,vV1, {u,v} E1 if and only if {f(u), f(v)} E2
If such a function exists, then the graphs G1 and G2 are called isomorphic graphs.
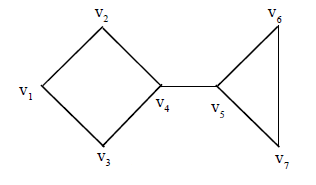
Example: Verify that the graphs given below are isomorphic.
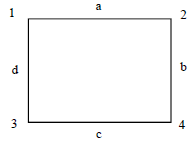
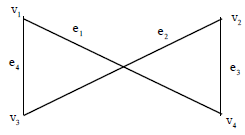
Sol:
The correspondance between the two graphs is as follows : The vertices 1, 2, 3 and 4 in G is corresponds to v1, v4, v3 and v2 respectively in
H. The edges a, b, c, d in G corresponds to e1, e3, e2, e4 respectively.
Note: i) Two isomorphic graphs have equal number of vertices and edges.
Ii) Two isomorphic graphs have equal number of vertices with same degree.
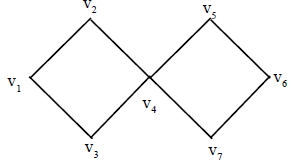
Example: Show that the graph displayed below are not isomorphic.
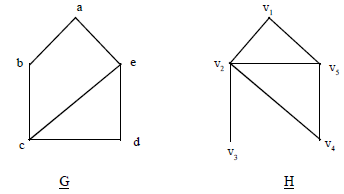
Sol:
The graph G and H both have five vertices and six edges. However the graph H has a vertex of degree one namely v3. Where as G has no vertices of egree one. Hence G and H are not isomorphic.
Example: Show that the simple graphs with the following adjacency matrices are isomorphic.
Sol:
Since the given adjacency matrices are of order three each, so its graph has three vertices namely v1, v2, v3 and u1, u2, u3 respectively.
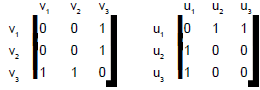
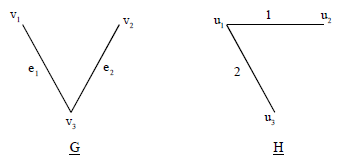
There is a one-to-one correspondence between the vertices and edges of the graph G and H. Both the graph has there vertices and 3 edges each. Two vertices of the graph G has degree one and one vertex has degree two. Again two vertices of the graph H has degree one and one vertex has degree two. The vertices v1, v2 and v3 in G corresponds to u2, u3 and u1 in H respectively. The edges e1 and e2 in G corresponds to 1 and 2 in H respectively.
Hence both the graphs are isomorphic.
Connectivity of a graph:
Walk: A walk is defined as a finite alternating sequence of vertices and edges, beginning and ending with vertices, such that each edge is incident with the vertices preceding and following it. Let u, v be any two vertices in an undirected graph G. Then a walk u-v in G is finite alternating sequence u-v1 e1 v2 e2 ... ... ... En vn = V of vertices and edges. Vertices with which a walk begins and ends are called terminal vertices.
Open and closed walk: A walk is said to be closed walk if it is possible that a walk begins and end at the same vertex.
A walk that is not closed is called an open walk.
Path: An open walk in which no vertex appears more than once is called a path. The number of edges in a path is called the length of the path.
An edge which is not a loop is s path of length one. A loop can be included in a walk but not in a path.
Circuits: A circuit is a closed walk of non-zero length that contains no repeated edges except the initial and end vertex where initial and end vertex. That is, a circuit is a closed, nontersecting walk. A circuit is also called elementary cycle, circular path and polygon.
In figure above, examples of walk, path and circuits are given bellow.
Walk: v1 e1 v2 e2 v3 e3 v3 e4 v4 etc
Path: v1 e1 v2 e2 v3 e4 v4 etc
Circuit: v2 e1 v3 e4 v9 e5 v5 e6 v2 etc
Connected graphs: A graph is said to be connected if we can reach any vertex from any other vertex by traveling along the edges. More formally: A graph is said to be connected if there exists at least one path between every pair of its vertices, otherwise, the graph is disconnected.
That is a graph G is connected if give any vertices u and v, it is possible to travel from u to v along a sequence of adjacent edges fig. Given above is connected
Graph but in fig. Above is a disconnected graph.
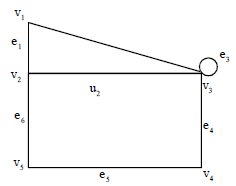
Cut points and Bridges: Vertex v in a connected graph G is called a cutpoint if G-v is disconnected, where G-v is the graph obtained from G by deleting the vertex v and all the edges connecting v. In fig., vertex v4 is the cutpoint
An edge e of a connected graph G is called a bridge or cut edge if Ge is disconnected. In fig. Below, the edge (v4, v5) is a bridge.
Paths-
Let G be a non-directed graph. A sequence P of zero or more edges of the form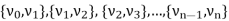 
, where 
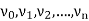are the vertices of G is called a path in G.
We denote this by P
The vertex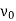 
is called the initial vertex and the vertex 
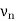is called the terminal vertex of the path P.
Note-
1. If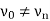
then the path P is called an open path and if 
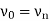then the path is called closed path.
2. If all the edges and vertices in a path P are distinct except possibly the end points then the path P is called a simple path.
Connectivity of a graph:
Edge connectivity: Each cut-set of a connected graph G consists of a certain number of edges. The number of edges in the smallest cut-set
(i,e cut-set with fewest number of edges) is defined as the edge connectivity
Of G.
Equivalently the edge connectivity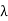 
(G) of a connected graph can be defined as the minimum number of edges whose removal reduces the graph disconnected. If G is a tree, then 
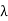(G) = 1, became removel of any one edges reduces the the tree disconnected.
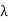(G) = 2
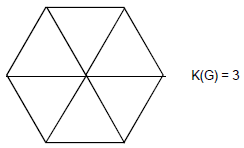
Vertex connectivity: The vertex connectivity K(G) of a connected graph G is defined as the minimum number of vertices whose removal from G leaves the graph disconnected. If G is a tree then K(G) = 1
EULERIAN AND HAMILTONIAN GRAPH:
Eulerian graph:
A undirected graph with no isolated vertices is said to have an Euler circuit if there is a circuit in G that traverses every edge of the graph exactly once. If there is an open trail from vertex u to v in G and this trail traverses each edge in G exactly once, the trail is called Euler trail. [A trail from a vertex u to v is a path that doesnot involve a repeated edge] An Eulerian tour is a closed walk that starts at some vertex, passes through each edge exactly once and returns to the starting vertex.
Since any closed walk in an undirected graph enters and leaves any vertex the same number of times, the subgraph composed of the edges in any closed walk is even. Thus, if the graph contains a closed walk passing through each edge exactly once, the graph must be even, conversely, if the graph is even, then it contains an Euler tour, A path that passes through each edge exactly once but vertices may be repeated is called Euler path. A graph that contains an Euler tour or Euler circuit is called an Eulerian graph.
Note: i) If a graph G has a vertex of odd degree, then there can be no Euler circuit in G.
Ii) if a graph G is connected and each vertex has even degree, then there is an Euler circuit.
For example the graph in fig below in an Eulerian graph because all the vertices are of even degree, so it has an Eulerian circuit
v1
v2
v3
v5
v4
v3
v1
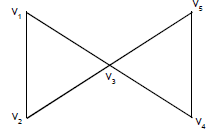
But the graph G in fig. Given below is not a Eulerian graph because all the vertices of G are not even degrees, so there does not have any Euler circuit.
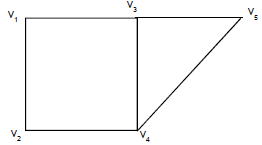
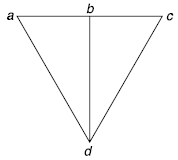
Hamiltonian graph: Let G be a connected graph with more than two vertices. If there is a path in G that uses each vertex of the graph exactly once, then such a path is called Hamiltonian path. If the path is a circuit that contains each vertex in G exactly once, except the initial vertex, then such a path is called a Hamiltonian circuit.
A graph that contains a Hamiltonian circuit is called a Hamiltonian graph.
Note: i) The complete bipartite graph km,n is Hamiltonian if m = n and m>1.
Ii) Eulerian circuit uses every edge exactly once but many repeat vertices, while Hamiltonian circuit uses each vertex exactly once except for the first and last vertex.
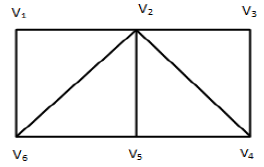
Example: Draw three graph which are
i) Hamiltonian but not a Eulerian
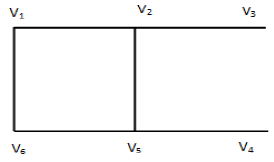
Ii) Neither Eulerian nor Hamiltonian
- Hamiltonian but not a Eulerian
2. Neither Eulerian nor Hamiltonian
The concept of a tree is important for these interested in applications of graphs. The important applications of trees include searching, sorting, syntax checking and database management. The tree is one of the most non-linear structures used for algorithm development in computer science. In this section, we shall define a tree and study its properties.
Definition of a tree- A tree is a connected graph without any circuits.
A graph is acyclic, if it has no cycles.
A tree is a connected acyclic graph. i, e a tree is a simple graph having neither a self-loop nor parallel edges. Trees with three, four and five vertices are given in fig.
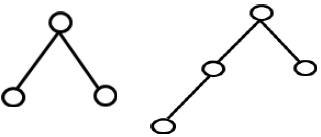
Some properties of trees:
Theorem: Prove that a graph G is a tree iff every pair of vertices is connected by a unique path.
Proof: First suppose that the graph G is a tree. So, G is a connected graph without any circuits. Since G is connected then there must exist at least one path between every pair of vertices in G. Now suppose that between two vertices u and v in G, there are two distinct path. The union of these two paths will contain a circuit and G cannot be a tree, which is a contradiction.
Hence in a tree every pair of vertices are connected by a unique path.
Conversely, suppose wehave a graph G, in which every pair of vertices are connected by a unique path, so G is connected. We need to show that G has no cycles. But if there is a cycle in G, then there are two paths between any two vertices on the cycle. Which is contradiction that there must be a unique path between any two vetices of G. Hence G can not contain any cycle. So G is a tree.
Theorem: Prove that a tree with n-vertices has n–1 edges.
Proof: We prove that theorem by induction on n vertices.
Base case: Let n = 1, then this is the trival tree with o edges. So the theorem is true for n = 1.
Inductive case:
Let us assume that the theorem holds for all trees with fewer than n vertices.
Let us consider a tree T with n vertices. Let e be an edge with end vertices u and v. Since T is a tree, so there is no other path between u and v except e then T-e is disconnected and has two components T1 and T2 has fewer than n vertices say n1 and n2 respectively and therefore by the induction by pthesis T1 has (n1–1) edges and t2 has (n2–1) edges. Number of edges in T = number of edges in T1+ number of edges in t2 + 1
= (n1–1) + (n2–1) + 1
= n1 + n2–1
= n1
Hence a tree with n vertices has n–1 edges.
Theorem: Prove that, in any tree with two or more vertices there are at least two pendant vertices.
Proof: Let T be a tree with n vertices, then T has n–1 edges,
Again, we know that,
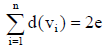
Where e is the number of edges in T
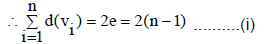
Since no vertex of T can be of zero degree. So, from (1), we must have at least two vertices of degree one in T. It means taht in any tree with two or more vertices there are at least two pendant vertices.
Distance and centres in a tree: In a connected graph G, the distance d(u,v) between two of its vertices u and v is the length of the shortest path. i,e the number of edges in the shortest path between them. It is very easier to determine the distance between any two vertices of a tree because, there is exactly one path between any two vertices of the tree.
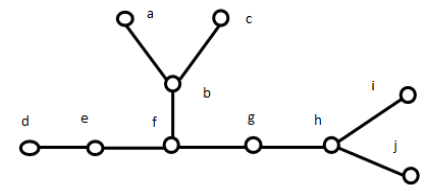
The graph in fig., d (a, b) = 1, d (a, d) = 4, d(b, h) = 3, d (a, j) = 5 and so on.
The eccentricity E (v) of a vertex v in a, graph G is the distance from
v to the vertex farthest from v in G, i.e E(v) = max {d(u,v) : uv}
The graph in fig. E(a) = 5, E(b) = 4, E(f) = 3, E(g) = 3, E(h) = 4 and so one.
A vertex with minimum eccentricity in a graph G is called the centre of G.
The diameter of a tree is the maximum distance between any two vertices of the tree.
Example: Find the eccentricities of all the vertices centers and diameter of the tree in the following fig.
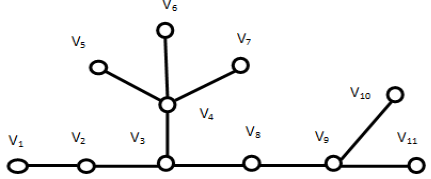
Sol:
E(v1) = 5 E(v2) = 4 E(v3) = 3 E(v4) = 4
E(v5) = 5 E(v6) = 5 E(v7) = 5 E(v8) = 3
E(v9) = 4 E(v10) = 5 E(v11) = 5
V3 is the center, diameter = 5
Theorem: Prove that every tree has either one or two centres.
Proof: The maximum distance, max d(u,v) from a given vertex v to any other vertex u occurs only when u is a is a pendant vertex. Now consider a tree T having more that n two vertices. We know that a tree must have two or more pendant vertices. Deleting all pendan vertices from T. The resulting graph T' is still a tree, decreases the eccentricities of the remaining vertices by one. Therefore, all vertices that T had as centres will still remain centers in T'. From T' we can again remove all pendant vertices and get another tree T". We continue this process until there is left either a vertex which id the confer of T or an edge whose end vertices are the two centers of T.
Rooted trees: A Tree in which one vertex, called the root of the tree is distinguished from all the others is called a rooted tree. Fig.11.34 is an example of a rooted tree where vertex v1 is the root of the tree that appears on the top of the tree. A rooted tree grows downwards i.e to form a rooted tree, we first place the root at the tree. Under the root and on the same level, we place the vestices that can be reached from the root on the same path of length one. Under each of these vertices and on the same level, we place the vertices that can be reached from the root a path of length two and so one.
Level of a vertex: The level of a vertex is the number of edges along the unique path between it and the root. The level of the root is defined as zero. The vertices immediately under the root are said to be in level one and so on.
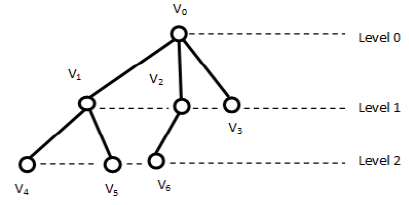
Height of the tree: The height of a tree is the maximum level of any vertex in the tree. This equals to the length of the longest path from the root of any pendent vertices. The depth of a vertex v in a tree is the length of the path from the root. The height of the tree in fig. Is 2 and depth of the vertex v3 is one.
Children, parent and siblings: The edges in a rooted tree is defined as predecessor-successor or parent-child relationship. In fig. Vertex v0 is the predecessor of vertices v1, v2 and v3. These vertices are called level 1 vertices, while v0 is said to at level 0. Here, v0 is called the parent of level 1 vertices. The vertices v1, v2 and v3 are called children of the vertex v0. Similarly v4 vs are children of v1 and v1is the parent of the vertex v4 and v5. The vertices having the same parent are called siblings of each other.
Binary tree: A binary tree is a rooted tree in which each vertex has at most two children (vertices), Each child is designated either as left child or as a right child and am internal vertex has atmost one left and one right child. A binary tree on also defined as a tree in which there exactly one vertex of degree two and each of the remaining vertices is of degree one or three.
Theorem: Prove that the number of vertices n in a binary tree is odd.
Proof: In a binary tree there is exactly one vertex of degree 2 i,e even and the remaining n–1 vertices are of odd degrees. Again, we know that, in a graph, the number of vertices of odd degree is even, So (n–1) is even, Hence n is odd.
Theorem: Prove that if T is a binary tree with n vertices and p be the number of pendant vertices then 2p = n + 1
Proof: Since P be the number of pendant vertices, of a binary tree with n vertices. Then n–p–1 is the number of degree three. (1 is corresponds to the root of the tree whose degree is two), Therefore, the total number of edges in T equals
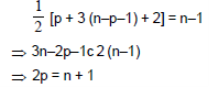
Remark: i) The minimum possible height of an n-vertex binary tree is [log2 (n +1)–1], where [n] denotes the smallest integer greater than or equal to n.
Ii) the maximum height of a binary tree of n vertices is- (n-1)/2
Example: Find the maximum and minimum height of a binary tree of 13 vertices.
Solution: The maximum height of abinary tree of 13 vertices-
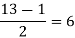
Again, the minimum height of the binary tree of 13 vertices
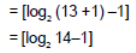
Spanning tree:
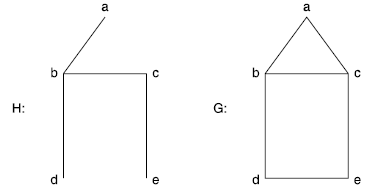
Let G be a connected graph. The sub-graph H of G is called a spanning tree of G if
(i) H is a tree and (ii) H contains all the vertices of G.
Example: In the Fig. Below H is spanning tree of G.
Sol:
Example: Find all the spanning trees of the graph G shown in the Fig.-
Solution: The spanning trees of G are given below
Theorem: A non-directed graph G is connected if and only f G contains a spanning tree.
Proof: Let T be a spanning tree of G. There exists a path between any pair of vertices in G along the tree T. G is connected.
Conversely let G be a connected graph and K be the number of cycles in G. If K = 0, then G has no cycles and G is connected. Therefore G is a tree when K = 0.
Let us suppose that all connected graphs with fewer than K cycles have a spanning tree. Let G be a connected graph with n cycles. Let e be an edges in one of the cycle. G – e is a connected graph and
G – e contains all the vertices of G.
∴ The spanning tree if G – e is also spanning tree for G.
Hence by mathematical induction the result holds for all connected graphs.
If G is a connected graph and T is a spanning tree of G. Edges of G present in T are called the branches of G with respect to Tj and the edges of G which do not belong to T are called the chords of G with respect to T. If G has n vertices and e edges then, the number of branches with respect to the spanning tree T of G is n – 1 and the number of chords is e – n + 1.
The number of branches in a connected graph G is called the rank of G and the number of chords is called the nullity of G. If G has k components then the rank of G is defined as the sum of ranks of the components; i.e.,
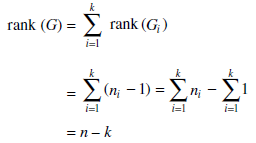
Where Gi, i = 1, 2, ..., K are K components of G. And nullity of
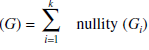
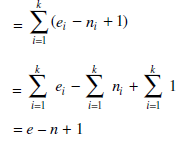
Minimal spanning tree: Definition: Let G be a connected weighted graph. A minimal spanning tree of G is a spanning tree of G whose total weight is as small as possible.
There are various methods to find a minimal spanning tree in connected weighted graph. Here we consider algorithms for generating such a minimal spanning tree.
Algorithm: A connected weighted graph with n vertices.
Step 1: Arrange the edges of G in the order of decreasing weights.
Step 2: Proceed sequentially, and delete each edge of G, that does not disconnect the graph G until n – 1 edges remain.
Step 3: Exit.
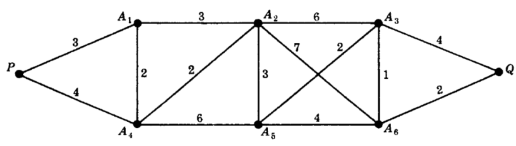
Example: Consider the graph G given below:
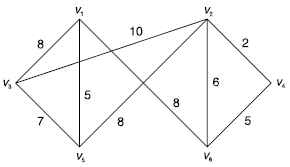
Number of vertices in G = n = 6.
We apply the algorithm given above.
We order the edged by decreasing weights and delete the edges of G until n – 1 = 6 – 1 = 5 edges
Remain.
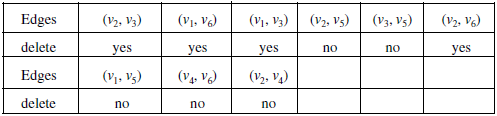
The minimal spanning tree of G is shown below:
The weight of the minimum spanning tree = 8 + 7 + 5 + 5 + 2 = 27.
Kruskal’s algorithm:
Input: A connected weighted graph G with n vertices.
Step 1: Arrange the edges of in order of increasing weights and select the edge with minimum weight.
Step 2: Proceed sequentially, add each edge which does not result in a cycle until n – 1, edges are selected.
Step 3: Exit.
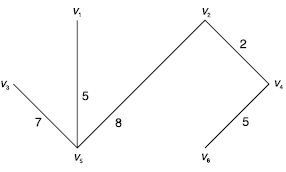
Example: Consider the graph in fig below:
We have n = 6
We order the edges by increasing weights (v2, v4) is edge with minimum weight. Select the edge
(v2, v4) we successively add edges to (v2, v4), without forming cycles until 6 – 1 = 5 edges are selected.
This yields-
Edges in the minimum spanning tree are
(v2, v4), (v1, v5), (v4, v6), (v3, v5), (v1, v6).
The resulting minimal (optimal) spanning tree is shown in Fig. Below
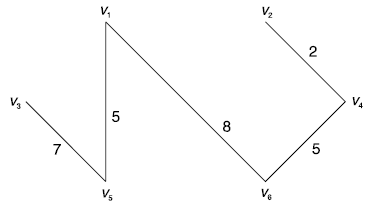
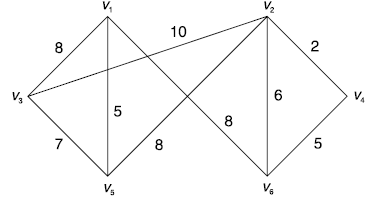
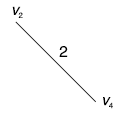
We apply the steps of Kruskal’s algorithm to the graph of Fig.(in question); as follows:
(v2, v4) is the edge with minimum weight, therefore we select the edge (v2, v4).
The next edge with minimum weight is (v1, v5), selection of (v1, v5) does not result in a cycle.
∴ edge (v1, v5) is selected.
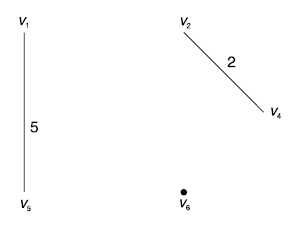
The edge to be considered, next is (v4, v6).
The next edge to be selected is (v4, v6).
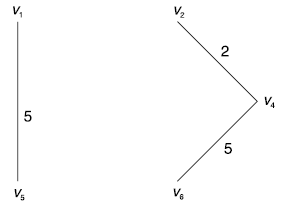
Selection of the edge (v2, v6) for the spanning tree results in a cycle. Therefore (v2, v6) is not selected we consider the edge (v3, v5) selection of edge (v3, v5) does not result in a cycle. Hence (v3, c5) is selected.
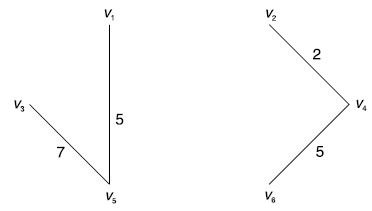
Next we consider the edge (v1, v3) from the list. Selection of the edge (v1, v3) results in a cycle.
Therefore edge (v1, v3) is not selected. Consider the edge (v1, v6) selection of edge (v1, v6) does not result in a cycle. Hence (v1, v6) is selected.
Number of edges selected is 5. We stop, and obtain the spanning trees as shown in Fig. Below
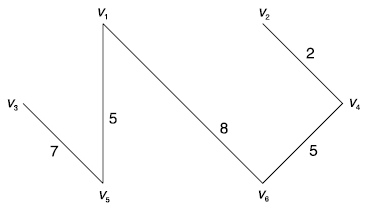
The weight of the minimal spanning tree.
= 2 + 5 + 5 + 7 + 8
= 27
Prim’s algorithm:
Input: A connected weighted graph G with n vertices.
Step 1: Select an arbitrary vertex v1 and an edge e1 with minimum weight incident with vertex v1.
Step 2: Having selected the vertices v1, v2, ..., vi and e1, e2, ..., ei – 1; select an edge ei such that ei connects a vertex of the set (v1, v2, ..., vi) and a vertex of V = (v1, v2, ..., vi) and of all such edges ei has the minimum weight.
Step 3: Stop if n – 1, edges are selected, else go to step 2.
Example: Consider the graph shown in Fig
Let
e1 = (v1, v2), e2 = (v2, v3)
e3 = (v3, v4), e4 = (v4, v1)
e5 = (v2, v5) and e6 = (v4, v6).
Denote the edge of G.
We apply Prims algorithm to the graph as follows:
The edge e3 = (v3, v4) is an edge with minimum weight. Hence, we start with the vertex v3 and select the edge e3 incident with v3.
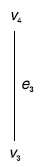
We next consider the edges connecting a vertex {v3, v4} with the vertex of the set V – {v3, v4}. We
Observe that e6 the edge with minimum weight.
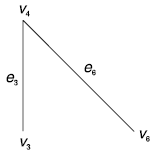
Consider the edges connecting the vertices of the set {v3, v4, v6} with the vertices of
V – {v3, v4, v6}. The edge e2 has the minimum weight. The edge e2 is selected.
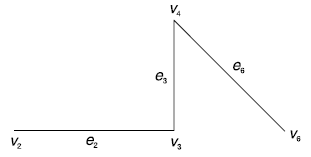
Of the connecting the vertices of {v2, v3, v4, v6}; with the vertex set V – {v2, v3, v4, v6}, e4 has minimum weight, therefore e4 is selected.
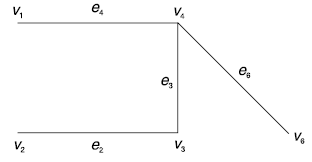
e1, e5 are the edges remaining. e5 is the only edge connecting {v1, v2, v3, v4, v5, v6} and {v5} such that the inclusion of e5 does not result in a cycle. Hence e5 is selected.
Since number of edges selected is 5 we stop.
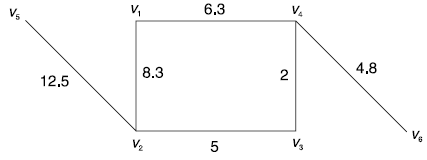
The minimal spanning tree obtained is shown in Fig. Below
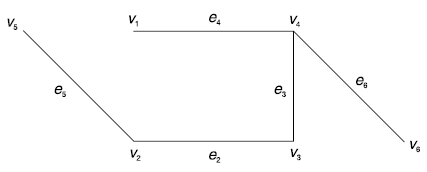
Weight of the minimal spanning tree
= 2 + 4.8 + 5 + 6.3 + 12.5
= 30.6
Binary tree:
A binary tree T is defined as a finite set of elements, called nodes, such that:
(1) T is empty (called the null tree or empty tree), or
(2) T contains a distinguished node R, called the root of T , and the remaining nodes of T form an
Ordered pair of disjoint binary trees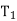 
and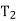 
.
If T does contain a root R, then the two trees T1 and T2 are called, respectively, the left and right subtrees of R.
If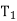 
is nonempty, then its root is called the left successor of R; similarly, if 
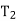is nonempty, then its root is called
The right successor of R.
The above definition of a binary tree T is recursive since T is defined in terms of the binary subtrees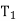 
and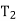 
.
This means, in particular, that every node N of T contains a left and a right subtree, and either subtree or both
Subtrees may be empty. Thus every node N in T has 0, 1, or 2 successors. A node with no successors is called a
Terminal node. Thus both subtrees of a terminal node are empty.
Algebraic Expressions and Polish Notation:
Let E be any algebraic expression which uses only binary operations, such as,
E = (a − b)/((c × d) + e)
Then E can be represented by a 2-tree as in fig below where the variables in E appear as the external nodes, and the operations in E appear as internal nodes.
The Polish mathematician Lukasiewicz observed that by placing the binary operation symbol before its arguments, e.g.,
+ab instead of a + b and /cd instead of c/d
One does not need to use any parentheses. This notation is called Polish notation in prefix form. (Analogously, one can place the symbol after its arguments, called Polish notation in postfix form.) Rewriting E in prefix form we obtain:
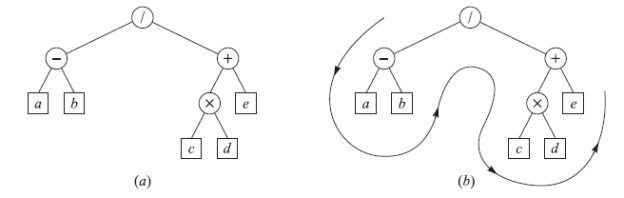
E = / − a b+×c d e
Observe that this is precisely the lexicographic order of the vertices in its 2-tree which can be obtained by scanning the tree as in Fig.
References:
1. “Discrete Mathematics and its Applications” by Kenneth H Rosen
2. “Discrete Mathematics” by Norman L Biggs
3. “Discrete Mathematics for Computer Science” by Kenneth Bogart and Robert L Drysdale
