Unit - 5
Combinatorics
Permutations-
A permutation of n objects taken r at a time is an arrangement of r of the objects
(r≤n).
The symbols of permutations of n things taken r at a time are- 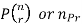
Example 1: Consider the three letters x, y, z. The arrangements of the letter x, y, ztaken two at a time are-
Xy, yx, xz, zx, yz, zy
∴The number of 2-arrangements are 6 i.e., the number of permutation of 3 letters taken 2 at a time
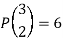
Note-A permutation of n objects taken r at a time is also called r-permutation
Factorial function-
The product of the positive integers from 1 to n is deoted by n!and we read it as “factorial “
Expressed as-
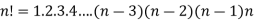
Note- 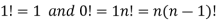
Binomial coefficient-
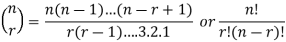
Example:
1. 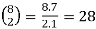
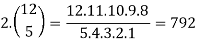
Permutation-
The arrangement of a set of n objects in a given order is called a permutation.
Any arrangement of any 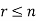 of these objects in a given order is said to be r-permutation.
of these objects in a given order is said to be r-permutation.
The number of permutations of n objects taken r will be denoted as-
P(n, r)
Formula- 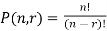
Permutation with repetitions-
The number of permutations of n objects of which are 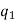 are alike,
are alike, 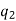 are alike,
are alike, 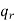
Are alike is-
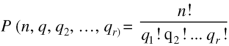
Sampling with or without replacement-
Suppose we chose the samples with repetition, fro example if we draw a ball from a urn then we put back that ball in the urn and again we pick a ball and we continue the process, so this is the case of sampling with repetition
Then the product rule tells us that the number of such samples is-
n.n.n.n.n……….n.n = 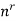
And if we pick a ball from the urn and we do not put it back to the urn, then this is the case of sampling without replacement.
So that in this case the number of samples are given as-
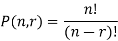
Example-
Three cards are chosen one after the other from a 52-card deck. Find the number m of ways
This can be done: (a) with replacement; (b) without replacement.
Sol.
(a) Each card can be chosen in 52 ways. Thus m = 52(52)(52) = 140 608.
(b) Here there is no replacement. Thus the first card can be chosen in 52 ways, the second in 51 ways, and the third in 50 ways. So that-
P(52, 3) = 52(51)(50) = 132 600
Example-
There are 4 black, 3 green and 5 red balls. In how many ways can they be arranged in a row?
Solution: Total number of balls = 4 black + 3 green + 5 red = 12
The black balls are alike,
The green balls are, and the red balls are alike,
The number of ways in which the balls can be arranged in a row =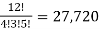
Example- A box contains 10 light bulbs. Find the number n of ordered samples of:
(a) Size 3 with replacement,
(b) Size 3 without replacement.
Solution:
(a) n= 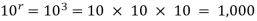
(b) P (10, 3) = 10 × 9 × 8 = 720
Circular permutations-
A circular permutation of n objects is an arrangement of the objects around a circle.
If the n objects are to be arranged round a circle we take an objects and fix it in one position.
Now the remaining (n – 1) objects can be arranged to fill the (n – 1) positions the circle in (n – 1)! ways.
Hence the number of circular permutations of n different objects = (n – 1)!
Combinations-
A combination of n objects taken at a time is an unordered selection of r of the n
Objects (r ≤n).
A combination of n objects taken r at a time is also called r-combination of n objects.
The number of combinations is given by-
C(n, r)
Note-
1. Property-1
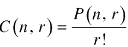
2. Property-2
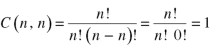
3. Property-3
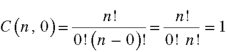
Generalized permutations and combinations
Generalized sum rule-
If we have tasks 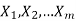 that can be done in
that can be done in 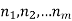 ways respectively, and no two of these tasks can be done at the same time then there are
ways respectively, and no two of these tasks can be done at the same time then there are 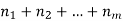 ways to do one of these task.
ways to do one of these task.
Generalized product rule-
If we have sequential task 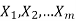 that can be done in
that can be done in 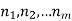 , then there are
, then there are 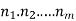 to do the procedure.
to do the procedure.
Permutation and combination with unlimited repetitions-
Suppose U (n, r) denotes r-permutations of n-objects with unlimited repetitions and v (r, n) denotes the r-combination with unlimited repetitions, then-
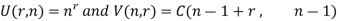
Let us consider a set 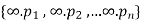 where
where 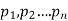 are all distinct.
are all distinct.
Any r-combination is of the form 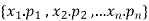 here each
here each 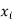 is a non-negative integer and
is a non-negative integer and 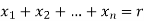
The numbers 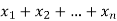 are called repetition numbers. Conversely any sequence of non-negative integers-
are called repetition numbers. Conversely any sequence of non-negative integers-
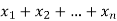
Corresponds to a r-combination 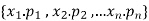 .
.
The following observation we get-
The number of r-combination of 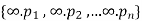
= the number of non-negative integer solution of 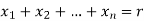
= the number of ways of placing r indistinguishable balls in n numbered boxes.
= the number of binary numbers with n – 1 one’s and zeros.
= C (n – 1 + r, r)
= C (n – 1 + r, n - 1)
Example: Find the number of non-negative integral solutions to 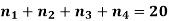
Sol: We have n = 4, r = 20
The number of non-negative integral solutions
= C (4 – 1 + 20, 20)
= C (23, 20)
= 1,771
Example-Find the number of ways of placing 8 similar balls in 5 numbered boxes.
Solution:
The number of ways of placing similar balls in 5 numbered boxes is
= C (5 – 1 + 8, 8)
= C (12, 8) = 495
Example-How many outcomes are possible by costing a 6 faced die 10 times?
Solution:
This is same as placing 10 similar balls into 6 numbered boxes.
There are C (6 – 1 + 10, 10)
= C (15, 10) possible outcomes.
Pigeonhole principle (statement)-
If n pigeonholes are occupied by n + 1 or more pigeons, then at least one pigeonhole is occupied by more than one pigeon.
This principle can be applied to many problems where we want to show that a given situation can occur.
Example-1: Suppose a class contains 13 students, then two of the students (pigeons) were born in the same months (pigeonholes)
Example-2: Suppose a department contains 13 professors, then two of the professors (pigeons) were born in the same month (pigeonholes).
Example-3: Find the minimum number of elements that one needs to take from the set S = {1, 2, 3, . . . , 9} to be sure that two of the numbers add up to 10.
Here the pigeonholes are the five sets {1, 9}, {2, 8}, {3, 7}, {4, 6}, {5}. Thus any choice of six elements (pigeons) of S will guarantee that two of the numbers add up to ten.
Example-4: Show that if seven numbers from 1 to 12 are chosen, then two of them will add up to 13.
Sol.
First we will construct six different sets, each containing two numbers that add up to 13 as follows-
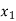 = {1, 12},
= {1, 12}, 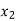 = {2, 11},
= {2, 11}, 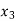 = {3, 10},
= {3, 10}, 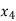 = {4, 9},
= {4, 9}, 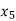 = {5, 8},
= {5, 8}, 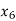 = {6, 7}.
= {6, 7}.
Each of the seven numbers belong to one of these six sets.
Since there are six sets, then according to the pigeonhole principle that two of the numbers chosen belong to the same set. These numbers add upto 13.
Generalized pigeonhole principle-
If n pigeonholes are occupied by kn+ 1 or more pigeons, where k is a positive integer, then at least one pigeonhole is occupied by k + 1 or more pigeons.
Example- Find the minimum number of persons in a group that three of them are born in the same month.
Sol.
Here the n = 12 months are the pigeonholes, and k + 1 = 3 so k = 2. Hence among any kn+ 1 = 25 students (pigeons), three of them are born in the same month.
Example: Find the minimum number of students in a class to be sure that three of them are born in the same month.
Sol:
Here the n = 12 months are the pigeonholes, and k + 1 = 3 so k = 2. Hence among any kn + 1 = 25 students (pigeons), three of them are born in the same month.
Key takeaways
- If n pigeonholes are occupied by n + 1 or more pigeons, then at least one pigeonhole is occupied by more than one pigeon.
- If n pigeonholes are occupied by kn+ 1 or more pigeons, where k is a positive integer, then at least one pigeonhole is occupied by k + 1 or more pigeons.
Recursion is a technique of defining a function, a set or an algorithm in terms of itself.
Suppose the set of natural numbers, we introduce the method of generating the set of natural numbers by recursion.
The natural numbers with zero are those objects which can be generated by starting with an initial object 0 and from any object “n” already generated passing to another uniquely determined object 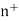 , the successor of n. The objects differently generated are always distinct. Thus the natural numbers appear as a set of objects 0,
, the successor of n. The objects differently generated are always distinct. Thus the natural numbers appear as a set of objects 0,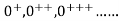
The transition to the usual notation is made upon introducing 1, 2, 3, 4, … to stand for 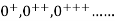 and then employing the notation.
and then employing the notation.
The recursive formula for defining a sequence (or numeric function) is called a recurrence relation.
A recurrence relation is also called a difference equation.
The information accompanying a recursive formula about the beginning of the numeric function is called initial condition.
Example: Find a recurrence relation and initial conditions for 1, 5, 17, 53, 161, 485.
Sol.
Here 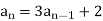 is the recurrence relation and the initial condition is
is the recurrence relation and the initial condition is 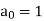
Example: Check whether 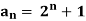 is a solution to the recurrence relation
is a solution to the recurrence relation 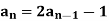 with
with 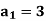 .
.
Sol.
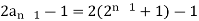
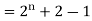
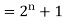
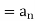
Key takeaways
- The recursive formula for defining a sequence (or numeric function) is called a recurrence relation.
- A recurrence relation is also called a difference equation.
- The information accompanying a recursive formula about the beginning of the numeric function is called initial condition.
Linear recurrence relation with constant coefficient-
If 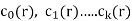 are constants then the recurrence relation is called a linear recurrence relation with constant coefficients.
are constants then the recurrence relation is called a linear recurrence relation with constant coefficients.
A linear kth-order recurrence relation with constant coefficients is a recurrence relation of the form
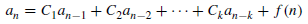
Where 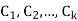 are constant with
are constant with 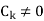 and f(n) is a function of ’n’.
and f(n) is a function of ’n’.
Example: Consider a following recurrence relation-
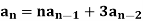
Sol.
It is a homogeneous linear second-order recurrence relation but it does not have constant coefficients because the coefficient of 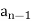 is not a constant given initial conditions
is not a constant given initial conditions 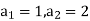 , the next elements of the sequence follows-
, the next elements of the sequence follows-
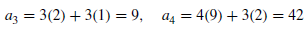
Note-
If if f (r) = 0, then the recurrence relation is called a linear homogenous relation.
For example:
The following relations are linear recurrence relations with constant coefficients-
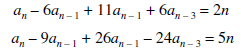
Key takeaways
- If
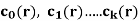 are constants then the recurrence relation is called a linear recurrence relation with constant coefficients.
are constants then the recurrence relation is called a linear recurrence relation with constant coefficients. - A linear kth-order recurrence relation with constant coefficients is a recurrence relation of the form
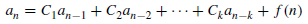
Where 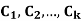 are constant with
are constant with 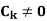 and f(n) is a function of ’n’.
and f(n) is a function of ’n’.
For a numeric function-
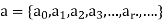
An infinite series is defined as-
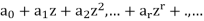 which is called the generating function of a.
which is called the generating function of a.
We denote it by A(Z).
The coefficient of 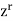 is A (z) is the value of the numeric function a.
is A (z) is the value of the numeric function a.
For example:
If the generating function is
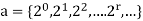
Is
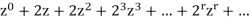
We can write the above series as below-
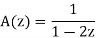
In 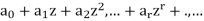 the term
the term 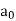 is called the constant term.
is called the constant term.
Let
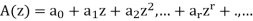
And
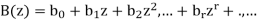
Are the generating functions.
A(z) and B(z) are equal if 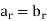 , for each
, for each
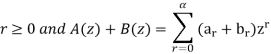
The product can be defined as-
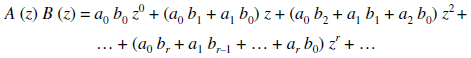
Note-
- The ordinary generating function is the formal power series-
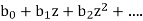
2. the exponential generating function (egf) is the formal power series
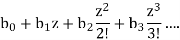
3. If the sequence has finitely many elements then the generating functions have finitely many terms.
Solution of recurrence relations by the method of generating functions
Any numeric function that can be described by a recurrence relation together with an appropriate set of boundary conditions is called a solution of the recurrence relation.
If 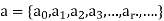
Is a solution to a recurrence relation then it is said to satisfy the relation.
A given recurrence relation may or may not have a solution.
Method of generating functions-
Recurrence relations can also be solved by using generating functions. Some equivalent expressions used are given below-
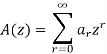
Then
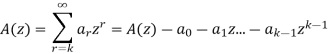
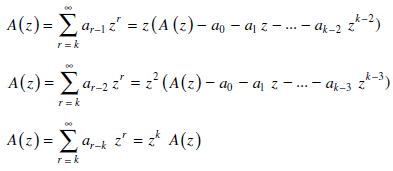
Example: Solve the recurrence relation-
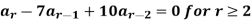
Sol.
Multiplying each term of the recurrence relation by 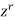 , we find-
, we find-
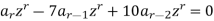
Now taking the sum to 2 to 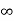 , we get
, we get
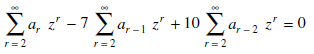
Replace each infinite sum by the corresponding equivalent expression given above, we obtain-
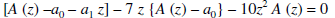
On simplifying, we obtain-
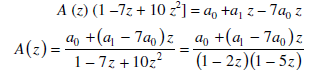
Decomposing A (z) as a sum of partial fractions, we can write
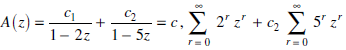
The solution is-
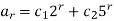
References:
1. “Discrete Mathematics and its Applications” by Kenneth H Rosen
2. “Discrete Mathematics” by Norman L Biggs
3. “Discrete Mathematics for Computer Science” by Kenneth Bogart and Robert L Drysdale