Unit - 4
Uncertainty
We had previously acquired knowledge representation using first-order logic and propositional logic with certainty, implying that we knew the predicates. With this knowledge representation, we could write AB, which implies that if A is true, then B is true; however, if we aren't sure if A is true or not, we won't be able to make this assertion; this is known as uncertainty.
So we require uncertain reasoning or probabilistic reasoning to describe uncertain information, when we aren't confident about the predicates.
Causes of uncertainty:
In the real world, the following are some of the most common sources of uncertainty.
● Information occurred from unreliable sources.
● Experimental Errors
● Equipment fault
● Temperature variation
● Climate change.
Probabilistic reasoning is a knowledge representation method that uses the concept of probability to indicate uncertainty in knowledge. We employ probabilistic reasoning, which integrates probability theory and logic, to deal with uncertainty.
Probability is employed in probabilistic reasoning because it helps us to deal with uncertainty caused by someone's indifference or ignorance.
There are many situations in the real world when nothing is certain, such as "it will rain today," "behavior of someone in specific surroundings," and "a competition between two teams or two players." These are probable sentences for which we can presume that something will happen but are unsure, thus we utilize probabilistic reasoning in this case.
Probability: Probability is a measure of the likelihood of an uncertain event occurring. It's a numerical representation of the likelihood of something happening. The probability value is always between 0 and 1, indicating complete unpredictability.
0 ≤ P(A) ≤ 1, where P(A) is the probability of an event A.
P(A) = 0, indicates total uncertainty in an event A.
P(A) =1, indicates total certainty in an event A.
We can compute the probability of an uncertain event using the formula below.
P(¬A) = probability of a not happening event.
P(¬A) + P(A) = 1.
Event: An event is the name given to each conceivable consequence of a variable.
Sample space: Sample space is a collection of all potential events.
Random variables: Random variables are used to represent real-world events and objects.
Prior probability: The prior probability of an occurrence is the probability calculated before fresh information is observed.
Posterior Probability: After all evidence or information has been considered, the likelihood is computed. It's a mix of known probabilities and new information.
Conditional probability: The likelihood of an event occurring when another event has already occurred is known as conditional probability.
Key takeaway
- Probabilistic reasoning is a method of knowledge representation in which the concept of probability is used to convey the uncertainty in knowledge.
- Probability is used in probabilistic reasoning because it allows us to deal with the uncertainty that arises from someone's laziness or ignorance.
It is critical to first comprehend what rational choice is, and to do so, one must first comprehend the meanings of the terms rational and choice (Green and Shapiro, 1994; Friedman, 1996). The google dictionary defines rational as "based on or in accordance with reason or logic," while choice is described as "the act of selecting between two or more options."
The process of making rational judgments based on relevant information in a logical, timely, and optimum manner is known as rational choice.
Let's say a man named Then do wants to figure out how much coffee he should drink today, so he phones his sister Denga to find out what color shoes she's wearing and uses that knowledge to figure out how much coffee he should drink that day. This will be an unreasonable decision because Thendo is deciding how much coffee he will drink based on irrelevant information (the color of shoes his sister Denga is wearing).
On the other hand, if Thendo determines that every time he takes a sip of that coffee, he must walk 1km, we will infer that he is acting irrationally because he is wasting energy by walking 1km to take a sip of coffee. This waste of energy is irrational, and it is referred to as an un-optimized solution in mathematical terms. If Then decides to pour the coffee from one glass to another every time he takes it for no other reason than to complete the chore of drinking coffee, he is taking an irrational course of action because it is not only illogical but also inefficient.
Figure shows an illustration of a rational decision-making framework. This diagram depicts how one studies the surroundings, or more technically, a decision-making area, when engaging in a rational decision-making process. The next step is to find the information that will help you make a decision. The input is then submitted to a logical and consistent decision engine, which examines all choices and their associated utilities before selecting the decision with the highest utility. Any flaw in this framework, such as the lack of complete knowledge, imprecise and defective information, or the inability to analyze all options, limits the theory of rational choice, and it becomes a bounded rational choice, as described by Herbert Simon (1991).
Classical economics is predicated on the notion that economic agents make decisions based on the principle of rational choice. Because this agent is a human person, many researchers have studied how humans make decisions, which is now known as behavioral economics. In his book Thinking Fast and Slow, Kahneman delves deeply into behavioral economics (Kahneman, 1991). Artificially intelligent machines are increasingly making decisions today. The assumption of rationality is stronger when decisions are made by artificial intelligent computers than when decisions are made by humans.
In this aspect, machine-made decisions are not as irrational as those produced by humans; but, they are not totally rational, and so are still susceptible to Herbert Simon's bounded rationality theory.
Fig 1: Steps for rational decision making
What are the characteristics of an isolated economic system in which all decision-making agents are human beings, for example? Behavioral economics will describe that economy. If, on the other hand, all of the decision-making agents are artificially intelligent machines that make rational-choice decisions, neoclassical economics will most likely apply. If half of these decision-making agents are people and the other half are machines, a half-neoclassical, half-behavioral economic system will emerge.
● Sample spaces S with events Ai, probabilities P(Ai); union A ∪ B and intersection AB, complement Ac .
● Axioms: P(A) ≤ 1; P(S) = 1; for exclusive Ai, P(∪iAi) = Σi P(Ai).
● Conditional probability: P(A|B) = P(AB)/P(B); P(A) = P(A|B)P(B) + P(A|Bc )P(Bc)
● Random variables (RVs) X; the cumulative distribution function (cdf) F(x) = P{X ≤ x};
For a discrete RV, probability mass function (pmf)
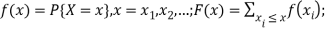
For a continuous RV, probability density function (pdf)
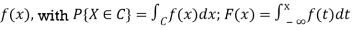
● Generalizations for more than one variable, e.g
Two RVs X and Y: joint cdf F(x, y) = P{X ≤ x, Y ≤ y};
Pmf f(x, y) = P{X = x, Y = y}; or
Pdf f(x, y), with
Independent X and Y iff f(x, y) = fX(x) fY (y)
● Expected value or mean: for RV X, µ = E[X]; discrete RVs
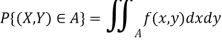
Continuous RVs
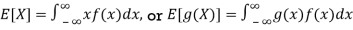
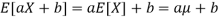
Probability Theory provides the formal techniques and principles for manipulating probabilistically represented propositions. The following are the three assumptions of probability theory:
● 0 <= P(A=a) <= 1 for all a in sample space of A
● P(True)=1, P(False)=0
● P(A v B) = P(A) + P(B) - P(A ^ B)
The following qualities can be deduced from these axioms:
● P(~A) = 1 - P(A)
● P(A) = P(A ^ B) + P(A ^ ~B)
● Sum{P(A=a)} = 1, where the sum is over all possible values a in the sample space of A
Bayes' theorem is a mathematical formula for calculating the probability of an event based on ambiguous information. It is also known as Bayes' rule, Bayes' law, or Bayesian reasoning.
In probability theory, it relates the conditional and marginal probabilities of two random events.
The inspiration for Bayes' theorem came from British mathematician Thomas Bayes. Bayesian inference is a technique for applying Bayes' theorem, which is at the heart of Bayesian statistics.
It's a method for calculating the value of P(B|A) using P(A|B) knowledge.
Bayes' theorem can update the probability forecast of an occurrence based on new information from the real world.
Example: If cancer is linked to one's age, we can apply Bayes' theorem to more precisely forecast cancer risk based on age.
Bayes' theorem can be derived using the product rule and conditional probability of event A with known event B:
As a result of the product rule, we can write:
P(A ⋀ B)= P(A|B) P(B) or
In the same way, the likelihood of event B if event A is known is:
P(A ⋀ B)= P(B|A) P(A)
When we combine the right-hand sides of both equations, we get:
The above equation is known as Bayes' rule or Bayes' theorem (a). This equation is the starting point for most current AI systems for probabilistic inference.
It displays the simple relationship between joint and conditional probabilities. Here,
P(A|B) is the posterior, which we must compute, and it stands for Probability of hypothesis A when evidence B is present.
The likelihood is defined as P(B|A), in which the probability of evidence is computed after assuming that the hypothesis is valid.
Prior probability, or the likelihood of a hypothesis before taking into account the evidence, is denoted by P(A).
Marginal probability, or the likelihood of a single piece of evidence, is denoted by P(B).
In general, we can write P (B) = P(A)*P(B|Ai) in the equation (a), therefore the Bayes' rule can be expressed as:
Where A1, A2, A3,..... Is a set of mutually exclusive and exhaustive events, and An is a set of mutually exclusive and exhaustive events.
- Bayesian Networks, also known as Bayes Nets, Belief Nets, Causal Nets, and Probability Nets, are a data structure for capturing all of the information in a domain's entire joint probability distribution. The Bayesian Net can compute every value in the entire joint probability distribution of a collection of random variables.
- This variable represents all direct causal relationships between variables.
- To construct a Bayesian net for a given set of variables, draw arcs from cause variables to immediate effects.
- It saves space by taking advantage of the fact that variable dependencies are generally local in many real-world problem domains, resulting in a high number of conditionally independent variables.
- In both qualitative and quantitative terms, the link between variables is captured.
- It's possible to use it to construct a case.
- Predictive reasoning (sometimes referred to as causal reasoning) is a sort of reasoning that proceeds from the top down (from causes to effects).
- From effects to causes, diagnostic thinking goes backwards (bottom-up).
- When A has a direct causal influence on B, a Bayesian Net is a directed acyclic graph (DAG) in which each random variable has its own node and a directed arc from A to B. As a result, the nodes represent states of affairs, whereas the arcs represent causal relationships. When A is present, B is more likely to occur, and vice versa. The backward influence is referred to as "diagnostic" or "evidential" support for A due to the presence of B.
- Each node A in a network is conditionally independent of any subset of nodes that are not children of A, given its parents.
A Bayesian network that depicts and solves decision issues under uncertain knowledge is known as an influence diagram.
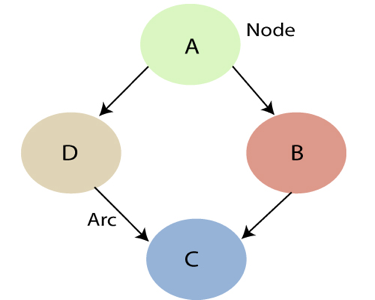
Fig 2: Bayesian network graph
- Each node represents a random variable that can be continuous or discontinuous in nature.
- Arcs or directed arrows represent the causal relationship or conditional probabilities between random variables. The graph's two nodes are connected by these directed links, also known as arrows.
These ties imply that one node has a direct influence on another, and nodes are independent of one another if there are no directed relationships.
Key takeaway
Bayesian Networks, also known as Bayes Nets, Belief Nets, Causal Nets, and Probability Nets.
Bayesian Networks are a data structure for capturing all of the information in the whole joint probability distribution for the collection of random variables that define a domain.
● In general, Bayes Net inference is an NP-hard problem (exponential in the size of the graph).
● There are linear time techniques based on belief propagation for singly-connected networks or polytrees with no undirected loops.
● Local evidence messages are sent by each node to their children and parents.
● Based on incoming messages from its neighbors, each node updates its belief in each of its possible values and propagates evidence to its neighbors.
● Inference for generic networks can be approximated using loopy belief propagation, which iteratively refines probabilities until they reach an exact limit.
Temporal model
- Monitoring or filtering
- Prediction
Approximate inference
Direct sampling method
The most basic sort of random sampling process for Bayesian networks generates events from a network with no evidence associated with them. The idea is that each variable is sampled in topological order. The value is drawn from a probability distribution based on the values that have previously been assigned to the variable's parents.
Function PRIOR-SAMPLE(bn) returns an event sampled from the prior specified by bn
Inputs: bn, a Bayesian network specifying joint distribution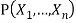 
an event with 
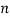elements
For each variable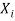 
in 
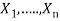do
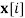a random sample from 
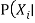parents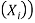 
Return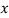 
Likelihood weighting
Likelihood weighting eliminates the inefficiencies of rejection sampling by creating only events that are consistent with the evidence. It's a tailored version of the general statistical approach of importance sampling for Bayesian network inference.
Function LIKELIHOOD-WEIGHTING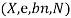 
returns an estimate of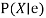 
Inputs: 
, the query variable
e, observed values for variables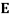 
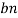, a Bayesian network specifying joint distribution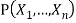 
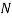, the total number of samples to be generated
Local variables: W, a vector of weighted counts for each value of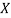 
, initially zero
For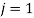 
to 
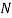do
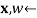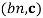
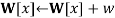WEIGHTED-SAMPLE 
where 
is the value of 
in 
Return NORMALIZE(W)
Inference by Markov chain simulation
Rejection sampling and likelihood weighting are not the same as Markov chain (MCMC) approaches. Rather of starting from scratch, MCMC approaches create each sample by making a random change to the preceding sample. It's easier to think of an MCMC algorithm as being in a current state where each variable has a value and then randomly modifying that state to get a new state.
Key takeaway
- For Bayesian networks, the most basic type of random sampling procedure generates events from a network with no evidence connected with them.
- It's a variant of the broad statistical technique of importance sampling that's been customized for Bayesian network inference.
- Markov chain (MCMC) MARKOV CHAIN methods are not the same as rejection sampling and likelihood weighting.
Fuzzy Logic (FL) is that of a method of the reasoning that resembles human reasoning. The approach of the FL imitates the way of decision making in humans that involves all intermediate possibilities between that of the digital values YES and NO.
The conventional logic block that a computer can understand takes the precise input and produces that of a definite output as TRUE or FALSE, which is equivalent to that of a human’s YES or NO.
The inventor of fuzzy logic, Lotfi Zadeh, observed that unlike the computers, the human decision making includes that of a range of the possibilities between YES and NO, example −
CERTAINLY YES |
POSSIBLY YES |
CANNOT SAY |
POSSIBLY NO |
CERTAINLY NO |
The fuzzy logic works on the levels of that of the possibilities of the input to achieve that of the definite output.
Implementation
● It can be implemented in the systems with the various sizes and the capabilities ranging from that of the small microcontrollers to large, the networked, and the workstation-based control systems.
● It can be implemented in the hardware, the software, or a combination of both.
Why Fuzzy Logic?
Fuzzy logic is useful for commercial and practical purposes.
● It can control the machines and the consumer products.
● It may not give the accurate reasoning, but acceptable to that of the reasoning.
● Fuzzy logic helps to deal with that uncertainty in engineering.
Fuzzy Logic Systems Architecture
It has four main parts as shown below −
● Fuzzification Module − It transforms that of the system inputs, which are crisp numbers, into that of the fuzzy sets. It splits the input signal into five steps example −
LP | x is Large Positive |
MP | x is Medium Positive |
S | x is Small |
MN | x is Medium Negative |
LN | x is Large Negative
|
● Knowledge Base − It stores IF-THEN rules provided by that of the experts.
● Inference Engine − It simulates that of the human reasoning process by making the fuzzy inference on the inputs and IF-THEN rules.
● Defuzzification Module − It transforms the fuzzy set obtained by that of the inference engine into a crisp value.
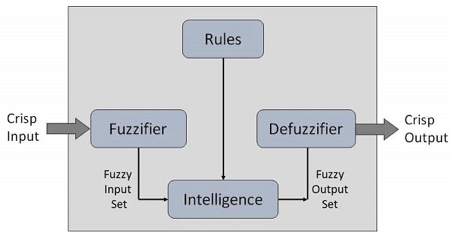
The membership functions work on that of the fuzzy sets of variables.
Membership Function
Membership functions allow you to quantify that of the linguistic term and represent a fuzzy set graphically. A membership function for that of a fuzzy set A on the universe of that of the discourse X is defined as μA:X → [0,1].
Here, each element of X is mapped to that of a value between 0 and 1. It is called the membership value or that of the degree of membership. It quantifies the degree of that of the membership of the element in X to that of the fuzzy set A.
● x axis represents that of the universe of discourse.
● y axis represents that of the degrees of membership in the [0, 1] interval.
There can be multiple membership functions applicable to that of the fuzzify a numerical value. Simple membership functions are used as use of that of the complex functions does not add more precision in the output.
All membership functions for LP, MP, S, MN, and LN are shown as below −
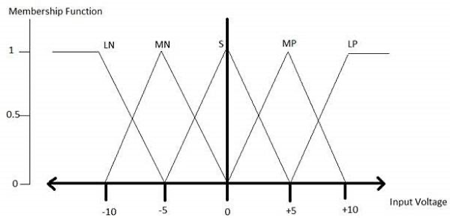
The triangular membership function shapes are the most of the common among various of the other membership function shapes for example trapezoidal, singleton, and Gaussian.
Here, the input to that of the 5-level fuzzifier varies from that of the -10 volts to +10 volts. Hence the corresponding output will also change.
Example of a Fuzzy Logic System
Let us consider that an air conditioning system with that of the 5-level fuzzy logic system. This system adjusts that of the temperature of the air conditioner by comparing that of the room temperature and that of the target temperature value.
Fig 3: Example
Algorithm
● Define linguistic Variables and terms (start)
● Construct membership functions for them. (start)
● Construct knowledge base of rules (start)
● Convert crisp data into fuzzy data sets using membership functions. (fuzzification)
● Evaluate rules in the rule base. (Inference Engine)
● Combine results from each rule. (Inference Engine)
● Convert output data into non-fuzzy values. (defuzzification)
Development
Step 1 − Define linguistic variables and terms
Linguistic variables are the input and the output variables in that of the form of the simple words or the sentences. For that of the room temperature, cold, warm, hot, etc., are the linguistic terms.
Temperature (t) = {very-cold, cold, warm, very-warm, hot}
Every member of this set is that of a linguistic term and it can cover that of the some portion of overall temperature of the values.
Step 2 − Construct membership functions for them
The membership functions of temperature variable are as shown −
Step3 − Construct knowledge base rules
Create a matrix of room temperature values versus target temperature values that an air conditioning system is expected to provide.
RoomTemp. /Target | Very_Cold | Cold | Warm | Hot | Very_Hot |
Very_Cold | No_Change | Heat | Heat | Heat | Heat |
Cold | Cool | No_Change | Heat | Heat | Heat |
Warm | Cool | Cool | No_Change | Heat | Heat |
Hot | Cool | Cool | Cool | No_Change | Heat |
Very_Hot | Cool | Cool | Cool | Cool | No_Change |
Build a set of rules into the knowledge base in the form of IF-THEN-ELSE structures.
Sr. No. | Condition | Action |
1 | IF temperature=(Cold OR Very_Cold) AND target=Warm THEN | Heat |
2 | IF temperature=(Hot OR Very_Hot) AND target=Warm THEN | Cool |
3 | IF (temperature=Warm) AND (target=Warm) THEN | No_Change |
Step 4 − Obtain fuzzy value
Fuzzy set operations perform evaluation of rules. The operations used for that of the OR and AND are the Max and Min respectively. Combine all of the results of the evaluation to form that of a final result. This result is that of a fuzzy value.
Step 5 − Perform defuzzification
Defuzzification is then performed according to that of the membership function for output variable.
Application Areas of Fuzzy Logic
The key application areas of fuzzy logic are as follows −
Automotive Systems
● Automatic Gearboxes
● Four-Wheel Steering
● Vehicle environment control
Consumer Electronic Goods
● Hi-Fi Systems
● Photocopiers
● Still and Video Cameras
● Television
Domestic Goods
● Microwave Ovens
● Refrigerators
● Toasters
● Vacuum Cleaners
● Washing Machines
Environment Control
● Air Conditioners/Dryers/Heaters
● Humidifiers
Advantages of FLSs
● Mathematical concepts within that of the fuzzy reasoning are very simple.
● You can modify a FLS by just adding or deleting the rules due to the flexibility of fuzzy logic.
● Fuzzy logic Systems can take the imprecise, the distorted, noisy input information.
● FLSs are easy to construct and to understand.
● Fuzzy logic is that of a solution to complex problems in all of the fields of life, including medicine, as it resembles human reasoning and that of the decision making.
Disadvantages of FLSs
● There is no systematic approach to that of fuzzy system designing.
● They are understandable only when they are simple.
● They are suitable for problems which do not need very high accuracy.
Key takeaway
Fuzzy Logic (FL) is that of a method of the reasoning that resembles human reasoning. The approach of the FL imitates the way of decision making in humans that involves all intermediate possibilities between that of the digital values YES and NO.
References:
- Elaine Rich, Kevin Knight and Shivashankar B Nair, “Artificial Intelligence”, Mc Graw Hill Publication, 2009.
- Dan W. Patterson, “Introduction to Artificial Intelligence and Expert System”, Pearson Publication,2015.
- Saroj Kaushik, “Artificial Intelligence”, Cengage Learning, 2011.
Unit - 4
Uncertainty
We had previously acquired knowledge representation using first-order logic and propositional logic with certainty, implying that we knew the predicates. With this knowledge representation, we could write AB, which implies that if A is true, then B is true; however, if we aren't sure if A is true or not, we won't be able to make this assertion; this is known as uncertainty.
So we require uncertain reasoning or probabilistic reasoning to describe uncertain information, when we aren't confident about the predicates.
Causes of uncertainty:
In the real world, the following are some of the most common sources of uncertainty.
● Information occurred from unreliable sources.
● Experimental Errors
● Equipment fault
● Temperature variation
● Climate change.
Probabilistic reasoning is a knowledge representation method that uses the concept of probability to indicate uncertainty in knowledge. We employ probabilistic reasoning, which integrates probability theory and logic, to deal with uncertainty.
Probability is employed in probabilistic reasoning because it helps us to deal with uncertainty caused by someone's indifference or ignorance.
There are many situations in the real world when nothing is certain, such as "it will rain today," "behavior of someone in specific surroundings," and "a competition between two teams or two players." These are probable sentences for which we can presume that something will happen but are unsure, thus we utilize probabilistic reasoning in this case.
Probability: Probability is a measure of the likelihood of an uncertain event occurring. It's a numerical representation of the likelihood of something happening. The probability value is always between 0 and 1, indicating complete unpredictability.
0 ≤ P(A) ≤ 1, where P(A) is the probability of an event A.
P(A) = 0, indicates total uncertainty in an event A.
P(A) =1, indicates total certainty in an event A.
We can compute the probability of an uncertain event using the formula below.
P(¬A) = probability of a not happening event.
P(¬A) + P(A) = 1.
Event: An event is the name given to each conceivable consequence of a variable.
Sample space: Sample space is a collection of all potential events.
Random variables: Random variables are used to represent real-world events and objects.
Prior probability: The prior probability of an occurrence is the probability calculated before fresh information is observed.
Posterior Probability: After all evidence or information has been considered, the likelihood is computed. It's a mix of known probabilities and new information.
Conditional probability: The likelihood of an event occurring when another event has already occurred is known as conditional probability.
Key takeaway
- Probabilistic reasoning is a method of knowledge representation in which the concept of probability is used to convey the uncertainty in knowledge.
- Probability is used in probabilistic reasoning because it allows us to deal with the uncertainty that arises from someone's laziness or ignorance.
It is critical to first comprehend what rational choice is, and to do so, one must first comprehend the meanings of the terms rational and choice (Green and Shapiro, 1994; Friedman, 1996). The google dictionary defines rational as "based on or in accordance with reason or logic," while choice is described as "the act of selecting between two or more options."
The process of making rational judgments based on relevant information in a logical, timely, and optimum manner is known as rational choice.
Let's say a man named Then do wants to figure out how much coffee he should drink today, so he phones his sister Denga to find out what color shoes she's wearing and uses that knowledge to figure out how much coffee he should drink that day. This will be an unreasonable decision because Thendo is deciding how much coffee he will drink based on irrelevant information (the color of shoes his sister Denga is wearing).
On the other hand, if Thendo determines that every time he takes a sip of that coffee, he must walk 1km, we will infer that he is acting irrationally because he is wasting energy by walking 1km to take a sip of coffee. This waste of energy is irrational, and it is referred to as an un-optimized solution in mathematical terms. If Then decides to pour the coffee from one glass to another every time he takes it for no other reason than to complete the chore of drinking coffee, he is taking an irrational course of action because it is not only illogical but also inefficient.
Figure shows an illustration of a rational decision-making framework. This diagram depicts how one studies the surroundings, or more technically, a decision-making area, when engaging in a rational decision-making process. The next step is to find the information that will help you make a decision. The input is then submitted to a logical and consistent decision engine, which examines all choices and their associated utilities before selecting the decision with the highest utility. Any flaw in this framework, such as the lack of complete knowledge, imprecise and defective information, or the inability to analyze all options, limits the theory of rational choice, and it becomes a bounded rational choice, as described by Herbert Simon (1991).
Classical economics is predicated on the notion that economic agents make decisions based on the principle of rational choice. Because this agent is a human person, many researchers have studied how humans make decisions, which is now known as behavioral economics. In his book Thinking Fast and Slow, Kahneman delves deeply into behavioral economics (Kahneman, 1991). Artificially intelligent machines are increasingly making decisions today. The assumption of rationality is stronger when decisions are made by artificial intelligent computers than when decisions are made by humans.
In this aspect, machine-made decisions are not as irrational as those produced by humans; but, they are not totally rational, and so are still susceptible to Herbert Simon's bounded rationality theory.
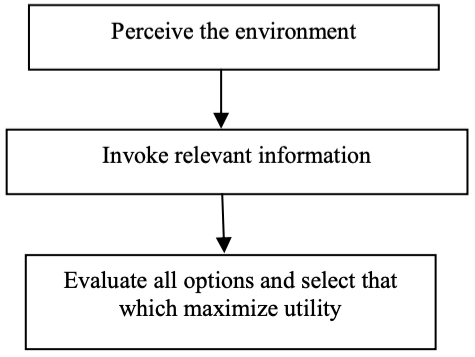
Fig 1: Steps for rational decision making
What are the characteristics of an isolated economic system in which all decision-making agents are human beings, for example? Behavioral economics will describe that economy. If, on the other hand, all of the decision-making agents are artificially intelligent machines that make rational-choice decisions, neoclassical economics will most likely apply. If half of these decision-making agents are people and the other half are machines, a half-neoclassical, half-behavioral economic system will emerge.
● Sample spaces S with events Ai, probabilities P(Ai); union A ∪ B and intersection AB, complement Ac .
● Axioms: P(A) ≤ 1; P(S) = 1; for exclusive Ai, P(∪iAi) = Σi P(Ai).
● Conditional probability: P(A|B) = P(AB)/P(B); P(A) = P(A|B)P(B) + P(A|Bc )P(Bc)
● Random variables (RVs) X; the cumulative distribution function (cdf) F(x) = P{X ≤ x};
For a discrete RV, probability mass function (pmf)
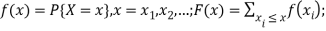
For a continuous RV, probability density function (pdf)
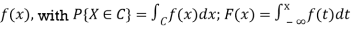
● Generalizations for more than one variable, e.g
Two RVs X and Y: joint cdf F(x, y) = P{X ≤ x, Y ≤ y};
Pmf f(x, y) = P{X = x, Y = y}; or
Pdf f(x, y), with
Independent X and Y iff f(x, y) = fX(x) fY (y)
● Expected value or mean: for RV X, µ = E[X]; discrete RVs
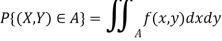
Continuous RVs
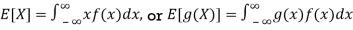
Probability Theory provides the formal techniques and principles for manipulating probabilistically represented propositions. The following are the three assumptions of probability theory:
● 0 <= P(A=a) <= 1 for all a in sample space of A
● P(True)=1, P(False)=0
● P(A v B) = P(A) + P(B) - P(A ^ B)
The following qualities can be deduced from these axioms:
● P(~A) = 1 - P(A)
● P(A) = P(A ^ B) + P(A ^ ~B)
● Sum{P(A=a)} = 1, where the sum is over all possible values a in the sample space of A
Bayes' theorem is a mathematical formula for calculating the probability of an event based on ambiguous information. It is also known as Bayes' rule, Bayes' law, or Bayesian reasoning.
In probability theory, it relates the conditional and marginal probabilities of two random events.
The inspiration for Bayes' theorem came from British mathematician Thomas Bayes. Bayesian inference is a technique for applying Bayes' theorem, which is at the heart of Bayesian statistics.
It's a method for calculating the value of P(B|A) using P(A|B) knowledge.
Bayes' theorem can update the probability forecast of an occurrence based on new information from the real world.
Example: If cancer is linked to one's age, we can apply Bayes' theorem to more precisely forecast cancer risk based on age.
Bayes' theorem can be derived using the product rule and conditional probability of event A with known event B:
As a result of the product rule, we can write:
P(A ⋀ B)= P(A|B) P(B) or
In the same way, the likelihood of event B if event A is known is:
P(A ⋀ B)= P(B|A) P(A)
When we combine the right-hand sides of both equations, we get:
The above equation is known as Bayes' rule or Bayes' theorem (a). This equation is the starting point for most current AI systems for probabilistic inference.
It displays the simple relationship between joint and conditional probabilities. Here,
P(A|B) is the posterior, which we must compute, and it stands for Probability of hypothesis A when evidence B is present.
The likelihood is defined as P(B|A), in which the probability of evidence is computed after assuming that the hypothesis is valid.
Prior probability, or the likelihood of a hypothesis before taking into account the evidence, is denoted by P(A).
Marginal probability, or the likelihood of a single piece of evidence, is denoted by P(B).
In general, we can write P (B) = P(A)*P(B|Ai) in the equation (a), therefore the Bayes' rule can be expressed as:
Where A1, A2, A3,..... Is a set of mutually exclusive and exhaustive events, and An is a set of mutually exclusive and exhaustive events.
- Bayesian Networks, also known as Bayes Nets, Belief Nets, Causal Nets, and Probability Nets, are a data structure for capturing all of the information in a domain's entire joint probability distribution. The Bayesian Net can compute every value in the entire joint probability distribution of a collection of random variables.
- This variable represents all direct causal relationships between variables.
- To construct a Bayesian net for a given set of variables, draw arcs from cause variables to immediate effects.
- It saves space by taking advantage of the fact that variable dependencies are generally local in many real-world problem domains, resulting in a high number of conditionally independent variables.
- In both qualitative and quantitative terms, the link between variables is captured.
- It's possible to use it to construct a case.
- Predictive reasoning (sometimes referred to as causal reasoning) is a sort of reasoning that proceeds from the top down (from causes to effects).
- From effects to causes, diagnostic thinking goes backwards (bottom-up).
- When A has a direct causal influence on B, a Bayesian Net is a directed acyclic graph (DAG) in which each random variable has its own node and a directed arc from A to B. As a result, the nodes represent states of affairs, whereas the arcs represent causal relationships. When A is present, B is more likely to occur, and vice versa. The backward influence is referred to as "diagnostic" or "evidential" support for A due to the presence of B.
- Each node A in a network is conditionally independent of any subset of nodes that are not children of A, given its parents.
A Bayesian network that depicts and solves decision issues under uncertain knowledge is known as an influence diagram.
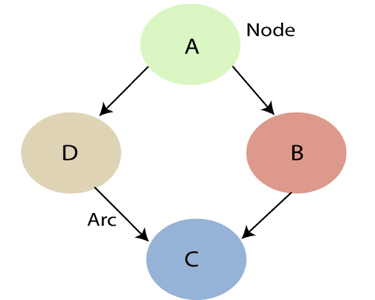
Fig 2: Bayesian network graph
- Each node represents a random variable that can be continuous or discontinuous in nature.
- Arcs or directed arrows represent the causal relationship or conditional probabilities between random variables. The graph's two nodes are connected by these directed links, also known as arrows.
These ties imply that one node has a direct influence on another, and nodes are independent of one another if there are no directed relationships.
Key takeaway
Bayesian Networks, also known as Bayes Nets, Belief Nets, Causal Nets, and Probability Nets.
Bayesian Networks are a data structure for capturing all of the information in the whole joint probability distribution for the collection of random variables that define a domain.
● In general, Bayes Net inference is an NP-hard problem (exponential in the size of the graph).
● There are linear time techniques based on belief propagation for singly-connected networks or polytrees with no undirected loops.
● Local evidence messages are sent by each node to their children and parents.
● Based on incoming messages from its neighbors, each node updates its belief in each of its possible values and propagates evidence to its neighbors.
● Inference for generic networks can be approximated using loopy belief propagation, which iteratively refines probabilities until they reach an exact limit.
Temporal model
- Monitoring or filtering
- Prediction
Approximate inference
Direct sampling method
The most basic sort of random sampling process for Bayesian networks generates events from a network with no evidence associated with them. The idea is that each variable is sampled in topological order. The value is drawn from a probability distribution based on the values that have previously been assigned to the variable's parents.
Function PRIOR-SAMPLE(bn) returns an event sampled from the prior specified by bn
Inputs: bn, a Bayesian network specifying joint distribution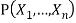 
an event with 
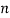elements
For each variable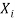 
in 
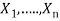do
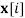a random sample from 
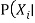parents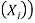 
Return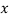 
Likelihood weighting
Likelihood weighting eliminates the inefficiencies of rejection sampling by creating only events that are consistent with the evidence. It's a tailored version of the general statistical approach of importance sampling for Bayesian network inference.
Function LIKELIHOOD-WEIGHTING 
returns an estimate of 
Inputs: 
, the query variable
e, observed values for variables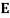 
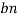, a Bayesian network specifying joint distribution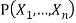 
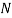, the total number of samples to be generated
Local variables: W, a vector of weighted counts for each value of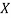 
, initially zero
For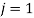 
to 
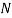do
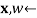WEIGHTED-SAMPLE 
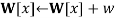where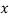 
is the value of 
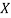in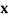 
Return NORMALIZE(W)
Inference by Markov chain simulation
Rejection sampling and likelihood weighting are not the same as Markov chain (MCMC) approaches. Rather of starting from scratch, MCMC approaches create each sample by making a random change to the preceding sample. It's easier to think of an MCMC algorithm as being in a current state where each variable has a value and then randomly modifying that state to get a new state.
Key takeaway
- For Bayesian networks, the most basic type of random sampling procedure generates events from a network with no evidence connected with them.
- It's a variant of the broad statistical technique of importance sampling that's been customized for Bayesian network inference.
- Markov chain (MCMC) MARKOV CHAIN methods are not the same as rejection sampling and likelihood weighting.
Fuzzy Logic (FL) is that of a method of the reasoning that resembles human reasoning. The approach of the FL imitates the way of decision making in humans that involves all intermediate possibilities between that of the digital values YES and NO.
The conventional logic block that a computer can understand takes the precise input and produces that of a definite output as TRUE or FALSE, which is equivalent to that of a human’s YES or NO.
The inventor of fuzzy logic, Lotfi Zadeh, observed that unlike the computers, the human decision making includes that of a range of the possibilities between YES and NO, example −
CERTAINLY YES |
POSSIBLY YES |
CANNOT SAY |
POSSIBLY NO |
CERTAINLY NO |
The fuzzy logic works on the levels of that of the possibilities of the input to achieve that of the definite output.
Implementation
● It can be implemented in the systems with the various sizes and the capabilities ranging from that of the small microcontrollers to large, the networked, and the workstation-based control systems.
● It can be implemented in the hardware, the software, or a combination of both.
Why Fuzzy Logic?
Fuzzy logic is useful for commercial and practical purposes.
● It can control the machines and the consumer products.
● It may not give the accurate reasoning, but acceptable to that of the reasoning.
● Fuzzy logic helps to deal with that uncertainty in engineering.
Fuzzy Logic Systems Architecture
It has four main parts as shown below −
● Fuzzification Module − It transforms that of the system inputs, which are crisp numbers, into that of the fuzzy sets. It splits the input signal into five steps example −
LP | x is Large Positive |
MP | x is Medium Positive |
S | x is Small |
MN | x is Medium Negative |
LN | x is Large Negative
|
● Knowledge Base − It stores IF-THEN rules provided by that of the experts.
● Inference Engine − It simulates that of the human reasoning process by making the fuzzy inference on the inputs and IF-THEN rules.
● Defuzzification Module − It transforms the fuzzy set obtained by that of the inference engine into a crisp value.
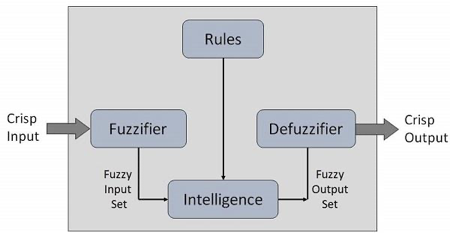
The membership functions work on that of the fuzzy sets of variables.
Membership Function
Membership functions allow you to quantify that of the linguistic term and represent a fuzzy set graphically. A membership function for that of a fuzzy set A on the universe of that of the discourse X is defined as μA:X → [0,1].
Here, each element of X is mapped to that of a value between 0 and 1. It is called the membership value or that of the degree of membership. It quantifies the degree of that of the membership of the element in X to that of the fuzzy set A.
● x axis represents that of the universe of discourse.
● y axis represents that of the degrees of membership in the [0, 1] interval.
There can be multiple membership functions applicable to that of the fuzzify a numerical value. Simple membership functions are used as use of that of the complex functions does not add more precision in the output.
All membership functions for LP, MP, S, MN, and LN are shown as below −
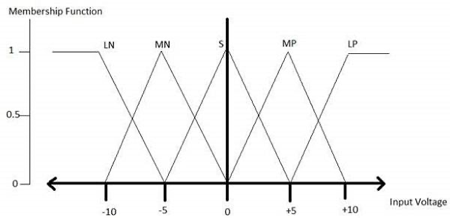
The triangular membership function shapes are the most of the common among various of the other membership function shapes for example trapezoidal, singleton, and Gaussian.
Here, the input to that of the 5-level fuzzifier varies from that of the -10 volts to +10 volts. Hence the corresponding output will also change.
Example of a Fuzzy Logic System
Let us consider that an air conditioning system with that of the 5-level fuzzy logic system. This system adjusts that of the temperature of the air conditioner by comparing that of the room temperature and that of the target temperature value.
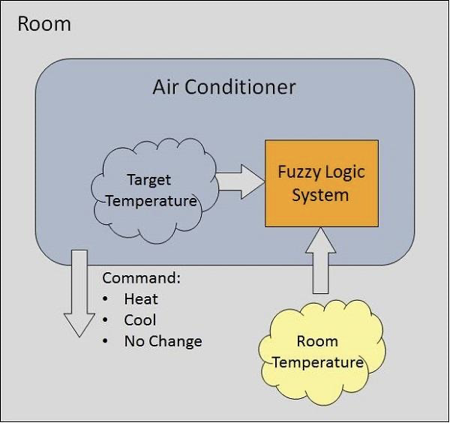
Fig 3: Example
Algorithm
● Define linguistic Variables and terms (start)
● Construct membership functions for them. (start)
● Construct knowledge base of rules (start)
● Convert crisp data into fuzzy data sets using membership functions. (fuzzification)
● Evaluate rules in the rule base. (Inference Engine)
● Combine results from each rule. (Inference Engine)
● Convert output data into non-fuzzy values. (defuzzification)
Development
Step 1 − Define linguistic variables and terms
Linguistic variables are the input and the output variables in that of the form of the simple words or the sentences. For that of the room temperature, cold, warm, hot, etc., are the linguistic terms.
Temperature (t) = {very-cold, cold, warm, very-warm, hot}
Every member of this set is that of a linguistic term and it can cover that of the some portion of overall temperature of the values.
Step 2 − Construct membership functions for them
The membership functions of temperature variable are as shown −
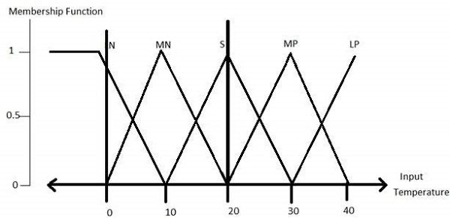
Step3 − Construct knowledge base rules
Create a matrix of room temperature values versus target temperature values that an air conditioning system is expected to provide.
RoomTemp. /Target | Very_Cold | Cold | Warm | Hot | Very_Hot |
Very_Cold | No_Change | Heat | Heat | Heat | Heat |
Cold | Cool | No_Change | Heat | Heat | Heat |
Warm | Cool | Cool | No_Change | Heat | Heat |
Hot | Cool | Cool | Cool | No_Change | Heat |
Very_Hot | Cool | Cool | Cool | Cool | No_Change |
Build a set of rules into the knowledge base in the form of IF-THEN-ELSE structures.
Sr. No. | Condition | Action |
1 | IF temperature=(Cold OR Very_Cold) AND target=Warm THEN | Heat |
2 | IF temperature=(Hot OR Very_Hot) AND target=Warm THEN | Cool |
3 | IF (temperature=Warm) AND (target=Warm) THEN | No_Change |
Step 4 − Obtain fuzzy value
Fuzzy set operations perform evaluation of rules. The operations used for that of the OR and AND are the Max and Min respectively. Combine all of the results of the evaluation to form that of a final result. This result is that of a fuzzy value.
Step 5 − Perform defuzzification
Defuzzification is then performed according to that of the membership function for output variable.
Application Areas of Fuzzy Logic
The key application areas of fuzzy logic are as follows −
Automotive Systems
● Automatic Gearboxes
● Four-Wheel Steering
● Vehicle environment control
Consumer Electronic Goods
● Hi-Fi Systems
● Photocopiers
● Still and Video Cameras
● Television
Domestic Goods
● Microwave Ovens
● Refrigerators
● Toasters
● Vacuum Cleaners
● Washing Machines
Environment Control
● Air Conditioners/Dryers/Heaters
● Humidifiers
Advantages of FLSs
● Mathematical concepts within that of the fuzzy reasoning are very simple.
● You can modify a FLS by just adding or deleting the rules due to the flexibility of fuzzy logic.
● Fuzzy logic Systems can take the imprecise, the distorted, noisy input information.
● FLSs are easy to construct and to understand.
● Fuzzy logic is that of a solution to complex problems in all of the fields of life, including medicine, as it resembles human reasoning and that of the decision making.
Disadvantages of FLSs
● There is no systematic approach to that of fuzzy system designing.
● They are understandable only when they are simple.
● They are suitable for problems which do not need very high accuracy.
Key takeaway
Fuzzy Logic (FL) is that of a method of the reasoning that resembles human reasoning. The approach of the FL imitates the way of decision making in humans that involves all intermediate possibilities between that of the digital values YES and NO.
References:
- Elaine Rich, Kevin Knight and Shivashankar B Nair, “Artificial Intelligence”, Mc Graw Hill Publication, 2009.
- Dan W. Patterson, “Introduction to Artificial Intelligence and Expert System”, Pearson Publication,2015.
- Saroj Kaushik, “Artificial Intelligence”, Cengage Learning, 2011.
