Unit - 6
Expert Systems
Expert systems are computer programs that are designed to tackle complicated issues in a certain domain at a level of human intellect and expertise.
An expert system is a piece of software that can deal with difficult problems and make choices in the same way as a human expert can. It achieves it by using reasoning and inference techniques to retrieve knowledge from its knowledge base based on the user's requests.
The performance of an expert system is based on the knowledge stored in its knowledge base by the expert. The better the system functions, the more knowledge is saved in the KB. When typing in the Google search box, one of the most common examples of an ES is a suggestion of spelling problems.
An expert system is a computer simulation of a human expert. It can alternatively be described as a computer software that imitates the judgment and conduct of a human or an organization with substantial knowledge and experience in a certain field.
In such a system, a knowledge base containing accumulated experience and a set of rules for applying the knowledge base to each specific case presented to the program are usually provided. Expert systems also leverage human knowledge to solve problems that would normally necessitate human intelligence. These expert systems use computers to transmit expertise knowledge as data or rules.
The expert system is a type of AI, and the first ES was created in 1970, making it the first successful artificial intelligence approach. As an expert, it solves the most difficult problems by extracting knowledge from its knowledge base. Like a human expert, the system assists in decision making for complex problems by employing both facts and heuristics. It is so named because it comprises expert knowledge of a certain subject and is capable of solving any complex problem in that domain. These systems are tailored to a particular field, such as medicine or science.
An expert system's performance is determined on the knowledge stored in its knowledge base by the expert. The more knowledge that is stored in the KB, the better the system performs. When typing in the Google search box, one of the most common examples of an ES is a suggestion of spelling problems.
The following is a block diagram that depicts how an expert system works:
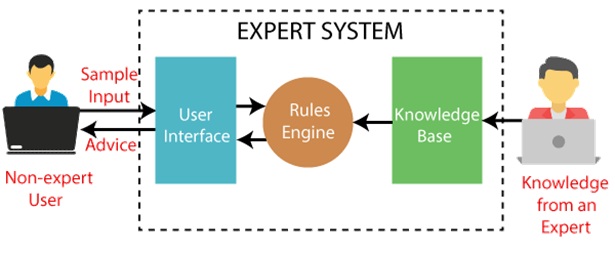
Fig 1: Expert system
Characteristics of Expert System
● High Efficiency and Accuracy - The expert system provides high efficiency and accuracy when addressing any type of complex problem in a specified domain.
● Understandable - It replies in a way that the user can easily comprehend. It can accept human-language input and produce human-language output.
● Reliable - It is really dependable in terms of producing an efficient and accurate result.
● Highly responsive - ES returns the answer to any sophisticated query in a matter of seconds.
Key takeaway
Expert systems are computer programs that are designed to tackle complicated issues in a certain domain at a level of human intellect and expertise.
An expert system is a piece of software that can deal with difficult problems and make choices in the same way as a human expert can.
Inference is used in First-Order Logic to generate new facts or sentences from current ones. It's crucial to understand some basic FOL terms before diving into the FOL inference rule.
Substitution:
Substitution is a fundamental approach for modifying phrases and formulations. All first-order logic inference systems contain it. The substitution becomes more difficult when there are quantifiers in FOL. We refer to the replacement of a constant "a" for the variable "x" when we write F[a/x].
Equality:
Atomic sentences are generated in First-Order Logic not only through the employment of predicate and words, but also through the application of equality. We can do this by using equality symbols, which indicate that the two terms relate to the same thing.
FOL inference rules for quantifier:
Because inference rules in first-order logic are comparable to those in propositional logic, below are some basic inference rules in FOL:
● Universal Generalization
● Universal Instantiation
● Existential Instantiation
● Existential introduction
Universal Generalization:
- Universal generalization is a valid inference rule that states that if premise P(c) is true for any arbitrary element c in the universe of discourse, we can arrive at the conclusion x P. (x).
- It can be represented as:
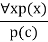
- If we want to prove that every element has a similar property, we can apply this rule.
- x must not be used as a free variable in this rule.
Example: Let's represent, P(c): "A byte contains 8 bits", so for ∀ x P(x) "All bytes contain 8 bits.", it will also be true.
Universal Instantiation:
- Universal instantiation, often known as universal elimination or UI, is a valid inference rule. It can be used numerous times to add more sentences.
- The new knowledge base is logically equivalent to the previous one.
- We can infer any phrase by replacing a ground word for the variable, according to the UI.
- According to the UI rule, any phrase P(c) can be inferred by substituting a ground term c (a constant inside domain x) for any object in the universe of discourse in x P(x).
- It can be represented as:
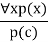
Example: IF "Every person like ice-cream"=> ∀x P(x) so we can infer that
"John likes ice-cream" => P(c)
Existential Instantiation:
- Existential Elimination, also known as Existential Instantiation, is a valid first-order logic inference rule.
- It can only be used once to substitute for the existential sentence.
- Despite the fact that the new KB is not conceptually identical to the previous KB, it will suffice if the old KB was.
- This rule states that one can infer P(c) from the formula given in the form of ∃x P(x) for a new constant symbol c.
- The only constraint with this rule is that c must be a new word for which P(c) is true.
- It can be represented as:
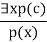
Existential introduction
- An existential generalization, also known as an existential introduction, is a valid inference rule in first-order logic.
- If some element c in the world of discourse has the characteristic P, we can infer that something else in the universe has the attribute P, according to this rule.
- It can be represented as:
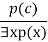
Example: Let's say that,
"Pritisha got good marks in English."
"Therefore, someone got good marks in English."
Propositional vs. First-Order Inference
Previously, inference in first order logic was checked via propositionalization, which is the act of turning the Knowledge Base included in first order logic into propositional logic and then utilizing any of the propositional logic inference mechanisms to check inference.
Inference rules for quantifiers:
To get sentences without quantifiers, several inference techniques can be applied to sentences containing quantifiers. We'll be able to make the conversion if we follow these requirements.
Universal Instantiation (UI):
The rule states that by substituting a ground word (a term without variables) for the variable, we can deduce any sentence. Let SUBST () stand for the outcome of the substitution on the sentence a. The rule is then written.
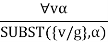
For any v and g ground term combinations. For example, in the knowledge base, there is a statement that states that all greedy rulers are Evil.
x King(x)A Greedy(x) Evil(x)
For the variable x, with the substitutions like {x/John}, {x/Richard} the following sentences can be inferred
King(John) A Greedy(John) Evil(John)
King(Richard) A Greedy(Richard) Evil(Richard)
As a result, the set of all potential instantiations can be used to substitute a globally quantified phrase.
Existential Instantiation (EI):
The existential statement states that there is some object that fulfills a requirement, and that the instantiation process is simply giving that object a name that does not already belong to another object. A Skolem constant is the moniker given to this new name. Existential Instantiation is a subset of a broader process known as "skolemization."
If the statement a, variable v, and constant symbol k do not occur anywhere else in the knowledge base,
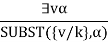
For example, from the sentence
3x Crown(x)A OnHead(x, John)
So we can infer the sentence
Crown(C1)A OnHead(C1, John)
As long as C1 does not appear elsewhere in the knowledge base. Thus, an existentially quantified sentence can be replaced by one instantiation
Elimination of Universal and Existential quantifiers should give new knowledge base which can be shown to be inferentially equivalent to old in the sense that it is satisfiable exactly when the original knowledge base is satisfiable.
Key takeaway
In First-Order Logic, inference is used to derive new facts or sentences from existing ones.
In First-Order Logic, atomic sentences are formed not only via the use of predicate and words, but also via the application of equality.
There are some Inference rules that can be applied to sentences with quantifiers to obtain sentences without quantifiers.
Knowledge acquisition is the process of gathering or collecting information from a variety of sources. It refers to the process of adding new information to a knowledge base while simultaneously refining or upgrading current information. Acquisition is the process of increasing a system's capabilities or improving its performance at a certain activity.
As a result, it is the creation and refinement of knowledge toward a certain goal. Acquired knowledge contains facts, rules, concepts, procedures, heuristics, formulas, correlations, statistics, and any other important information. Experts in the field, text books, technical papers, database reports, periodicals, and the environment are all possible sources of this knowledge.
Knowledge acquisition is a continuous process that takes place throughout a person's life. Knowledge acquisition is exemplified via machine learning. It could be a method of self-study or refining aided by computer programs. The newly acquired knowledge should be meaningfully linked to previously acquired knowledge.
The data should be accurate, non-redundant, consistent, and thorough. Knowledge acquisition helps with tasks like knowledge entry and knowledge base upkeep. The knowledge acquisition process builds dynamic data structures in order to refine current information.
The knowledge engineer's role is equally important in the development of knowledge refinements. Knowledge engineers are professionals who elicit knowledge from specialists. They write and edit code, operate several interactive tools, and create a knowledge base, among other things, to combine knowledge from multiple sources.
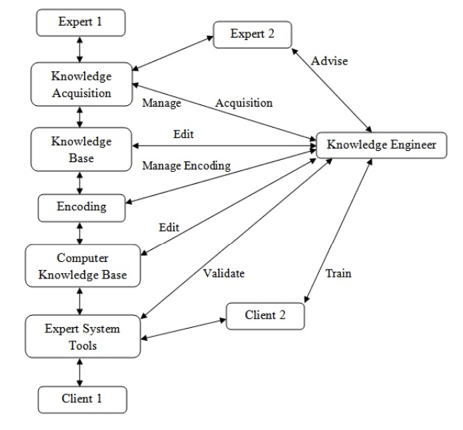
Fig 2: Knowledge Engineer’s Roles in Interactive Knowledge Acquisition
Key takeaway
- The gathering or collection of knowledge from multiple sources is known as knowledge acquisition.
- Knowledge acquisition is an ongoing process that spans a person's entire life.
- Machine learning is an example of knowledge acquisition.
A knowledge-based system (KBS) is a computer programme that collects and applies information from various sources. Artificial intelligence aids in the solution of problems, particularly difficult challenges, with a KBS. These systems are largely used to assist humans in making decisions, learning, and doing other tasks.
A knowledge-based system is a popular artificial intelligence application. These systems are capable of making decisions based on the data and information in their databases. They can also understand the context of the data being processed.
An interface engine plus a knowledge base make up a knowledge-based system. The interface engine serves as a search engine, while the knowledge base serves as a knowledge repository. Learning is an important part of any knowledge-based system, and learning simulation helps to enhance it over time. Expert systems, intelligent tutoring systems, hypertext manipulation systems, CASE-based systems, and databases with an intelligent user interface are all examples of knowledge-based systems.
The following are examples of knowledge-based systems:
● Medical diagnosis systems - There are systems that can assist with disease diagnosis, such as Mycin, one of the earliest KBS. Such algorithms can identify likely diagnoses (and include a confidence level around the diagnosis) as well as make therapy suggestions by inputting data or answering a series of questions.
● Eligibility analysis systems - It is possible to determine whether a person is eligible for a particular service by answering guided questions. When determining eligibility, a system would ask questions until it received an answer that was processed as disqualifying, and then transmit that information to the individual, all without the requirement for a third-party person's involvement.
● Blackboard systems - A blackboard system, in contrast to other KBS, is highly reliant on updates from human specialists. A varied collection of people will collaborate to discover the best answer to an issue. Each individual will update the blackboard with a partial solution as they work on the problem until it is eventually solved.
● Classification systems - KBS can also be used to examine various pieces of information in order to determine their classification status. For example, by studying mass spectra and chemical components, information might be inputted to determine distinct chemical compounds.
Key takeaway
A knowledge-based system (KBS) is a computer programme that collects and applies information from various sources. Artificial intelligence aids in the solution of problems, particularly difficult challenges, with a KBS.
Automated reasoning is a generic method that provides an orderly framework for machine learning algorithms to conceive, approach, and solve problems. Automated reasoning underpins several machine learning approaches, such as logic programming, fuzzy logic, Bayesian inference, and maximal entropy reasoning, and is more of a theoretical field of research than a specific technique. The ultimate goal is to develop deep learning systems capable of simulating human deduction without the need for human intervention.
The field of automated reasoning is dedicated to studying diverse elements of reasoning in computer science, particularly in knowledge representation and reasoning and meta logic. Automated reasoning research aids in the development of computer programmes that enable computers to reason totally or nearly completely automatically. Although automated reasoning is classified as an artificial intelligence subfield, it also has ties to theoretical computer science and philosophy.
Automated theorem proving (including the less automated but more pragmatic subcategory of interactive theorem proving) and automated proof checking are the most developed subfields of automated reasoning (viewed as guaranteed correct reasoning under fixed assumptions). Induction and abduction have also been used extensively in reasoning through analogy.
Classical logics and calculi, fuzzy logic, Bayesian inference, reasoning with maximum entropy, and many less formal ad hoc procedures are all examples of automated reasoning tools and techniques.
How is Automated Reasoning Created?
There are numerous methods of reasoning, but all frameworks require:
● Problem Domain - Define in mathematical terms the problems that the software will be required to solve.
● Language - Choose the programming language, logic, and functions that will be used by the programme to represent the training data as well as new data inferred by it.
● Deduction Calculus - Describe the method and tools that the software will employ to analyze data and draw conclusions.
● Resolution - Create a control flow method to efficiently complete all of these calculations.
Application
For the most part, automated reasoning has been employed to create automated theorem provers. Theorem provers, on the other hand, frequently require human assistance to be effective and hence fall within the category of proof assistants. In some circumstances, such provers have devised novel methods for proving a theorem. A good example of this is Logic Theorist. The software devised a proof for one of the theorems in Principia Mathematica that was more efficient (in terms of steps) than Whitehead and Russell's proof.
Automated reasoning programmes are being used to tackle an increasing number of issues in formal logic, mathematics and computer science, logic programming, software and hardware verification, circuit design, and a variety of other fields. Sutcliffe and Suttner's TPTP (Sutcliffe and Suttner, 1998) is a library of similar problems that is regularly updated. A competition for automated theorem provers is organized every year at the CADE conference (Pelletier, Sutcliffe, and Suttner 2002), using problems chosen from the TPTP collection.
Key takeaway
Automated reasoning is a generic method that provides an orderly framework for machine learning algorithms to conceive, approach, and solve problems. Automated reasoning underpins several machine learning approaches, such as logic programming, fuzzy logic, Bayesian inference, and maximal entropy reasoning, and is more of a theoretical field of research than a specific technique.
Natural Language Processing (NLP) is an artificial intelligence (AI) way of communicating with intelligent computers using natural language such as English.
Natural language processing is essential when you want an intelligent system, such as a robot, to follow your commands, when you want to hear a decision from a dialogue-based clinical expert system, and so on.
Computational linguistics—rule-based human language modeling—is combined with statistical, machine learning, and deep learning models in NLP. These technologies, when used together, allow computers to process human language in the form of text or speech data and 'understand' its full meaning, including the speaker's or writer's intent and sentiment.
NLP is used to power computer programmes that translate text from one language to another, respond to spoken commands, and quickly summarise vast amounts of material—even in real time. Voice-activated GPS systems, digital assistants, speech-to-text dictation software, customer care chatbots, and other consumer conveniences are all examples of NLP in action. However, NLP is increasingly being used in corporate solutions to help businesses streamline operations, boost employee productivity, and simplify mission-critical business processes.
An NLP system's input and output can be anything -
● Speech
● Written Text
Components of NLP
As stated previously, NLP has two components. −
Natural Language Understanding (NLU)
The following tasks are required for comprehension:
● Translating natural language input into meaningful representations.
● Examining many features of the language.
Natural Language Generation (NLG)
It's the process of turning some internal information into meaningful words and sentences in natural language.
It involves −
● Text planning − It comprises obtaining appropriate content from the knowledge base as part of the text planning process.
● Sentence planning − Sentence planning entails selecting necessary words, generating meaningful phrases, and determining the tone of the sentence.
● Text Realization − It is the mapping of a sentence plan into a sentence structure that is known as text realization.
The NLU is more difficult than the NLG.
NLP Terminology
● Phonology - It is the systematic organization of sounds.
● Morphology - It is the study of how words are constructed from simple meaningful units.
● Morpheme − In a language, a morphe is a basic unit of meaning.
● Syntax - It is the process of putting words together to form a sentence. It also entails figuring out what structural role words have in sentences and phrases.
● Semantics - It is the study of the meaning of words and how to put them together to form meaningful phrases and sentences.
● Pragmatics - It is the study of how to use and understand sentences in various settings, as well as how this affects the sentence's meaning.
● Discourse - It is concerned with how the prior sentence influences the interpretation of the following sentence.
● World Knowledge − The term "world knowledge" refers to general knowledge about the world.
NLP Tasks
Because human language is riddled with ambiguities, writing software that accurately interprets the intended meaning of text or voice input is extremely challenging. Homonyms, homophones, sarcasm, idioms, metaphors, grammar and usage exceptions, sentence structure variations—these are just a few of the irregularities in human language that take humans years to learn, but that programmers must teach natural language-driven applications to recognise and understand accurately from the start if those applications are to be useful.
Several NLP activities help the machine understand what it's absorbing by breaking down human text and speech input in ways that the computer can understand. The following are some of these responsibilities:
● Speech recognition, The task of consistently turning voice data into text data is known as speech recognition, or speech-to-text. Any programme that follows voice commands or responds to spoken questions requires speech recognition. The way individuals speak—quickly, slurring words together, with varied emphasis and intonation, in diverse dialects, and frequently using improper grammar—makes speech recognition particularly difficult.
● Part of speech tagging, The method of determining the part of speech of a particular word or piece of text based on its use and context is known as part of speech tagging, or grammatical tagging. 'Make' is a verb in 'I can make a paper aircraft,' and a noun in 'What make of car do you own?' according to part of speech.
● Natural language generation is the job of converting structured data into human language; it is frequently referred to as the polar opposite of voice recognition or speech-to-text.
● Word sense disambiguation is the process of determining the meaning of a word with several meanings using a semantic analysis procedure to discover which word makes the most sense in the current context. The meaning of the verb 'make' in 'make the grade' (achieve) vs.'make a bet', for example, can be distinguished via word sense disambiguation (place).
● NEM (named entity recognition) is a technique for recognising words or sentences as useful entities. 'Kentucky' is a region, and 'Fred' is a man's name, according to NEM.
References:
- Introduction to Artificial Intelligence & Expert Systems, Dan W Patterson, PHI.,2010
- S Kaushik, Artificial Intelligence, Cengage Learning, 1st ed.2011
- Stuart Russell, Peter Norvig, Artificial Intelligence -A Modern Approach, 2/e, Pearson, 2003.
Unit - 6
Expert Systems
Expert systems are computer programs that are designed to tackle complicated issues in a certain domain at a level of human intellect and expertise.
An expert system is a piece of software that can deal with difficult problems and make choices in the same way as a human expert can. It achieves it by using reasoning and inference techniques to retrieve knowledge from its knowledge base based on the user's requests.
The performance of an expert system is based on the knowledge stored in its knowledge base by the expert. The better the system functions, the more knowledge is saved in the KB. When typing in the Google search box, one of the most common examples of an ES is a suggestion of spelling problems.
An expert system is a computer simulation of a human expert. It can alternatively be described as a computer software that imitates the judgment and conduct of a human or an organization with substantial knowledge and experience in a certain field.
In such a system, a knowledge base containing accumulated experience and a set of rules for applying the knowledge base to each specific case presented to the program are usually provided. Expert systems also leverage human knowledge to solve problems that would normally necessitate human intelligence. These expert systems use computers to transmit expertise knowledge as data or rules.
The expert system is a type of AI, and the first ES was created in 1970, making it the first successful artificial intelligence approach. As an expert, it solves the most difficult problems by extracting knowledge from its knowledge base. Like a human expert, the system assists in decision making for complex problems by employing both facts and heuristics. It is so named because it comprises expert knowledge of a certain subject and is capable of solving any complex problem in that domain. These systems are tailored to a particular field, such as medicine or science.
An expert system's performance is determined on the knowledge stored in its knowledge base by the expert. The more knowledge that is stored in the KB, the better the system performs. When typing in the Google search box, one of the most common examples of an ES is a suggestion of spelling problems.
The following is a block diagram that depicts how an expert system works:
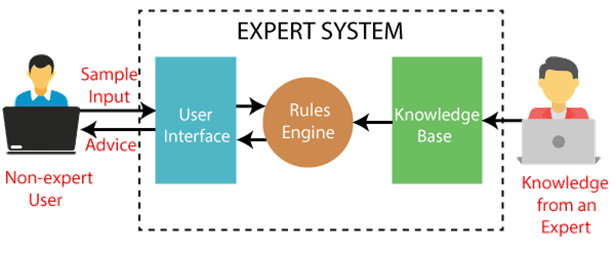
Fig 1: Expert system
Characteristics of Expert System
● High Efficiency and Accuracy - The expert system provides high efficiency and accuracy when addressing any type of complex problem in a specified domain.
● Understandable - It replies in a way that the user can easily comprehend. It can accept human-language input and produce human-language output.
● Reliable - It is really dependable in terms of producing an efficient and accurate result.
● Highly responsive - ES returns the answer to any sophisticated query in a matter of seconds.
Key takeaway
Expert systems are computer programs that are designed to tackle complicated issues in a certain domain at a level of human intellect and expertise.
An expert system is a piece of software that can deal with difficult problems and make choices in the same way as a human expert can.
Inference is used in First-Order Logic to generate new facts or sentences from current ones. It's crucial to understand some basic FOL terms before diving into the FOL inference rule.
Substitution:
Substitution is a fundamental approach for modifying phrases and formulations. All first-order logic inference systems contain it. The substitution becomes more difficult when there are quantifiers in FOL. We refer to the replacement of a constant "a" for the variable "x" when we write F[a/x].
Equality:
Atomic sentences are generated in First-Order Logic not only through the employment of predicate and words, but also through the application of equality. We can do this by using equality symbols, which indicate that the two terms relate to the same thing.
FOL inference rules for quantifier:
Because inference rules in first-order logic are comparable to those in propositional logic, below are some basic inference rules in FOL:
● Universal Generalization
● Universal Instantiation
● Existential Instantiation
● Existential introduction
Universal Generalization:
- Universal generalization is a valid inference rule that states that if premise P(c) is true for any arbitrary element c in the universe of discourse, we can arrive at the conclusion x P. (x).
- It can be represented as:

- If we want to prove that every element has a similar property, we can apply this rule.
- x must not be used as a free variable in this rule.
Example: Let's represent, P(c): "A byte contains 8 bits", so for ∀ x P(x) "All bytes contain 8 bits.", it will also be true.
Universal Instantiation:
- Universal instantiation, often known as universal elimination or UI, is a valid inference rule. It can be used numerous times to add more sentences.
- The new knowledge base is logically equivalent to the previous one.
- We can infer any phrase by replacing a ground word for the variable, according to the UI.
- According to the UI rule, any phrase P(c) can be inferred by substituting a ground term c (a constant inside domain x) for any object in the universe of discourse in x P(x).
- It can be represented as:
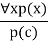
Example: IF "Every person like ice-cream"=> ∀x P(x) so we can infer that
"John likes ice-cream" => P(c)
Existential Instantiation:
- Existential Elimination, also known as Existential Instantiation, is a valid first-order logic inference rule.
- It can only be used once to substitute for the existential sentence.
- Despite the fact that the new KB is not conceptually identical to the previous KB, it will suffice if the old KB was.
- This rule states that one can infer P(c) from the formula given in the form of ∃x P(x) for a new constant symbol c.
- The only constraint with this rule is that c must be a new word for which P(c) is true.
- It can be represented as:
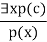
Existential introduction
- An existential generalization, also known as an existential introduction, is a valid inference rule in first-order logic.
- If some element c in the world of discourse has the characteristic P, we can infer that something else in the universe has the attribute P, according to this rule.
- It can be represented as:
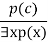
Example: Let's say that,
"Pritisha got good marks in English."
"Therefore, someone got good marks in English."
Propositional vs. First-Order Inference
Previously, inference in first order logic was checked via propositionalization, which is the act of turning the Knowledge Base included in first order logic into propositional logic and then utilizing any of the propositional logic inference mechanisms to check inference.
Inference rules for quantifiers:
To get sentences without quantifiers, several inference techniques can be applied to sentences containing quantifiers. We'll be able to make the conversion if we follow these requirements.
Universal Instantiation (UI):
The rule states that by substituting a ground word (a term without variables) for the variable, we can deduce any sentence. Let SUBST () stand for the outcome of the substitution on the sentence a. The rule is then written.
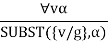
For any v and g ground term combinations. For example, in the knowledge base, there is a statement that states that all greedy rulers are Evil.
x King(x)A Greedy(x) Evil(x)
For the variable x, with the substitutions like {x/John}, {x/Richard} the following sentences can be inferred
King(John) A Greedy(John) Evil(John)
King(Richard) A Greedy(Richard) Evil(Richard)
As a result, the set of all potential instantiations can be used to substitute a globally quantified phrase.
Existential Instantiation (EI):
The existential statement states that there is some object that fulfills a requirement, and that the instantiation process is simply giving that object a name that does not already belong to another object. A Skolem constant is the moniker given to this new name. Existential Instantiation is a subset of a broader process known as "skolemization."
If the statement a, variable v, and constant symbol k do not occur anywhere else in the knowledge base,
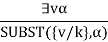
For example, from the sentence
3x Crown(x)A OnHead(x, John)
So we can infer the sentence
Crown(C1)A OnHead(C1, John)
As long as C1 does not appear elsewhere in the knowledge base. Thus, an existentially quantified sentence can be replaced by one instantiation
Elimination of Universal and Existential quantifiers should give new knowledge base which can be shown to be inferentially equivalent to old in the sense that it is satisfiable exactly when the original knowledge base is satisfiable.
Key takeaway
In First-Order Logic, inference is used to derive new facts or sentences from existing ones.
In First-Order Logic, atomic sentences are formed not only via the use of predicate and words, but also via the application of equality.
There are some Inference rules that can be applied to sentences with quantifiers to obtain sentences without quantifiers.
Knowledge acquisition is the process of gathering or collecting information from a variety of sources. It refers to the process of adding new information to a knowledge base while simultaneously refining or upgrading current information. Acquisition is the process of increasing a system's capabilities or improving its performance at a certain activity.
As a result, it is the creation and refinement of knowledge toward a certain goal. Acquired knowledge contains facts, rules, concepts, procedures, heuristics, formulas, correlations, statistics, and any other important information. Experts in the field, text books, technical papers, database reports, periodicals, and the environment are all possible sources of this knowledge.
Knowledge acquisition is a continuous process that takes place throughout a person's life. Knowledge acquisition is exemplified via machine learning. It could be a method of self-study or refining aided by computer programs. The newly acquired knowledge should be meaningfully linked to previously acquired knowledge.
The data should be accurate, non-redundant, consistent, and thorough. Knowledge acquisition helps with tasks like knowledge entry and knowledge base upkeep. The knowledge acquisition process builds dynamic data structures in order to refine current information.
The knowledge engineer's role is equally important in the development of knowledge refinements. Knowledge engineers are professionals who elicit knowledge from specialists. They write and edit code, operate several interactive tools, and create a knowledge base, among other things, to combine knowledge from multiple sources.
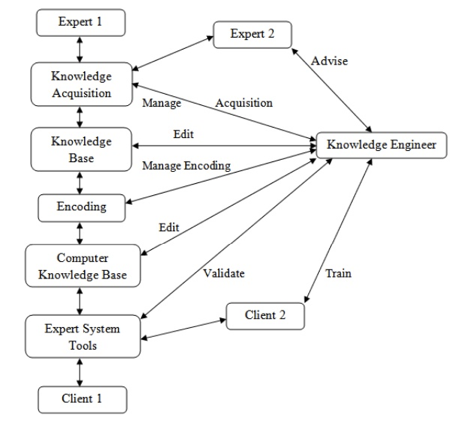
Fig 2: Knowledge Engineer’s Roles in Interactive Knowledge Acquisition
Key takeaway
- The gathering or collection of knowledge from multiple sources is known as knowledge acquisition.
- Knowledge acquisition is an ongoing process that spans a person's entire life.
- Machine learning is an example of knowledge acquisition.
A knowledge-based system (KBS) is a computer programme that collects and applies information from various sources. Artificial intelligence aids in the solution of problems, particularly difficult challenges, with a KBS. These systems are largely used to assist humans in making decisions, learning, and doing other tasks.
A knowledge-based system is a popular artificial intelligence application. These systems are capable of making decisions based on the data and information in their databases. They can also understand the context of the data being processed.
An interface engine plus a knowledge base make up a knowledge-based system. The interface engine serves as a search engine, while the knowledge base serves as a knowledge repository. Learning is an important part of any knowledge-based system, and learning simulation helps to enhance it over time. Expert systems, intelligent tutoring systems, hypertext manipulation systems, CASE-based systems, and databases with an intelligent user interface are all examples of knowledge-based systems.
The following are examples of knowledge-based systems:
● Medical diagnosis systems - There are systems that can assist with disease diagnosis, such as Mycin, one of the earliest KBS. Such algorithms can identify likely diagnoses (and include a confidence level around the diagnosis) as well as make therapy suggestions by inputting data or answering a series of questions.
● Eligibility analysis systems - It is possible to determine whether a person is eligible for a particular service by answering guided questions. When determining eligibility, a system would ask questions until it received an answer that was processed as disqualifying, and then transmit that information to the individual, all without the requirement for a third-party person's involvement.
● Blackboard systems - A blackboard system, in contrast to other KBS, is highly reliant on updates from human specialists. A varied collection of people will collaborate to discover the best answer to an issue. Each individual will update the blackboard with a partial solution as they work on the problem until it is eventually solved.
● Classification systems - KBS can also be used to examine various pieces of information in order to determine their classification status. For example, by studying mass spectra and chemical components, information might be inputted to determine distinct chemical compounds.
Key takeaway
A knowledge-based system (KBS) is a computer programme that collects and applies information from various sources. Artificial intelligence aids in the solution of problems, particularly difficult challenges, with a KBS.
Automated reasoning is a generic method that provides an orderly framework for machine learning algorithms to conceive, approach, and solve problems. Automated reasoning underpins several machine learning approaches, such as logic programming, fuzzy logic, Bayesian inference, and maximal entropy reasoning, and is more of a theoretical field of research than a specific technique. The ultimate goal is to develop deep learning systems capable of simulating human deduction without the need for human intervention.
The field of automated reasoning is dedicated to studying diverse elements of reasoning in computer science, particularly in knowledge representation and reasoning and meta logic. Automated reasoning research aids in the development of computer programmes that enable computers to reason totally or nearly completely automatically. Although automated reasoning is classified as an artificial intelligence subfield, it also has ties to theoretical computer science and philosophy.
Automated theorem proving (including the less automated but more pragmatic subcategory of interactive theorem proving) and automated proof checking are the most developed subfields of automated reasoning (viewed as guaranteed correct reasoning under fixed assumptions). Induction and abduction have also been used extensively in reasoning through analogy.
Classical logics and calculi, fuzzy logic, Bayesian inference, reasoning with maximum entropy, and many less formal ad hoc procedures are all examples of automated reasoning tools and techniques.
How is Automated Reasoning Created?
There are numerous methods of reasoning, but all frameworks require:
● Problem Domain - Define in mathematical terms the problems that the software will be required to solve.
● Language - Choose the programming language, logic, and functions that will be used by the programme to represent the training data as well as new data inferred by it.
● Deduction Calculus - Describe the method and tools that the software will employ to analyze data and draw conclusions.
● Resolution - Create a control flow method to efficiently complete all of these calculations.
Application
For the most part, automated reasoning has been employed to create automated theorem provers. Theorem provers, on the other hand, frequently require human assistance to be effective and hence fall within the category of proof assistants. In some circumstances, such provers have devised novel methods for proving a theorem. A good example of this is Logic Theorist. The software devised a proof for one of the theorems in Principia Mathematica that was more efficient (in terms of steps) than Whitehead and Russell's proof.
Automated reasoning programmes are being used to tackle an increasing number of issues in formal logic, mathematics and computer science, logic programming, software and hardware verification, circuit design, and a variety of other fields. Sutcliffe and Suttner's TPTP (Sutcliffe and Suttner, 1998) is a library of similar problems that is regularly updated. A competition for automated theorem provers is organized every year at the CADE conference (Pelletier, Sutcliffe, and Suttner 2002), using problems chosen from the TPTP collection.
Key takeaway
Automated reasoning is a generic method that provides an orderly framework for machine learning algorithms to conceive, approach, and solve problems. Automated reasoning underpins several machine learning approaches, such as logic programming, fuzzy logic, Bayesian inference, and maximal entropy reasoning, and is more of a theoretical field of research than a specific technique.
Natural Language Processing (NLP) is an artificial intelligence (AI) way of communicating with intelligent computers using natural language such as English.
Natural language processing is essential when you want an intelligent system, such as a robot, to follow your commands, when you want to hear a decision from a dialogue-based clinical expert system, and so on.
Computational linguistics—rule-based human language modeling—is combined with statistical, machine learning, and deep learning models in NLP. These technologies, when used together, allow computers to process human language in the form of text or speech data and 'understand' its full meaning, including the speaker's or writer's intent and sentiment.
NLP is used to power computer programmes that translate text from one language to another, respond to spoken commands, and quickly summarise vast amounts of material—even in real time. Voice-activated GPS systems, digital assistants, speech-to-text dictation software, customer care chatbots, and other consumer conveniences are all examples of NLP in action. However, NLP is increasingly being used in corporate solutions to help businesses streamline operations, boost employee productivity, and simplify mission-critical business processes.
An NLP system's input and output can be anything -
● Speech
● Written Text
Components of NLP
As stated previously, NLP has two components. −
Natural Language Understanding (NLU)
The following tasks are required for comprehension:
● Translating natural language input into meaningful representations.
● Examining many features of the language.
Natural Language Generation (NLG)
It's the process of turning some internal information into meaningful words and sentences in natural language.
It involves −
● Text planning − It comprises obtaining appropriate content from the knowledge base as part of the text planning process.
● Sentence planning − Sentence planning entails selecting necessary words, generating meaningful phrases, and determining the tone of the sentence.
● Text Realization − It is the mapping of a sentence plan into a sentence structure that is known as text realization.
The NLU is more difficult than the NLG.
NLP Terminology
● Phonology - It is the systematic organization of sounds.
● Morphology - It is the study of how words are constructed from simple meaningful units.
● Morpheme − In a language, a morphe is a basic unit of meaning.
● Syntax - It is the process of putting words together to form a sentence. It also entails figuring out what structural role words have in sentences and phrases.
● Semantics - It is the study of the meaning of words and how to put them together to form meaningful phrases and sentences.
● Pragmatics - It is the study of how to use and understand sentences in various settings, as well as how this affects the sentence's meaning.
● Discourse - It is concerned with how the prior sentence influences the interpretation of the following sentence.
● World Knowledge − The term "world knowledge" refers to general knowledge about the world.
NLP Tasks
Because human language is riddled with ambiguities, writing software that accurately interprets the intended meaning of text or voice input is extremely challenging. Homonyms, homophones, sarcasm, idioms, metaphors, grammar and usage exceptions, sentence structure variations—these are just a few of the irregularities in human language that take humans years to learn, but that programmers must teach natural language-driven applications to recognise and understand accurately from the start if those applications are to be useful.
Several NLP activities help the machine understand what it's absorbing by breaking down human text and speech input in ways that the computer can understand. The following are some of these responsibilities:
● Speech recognition, The task of consistently turning voice data into text data is known as speech recognition, or speech-to-text. Any programme that follows voice commands or responds to spoken questions requires speech recognition. The way individuals speak—quickly, slurring words together, with varied emphasis and intonation, in diverse dialects, and frequently using improper grammar—makes speech recognition particularly difficult.
● Part of speech tagging, The method of determining the part of speech of a particular word or piece of text based on its use and context is known as part of speech tagging, or grammatical tagging. 'Make' is a verb in 'I can make a paper aircraft,' and a noun in 'What make of car do you own?' according to part of speech.
● Natural language generation is the job of converting structured data into human language; it is frequently referred to as the polar opposite of voice recognition or speech-to-text.
● Word sense disambiguation is the process of determining the meaning of a word with several meanings using a semantic analysis procedure to discover which word makes the most sense in the current context. The meaning of the verb 'make' in 'make the grade' (achieve) vs.'make a bet', for example, can be distinguished via word sense disambiguation (place).
● NEM (named entity recognition) is a technique for recognising words or sentences as useful entities. 'Kentucky' is a region, and 'Fred' is a man's name, according to NEM.
References:
- Introduction to Artificial Intelligence & Expert Systems, Dan W Patterson, PHI.,2010
- S Kaushik, Artificial Intelligence, Cengage Learning, 1st ed.2011
- Stuart Russell, Peter Norvig, Artificial Intelligence -A Modern Approach, 2/e, Pearson, 2003.