UNIT 5
Higher Order Differential Equations
The linear homogeneous differential equation of the nth order with constant coefficients can be written as
Y(n) (x) + a1y(n-1)(x)+.....+an-1y’(x)+any(x) =0
Where a1,a2,…, an are constants which may be real or complex.
Using the linear differential operator L(D), this equation can be represented as
L(D)y(x)=0,
Where
L(D)=Dn +a1D(n-1)+⋯+an-1D+an.
Example 1:
Solve the differential equation y’’’+2y’’-y’-2y=0
Solution:
The corresponding characteristic equation is,
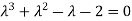
Solving it, we find the roots
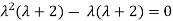
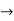
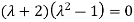
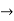
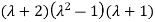 =0
=0
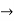
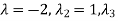 =-1
=-1
The general solution for the differential equation is
Y(x)= 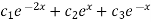
Where  are arbitrary constants.
are arbitrary constants.
Example 2:
Solve the equation y’’’+11y’-5y=0
Solution:
The characteristic equation of the give D.E is

Here one of the root is  then factorising the term
then factorising the term 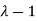 from the equation we obtain
from the equation we obtain
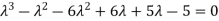
 (
(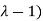 (
(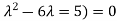
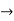 (
(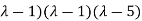 =0
=0
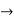 (
( (
(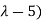 =0
=0
Thus the equation has two roots 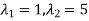
Hence the general equation of the D.E is
Y(x)=(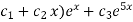
Where  are arbitrary constants.
are arbitrary constants.
This method is to solve the second order differential equations of the form:
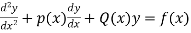
Where p(x),q(x)and f(x) are functions of x
The other form of equation is.,
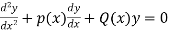
For the above D.E the general solutions are as follows
*The general solution of the homogeneous equation is ,
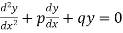
*particular solution for non-homogenous equation is,
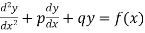
Example 1:
To find the general solution of 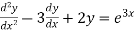
Solution:
The characteristic equation is r2 -3r+2 =0
The factors are (r-1)(r-2)=0
 r=1or r=2
r=1or r=2
Hence the general solution is A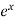 +B
+B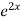
So in this case the fundamental solutions and their derivatives are as follows:
Y1(x) = ex
Y1’(x) = ex
Y2(x) =e2x
Y2’(x) =2.e2x
Example 2:
Find the general solution of the following D.E
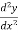 -y=2
-y=2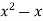 -3
-3
Solution :
Consider ,
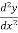 -y=0
-y=0
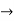 The characteristic equation is r2 -1 =0
The characteristic equation is r2 -1 =0
The factors are (r-1)(r+1)=0
 r= 1or-1
r= 1or-1
Hence the general solution is A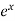 +B
+B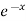
Y1(x) = ex
Y1’(x) =ex
Y2(x) =e-x
Y2’(x) =-e-x
Cauchy’s equation:
The most general form of Cauchy's equation is

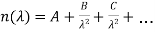
Where n is the refractive index, λ is the wavelength, A, B, C, etc., are coefficients that can be determined for a material by fitting the equation to measured refractive indices at known wavelengths. The coefficients are usually quoted for λ as the vacuum wavelength in micrometres.
Usually, it is sufficient to use a two-term form of the equation:
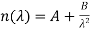
 where the coefficients A and B are determined specifically for this form of the equation.
where the coefficients A and B are determined specifically for this form of the equation.
The other form of cauchy’s euler equation is as stated,
Let y(n)(x) be the nth derivative of the unknown function y(x). Then a Cauchy–Euler equation of order n has the form
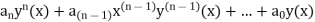
The most common Cauchy–Euler equates substitution x=eu (that is, u= ln(x) ; for x<0, one might replace all instances of x by 
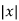 , which extends the solution's domain to
, which extends the solution's domain to 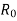
 ) may be used to reduce this equation to a linear differential equation with constant coefficients. Alternatively, the trial solution y=xm may be used to directly solve for the basic solutions.
) may be used to reduce this equation to a linear differential equation with constant coefficients. Alternatively, the trial solution y=xm may be used to directly solve for the basic solutions.
The second order Cauchy–Euler equation is
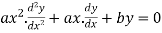
We assume a trial solution
Y=xm
Differentiating gives

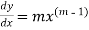
And
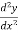 =m(m-1)x(m-2)
=m(m-1)x(m-2)

Substituting into the original equation leads to requiring
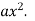 m(m-1)x(m-2)
m(m-1)x(m-2)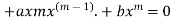
Rearranging and factoring gives the indicial equation
m2+m(a-1)=b=0
We then solve for m. There are three particular cases of interest:
Case #1 of two distinct roots, m1 and m2;
Case #2 of one real repeated root, m;
Case #3 of complex roots, α ± βi.
In case #1, the solution is
y= c1xm1 +c2xm2
In case #2, the solution is
C1xm .ln(x) +c2 xm
In case #3, the solution is
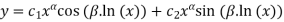
Where,
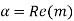
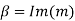
For c1 ,c2 R
R
This form of the solution is derived by setting x=et and using Euler’s formula.
Example 1:
Find the value of m for the following D.E
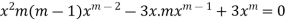

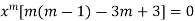
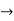 m (m-1)-3m+3=0
m (m-1)-3m+3=0
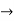 m2 – 4m +3=0
m2 – 4m +3=0
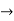 (m-1)(m-3)=0
(m-1)(m-3)=0
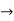 m= 1, 3
m= 1, 3
Example 2:
Solve y’=(y+1)x
= =x
=x
= 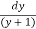 = xdx
= xdx
By integrating on both sides we get,
Ln(y+1) =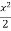 +c
+c
1+y=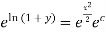
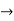 y(x)=
y(x)=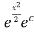 -1
-1
*Legendre’s homogeneous differential equation:
The Legendre differential equation is the second-order ordinary differential equation
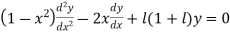 | (1) |
Which can be written as.,
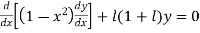 | (2) |
The above form is a special case of the so-called "associated Legendre differential equation" corresponding to the case m=0. The Legendre differential equation has regular singular points at -1, 1, and 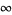 .
.
If the variable 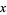 is replaced by cos
is replaced by cos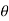 , then the Legendre differential equation becomes
, then the Legendre differential equation becomes
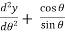  | (3) |
Example 1:
Find the Legendre’s equation for the following D.E
 -
-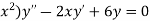
Solution:
n(l+n)=6 , n=2
c2 = -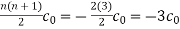
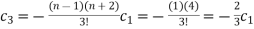
For k= 2,3,....
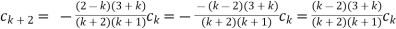
At k=2,  for m=2,3,.....
for m=2,3,.....
 the general solution is.,
the general solution is.,
Y=
= 
A simultaneous differential equation is one of the mathematical equations for an indefinite function of one or more than one variables that relate the values of the function. Differentiation of an equation in various orders. Differential equations play an important function in engineering, physics, economics, and other disciplines. This analysis concentrates on linear equations with Constant Coefficients.
Example 1:
Solve the given D.E
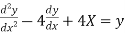
Solution:
The above equation can be writen as,
(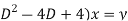 ....... (1)
....... (1)
(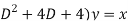 ........ (2)
........ (2)
Eliminating y from equations (1) and (2)
(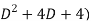 (
(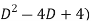 x=25x+16et
x=25x+16et
i.e.
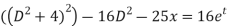
 (
(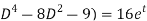

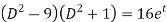
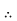 x=A.
x=A.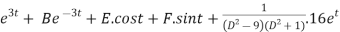
Thus the general equation is,
A.e3t +B.e-3t+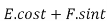 -et.
-et.
Example 2:
Solve the following equations using Legendre’s method:
(1).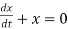
(2).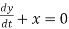
Solution:
Subtract eq(1)-eq(2)
i.e the given equations can be written as follow:
Dx+y=0......(1)
Dy+x=0.......(2)
(1)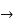 Dx+y=0 (
Dx+y=0 ( (2)
(2)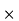 D
D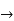 Dx+D2y=0
Dx+D2y=0
By subtracting the above two equations we get.,
y-D2y=0
 (D2 -1)y =0
(D2 -1)y =0
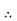 The general solution is given by,
The general solution is given by,
Aet+Be-t.
Example 1:
Verify that 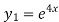 and
and 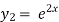 both satisfy the constant co-efficient linear homogeneous equation:
both satisfy the constant co-efficient linear homogeneous equation:
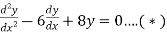
Solution:
Consider, 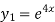
Deafferenting on both sides we get,
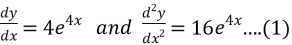
Now consider, 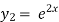
Differentiating on both sides we get,
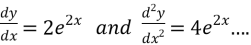 (2)
(2)
Substituting eq(1) and (2) in equation(*) we get the general solution as follow,
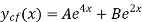
Example 2:
Find the order and degree of the following D.E

Solution:
Let x= sin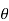 and y=sin
and y=sin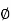
Then the given equation can be written as,

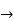 (
(
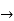 2cos
2cos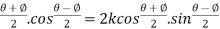
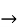
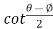
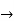
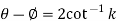
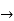
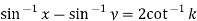
On differentiating both sides we get,
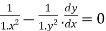
Thus the above equation completes the problem.
5.6.1. Applications of differential equations to oscillations of a spring:
It’s now time to take a look at an application of second order differential equations. We’re going to take a look at mechanical vibrations. In particular we are going to look at a mass that is hanging from a spring.
Vibrations can occur in pretty much all branches of engineering and so what we’re going to be doing here can be easily adapted to other situations, usually with just a change in notation.
Below is sketch of the spring with and without the object attached to it.
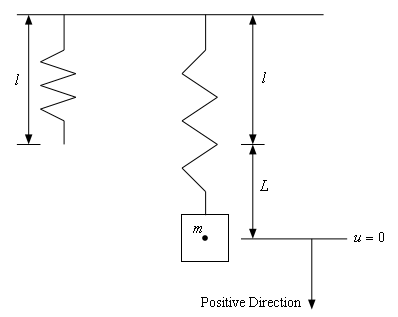
As denoted in the sketch we are going to assume that all forces, velocities, and displacements in the downward direction will be positive. All forces, velocities, and displacements in the upward direction will be negative.
Also, as shown in the sketch above, we will measure all displacement of the mass from its equilibrium position. Therefore, the u=0u=0 position will correspond to the center of gravity for the mass as it hangs on the spring and is at rest (i.e. no movement).
Now, we need to develop a differential equation that will give the displacement of the object at any time tt. First, recall Newton’s Second Law of Motion.
Ma=f
In this case we will use the second derivative of the displacement, uu, for the acceleration and so Newton<’s Second Law becomes,
Mu’’=F(t,u,u’)
We now need to determine all the forces that will act upon the object. There are four forces that we will assume act upon the object. Two that will always act on the object and two that may or may not act upon the object.
Here is a list of the forces that will act upon the object.
- Gravity, Fg
The force due to gravity will always act upon the object of course. This force is
Fg=mg
2. Spring, Fs
We are going to assume that Hooke’s Law will govern the force that the spring exerts on the object. This force will always be present as well and is
Fs=−k(L+u)
Example 1:
A spring with spring constant 18N/m is attached to a 2kg mass with negligible friction. Determine the period that the spring mass system will oscillate for any non-zero initial conditions.
Solution:
From above, we have a spring mass system modelled by the DE
2y’’ + 18y = 0 which has general solution given by
y(t) = 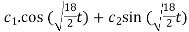 = c1 cos(3t)+c2 sin(3t)
= c1 cos(3t)+c2 sin(3t)
Since period of cost is 2π, then the period of cos(3t) and sin(3t) is 2π/ 3 .
Therefore, the period of c1 cos(3t) + c2 sin(3t) is also 2π /3 .
5.6.2 Applications of differential equations of oscillatory electric circuits:
As you probably already know, electric circuits can consist of a wide variety of complex components. These may be set up in series, or in parallel, or even as combinations of both. In this laboratory, however, we'll be considering only series circuits with especially simple components: resistors, inductors, and capacitors, along with some form of voltage supply.
The mathematics required to deal with such circuits goes a little beyond your high-school physics usage of Ohm's Law. After all, in these circuits the quantities of interest may be changing, and change implies that rates of change may get involved. It looks like once again we will be seeing equations involving derivatives—differential equations.
To start with, let's consider the picture of a simple series circuit in which one of each of the components that we mentioned above appears:

In this diagram we see each of the components that we just mentioned. The labels have the following meanings:
- L is a constant representing inductance, and is measured in henrys
- R is a constant representing resistance, and is measured in ohms
- C is a constant representing capacitance, and is measured in farads
- E represents the electromotive force, and is measured in volts. It is not necessarily a constant, and may be a function of time
Although they don't appear in the diagram, there are a few other quantities that will be involved in our analysis:
- q represents charge, and is measured in coulombs
- I represents current, and is measured in amperes
- t represents time, and is measured in seconds
So how do we start to find the relationships over time between these quantities? The key is to use Kirchoff's second law, which states:
The sum of the voltage drops across each component in a circuit is equal to the voltage, E, impressed upon the circuit.
Obviously then, in order to make use of this statement, we need to know what the voltage drop across each component is. Physics has the answer for us! Let's go through the components one at a time:
- The inductor: produces a voltage drop of
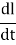 , or LI′.
, or LI′. - The resistor: produces a voltage drop of RI.
- The capacitor: produces a voltage drop of
 .
.
Restating Kirchhoff’s second law in abbreviated form, we get the following:
Sum of the voltage drops = E,
Which may be restated as
Inductor voltage drop + resistor voltage drop + capacitor voltage drop = E,
Into which we may substitute the actual voltage drops that we mentioned above, to get:
(1) | LI′ + RI + q/C = E. |
But, also according to physics, I = q′, so substituting, we can rewrite the equation purely in terms of the charge, q, rather than a mixture of charge and current:
(2) | Lq″ + Rq′ + q/C = E, |
Or alternatively, if we differentiate equation (1) and use the same substitution, we get an equation purely in terms of current:
(3) | L I″ + R I′ + I/C = E′. |
We will be mainly concerned with using the last of these three equivalent forms.
Notice that equation (3) is linear with constant coefficients, so in the case when
E′ = 0, (the homogeneous case), it may be solved very easily, even by hand.
The form of E′ will determine the method necessary when solving the non-homogeneous case by hand. We would need to use either undetermined coefficients, or variation of parameters. (Fortunately, in this laboratory we'll be letting the computer do the work for us.)
Example 1:
Two 9-volt batteries are connected to a series in which the inductance is ¼ henry and the resistance is 8 ohms. Determine the current i(t) if the initial current is zero.
Solution:
Given,
L= R=8 E(t)=18
R=8 E(t)=18
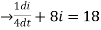
The requied D.E is,
L .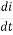 +Rt=E(t)
+Rt=E(t)
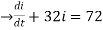
U(t) = 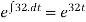
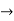
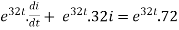
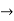 the above equation can be written as,
the above equation can be written as,
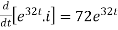
Beam deflection means the state of deformation of a beam from its original shape under the work of a force or load or weight. One of the most important applications of beam deflection is to obtain equations with which we can determine the accurate values of beam deflections in many practical cases. Deflections are also used in the analysis of statically indeterminate beams.
Methods to Determine Beam Deflection
Several methods are available for determining beam deflections. The principle is the same but differs in technique and in their immediate objective.
- Direct Integration Method
- Area moment Method
- Conjugate Beam Method
- Method of Superposition
Direct Integration Method:
Beam deflections due to bending are determined from deformation taking place along a span. This is based on the hypothesis that during bending, plane sections through a beam remains plain. For now, it will be assumed that bending takes place only about one of the principal axes of the cross-section. The edge view of the neutral surface of a deflected beam is called the elastic curve of the beam. The differential equation of the elastic curve of a beam:
EI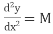
Some Boundary Conditions:
- Clamped or fixed support:

- Roller or pinned support:
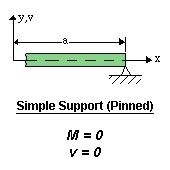
In this case. The end is free to rotate, that’s why the moment is zero.
3. Free end:
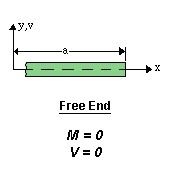
4. :Guided Support:

Example:
Given:
The rectangular beam, built in at the left end, having length, L, and cross-section of width, b, and height, h, is acted upon by a point load, P, at its free end.
Req'd: Determine the deflection at the end of the beam. 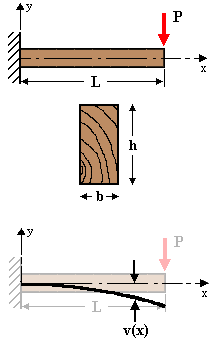
Sol'n: The bending moment in the beam is given by:
M(x)=-P(L-x)
Therefore the differential equation for bending is:
Elv”(x)=-P(L-x)
Integrating with respect to x
Elv’(x)=-P
Since the slope at the built-in end is zero, then
v’(x=0)=0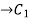 =0
=0
Integrating again gives:
Elv(x)= -P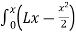 dx= -P
dx= -P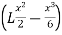 +
+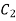
The deflection at the built-in end is zero, therefore:
v(x=0)=0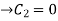 .
.
Therefore, the equation of the elastic curve is:
v(x)= 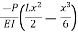
Deflection at the tip is then:
v(L)= =
=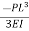
Since the sign of v(L) is negative, the deflection is downward.