Unit 2
Basic Electrical
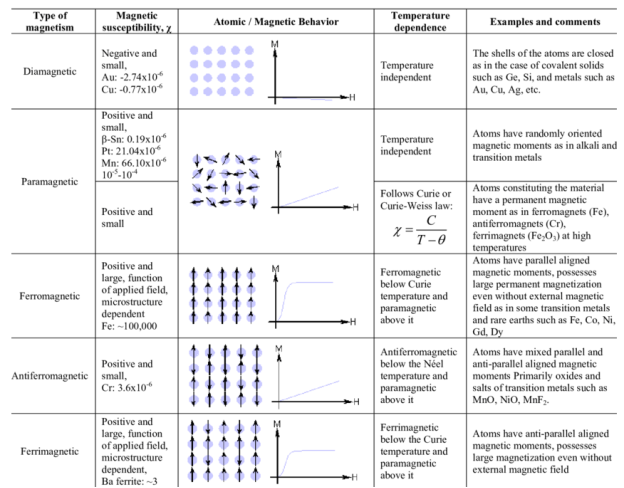
The number of magnetic lines of forces set up in a magnetic circuit is called Magnetic Flux. It is analogous to electric current, I in an electric circuit. Its SI unit is Weber (Wb) and its CGS unit is Maxwell. It is denoted by φB.
ΦB=B.S
ΦB=B.S Cos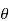
B – the magnitude of the magnetic field
S – area of surface
θ – angle between the magnetic field lines and perpendicular distance normal to the surface area
Magnetic flux for a closed surface
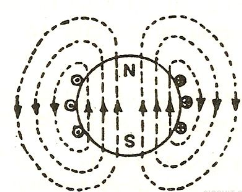
ΦB=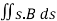
=0
Magnetic flux for open surface is
E=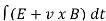
E=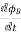
E – electromotive force
v – velocity of the boundary
E – electric field
B – magnetic field
øB- magnetic flux through the open surface
The magnetic flux through a closed surface is always zero, but in the open surface, it is not zero.
It is defined as the flux passing per unit area through a plane at right angles to the flux. It is denoted by B. Its unit is Weber/m2.
B=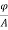 
Wb/m2
Isis also known as magnetic field strength. It is numerically equal to the force experienced by the N-pole of one weber placed at that point. It is denoted by H.
H=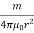 
A/m or N/Wb
The MMF is defined as the work done in moving the unit magnetic pole (1weber) once around the magnetic circuit.
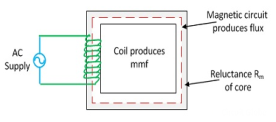
The magnetomotive force (MMF) is required to drive the magnetic flux in the magnetic circuit. The magnetic pressure, which sets up the magnetic flux in the circuit as called Magnetomotive Force. The SI unit of MMF is Ampere-turn (AT), and their CGS unit is G (gilbert). The MMF for the inductive coil shown in the figure below is expressed as
F=NI
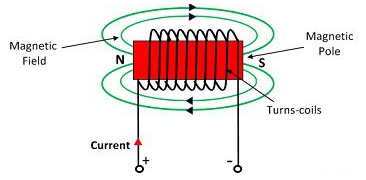
The strength of the MMF is equivalent to the product of the current around the turns and the number of turns of the coil.
The obstruction offered by a magnetic circuit to the magnetic flux is known as reluctance.
S=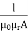
l – the length of the conductor
μo – permeability of vacuum which is equal to 4π Χ10-7 Henry/metre.
μr – relative permeability of the material.
A – cross-section area of the conductor.
Its SI unit is AT / Wb (ampere-turns / Weber)
Every medium is supposed to have two permittivities.
a) Absolute permitivitty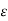 
b) Relative permittivity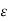 
r
To measure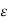 
rvacuum or free space is chosen. It has an absolute permittivity of 8.854 x 10-12 F/m. For any other medium
= 
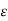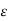0 
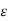r
The phenomenon of magnetism and electromagnetism depends on certain property of material called as permeability.Every medium is supposed to have two permeabilities.
a) Absolute permeability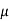
b) Relative permeability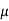
0
To measure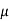 
r vacuum or free space is chosen. It has an absolute permeability of 4
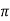x 10-7H/m. For any other medium
= 
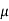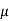0 
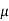r
Que)The amount of flux present in around magnetic bar was measured at 0.013 weber. If the material has a diameter of 14cm, calculate the flux density.
Sol: Area=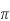
r2
Diameter=2r
r=14/2=7cm=0.07m
Area=3.14 x 0.072=0.0154m2
Flux Density B==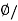
A=0.013/0.0154=0.843 Tesla
Que) Calculate the radius of the material having flux density of 0.5 T and flux present around the magnetic bar is 0.02T.
Sol: Flux Density B=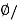
A
A=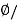
B=0.02/0.5=0.04 m2
Area=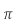
r2
r=0.113m
Que) A wire 2.5m long is bent into a square and into a circle. If the current flowing through the wire is 100 A, find the magnetizing force at the centre of the square and the centre of the circle?
Sol: Value of h at centre of square will be H=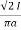
= 
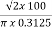=144 AT/m
Value of H at the centre of circle is H=I/2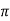
r
=125.6AT/m
Que) Calculate the magnetizing force and flux density at a distance of 4cm from a long straight circular conductor carrying a current of 250A and placed in air?
Sol: H=I/2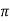
r
=250/2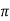
x 0.04=994.71 AT/m
B=μoH
=4
x10-7x994.71=1.25x10-3 Wb/m2
For magnetic circuits connected in series we can say that the total reluctance S is given as
S= S1+S2+S3+…..+Sn
Que) A closed magnetic circuit of cast steel contains a 6cm long path of cross-sectional area 1 cm2 and a 2cm path of cross sectional area 0.5 cm2. A coil of 200 turns is wound around the 6cm length of the circuit and a current of 0.4A flows. Determine the flux in the 2 cm path, if the relative permeability of the cast steel is 750?
Sol: For 6cm path:
S1 =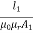 
= 
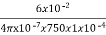= 6.37 x 105 /H
For 2cm path:
S2=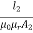 
= 
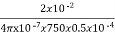= 4.24 x 105 /H
Total reluctance S= S1+S2 = 6.37 x 105+4.24 x 105= 10.61 x 105/H
S = mmf/φ
Φ = mmf/S = NI/S = (200x0.4)/(10.61 x 105) = 7.54x 10-5 Wb
Flux density in the 2cm path B=φ/A = 7.54x 10-5/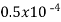
= 1.51 T
Leakage flux is a flux which follows a path not intended for it. Below shown is an iron ring wound with a coil having an air-gap. The flux in the air gap is known as useful flux because it is the only flux which is utilized. Air being the insulator of electricity is good magnetic conductor.
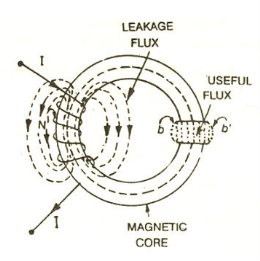
Leakage coefficient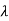 
= 
= 
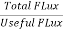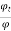
Magnetic leakage can be reduced by placing exciting coils very close to the air-gap. The spreading of lines of flux is called as fringing. This fringing increases the effective area of the air-gap.
Que)A laminated soft iron ring of relative permeability 800 has a mean circumference of 600mm and a cross sectional area of 400mm2. A radial air gap of 1mm width is cut in the ring which is wound with 800 turns. Calculate the current required to produce an air gap flux of 0.5mWb if leakage factor is 1.2 and stacking factor 0.9.
Sol: Required Ampere turn =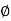 
gSg+ 
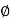iSi
=
+ 
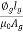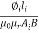
Air gap flux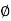 
s=0.5mWb
lg=1mm=1x10-3m
Ag=400mm2=400x10-6
Flux in iron ring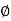 
i=1.2x0.5x10-3=0.6mWb
Net cross-sectional area = Ai x stacking factor=400x10-6 x 0.9=360x10-6
Total AT required=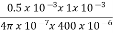
+ 
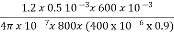= 994.72
I=A/N=994.72/800=1.24A
Que) An iron ring has X-section of 4cm2 and a mean diameter of 25cm. An air-gap of 0.3mm has been cut across the section of the ring. The ring is wound with a coil of 220 turns through which a current of 2A is passed. If the total magnetic flux is 0.24mWb, find relative permeability of iron?
Sol: φ=0.24mWb
A=4cm2=4 x 10-4
B=φ/A=0.24 x 10-3/4 x 10-4=0.6Wb/m2
AT for iron ring=H x l=(B/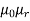
)/l=(0.6/
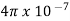x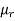
) x 0.25=1.19 x 105/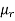
AT for air gap= H x l=( B/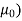
/l=(0.6/
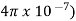x 0.3x10-3=143.24
Total AT required=(1.19 x 105/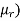
+143.24
Total AT provided=220 x 2=440
Therefore,
(1.19 x 105/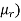
+143.24=440
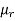= 400.99
In a magnetic circuit, this field is represented by magnetomotive force. It is analogous to the electromotive force in electrical circuit. This field is responsible to “set up” certain flux, which in turn gives rise to certain flux density B. Note that, here H is cause and B is its effect. The amount of flux which can be setup in a material is determined by an inherent property of the material, called as permeability, denoted by µ.
B = µH
When external magnetic field H is applied to a material, all the domains align in a particular direction, setting up net flux in the material. Due to domain alignment B (i.e. the magnitude of B) increases. However, after a certain value of B, the slope of B − H curve starts reducing as shown in Figure below
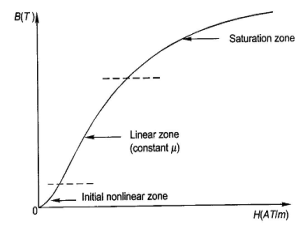
Fig: Magnetization curve
B-H Curve:
We cannot measure B and H directly. Further if we have transformer, we only have terminal measurements are with us. Hence, it is required to process the signals to get values of B and H. From Faraday’s law, V = N dφ/dt . Also, B is directly proportional to flux φ.
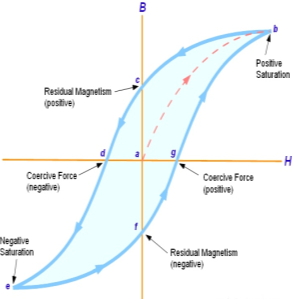
Fig: B-H curve
The lag or delay of a magnetic material known commonly as Magnetic Hysteresis.The Magnetic Hysteresis loop above, shows the behaviour of a ferromagnetic core graphically as the relationship between B and H is non-linear. Initially both B and H will be at zero, point 0 on the magnetisation curve.
If the magnetisation current, i is increased in a positive direction to some value than the magnetic field strength H increases linearly with i and the flux density B also increases (curve from point 0 to point a) as it heads towards saturation.
Now if the magnetising current in the coil is reduced to zero, the magnetic field circulating around the core also reduces to zero. However, the coils magnetic flux will not reach zero due to the residual magnetism present within the core and this is shown on the curve from point a to point b.
To reduce the flux density at point b to zero we need to reverse the current flowing through the coil. The magnetising force which must be applied to null the residual flux density is called a “Coercive Force”. This coercive force reverses the magnetic field re-arranging the molecular magnets until the core becomes unmagnetized at point c.
An increase in this reverse current causes the core to be magnetised in the opposite direction and increasing this magnetisation current further will cause the core to reach its saturation point but in the opposite direction, point d on the curve.
This point is symmetrical to point b. If the magnetising current is reduced again to zero the residual magnetism present in the core will be equal to the previous value but in reverse at point e.
Again, reversing the magnetising current flowing through the coil this time into a positive direction will cause the magnetic flux to reach zero, point f on the curve and as before increasing the magnetisation current further in a positive direction will cause the core to reach saturation at point a.
Then the B-H curve follows the path of a-b-c-d-e-f-a as the magnetising current flowing through the coil alternates between a positive and negative value such as the cycle of an AC voltage. This path is called a Magnetic Hysteresis Loop.
Discussed in above section.
