Unit - 4
Synchronous Machines
It is known that the electric supply used now-a-days for commercial, as well as domestic purposes, is of alternating type. Similar to d.c machines, the a.c machines associated with alternating voltages, are also classified as generators.
Machines generating ac EMF are called alternators or synchronous generators. While the machines accepting input from a.c supply to produce a mechanical output are called synchronous motors. Both these machines work at a specific constant speed called synchronous speed and hence is general called synchronous machines.
Construction of Synchronous Generator
In general, synchronous generator consists of two parts rotor and stator. The rotor part consists of field poles and stator part consists of armature conductors. The rotation of field poles in the presence of armature conductors induces an alternating voltage which results in electrical power generation.
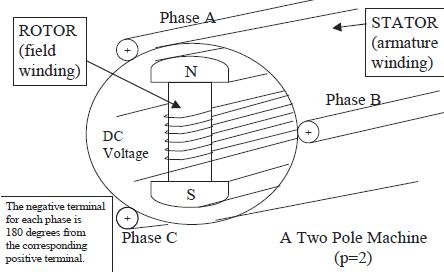
Fig. Construction of Synchronous Generator
The speed of field poles is synchronous speed and is given by
Ns = 120f/P
Where, ‘f’ indicates alternating current frequency and ‘P’ indicates number of poles.
Synchronous Generator Working Principle
The principle of operation of synchronous generator is electromagnetic induction. If there exists a relative motion between the flux and conductors, then an emf is induced in the conductors. To understand the synchronous generator working principle, let us consider two opposite magnetic poles in between them a rectangular coil or turn is placed as shown in the below figure.
If the rectangular turn rotates in clockwise direction against axis a-b as shown in the below figure, then after completing 90 degrees’ rotation the conductor sides AB and CD comes in front of the S-pole and N-pole respectively. Thus, now we can say that the conductor tangential motion is perpendicular to magnetic flux lines from north to south pole.

Fig. Direction of Rotation of Conductor perpendicular to Magnetic Flux
So, here rate of flux cutting by the conductor is maximum and induces current in the conductor, the direction of the induced current can be determined using Fleming’s right hand rule. Thus, we can say that current will pass from A to B and from C to D. If the conductor is rotated in a clockwise direction for another 90 degrees, then it will come to a vertical position as shown in the below figure.
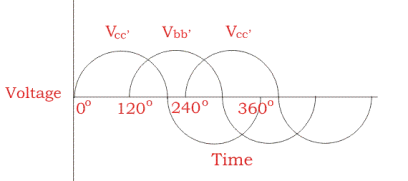
Now, if we consider a practical synchronous generator, then field magnets rotate between the stationary armature conductors. The synchronous generator rotor and shaft or turbine blades are mechanically coupled to each other and rotates at synchronous speed. Thus, the magnetic flux cutting produces an induced emf which causes the current flow in armature conductors. Thus, for each winding the current flows in one direction for the first half cycle and current flows in the other direction for the second half cycle with a time lag of 120 degrees (as they displaced by 120 degrees). Hence, the output power of synchronous generator can be shown as below figure.
Armature reaction as per Blondel’s two reaction theory for salient-pole machines
Two reaction theory
Two reaction theory was proposed by, Andre Blondel. The theory proposes to resolve the given armature mmfs into two mutually perpendicular components, with one located along the axis of the rotor salient pole. It is known as the Direct axis component. The other component is located perpendicular to the axis of the rotor salient pole. It is known as the quadrature axis component. The d axis component of the armature MMF 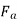 is denoted by
is denoted by 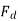 , and the q axis component by
, and the q axis component by 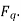 The component
The component 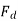 is either magnetizing or demagnetizing. The component
is either magnetizing or demagnetizing. The component  results in a cross-magnetizing effect.
results in a cross-magnetizing effect.
If 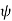 is the angle between the armature current
is the angle between the armature current 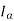 , and the excitation voltage
, and the excitation voltage 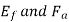 is the amplitude of the armature MMF, then
is the amplitude of the armature MMF, then
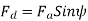
And 
The magnetic axes of the rotor
The axis of symmetry of the north magnetic poles of the rotor is called the Direct Access or d-axis.
The axis symmetry of the South magnetic poles is called the negative d-axis.
The axis of symmetry half way between adjacent North and South poles is called quadrature axis or q-axis. The q axis legging the north pole is taken as the positive q axis.
The quadrature access is so named because it is 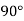 electrical degrees (one-quarter cycle) away from the direct axis.
electrical degrees (one-quarter cycle) away from the direct axis.
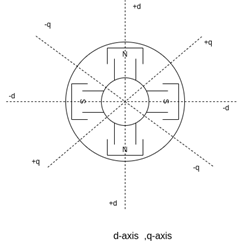
Fig, d-axis, q-axis [Direct axis, quadrature axis]
Salient pole synchronous machine two reaction model
In the cylindrical rotor synchronous machine, the air gap is uniform. The protruding pole structure of the rotor of a salient pole machine makes the air gap highly non-uniform. Consider a two-pole rotor rotating in the anticlockwise direction within a two-pole stator.
The Axis along the axis of the rotor is called the d axis, and the axis perpendicular to the d axis is called the quadrature axis.
It is seen that the direct Axis flux path involves too small air gaps, and is the path of minimum reluctance. The path denoted by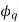 has too large air gaps, and is the path of maximum reluctance.
has too large air gaps, and is the path of maximum reluctance.
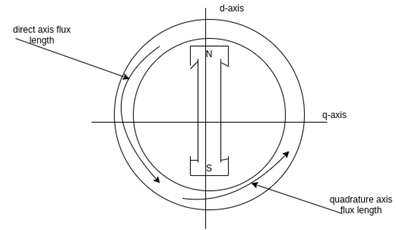
Fig. Salient pole synchronous machine two reaction model
The rotor flux 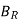 is shown vertically upwards, this rotor flux induces a voltage
is shown vertically upwards, this rotor flux induces a voltage 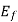 in the stator.
in the stator.
If a lagging p.f. The load is connected to the synchronous generator, a stator current 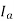 will flow, and it lags behind the generated voltage
will flow, and it lags behind the generated voltage 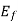 by an angle
by an angle 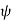 .
.
The armature current produces stator mmf which will lags behind
which will lags behind 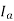 by 90°. The stator MMF
by 90°. The stator MMF  produces a magnetic field
produces a magnetic field 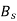 along its direction, and it can be resolved into two components the Direct axis component
along its direction, and it can be resolved into two components the Direct axis component 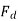 , and the quadrature axis component
, and the quadrature axis component 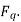
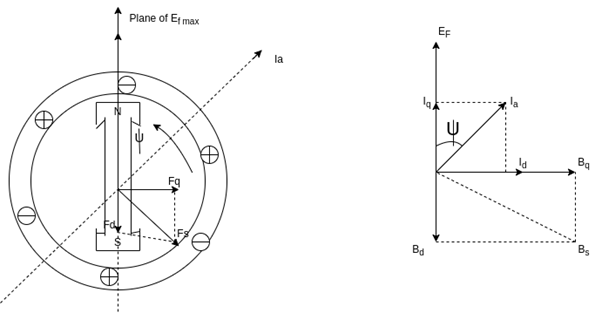
Fig. Phasor for d-axis and q-axis
If 
Where  =reluctance of direct Axis flux path
=reluctance of direct Axis flux path
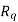 =reluctance of q axis flux path
=reluctance of q axis flux path
Since  the Direct axis component of mmf
the Direct axis component of mmf  produces more flux than the quadrature axis component mmf
produces more flux than the quadrature axis component mmf 
The direct, and quadrature axis stator flux is produced voltages in the stator winding by armature reaction.
Let 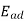 =direct Axis component of armature reaction voltage
=direct Axis component of armature reaction voltage
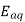 =quadrature Axis component of armature reaction voltage.
=quadrature Axis component of armature reaction voltage.
We can write
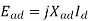
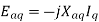
Where 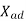 =armature reaction reactance in the Direct axis per phase.
=armature reaction reactance in the Direct axis per phase.
 = armature reaction reactance in the quadrature axis per phase.
= armature reaction reactance in the quadrature axis per phase.
The value of 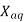 is always less than
is always less than 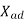 since the EMF induced by a given mmf acting on Direct access is smaller than for the quadrature axis due to its higher reluctance.
since the EMF induced by a given mmf acting on Direct access is smaller than for the quadrature axis due to its higher reluctance.
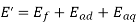
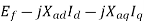
Considering the resistance, and leakage reactance of the armature,
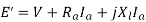
If  = the q-axis component of
= the q-axis component of  in phase with
in phase with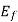 .
.
 =the d- axis component of
=the d- axis component of 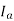 lagging
lagging 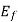 by 90°
by 90°
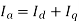
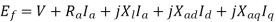
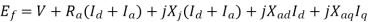
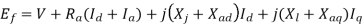
Let
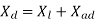
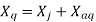
The reactance 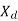 is called the direct Axis synchronous reactance, and the reactance
is called the direct Axis synchronous reactance, and the reactance 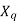 is called the quadrature axis synchronous reactance.
is called the quadrature axis synchronous reactance.

The above equation is the final form of the voltage equation for a salient pole synchronous generator.
Phasor diagram
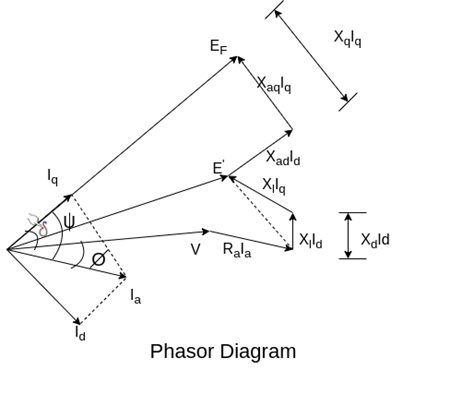
Fig. Phasor fo rsalient pole synchronous generator.
Simplified phasor diagram
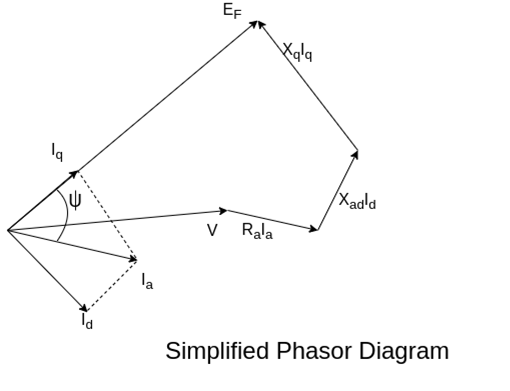
Fig. Simplified Phasor Diagram
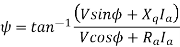
Since 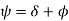
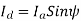
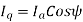
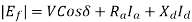
 is taken positive for lagging power factor, and it will be taken negative for the leading power factor.
is taken positive for lagging power factor, and it will be taken negative for the leading power factor.
If the armature resistance is neglected
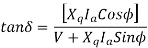
Determination of 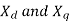
The direct, and quadrature axis synchronous reactance of a salient pole synchronous machine can be determined form a simple no-load test known as slip test.
In this test, a small voltage at rated frequency and not more than about 25 % of the rated value is applied to the 3 phase stator winding. The field winding is excited and left open-circuited.
The rotor is driven by an auxiliary motor at high speed slightly less or slightly more than synchronous speed. The direction of rotation should be the same as that of the rotating field produced by the stator. A small voltage reading indicated by the voltmeter across the open field winding terminal shows that the direction of rotation of the rotor is proper. Since the rotor is running at a speed 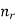 close to synchronous speed
close to synchronous speed 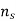 there will be a small slip between the rotating magnetic field produced by the armature, and the actual salient field poles.
there will be a small slip between the rotating magnetic field produced by the armature, and the actual salient field poles.
Since the stator mmf moves slowly past the actual field poles, there will be an instant when the peak of the armature mmf wave is in line with the axis of the actual salient field poles.

Fig. Determination of Xd and Xq
Construction:
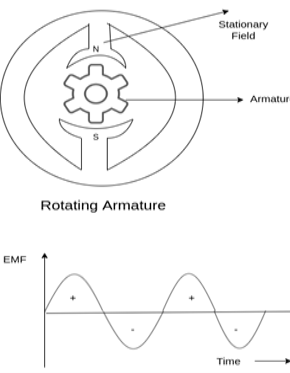
Fig. Construction
Rotating field type (stationary armature):
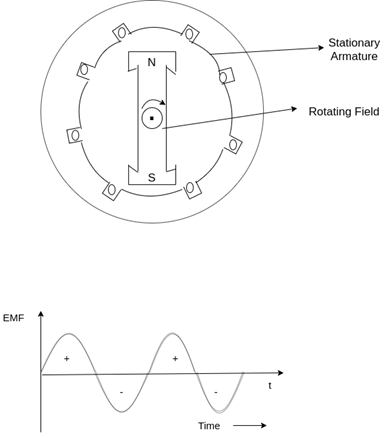
Fig. Rotating field type
Sr. No. | Salient pole type synchronous machine | Non-salient pole type synchronous machine |
1 | Diagram 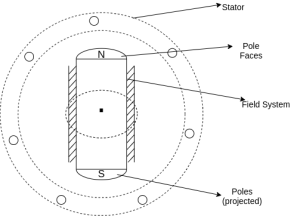 | Diagram  |
2 | Projected out poles | Merged in polls |
3 | Rotor surface is projected | Smooth rotor surface |
4 | The diameter of the machine is large | The small diameter of the machine |
5 | The axial length of the machine is small | The axial length of the machine is large |
6 | Speed is slow | Speed is high |
7 | Air gap is non uniform | Air gap is uniform |
8 | Damper bars/winding is used | Damper bar/winding not used |
9 | The air gap between stator and rotor is non-uniform | The air is uniform between stator and rotor |
10 | Centrifugal stress is more | Centrifugal stress is less |
11 | Aerodynamic resistance is more | Aerodynamic resistance is less |
Problem
A 3 phase 16 pole alternator has a star connected winding with 144 slots, and 10 conductors per slot. The flux per pole=0.03 Wb sinusoidally distributed, and speed is 375 rpm.
Find
1) Frequency
2) Phase voltage
3) Line voltage
Solution
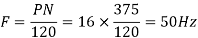
Total conductors= 144×10=1440
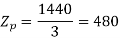
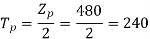
For 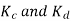 as coil pitch is not mentioned take full pitched coil.
as coil pitch is not mentioned take full pitched coil.
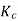 =1
=1
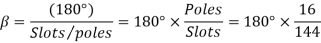
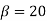

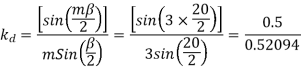
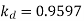
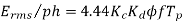
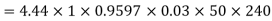
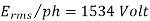
For star connection,
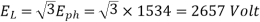
Problem
A 3 phase 4 pole alternator has 60 slots, two conductors per slot. The pitch of the coils is 3 slots less than full pitch. Find 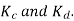
Pole pitch=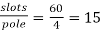
Now 15 slots=180
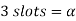
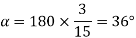
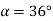
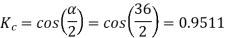
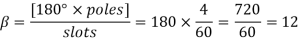

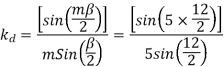
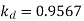
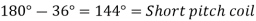
Armature reaction
The effect of armature flux  on the flux produced by the field poles or the main flux
on the flux produced by the field poles or the main flux  is called armature reaction.
is called armature reaction.
This effect is different for different nature of p.f. Of the load.
1) The effect may be cross magnetizing i.e.
2) It may be strong magnetizing or magnetizing i.e.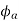 is in the same direction as
is in the same direction as  , So both are added, and the resultant field becomes stronger.
, So both are added, and the resultant field becomes stronger.
3) It may be demagnetizing i.e.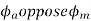 , and hence
, and hence 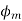 weakens.
weakens.
Different nature of p.f.
1) Unity PF
2) Zero PF lagging
3) Zero PF leading
Unity PF-: in this case  is in phase with E.
is in phase with E.
Phasors relations:
1) E lag 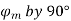
2) 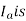 in phase with E
in phase with E
3) Field ampere-turns i.e. F and 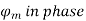
4) Flux produced by  in phase with
in phase with 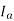 that is
that is 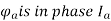
The armature flux 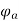 crosses the main flux
crosses the main flux  from the winding field, and vector diagram or Phasors.
from the winding field, and vector diagram or Phasors.
Also, the armature flux crosses the resultant flux so for the unit PF the armature reaction is such that the main flux  is crossed or distorted. It is a cross magnetizing effect.
is crossed or distorted. It is a cross magnetizing effect.
Zero lagging PF
It is seen that for lagging PF the armature flux is in direct opposition to flux  Hence it is demagnetizing, and resultant flux
Hence it is demagnetizing, and resultant flux 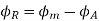
Hence in the case of lagging PF, the effect of armature reaction is demagnetizing.
Principle of operation: The rotor of the alternator is run at its proper speed by its prime mover. A prime mover is a machine that supplies the mechanical energy input to the alternator. Hydraulic turbines commerce steam and gas turbines are used as prime movers. As the poles of the rotor move under the armature conductor on the status of the file, and flux cut the armature conductors. Therefore voltage is generates in these conductors. This voltage of alternating nature of our sins poles of alternative polarity successively passes by a given stator conductor.
EMF equation and Winding Factor
Let 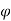 =useful flux per pole in weber
=useful flux per pole in weber
P=total number of poles.
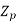 =total number of conductors or equal sides in series per phase.
=total number of conductors or equal sides in series per phase.
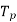 =total number of coils or turns per phase.
=total number of coils or turns per phase.
n=speed of rotation of rotator is revaluation per second.
F=frequency of generated voltage.
Since the flux per Pole is , each stator conductor cuts a flux
, each stator conductor cuts a flux 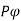 .
.
The average value of generated voltage per conductor
=(
Since n revolutions are made in one second, one revolution will be made in 1/n second. Therefore, the time for one revolution of the armature is 1/n second. The average voltage generated per conductor is
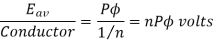
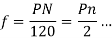
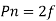
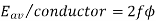
Since there are 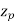 conductors in series per phase, the average voltage generated per phase are given by
conductors in series per phase, the average voltage generated per phase are given by
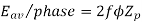
Since.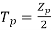
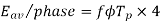
For the voltage wave, the form factor is given by
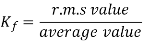
For sinusoidal voltage KF=1.11
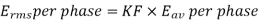
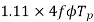
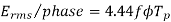
Above equation has been derived with the following assumptions
a) Coils have got a full pitch
b) All the conductors are concentrated in one stator slot.
The winding through which a current is passed to produce the main flux is called the field winding.
The winding in which voltage is induced is called the armature winding some basic terms related to the armature winding are defined as eternal consists of two conductors connected to one end by an end connector. A coil is formed by connecting several turns in series.
A winding is formed by connecting several coils in series.
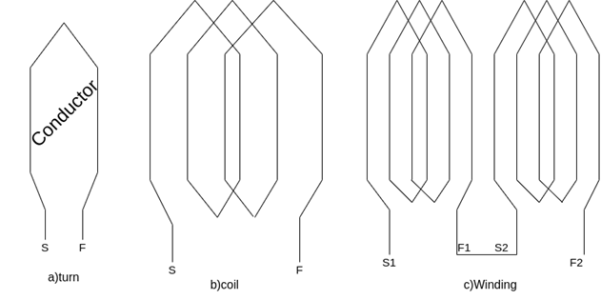
Fig. Winding formed by several coils in series
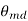 =Mechanical degrees or angular measure in space
=Mechanical degrees or angular measure in space
 = Electrical degree of angular measure in cycles
= Electrical degree of angular measure in cycles
For p pole machine, the electrical degree is defined as
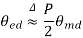
The angular distance between the centers of two adjacent pole on a machine is known as pole pitch or pole span.
One pole pitch=180° elect degree =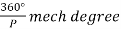
Regardless of the number of poles in the machine, a pole pitch is always 180° electrical degrees.
The two sides of a coil are placed in two slots on the stator surface. The distance between the two sides of a coil is called the coil pitch. If the coil pitch is one pole pitch coma it is called the full pitch coil. If the coil pitch is less than one pole pitch of the coil is called the short pitch coil for fractional pitch coil.
Coil span factor or pitch factor-
The distance between the two sides of a coil is called the coil span or coil pitch.
The angular distance between the central line of one pole to the central line of the next Pole is called pole pitch. A pole pitch is always 180 electrical degrees regardless of the number of poles on the machine.
A coil having a span equal to 180° electrical is called a full pitch coil.
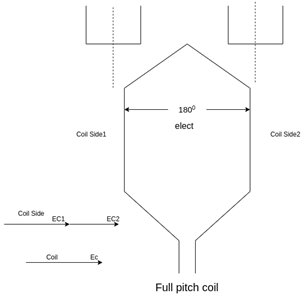
Fig. Full Pitch Coil
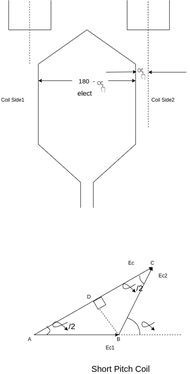
Fig. Short Pitch Coil
A coil having a span less than 180° electrical is called a short pitch coil, for fractional pitch coil. It is also called a chorded coil. A stator winding using fractional pitch coils is called a chorded winding. If the span of the coil is reduced by an angle 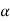 electrical degrees, the coil span will be (
electrical degrees, the coil span will be ( ) Electrical degrees.
) Electrical degrees.
The coil span factor or pitch factor 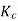 is defined as the ratio of the voltage generated in the short pitch coil to the voltage generated in the full pitch coil. The coil span factor is also called the chording factor.
is defined as the ratio of the voltage generated in the short pitch coil to the voltage generated in the full pitch coil. The coil span factor is also called the chording factor.
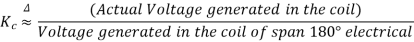
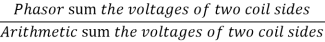
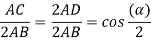
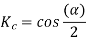
For full pitch coil,  , and
, and
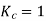 For short pitch coil
For short pitch coil 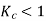
Advantages of short pitching or chording
1) Shortens the end of the winding, and therefore there is shaving in the conductor material.
2) Reduces the effects of distorting harmonics, and thus the waveform of the generated voltage is improved and making it approach A sine wave.
Winding Factor: The combined effect of coil span factor and distribution factor is known as winding factor. In fact, winding factor is the product of coil span factor and distribution factor.
EMF Equation of Synchronous Generator or Alternator:
We know that Synchronous Generator or Alternator will generate an EMF. The following is the derivation of emf equation of Synchronous Generator or Alternator.
Let Φ = Flux per pole, in Wb
P = Number of poles
N = Synchronous speed in r.p.m
f = Frequency of induced emf in Hz
Z = Total number of conductors
Zph = Conductors per phase connected in series
Zph = Z/3 as number of phases = 3
Consider a single conductor placed in a slot.
The average value of emf induced in a conductor = dΦ/dt
Or one revolution of a conductor,
eavg per conductor = (Flux cut in one revolution/Time taken for one revolution)
Total flux cut in one revolution is Φ x P.
Principle and working of Synchronous generator or alternator
Time taken for one revolution is 60/Ns seconds.
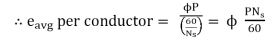
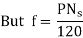

Substituting in above equation
eavg per conductor = 2 f Φ volts
Assume full pitch winding for simplicity i.e. this conductor is connected to a conductor which is 180° electrical apart. So these two emf's will try to set up a current in the same direction i.e. the two emf are helping each other and hence resultant emf per turn will be twice the emf induced in a conductor.
Emf per turn = 2 x (emf per conductor) = 2 x (2 f Φ)
= 4 f Φ volts.
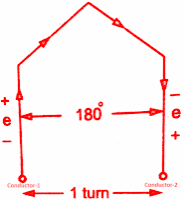
Turn of full pitch coil
Let Tph be the total number of turns per phase connected in series. Assuming concentrated winding, we can say that a are placed in single slot per pole per phase (So induced emf's in all turns will be in phase as placed in a single slot. Hence net emf per phase will be algebraic sum of the emf's per turn.
Average Eph = Tph x (Average emf per turn)
Average Eph = Tph x 4 f Φ
But in ac circuits, RMS value of an alternating quantity is used for the analysis. The form factor is 1.11 of sinusoidal emf.
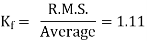
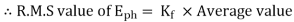

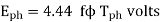
Armature leakage reactance:
In an AC machine, any flux set up by the load current which does not contribute to the useful flux of the machine is a leakage flux.
The effect of this leakage flux is to set up a self-induced emf in the armature winding the leakage flux is may be classified as
- Slot leakage
- Tooth head leakage
- Coil end for overhang leakage.
The voltage induced in the armature windings by the air gap flux is called air gap voltages.
The leakage flux also induces a voltage in the armature winding these are taken into account by introduction of leakage reactance drops. Most of the reluctances of the magnetic circuits for armature leakage fluxes are due to air paths. The fluxes are, therefore nearly proportional to the armature current producing them and are in phase with these currents. The voltage induced in the armature windings can be considered with the leakage reactance drops, and lead the current producing them by 90.
When current flows through the armature winding of an alternator the resultant MMF produces flux. The armature flux reacts with main Pole flux causing the resultant flux to become either less than or more than the original main field flux. (The effect of armature (stator) flux on the flux produced by the rotor field poles is called armature reaction).
For simplicity, we considered a 3 phase 2 pole alternator having a single layer winding but this treatment is valid for any number of poles. Also, the winding of each phase is assumed to be concentrated but the effect of armature reaction will be the same as if a distributed winding were used.
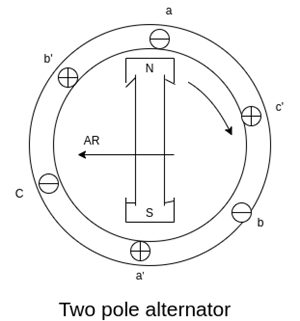
Fig. Two pole alternator
The power factor will be defined as the cosine of the angle between the armature phase current, and the induced EMF in the armature conductor in that phase.
a) Armature reaction at unity power factor:
Suppose that the alternator is supplying current at unity power factor the phase currents 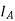 ,
, 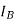 , and
, and 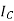 will be in phase with their respective generated voltage
will be in phase with their respective generated voltage 

Fig. Phasor for UPF
The projections of phasor on the vertical Axis gives its instantaneous value. At t=0, the instantaneous values of the currents and fluxes are given by.
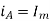
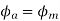
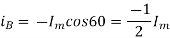
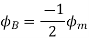


Where the subscript m denotes the maximum value of current, and flux.
Since the fluxes 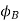 , and
, and  are negative. They are acting opposite to the direction shown above. They are shown by OB, and OC. The resultant of the fluxes can be found by resolving the fluxes horizontally and vertically
are negative. They are acting opposite to the direction shown above. They are shown by OB, and OC. The resultant of the fluxes can be found by resolving the fluxes horizontally and vertically
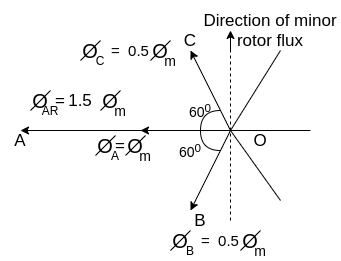
Fig. Direction of minor rotor flux
Resolving along the horizontal direction we get
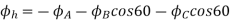
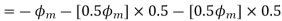
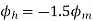
Resolving along the vertical direction we get
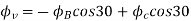
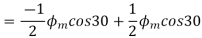
=0
The resultant armature reaction flux is given by

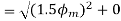
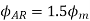
The direction of this resultant flux is along OA, and the resultant armature reaction flux 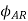 is constant in magnitude equal to 1.5
is constant in magnitude equal to 1.5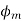 .
.
Also  lags behind 90 with the main field flux. This is called the cross-magnetizing flux.
lags behind 90 with the main field flux. This is called the cross-magnetizing flux.
b. Armature reaction: -Lagging power factor
Suppose that the alternator is loaded with an inductive load of zero power factor lagging. The phase current 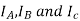 will be lacking with their respective phase voltage
will be lacking with their respective phase voltage 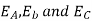 by 90°.
by 90°.
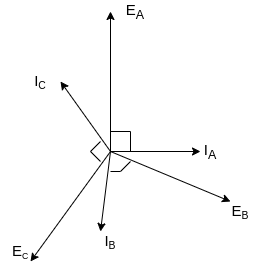
Fig. Phasor for Lagging power factor
At time t=0 the instantaneous values of currents and fluxes are given by
 ,
, 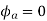
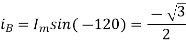
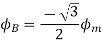
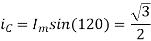
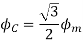
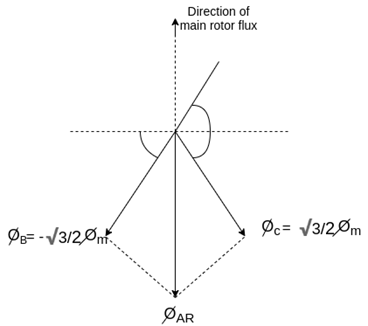
Fig. Direction of main rotor flux
The resultant flux is
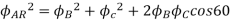
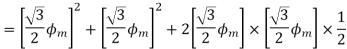
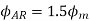
It is seen that the direction of the armature reaction flux is opposite to the main field flux. Therefore, it will oppose, and weaken the main field flux. It is said to be demagnetizing.

c. Armature reaction: Leading power factor
Suppose that the alternator is loaded with a load of zero power factor leading. The phase 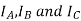 will be leading their respective phase voltages
will be leading their respective phase voltages 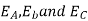 by 90°
by 90°
At time t=0 the instantaneous values of currents and fluxes are given by
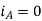 ,
,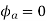
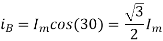
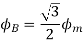
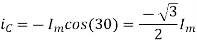
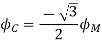
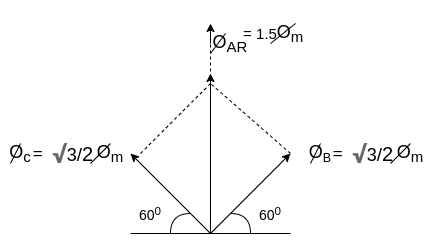
Fig. Phasor for Leading power factor
The resultant flux is given by
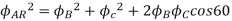
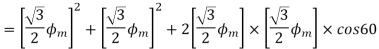
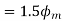
It is seen that the direction of the armature reaction flux is in the direction of the main field flux. Does it will aid it. In other words, it is a magnetizing flux.
- The synchronous impedance method of calculating voltage regulation of an alternator is otherwise called the EMF method.
- The synchronous impedance or the EMF method is based on the concept of replacing the effect of armature reaction with an imaginary reactance.
- This method is not accurate as it gives a result that is higher than the original value. That’s why it is called the pessimistic method.
- For calculating the regulation, the synchronous method requires the armature resistance per phase, the open-circuit characteristic, and the short circuit characteristics.
4. 10 Three Phase Synchronous Motor: Construction and Principle
Principle of operation
Asynchronous motor is a doubly excited machine. Its rotor poles are excited by direct current and its stator winding are connected to the AC supply. The air gap flux is, therefore, the resultant of the fluxes due to both rotor current and stator current. Any important feature of a synchronous motor is that it can draw either lagging or leading reactive current from the AC supply system.
Construction
3 phase armature winding is on the stator and is wound for the same number of poles as the rotor.
The rotor of a synchronous motor can be of the salient pole or cylindrical pole type of construction. Generally, it is of salient pole type, except for exceedingly high-speed machines.
An additional set of winding called the damper winding is mounted on the rotor. This winding is placed in slots located in the pole faces and parallel to the shaft.
The ends of the copper bars are short circuited in the same manner as in the case of rotor of an induction motor.
Damper winding provides a means of starting to the synchronous motor. They also serve to increase the stability of the motor during load transients.

Fig. Construction of 3-phase Armature Winding
Principle of operation:
Consider a 2 pole synchronous motor. When a three phase AC voltage is applied to the stator winding, a rotating magnetic field is produced in the air gap. The stator field rotates at synchronous speed.
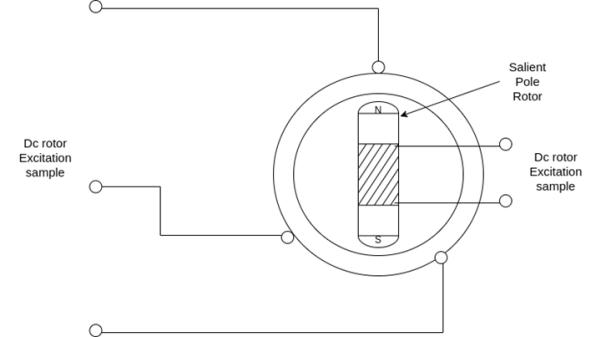
Fig. Synchronous Motor
The field current of the motor produces a steady state magnetic field. Therefore, there are two magnetic fields present in the machine. The rotor will tend to align if placed near each other to the stator field.
Since the stator magnetic field is rotating the rotor magnetic field and the rotor will tend to rotate with the rotating field of the stator.
In order to develop a continuous torque, the two fields must be stationary with respect to each other. This is possible when the rotor also rotates at synchronous speed.
The basic principle of synchronous motor operation is that the rotor chases stator magnetic field. In other words, the stator rotating magnetic field tends to drag the rotor along, as if north pole on the stator locks in with the South Pole of the rotor.
When a pair of rotating stator poles sweeps across the stationary rotor poles at synchronous speed, stator poles will tend to rotate the rotor in one direction and then in the other direction.
However, because of the rotor inertia the stator fields slide by so fast that the rotor cannot follow it. Consequently, the rotor does not move and we say that the starting torque is zero. In other words, a synchronous motor is not self-starting.
Key takeaway
The field current of the motor produces a steady state magnetic field. Therefore, there are two magnetic fields present in the machine. The rotor will tend to align if placed near each other to the stator field.
Since the stator magnetic field is rotating the rotor magnetic field and the rotor will tend to rotate with the rotating field of the stator.
Synchronous motor starting the synchronous motor must be brought to a speed sufficiently close to synchronous speed in order to lock into synchronism with the rotating field
- DC motor coupled to the synchronous motor shaft- this method sometimes used in Laboratories with synchronous Motors not equipped with damper winding generally the synchronous motor is intended as the constant speed Prime mover for the DC generator. But in order to bring the motor up to synchronism, the decision letter is operated as motor. The DC motor will now act as a generator if its field current is increased so that its generated EMF exceeds the DC bus.
- Using field excited generator as a DC motor-
- A small induction motor of at least one pair of poles less than the synchronous motor-this method in involve the same synchronizing procedure for AC synchronous motor as an alternator.
- Using the damper winding as a squirrel cage induction motor- it is practically impossible to start a synchronous motor with its DC field energized. Even when left to de-energized, the rapidly rotating magnetic field of the stator will induce extremely high voltages in the many turns of the field winding. Therefore, it is customary to short circuit the DC field winding during the starting period, whatever voltage and current are induced in it, it may then aid in producing induction motor action. In very large synchronous motors, field sectionalizing or field splitting switches are used with short circuit individual field windings to prevent cumulative addition of induced voltage is from pole to pole.
Hunting or phase swinging
When synchronous motor is loaded, the rotor falls back by an angle 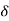 (called as load angle). Even if rotor falls back by
(called as load angle). Even if rotor falls back by  it continues to rotated at synchronous speed i.e. speed of the stator magnetic field.
it continues to rotated at synchronous speed i.e. speed of the stator magnetic field.
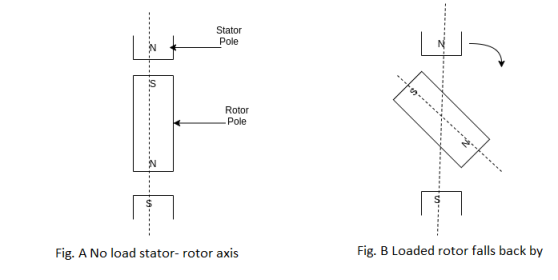
Fig. (a) No-load stator-rotor axis (b) Loaded falls back by
So for first figure a 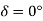 & for figure b
& for figure b 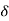 is having some angle and value. But in actual case, the rotor does not settle to angle
is having some angle and value. But in actual case, the rotor does not settle to angle 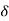 immediately i.e. when motor is loaded there are several oscillations of rotor around the final
immediately i.e. when motor is loaded there are several oscillations of rotor around the final 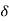 position. This is due to the inertia of the rotor. These oscillations are called hunting in synchronous motor.
position. This is due to the inertia of the rotor. These oscillations are called hunting in synchronous motor.
Due to hunting the load angle  changes its value about its final equilibrium value.
changes its value about its final equilibrium value.
Causes of hunting:
1) Sudden changes of load.
2) Fault occurring in the system which the generator supplies.
3) Sudden changes in the field current.
4) Cyclic variations in or of the load torque.
Effects of hunting:
1) It can be lead to loss of synchronism.
2) Variations of supply voltage producing undesirable lamp flicker.
3) Increases the possibility at resonance.
If the frequency of load torque component becomes equal to that of transient oscillations the resonance occurs.
4) Large mechanical stress on rotor shaft.
5) Increases in machine losses and temperature.
Remedies/ reduction of hunting:
1) By using the damper winding.
2) By using the fly wheels
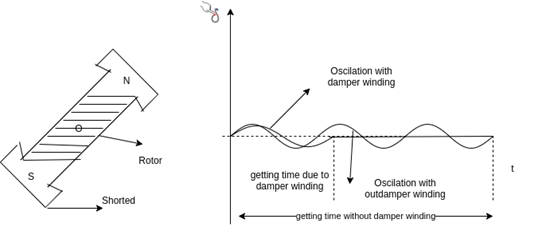
Fig. Effect of damping winding
Problems:
A 3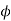 , 400V synchronous motor takes 52.5 A at a power factor of 0.8 leading. Determine the induced EMF and power supplied. The motor impedance per phase is
, 400V synchronous motor takes 52.5 A at a power factor of 0.8 leading. Determine the induced EMF and power supplied. The motor impedance per phase is 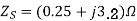
Given 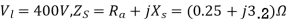 ,
, 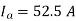
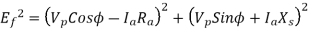
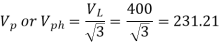
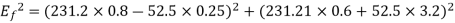
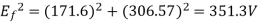
Line emf = 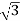 * Induced Emf
* Induced Emf
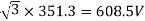
Power supplied =>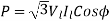

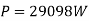
Ques-
A 2.3 KV, 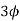 , star connected synchronous motor has
, star connected synchronous motor has 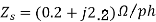 . The motor is operating at 0.5 P.F. Leading, with a line current of 200 A. Determine the generated Emf per phase.
. The motor is operating at 0.5 P.F. Leading, with a line current of 200 A. Determine the generated Emf per phase.
Solution-:
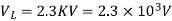
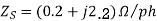
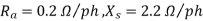
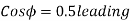
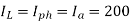
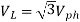
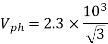
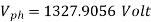
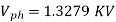
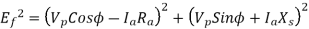
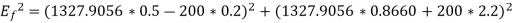
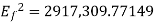

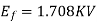
Line EMF= Induced EMF
Induced EMF
Line EMF =
Line emf=2.9583KV
Synchronous motor runs at absolutely constant synchronous speed, regardless of the load.
Consider a synchronous motor operating initially with a leading power factor. Suppose that the load on the shaft is increased. The rotor slows down momentarily since it takes some time for the motor to take increase power from the line. In other words, although still rotating at synchronous speed, the rotor slips back in space as a result of increased loading. In this process the torque angle 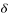 become larger and therefore the induced torque
become larger and therefore the induced torque
τinduced = V E 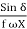 , Increases. The increased torque increases the rotor Speed the motor again picks up the synchronous speed but with a larger torque angle δ.
, Increases. The increased torque increases the rotor Speed the motor again picks up the synchronous speed but with a larger torque angle δ.
Since the excitation voltage Ef is proportional to ϕw it only depends upon the field current and the speed of the motor.
Since the motor is moving with a constant synchronous speed, and since the field circuit is also untouched, the field current remains constant.
Therefore, the magnitude of excitation voltage|Ef| remains constant with the change in load on the shaft.
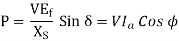
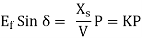
Where k =  = a constant
= a constant
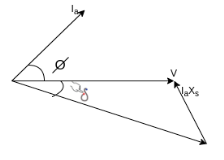
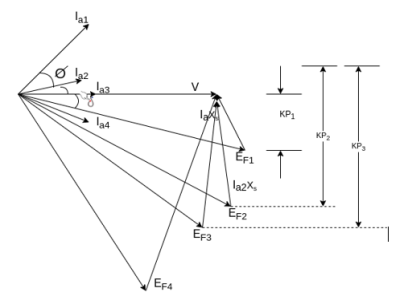
Fig. Effect of load changes on a synchronous motor
Thus, when the load on a synchronous motor is increased,
1) The motor continues to run at synchronous speed.
2) The torque angle δ increases.
3) The excitation voltage Ef remains constant.
4) The armature current Ia drawn from the supply increases.
5) The phase angle ϕ increases in the lagging direction.
Synchronous motor v curves
It has also been observed that the armature current Ia changes with change in field current IfLet us assume that the motor is operating at no load. If the field current is increased from this small value of the armature current Ia decreases until the armature current becomes minimum. At this minimum armature current the motor is operating at unity power factor. Up to this point the motor was operating at a lagging power factor. If the field current is increased further, the armature current increases again at the motor starts to operate at a leading power factor. If a graph is plotted between armature current Iaand field current Ifat no load the lowest curve is obtained. If this procedure is repeated for various increased loads, a family of curves is obtained as shown.

Fig. Synchronous Motor V curve
This V curves are plots of stator current versus field current for different constant loads.
Inverted V curves:
A family of curves is obtained by plotting the power factor versus field current. These are inverted V curves as shown in figure below.
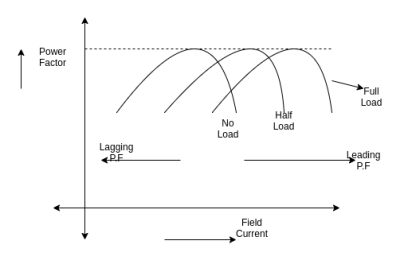
Fig. Inverted V curve
The highest point on each of these curves indicate unity power factor. The field current for unity power factor at full load is more than the field current at unity power factor at no load.
Key takeaway
Thus, when the load on a synchronous motor is increased,
1) The motor continues to run at synchronous speed.
2) The torque angle δ increases.
3) The excitation voltage Ef remains constant.
4) The armature current Ia drawn from the supply increases.
5) The phase angle ϕ increases in the lagging direction.
The important characteristics of the synchronous motor are its constant speed irrespective of the load conditions and variable power factor operation. Due to constant speed characteristics it is used in
- Machine tools
- Motor generator sets
- Synchronous clocks
- Stroboscopic devices
- Timing devices
- Belt driven reciprocating compressors
- Fans and blowers
- Centrifugal pumps, vacuum pumps
- Pulp grinders
- Textile mills, paper mills, rolling Mills, cement Mills
Synchronous motor operating under over excited condition, its operating power factor is leading in nature. It is very important from the power factor correction point of view. Synchronous Motors are used as a power factor correction devices, phase advancer and phase modifiers for voltage regulation of the transmission lines.
Comparison of 3 - phase synchronous motor with 3-phase induction motor
Sr. No. | Synchronous motor | Induction motor |
1 | Construction is complicated | Simple construction particularly in case of cage rotor motor. |
2 | Not self-starting | Self-starting |
3 | Separate DC source required for rotor excitation | Rotor excites by the induced EMF. Separate force is not required |
4 | The speed is always synchronous irrespective at load. | Speed is always less than synchronous speed and never synchronous speed |
5 | Speed control is not possible | Speed control is possible though it is different. |
6 | As load increases, the load angle increases, keeping the speed constant as synchronous | As load increases the speed decreases. |
7 | By changing excitation, the PF can be changed from lagging and leading | It always operates at lagging PF and PF control is not possible. |
8 | It can be used as synchronous condenser for PF improvement. | It can't be used for PF improvement. |
9 | Motor is sensitive to sudden load changes and hunting effect | Phenomenon of hunting is absent. |
10 | Motor is costly and requires frequent maintenance | Motors are less costly and cage motors are housing less maintenance |
Examples
Q1) A 1492 kW, unity power factor,3-phase, star-connected ,2300 V, 50 Hz, synchronous motor has a synchronous reactance of 1.95 ohm/phase. Compute the max. Torque in N-m which this motor can deliver if it is supplied from a constant frequency source and if the field excitation is constant at the value which would result in unity power factor at rated load. Assume that the motor is of cylindrical rotor type. Neglect all losses.
A1)
Rated kVA, 3-phase= S = 1492
Rated kVA per phase = 1492/3 = 497.333
Rated Voltage/phase = V =2300/√3 = 1327.906
E = 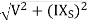 = 1515.489 Volts
= 1515.489 Volts
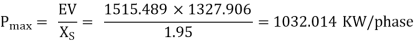
ω = 2π f = 2π × 50 = 314.159

3 – phase max. Torque = 9855 N.m
Q2) Example: A factory takes 600 kVA at a lagging power factor of 0.6. A synchronous motor is to be installed to raise the power factor to 0.9 lagging when the motor is taking 200 kW. Calculate the corresponding apparent power (in kVA) taken by the motor and the power factor at which it operates.
A2)
Load power factor, Cos φ= 0.6
Sin φ = 0.8
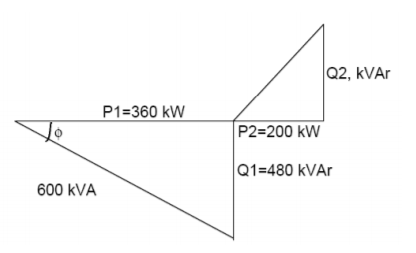
Load kVA = 600
P1, Load power = load kVA*cos φ = 360 kW
Q1, Load reactive power = kVA*Sin φ = 480 kVAr
P2, Motor power = 200 kW
Overall P.F., Cos α= 0.9 lag
Tan α = 0.484
Since, tan ∝ = (Q1-Q2)/P1+P2
𝑄2 = 𝑄1− (𝑃1 + 𝑃2) tan ∝ = 208.78 KVAr
S2, Apparent power of the motor = 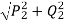 = 289.118 kVA
= 289.118 kVA
Motor P.F. =P2/S2= 0.692 lead
Q3) A 75-kW, 3-ϕ, Y-connected, 50-Hz, 440-V cylindrical rotor synchronous motor operates at rated condition with 0.8 p.f. Leading. The motor efficiency excluding field and stator losses, is 95% and XS = 2.5 Ω. Calculate (i) mechanical power developed (ii) armature current (iii) back e.m.f. (iv) power angle and (v) maximum or pull-out torque of the motor.
A3)
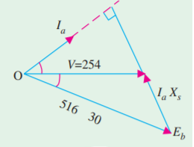
NS = 120 × 50/4 = 1500 rpm = 25rps
(i) Pm = Pin = Pout /η = 75 × 103/0.95 = 78,950 W
(ii) Since power input is known
∴ √3 × 440 × Ia × 0.8 = 78,950; Ia = 129 A
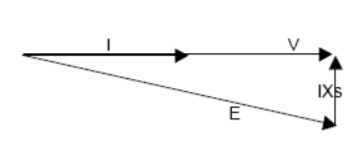
(iii) Applied voltage/ phase = 440/ √3 = 254 V. Let V = 254 ∠0o as shown in Fig.
Now, V = Eb + j I XS or Eb = V – j Ia XS = 254 ∠0o – 129 ∠36.9o × 2.5 ∠90o = 250 ∠0o -322 ∠126.9o = 254 – 322 (cos 126.9o + j sin 126.9o) = 254 – 322 ( - 0.6 + j 0.8) = 516 ∠-30o
(iv) ∴ α = - 30o
(v) pull-out torque occurs when α = 90o
Maximum Pm = 3 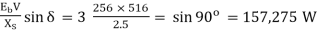
∴ pull-out torque = 9.55 × 157,275/1500 = 1,000 N-m
Q4) A 3-ϕ, 150-kW, 2300-V, 50-Hz, 1000-rpm salient-pole synchronous motor has Xd = 32 Ω / phase and Xq = 20 Ω / phase. Neglecting losses, calculate the torque developed by the motor if field excitation is so adjusted as to make the back e.m.f. Twice the applied voltage and α = 16o.
A4)
V = 2300 / 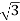 = 1328 V; Eb = 2 × 1328 = 2656 V
= 1328 V; Eb = 2 × 1328 = 2656 V
Excitation power / phase = 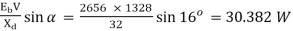
Reluctance power / phase = 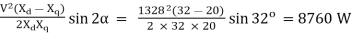
Total power developed, Pm = 3(30382 + 8760) = 117,425 W
Tg = 9.55 × 117,425 / 1000 = 1120 N-m
Q5) A 3300-V, 1.5-MW, 3-ϕ, Y-connected synchronous motor has Xd = 4Ω/phase and Xq = 3 Ω/phase. Neglecting all losses, calculate the excitation e.m.f. When motor supplies rated load at unity p.f. Calculate the maximum mechanical power which the motor would develop for this field excitation.
A5)
V = 3300/ 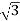 = 1905 V; cos ϕ = 1; sin ϕ = 0; ϕ = 0o
= 1905 V; cos ϕ = 1; sin ϕ = 0; ϕ = 0o
Ia = 1.5 × 106 / 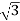 × 3300 × 1 = 262 A
× 3300 × 1 = 262 A
Tan Ψ = 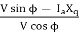 =
= 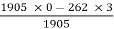 = - 0.4125; Ψ = - 22.4o
= - 0.4125; Ψ = - 22.4o
α = ϕ – Ψ = 0 – ( - 22.4o) = 22.4o
Id = 262 × sin (- 22.4o) = - 100 A; Iq = 262 cos ( - 22.4o) = 242 A
Eb = V cos α – Id Xd = 1905 cos ( -22.4o) – (- 100 × 4) = 2160 V
= 1029 sin α + 151 sin 2 α
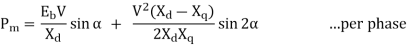
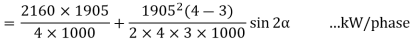
= 1029 sin α + 151 sin 2α ... KW/phase
If developed power has to achieve maximum value, then
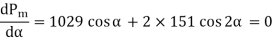
∴ 1029 cos α + 302 (2 cos2 α – 1) = 0 or 604 cos2 α + 1029 cos α – 302 = 0
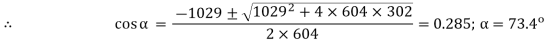
∴ maximum Pm = 1029 sin 73.4o + 151 sin 2 × 73.4o = 1070 kW/phase
Hence, maximum power developed for three phases = 3 × 1070 = 3210 kW
Q6) The input to an 11000-V, 3-phase, star-connected synchronous motor is 60 A. The effective resistance and synchronous reactance per phase are respectively 1 ohm and 30 ohm. Find (i) the power supplied to the motor (ii) mechanical power developed and (iii) induced emf for a power factor of 0.8 leading.
A6)
(i) Motor power input =  × 11000 × 60 × 0.8 = 915 kW
× 11000 × 60 × 0.8 = 915 kW
(ii) stator Cu loss/phase = 602 × 1 = 3600 W; Cu loss for three phases = 3 × 3600 = 10.8 kW
Pm = P2 – rotor Cu loss = 915 – 10.8 = 904.2 kW
Vp = 11000/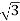 = 6350 V ; ϕ = cos-1 0.8 = 36.9o;
= 6350 V ; ϕ = cos-1 0.8 = 36.9o;
θ = tan-1 (30/1) = 88.1o
Zs ≡ 30 Ω; stator impedance drop/ phase = Ia ZS
= 60 × 30 = 1800 V
As seen from Fig.

Eb2 = 63502 + 18002 – 2 × 6350 × 1800 × cos ( 88.1o + 36.9o)
= 63502 + 18002 – 2 × 6350 × 1800 × - 0.572
∴ Eb = 7528 V; line value of Eb = 7528 × 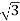 = 13042
= 13042
Q7) A 500 - V, I-phase synchronous motor gives a net output mechanical power of 7.46 kW and operates at 0.9 p.f. Lagging. Its effective resistance is 0.8Ω. If the iron and friction losses are 500 W and excitation losses are 800 W, estimate the armature current. Calculate the commercial efficiency.
A7)
Motor input = V Ia cos ϕ ; Armature Cu loss = Ia Ra2
Power developed in armature is Pm = V Ia cos ϕ – Ia2Ra
∴ Ia2Ra - V Ia cos ϕ + Pm = 0 or Ia = 
Now, Pout = 7.46 kW = 7,460 W
Pm = Pout + iron and friction losses + excitation losses
= 7460 + 500 + 800 = 8760 W

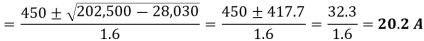
Motor input = 500 × 20.2 × 0.9 = 9090 W
ηc = net output / input = 7460 / 9090 = 0.8206 or 82.06$.
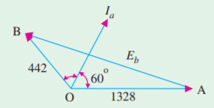
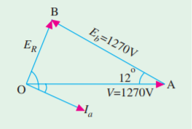
Q8) A 2,300- V, 3-phase, star – connected synchronous motor has a resistance of 0.2 ohm per phase and a synchronous reactance of 2.2 ohm per phase. The motor is operating at 0.5 power factor leading with a line current of 200 A. Determine the value of the generated e.m.f. Per phase.
A8)
Here, ϕ = cos-1 (0.5) = 60o (lead)
θ = tan-1 (2.2/0.2) = 84.8o
(θ+ ϕ) = 84.8o + 60o = 144. 8o
Cos 144.8o = - cos 35.2o
v = 2300 / √3 = 1328 VOLT
zs = 
IZS = 200 × 2.209= 442 V
The vector is shown in the Fig.
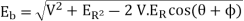
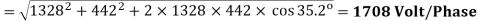
Q9) A synchronous motor having 40% reactance and a negligible resistance is to be operated at reated load at (i) u.p.f. (ii) 0.8 p.f. Lag (iii) 0.8 p.f. Lead. What are the values of induced e.m.f.? Indicate assumptions made, if any
A9)
Let V = 100 V, then reactance drop = IaXS = 40 V
(i) At unity p.f.
Here, θ = 90o , Eb = 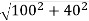 = 108 V
= 108 V
(ii) At p.f.0.8 (lag.) Here ∠ BOA = θ – ϕ = 90o – 36o54’ = 53o6’
Eb2 = 1002 + 402 - 2× 100 × 40 × cos 53o6’ ; Eb = 82.5 V,
Alternatively, Eb = AB =  =
=  = 82.5 V
= 82.5 V
(iii) At p.f.0.8 (lead,) Here, (θ+ϕ) = 90o+ 36.9o = 126.9o
Eb2 = 1002 + 402 – 2 × 40 × cos 126.9o = 128 V
Again from Fig. Eb2 = (OM + OA)2 + MB2 = 1242+ 322 ; Eb = 128 V.
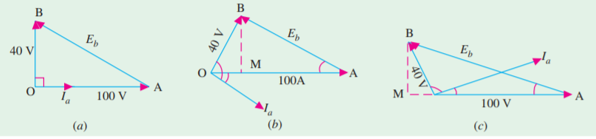
Q10) A 2200- V, 3-ϕ, Y- connected, 50 – Hz, 8 – pole synchronous motor has Zs = (0.4 + j 6) ohm/phase. When the motor runs at no-load, the field excitation is adjusted so that E is made equal to V. When the motor is loaded, the rotor is retarded by 3o mechanical.
Draw the phase diagram and calculate the armature current, power factor and power of the motor. What is the maximum power the motor can supply without falling out of step?
A10)
Per phase Eb = V = 2200 / √3 = 1270 V
α = 3o (mech) = 3o ×(8/2) = 12o(elect).
As seen from Fig
ER = (12702 + 12702 – 2 × 1270 × 1270 cos 12o)1/2
= 266 V ; ZS = 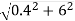 = 6.013 Ω
= 6.013 Ω
Ia = ER / ZS = 266 / 6.013 = 44.2 A. From ∆ OAB,
We get, 
∴ sin (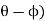 = 1270 × 0.2079/266 = 0.9926 ∴ (
= 1270 × 0.2079/266 = 0.9926 ∴ (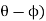 = 83o
= 83o
Now, θ = tan-1 (XS / Ra) = tan-1 (6/0.4) = 86.18o
ϕ = 86.18o – 83o = 3.18o ∴ p.f. = cos 3.18o = 0.998(lag)
Total motor power input = 3 V Ia cos ϕ = 3 × 1270 × 44.2 × 0.998 = 168 kW
Total Cu loss = 3 Ia2Ra = 3 × 44.22× 0.4 = 2.34 k W
Power developed by motor = 168 – 2.34 = 165.66 kW
Pm(max) = 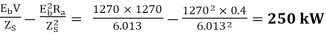
References:
1. I. J. Nagrath, D.P. Kothari, “Electrical Machines,”, Tata McGraw- Hill Publishing
Company Ltd.
2. P.S. Bhimbra, “Electrical Machinery”, Khanna Publishers.
3. P.K. Mukherjee, S. Chakrabvorty, “Electrical Machines”, Dhanpat Rai Publications.
4. P.S. Bhimbra, “Generalized Theory in Electrical Machines”, KhannaPublishers.
5. D C Kulshreshtha, “Basic Electrical Engineering,” The McGraw Hill Higher EducationPrivate Limited, New Delhi.