Unit - 1
Review of Vector Analysis
Vector algebra is essential in developing the concepts of electromagnetic field theory. The widespread acceptance of vectors in electromagnetic field theory is because they provide compact mathematical representations of complicated phenomena and allow for easy visualization and manipulation.
Scalar and vector quantities
Most of the quantities encountered in electromagnetic fields can easily be divided into two classes, scalars, and vectors.
Scalar
A physical quantity that can be completely described by its magnitude is called a scalar. Some examples of scalar quantities are mass, time, temperature, work, and electric charge.
Vector
A physical quantity having a magnitude as well as a direction is called a vector. Force, velocity, torque, electric field, and acceleration are vector quantities.
Unit Vector
Vector having unit magnitude is called unit vector. The most common unit vectors are those which have the directions of the right handed Cartesian co-ordinate system as shown in figure.
The vector 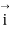 is a unit vector having the X direction of the co-ordinate system, the unit vector
is a unit vector having the X direction of the co-ordinate system, the unit vector  has the z direction. The vectors are also denoted by suffixing x, y and z or axis direction to an alphabet.
has the z direction. The vectors are also denoted by suffixing x, y and z or axis direction to an alphabet.
If are the projections of P on the three axes x, y, z respectively we can write
are the projections of P on the three axes x, y, z respectively we can write
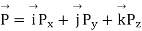
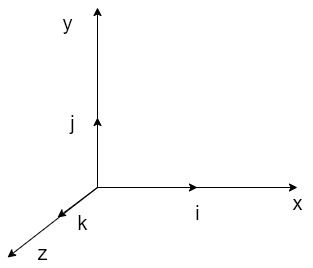
If a vector 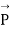 Is given in magnitude and direction, then its components along the three axes of a cartesian system are given by
Is given in magnitude and direction, then its components along the three axes of a cartesian system are given by
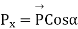 ---1.6(a)
---1.6(a)
 ----1.6(b)
----1.6(b)
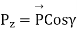 ----1.6©
----1.6©
Where 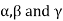 are respectively the angles made by the vector with the X, y and z axis as shown in figure 1.6
are respectively the angles made by the vector with the X, y and z axis as shown in figure 1.6
The three cosines of angles between a given direction as the direction of the vector p, and the three axes x, y and z are called direction cosines.

Since the magnitude of a vector is length in three dimension this length will be the square of the diagonal of the rectangular which in turn will be the sum of the square of three sides.
 ----1.7
----1.7
From equation 1.6 & 1.7 the direction cosines are given by
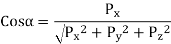
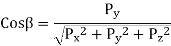
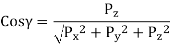
Squaring and adding above

Since the angle between 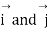 is zero.
is zero. 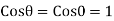 and dot product
and dot product 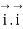 will be zero. The dot product of like vectors will be unity, while the dot product of unlike unit vectors will be zero.
will be zero. The dot product of like vectors will be unity, while the dot product of unlike unit vectors will be zero.
The cross product of 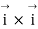 Involves the sine of 0 and the result is 0 while the cross product of
Involves the sine of 0 and the result is 0 while the cross product of 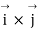 Involves sine of 90 degree and the result is unit vector.
Involves sine of 90 degree and the result is unit vector.
The cross product of two like unit vectors is zero while cross product of two unlike unit vector is the third unit vector, positive if rotation is normal and negative rotation is reversed.



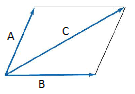
- Addition
- Addition is commutative:
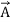 +
+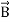 =
=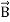 +
+
- It is also commutative: (
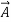 +
+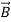 ) +
) + 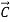 = (
= (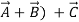
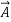 +
+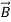 =
= 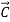
2. Subtraction
 -
-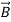 =
= 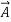 +
+
- It does not follow commutative law:
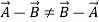
But follows associative law

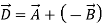
-ve sign shows reversal of direction
3. Multiplication
- Dot Product or Scalar Product
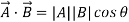
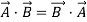
Dot product of vector is scalar
- Vector or Cross Product
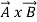 =
= 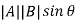 î
î
î = unit vector in the direction of perpendicular to 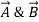
To find direction î, use right hand screw rule.
Cross Product of two vector is always a vector
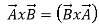
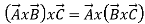
- A vector multiplied/divided by a scalar
 = it increases the magnitude by s unit
= it increases the magnitude by s unit
 = it decreases the magnitude by s unit
= it decreases the magnitude by s unit
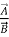 = it does not exist
= it does not exist
Key takeaway
- Addition is commutative as well as associative.
- Subtraction follows only associative law.
- Dot product of vector is scalar
- Cross productor of vector is vector
Representing a point in Rectangular Co-ordinate system
A point in rectangular co-ordinate system is located by three co-ordinates namely x,y and z co-ordinates. The point can be reached by moving from origin the distance of x in x-direction , distance of y in y-direction and finally distance of z in z direction.
Consider a point P having co-ordinates x1,y1 and z1 which can be positive or negative.
The point Q(3,-1,2) can be shown as
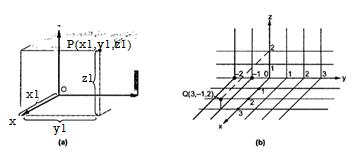
Figure 1. Rectangular co-ordinate system
Base vector :
The base vector are the unit vectors that are oriented along the directions of the co-ordinate axes of the given co-ordinate system. Thus for cartesian co-ordinate system the three base vectors are unit vectors oriented in x,y and z axis of the system. Therefore
given co-ordinate system. Thus for cartesian co-ordinate system the three base vectors are unit vectors oriented in x,y and z axis of the system. Therefore 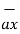 ,
,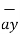 and
and 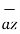 are the base vectors of the cartesian co-ordinate system.
are the base vectors of the cartesian co-ordinate system.
Any point of the x-axis having (x1,0,0) can be represented by a vector joining origin to this point to this point and denoted as x1 .
.
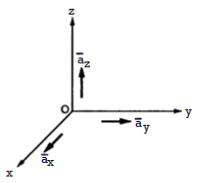
Figure 2. Base vector
Position and Distance vectors :
Consider a point P(x1,y1,z1) in cartesian co-ordinate system as shown in figure. Then the position vector of point P from the origin directed from origin to point P. This is called radius vector as shown in figure.
The three components of position vector oriented along the three co-ordinate axes with magnitudes x1,y1and z1. Thus the position vector of point P can be represented as

Figure. 3 Position vector
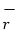 OP= x1
OP= x1  + y1
+ y1 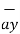 + z1
+ z1 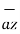
The magnitude of this vector in terms of three mutually perpendicular components is given by
| OP|=
OP|=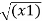 2 + (y1) 2+ (z1) 2
2 + (y1) 2+ (z1) 2
Thus, if point P has co-ordinates (1,2,3) then its position vector is
 OP=1
OP=1 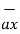 + 2
+ 2 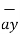 + 3
+ 3 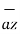
And
 OP =
OP =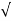 (1) 2 + (2) 2 + (3) 2 =
(1) 2 + (2) 2 + (3) 2 =  = 3.7416
= 3.7416
Consider two points in a cartesian coordinate system P and Q with the co-ordinates (x1,y1,z1) and (x2,y2,z2) respectively. The individual position vectors of the points are
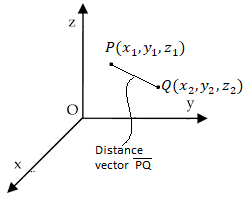
Figure 4. Cartesian coordinate system
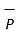 = x1
= x1 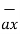 + y1
+ y1 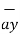 + z1
+ z1 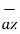
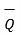 = x2
= x2 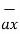 + y2
+ y2 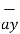 + z2
+ z2 
Then the displacement from P to Q is represented by the distance vector 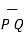 and is given by
and is given by
 =
= 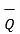 -
-  = [x2 -x1]
= [x2 -x1] 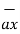 + [ y2 -y1]
+ [ y2 -y1] 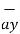 + [z2 -z1]
+ [z2 -z1] 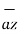
This is called separation vector.
The magnitude of the vector is given by
| | = √ (x2 -x1) 2 + (y2 -y1) 2 +(z2 – z1) 2
| = √ (x2 -x1) 2 + (y2 -y1) 2 +(z2 – z1) 2
This is called as distance formula.
The unit vector along the direction PQ is given by
 PQ= Unit vector along PQ =
PQ= Unit vector along PQ = 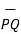 / |PQ|
/ |PQ|
Obtain the unit vector in the direction from the origin towards the point P(3,-3,-2)
Solution:
The origin O(0,0,0) while P(3,-3,-2) hence the distance vector 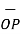 is
is
 = (3-0)
= (3-0) 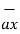 + (-3-0)
+ (-3-0) 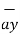 +(-2-0)
+(-2-0)  = 3
= 3 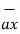 -3
-3 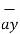 -2
-2 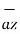
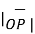 =
=  (3) 2 + (-3) 2 + (-2) 2 = 4.6904
(3) 2 + (-3) 2 + (-2) 2 = 4.6904
Hence the unit vector along the direction OP is
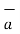 OP=
OP= 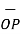 / |
/ |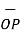 | = 3
| = 3 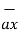 -3
-3 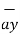 -2
-2 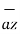 / 4.6904 =
/ 4.6904 =
= 0.6396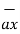 -0.63963
-0.63963 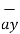 -0.4264
-0.4264 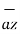
Differential Elements in Cartesian Co-ordinate System
Consider a point P(x,y,z) in the rectangular co-ordinate system . If we increase each co-ordinate by a differential amount a new point P’ will be obtained having co-ordinates (x+dx, y +dy ,z+dz)
Dx = differential length in x-direction
Dy = differential length in y-direction
Dz = differential length in z-direction
Hence differential vector length called elementary vector length
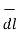 = dx
= dx 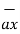 -dy
-dy -dz
-dz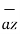 .
.
P is the intersection of the three planes and P’ is the intersection of the new three planes which are displaced from original three planes. These six planes together define a differential volume which is a rectangular parallelepiped as shown in the figure.
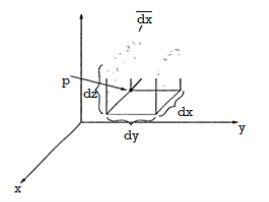
Figure 5. Cartesian coordinate system
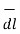 = dx
= dx 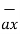 -dy
-dy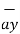 -dz
-dz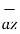 .
.
Hence the differential volume of the rectangular parallel piped is given by
Dv = dx dydz
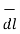 is vector and dv is scalar.
is vector and dv is scalar.
The differential surface area is given by
 =
= 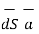 n
n
Ds = Different surfaces area of the element
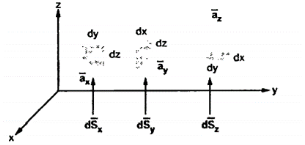
Figure 6. Differential vector system
d = Differential vector surface area normal to x direction dy dz
= Differential vector surface area normal to x direction dy dz 
d = = Differential vector surface area normal to y direction dx dz
= = Differential vector surface area normal to y direction dx dz 
d = = Differential vector surface area normal to y direction dx dy
= = Differential vector surface area normal to y direction dx dy 
Given the three points in cartesian co-ordinate system as A(3,-2,1) B (-3,-3,5) , C (2,6,-4)
Find
i) The vector from A to C
Ii) The unit vector from B to A
Iii) The distance from B to C
Iv) The vector from A to the mid-point of the straight line joining B to C.
The position vectors for the given points are:
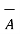 = 3
= 3 - 2
- 2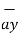 +
+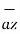 .
.
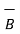 = -3
= -3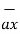 - 3
- 3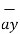 +5
+5 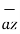 .
.
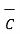 = 2
= 2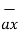 +6
+6 -4
-4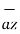 .
.
i) The vector from A to C is
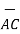 =
= 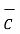 -
- 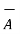 = [ 2-3]
= [ 2-3] 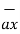 +[6–(-2)]
+[6–(-2)]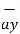 +[-4-1]
+[-4-1] 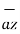 .
.
= - 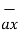 + 8
+ 8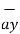 -5
-5  .
.
Ii) For unit vector from B to A obtain the distance vector  first
first
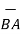 =
= 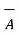 -
- 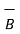
= [ 3 – (-3)]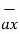 + [ (-2) –(-3) ]
+ [ (-2) –(-3) ] 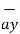 + [ -4-1]
+ [ -4-1] 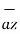
= 6 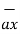 +
+ 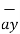 -4
-4 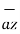 .
.
| | =
| =  (6) 2 + (1) 2 + (-4)2 = 7.2801.
(6) 2 + (1) 2 + (-4)2 = 7.2801.
 BA =
BA =  / |
/ | | = 6
| = 6 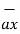 +
+ 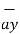 -4
-4 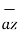 ./ 7.2801
./ 7.2801
Iii) For distance between B and C
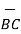 =
= 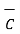 -
- 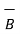 = [ 2 –(-3 ]
= [ 2 –(-3 ]  + [6-(-3)]
+ [6-(-3)] 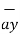 +[-4) –(-5)]
+[-4) –(-5)]  = 5
= 5 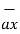 + 9
+ 9  – 9
– 9 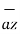
Distance BC =  2 + (9) 2 + (-9) 2 = 13.6747
2 + (9) 2 + (-9) 2 = 13.6747
Iv) Let B(x1,y1,z1 ) and C(x2,y2,z2) then the co-ordinates of the mid-point BC are (x1+x2/2 , y1+y2/2 , z1+z2/2)
The circular cylindrical co-ordinate system is a three-dimensional version of polar co-ordinate system. The surfaces used to define the cylindrical co-ordinate system are:
- Plane of constant z which is parallel to xy plane.
- A cylinder of radius r with z-axis of the cylinder
- A half plane perpendicular to xy plane at angle Ø with respect to x-z plane. The angle Ø is called the azimuth angle.
The ranges of the variable are:
0 ≤ r ≤ ∞------------------(1)
0 ≤Ø≤ 2π------------------------------(2)
-∞≤z≤∞--------------------------------------------------(3)
The point P in cylindrical co-ordinate system has three co-ordinates r, Ø and z whose values lie in the ranges given by equations 1,2,3.
The point P(r,Ø1,z1) can be shown in figure (b)
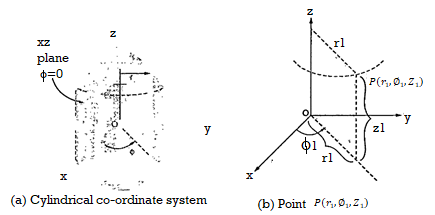
Figure.7 Cylindrical coordinate system
The point P can be defined as the intersection of three surfaces in cylindrical co-ordinate system. These three surfaces are,
r = Constant which is circular cylinder with z axis as its axis
Ø= Constant plane which is a vertical plane perpendicular to xy plane making angle Ø with respect to xz plane.
z= Constant plane is a plane parallel to xy plane.
These surfaces are shown in figure.

Figure.8 Surfaces of cylindrical coordinate system
The intersction of any two surfaces out of the above three surfaces is either a line or a circle and intersection of three surfaces define a point.
The intersection of z=constant and r=constant is a circle. The intersection of ɸ=constant and r=constant is a line. The point P which is intersection of all three surfaces is shown in the figure.

Figure.9 Intersection
Base vectors:
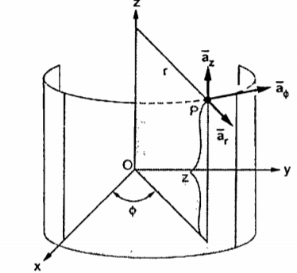
Figure. 10 Base vector
These are mutually perpendicular to each other. The 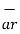 lies in a plane parallel to xy plane and perpendicular to the surface of the cylinder at a given point coming radially outwards. The vector
lies in a plane parallel to xy plane and perpendicular to the surface of the cylinder at a given point coming radially outwards. The vector 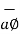 lies also in a plane parallel to xy plane but it is tangent to the cylinder and pointing in the direction of increasing
lies also in a plane parallel to xy plane but it is tangent to the cylinder and pointing in the direction of increasing 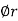 at the given point.
at the given point.
The unit vector 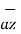 is parallel to z-axis and directed towards increasing z . Hence, vector of point P can be represented as
is parallel to z-axis and directed towards increasing z . Hence, vector of point P can be represented as
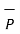 = P r
= P r  + P ɸ
+ P ɸ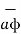 + P z
+ P z 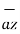
Differential Elements in Cylindrical co-ordinate system
Consider o point P(r,ɸ,z) in a cylindrical co-ordinate system. Let each co-ordinate be increased by differential amount. The differential increments in r,ɸ,z are dr,dɸ and dz respectively.
There are two cylinders of radius r and r+dr. There are two radial planes at the angles ɸ and ɸ+dɸ. And there are two horizontal planes at the heights z+dz. All these surfaces enclose a small volume as shown in figure.
The different lengths in r and z are dz and dr respectively. In ɸ direction dɸ is the change in angle ɸ and is not the differential length. Due to this change dɸ there exists a differential arc length in ɸ direction. This differential length due to dɸ in ɸ direction is r dɸ as shown in figure.
Thus the differential lengths are:
Dr = Differential length in r direction.
r dɸ = Differential length in ɸ direction
Dz = Differential length in z direction
Hence the differential vector length in cylindrical co-ordinate system is given by
 = dr
= dr 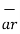 + r dɸ
+ r dɸ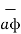 + dz
+ dz 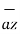
The magnitude of the differential length vector is given y
|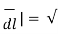 (dr) 2 +( r d ɸ) 2 + (dz) 2
(dr) 2 +( r d ɸ) 2 + (dz) 2
Hence the differential volume of the differential element is given by
Dv = r drdɸdz
The surfaces which are used to define the spherical co-ordinate system on the three cartesian axes are:
- Sphere of radius r, origin as the centre of the sphere.
- A right circular cone with its apex at the origin and its axis as z-axis. It half angle is Ѳ varies from 0 to 180.
- A half plane perpendicular to xy plane containing z axis making an angle Ø with xz plane.
Thus the three co-ordinates of a point P in the spherical co-ordinate system are (r,Ѳ,Ø). These surfaces are shown in figure
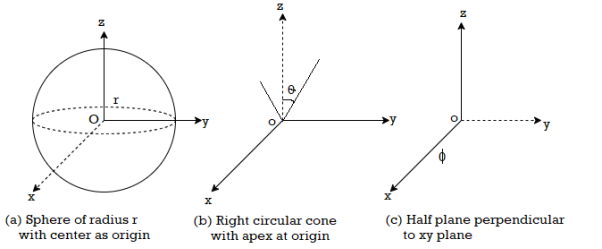
Figure. 11 Spherical coordinate system.
The ranges of the variables are,
 (1)
(1)
 (2)
(2)
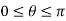 as half angle (3)
as half angle (3)
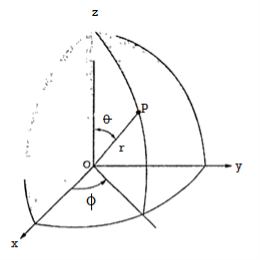
Figure. 12 Points in the spherical coordinate system
The point P(r,Ѳ,Ø) can be represented in the spherical co-ordinate system as shown in figure. The angles Ѳ and Ø are measured in radians. The point P can be defined as the intersection of three surfaces in spherical co-ordinate system. These three surfaces are:
r = Constant which is a sphere with cenre as origin
Ɵ = Constant which is right circular cone with apex as origin and axis a z axis
ɸ= Constant is a plane perpendicular to xy plane.
Base Vector:
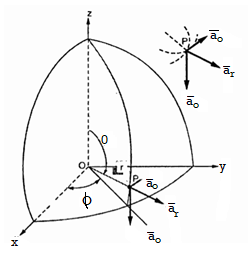
Figure.13 Base vector
There are three unit vectors in r, Ɵ and ɸ directions denoted as  ,
,  and
and 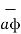 . These unit vectors are mutually perpendicular to each other as shown in figure. The unit vector
. These unit vectors are mutually perpendicular to each other as shown in figure. The unit vector  is directed from the centre of the sphere that is the origin to the given point P. It is radially outward normal to the sphere. It lies in the cone Ɵ = constant and plane ɸ= constant.
is directed from the centre of the sphere that is the origin to the given point P. It is radially outward normal to the sphere. It lies in the cone Ɵ = constant and plane ɸ= constant.
The unit vector 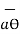 is tangent to the sphere and oriented in the direction of increasing Ɵ. It is normal to the conical surface.
is tangent to the sphere and oriented in the direction of increasing Ɵ. It is normal to the conical surface.
The third unit vector 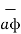 is tangent to the sphere and also tangent to the conical surface . It is oriented in the direction of increasing ɸ. It is same as defined in the cylindrical co-ordinate system.
is tangent to the sphere and also tangent to the conical surface . It is oriented in the direction of increasing ɸ. It is same as defined in the cylindrical co-ordinate system.
Hence, vector P is
 = Pr
= Pr 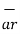 + P
+ P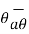 + Pɸ
+ Pɸ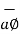
Differential elements in Spherical co-ordinate system

Figure.14 Spherical coordinate system
Consider a point P(r,Ɵ,ɸ) in spherical co-ordinate system. Let each co-ordinate be increased by the differential amount. The differential increments in r,Ɵ,ɸ are dr,dƟ and dɸ.
Now there are two spheres of radius r and r+dr . There are two cones with half angles Ɵ and Ɵ+dƟ. There are two planes at the angles ɸ+dɸ measured from xz plane. All these surfaces enclose a small volume as shown in figure.
Dr= Differential length in r direction
r d Ɵ = Differential length in Ɵ direction
r sin Ɵdɸ = Differential length in ɸ direction.
Hence the differential vector length in spherical coordinate system is
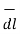 = dr
= dr 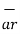 + r d
+ r d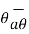 + r sin
+ r sin  dɸ
dɸ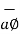
The magnitude of the differential length vector is
|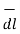 | = √ (dr) 2 + (r d
| = √ (dr) 2 + (r d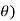 2 + (r sin
2 + (r sin 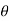 dɸ) 2
dɸ) 2
Hence differential volume is given by
Dv = r 2 sin 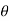 dr d
dr d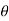 d
d 
Key Takeaways:
A Cartesian coordinate system is a coordinate system that specifies each point uniquely in a plane by a set of numerical coordinates, which are the signed distances to the point from two fixed perpendicular oriented lines, measured in the same unit of length.
Rectangular to cylindrical
The transformation of rectangular to cylindrical coordinates requires that we find the components of the rectangular coordinate vector A in the direction of the cylindrical coordinate unit vectors using dot product.
Transformation:
(Ax,Ay,Az) ----- (Ar,Aɸ,Az)
The required dot products are
Ar = A.  = Ax .
= Ax .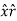 + Ay
+ Ay 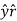 + A.
+ A. 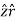 = Ax .
= Ax .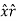 + Ay
+ Ay 
Aɸ = A. 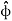 = Ax .
= Ax .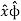 + Ay
+ Ay  + A.
+ A.  = Ax .
= Ax .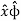 + Ay
+ Ay 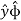
Az = A.  = Ax .
= Ax . + Ay
+ Ay  + Az.
+ Az. 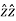 = Az
= Az
Where 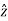 .
. 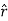 =0
=0 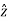 .
. 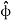 =0
=0 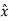 .
.  =0
=0 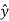 .
.  =0
=0  .
.  =1
=1
The four remaining unit vector dot products are determined according to the geometry relationships between the two coordinate systems.
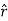 = cos ɸ
= cos ɸ + sin ɸ
+ sin ɸ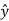
ɸ = - sin ɸ  + cos ɸ
+ cos ɸ 
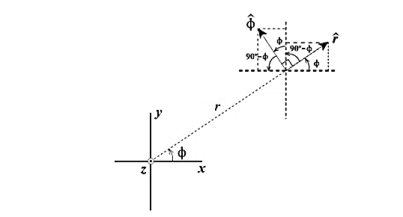
Figure. 15. Rectangular co-ordinate
 .
.  =
= 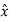 . ( cos ɸ
. ( cos ɸ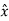 + sin ɸ
+ sin ɸ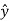 ) = cos ɸ
) = cos ɸ
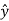 .
.  =
= 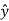 . ( cos ɸ
. ( cos ɸ + sin ɸ
+ sin ɸ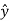 ) = sinɸ
) = sinɸ
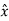 . ɸ =
. ɸ = 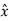 . ( -sin ɸ
. ( -sin ɸ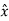 + cos ɸ
+ cos ɸ ) = -sin ɸ
) = -sin ɸ
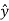 . ɸ =
. ɸ =  . ( -sin ɸ
. ( -sin ɸ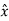 + cos ɸ
+ cos ɸ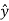 ) = cos ɸ
) = cos ɸ
The resulting cylindrical coordinate vector is A = Ar . 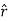 + A ɸɸ + Az
+ A ɸɸ + Az 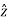
= (Ax cos ɸ + Ay sin ɸ) 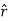 + (Ay cos ɸ - Ax sin ɸ) ɸ + Az
+ (Ay cos ɸ - Ax sin ɸ) ɸ + Az 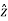
The rectangular to cylindrical transformation is

Rectangular to spherical
Transformation:
(Ax,Ay,Az) ----- (AR,A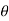 ,Aɸ)
,Aɸ)
The required dot products from rectangular to spherical are
Ar = A.  = Ax .
= Ax .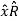 + Ay
+ Ay 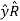 + Az
+ Az 
A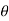 = A.
= A. 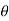 = Ax .
= Ax .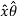 + Ay
+ Ay 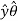 + Az
+ Az 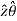
A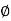 = A.ɸ =Ax .
= A.ɸ =Ax . 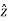 ɸ + Ay
ɸ + Ay 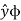 + Az.
+ Az. 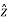 ɸ
ɸ
The geometry relationships between the rectangular and spherical unit vectors are shown below:
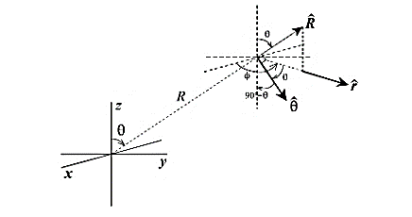
Figure. 16 Rectangular to spherical
 = sin
= sin  .
.  + cos .
+ cos . 
= sin 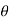 [ cos ɸ
[ cos ɸ + sin ɸ
+ sin ɸ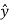 ] + cos
] + cos 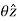
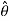 = cos
= cos 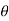 .
. 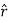 - cos( 90 –
- cos( 90 –  )
) 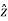
= cos  .cos ɸ
.cos ɸ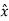 + cos
+ cos 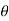 . Sin ɸ.
. Sin ɸ.  – sin
– sin 
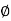 = - sin
= - sin 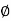 .
. 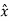 + cos ɸ .
+ cos ɸ .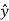
The dot products are then
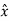 .
. 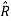 = sin
= sin  . Cos
. Cos 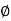
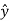 .
. 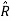 = sin
= sin 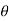 . Sin
. Sin 
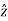 .
. 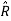 = cos
= cos 
 .
. 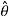 = cos
= cos  . Cos
. Cos 
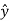 .
.  = cos
= cos 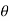 . Sin ɸ
. Sin ɸ
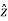 .
. 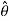 = - sin
= - sin 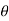
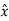 .
. 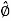 = - sin ɸ
= - sin ɸ
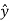 .
. 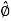 = cosɸ
= cosɸ
 .
.  = 0
= 0
The rectangular to spherical transformation may be written as
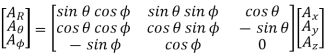
Spherical to Rectangular
(AR,A ,Aɸ) -------- (Ax,Ay,Az)
,Aɸ) -------- (Ax,Ay,Az)
The spherical to rectangular coordinate transformation is the inverse of the rectangular to spherical coordinate transformation so that
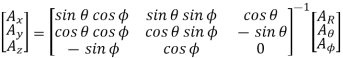
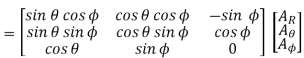
The spherical coordinate variables in terms of the rectangular coordinate variables are
Sin 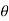 = r/R = √ x2 + y2 / √ x2 + y2 + z2 cos
= r/R = √ x2 + y2 / √ x2 + y2 + z2 cos 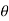 = z/R = z / √x2 + y2 + z2
= z/R = z / √x2 + y2 + z2
The complete spherical to rectangular transformation is
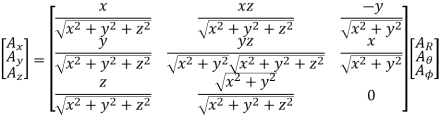
Cylindrical to rectangular:
The transformation from cylindrical to rectangular can be determined as the inverse of the rectangular to cylindrical transformation.
Transformation:
(Ar,Aɸ,Az) = (Ax,Ay,Az)
The transformation from cylindrical to rectangular coordinates can be determined as the inverse of rectangular to cylindrical transformation.
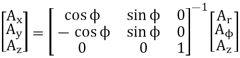
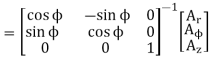
The cylindrical coordinates variables in the transformation matrix must be expressed in the terms of rectangular coordinates
Cosɸ = x/r = x / √x2 + y2
Sin ɸ = y/r = y/ √ x2 + y2
The resulting transformation is

The cylindrical to rectangular transformation can be written as
A = Ax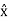 + Ay
+ Ay  + Az
+ Az 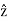
= (Ar cos ɸ - Aɸ sin ɸ) 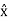 + (Ar sin ɸ + Aɸ cos ɸ)
+ (Ar sin ɸ + Aɸ cos ɸ)  + Az
+ Az
= Ar . x/ √ x 2 + y 2 – A ɸ . y / √ x 2 + y2 ) 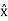 + Ar( y/ √ x 2 + y 2 + Aɸ . x / √ x 2 + y 2 )
+ Ar( y/ √ x 2 + y 2 + Aɸ . x / √ x 2 + y 2 )  + Az
+ Az 
Key Takeaway:
Vector can be converted from one co-ordinate system to another.
References:
- W.H. Hayt, “Engineering Electromagnetics” ,TMH Publication 2006
- N.N.Rao Electromagnetic Engg. V Edition , Prentice Hall. 2005
- Fawwaz T. Ulaby Applied Electromagnetics, Prentice Hall. 1999
- Krauss Electromagnetic Engg. IV Edition, Tata Mc Graw Hill. 2003
- Shevgaonkar Electromagnetic Waves, Tata Mc Graw Hill 2002