Unit - 2
Coulomb’s law, Electrical field intensity and electric flux density, Gauss’s law, Divergence
According to this law, the force of interaction between any two point charges is directly proportional to the product of the charges and inversely proportional to the square of the distance between them.
Suppose two bodies having charges  are separated in vacuum by distance r. Their linear dimensions be much smaller than the distance r so that they act as point charges.
are separated in vacuum by distance r. Their linear dimensions be much smaller than the distance r so that they act as point charges.
According to coulomb’s law
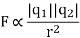
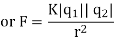
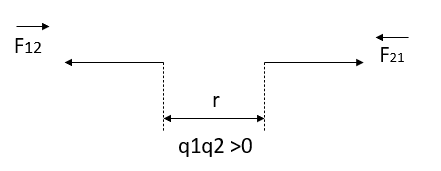
Where k is electrostatic force constant if  i.e. both the charges
i.e. both the charges  are positive or both are negative, bodies repel each other as shown in figure 1 (a).
are positive or both are negative, bodies repel each other as shown in figure 1 (a).
Let, 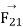 = force on
= force on  due to
due to  and
and , unit vector pointing from
, unit vector pointing from 
According to coulomb’s law
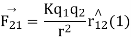
K is electrostatic force constant similarly the force on q due to 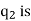

Pointing from 
If  if one of the charges is positive and other is negative, the bodies attract each other, figure 1 (b)
if one of the charges is positive and other is negative, the bodies attract each other, figure 1 (b)
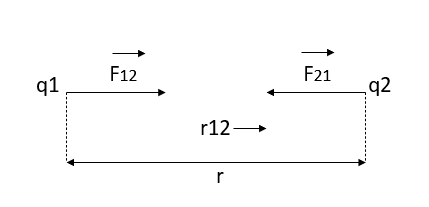
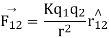
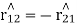
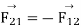
This shows that the force exerted by the two charges on each other are equal and opposite. Coulomb’s law is valid only for point charges.
The value of electrostatic force constant depends on the nature of medium separating the charges and on the system of units. When charges are situated in free space (air/vacuum) then CGS system K=1
In SI we write
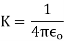
Where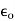 is called absolute electric permeability of the free space.
is called absolute electric permeability of the free space.
The experimentally measured value of K is 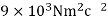
Therefore

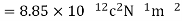
From equation 1 we can re write coulombs law in SI unit

The magnitude force is
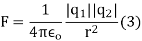
Solved Examples
Q1. A) Two insulated charged copper spheres A and B half their centres separated by 50 cm. What is the mutual force of repulsion if charge on each is  coulomb? The radii of A and B is negligible compared to distance of separation.
coulomb? The radii of A and B is negligible compared to distance of separation.
B) What is the force of repulsion of each sphere is charged double of the above amount and the distance between them is halved?
Sol. A) 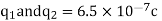

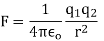
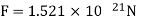
B) 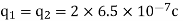
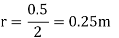
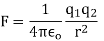
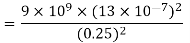

Q2. The electrostatic force on a small sphere of charge 0.4μc due to another small sphere of charge -0.8μc in air is 0.2 N.
(a) What is the distance between the two spheres?
(b) What is the force on the second sphere due to the first?
Sol. A) Here,

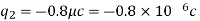
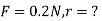
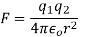
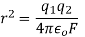
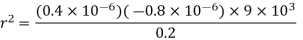
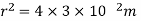

B) Force on second sphere is same 0.2N=F
Q3. A point charge of 2.0 μc is at the centre of a cubic Gaussian surface 90 cm on edge. What is the electric flux through the surface?
Sol. Here q= 20 μc=2×
L=90 cm
 =
= 

Q4. Consider uniform electric field E, 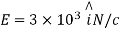
Field is along positive x direction
Surface area =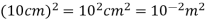
(a)What is the flux of this field through a square of 10 cm on a side whose plane is parallel to y z plane?
(b)What is the flux through the same square is the normal to its plane 30 degree angle with x axis?
Sol.(a) When plane is parallel to y z plane

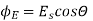
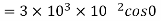

(b)When normal to the plane makes an angle of 30 degree with x-axis then  =30°
=30°
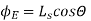
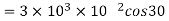
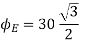
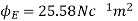
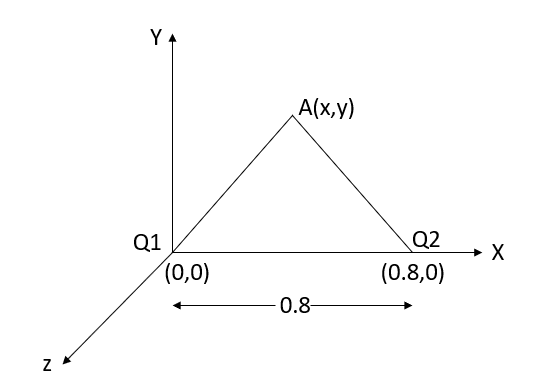
Q5. Two particles having charges 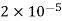 and
and  coulombs are spaced 0.8 metre apart. Determine the electric field at a point A situated at a distance of 0.5 metre from each of the particles.
coulombs are spaced 0.8 metre apart. Determine the electric field at a point A situated at a distance of 0.5 metre from each of the particles.
Sol. Let the two particles have charge 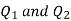 coulombs then the point A will be as shown in (1). Let the origin of the three axis be located at the point charge
coulombs then the point A will be as shown in (1). Let the origin of the three axis be located at the point charge 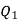 then the coordinates of
then the coordinates of  will be (0,0) (0.8,0) respectively.
will be (0,0) (0.8,0) respectively.
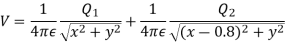
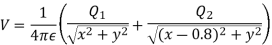
Differentiating partially with respect to x and y we get
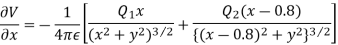
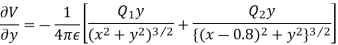
For the location of point A
x=0.4 and y= 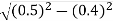 =0.3
=0.3
Substituting these values we have
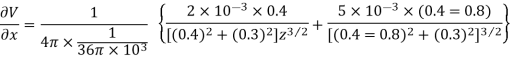
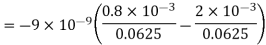
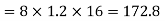
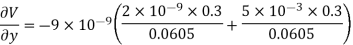

Since the field is desired in xy plane
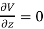 and field intensity E is given by
and field intensity E is given by
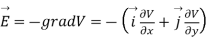
Substituting the values of 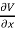 and
and 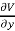 we get
we get
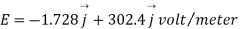
We have seen so far, the charge distributions have been discrete i.e. made up of individual point particles.
If a charge distribution is continuous rather than discrete, we can generalize the definition of the electric field. We simply divide the charge into infinitesimal pieces and treat each piece as a point charge.
We know that charge is quantized so there is no such thing as a truly continuous charge distribution. However, in most practical cases, the total charge creating the field involves such a huge number of discrete charges.
For simplicity we can safely ignore the discrete nature of the charge and consider it to be continuous. This is exactly the kind of approximation we make when we deal with a bucket of water as a continuous fluid rather than a collection of H2O molecules.
Continuous charge distribution: an arrangement of many discrete charges so closely spaced that the charge is treated as a continuum, resulting in a replacement of discrete sums with integrals.
Distribution of charges
(a) Line charge density
(b) Surface charge density
(c) Volume charge density
(d) Some of the components of the total electric field cancel out, with the remainder resulting in a net electric field
Definitions of charge density:
(a) λ - Line charge: charge per unit length (linear charge density); units are coulombs per meter (C/m)
(b) - Surface charge density: Charge per unit area; units are coulombs per square meter (C/m2)
(c) - Volume charge density: Charge per unit volume; units are coulombs per cubic meter (C/m3)
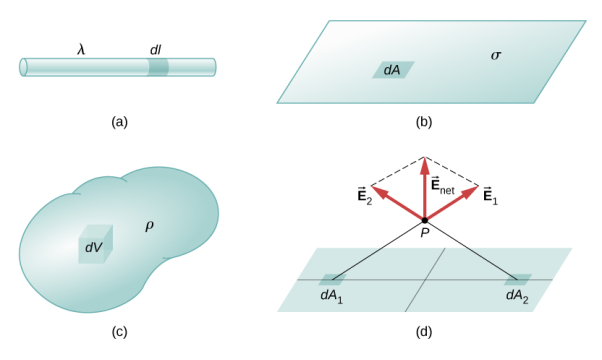
Figure 1: Charge Distribution
Some of the important result for electric field due to point charge, line charge density, surface charge density and volume charge density.
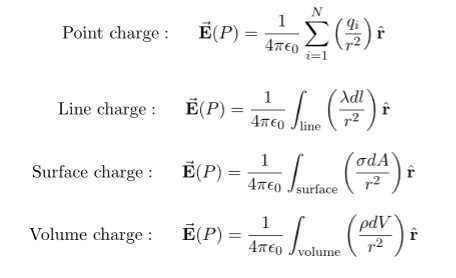
Note carefully the meaning of r in these equations: It is the distance from the charge element λdl, ds, dV to the location of interest, P(x,y,z) (the point in space where you want to determine the field). However, don’t confuse this with the meaning of 
If the charge distribution is continuous, the potential at a point P can be found by summing over the contributions from individual differential elements of charge. Dq
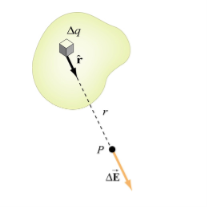
Figure 2: Continuous charge distribution
Consider the charge distribution shown in Figure. Taking infinity as our reference point with zero potential, the electric potential at P due to dq is
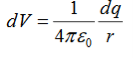
Summing over contributions from all differential elements, we have
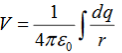
We established the relation between 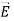 and V. If we consider two points which are separated by a small distance
and V. If we consider two points which are separated by a small distance 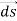 , the following differential form is obtained.
, the following differential form is obtained.
DV = -
In Cartesian coordinates,
E = Ex 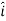 + Ey
+ Ey + Ez
+ Ez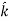
And 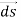 = dx
= dx  + dy
+ dy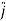 + dz
+ dz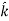
DV = ( Ex + Ey
+ Ey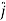 + Ez
+ Ez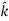 ) .( dx
) .( dx 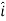 + dy
+ dy + dz
+ dz )
)
DV = ( Ex dx+ Eydy + Ezdz
This implies
Ex = 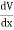 Ey =
Ey = 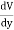 Ez =
Ez = 
By introducing a differential quantity called the “del (gradient) operator”
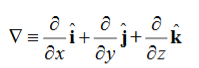
The electric field can be written as
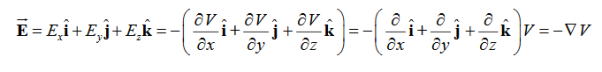
 =-
=- 
Notice that ∇ operates on a scalar quantity (electric potential) and results in a vector quantity (electric field). Mathematically, we can think of  as the negative of the gradient of the electric potential V. Physically, the negative sign implies that if V increases as a positive charge moves along some direction, say x, with, then there is a non-vanishing component of
as the negative of the gradient of the electric potential V. Physically, the negative sign implies that if V increases as a positive charge moves along some direction, say x, with, then there is a non-vanishing component of 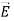 in the opposite direction(-Ex 0)
in the opposite direction(-Ex 0)
In the case of gravity, if the gravitational potential increases when a mass is lifted a distance h, the gravitational force must be downward.
If the charge distribution possesses spherical symmetry, then the resulting electric field is a function of the radial distance r, i.e. 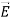 = Er
= Er 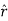
In this case, .dV=- Er dr.
If V(r) is known, then 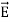 may be obtained as
may be obtained as
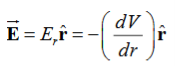
For example, the electric potential due to a point charge q is
V = 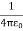

Using the above formula, the electric field is simply
E = 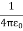
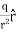
Let us find the electric field a distance z above the midpoint of a straight-line segment of length L that carries a uniform line charge density λ.
Since this is a continuous charge distribution, we conceptually break the wire segment into differential pieces of length dl, each of which carries a differential amount of charge dq = λdl.
We proceed as follow to obtain the complete electric field expression.
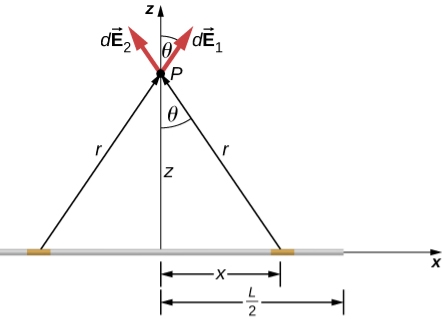
Figure 3: A uniformly charged segment of wire. The electric field at point P can be found by applying the superposition principle to symmetrically placed charge elements and integrating.
Since it is a finite line segment, from far away, it should look like a point charge. We will check the expression we get to see if it meets this expectation.
The electric field for a line charge is given by the general expression
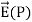 =
=  …………..(1)
…………..(1)
The symmetry of the situation (our choice of the two identical differential pieces of charge) implies the horizontal (x)-components of the field cancel, so that the net field points in the  -direction. Let’s check this formally.
-direction. Let’s check this formally.
The total field  is the vector sum of the fields from each of the two charge elements are E1 and E2.
is the vector sum of the fields from each of the two charge elements are E1 and E2.
 = E1+ E2 =
= E1+ E2 =  +
+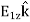 +
+ +
+ …………..(2)
…………..(2)
Because the two charge elements are identical and are the same distance away from the point P where we want to calculate the field, =
=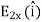 , so those components cancel. This leaves
, so those components cancel. This leaves
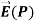 = E1+ E2 =
= E1+ E2 =  +
+ = E1Cosθ
= E1Cosθ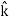 + E2Cosθ
+ E2Cosθ …………..(3)
…………..(3)
These components are also equal, so we have
 …………..(4)
…………..(4)
Here our differential line element dl is dx, in this example, since we are integrating along a line of charge that lies on the x-axis.
The limits of integration are 0 to  , not
, not  to L, because we have constructed the net field from two differential pieces of charge dq. If we integrated along the entire length, we would pick up an erroneous factor of 2.
to L, because we have constructed the net field from two differential pieces of charge dq. If we integrated along the entire length, we would pick up an erroneous factor of 2.
In principle, this is complete. However, to actually calculate this integral, we need to eliminate all the variables that are not given. In this case, both r and θ change as we integrate outward to the end of the line charge, so those are the variables to get rid of as follow
r = 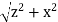
And
Cos θ =  =
=  …………..(5)
…………..(5)
Substituting, we obtain
 …………..(6)
…………..(6)
This simplifies to
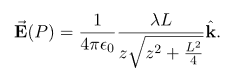 …………..(7)
…………..(7)
With the use of symmetry, we are able to find electric field due to line element. This is a very common strategy for calculating electric fields. The fields of non-symmetrical charge distributions have to be handled with multiple integrals.
ELECTRIC FIELD OF AN INFINITE LINE OF CHARGE
Find the electric field a distance z above the midpoint of an infinite line of charge that carries a uniform line charge density λ.
This is exactly like the 1.12 article except the limits of integration will be - to +
Again, the horizontal components cancel out, so we wind up with

Where our differential line element dl is dx, in this example, since we are integrating along a line of charge that lies on the x-axis. Again,
Cos θ =  =
= 
Substituting, we obtain
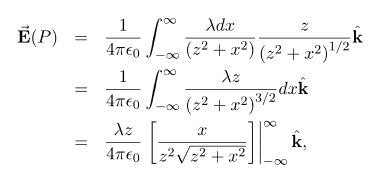
This simplifies to
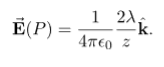
In the case of a finite line of charge, note that for z >>L, z2 dominates L the  in the denominator, so that Equation simplifies to
in the denominator, so that Equation simplifies to
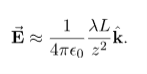
If you recall that λL=q, the total charge on the wire, we have retrieved the expression for the field of a point charge, as expected.
In the limit L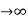 , on the other hand, we get the field of an infinite straight wire, which is a straight wire whose length is much, much greater than either of its other dimensions, and also much, much greater than the distance at which the field is to be calculated:
, on the other hand, we get the field of an infinite straight wire, which is a straight wire whose length is much, much greater than either of its other dimensions, and also much, much greater than the distance at which the field is to be calculated:
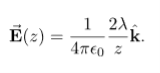
ELECTRIC FIELD DUE TO A RING OF CHARGE
A ring has a uniform charge density λ, with units of coulomb per unit meter of arc. Find the electric potential at a point on the axis passing through the center of the ring.
We use the same procedure as for the charged wire. The difference here is that the charge is distributed on a circle. We divide the circle into infinitesimal elements shaped as arcs on the circle and use polar coordinates shown in figure
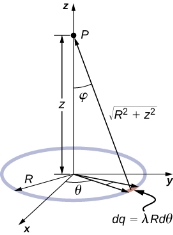
Figure 4: The system and variable for calculating the electric field due to a ring of charge.
 =
= 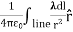 …………..(1)
…………..(1)
A general element of the arc between θ and dθ is of length Rdθ and therefore contains a charge equal to λRdθ. The element is at a distance of r =  from P, the angle is,
from P, the angle is,
Cos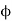 =
=  =
= 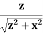
And therefore, the electric field is
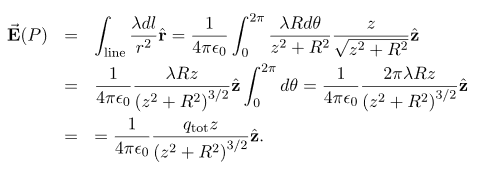
Significance
As usual, symmetry simplified this problem, in this particular case resulting in a trivial integral. Also, when we take the limit of Z >> R, we find that
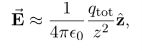
ELECTRIC POTENTIAL FOR UNIFORMLY CHARGED ROD
Electric Potential
Electric potential is the work done by an applied force on a unit charge bringing it from infinity to a specific point. The work done is called electric Potential.
Consider a non-conducting rod of length A having a uniform charge density λ. Find the electric potential at P, a perpendicular distance y above the midpoint of the rod.

Figure 5: A non-conducting rod of length l and uniform charge density λ
Consider a differential element of length dx′ which carries a charge dq =λdx′, as shown in Figure. The source element is located at (x′,0) while the field point P is located on the y-axis at (0,y). The distance from dx′ to P is r =  . Its contribution to the potential is given by
. Its contribution to the potential is given by
DV = 
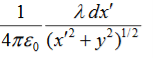
Taking V to be zero at infinity, the total potential due to the entire rod is

Where we have used the integration formula
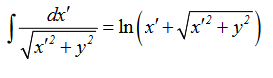
In the limit the potential becomes l>>y
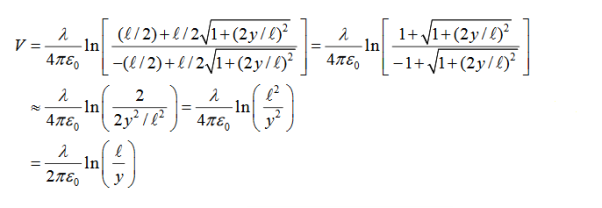
The corresponding electric field can be obtained as
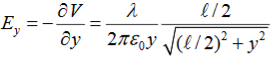
ELECTRIC POTENTIAL FOR UNIFORMLY CHARGED RING
Uniformly consider a uniformly charged ring of radius R and charge density λ. Electric potential at a distance z from the central axis
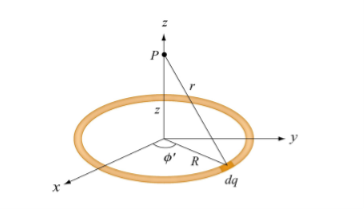
Figure 6: A non-conducting ring of radius R with uniform charge density λ
Consider a small differential element dl= Rd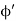 on the ring. The element carries a charge
on the ring. The element carries a charge
Dq =λdl = λ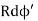 ………….(1)
………….(1)
And its contribution to the electric potential at P is

The electric potential at P due to the entire ring is
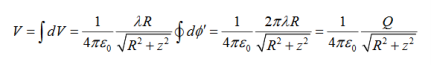 ………….(2)
………….(2)
Where we have substituted Q=2πRλ for the total charge on the ring. In the limit z>>R, the potential approaches its “point-charge” limit:
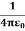

From Equation 2, the z-component of the electric field may be obtained as
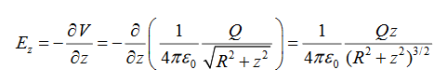
This is in agreement with the result of article 1.14
Key Takeaways
- Continuous charge distribution: an arrangement of many discrete charges so closely spaced that the charge is treated as a continuum, resulting in a replacement of discrete sums with integrals.
- Distribution of charges can be Line charge density, Surface charge density and Volume charge density
- Electric field for a continuous charge distribution can be written as =-
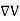
- Electric field of a line segment or rod is given by

5. Electric field of an infinite line of charge
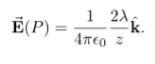
6. Electric field due to a ring of charge
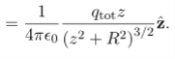
7. Electric potential is the work done by an applied force on a unit charge bringing it from infinity to a specific point. The work done is called electric Potential.
The region in which the influence of an electric charge can be felt is known as electric field. The force experienced by a unit positive charge at a point is called is electric field strength.
E= F/q N/C or V/m
Electric flux density is defined as the amount of flux passes through unit surface area in the space at right angle to the direction of electric field.
E = 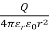
Q: charge
r: distance between the object and field
Definition:
The electric flux passing through any closed surface is equal to the total charge enclosed by that surface.
The total charge enclosed by the irregular closed surface is Q coulombs. Hence the total flux has to pass through the closed surface is Q. Consider a small differential surface dS at point P. As the surface is irregular the direction of D as well as its magnitude is going from point to point on the surface. The surface dS under consideration can be represented in vector form.
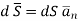
Where 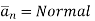 to the surface dS at point P
to the surface dS at point P
The flux density at point P is D and its direction is such that it makes an angle Ѳ with the normal direction at point P.
The flux d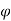 passing through the surface dS is the product of the component normal to dS and d
passing through the surface dS is the product of the component normal to dS and d .
.
Mathematically this can be represented as,
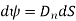
Where 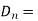 Component of
Component of 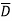 in the direction of normal to the surface dS
in the direction of normal to the surface dS
From fig. We can write
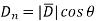
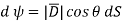
From the definition of the dot product
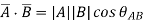
We can write

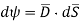
This is the flux passing through incremental surface area dS. Hence the total flux passing through the entire closed surface is to be obtained by finding the surface integration of the equation (5)
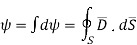
 sign indicates the integration over the closed surface is called closed surface integral.
sign indicates the integration over the closed surface is called closed surface integral.
Such a closed surface over which the integration in eq (6) is carried out is called Gaussian surface.
Total charge enclosed by the surface is given by
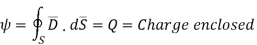
Applications:
Infinite line charge:
Consider an infinite line charge of density 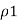 C/m lying along the z-axis from -
C/m lying along the z-axis from - 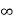 to
to  as shown in figure.
as shown in figure.
Consider the Gaussian surface as the right circular cylinder with z-axis as its axis and radius r as shown in figure. The length of the cylinder is L.
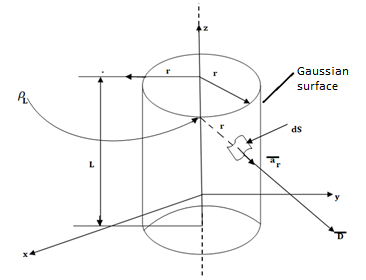
Fig 7. Infinite Line charge
The flux density at any point on the surface is directed radially towards that is in the  direction according to cylindrical co-ordinate system.
direction according to cylindrical co-ordinate system.
Consider differential surface area dS as shown which is at a radial distance r from the line charge. The direction is normal to dS is 
As the line charge is along z-axis there cannot be any component D in z direction. So, D has only radial component.
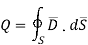
The integration is to be evaluated for side surface, top surface and bottom surface.
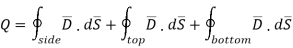
Now  as has only radial component
as has only radial component
And 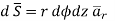 normal to
normal to 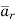 direction.
direction.
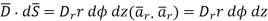 … as
… as 
Now 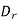 is constant over the side surface.
is constant over the side surface.
As 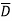 has only radial component and no component along
has only radial component and no component along  and
and 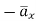 hence integrations over top and bottom surfaces is zero.
hence integrations over top and bottom surfaces is zero.
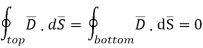
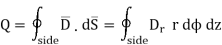
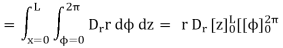

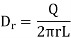
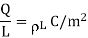
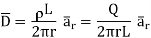
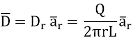
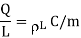
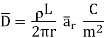
And 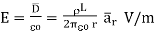
The results are same as obtained from the Coulomb’s law.
It is instructive at this point to continue using the integral and differential equations just developed for Maxwell’s Equation No.1 in order to illustrate a vector identity called, "Gauss’ Divergence Theorem". This identity equates a vector surface integral to a vector volume integral.
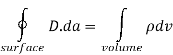
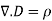
By substituting 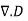 for r in the integral equation we obtain;
for r in the integral equation we obtain;

This is a typical illustration of Gauss’ divergence theorem, using vector D as the example. The point here is that any time we have a vector surface integral of this type we can substitute the volume integral. If we have a vector volume integral of the above type, we can substitute the surface integral. The integral of the divergence of a vector summed throughout the volume is equal to the integral of the product of the vector times its effective area summed over the area. This is analogous to stating that the volume of a ball is contained within its surface area. The circle on the integral sign indicates that the integral is taken over a continuous area.
Key takeaway
Vector surface integral to a vector volume integral.

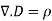
References:
- W.H. Hayt, “Engineering Electromagnetics”, TMH Publication 2006
- N.N.R ao Electromagnetic Engg. V Edition, Prentice Hall. 2005
- Fawwaz T. Ulaby Applied Electromagnetics, Prentice Hall. 1999
- Krauss Electromagnetic Engg. IV Edition, Tata Mc Graw Hill. 2003
- Shevgaonkar Electromagnetic Waves, Tata Mc Graw Hill 2002