Unit - 5
Load Flow Studies
Load flow studies are important in planning and designing future expansion of power systems. The study gives steady state solutions of the voltages at all the buses, for a particular load condition. Different steady state solutions can be obtained, for different operating conditions, to help in planning, design and operation of the power system. Generally, load flow studies are limited to the transmission system, which involves bulk power transmission. The load at the buses is assumed to be known. Load flow studies throw light on some of the important aspects of the system operation, such as: violation of voltage magnitudes at the buses, overloading of lines, overloading of generators, stability margin reduction, indicated by power angle differences between buses linked by a line, effect of contingencies like line voltages, emergency shutdown of generators, etc. Load flow studies are required for deciding the economic operation of the power system.
They are also required in transient stability studies. Hence, load-flow studies play a vital role in power system studies. Thus, the load flow problem consists of finding the power flows (real and reactive) and voltages of a network for given bus conditions. At each bus, there are four quantities of interest to be known for further analysis: the real and reactive power, the voltage magnitude and its phase angle. Because of the nonlinearity of the algebraic equations, describing the given power system, their solutions are obviously, based on the iterative methods only. The constraints placed on the load flow solutions could be: The Kirchhoff’s relations holding good, Capability limits of reactive power sources, Tap-setting range of tap-changing transformers, Specified power interchange between interconnected systems, Selection of initial values, acceleration factor, convergence limit, etc.
The following variables are associated with each bus or node:
1) Magnitude of voltage, |Vi|
2) phase angle of the voltage, 
3) Active power, Pi
4) Reactive volt ampere, Qi
Three types of buses or nodes are identified in a power system network for load flow studies. In each bus two variables are known (specified) and 2 are to be determined. The bus classification depends upon the specified variables.
a) Spring bus or reference bus or slackbus - Voltage magnitude |Vi| and phase angle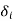 
are specified for this bus. This bus is first to respond to a changing load condition.
b) Generator bus or voltage controlled bus or PV- Here |Vi| and |Pi| are specified. Often the upper and lower limits of Q are also specified. The phase angles of the voltages and the reactive powers are to be determined.
c) Load bus or P-Q bus- Here, the active power Pi and reactive voltamperes Qi are specified. Buses with neither generator nor load may be considered as load buses where P==Qi=0. If any bus in a power system network has both load and generator, then load is generally treated as negative generator.
In a power system, power is injected into a bus from generators, while the loads are tapped from it. There may be some buses with only generators and there may be other only with loads. Some buses have generators and loads while some other may have static capacitors for reactive power compensation. The surplus power at some of the buses is transported through transmission lines to the bus deficient in power. Single line diagram of a simple 4-bus system with generators and load at each bus is shown in the figure. Let SGi denote the 3-phase complex generator power flowing into the ith bus and SDi denotes the 3-phase complex power demand at the ith bus. Let SGi and SDi may be represented as-
SGi = PGi + jQGi
SDi = PDi + jQGi
Net complex power injected into the bus is given as
Si= Pi + jQi = (PGi – PDi) + j (QGi – QDi)
The real & reactive power injected into the ith bus is then,
Pi = PGi - PDi
Qi = QGi - QDi
Where i = 1, 2, 3, 4…n
A network model of the given power system worked out on the above line is shown below in the figure. S1, S2, S3, S4 denote the net 3-phase complex power flowing into the buses and I1, I2, I3, I4 denotes the current flowing into the buses. Each transmission line is represented by a π-circuit.
The equivalent circuit of 4-bus system is shown in the figure below. All the sources of the bus system connected to the common reference at ground potential and the shunt admittance at the busses have been lumped. Besides the ground node, it has four other nodes or buses at which the current from the source is injected into the network. The line admittance between nodes i and k is represented by yik = yki. Further, the mutual admittance between lines is assumed to be zero.
Applications of Kirchhoff’s current law to the four nodes gives the following equation.
I1 = V1y10 + (V1-V2) y12 + (V1-V2)
I2 = V2y20 + (V2-V1) y12 + (V2-V3) y23 + (V2-V4) y24
I3 = V3y30 + (V3-V1) y13 + (V3-V2) y23 + (V3-V4) y34
I4 = V4y40 + (V4-V2) y24 + (V4-V3) y34
The above equation can be arranged & written in matrix form as below
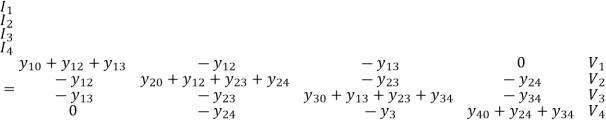
The self-admittance matrix is given as
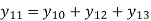
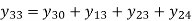
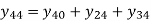
The mutual admittances for the matrix are given as
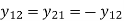
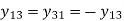
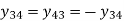
Matrix is written in terms of self-bus admittance Yi and mutual-bus admittance Yik as follows: -
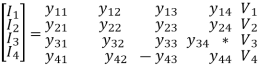
Yii is known as self-admittance (or driving point admittance) of the ith node and is equal to the sum of the admittance connected to the ith node. Each off-diagonal term Yik is known as mutual admittance (or transfer admittance) between ith and kth node and is equal to the negative of the sum of all the admittances connected directly between ith and kth node.
The equation can be written in compact form as
Ibus = Ybus * V
Where [ I] is the n-bus matrix, [ V] is the n-bus voltage matrix and, [ Ybus] is called bus admittance matrix and is written as
Ibus = Ybus V
And is called the bus admittance matrix and V and I are the n-element node voltage matrix and current node matrix respectively.
Key Takeaway
Diagonal elements are dominating. Off diagonal elements are symmetric. The diagonal element of each node is the sum of the admittances connected to it. The off-diagonal element is negated admittance
Here, the analysis is restricted to a balanced three-phase power system, so that the analysis can be carried out on a single phase basis. The per unit quantities are used for all quantities. The first step in the analysis is the formulation of suitable equations for the power flows in the system. The power system is a large interconnected system, where various buses are connected by transmission lines. At any bus, complex power is injected into the bus by the generators and complex power is drawn by the loads. Ofcourse at any bus, either one of them may not be present. The power is transported from one bus to other via the transmission lines. At any bus i, the complex power Si (injected), shown in figure 1, is defined as
Si = SGi - SDi
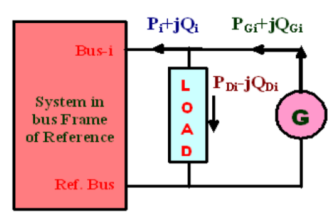
Where Si = net complex power injected into bus i, SGi = complex power injected by the generator at bus i, and SDi = complex power drawn by the load at bus i. According to conservation of complex power, at any bus i, the complex power injected into the bus must be equal to the sum of complex power flows out of the bus via the transmission lines. Hence,
Si = _Sij " i = 1, 2, ………..n
Where Sij is the sum over all lines connected to the bus and n is the number of buses in the system (excluding the ground). The bus current injected at the bus-i is defined as
Ii = IGi – IDi " i = 1, 2, ………..n
Where IGi is the current injected by the generator at the bus and IDi is the current drawn by the load (demand) at that bus. In the bus frame of reference
IBUS = YBUS VBUS
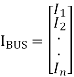
Is the vector of currents injected at the bus
YBUS is the bus admittance matrix and
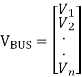
VBUS is the vector of complex bus voltages
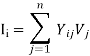
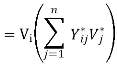
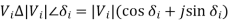
Hence,
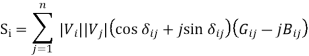
Separating real and imaginary parts
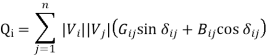
An alternate form of Pi and Qi can be obtained by representing Yik also in polar form as
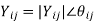
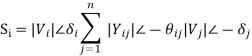
The real part of above equation gives Pi
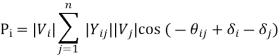
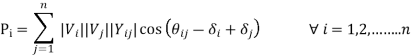
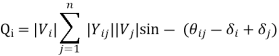
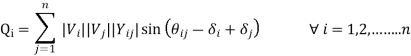
The load flow equations can be solved for any 2n unknowns, if the other 2n variables are specified. This establishes the need for classification of buses of the system for load flow analysis into: PV bus, PQ bus, etc.
Gauss Seidel Method
The Gauss-Seidel method is based on substituting nodal equations into each other. It is the slower of the two but is the more stable technique. Its convergence is said to be Monotonic. The iteration process can be visualized for two equations
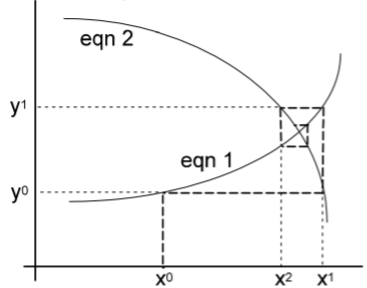
Although not the best load-flow method, Gauss-Seidel is the easiest to understand and was the most widely used technique until the early 1970s. Gauss-Seidel method is used to solve a set of algebraic equations. Consider
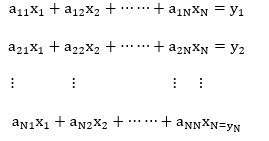
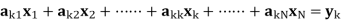
Thus,
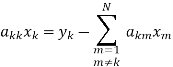
k = 1,2,….,N
In Gauss-Seidel method, initially, values of x1, x2 x3……xN are assumed. Updated values are calculated using the above equation. In any iteration h1, up to m k1, values of xm calculated in h1 iteration are used and for m k1 to N, values of xm calculated in h iteration are used. Thus,
In this method, first an initial estimate of bus voltages is assumed. By substituting this estimate in the given set of equations, a second estimate, better than the first one, is obtained. This process is repeated and better and better estimates of the solution are obtained until the difference between two successive estimates becomes lesser than a prescribed tolerance. First let us consider a power system without any P-V bus. Later, the modification required to include the P-V busses will be discussed. This means that given the net power injection at all the load bus, it is required to find the bus voltages at all the load busses. The expression for net power injection being Vk Ik * , the equations to be solved are
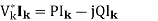
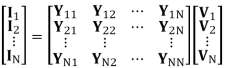
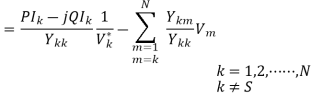
A significant reduction in computing time for a solution can be achieved by performing as many arithmetic operations as possible before initiating the iterative calculation. Let us define
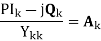
Having defined Ak and Bkm equation
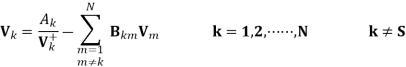
When Gauss-Seidel iterative procedure is used, the voltage at the th k bus during th h 1 iteration, can be computed as
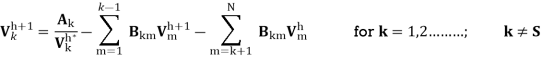
Newton-Raphson method
Load flow solution is an unavoidable tool for power system planning and operation. NR and its derivatives are the most popular and widely used ones among the various methods of load flow solution techniques. In NR method one of the generator buses is treated as slack bus which is kept out of calculation during iterations. This is because of the fact that the slack bus is to carry entire loss of the system and total loss cannot be calculated before the end of iterations [8]. The exclusion of slack bus from the load flow iteration restricts many analyses to make. Consideration of distributed slack bus, load flow for Micro grids, study on minimization of system losses etc. cannot be performed when the slack bus is excluded from the iterations.
The results obtained from this analysis comprises the real and reactive power flow on transmission lines, reactive powers on generator buses, magnitudes and phase angles of load bus voltages. NR method of load flow analysis is an iterative method which approximates the set of nonlinear simultaneous equations to a set of linear simultaneous equations using Taylor’s series expansion and the terms are limited to first order approximation. The non-linear equations governing the power system network are:
Where, Si is the complex power in bus i
Vi is the bus voltage at bus i given as
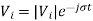
And
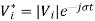
Where, i = is the bus angle at node i
e is the Euler’s constant
is the complex voltage at node i
Also
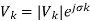
Where Vk is the voltage at bus k
k is the bus angle at node k
Ii is the current injected into bus i, given by
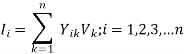
Where Yik is the admittance at bus I & k
Qik is the admittance angle at nodes i & k
Pi & Qi is the real & reactive power respectively at bus i
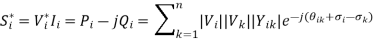
Separate the conjugate complex power in to real & imaginary power & we will get
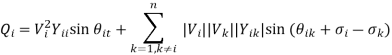
The above equations constitute the polar form of the power flow equations that provide the calculated values for the net real power Pi & reactive power Qi entering the bus i. Denoting the calculated values of Pi by Pi cal and Qi by Qi cal leads to definition of mismatches ΔPi & ΔQi
Hence,
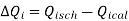
Mismatches occur when Pi cal & Qi cal do not coincide with scheduled values.
The set of linear equations formed expressing the relationship between changes in real and reactive power components of the bus voltages can be written in compact form as
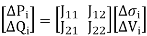
The Jacobian Matrix J11 J12 is set up as a partitioned matrix by conventional form
The off diagonal and diagonal term in the sub-matrices are real numbers calculated by partial differentiation of above equations 𝜎𝑖 and |𝑉𝑖 |. The Newton-Raphson method solves the polar form of the power flow equations until the mismatches at all buses fall within specified tolerances.
Flowchart of Newton Raphson Method
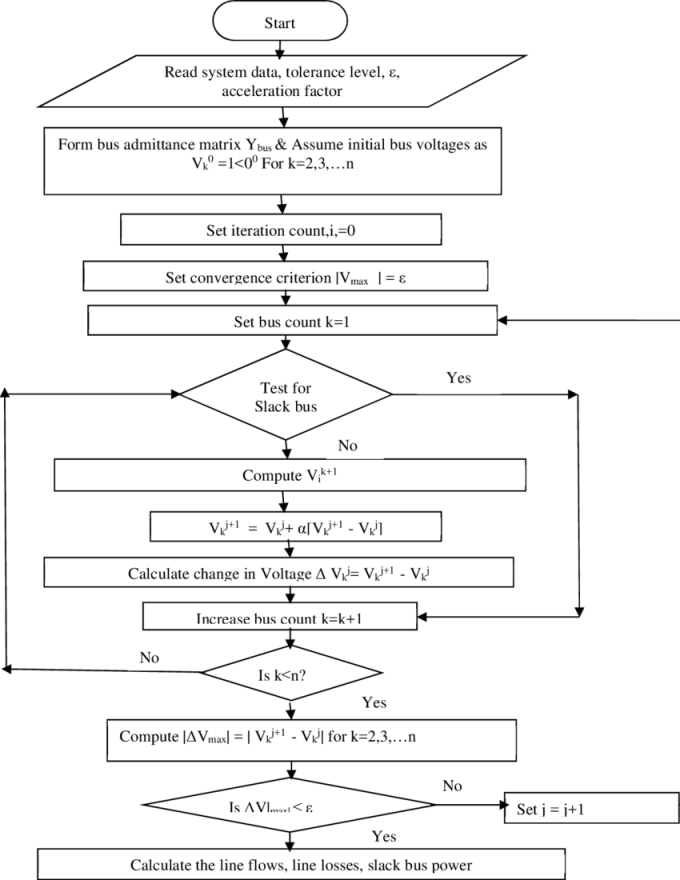
Key Takeaway
Iterative method to calculate line flows, line losses & output of load flow analysis in a power system.
Consider that a purely inductive load is connected to a source through a lossless line as shown in Figure below. Here, P = 0 and δ = 0 since the load is purely inductive; therefore, the reactive power at the receiving end is expressed as
Qr = (Vs Vr /X) - (Vr2/X)
The condition for maximum reactive power transfer is dQr/dVr = 0
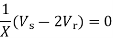
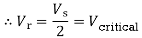
Where Vcritical is the receiving-end voltage for maximum reactive power transfer. Therefore, the maximum reactive power is expressed as
As half of the drop will be across the line and another half across the load, Xload = X; hence
Qrmax = Vr2/Xload
The maximum reactive power is transferred when the load reactance is equal to the line reactance or the source reactance. The short-circuit reactive power of the line is
Qsc= Vs2/X
Hence, the normalized maximum reactive power is
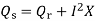
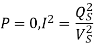
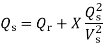
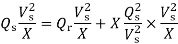
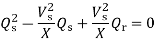
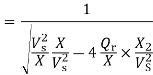
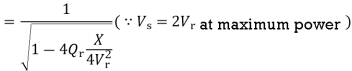
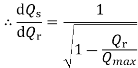
The differentiation of the sending-end reactive power Qs with respect to the receiving-end reactive power Qr, dQs/dQr is known as the voltage collapse proximate indicator (VCPI) of a radial line. The receiving-end voltage varies from Vs at no load to Vs/2 at maximum load Qmax. However, VCPI is unity at no load since at no load Qr =0 and dQs/dQr =1 for Qr=0 and it is infinity at maximum load since at this load Qr = Qrmax and hence dQs/dQr is infinity.
It is clear that near the maximum load, an extremely large amount of reactive power is required at the sending end to supply an incremental increase in load. Thus, VCPI is a very sensitive indicator of impeding voltage collapse. There, lated quantities reactive reserve activation and reactive losses are also sensitive indicators.
Voltage stability refers to the ability of a power system to maintain steady voltages at all buses in the system after being subjected to a disturbance. It depends on the ability of the system to maintain equilibrium between load demand and load supply. Instability results in a progressive fall or rise of voltages of some buses, which could lead to loss of load in an area or tripping of transmission lines, leading to cascading outages. This may eventually lead to loss of synchronism of some generators.
The cause of voltage instability is usually the loads. A run-down situation causing voltage instability occurs when load dynamics attempt to restore power consumption beyond the capability of the transmission network. Voltage stability is also threatened when a disturbance increases the reactive power demand beyond the sustainable capacity of the available reactive power resources. Voltage stability is categorized into the following sub-categories:
Small – disturbance voltage stability: It refers to the system’s ability to maintain steady voltages when subjected to small perturbations such as incremental changes in load. This is primarily influenced by the load characteristics and the controls at a given point of time.
Large disturbance voltage stability: It refers to the systems ability to maintain steady voltages following large disturbances; It requires computation of the non-linear response of the power system to include interaction between various devices like motors, transformer tap changers and field current limiters. Short term voltage stability involves dynamics of fast acting load components and period of interest is in the order of several seconds. Long term voltage stability involves slower acting equipment like tap-changing transformers and generator current limiters. Instability is due to loss of long-term equilibrium.
Voltage stability of a simple 2-bus system.
The basic concept of voltage stability can be explained with a simple 2-bus system shown in Figure. The load is of constant power type. Real power transfer from bus 1 to 2 is given by
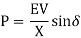
Reactive power transfer from bus 1 to 2 is given by
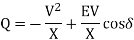
Where, E = E ∠δ is the voltage at bus 1, V = V ∠0 is the voltage at bus 2, X= impedance of the line (neglecting resistance), δ = power angle.
Normalizing the terms in above equations with v = V/E, p = P.X/E2 and q = Q.X/E2, one obtains
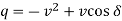
Squaring the two equations above and rearranging,
v2 (sin2 δ + cos2 δ) = p2 +(q + v2)2
v4 + v2 (2q - 1) + (p2 +q2) = 0
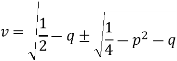
A plot of v on the p-q-v plane corresponding to each point (p,q), there are two solutions for voltage, one is the high voltage or stable solution, which is the actual voltage at the bus, and the other one is the low voltage or unstable solution. The equator, along which the two solutions of v are equal, represents maximum power points. Starting from any operating point on the upper part of the surface, an increase in p or q or both brings the system closer to the maximum power point. An increase in p or q beyond the maximum power point makes the voltage unstable. The preceding discussion illustrates voltage instability caused by an increase in system loading. In a real power system, voltage instability is caused by a combination of many additional factors which includes the transmission capability of the network, generator reactive power and voltage control limits, voltage sensitivity of the load, characteristics of reactive compensation devices, action of voltage control devices such as transformer under load tap changers (ULTCs) etc.
PV Curves
This is one of the widely used methods of voltage stability analysis. This gives the available amount of active power margin before the point of voltage instability. For radial systems, the voltage of the critical bus is monitored against the changes in real power consumption. For large meshed networks, P can be the total active load in the load area and V can be the voltage of the critical or representative bus. Real power transfer through a transmission interface or interconnection also can be studied by this method. For a simple two-bus system as shown in Figure above, equation above gives real solutions of v2, provided (1 – 4q – 4p2) ≥ 0.
Assuming a constant power factor load such that q/p = k (constant), the inequality can be expressed as
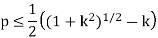
For values of ‘p’ satisfying above equation, there are two solutions of v as follows:
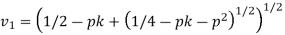
For real values of v1 and v2, the terms under the square roots should be positive.
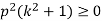
In practice, it is possible to find the Thevenin equivalent of any system with respect to the bus under consideration. It is to be noted that the generations are rescheduled at each step of change of the load. Some of the generators may hit the reactive power limit. The network topology may keep changing with respect to the critical bus, with change in the loading, thereby reducing the accuracy of the method. This method works well in the case of an infinite bus and isolated load scenario.
V-Q curve method
The V-Q curve method is one of the most popular ways to investigate voltage instability problems in power systems during the post transient period. Unlike the P-V curve method, it doesn’t require the system to be represented as two-bus equivalent. Voltage at a test bus or critical bus is plotted against reactive power at that bus. A fictitious synchronous generator with zero active power and no reactive power limit is connected to the test bus. The power-flow program is run for a range of specified voltages with the test bus treated as the generator bus. Reactive power at the bus is noted from the power flow solutions and plotted against the specified voltage. The operating point corresponding to zero reactive power represents the condition when the fictitious reactive power source is removed from the test bus. Voltage security of a bus is closely related to the available reactive power reserve, which can be easily found from the V-Q curve of the bus under consideration. The reactive power margin is the MVAR distance between the operating point and either the nose point of the V-Q curve or the point where capacitor characteristics at the bus are tangent to the V-Q curve. Stiffness of the bus can be qualitatively evaluated from the slope of the right portion of the V-Q curve. The greater the slope is, the less stiff is the bus, and therefore the more vulnerable to voltage collapse it is. Weak busses in the system can be determined from the slope of V-Q curve. For the simple two-bus system equations of V-Q curves for constant power loads can be derived as follows. From the power angle δ is computed for specified active power.
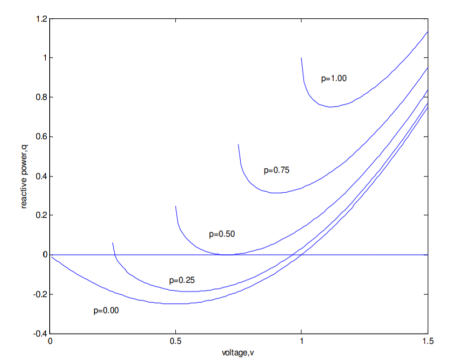
For a range of values of voltage and different active power levels, normalized V-Q curves are shown in Figure below. The critical point or nose point of the characteristics corresponds to the voltage where dQ/dV becomes zero. If the minimum point of the V-Q curve is above the horizontal axis, then the system is reactive power deficient. Additional reactive power sources are needed to prevent a voltage collapse. In Figure, curves for p=1.00 and p=0.75 signify reactive power deficient busses. Busses having V-Q curves below the horizontal axis have a positive reactive power margin. The system may still be called reactive power deficient, depending on the desired margin.
The various methods to improve voltage stability are
- Planning of generation system- The reliability aspect of supply can be improved by sitting generating plants in the load areas
- Maintenance of generation system: Over excitation and under excitation limiters, alarm settings, tap changer settings need to be verified and maintained
- Operation of generation system: During peak load power import over the transmission network should be reduced
- Reactive power compensation: Extra high voltage transmission lines require shunt reactors for energization and under lightly loaded condition. These shunt reactors should be switched off during voltage emergencies
- Capacitor bank: Shunt capacitor banks acts as constant reactive power sources.
- Tap changing: The tap changing transformers change the transformation ratio and thus the voltage in the secondary circuit is varied and voltage control is obtained.
References:
1. I. J. Nagrath, D. P. Kothari, Power System Engineering, Tata McGraw-Hill publications,
2008
2. Ashfaq Husain, Electrical Power System, CBS Publication, 5th Edition
3. C. L. Wadhwa, Electrical Power Systems, New Age International Publiser, 6th Edition
4. V. K. Mehta and Rohit Mehta, Principles of Power System, S. Chand Publication, 2008
