Unit - 4
Time and Frequency Domain Transformations
A signal is said to be periodic if it satisfies the condition x (t) = x (t + T) or x (n) = x (n + N).
Where T = fundamental time period,
ω0= fundamental frequency = 2π/T
There are two basic periodic signals:
x(t) = cos wot (sinusoidal)
x(t) = e jwot (complex exponential)
These two signals are periodic with period T=2π/ω0
A set of harmonically related complex exponentials can be represented as ɸk(t)
ɸk(t) = {e jkwot} = {e jk(2π/T) t} where k=0, ±1, ±2, ±3,………(1)
All these signals are periodic with period T.
According to orthogonal signal space approximation of a function f(x) with n mutually orthogonal functions is given by
x(t) =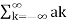 
e jkwot ……………………………………………….(2)
=
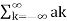k ejkwot
Where ak= Fourier coefficient = coefficient of approximation.
This signal x(t) is also periodic with period T.
Equation 2 represents Fourier series representation of periodic signal x(t).
The term k = 0 is constant.
The term k=±1 having fundamental frequency ω0, is called as 1st harmonics.
The term k=±2 having fundamental frequency 2ω0, is called as 2nd harmonics, and so on...
The term k=±n having fundamental frequency nω0, is called as nth harmonics.
Key Takeaways:
The Fourier series represents periodic; continuous-time signals as a weighted sum of continuous-time sinusoids.
- Even function symmetry
A function is defined to be even if and only if
f(t) = f(-t) -------------------------------------------------------------(1)
If the condition is satisfied then eq(1) is said to be even because polynomial functions with even components
For any even periodic functions, the equations for the Fourier coefficients
Av = 2/T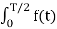 
dt ---------------------------------------------------(2)
Ak = 4/T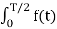 
coskwot dt --------------------------------------------(3)
Bk=0 for all k --------------------------------------------------(4)
In eq(4) all b co-effecients are zero if the function is even. The figure depicts the even periodic function.
Figure 1. Even symmetry
Av = 1/T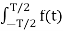 
dt
= 1/T 
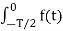dt +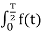 
- Odd function symmetry
A periodic function is defined to be odd if
f(t) = -f(t) ---------------------------------(1)
The function that satisfies eq(1) is said to be odd because polynomial funtions with odd exponents. The expression for Fourier co-effecients are:
Av=0
Ak=0 for all k;
Bk = 4T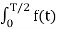
sinkwo dt ---------------------------------(2)
Figure 2. Odd function symmetry
- Half Wave Symmetry
A function is said to have half-wave symmetry if it satisfies the following constraint:
f(t) = -f(t - T/2) ------------------------------------ (1)
Equation 1 expresses that a periodic function has a half-wave symmetry if, after it has been shifted by one-half of a period and inverted, it is said to be identical to the original periodic function.
For instance, the periodic functions illustrated in Figures possess half-wave symmetry.
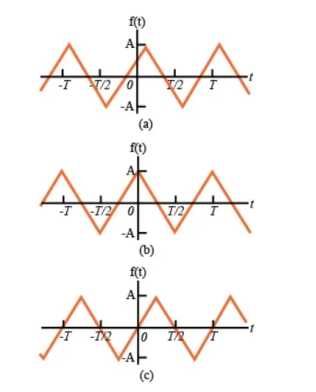
Figure 3. Half wave Symmetry
- Quarter Wave Symmetry
If a function has half-wave symmetry and symmetry about the midpoint of the positive and negative half-cycles, the periodic function is said to have quarter--wave symmetry. This function is illustrated in Figure
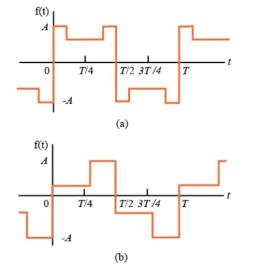
Figure 4. Quarter Wave Symmetry
Key Takeaway:
These types, even, odd, half-wave, quarter-wave half-wave even, and quarter-wave half-wave odd are all used to simplify the computation of the Fourier coefficients.
We know that x(t) = 
e jkwot ------------------------(1)
Multiply e-jnwot on both sides we get
x(t) e -jnwot =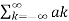 
e jkwot . e- jnwot
Consider integral on both sides we get
e jkwot dt = 
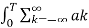e jkwot . e- jnwot
= 
e j(k-n)wot dt
= 
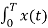e jkwot dt =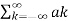 
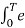j(k-n)wot dt --------------------------(2)
By Eulers formula
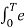j(k-n)wot dt = 
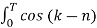wo dt + j 
wo dt
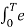j(k-n) wot dt = {T k=n
k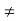 
n
Hence in equation (2) the integral is zero for all values of k except at k=n. Put k=n is equation 2
= 
j(k-n)wot dt = anT
=an = 1/T 
-jnwot
Replace n by k we get
= ak = 1/T 
-jkwot dt
x(t) =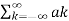
e j(k-n) wot
Where ak = 1/T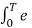 
-jkwot dt
Key Takeaway:
Fourier coefficients and can be found from f(t). The term ω0 (or 2πT 2 π T) represents the fundamental frequency of the periodic function f(t)
The (CT) Fourier transform (or spectrum) of x(t) is
X(jw) =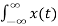 
e -jwt dt ---------------------------------------(1)
x(t) can be reconstructed from its spectrum using the inverse Fourier transform
x(t) = 1/ 2 π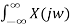 
e jwt dw ------------------------------------------(2)
The above two equations are referred as Fourier transform pair with the first one being the analysis equation and the second being the synthesis equation.
Notation
X(jw) = F{x(t)}
x(t) = F -1 {X(jw)}
x(t) and X(jw) form a Fourier transform pair denoted by
Key Takeaways:
Aperiodic signals in continuous time are represented by the Fourier transform
Imagine we have a function f[t] whose Fourier transform is F[w] and another function g[t] whose transform is G[w]. Then the convolution is
f[t] * g[t] =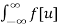 
g[t-u] du
We write g[t-u] in terms of Inverse Fourier transform
g[t-u] = 1/2π 
E Iw(t-u) dw dw
Thus
f[t] * g[t] = 
1/2π 
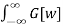E Iw(t-u) dw dw du
= 1/2π 
E Iwt 
E -Iwu du dw
But the right hand integral above is the Fourier transform of f[u] so
f[t] * g[t] = 1/2π 
G[w] E -Iwu dw
The convolution property states that:
x(t) * h(t) > X(w) H(w)
Let
y(t) =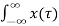 
h(t-τ) dτ = x(t) * h(t)
Y(w) = 
e -jwt dt = 
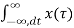h(t-τ) dτ e -jwt dt
If we switch the order of the two integrals we get
Y(w) =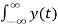 
e -jwt dt =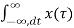 
h(t-τ) dτ e -jwt dt let u=t-τ
= 
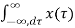
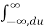h(u) e -jw(u+τ) du dτ
= 
e -jwτ dτ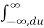 
h(u) e -jwu du
= X(w) H(w)
Therefore,
y(t) = x(t) * h(t) <-> Y(w) = X(w) H(w)
Fourier Transform of the convolution of two functions is simply the product of the Fourier Transforms of the functions.
Multiplication of Signals
It states that the Fourier Transform of the product of two signals in time is the convolution of the two Fourier Transforms.
x1(t) x2(t) <-> 1/2π X1(w) * X2(w)
x1(t) x2(t) <-> 1/2π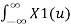 
X2(w-u) du
Proof:
F[x1(t) x2(t)] =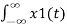 
x2(t) e-jwt dt
Write x1 (t) as an inverse Fourier Transform
F[x1(t) x2(t)] =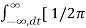 
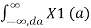e-jat da] x2(t) e -jwt dt
= 
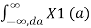
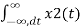e -j(w-a)t dt da
= 1/2π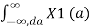 
X2(w-a) da
= 1/2π X1(w) * X2(w)
Therefore,
x1(t) x2(t) > 1/2π X1(w) * X2(w)
H(e jw) = H R ( e jw) + j H I ( e jw) = | H ( e jw) | e j 
1 (w)
1 (w) = angle H(e jw)
Example:
h[n] = - δ[n]
| H (ejw)| = 1 angle H(e jw) = π
In the magnitude or phase representation a real valued frequency response does not mean that the system is zero-phase.
Using this representation,
|Y (e jw) | = | H ( ejw)| | X (ejw)|
Thus, |H(ejω) | and angle H(ejω) are commonly referred to as the gain and the phase shift of the system, respectively.
In magnitude and phase plots, as ω goes through a zero on the unit circle, the magnitude will go to zero and the phase will flip by π, as shown in the figure below.
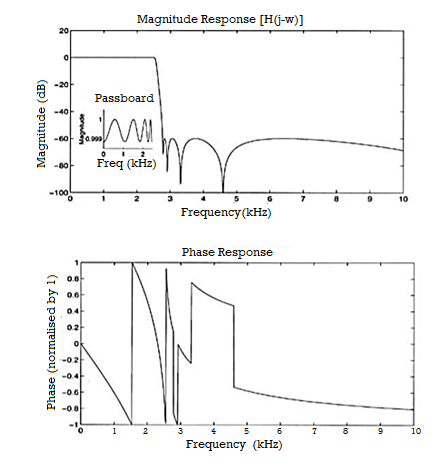
Figure 5. Magnitude and Phase response
The Duality Property states that if x(t) has a Fourier Transform X(w), then if we form a new function of time of form of the transform, X(t), it will have a Fourier Transform x(ω) that has the functional form of the original time.
x(t) > X(w)
X(t) <-> 2πx(-w)
The second term in the last line is simply the Fourier Transform integral of the function X(t), i.e.
F[X(t)] = 
e -jbw db
Therefore, we get duality property
x(t) <-> X(w)
X(t) <-> 2π x(-w)
Key Takeaways:
If two signals x(t) and y(t) are Fourier Transformable, and their convolution is also Fourier Transformable, then the Fourier Transform of their convolution is the product of their Fourier Transforms.
The discrete-time Fourier transform (DTFT) or the Fourier transform of a discrete–time sequence x[n] is a representation of the sequence in terms of the complex exponential sequence ejωn.
The DTFT sequence x[n] is given by
X(w) =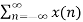 
e-jwn ---------------(1)
Here X(w) is a complex function of real frequency variable w and can be written as
X(w) = Xre (w) + j X img(w)
Where Xre (w), j X img(w) are real and Imaginary parts of X(w)
Xre(w) = |X(w)| cos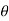 
(w)
Ximg(w) = |X(w)| sin 
(w)
|X(w)| 2 = |Xre(w)| 2 + |Xim(w)| 2
And | X(w)| can be represented as
X(w) = |X(w)| e j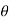
(w)
Inverse Discrete Fourier Transform is given by
x(n) = 1/2π 
e jwn dw
Discrete Fourier Transform
Let f(t) be the continuous signal which is the source of the data. Let N samples be denoted f[0], f[1],f[2],………..,f[k],…….,f[N-1].
The Fourier Transform of the original signal f(t) would be
F(jw) =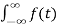 
e-jwt dt
Each sample f[k] as an impulse has area f[k]. Then since the integrand exists only at the sample points:
F(jw) =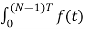 
e -jwt dt
= f(0) e -j0 + f[1] e -jwT + …… + f[k] e -jwT + …. F(N-1) e -jw(N-1)T
That is F(jw) =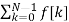 
e -jwkT
The continuous Fourier transform could be evaluated over a finite interval usually the fundamental period rather than from -∞ to ∞. Similarly, since there are only a finite number of input data points, the DFT treats the data as if it were periodic form f(N) to f(2N-1).
Hence the sequence shown below in Figure (a) is one period of the periodic sequence in plot (b)
Figure.6 (a) Sequence of N=10 pts. (b) implicit periodicity in DFT
Since the operation treats the data as periodic, we evaluate the DFT equation for the fundamental frequency (one cycle per sequence, 1/NT Hz, 2π/NT rad/sec and its harmonics at w=0.
In general
F[n] = 
e -j2π/N nk (n=0:N-1)
F[n] is the Discrete Fourier Transform of the sequence f[k].
In matrix form we get
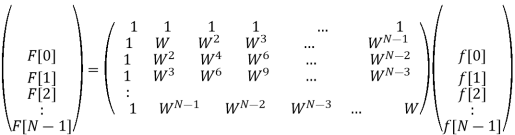
Where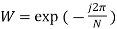 
and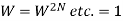 
Problem:
Find the DFT of the sequence
f(n) = {8,4,8,0}
F[n] = 
e -j π/2 nk = 
(-j) nk
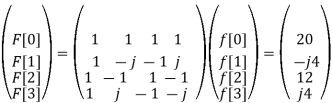
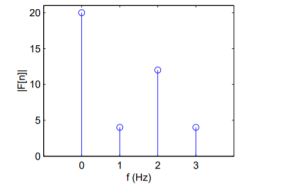
Figure7. Magnitude of the four point sequence.
The inverse transform of
F[n] =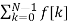 
e -j 2π/N nk
That is
f[k] = 1/N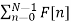 
e j 2π/N nk
Key Takeaways:
DFT converts a finite sequence of equally-spaced samples of a function into a same-length sequence
Consider two periodic signals x1(t) and x2(t) with equal period T. If the Fourier series co-efficient of these two signals are cn and dn then
1/T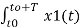 
x2(t) = 1/T 
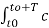n e j n Ωot [ 
m e jmΩot ] dt ---------(1)
= 1/T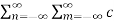 
n d *m 
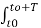e j(n-m)Ωot dt ------------------------------(2)
= 0 n≠ m
= 
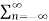n d *n n=m --------------------------------(3)
If x1(t) = x2(t) = x(t) then eq(3) becomes
1/T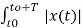 
2 =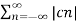 
2 --------------------------------(4)
The above equation can be written as
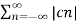2 = c0 2 + 
2
n≠0
= c0 2 + 
n c *n
n≠0
a0 2 +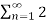 
[Re(c 2 n ) + Im (cn ) 2]
= a0 2 +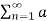 
2 n /2 + b 2 n /2 ---------------------------(5)
Key Takeaways:
Parseval's theorem usually refers to the result that the Fourier transform is unitary
Given a continuous-time signal x(t), the Laplace transform of x(t) is defined as
X(s) =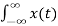 
e -st dt -------------------------------------------------------(1)
X(s) is a function which takes complex numbers and returns complex number X(s) that is X(s) is function that maps the complex plane into the complex value.
The set of values of s for which the integral in (1) is well defined is called Region of Convergence.
Find the Laplace transform of e –t.
F(s) =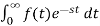 
F(s) =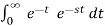 
F(s) =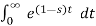 
F(s) = 1 / 1-s [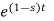
]0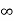 
F (s = 1/ s-1.
Find the Laplace transform of unit -step function.
f(t) = 1 (t≥0)
F(s) = 
-st dt = -1/s e -st | 0 ∞ = 1/s [ e -∞ - e -0] = 1
F(s) = 1/s.
Find the Laplace transform of e-at u(t)
X(s) =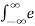 
at u(t) e -st dt = 
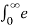at e -st dt = 
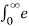–(s-a) t dt
= 1 – e –(s-a) ∞ / s-a
Key Takeaways:
This is the operator that transforms the signal in time domain in to a signal in a complex frequency domain called as ‘S’ domain. The complex frequency domain will be denoted by S and the complex frequency variable will be denoted by ‘s’
The response of an LTI system with impulse response h(t) to complex exponential input x(t) = e st is y(t) = H(s) e st where s ia complex number and
H(s) =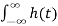 
e -st dt
When s is purely imaginary this is Fourier transform H(jw)
When s is complex this is Laplace transform of h(t) , H(s )
Let z = r e jw and z n = r n e jwn
Then for input z n we get output H(z) z n
Figure 8. I/O relationship
Here H(z) is called the system function.
y[n] = 
x[n-k]
= z n 
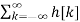z-k
Here z transform of h[k] is H[z].
Key Takeaways:
H(z) represents the Fourier transform
Consider the difference equation given by
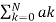y[n-k] = 
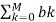x[n-k]
H(z) =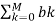 
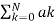z -k / 
z -k
Poles : H(z) - ∞ ; 
z -k = 0 , z=0 if bo=0.
Zeros : H(z) -> 0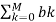 
z -k =0
In factored form
H(z) =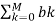 
z -k / 
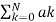z -k = bo 
1 – ck z-1 ) / ao 
1 – dk z-1 )
Here bo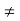
0 , ao 
0 .
Ck represents zeros denoted by “o”
Dk represents poles denoted by “x”
Example :
Find H(z), poles and zeros for the difference equation given by
y[n] – 3/8 y[n-1] – 7/16 y[n-2] = x[n] + x[n-2]
Solution:
Here ao=1,a1=-3/8,a2=-7/6,bo=1,b1=0,b2=1
H[z] = 1 + z -2 / 1 -3/8 z-1 -7/16 z -2
= (1+j z-1 ) (1 -jz-1) / (1-7/8 z-1) ( 1+1/2 z-1)
Zeros : z=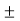
j represented by o.
Poles z= 7/8 , z=-1/2 represented by x.
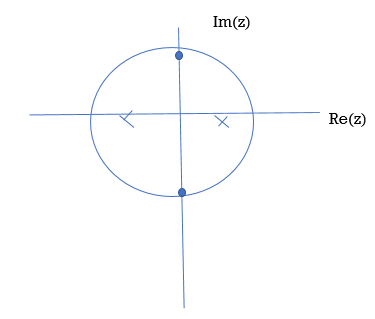
Figure 9. Poles and Zeros
Key Takeaways:
The poles of the system are indicated in the plot by an X while the zeros are indicated by a circle or O
Find io(t) using Laplace
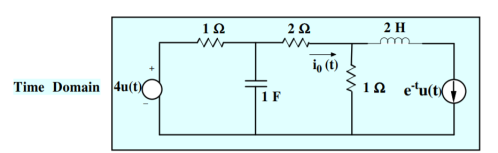
Fogure 10. Mesh Network
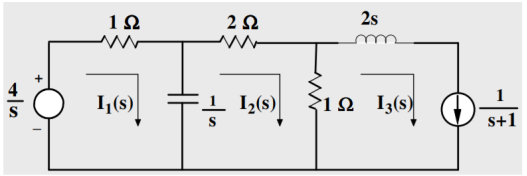
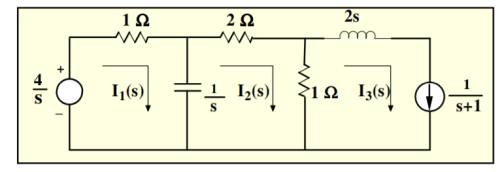
Figure 11. Laplace network
Mesh 1:
(s+1)/s I1(s) – I2(s)/s = 4/s
(s+1) I1(s) – I2(s) = 4
Mesh 2:
-1/s I1(s) + 3s+1/s I2(s) – I3(s) =0
-1/s I1(s) + 3s+1/s I2(s) – 1/s+1 =0
-I1(s) + (3s+1) I2(s) = s/s+1
-(s+1) I1(s) + (s+1)(3s+1) I2(s) = s
Adding these two equations we get
S(3s+4) I2(s) = s+4
I2(s) = (1/3) (s+4)/ s(s+4/3) = 1/s -2/3/ s+4/3
i2(t) = [ 1-2/3 e -4/3 t ] u(t)
-I1(s) + 3s+1/s . [1/s -2/3 /s+4/3] =s/s+1
-I1(s) = s/s+1 – 3s+1/s[ 1/s -2/3/s+4/3]
Key Takeaways:
Laplace techniques convert circuits with voltage and current signals that change with time to the s-domain so you can analyse the circuit's action using only algebraic techniques.
Using Laplce transform solve the differential equations :
y” – 3y’ -4y = -16x
y(0) = -4
y’(0) = -5
Apply the operator L to both sides of the differential equation; then use linearity, the initial conditions,
L[ y” – 3y’ -4y] = L[-16x]
L[ y”] – 3L[y’] -4L[y] = L[-16x]
[p 2 L[y] – p y’(0)] –[p L[y] – y[0]] – 4 L[y] = L[-16x]
p 2 L[y] +4p+5]-3[pL[y] +4] -4L[y] = -16/p2
(p2 -3p-4) L[y] + 4p -7 = -16/p2
L[y] = -16/p2 -4p +7/p2 – 3p -4
But the partial fraction decomposition of this expression for L[ y] is
-16/p2 -4p+7/ p2 -3p-4 = -16/p2 -4p+7/ p2 -3p-4 = -16-4p3+7p2/ p2(p+1)(p-4)
= -3/p + 4/p2 +1/p+1 +-2/p-4
Therefore,
y= L-1 [-3/p + 4/p2 + 1/p+1+-2/p-4]
Which yields
y=-3 +4x+e-x -2 e 4x
Key Takeaways:
The first step in using Laplace transforms to solve an IVP is to take the transform of every term in the differential equation
Given an analog signal x(t) the discrete time signal is represented by a sequence of weighted and delayed impulses.
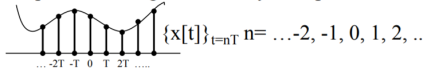
Figure12. Discrete time signal
A discrete time system is a mathematucal algorithm that takes an input sequence x[n] and produces output sequence y[n].
For any given sequence x[n] its z-transform is defined as :
X(z) =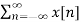 
z -n
= …….+x[-2] z2 + x[-1] z1 + x[0] zo + x[1] z -1 + x[2] z -2 +……..
Where z is complex variable.
Given xn=un that is step function input to the system
G(z) = 1/(1-0.9z-1) Then output yn is given by
Y(z) = G(z) X(z)
X(z) = z(un) = 1/1-z-1
Y(z) = G(z) . 1/1-z-1
Yn = z-1(G(z) / 1-z-1)
= z-1 ( 1/1-0.9 z-1 ). 1(1-z-1)
= 1/(1-0.9 z-1 )(1-z-1) = -0.9 / 1-0.9z-1 + 10/ 1-z-1
Yn = -9(0.9) n + 10
Poles are the values of z that make the denominator zero, and zeros are the values of z that make the numerator go to zero.
G(z) = 1/ 1+0.2 z-1 -0.48 z-2
= z 2/ z2 +0.2 z-0.48
= z2 / (z+0.8) (z-0.6)
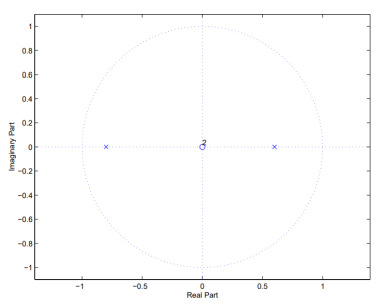
Figure 13. Poles and Zeros
Lets look at the system G(z)
G(z) = 1/1-az-1
The system has a pole at z=a and zero at z=0.
The impulse response of the system above is hn= an
Hence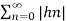 
= 
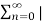a n |= 
n.
For the system to be stable it must have finite sum. As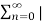 
a n represents geometric expression te sum is finite if and only if |a|<1.
That means that the POLE must be within the unit circle!
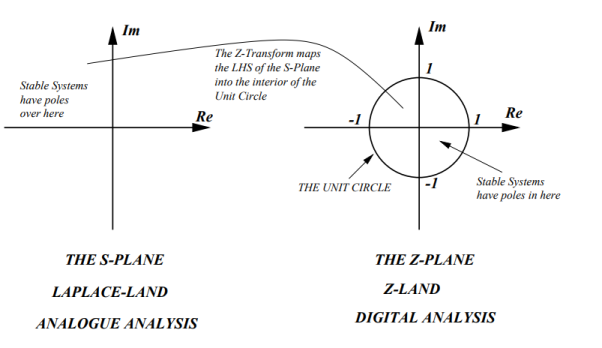
Figure 14. s-plane to z-plane
Key Takeaways:
The Z-transform converts a discrete-time signal, which is a sequence of real or complex numbers, into a complex frequency-domain representation.
References:
- Signals and Systems by Simon Haykin
- Signals and Systems by Ganesh Rao
- Signals and Systems by P. Ramesh Babu
- Signals and Systems by Chitode
