Unit - 5
Frequency response method
The calculation of system parameters for higher order systems is difficult in time domain analysis. This can be overcome by frequency domain analysis. As the frequency response of a linear time invariant system is independent of amplitude and phase of the input test signal. The effect of noise and parameter variation in frequency domain can be easily computed.
In frequency response can be determine by calculating the phase and amplitude oof the given system transfer function. If a sinusoidal signal XG(j)sint then its amplitude will be
C(t) = XG(j)sint
= X|G(j)| 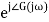 sint
sint
Magnitude = |G(j)|
Phase = G(j)
In polar form = |G(j)| 
Resonant Peak (Mr): The maximum value of magnitude is known as Resonant peak. The relative stability of the system can be determined by Mr. The larger the value of Mr the undesirable is the transient response.
Resonant Frequency (Wr): The frequency at which magnitude has maximum value.
Bandwidth: The band of frequencies lying between -3db points.
Cut-off frequency –The frequency at which the magnitude is 3db below its zero frequency.
Cut-off Rate – It is the slope of the log magnitude curve near the cut off frequency.

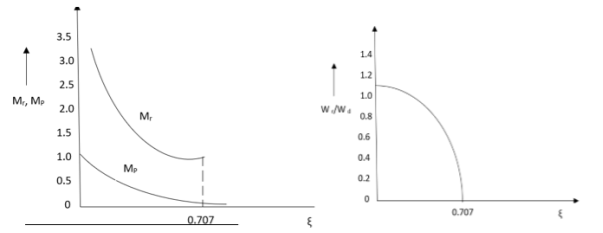
Fig 1 Frequency Domain Specification
It gives the frequency response of the system. If the transfer function is given, then from the plot number of poles and zeros can be calculated.
Polar plot of some standard functions:
# TYPE ‘O’
Ex :1T(S) = 1/S + 1
(1). For polar plot substitute S=jw.
TF = 1/1 + jw
(2). Magnitude M = 1 + 0j / 1 + jw = 1/√1 + w2
(3). Phase φ = tan-1(0)/ tan-1w = - tan-1w
WMφ
0100
10.707-450
∞0-900
The plot is shown in fig. 2(a)

Fig 2(a) Polar Plot T(S) = 1/S + 1
Ex.2>. T(S) = 1/(S+1)(S+2)
(1). S = jw
TF = 1/(1+jw)(2+jw)
(2). M = 1/(1+jw)(2+jw) = 1/-w2 + 3jw + 2
M = 1/√1 + w2√4 + w2
(3). Φ = - tan-1 w - tan-1(w/2)
WMΦ
00.500
10.316-71.560
20.158-108.430
∞0-1800
The plot is shown in fig2(b)
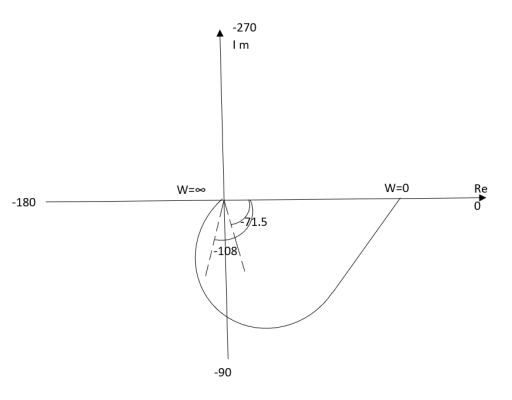
Fig2(b) Polar Plot T(S) = 1/(S+1)(S+2)
Intersection of polar plot with imaginary axis will be when real part of Transfer function = 0
M = 1/(jw + 1)(jw + 2)
= 1/-w2 + j3w + 2
TYPE ‘1’
Ex.1 T(S) = 1/S
(1). S = jw
(2). M = 1/W
(3). Φ = -tan-1(W/O) = -900
WMφ
0∞-900
11-900
20.5-900
∞0-900
The plot is shown in fig.3(a)
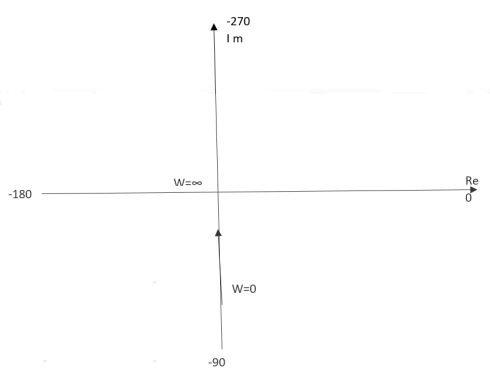
Fig 3(a) Polar Plot T(S) = 1/S
Ex.2 T(S) = 1/S2
(1). S = jw
(2). M = 1/w2
(3). Φ = -tan-1(W/O)-tan-1(W/O) = -1800
WMΦ
0∞-1800
11-1800
20.25-1800
∞0-1800
The plot is shown in fig.3(b)
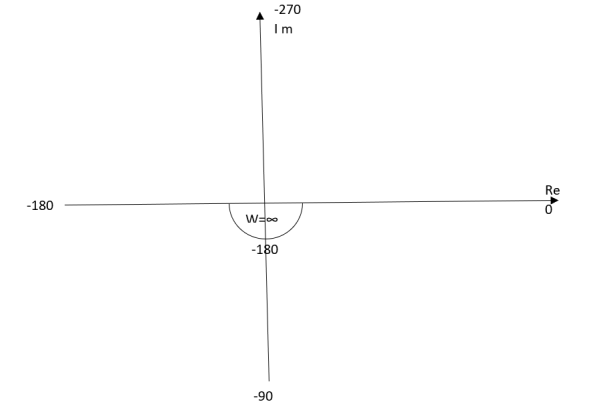
Fig 3(b) Polar Plot T(S) = 1/S2
Key takeaway
- For Polar Plot starting point depends upon type of system
- The terminating phase depends on order of the system.
TYPE 1 ORDER 2
Ex.1 T(S) = 1/S(S+1)
(1). M = 1/W√1+w2
(2). Φ = -900 - tan -1(W/T)
WMφ
0∞-900
10.707-1350
20.45-153.40
∞0-1800
The plot is shown in fig.4(a)
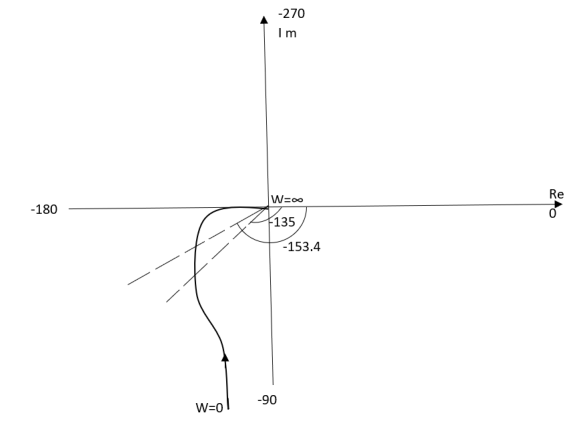
Fig 4(a) Polar Plot T(S) = 1/S(S+1)
Ex.2TYPE 2 ORDER 3
T(s) = 1/S2(S+1)
(1). M = 1/w2√1+jw
(2). Φ = -1800 – tan-1W/T
The plot is shown in fig.4(b)
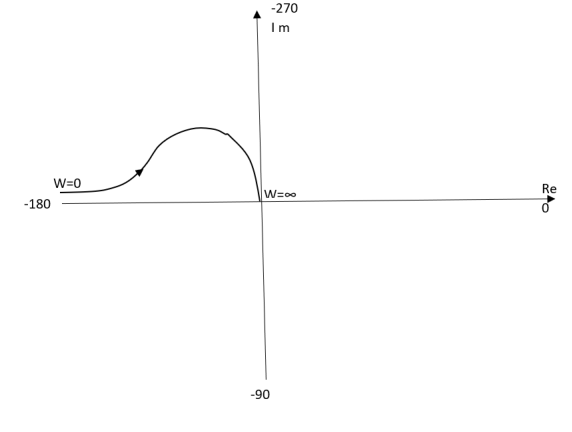
Fig 4(b) Polar Plot T(s) = 1/S2(S+1)
Nyquist Stability Criteria:
The Nyquist criteria is a semi graphical method that determines stability of CL system investigating the properties of the frequency domain plot (Polar plot), the Nyquist plot of the OLTF G(S) H(S) is represented as L(S)
L(S) = G(S)H(S)
Specially the Nyquist plot of L(S) is a plot drawn by substituting S=jw and varying the value of w as per in polar plot. In polar plot we take one sided frequency response ( 0 - ∞) in Nyquist plot we will vary the frequency in entire range possible from ( -∞ to 0 ) and (0 to ∞ )
Nyquist Criteria also gives:
(1). In addition to providing the absolute stability like other plots, the Nyquist criteria also gives information on the relative stability of a stable system and the degree of instability of an unstable system.
(2). It also gives indications on how the system stability can be improved.
(3). The Nyquist plot of G(S) H(S) is the polar plot of G(S) H(S) drawn with wider range of frequency ( -∞ to ∞ ) and along the Nyquist path.
(4). The Nyquist plot of G(S) H(S) gives information on frequency domain characteristics such as B.W, gain margin and phase margin.
Construction of Nyquist Plot
Encircled: A point or region in a complex function phase i.e. S-plane is said to be encircled by a closed path if it is found inside the path.
Assumption:
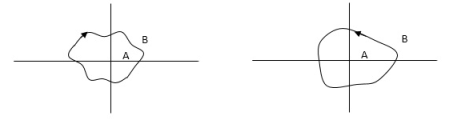
Fig 5. Encirclement
In this example point A is encircled by the closed path Y. Since, A is inside the closed path point B is not encircled by y. It is outside the path. Furthermore when the closed path Y, has a direction assign to it, encirclement, if made can be in the clockwise direction or in the anti-clockwise direction.
Point A is encircled by Y by anticlockwise direction. We can say that the region inside the path is encircled in the prescribed direction and the region outside the path is not encircled.
Enclosed:
A point or region is said to be enclosed by a closed path if it is encircled in the counter clockwise direction, or the point or region lies to the left of the path (always), when the path is traveling in the prescribed direction.
The concept of enclosure is particularly useful, if only a portion of a closed path is shown.
In this example the shaded region are
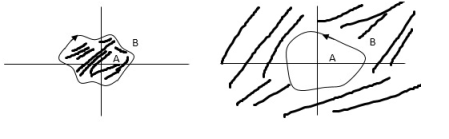
Fig 6. Enclosure
Considered to be enclosed by the closed path Y. In other words, point A is enclosed by Y in fig a. But is not enclosed by Y in fig b. And for point B it is viceversa.
No of encirclements and enclosure:
For A line is cut once
For B line is cut twice
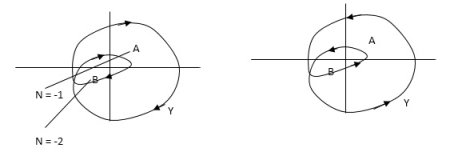
Fig 7. Encirclement and Enclosure with example
As it’s overlapping but 2 times in Same direction
When a point is encircled by a closed path Y, a no. N can be assigned to the no. Of times it is encircled. The magnitude of N can be determined by drawing an arrow around the closed path Y.
Taking an arbitrary point S, and moving around in clockwise direction and anti-clockwise direction respectively. We are getting a direction.
The path followed by S1 gives us the direction and this path which covers the total number of revolution travelled by this point S1 is N or the net angle is ‘ 2 π N ’.
For B = 2 = N for A = 1 = N
In this eg. Point A is encircled ones (or 2 π radians) by function Y and point B is encircled twice (or 4 π radians)all in clockwise direction.
In diagram b again A and B are encircled but in counter clockwise direction thus for this diagram A is enclosed one’s and B is enclosed twice.
By definition M is +ve for anticlockwise(direction) encirclement and –ve for clockwise encirclement.
OLTF G(S) = (S + Z1)(S + Z2)/(S + P1)(S + P2) H(S) = 1 - - (1)
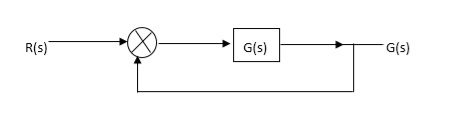
Fig 8. Unity feedback control system
CLTF G(S)/1 + G(S)
CE = 1 + G(S)
= 1 + (S + Z1)(S + Z2)/(S + P1)(S + P2)
CE = (S + P1)(S + P2) + (S + Z1)(S + Z2)/ (S + P1)(S + P2) - - (2)
Key takeaway:
# OLTF poles is equal to CE poles.
CE = (S + Z’1)( S + Z’2)/( S + P1)( S + P2) - - (3)
CLTF = G(S) –(1) / 1 + G(S) –(3)
= (S + Z1)( S + Z2) / (S + Z’1)( S + Z’2) - - (4)
# Zeros of characteristic equation is poles of CLTF (3 and 4).
For the closed loop system to be stable zeros of CE(i.e. poles of CLTF) should not be located at right half of the S-plane.
Consider a contour, which covers the entire right half of S-plane.
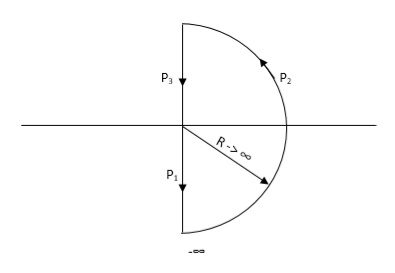
Fig 9. Contour For Right half of S-plane
P1 W(0 - ∞)
P2 RejR ∞
ϴ - π/2 to 0 to + π/2
P3 W(∞ to 0 )
If each and every point along the boundary of contour is mapped in q(S) where q(S) is 1+G(S)H(S)[CE]. The CE is drawn in S-domain. Now, as the CE : q(s) = 1 + G(S)H(S) contour is drawn into S-plane.
This q(S) contour may encircle the origin. Thus, the number of encirclement of q(S) contour with respect to origin is given by
N = Z – P
Where : Z1P zeros and poles of q(S)[CE]
N Total no of encirclement of origin
Z1P Zeros and poles of CE in the right half of S-plane
** for the CL system to be stable Z=0 always.
Important:
# Open loop System(stable): When OL system is stable P=0 i.e. no of poles on right half
N = Z – P
If P = 0
N = Z
- Now for CL system to be stable Z = 0
- N = 0
- i.e. q(s) contour should not encircle the origin.
# Open loop system(unstable): Let P = 1 i.e. one OL pole is located in right half of S-plane i.e. OLTF is unstable.
As N = Z – P
N = Z – 1
For CL system to be stable the only criteria is (Z=0) i.e.
N = -1
Which means q(S) contour should encircle the origin one’s in CW direction.
Key takeaway:
(1). When OL system is unstable then corresponding CL will be stable only when q(S) contour will encircle origin in CW direction.
(2). The no of encirclements should be equal to no of open loop poles located in right half of S-plane.
** the no of encirclements(N) can also be calculated by using G(S) contour (instead of q(S) contour) but the reference is -1+j0 instead of 0+j0 i.e. the no of encirclements should be considered w.r.t -1+j0 and not with the origin.
Explanation Mapping
q(S) = 1 + G(S)
G(S) is always given to us, so we can relate G(S) with q(S).
G(S) = q(S) – 1
But q(S) can be drawn by adding 1 real part to the q(S).
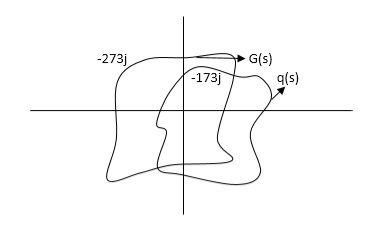
Fig 10. Mapping
G(S) given then q(S) shift to right side.
Nyquist criterion
Nyquist plots are the continuation of polar plots for finding the stability of the closed loop control systems by varying ω from −∞ to ∞. That means, Nyquist plots are used to draw the complete frequency response of the open loop transfer function.
The Nyquist stability criterion works on the principle of argument. It states that if there are P poles and Z zeros are enclosed by the ‘s’ plane closed path, then the corresponding G(s)H(s) plane must encircle the origin P−Z times. So, we can write the number of encirclements N as,
N=P-Z
Nyquist Contour: is the contour in the s-plane that includes the entire right half plane. Now, let’s consider F (s) = 1 + G(s)H(s) and the contour in the s-plane is the Nyquist contour (i.e., the entire right half plane).
Applying the Cauchy’s Principle of Argument, we should have
The number of rotations about the origin of the mapping through 1+ G(s) (H)
N = The number of zeros of 1+ G(s) (H) in the right half plane, Z - The number of poles of 1+ G(s) (H) in the right half plane, P
Please note
The mapping through G(s) (H) is virtually the same as the one through 1+ G(s) (H)
except that the contour is shifted one unit to the left. Thus, we can count rotations
about -1 instead of rotations about the origin in the above statement.
The zeros of 1+ G(s) (H) = the closed-loop poles.
The poles of 1+ G(s) (H) = the open-loop poles or the poles of 1+ G(s) (H)
Therefore
The number of rotations about -1 of the mapping through 1+ G(s) (H),
N = The number of closed-loop poles in the right half plane, Z - The number of open-loop poles in the right half plane, P
The above relationship is called the Nyquist Criterion; and the mapping through G(S)H(S) is called the Nyquist Diagram of G(S)H(S)
For a system to be stable, Z must be zero.
Sketching the Nyquist Diagram
Suppose the open-loop transfer function
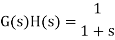
Sketch its Nyquist diagram
| | GH | | GH |
= 0 | 1 | 0 |
= | o | 
|
Cross re: = 0 = | See above | See above |
= 1 rad/s | 0.707 | 
|
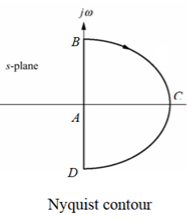
Sketching the Nyquist diagram includes two steps:
(1) Sketch the mapping of Point A to Point B, which is the same as the polar plot of frequency response for G(S)H(S).
Note that the semicircle with an infinite radius, i.e., B-C-D, is mapped to the origin if the order the denominator of G(S)H(S) is greater than the order the numerator of G(S)H(S).
(2) Sketch the mapping of Point A to Point D, which is the mirror image about the real axis of the mapping of Point A to Point B.
Plotting
Q1. For the transfer function below plot the Nyquist plot and also comment on stability?
G(S) = 1/S+1
Sol: N = Z – P ( No pole of right half of S plane P = 0 )
P = 0, N = Z
NYQUIST PATH:
P1 = W – (0 to - ∞)
P2 = ϴ( - π/2 to 0 to π/2 )
P3 = W(+∞ to 0)
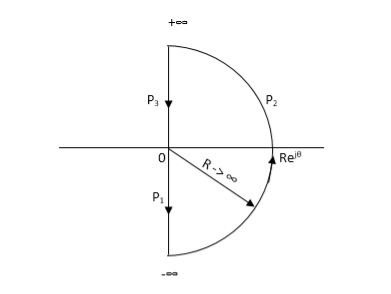
Fig 11. Nyquist path
Substituting S = jw
G(jw) = 1/jw + 1
M = 1/√1+W2
Φ = -tan-1(W/I)
For P1 :- W(0 to -∞)
W M φ
0 1 0
-1 1/√2 +450
-∞ 0 +900
Path P2:
W = Rejϴ R ∞ϴ -π/2 to 0 to π/2
G(jw) = 1/1+jw
= 1/1+j(Rejϴ) (neglecting 1 as R ∞)
M = 1/Rejϴ = 1/R e-jϴ
M = 0 e-jϴ = 0
Path P3:
W = -∞ to 0
M = 1/√1+W2, φ = -tan-1(W/I)
W M φ
∞ 0 -900
1 1/√2 -450
0 1 00
The Nyquist Plot is shown in fig 12.
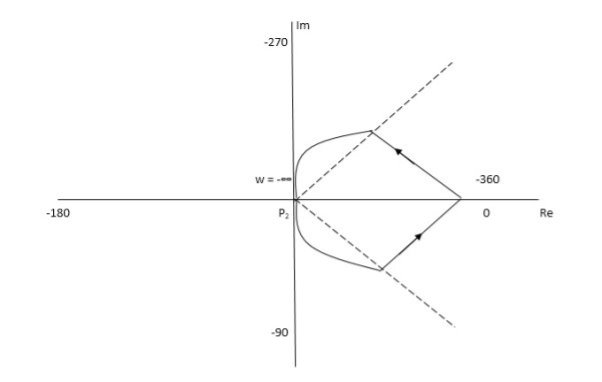
Fig 12. Nyquist Plot G(S) = 1/S+1
From plot we can see that -1 is not encircled so, N = 0
But N = Z, Z = 0
So, system is stable.
Q.2. For the transfer function below plot the Nyquist Plot and comment on stability G(S) = 1/(S + 4)(S + 5)
Soln: N = Z – P, P = 0, No pole on right half of S-plane
N = Z
NYQUIST PATH
P1 = W(0 to -∞)
P2 = ϴ(-π/2 to 0 to +π/2)
P3 = W(∞ to 0)
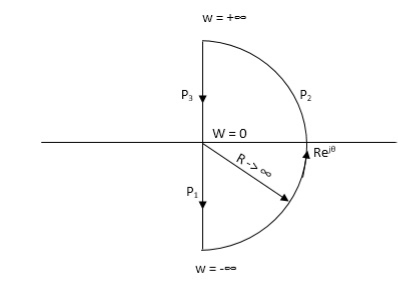
Fig 13. Nyquist Path
Path P1 W(0 to -∞)
M = 1/√42 + w2 √52 + w2
Φ = -tan-1(W/4) – tan-1(W/5)
W M Φ
0 1/20 00
-1 0.047 25.350
-∞ 0 +1800
Path P3 will be the mirror image across the real axis.
Path P2: ϴ(-π/2 to 0 to +π/2)
S = Rejϴ
G(S) = 1/(Rejϴ + 4)( Rejϴ + 5)
R∞
= 1/ R2e2jϴ = 0.e-j2ϴ = 0
The plot is shown in fig 14. From plot N=0, Z=0, system stable.
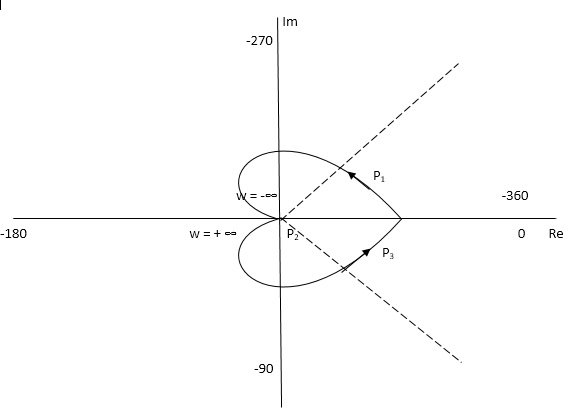
Fig 14. Nyquist Plot G(S) = 1/(S + 4)(S + 5)
Q.3. For the given transfer function, plot the Nyquist plot and comment on stability G(S) = k/S2(S + 10)?
Soln: As the poles exists at origin. So, first time we do not include poles in Nyquist plot. Then check the stability for second case we include the poles at origin in Nyquist path. Then again check the stability.
PART – 1: Not including poles at origin in the Nyquist Path.
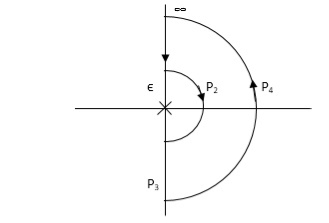
Fig 15. Nyquist Path
P1 W(∞ Ɛ) where Ɛ 0
P2 S = Ɛejϴ ϴ(+π/2 to 0 to -π/2)
P3 W = -Ɛ to -∞
P4 S = Rejϴ, R ∞, ϴ = -π/2 to 0 to +π/2
For P1
M = 1/w.w√102 + w2 = 1/w2√102 + w2
Φ = -1800 – tan-1(w/10)
W M Φ
∞ 0 -3 π/2
Ɛ ∞ -1800
Path P3 will be mirror image of P1 about Real axis.
G(Ɛ ejϴ) = 1/( Ɛ ejϴ)2(Ɛ ejϴ + 10)
Ɛ 0, ϴ = π/2 to 0 to -π/2
= 1/ Ɛ2 e2jϴ(Ɛ ejϴ + 10)
= ∞. e-j2ϴ [ -2ϴ = -π to 0 to +π ]
Path P2 will be formed by rotating through -π to 0 to +π
Path P4 S = Rejϴ R ∞ ϴ = -π/2 to 0 to +π/2
G(Rejϴ) = 1/ (Rejϴ)2(10 + Rejϴ)
= 0
N = Z – P
No poles on right half of S plane so, P = 0
N = Z – 0
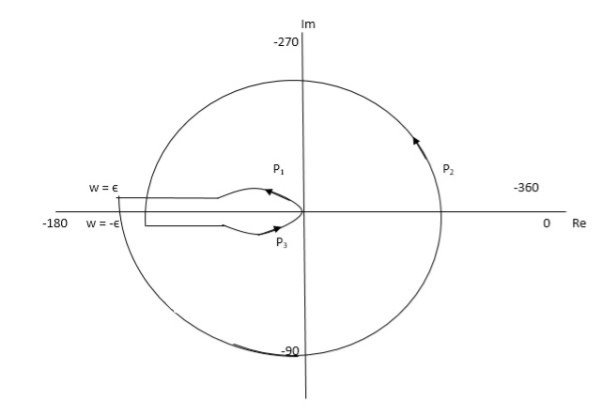
Fig 16. Nyquist Plot for G(S) = k/S2(S + 10)
But from plot shown in fig 16. It is clear that number of encirclements in Anticlockwise direction. So,
N = 2
N = Z – P
2 = Z – 0
Z = 2
Hence, system unstable.
PART 2 Including poles at origin in the Nyquist Path.
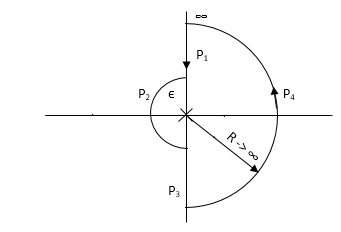
Fig 17. Nyquist Path
P1 W(∞ to Ɛ) Ɛ 0
P2 S = Ɛejϴ Ɛ 0 ϴ(+π/2 to +π to +3π/2)
P3 W(-Ɛ to -∞) Ɛ 0
P4 S = Rejϴ, R ∞, ϴ(3π/2 to 2π to +5π/2)
M = 1/W2√102 + W2 , φ = - π – tan-1(W/10)
P1 W(∞ to Ɛ)
W M φ
∞ 0 -3 π/2
Ɛ ∞ -1800
P3 (mirror image of P1)
P2 S = Ɛejϴ
G(Ɛejϴ) = 1/ Ɛ2e2jϴ(10 + Ɛejϴ)
Ɛ 0
G(Ɛejϴ) = 1/ Ɛ2e2jϴ(10)
= ∞. e-j2ϴϴ(π/2 to π to 3π/2)
-2ϴ = (-π to -2π to -3π)
P4 = 0
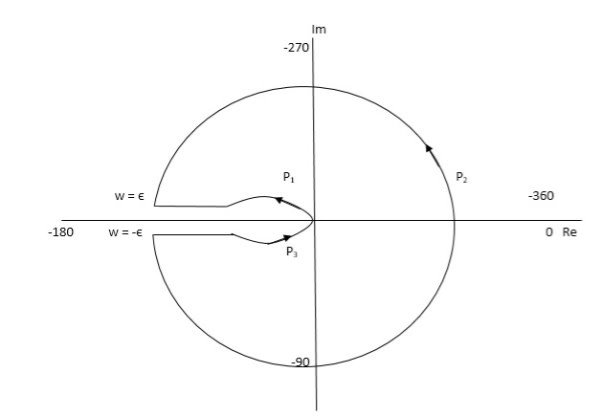
Fig 18. Nyquist Plot G(S) = k/S2(S + 10)
The plot is shown in fig 18. From the plot it is clear that there is no encirclement of -1 in Nyquist path. (N = 0). But the two poles at origin lies to the right half of S-plane in Nyquist path.(P = 2)[see path P2]
N = Z – P
0 = Z – 2
Z = 2
Hence, system is unstable.
Path P2 will be formed by rotating through -π to -2π to -3π
NOTE: The sign convention for angles is shown
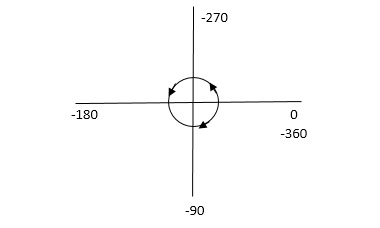
Fig 19. Sign for Angle Directions
NOTE: Angles are considered –ve for anticlockwise directions and +ve for clockwise directions.
Bode Plot
In polar plot any point gives the magnitude phase of the transfer function in bode we split magnitude and  plot.
plot.
Advantages
By looking at bode plot we can write the transfer function of system
Q. G(S) = 
Substitute S = j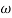
G(j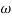 ) =
) = 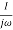
M = 
 = tan-1
= tan-1 = -900
= -900
Magnitude varies with ‘w’ but phase is constant.
MdB = +20 log10
MdB = -20 log10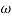
Decade frequency:
W present = 10 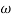 past
past
Then 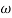 present is called decade frequency of
present is called decade frequency of 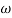 past
past
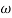 2 = 10
2 = 10 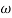 1
1
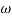 2 is decade frequency of
2 is decade frequency of  1
1
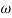 MdB
MdB
0.0140
0.120
10 (shows pole at origin)
0-20
10-40
100-60
Slope = (20db/decade)
MAGNITUDE PLOT
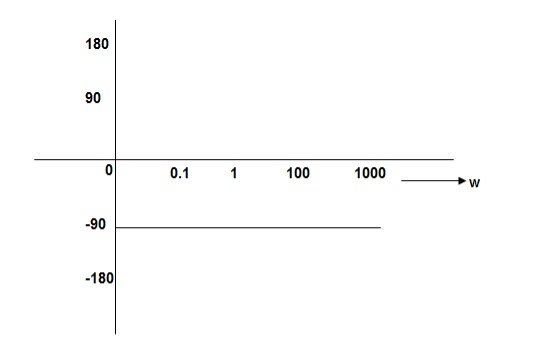
PHASE PLOT
Q.G(S) = 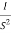
G(j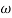 ) =
) = 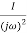
M = 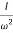 ;
;  = -1800 (-20tan-1
= -1800 (-20tan-1 )
)
MdB = +20 log 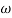 -2
-2
MdB = -40 log10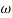
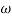 MdB
MdB
0.0180
0.140
10(pole at origin)
10-40
100-80
Slope = 40dbdecade
Q. G(S) = S
M= W
 = 900
= 900
MdB = 20 log10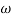
 MdB
MdB
0.01-40
0.1-20
10
1020
10090
100060
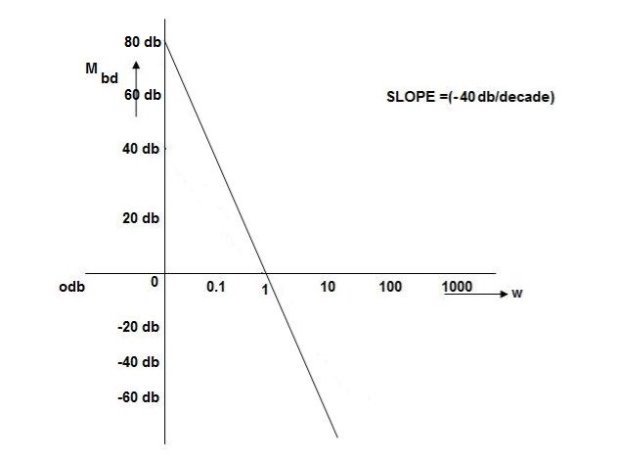
Q. G(S) = S2
M=  2MdB = 20 log10
2MdB = 20 log10 2
2
 = 1800 = 40 log10
= 1800 = 40 log10
WMdB
0.01-80
0.1-40
10
1040
10080
Q. (S) = 
G(j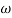 ) =
) = 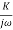
M = 
MdB = 20 log10 K-20 log10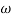
 = tan-1(
= tan-1( ) –tan-1(
) –tan-1(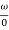 )
)
 = 0-900 = -900
= 0-900 = -900
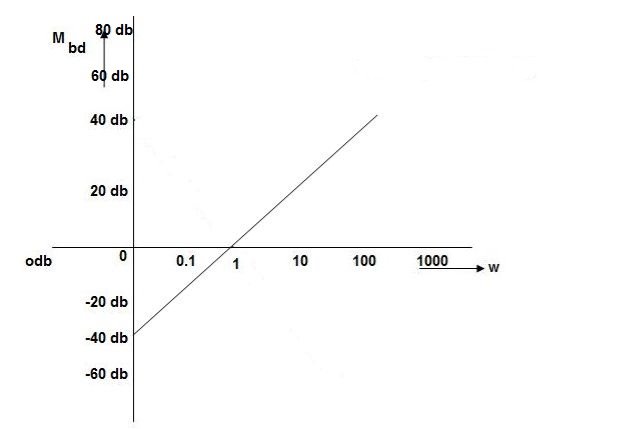
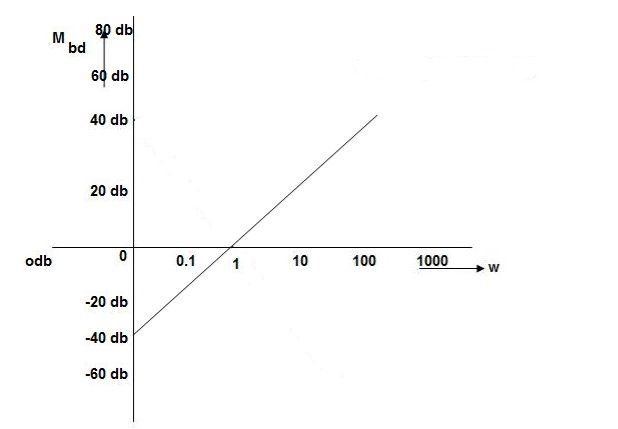
K=1K=10 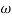 =-20 log10 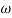 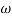 0.014060 0.12040 1020 10-200 100-40-20 |
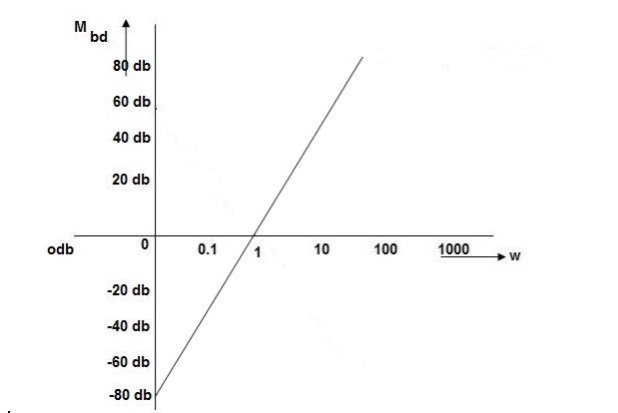
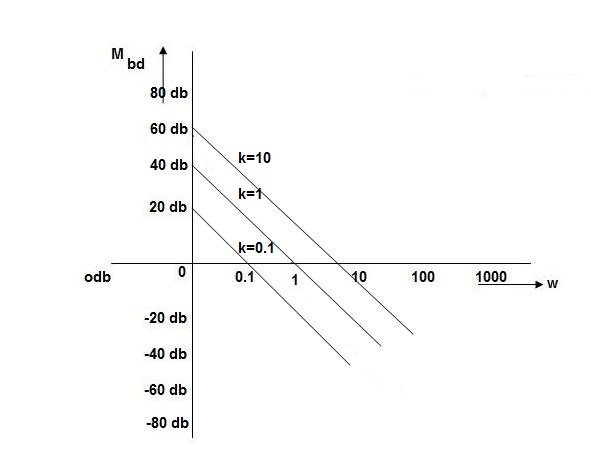
As we vary K  then plot shift by 20 log10K
then plot shift by 20 log10K
i.e adding a d.c. To a.c. Quantity
Approximation of Bode Plot:
IF poles and zeros are not located at origin
G(S) = 
TF = 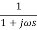
M = 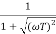
MdB = -20 log10 (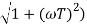
 = -tan-1
= -tan-1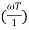
Approximation: 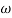 T >> 1. So, we can neglect 1.
T >> 1. So, we can neglect 1.
MdB = -20 log10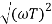
MdB = -20 log10 T . ;
T . ;  = -tan-1(
= -tan-1( T)
T)
Approximation:  T << 1. So, we can neglecting
T << 1. So, we can neglecting 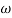 T.
T.
MdB= 0dB,  = 00
= 00
At a point both meet so equal i.e a time will come hence both approx become equal
-20 log10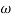 T= 0
T= 0
 T= 1
T= 1
 corner frequency
corner frequency
At this frequency both the cases are equal
MdB = -20 log10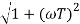
Now for 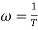
MdB = -20 log10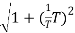
= -20 log10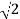
= -10 log102
MdB = 10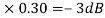
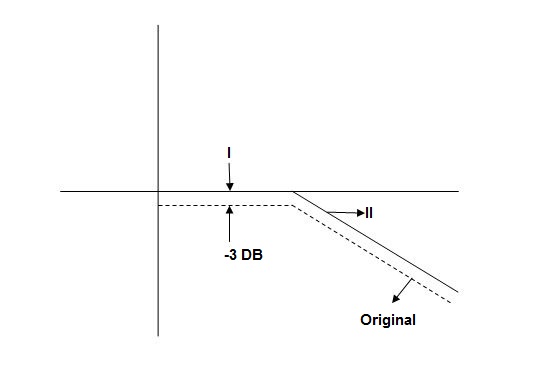
When we increase the value of  in app 2 and decrease the
in app 2 and decrease the  of app 1 so a RT comes when both cases are equal and hence for that value of
of app 1 so a RT comes when both cases are equal and hence for that value of  where both app are equal gives max. Error we found above and is equal to 3dB
where both app are equal gives max. Error we found above and is equal to 3dB
At corner frequency we have max error of -3dB
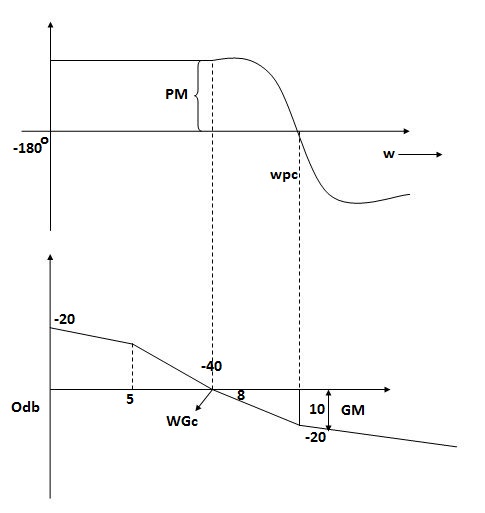
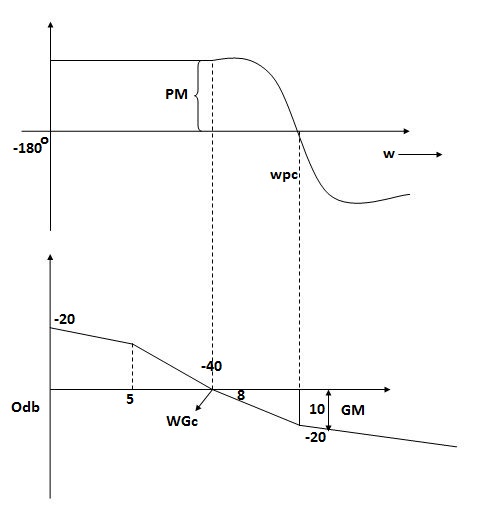
Gain margin (GM): The gain margin is the change in open-loop gain, expressed in decibels (dB), required at 180◦ of phase shift to make the closed-loop system unstable.
Phase margin (PM): The phase margin is the change in open-loop phase shift, required at unity gain to make the closed-loop system unstable.
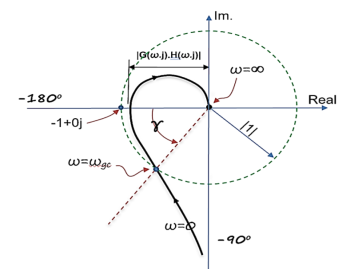
GM = 1/|G(jw)H(jw)| for w=wpc
=20log10(1/|G(jw)H(jw)|)
=-20 log10 (|G(jw)H(jw)|)
For PM refer figure
PM = 1800+ɸ
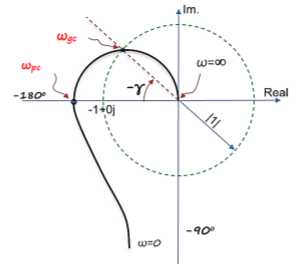
Gain crossover frequency (ωgc):
The frequency at which magnitude of G(wj)H(wj) is unity (i.e. |G(wj)H(wj)| =1) called gain frequency crossover.
ωpc > ωgc
GM & PM are stable (+ve) Stable system
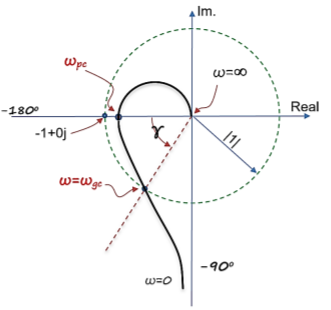
Phase crossover frequency (ωpc):
The frequency at which phase angle of G(wj)H(wj) is -180o
ωgc > ωpc GM & PM are stable (-ve) Unstable system.
Closed loop frequency response
The closed-loop frequency response reveals important information about the relative stability and the speed of response in the time-domain. For unity-gain feedback configuration (H(s)=1), the closed-loop frequency response is computed as
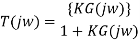
To proceed further, use rectangular form for the open loop frequency response:
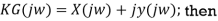
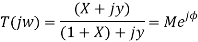
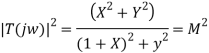

The above relation represents the equation of a circle with centre at
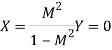
And radius; 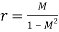
These are described as constant M circles on the
Frequency response plot
Further, as M→1, X=−1/2, which is a vertical line that separates the circles for M<1 from those with M>1.
The phase relationship similarly reveals an equation for constant phase circles:
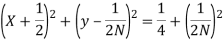
Where N = tan  . The constant phase circle is centred at X =
. The constant phase circle is centred at X =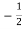 , Y=
, Y=  , and have radius
, and have radius
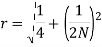
Resonance Peak
The resonance peak in the frequency response occurs at ω=ωr for ζ<0.7. For a prototype second-order system, we have
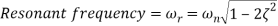
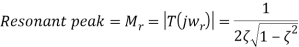
When the polar plot of the loop gain, KGH(jω), is superimposed onto the constant M and constant N contours, it reveals the magnitude peak Mr in T(jω).
The magnitude peak represents a measure of relative stability, while the resonant frequency associated with it is a measure of speed of response in the time-domain. A value of Mr=1.3 (or 2.5dB) is considered a good compromise between speed and stability.
Open loop frequency response
“Open Loop Gain” which is defined as the amplifiers output amplification without any external feedback signals connected to it and for a typical operational amplifier is about 100dB at DC (zero Hz). This output gain decreases linearly with frequency down to “Unity Gain” or 1, at about 1MHz and this is shown in the following open loop gain response curve.
Open-loop Frequency Response Curve
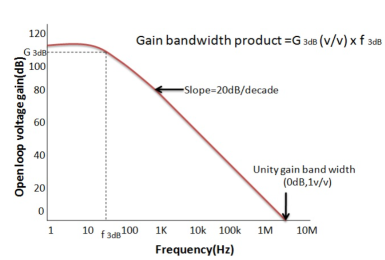
Fig 20. Frequency Response Curve
From this frequency response curve, we can see that the product of the gain against frequency is constant at any point along the curve. Also, that the unity gain (0dB) frequency also determines the gain of the amplifier at any point along the curve. This constant is generally known as the Gain Bandwidth Product or GBP. Therefore:
GBP = Gain x Bandwidth = A x BW
For example, from the graph above the gain of the amplifier at 100kHz is given as 20dB or 10, then the gain bandwidth product is calculated as:
GBP = A x BW = 10 x 100,000Hz = 1,000,000.
Similarly, the operational amplifiers gain at 1kHz = 60dB or 1000, therefore the GBP is given as:
GBP = A x BW = 1,000 x 1,000Hz = 1,000,000.
The Voltage Gain (AV) of the operational amplifier can be found using the following formula:
Av = Vout/ Vin
And in Decibels or (dB) is given as:
20 log (A) or 20 log (Vout/ Vin ) in dB
An Op- Amp Bandwidth
The operational amplifiers bandwidth is the frequency range over which the voltage gain of the amplifier is above 70.7% or -3dB (where 0dB is the maximum) of its maximum output value.

Fig 21. Frequency Response
Example-1
Using the formula 20 log (A), we can calculate the bandwidth of the amplifier as:
37 = 20 log (A) therefore, A = anti-log (37 /20) = 70.8
GBP/ A = Bandwidth, therefore, 1,000,000 / 70.8 = 14,124Hz, or 14kHz
Then the bandwidth of the amplifier at a gain of 40dB is given as 14kHz as previously predicted from the graph.
Key takeaways
“Open Loop Gain” which is defined as the amplifiers output amplification without any external feedback signals connected to it and for a typical operational amplifier is about 100dB at DC (zero Hz).
Que. G(S) = 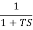
TF = 
M = 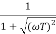
MdB = -20 log10 (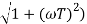 at T=2
at T=2
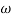 MdB
MdB
1-20 log10
10-20 log10
100-20 log10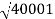
 MdB
MdB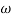 =
= =
= 
0.1-20 log10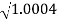 = 1.73
= 1.73  10-3
10-3
0.1-20 log10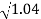 = -0.1703
= -0.1703
0.5-20 log10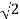 = -3dB
= -3dB
1-20 log10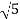 = -6.98
= -6.98
10-20 log10 = -26.03
= -26.03
100 -20 log10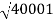 = -46.02
= -46.02
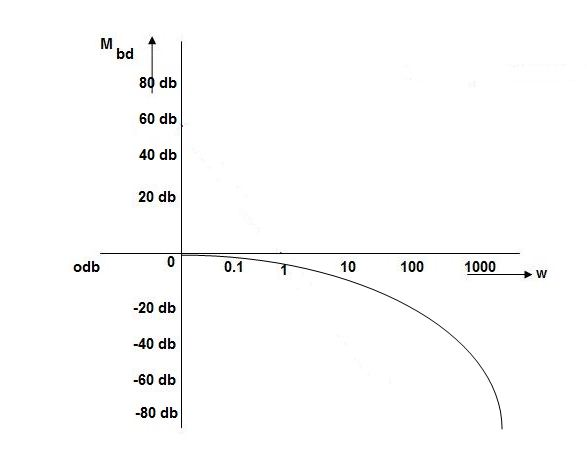
Fig 22. Magnitude Plot with approximation
Without approximation
For second order system
TF = 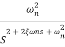
TF = 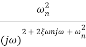
= 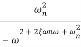
= 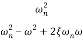
= 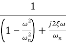
M= 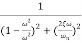
MdB= 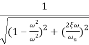
Case 1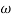 <<
<<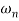
 << 1
<< 1
MdB= 20 log10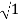 = 0 dB
= 0 dB
Case 2 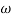 >>
>>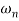
 >> 1
>> 1
MdB = -20 log10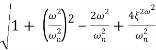
= -20 log10
= -20 log10
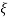 < 1
< 1  is very large so neglecting other two terms
is very large so neglecting other two terms
MdB = -20 log10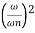
= -40 log10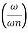
Case 3 . When case 1 is equal to case 2
-40 log10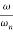 = 0
= 0
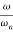 = 1
= 1
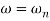
The natural frequency is our corner frequency
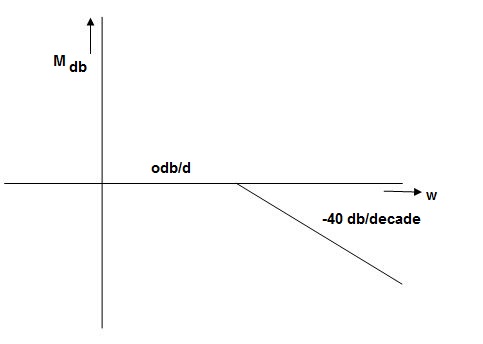
Fig 23. Magnitude Plot
Max error at 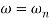 i.e at corner frequency
i.e at corner frequency
MdB = -20 log10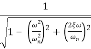
For 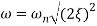
MdB = -20 log10 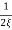
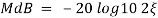 error for
error for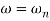
Completely the error depends upon the value of  (error at corner frequency)
(error at corner frequency)
The maximum error will be
MdB = -20 log10 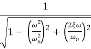
M = -20 log10 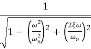
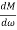 = 0
= 0
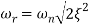
 is resonant frequency and at this frequency we are getting the maximum error so the magnitude will be
is resonant frequency and at this frequency we are getting the maximum error so the magnitude will be
M = -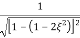 +
+ 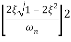
= 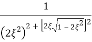
Mr =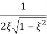
MdB = -20 log10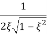
MdB = -20 log10 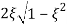
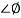 = tan-1
= tan-1
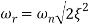
Mr = 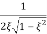
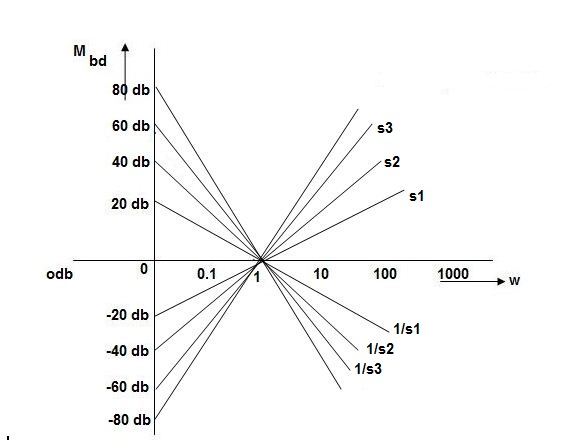
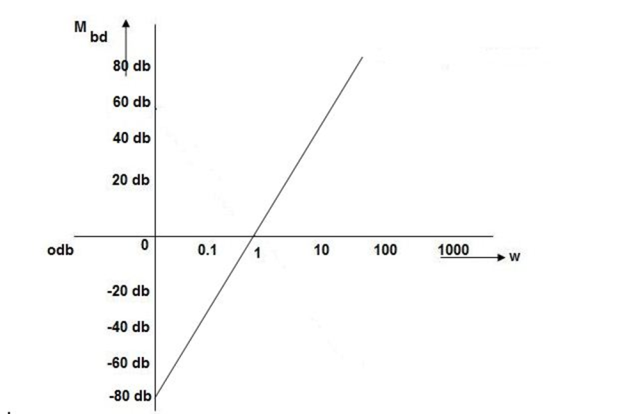
Type of system | Initial slope | Intersection |
0 | 0 dB/decade | Parallel to 0 axis |
1 | -20 dB/decade | =K1 |
2 | -40 dB/decade | =K1/2 |
3 | -60 dB/decade | =K1/3 |
. | . | 1 |
. | . | 1 |
. | . | 1 |
N | -20N dB/decade | =K1/N |
Q.1 Sketch the bode plot for transfer function
G(S) = 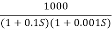
- Replace S = j
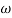
G(j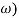 =
= 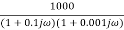
This is type 0 system. So initial slope is 0 dB decade. The starting point is given as
20 log10 K = 20 log10 1000
= 60 dB
Corner frequency  1 =
1 = 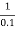 = 10 rad/sec
= 10 rad/sec
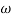 2 =
2 = 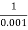 = 1000 rad/sec
= 1000 rad/sec
Slope after 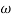 1 will be -20 dB/decade till second corner frequency i.e
1 will be -20 dB/decade till second corner frequency i.e 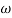 2 after
2 after 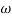 2 the slope will be -40 dB/decade (-20+(-20)) as there are poles
2 the slope will be -40 dB/decade (-20+(-20)) as there are poles
2. For phase plot
 = tan-1 0.1
= tan-1 0.1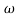 - tan-1 0.001
- tan-1 0.001 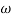
For phase plot
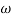

100-900
200-9.450
300-104.80
400-110.360
500-115.420
600-120.00
700-124.170
800-127.940
900-131.350
1000 -134.420
The plot is shown in figure 24.
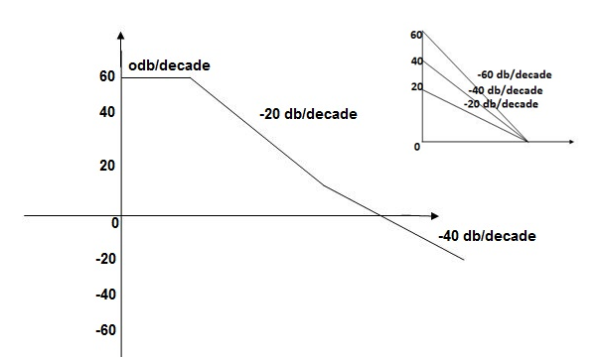
Fig 24. Magnitude Plot for G(S) = 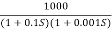
Q.2 For the given transfer function determine
G(S) = 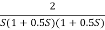
Gain cross over frequency phase cross over frequency phase mergence and gain margin
Initial slope = 1
N = 1, (K)1/N = 2
K = 2
Corner frequency
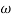 1 =
1 = 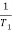 = 2 (slope -20 dB/decade
= 2 (slope -20 dB/decade
 2 =
2 = 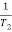 = 20 (slope -40 dB/decade
= 20 (slope -40 dB/decade
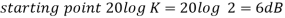
Phase
 = tan-1
= tan-1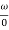 - tan-1 0.5
- tan-1 0.5 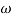 - tan-1 0.05
- tan-1 0.05 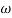
 = 900- tan-1 0.5
= 900- tan-1 0.5 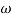 - tan-1 0.05
- tan-1 0.05 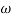


1-119.430
5-172.230
10-195.250
15-209.270
20-219.30
25-226.760
30-232.490
35-236.980
40-240.570
45-243.490
50-245.910
Finding 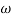 gc (gain cross over frequency
gc (gain cross over frequency
M = 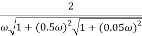
4 = 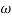 2 (
2 (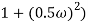 (
(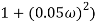
 6 (6.25
6 (6.25 104) + 0.252
104) + 0.252 4 +
4 +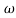 2 = 4
2 = 4
Let 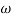 2 = x
2 = x
X3 (6.25 104) + 0.252
104) + 0.252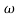 2 + x = 4
2 + x = 4
X1 = 2.46
X2 = -399.9
X3 = -6.50
For x1 = 2.46
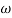 gc = 3.99 rad/sec(from plot )
gc = 3.99 rad/sec(from plot )
For phase margin
PM = 1800 - 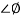
 = 900 – tan-1 (0.5×
= 900 – tan-1 (0.5×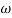 gc) – tan-1 (0.05 ×
gc) – tan-1 (0.05 × 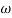 gc)
gc)
= -164.50
PM = 1800 - 164.50
= 15.50
For phase cross over frequency (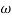 pc)
pc)
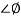 = 900 – tan-1 (0.5
= 900 – tan-1 (0.5 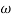 ) – tan-1 (0.05
) – tan-1 (0.05 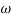 )
)
-1800 = -900 – tan-1 (0.5 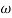 pc) – tan-1 (0.05
pc) – tan-1 (0.05 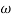 pc)
pc)
-900 – tan-1 (0.5 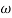 pc) – tan-1 (0.05
pc) – tan-1 (0.05 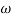 pc)
pc)
Taking than on both sides
Tan 900 = tan-1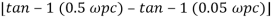
Let tan-1 0.5 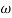 pc = A, tan-1 0.05
pc = A, tan-1 0.05 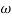 pc = B
pc = B
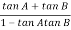 = 00
= 00
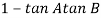 = 0
= 0
1 =0.5 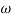 pc 0.05
pc 0.05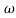 pc
pc
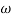 pc = 6.32 rad/sec
pc = 6.32 rad/sec
The plot is shown in figure 25.

Fig 25. Magnitude Plot G(S) = 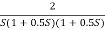
Q3. For the given transfer function
G(S) = 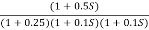
Plot the rode plot find PM and GM
T1 = 0.5 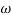 1 =
1 = 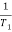 = 2 rad/sec
= 2 rad/sec
Zero so, slope (20 dB/decade)
T2 = 0.2 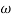 2 =
2 = 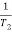 = 5 rad/sec
= 5 rad/sec
Pole, so slope (-20 dB/decade)
T3 = 0.1 = T4 = 0.1
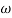 3 =
3 = 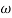 4 = 10 (2 pole) (-40 db/decade)
4 = 10 (2 pole) (-40 db/decade)
- Initial slope 0 dB/decade till
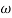 1 = 2 rad/sec
1 = 2 rad/sec - From
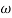 1 to
1 to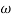 2 (i.e. 2 rad /sec to 5 rad/sec) slope will be 20 dB/decade
2 (i.e. 2 rad /sec to 5 rad/sec) slope will be 20 dB/decade - From
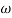 2 to
2 to 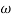 3 the slope will be 0 dB/decade (20 + (-20))
3 the slope will be 0 dB/decade (20 + (-20)) - From
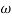 3,
3,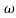 4 the slope will be -40 dB/decade (0-20-20)
4 the slope will be -40 dB/decade (0-20-20)
Phase plot
 = tan-1 0.5
= tan-1 0.5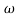 - tan-1 0.2
- tan-1 0.2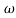 - tan-1 0.1
- tan-1 0.1 - tan-1 0.1
- tan-1 0.1

500-177.30
1000-178.60
1500-179.10
2000-179.40
2500-179.50
3000-179.530
3500-179.60
GM = 00
PM = 61.460
The plot is shown in figure 26.
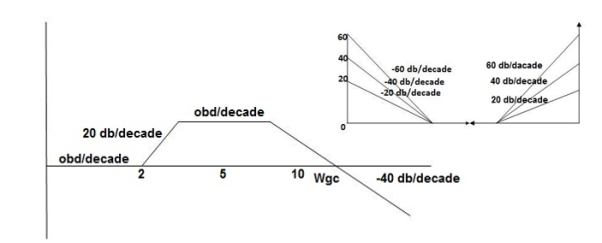
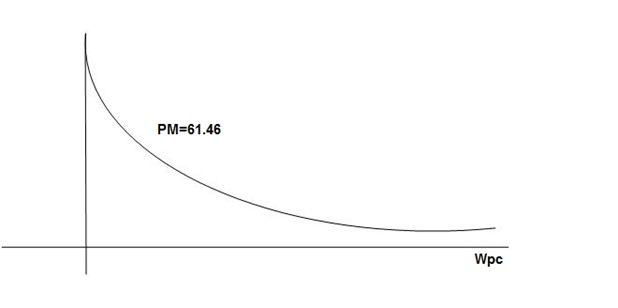
Fig 26. Magnitude and phase Plot for G(S) = 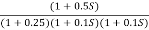
Q4. For the given transfer function plot the bode plot (magnitude plot)
G(S) = 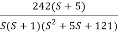
Given transfer function
G(S) = 
Converting above transfer function to standard from
G(S) = 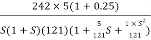
= 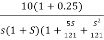
1. As type 1 system, so initial slope will be -20 dB/decade
2. Final slope will be -60 dB/decade as order of system decides the final slope
3. Corner frequency
T1 =  ,
, 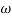 11= 5 (zero)
11= 5 (zero)
T2 = 1,  2 = 1 (pole)
2 = 1 (pole)
4. Initial slope will cut zero dB axis at
(K)1/N = 10
i.e 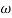 = 10
= 10
5. Finding  n and
n and 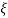
T(S) = 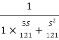
T(S)= 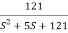
Comparing with standard second order system equation
S2+2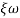 ns +
ns +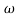 n2
n2
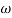 n = 11 rad/sec
n = 11 rad/sec
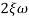 n = 5
n = 5
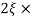 11 = 5
11 = 5
 =
= 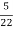 = 0.27
= 0.27
6. Maximum error
M = -20 log 2
= +6.5 dB
7. As K = 10, so whole plot will shift by 20 log 10 10 = 20 dB
The plot is shown in figure 27.
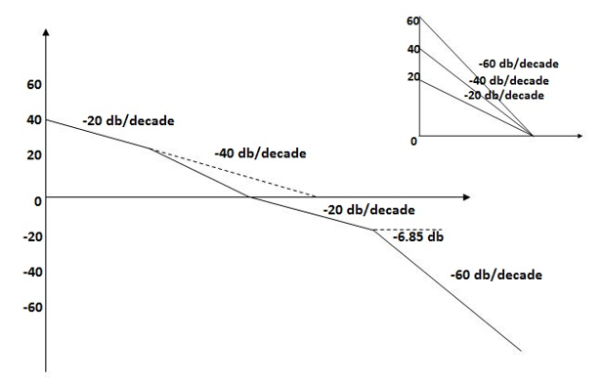
Fig 27. Magnitude Plot for G(S) = 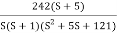
Q5. For the given plot determine the transfer function
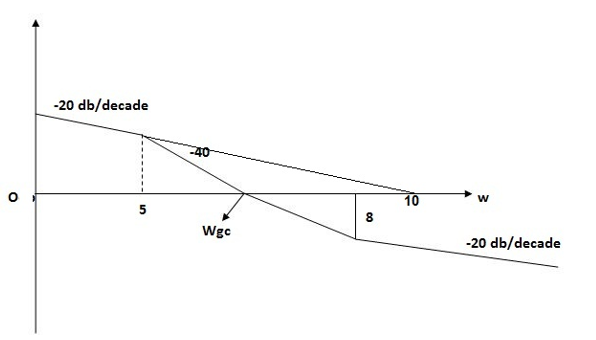
From above figure we can conclude that
1. Initial slope = -20 dB/decade so type -1
2. Initial slope alls 0 dB axis at  = 10 so
= 10 so
K1/N N = 1
(K)1/N = 10.
3. Corner frequency
 1 =
1 =  = 0.2 rad/sec
= 0.2 rad/sec
 2 =
2 =  = 0.125 rad/sec
= 0.125 rad/sec
4. At  = 5 the slope becomes -40 dB/decade, so there is a pole at
= 5 the slope becomes -40 dB/decade, so there is a pole at  = 5 as slope changes from -20 dB/decade to -40 dB/decade
= 5 as slope changes from -20 dB/decade to -40 dB/decade
5. At  = 8 the slope changes from -40 dB/decade to -20 dB/decade hence is a zero at
= 8 the slope changes from -40 dB/decade to -20 dB/decade hence is a zero at  = 8 (-40+(+20)=20)
= 8 (-40+(+20)=20)
6. Hence transfer function is
T(S) = 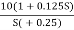
Gain Cross Over Frequency:
The frequency at which the bode plot culls the 0db axis is called Gain Cross Over Frequency.
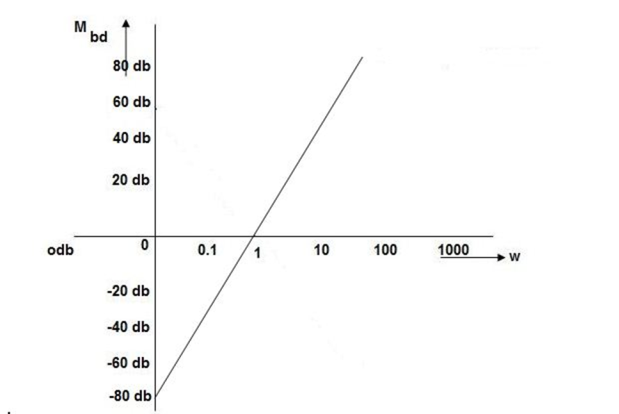
Phase Cross Over Frequency-:
The frequency at which the phase plot culls the -1800 axis.
GM=MdB= -20 log [ G (jw)]
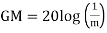 .:
.: 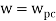
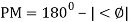 .:
.: 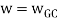
When gain cross over frequency is smaller than phase curves over frequency the system is stable and vice versa.
Key takeaway:
- More the difference between b/WPC and WGC core is the stability of the system
- If GM is below 0dB axis then take ilb +ve and stable. If GM above 0dB axis, that takes -ve
GM= ODB - 20 log M
3. The IM should also lie above -1800 for making the system (i.e. pm=+ve
4. For a stable system, GM and PM should be -ve
5. GM and PM both should be +ve more the value of GM and PM more the system is stable.
6. If Wpc and Wgc are in the same line Wpc= Wgc then the system is marginally stable. As we get GM=0dB.
References:
1. Control Systems Engineering, I.J. Nagrath, M. Gopal
2. Modern Control system (II Edition) – Katsuhiko Ogata
3. Control systems by Smarajit Ghosh (second Edition, Pearson Education)
Unit - 5
Frequency response method
The calculation of system parameters for higher order systems is difficult in time domain analysis. This can be overcome by frequency domain analysis. As the frequency response of a linear time invariant system is independent of amplitude and phase of the input test signal. The effect of noise and parameter variation in frequency domain can be easily computed.
In frequency response can be determine by calculating the phase and amplitude oof the given system transfer function. If a sinusoidal signal XG(j)sint then its amplitude will be
C(t) = XG(j)sint
= X|G(j)| 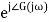 sint
sint
Magnitude = |G(j)|
Phase = G(j)
In polar form = |G(j)| 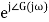
Resonant Peak (Mr): The maximum value of magnitude is known as Resonant peak. The relative stability of the system can be determined by Mr. The larger the value of Mr the undesirable is the transient response.
Resonant Frequency (Wr): The frequency at which magnitude has maximum value.
Bandwidth: The band of frequencies lying between -3db points.
Cut-off frequency –The frequency at which the magnitude is 3db below its zero frequency.
Cut-off Rate – It is the slope of the log magnitude curve near the cut off frequency.
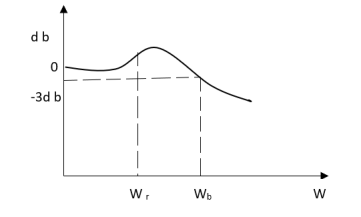

Fig 1 Frequency Domain Specification
It gives the frequency response of the system. If the transfer function is given, then from the plot number of poles and zeros can be calculated.
Polar plot of some standard functions:
# TYPE ‘O’
Ex :1T(S) = 1/S + 1
(1). For polar plot substitute S=jw.
TF = 1/1 + jw
(2). Magnitude M = 1 + 0j / 1 + jw = 1/√1 + w2
(3). Phase φ = tan-1(0)/ tan-1w = - tan-1w
WMφ
0100
10.707-450
∞0-900
The plot is shown in fig. 2(a)
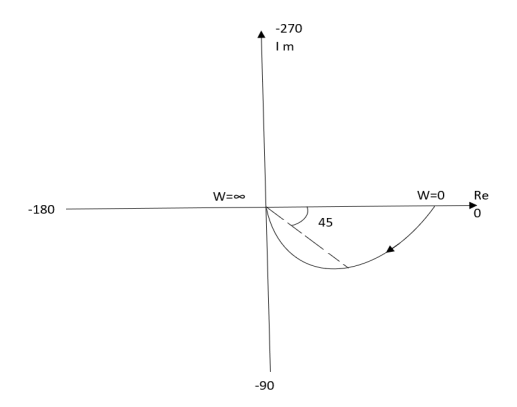
Fig 2(a) Polar Plot T(S) = 1/S + 1
Ex.2>. T(S) = 1/(S+1)(S+2)
(1). S = jw
TF = 1/(1+jw)(2+jw)
(2). M = 1/(1+jw)(2+jw) = 1/-w2 + 3jw + 2
M = 1/√1 + w2√4 + w2
(3). Φ = - tan-1 w - tan-1(w/2)
WMΦ
00.500
10.316-71.560
20.158-108.430
∞0-1800
The plot is shown in fig2(b)
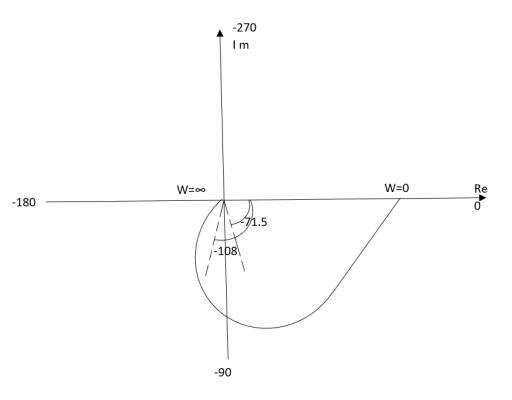
Fig2(b) Polar Plot T(S) = 1/(S+1)(S+2)
Intersection of polar plot with imaginary axis will be when real part of Transfer function = 0
M = 1/(jw + 1)(jw + 2)
= 1/-w2 + j3w + 2
TYPE ‘1’
Ex.1 T(S) = 1/S
(1). S = jw
(2). M = 1/W
(3). Φ = -tan-1(W/O) = -900
WMφ
0∞-900
11-900
20.5-900
∞0-900
The plot is shown in fig.3(a)
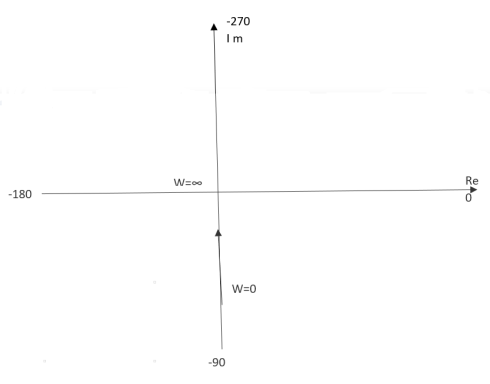
Fig 3(a) Polar Plot T(S) = 1/S
Ex.2 T(S) = 1/S2
(1). S = jw
(2). M = 1/w2
(3). Φ = -tan-1(W/O)-tan-1(W/O) = -1800
WMΦ
0∞-1800
11-1800
20.25-1800
∞0-1800
The plot is shown in fig.3(b)
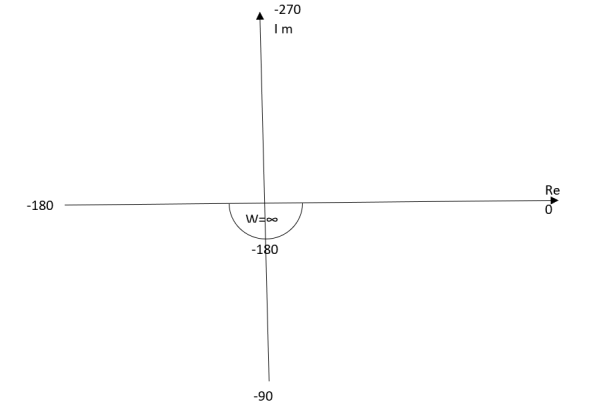
Fig 3(b) Polar Plot T(S) = 1/S2
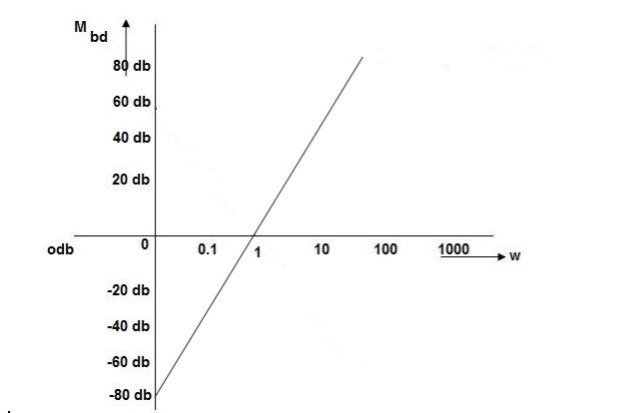
Key takeaway
- For Polar Plot starting point depends upon type of system
- The terminating phase depends on order of the system.
TYPE 1 ORDER 2
Ex.1 T(S) = 1/S(S+1)
(1). M = 1/W√1+w2
(2). Φ = -900 - tan -1(W/T)
WMφ
0∞-900
10.707-1350
20.45-153.40
∞0-1800
The plot is shown in fig.4(a)
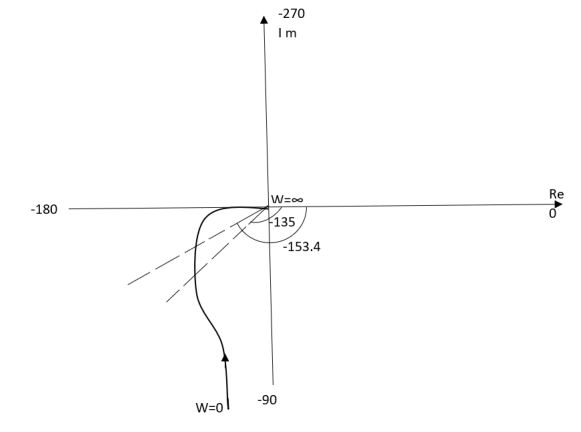
Fig 4(a) Polar Plot T(S) = 1/S(S+1)
Ex.2TYPE 2 ORDER 3
T(s) = 1/S2(S+1)
(1). M = 1/w2√1+jw
(2). Φ = -1800 – tan-1W/T
The plot is shown in fig.4(b)
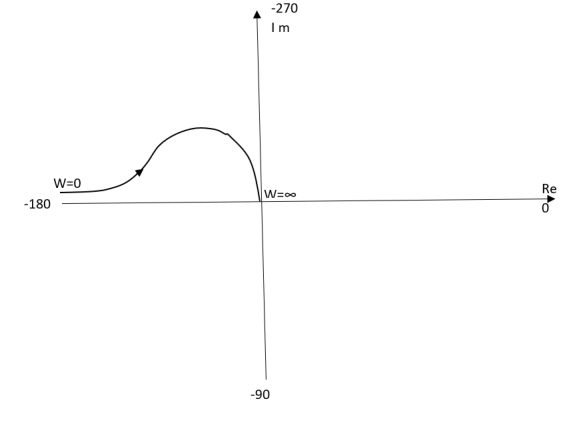
Fig 4(b) Polar Plot T(s) = 1/S2(S+1)
Nyquist Stability Criteria:
The Nyquist criteria is a semi graphical method that determines stability of CL system investigating the properties of the frequency domain plot (Polar plot), the Nyquist plot of the OLTF G(S) H(S) is represented as L(S)
L(S) = G(S)H(S)
Specially the Nyquist plot of L(S) is a plot drawn by substituting S=jw and varying the value of w as per in polar plot. In polar plot we take one sided frequency response ( 0 - ∞) in Nyquist plot we will vary the frequency in entire range possible from ( -∞ to 0 ) and (0 to ∞ )
Nyquist Criteria also gives:
(1). In addition to providing the absolute stability like other plots, the Nyquist criteria also gives information on the relative stability of a stable system and the degree of instability of an unstable system.
(2). It also gives indications on how the system stability can be improved.
(3). The Nyquist plot of G(S) H(S) is the polar plot of G(S) H(S) drawn with wider range of frequency ( -∞ to ∞ ) and along the Nyquist path.
(4). The Nyquist plot of G(S) H(S) gives information on frequency domain characteristics such as B.W, gain margin and phase margin.
Construction of Nyquist Plot
Encircled: A point or region in a complex function phase i.e. S-plane is said to be encircled by a closed path if it is found inside the path.
Assumption:
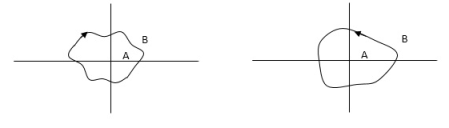
Fig 5. Encirclement
In this example point A is encircled by the closed path Y. Since, A is inside the closed path point B is not encircled by y. It is outside the path. Furthermore when the closed path Y, has a direction assign to it, encirclement, if made can be in the clockwise direction or in the anti-clockwise direction.
Point A is encircled by Y by anticlockwise direction. We can say that the region inside the path is encircled in the prescribed direction and the region outside the path is not encircled.
Enclosed:
A point or region is said to be enclosed by a closed path if it is encircled in the counter clockwise direction, or the point or region lies to the left of the path (always), when the path is traveling in the prescribed direction.
The concept of enclosure is particularly useful, if only a portion of a closed path is shown.
In this example the shaded region are
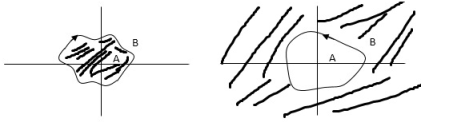
Fig 6. Enclosure
Considered to be enclosed by the closed path Y. In other words, point A is enclosed by Y in fig a. But is not enclosed by Y in fig b. And for point B it is viceversa.
No of encirclements and enclosure:
For A line is cut once
For B line is cut twice

Fig 7. Encirclement and Enclosure with example
As it’s overlapping but 2 times in Same direction
When a point is encircled by a closed path Y, a no. N can be assigned to the no. Of times it is encircled. The magnitude of N can be determined by drawing an arrow around the closed path Y.
Taking an arbitrary point S, and moving around in clockwise direction and anti-clockwise direction respectively. We are getting a direction.
The path followed by S1 gives us the direction and this path which covers the total number of revolution travelled by this point S1 is N or the net angle is ‘ 2 π N ’.
For B = 2 = N for A = 1 = N
In this eg. Point A is encircled ones (or 2 π radians) by function Y and point B is encircled twice (or 4 π radians)all in clockwise direction.
In diagram b again A and B are encircled but in counter clockwise direction thus for this diagram A is enclosed one’s and B is enclosed twice.
By definition M is +ve for anticlockwise(direction) encirclement and –ve for clockwise encirclement.
OLTF G(S) = (S + Z1)(S + Z2)/(S + P1)(S + P2) H(S) = 1 - - (1)
Fig 8. Unity feedback control system
CLTF G(S)/1 + G(S)
CE = 1 + G(S)
= 1 + (S + Z1)(S + Z2)/(S + P1)(S + P2)
CE = (S + P1)(S + P2) + (S + Z1)(S + Z2)/ (S + P1)(S + P2) - - (2)
Key takeaway:
# OLTF poles is equal to CE poles.
CE = (S + Z’1)( S + Z’2)/( S + P1)( S + P2) - - (3)
CLTF = G(S) –(1) / 1 + G(S) –(3)
= (S + Z1)( S + Z2) / (S + Z’1)( S + Z’2) - - (4)
# Zeros of characteristic equation is poles of CLTF (3 and 4).
For the closed loop system to be stable zeros of CE(i.e. poles of CLTF) should not be located at right half of the S-plane.
Consider a contour, which covers the entire right half of S-plane.
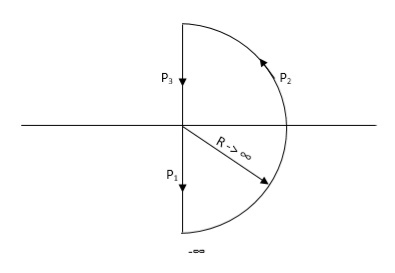
Fig 9. Contour For Right half of S-plane
P1 W(0 - ∞)
P2 RejR ∞
ϴ - π/2 to 0 to + π/2
P3 W(∞ to 0 )
If each and every point along the boundary of contour is mapped in q(S) where q(S) is 1+G(S)H(S)[CE]. The CE is drawn in S-domain. Now, as the CE : q(s) = 1 + G(S)H(S) contour is drawn into S-plane.
This q(S) contour may encircle the origin. Thus, the number of encirclement of q(S) contour with respect to origin is given by
N = Z – P
Where : Z1P zeros and poles of q(S)[CE]
N Total no of encirclement of origin
Z1P Zeros and poles of CE in the right half of S-plane
** for the CL system to be stable Z=0 always.
Important:
# Open loop System(stable): When OL system is stable P=0 i.e. no of poles on right half
N = Z – P
If P = 0
N = Z
- Now for CL system to be stable Z = 0
- N = 0
- i.e. q(s) contour should not encircle the origin.
# Open loop system(unstable): Let P = 1 i.e. one OL pole is located in right half of S-plane i.e. OLTF is unstable.
As N = Z – P
N = Z – 1
For CL system to be stable the only criteria is (Z=0) i.e.
N = -1
Which means q(S) contour should encircle the origin one’s in CW direction.
Key takeaway:
(1). When OL system is unstable then corresponding CL will be stable only when q(S) contour will encircle origin in CW direction.
(2). The no of encirclements should be equal to no of open loop poles located in right half of S-plane.
** the no of encirclements(N) can also be calculated by using G(S) contour (instead of q(S) contour) but the reference is -1+j0 instead of 0+j0 i.e. the no of encirclements should be considered w.r.t -1+j0 and not with the origin.
Explanation Mapping
q(S) = 1 + G(S)
G(S) is always given to us, so we can relate G(S) with q(S).
G(S) = q(S) – 1
But q(S) can be drawn by adding 1 real part to the q(S).
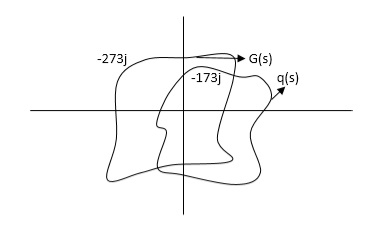
Fig 10. Mapping
G(S) given then q(S) shift to right side.
Nyquist criterion
Nyquist plots are the continuation of polar plots for finding the stability of the closed loop control systems by varying ω from −∞ to ∞. That means, Nyquist plots are used to draw the complete frequency response of the open loop transfer function.
The Nyquist stability criterion works on the principle of argument. It states that if there are P poles and Z zeros are enclosed by the ‘s’ plane closed path, then the corresponding G(s)H(s) plane must encircle the origin P−Z times. So, we can write the number of encirclements N as,
N=P-Z
Nyquist Contour: is the contour in the s-plane that includes the entire right half plane. Now, let’s consider F (s) = 1 + G(s)H(s) and the contour in the s-plane is the Nyquist contour (i.e., the entire right half plane).
Applying the Cauchy’s Principle of Argument, we should have
The number of rotations about the origin of the mapping through 1+ G(s) (H)
N = The number of zeros of 1+ G(s) (H) in the right half plane, Z - The number of poles of 1+ G(s) (H) in the right half plane, P
Please note
The mapping through G(s) (H) is virtually the same as the one through 1+ G(s) (H)
except that the contour is shifted one unit to the left. Thus, we can count rotations
about -1 instead of rotations about the origin in the above statement.
The zeros of 1+ G(s) (H) = the closed-loop poles.
The poles of 1+ G(s) (H) = the open-loop poles or the poles of 1+ G(s) (H)
Therefore
The number of rotations about -1 of the mapping through 1+ G(s) (H),
N = The number of closed-loop poles in the right half plane, Z - The number of open-loop poles in the right half plane, P
The above relationship is called the Nyquist Criterion; and the mapping through G(S)H(S) is called the Nyquist Diagram of G(S)H(S)
For a system to be stable, Z must be zero.
Sketching the Nyquist Diagram
Suppose the open-loop transfer function
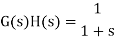
Sketch its Nyquist diagram
| | GH | | GH |
= 0 | 1 | 0 |
= | o | 
|
Cross re: = 0 = | See above | See above |
= 1 rad/s | 0.707 | 
|
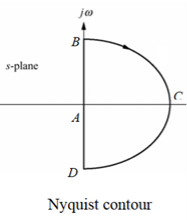
Sketching the Nyquist diagram includes two steps:
(1) Sketch the mapping of Point A to Point B, which is the same as the polar plot of frequency response for G(S)H(S).
Note that the semicircle with an infinite radius, i.e., B-C-D, is mapped to the origin if the order the denominator of G(S)H(S) is greater than the order the numerator of G(S)H(S).
(2) Sketch the mapping of Point A to Point D, which is the mirror image about the real axis of the mapping of Point A to Point B.
Plotting
Q1. For the transfer function below plot the Nyquist plot and also comment on stability?
G(S) = 1/S+1
Sol: N = Z – P ( No pole of right half of S plane P = 0 )
P = 0, N = Z
NYQUIST PATH:
P1 = W – (0 to - ∞)
P2 = ϴ( - π/2 to 0 to π/2 )
P3 = W(+∞ to 0)
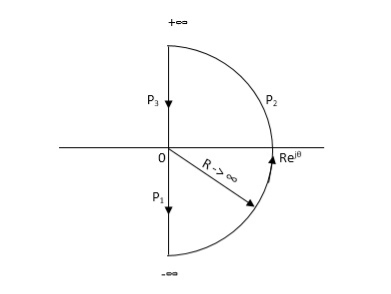
Fig 11. Nyquist path
Substituting S = jw
G(jw) = 1/jw + 1
M = 1/√1+W2
Φ = -tan-1(W/I)
For P1 :- W(0 to -∞)
W M φ
0 1 0
-1 1/√2 +450
-∞ 0 +900
Path P2:
W = Rejϴ R ∞ϴ -π/2 to 0 to π/2
G(jw) = 1/1+jw
= 1/1+j(Rejϴ) (neglecting 1 as R ∞)
M = 1/Rejϴ = 1/R e-jϴ
M = 0 e-jϴ = 0
Path P3:
W = -∞ to 0
M = 1/√1+W2, φ = -tan-1(W/I)
W M φ
∞ 0 -900
1 1/√2 -450
0 1 00
The Nyquist Plot is shown in fig 12.

Fig 12. Nyquist Plot G(S) = 1/S+1
From plot we can see that -1 is not encircled so, N = 0
But N = Z, Z = 0
So, system is stable.
Q.2. For the transfer function below plot the Nyquist Plot and comment on stability G(S) = 1/(S + 4)(S + 5)
Soln: N = Z – P, P = 0, No pole on right half of S-plane
N = Z
NYQUIST PATH
P1 = W(0 to -∞)
P2 = ϴ(-π/2 to 0 to +π/2)
P3 = W(∞ to 0)

Fig 13. Nyquist Path
Path P1 W(0 to -∞)
M = 1/√42 + w2 √52 + w2
Φ = -tan-1(W/4) – tan-1(W/5)
W M Φ
0 1/20 00
-1 0.047 25.350
-∞ 0 +1800
Path P3 will be the mirror image across the real axis.
Path P2: ϴ(-π/2 to 0 to +π/2)
S = Rejϴ
G(S) = 1/(Rejϴ + 4)( Rejϴ + 5)
R∞
= 1/ R2e2jϴ = 0.e-j2ϴ = 0
The plot is shown in fig 14. From plot N=0, Z=0, system stable.
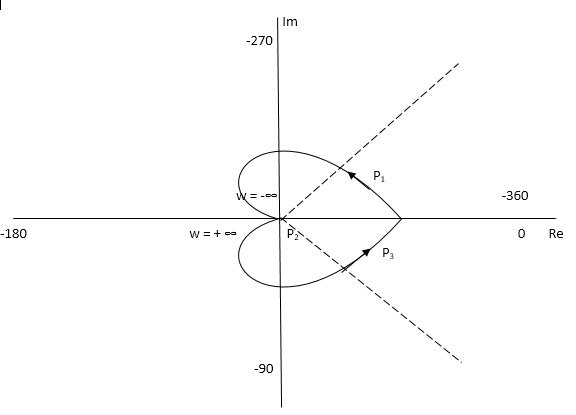
Fig 14. Nyquist Plot G(S) = 1/(S + 4)(S + 5)
Q.3. For the given transfer function, plot the Nyquist plot and comment on stability G(S) = k/S2(S + 10)?
Soln: As the poles exists at origin. So, first time we do not include poles in Nyquist plot. Then check the stability for second case we include the poles at origin in Nyquist path. Then again check the stability.
PART – 1: Not including poles at origin in the Nyquist Path.
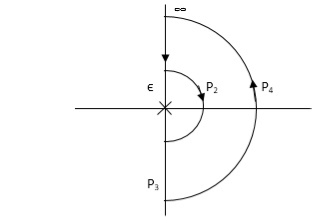
Fig 15. Nyquist Path
P1 W(∞ Ɛ) where Ɛ 0
P2 S = Ɛejϴ ϴ(+π/2 to 0 to -π/2)
P3 W = -Ɛ to -∞
P4 S = Rejϴ, R ∞, ϴ = -π/2 to 0 to +π/2
For P1
M = 1/w.w√102 + w2 = 1/w2√102 + w2
Φ = -1800 – tan-1(w/10)
W M Φ
∞ 0 -3 π/2
Ɛ ∞ -1800
Path P3 will be mirror image of P1 about Real axis.
G(Ɛ ejϴ) = 1/( Ɛ ejϴ)2(Ɛ ejϴ + 10)
Ɛ 0, ϴ = π/2 to 0 to -π/2
= 1/ Ɛ2 e2jϴ(Ɛ ejϴ + 10)
= ∞. e-j2ϴ [ -2ϴ = -π to 0 to +π ]
Path P2 will be formed by rotating through -π to 0 to +π
Path P4 S = Rejϴ R ∞ ϴ = -π/2 to 0 to +π/2
G(Rejϴ) = 1/ (Rejϴ)2(10 + Rejϴ)
= 0
N = Z – P
No poles on right half of S plane so, P = 0
N = Z – 0

Fig 16. Nyquist Plot for G(S) = k/S2(S + 10)
But from plot shown in fig 16. It is clear that number of encirclements in Anticlockwise direction. So,
N = 2
N = Z – P
2 = Z – 0
Z = 2
Hence, system unstable.
PART 2 Including poles at origin in the Nyquist Path.
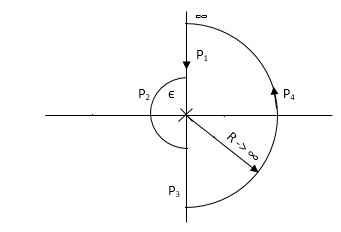
Fig 17. Nyquist Path
P1 W(∞ to Ɛ) Ɛ 0
P2 S = Ɛejϴ Ɛ 0 ϴ(+π/2 to +π to +3π/2)
P3 W(-Ɛ to -∞) Ɛ 0
P4 S = Rejϴ, R ∞, ϴ(3π/2 to 2π to +5π/2)
M = 1/W2√102 + W2 , φ = - π – tan-1(W/10)
P1 W(∞ to Ɛ)
W M φ
∞ 0 -3 π/2
Ɛ ∞ -1800
P3 (mirror image of P1)
P2 S = Ɛejϴ
G(Ɛejϴ) = 1/ Ɛ2e2jϴ(10 + Ɛejϴ)
Ɛ 0
G(Ɛejϴ) = 1/ Ɛ2e2jϴ(10)
= ∞. e-j2ϴϴ(π/2 to π to 3π/2)
-2ϴ = (-π to -2π to -3π)
P4 = 0
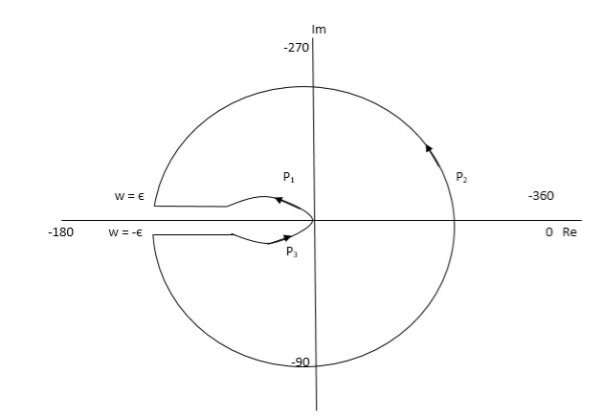
Fig 18. Nyquist Plot G(S) = k/S2(S + 10)
The plot is shown in fig 18. From the plot it is clear that there is no encirclement of -1 in Nyquist path. (N = 0). But the two poles at origin lies to the right half of S-plane in Nyquist path.(P = 2)[see path P2]
N = Z – P
0 = Z – 2
Z = 2
Hence, system is unstable.
Path P2 will be formed by rotating through -π to -2π to -3π
NOTE: The sign convention for angles is shown
Fig 19. Sign for Angle Directions
NOTE: Angles are considered –ve for anticlockwise directions and +ve for clockwise directions.
Bode Plot
In polar plot any point gives the magnitude phase of the transfer function in bode we split magnitude and  plot.
plot.
Advantages
By looking at bode plot we can write the transfer function of system
Q. G(S) = 
Substitute S = j
G(j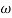 ) =
) = 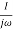
M = 
 = tan-1
= tan-1 = -900
= -900
Magnitude varies with ‘w’ but phase is constant.
MdB = +20 log10
MdB = -20 log10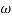
Decade frequency:
W present = 10 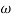 past
past
Then 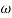 present is called decade frequency of
present is called decade frequency of 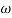 past
past
 2 = 10
2 = 10 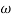 1
1
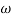 2 is decade frequency of
2 is decade frequency of  1
1
 MdB
MdB
0.0140
0.120
10 (shows pole at origin)
0-20
10-40
100-60
Slope = (20db/decade)
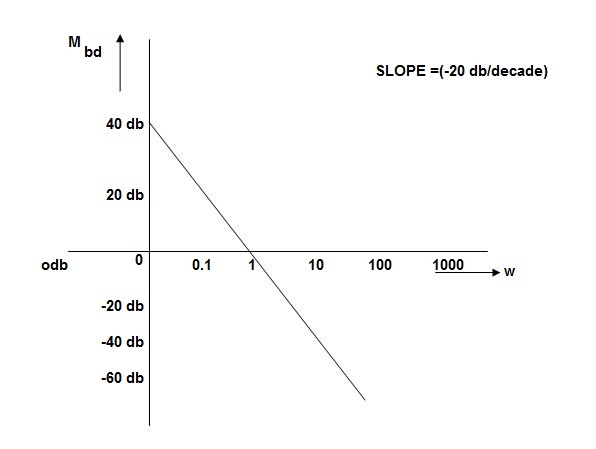
MAGNITUDE PLOT
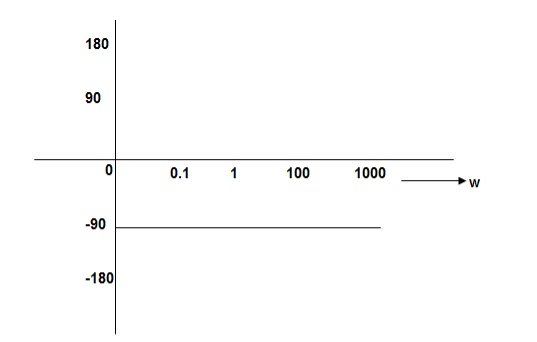
PHASE PLOT
Q.G(S) = 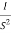
G(j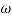 ) =
) = 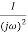
M = 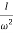 ;
;  = -1800 (-20tan-1
= -1800 (-20tan-1 )
)
MdB = +20 log 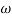 -2
-2
MdB = -40 log10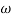
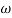 MdB
MdB
0.0180
0.140
10(pole at origin)
10-40
100-80
Slope = 40dbdecade
Q. G(S) = S
M= W
 = 900
= 900
MdB = 20 log10
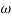 MdB
MdB
0.01-40
0.1-20
10
1020
10090
100060
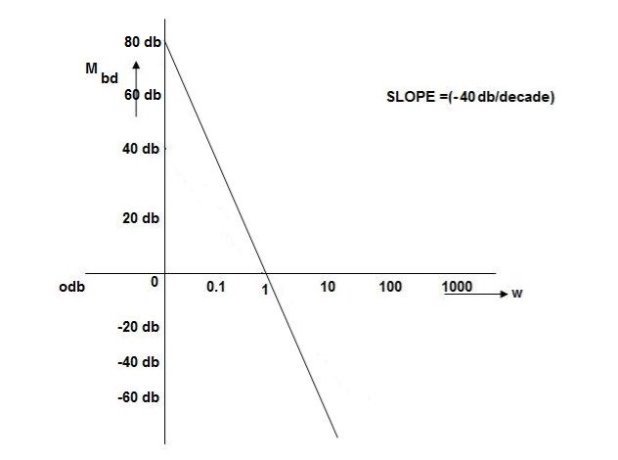
Q. G(S) = S2
M= 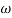 2MdB = 20 log10
2MdB = 20 log10 2
2
 = 1800 = 40 log10
= 1800 = 40 log10
WMdB
0.01-80
0.1-40
10
1040
10080
Q. (S) = 
G(j ) =
) = 
M = 
MdB = 20 log10 K-20 log10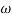
 = tan-1(
= tan-1( ) –tan-1(
) –tan-1(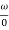 )
)
 = 0-900 = -900
= 0-900 = -900
K=1K=10 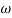 =-20 log10 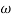 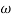 0.014060 0.12040 1020 10-200 100-40-20 |
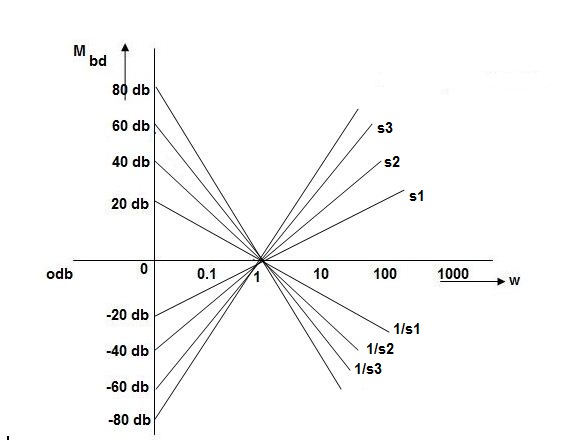
As we vary K  then plot shift by 20 log10K
then plot shift by 20 log10K
i.e adding a d.c. To a.c. Quantity
Approximation of Bode Plot:
IF poles and zeros are not located at origin
G(S) = 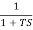
TF = 
M = 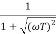
MdB = -20 log10 (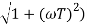
 = -tan-1
= -tan-1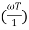
Approximation: 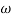 T >> 1. So, we can neglect 1.
T >> 1. So, we can neglect 1.
MdB = -20 log10
MdB = -20 log10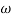 T . ;
T . ;  = -tan-1(
= -tan-1(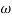 T)
T)
Approximation: 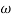 T << 1. So, we can neglecting
T << 1. So, we can neglecting 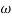 T.
T.
MdB= 0dB,  = 00
= 00
At a point both meet so equal i.e a time will come hence both approx become equal
-20 log10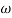 T= 0
T= 0
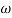 T= 1
T= 1
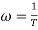 corner frequency
corner frequency
At this frequency both the cases are equal
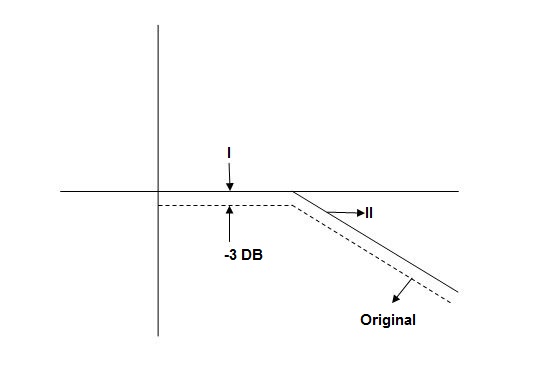
MdB = -20 log10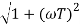
Now for 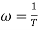
MdB = -20 log10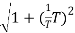
= -20 log10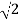
= -10 log102
MdB = 10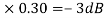
When we increase the value of 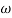 in app 2 and decrease the
in app 2 and decrease the 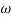 of app 1 so a RT comes when both cases are equal and hence for that value of
of app 1 so a RT comes when both cases are equal and hence for that value of 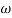 where both app are equal gives max. Error we found above and is equal to 3dB
where both app are equal gives max. Error we found above and is equal to 3dB
At corner frequency we have max error of -3dB
Gain margin (GM): The gain margin is the change in open-loop gain, expressed in decibels (dB), required at 180◦ of phase shift to make the closed-loop system unstable.
Phase margin (PM): The phase margin is the change in open-loop phase shift, required at unity gain to make the closed-loop system unstable.
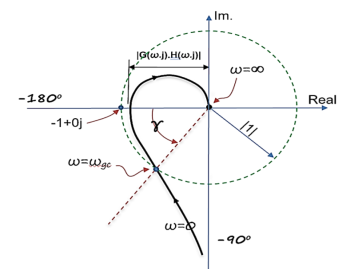
GM = 1/|G(jw)H(jw)| for w=wpc
=20log10(1/|G(jw)H(jw)|)
=-20 log10 (|G(jw)H(jw)|)
For PM refer figure
PM = 1800+ɸ
Gain crossover frequency (ωgc):
The frequency at which magnitude of G(wj)H(wj) is unity (i.e. |G(wj)H(wj)| =1) called gain frequency crossover.
ωpc > ωgc
GM & PM are stable (+ve) Stable system
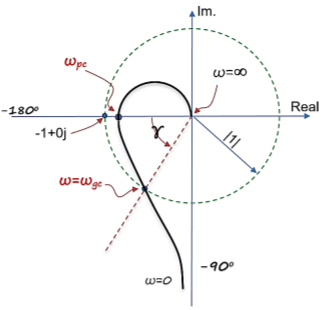
Phase crossover frequency (ωpc):
The frequency at which phase angle of G(wj)H(wj) is -180o
ωgc > ωpc GM & PM are stable (-ve) Unstable system.
Closed loop frequency response
The closed-loop frequency response reveals important information about the relative stability and the speed of response in the time-domain. For unity-gain feedback configuration (H(s)=1), the closed-loop frequency response is computed as
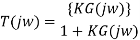
To proceed further, use rectangular form for the open loop frequency response:
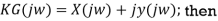
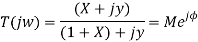
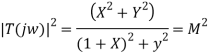
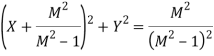
The above relation represents the equation of a circle with centre at
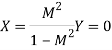
And radius; 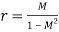
These are described as constant M circles on the
Frequency response plot
Further, as M→1, X=−1/2, which is a vertical line that separates the circles for M<1 from those with M>1.
The phase relationship similarly reveals an equation for constant phase circles:
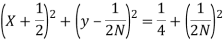
Where N = tan  . The constant phase circle is centred at X =
. The constant phase circle is centred at X =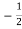 , Y=
, Y= 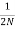 , and have radius
, and have radius
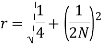
Resonance Peak
The resonance peak in the frequency response occurs at ω=ωr for ζ<0.7. For a prototype second-order system, we have

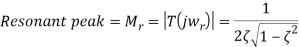
When the polar plot of the loop gain, KGH(jω), is superimposed onto the constant M and constant N contours, it reveals the magnitude peak Mr in T(jω).
The magnitude peak represents a measure of relative stability, while the resonant frequency associated with it is a measure of speed of response in the time-domain. A value of Mr=1.3 (or 2.5dB) is considered a good compromise between speed and stability.
Open loop frequency response
“Open Loop Gain” which is defined as the amplifiers output amplification without any external feedback signals connected to it and for a typical operational amplifier is about 100dB at DC (zero Hz). This output gain decreases linearly with frequency down to “Unity Gain” or 1, at about 1MHz and this is shown in the following open loop gain response curve.
Open-loop Frequency Response Curve
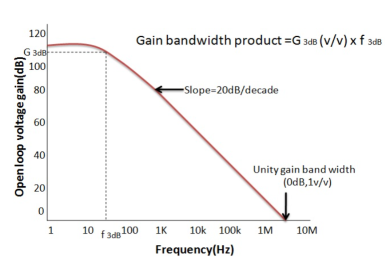
Fig 20. Frequency Response Curve
From this frequency response curve, we can see that the product of the gain against frequency is constant at any point along the curve. Also, that the unity gain (0dB) frequency also determines the gain of the amplifier at any point along the curve. This constant is generally known as the Gain Bandwidth Product or GBP. Therefore:
GBP = Gain x Bandwidth = A x BW
For example, from the graph above the gain of the amplifier at 100kHz is given as 20dB or 10, then the gain bandwidth product is calculated as:
GBP = A x BW = 10 x 100,000Hz = 1,000,000.
Similarly, the operational amplifiers gain at 1kHz = 60dB or 1000, therefore the GBP is given as:
GBP = A x BW = 1,000 x 1,000Hz = 1,000,000.
The Voltage Gain (AV) of the operational amplifier can be found using the following formula:
Av = Vout/ Vin
And in Decibels or (dB) is given as:
20 log (A) or 20 log (Vout/ Vin ) in dB
An Op- Amp Bandwidth
The operational amplifiers bandwidth is the frequency range over which the voltage gain of the amplifier is above 70.7% or -3dB (where 0dB is the maximum) of its maximum output value.
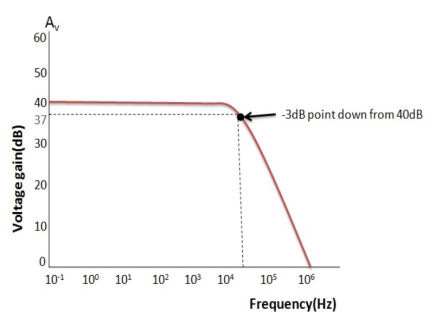
Fig 21. Frequency Response
Example-1
Using the formula 20 log (A), we can calculate the bandwidth of the amplifier as:
37 = 20 log (A) therefore, A = anti-log (37 /20) = 70.8
GBP/ A = Bandwidth, therefore, 1,000,000 / 70.8 = 14,124Hz, or 14kHz
Then the bandwidth of the amplifier at a gain of 40dB is given as 14kHz as previously predicted from the graph.
Key takeaways
“Open Loop Gain” which is defined as the amplifiers output amplification without any external feedback signals connected to it and for a typical operational amplifier is about 100dB at DC (zero Hz).
Que. G(S) = 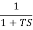
TF = 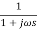
M = 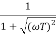
MdB = -20 log10 (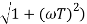 at T=2
at T=2
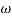 MdB
MdB
1-20 log10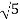
10-20 log10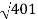
100-20 log10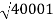
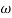 MdB
MdB =
= =
= 
0.1-20 log10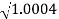 = 1.73
= 1.73  10-3
10-3
0.1-20 log10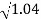 = -0.1703
= -0.1703
0.5-20 log10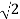 = -3dB
= -3dB
1-20 log10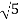 = -6.98
= -6.98
10-20 log10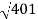 = -26.03
= -26.03
100 -20 log10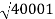 = -46.02
= -46.02
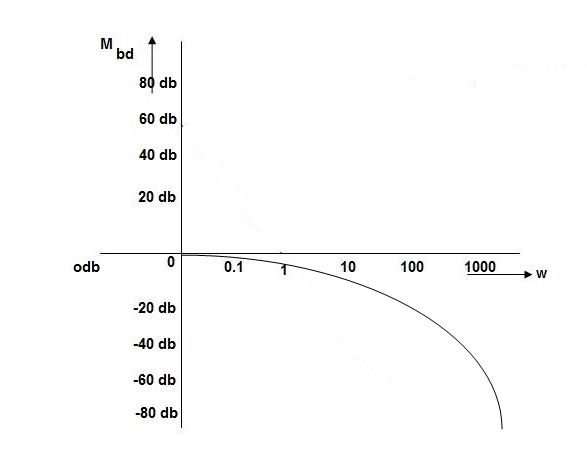
Fig 22. Magnitude Plot with approximation
Without approximation
For second order system
TF = 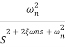
TF = 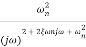
= 
= 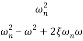
= 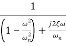
M= 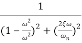
MdB= 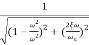
Case 1 <<
<<
 << 1
<< 1
MdB= 20 log10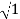 = 0 dB
= 0 dB
Case 2 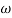 >>
>>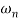
 >> 1
>> 1
MdB = -20 log10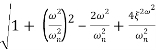
= -20 log10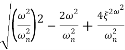
= -20 log10
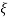 < 1
< 1 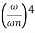 is very large so neglecting other two terms
is very large so neglecting other two terms
MdB = -20 log10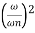
= -40 log10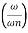
Case 3 . When case 1 is equal to case 2
-40 log10 = 0
= 0
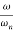 = 1
= 1
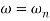
The natural frequency is our corner frequency
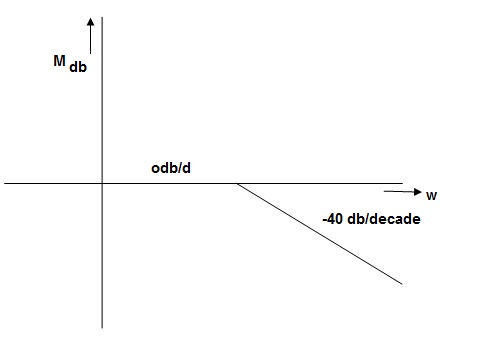
Fig 23. Magnitude Plot
Max error at 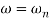 i.e at corner frequency
i.e at corner frequency
MdB = -20 log10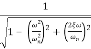
For 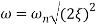
MdB = -20 log10 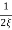
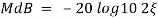 error for
error for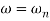
Completely the error depends upon the value of 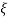 (error at corner frequency)
(error at corner frequency)
The maximum error will be
MdB = -20 log10 
M = -20 log10 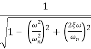
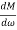 = 0
= 0
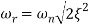
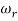 is resonant frequency and at this frequency we are getting the maximum error so the magnitude will be
is resonant frequency and at this frequency we are getting the maximum error so the magnitude will be
M = -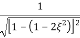 +
+ 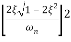
= 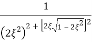
Mr =
MdB = -20 log10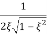
MdB = -20 log10 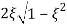
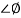 = tan-1
= tan-1
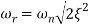
Mr = 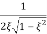
Type of system | Initial slope | Intersection |
0 | 0 dB/decade | Parallel to 0 axis |
1 | -20 dB/decade | =K1 |
2 | -40 dB/decade | =K1/2 |
3 | -60 dB/decade | =K1/3 |
. | . | 1 |
. | . | 1 |
. | . | 1 |
N | -20N dB/decade | =K1/N |
Q.1 Sketch the bode plot for transfer function
G(S) = 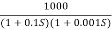
- Replace S = j

G(j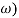 =
= 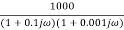
This is type 0 system. So initial slope is 0 dB decade. The starting point is given as
20 log10 K = 20 log10 1000
= 60 dB
Corner frequency 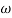 1 =
1 = 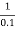 = 10 rad/sec
= 10 rad/sec
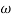 2 =
2 = 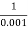 = 1000 rad/sec
= 1000 rad/sec
Slope after 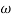 1 will be -20 dB/decade till second corner frequency i.e
1 will be -20 dB/decade till second corner frequency i.e 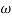 2 after
2 after 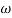 2 the slope will be -40 dB/decade (-20+(-20)) as there are poles
2 the slope will be -40 dB/decade (-20+(-20)) as there are poles
2. For phase plot
 = tan-1 0.1
= tan-1 0.1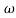 - tan-1 0.001
- tan-1 0.001 
For phase plot

100-900
200-9.450
300-104.80
400-110.360
500-115.420
600-120.00
700-124.170
800-127.940
900-131.350
1000 -134.420
The plot is shown in figure 24.
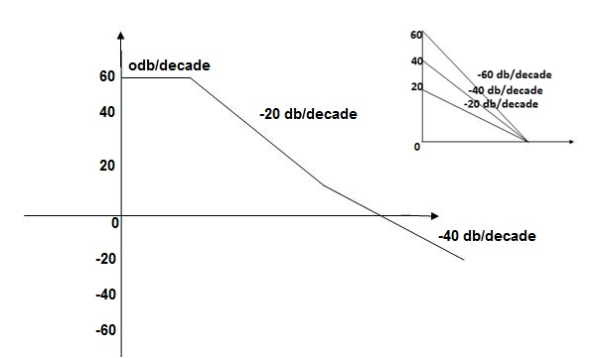
Fig 24. Magnitude Plot for G(S) = 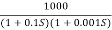
Q.2 For the given transfer function determine
G(S) = 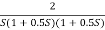
Gain cross over frequency phase cross over frequency phase mergence and gain margin
Initial slope = 1
N = 1, (K)1/N = 2
K = 2
Corner frequency
 1 =
1 = 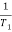 = 2 (slope -20 dB/decade
= 2 (slope -20 dB/decade
 2 =
2 =  = 20 (slope -40 dB/decade
= 20 (slope -40 dB/decade
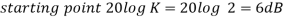
Phase
 = tan-1
= tan-1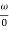 - tan-1 0.5
- tan-1 0.5 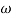 - tan-1 0.05
- tan-1 0.05 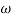
 = 900- tan-1 0.5
= 900- tan-1 0.5 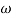 - tan-1 0.05
- tan-1 0.05 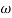

1-119.430
5-172.230
10-195.250
15-209.270
20-219.30
25-226.760
30-232.490
35-236.980
40-240.570
45-243.490
50-245.910
Finding 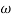 gc (gain cross over frequency
gc (gain cross over frequency
M = 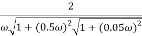
4 = 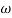 2 (
2 (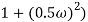 (
(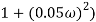
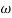 6 (6.25
6 (6.25 104) + 0.252
104) + 0.252 4 +
4 +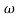 2 = 4
2 = 4
Let  2 = x
2 = x
X3 (6.25 104) + 0.252
104) + 0.252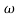 2 + x = 4
2 + x = 4
X1 = 2.46
X2 = -399.9
X3 = -6.50
For x1 = 2.46
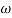 gc = 3.99 rad/sec(from plot )
gc = 3.99 rad/sec(from plot )
For phase margin
PM = 1800 - 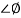
 = 900 – tan-1 (0.5×
= 900 – tan-1 (0.5× gc) – tan-1 (0.05 ×
gc) – tan-1 (0.05 × 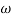 gc)
gc)
= -164.50
PM = 1800 - 164.50
= 15.50
For phase cross over frequency (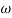 pc)
pc)
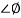 = 900 – tan-1 (0.5
= 900 – tan-1 (0.5 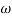 ) – tan-1 (0.05
) – tan-1 (0.05 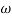 )
)
-1800 = -900 – tan-1 (0.5 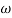 pc) – tan-1 (0.05
pc) – tan-1 (0.05 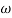 pc)
pc)
-900 – tan-1 (0.5 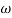 pc) – tan-1 (0.05
pc) – tan-1 (0.05 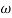 pc)
pc)
Taking than on both sides
Tan 900 = tan-1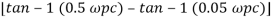
Let tan-1 0.5 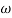 pc = A, tan-1 0.05
pc = A, tan-1 0.05 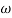 pc = B
pc = B
 = 00
= 00
 = 0
= 0
1 =0.5 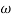 pc 0.05
pc 0.05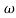 pc
pc
 pc = 6.32 rad/sec
pc = 6.32 rad/sec
The plot is shown in figure 25.
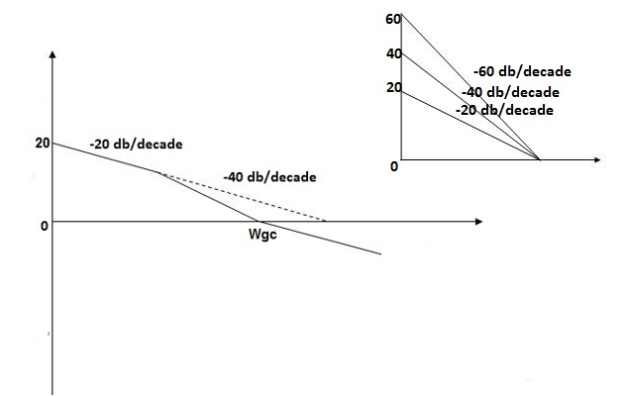
Fig 25. Magnitude Plot G(S) = 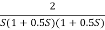
Q3. For the given transfer function
G(S) = 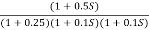
Plot the rode plot find PM and GM
T1 = 0.5  1 =
1 = 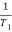 = 2 rad/sec
= 2 rad/sec
Zero so, slope (20 dB/decade)
T2 = 0.2 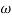 2 =
2 = 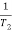 = 5 rad/sec
= 5 rad/sec
Pole, so slope (-20 dB/decade)
T3 = 0.1 = T4 = 0.1
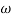 3 =
3 =  4 = 10 (2 pole) (-40 db/decade)
4 = 10 (2 pole) (-40 db/decade)
- Initial slope 0 dB/decade till
 1 = 2 rad/sec
1 = 2 rad/sec - From
 1 to
1 to 2 (i.e. 2 rad /sec to 5 rad/sec) slope will be 20 dB/decade
2 (i.e. 2 rad /sec to 5 rad/sec) slope will be 20 dB/decade - From
 2 to
2 to  3 the slope will be 0 dB/decade (20 + (-20))
3 the slope will be 0 dB/decade (20 + (-20)) - From
 3,
3, 4 the slope will be -40 dB/decade (0-20-20)
4 the slope will be -40 dB/decade (0-20-20)
Phase plot
 = tan-1 0.5
= tan-1 0.5 - tan-1 0.2
- tan-1 0.2 - tan-1 0.1
- tan-1 0.1 - tan-1 0.1
- tan-1 0.1

500-177.30
1000-178.60
1500-179.10
2000-179.40
2500-179.50
3000-179.530
3500-179.60
GM = 00
PM = 61.460
The plot is shown in figure 26.
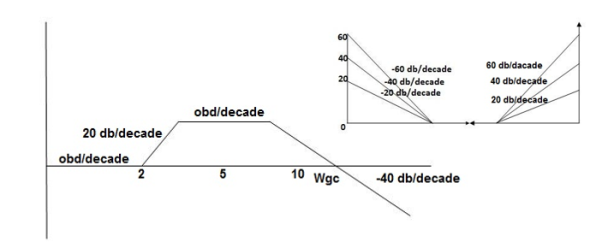

Fig 26. Magnitude and phase Plot for G(S) = 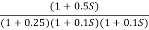
Q4. For the given transfer function plot the bode plot (magnitude plot)
G(S) = 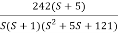
Given transfer function
G(S) = 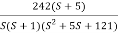
Converting above transfer function to standard from
G(S) = 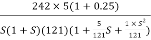
= 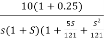
1. As type 1 system, so initial slope will be -20 dB/decade
2. Final slope will be -60 dB/decade as order of system decides the final slope
3. Corner frequency
T1 =  ,
,  11= 5 (zero)
11= 5 (zero)
T2 = 1, 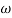 2 = 1 (pole)
2 = 1 (pole)
4. Initial slope will cut zero dB axis at
(K)1/N = 10
i.e 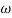 = 10
= 10
5. Finding 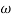 n and
n and 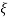
T(S) = 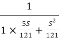
T(S)= 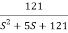
Comparing with standard second order system equation
S2+2 ns +
ns + n2
n2
 n = 11 rad/sec
n = 11 rad/sec
 n = 5
n = 5
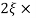 11 = 5
11 = 5
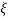 =
= 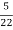 = 0.27
= 0.27
6. Maximum error
M = -20 log 2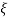
= +6.5 dB
7. As K = 10, so whole plot will shift by 20 log 10 10 = 20 dB
The plot is shown in figure 27.
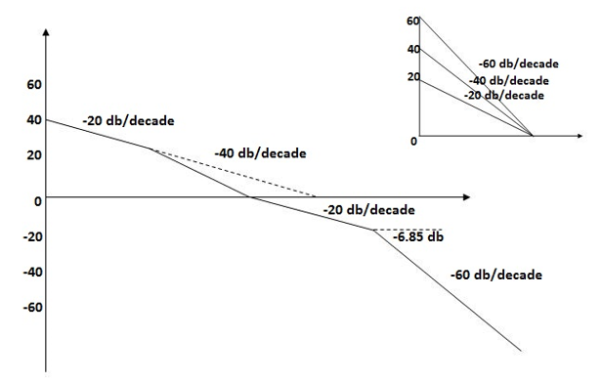
Fig 27. Magnitude Plot for G(S) = 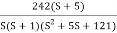
Q5. For the given plot determine the transfer function
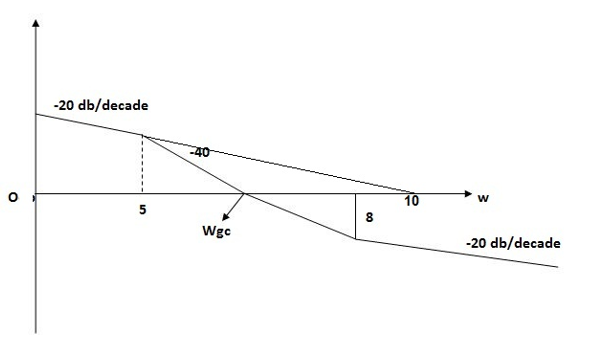
From above figure we can conclude that
1. Initial slope = -20 dB/decade so type -1
2. Initial slope alls 0 dB axis at  = 10 so
= 10 so
K1/N N = 1
(K)1/N = 10.
3. Corner frequency
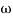 1 =
1 =  = 0.2 rad/sec
= 0.2 rad/sec
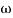 2 =
2 =  = 0.125 rad/sec
= 0.125 rad/sec
4. At 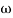 = 5 the slope becomes -40 dB/decade, so there is a pole at
= 5 the slope becomes -40 dB/decade, so there is a pole at 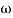 = 5 as slope changes from -20 dB/decade to -40 dB/decade
= 5 as slope changes from -20 dB/decade to -40 dB/decade
5. At 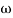 = 8 the slope changes from -40 dB/decade to -20 dB/decade hence is a zero at
= 8 the slope changes from -40 dB/decade to -20 dB/decade hence is a zero at  = 8 (-40+(+20)=20)
= 8 (-40+(+20)=20)
6. Hence transfer function is
T(S) = 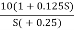
Gain Cross Over Frequency:
The frequency at which the bode plot culls the 0db axis is called Gain Cross Over Frequency.
Phase Cross Over Frequency-:
The frequency at which the phase plot culls the -1800 axis.
GM=MdB= -20 log [ G (jw)]
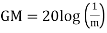 .:
.: 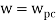
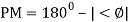 .:
.: 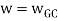
When gain cross over frequency is smaller than phase curves over frequency the system is stable and vice versa.
Key takeaway:
- More the difference between b/WPC and WGC core is the stability of the system
- If GM is below 0dB axis then take ilb +ve and stable. If GM above 0dB axis, that takes -ve
GM= ODB - 20 log M
3. The IM should also lie above -1800 for making the system (i.e. pm=+ve
4. For a stable system, GM and PM should be -ve
5. GM and PM both should be +ve more the value of GM and PM more the system is stable.
6. If Wpc and Wgc are in the same line Wpc= Wgc then the system is marginally stable. As we get GM=0dB.
References:
1. Control Systems Engineering, I.J. Nagrath, M. Gopal
2. Modern Control system (II Edition) – Katsuhiko Ogata
3. Control systems by Smarajit Ghosh (second Edition, Pearson Education)
Unit - 5
Frequency response method
The calculation of system parameters for higher order systems is difficult in time domain analysis. This can be overcome by frequency domain analysis. As the frequency response of a linear time invariant system is independent of amplitude and phase of the input test signal. The effect of noise and parameter variation in frequency domain can be easily computed.
In frequency response can be determine by calculating the phase and amplitude oof the given system transfer function. If a sinusoidal signal XG(j)sint then its amplitude will be
C(t) = XG(j)sint
= X|G(j)|  sint
sint
Magnitude = |G(j)|
Phase = G(j)
In polar form = |G(j)| 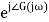
Resonant Peak (Mr): The maximum value of magnitude is known as Resonant peak. The relative stability of the system can be determined by Mr. The larger the value of Mr the undesirable is the transient response.
Resonant Frequency (Wr): The frequency at which magnitude has maximum value.
Bandwidth: The band of frequencies lying between -3db points.
Cut-off frequency –The frequency at which the magnitude is 3db below its zero frequency.
Cut-off Rate – It is the slope of the log magnitude curve near the cut off frequency.
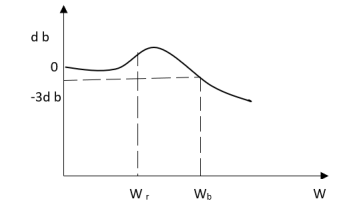
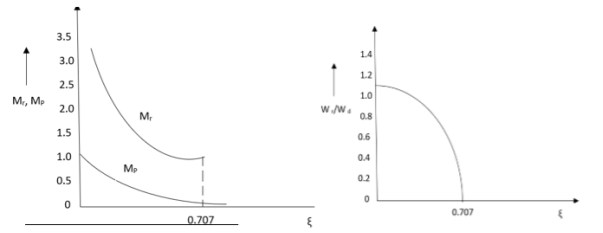
Fig 1 Frequency Domain Specification
It gives the frequency response of the system. If the transfer function is given, then from the plot number of poles and zeros can be calculated.
Polar plot of some standard functions:
# TYPE ‘O’
Ex :1T(S) = 1/S + 1
(1). For polar plot substitute S=jw.
TF = 1/1 + jw
(2). Magnitude M = 1 + 0j / 1 + jw = 1/√1 + w2
(3). Phase φ = tan-1(0)/ tan-1w = - tan-1w
WMφ
0100
10.707-450
∞0-900
The plot is shown in fig. 2(a)
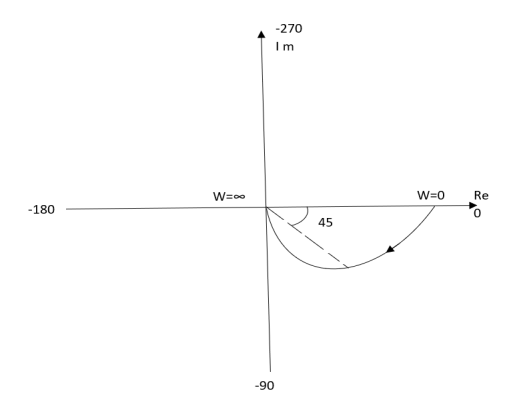
Fig 2(a) Polar Plot T(S) = 1/S + 1
Ex.2>. T(S) = 1/(S+1)(S+2)
(1). S = jw
TF = 1/(1+jw)(2+jw)
(2). M = 1/(1+jw)(2+jw) = 1/-w2 + 3jw + 2
M = 1/√1 + w2√4 + w2
(3). Φ = - tan-1 w - tan-1(w/2)
WMΦ
00.500
10.316-71.560
20.158-108.430
∞0-1800
The plot is shown in fig2(b)
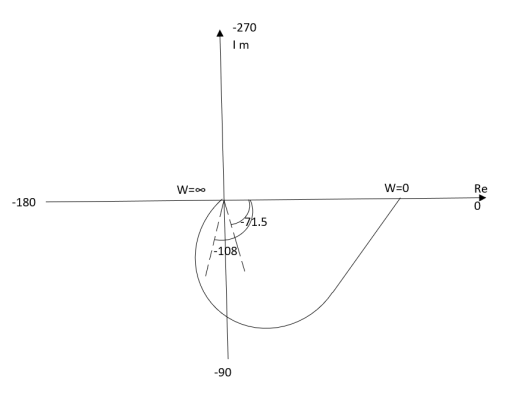
Fig2(b) Polar Plot T(S) = 1/(S+1)(S+2)
Intersection of polar plot with imaginary axis will be when real part of Transfer function = 0
M = 1/(jw + 1)(jw + 2)
= 1/-w2 + j3w + 2
TYPE ‘1’
Ex.1 T(S) = 1/S
(1). S = jw
(2). M = 1/W
(3). Φ = -tan-1(W/O) = -900
WMφ
0∞-900
11-900
20.5-900
∞0-900
The plot is shown in fig.3(a)
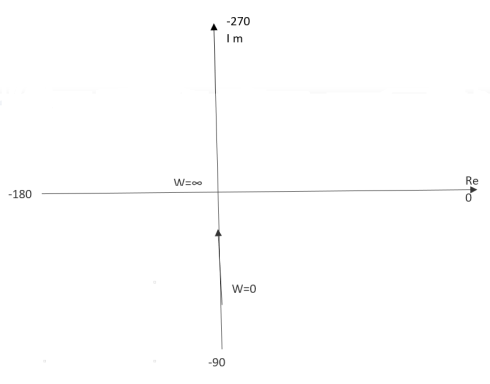
Fig 3(a) Polar Plot T(S) = 1/S
Ex.2 T(S) = 1/S2
(1). S = jw
(2). M = 1/w2
(3). Φ = -tan-1(W/O)-tan-1(W/O) = -1800
WMΦ
0∞-1800
11-1800
20.25-1800
∞0-1800
The plot is shown in fig.3(b)
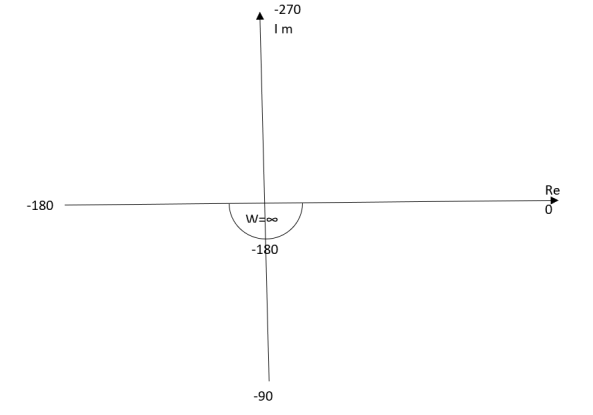
Fig 3(b) Polar Plot T(S) = 1/S2
Key takeaway
- For Polar Plot starting point depends upon type of system
- The terminating phase depends on order of the system.
TYPE 1 ORDER 2
Ex.1 T(S) = 1/S(S+1)
(1). M = 1/W√1+w2
(2). Φ = -900 - tan -1(W/T)
WMφ
0∞-900
10.707-1350
20.45-153.40
∞0-1800
The plot is shown in fig.4(a)
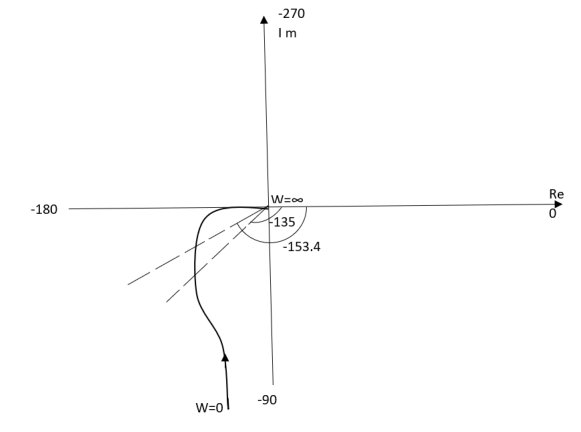
Fig 4(a) Polar Plot T(S) = 1/S(S+1)
Ex.2TYPE 2 ORDER 3
T(s) = 1/S2(S+1)
(1). M = 1/w2√1+jw
(2). Φ = -1800 – tan-1W/T
The plot is shown in fig.4(b)
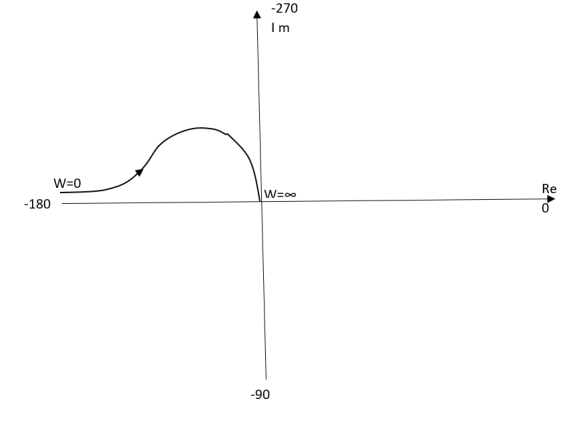
Fig 4(b) Polar Plot T(s) = 1/S2(S+1)
Nyquist Stability Criteria:
The Nyquist criteria is a semi graphical method that determines stability of CL system investigating the properties of the frequency domain plot (Polar plot), the Nyquist plot of the OLTF G(S) H(S) is represented as L(S)
L(S) = G(S)H(S)
Specially the Nyquist plot of L(S) is a plot drawn by substituting S=jw and varying the value of w as per in polar plot. In polar plot we take one sided frequency response ( 0 - ∞) in Nyquist plot we will vary the frequency in entire range possible from ( -∞ to 0 ) and (0 to ∞ )
Nyquist Criteria also gives:
(1). In addition to providing the absolute stability like other plots, the Nyquist criteria also gives information on the relative stability of a stable system and the degree of instability of an unstable system.
(2). It also gives indications on how the system stability can be improved.
(3). The Nyquist plot of G(S) H(S) is the polar plot of G(S) H(S) drawn with wider range of frequency ( -∞ to ∞ ) and along the Nyquist path.
(4). The Nyquist plot of G(S) H(S) gives information on frequency domain characteristics such as B.W, gain margin and phase margin.
Construction of Nyquist Plot
Encircled: A point or region in a complex function phase i.e. S-plane is said to be encircled by a closed path if it is found inside the path.
Assumption:
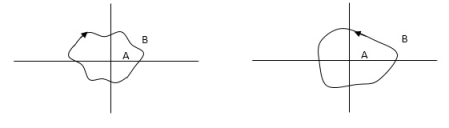
Fig 5. Encirclement
In this example point A is encircled by the closed path Y. Since, A is inside the closed path point B is not encircled by y. It is outside the path. Furthermore when the closed path Y, has a direction assign to it, encirclement, if made can be in the clockwise direction or in the anti-clockwise direction.
Point A is encircled by Y by anticlockwise direction. We can say that the region inside the path is encircled in the prescribed direction and the region outside the path is not encircled.
Enclosed:
A point or region is said to be enclosed by a closed path if it is encircled in the counter clockwise direction, or the point or region lies to the left of the path (always), when the path is traveling in the prescribed direction.
The concept of enclosure is particularly useful, if only a portion of a closed path is shown.
In this example the shaded region are
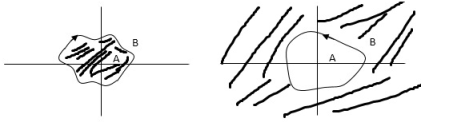
Fig 6. Enclosure
Considered to be enclosed by the closed path Y. In other words, point A is enclosed by Y in fig a. But is not enclosed by Y in fig b. And for point B it is viceversa.
No of encirclements and enclosure:
For A line is cut once
For B line is cut twice
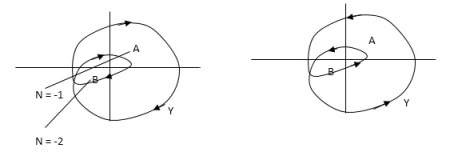
Fig 7. Encirclement and Enclosure with example
As it’s overlapping but 2 times in Same direction
When a point is encircled by a closed path Y, a no. N can be assigned to the no. Of times it is encircled. The magnitude of N can be determined by drawing an arrow around the closed path Y.
Taking an arbitrary point S, and moving around in clockwise direction and anti-clockwise direction respectively. We are getting a direction.
The path followed by S1 gives us the direction and this path which covers the total number of revolution travelled by this point S1 is N or the net angle is ‘ 2 π N ’.
For B = 2 = N for A = 1 = N
In this eg. Point A is encircled ones (or 2 π radians) by function Y and point B is encircled twice (or 4 π radians)all in clockwise direction.
In diagram b again A and B are encircled but in counter clockwise direction thus for this diagram A is enclosed one’s and B is enclosed twice.
By definition M is +ve for anticlockwise(direction) encirclement and –ve for clockwise encirclement.
OLTF G(S) = (S + Z1)(S + Z2)/(S + P1)(S + P2) H(S) = 1 - - (1)
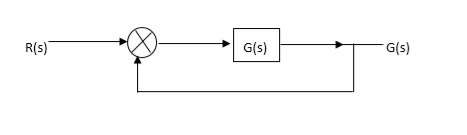
Fig 8. Unity feedback control system
CLTF G(S)/1 + G(S)
CE = 1 + G(S)
= 1 + (S + Z1)(S + Z2)/(S + P1)(S + P2)
CE = (S + P1)(S + P2) + (S + Z1)(S + Z2)/ (S + P1)(S + P2) - - (2)
Key takeaway:
# OLTF poles is equal to CE poles.
CE = (S + Z’1)( S + Z’2)/( S + P1)( S + P2) - - (3)
CLTF = G(S) –(1) / 1 + G(S) –(3)
= (S + Z1)( S + Z2) / (S + Z’1)( S + Z’2) - - (4)
# Zeros of characteristic equation is poles of CLTF (3 and 4).
For the closed loop system to be stable zeros of CE(i.e. poles of CLTF) should not be located at right half of the S-plane.
Consider a contour, which covers the entire right half of S-plane.
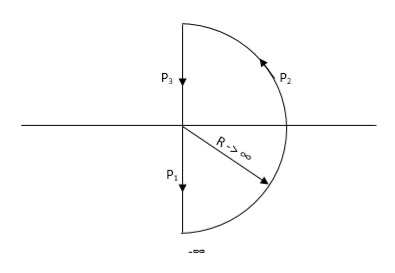
Fig 9. Contour For Right half of S-plane
P1 W(0 - ∞)
P2 RejR ∞
ϴ - π/2 to 0 to + π/2
P3 W(∞ to 0 )
If each and every point along the boundary of contour is mapped in q(S) where q(S) is 1+G(S)H(S)[CE]. The CE is drawn in S-domain. Now, as the CE : q(s) = 1 + G(S)H(S) contour is drawn into S-plane.
This q(S) contour may encircle the origin. Thus, the number of encirclement of q(S) contour with respect to origin is given by
N = Z – P
Where : Z1P zeros and poles of q(S)[CE]
N Total no of encirclement of origin
Z1P Zeros and poles of CE in the right half of S-plane
** for the CL system to be stable Z=0 always.
Important:
# Open loop System(stable): When OL system is stable P=0 i.e. no of poles on right half
N = Z – P
If P = 0
N = Z
- Now for CL system to be stable Z = 0
- N = 0
- i.e. q(s) contour should not encircle the origin.
# Open loop system(unstable): Let P = 1 i.e. one OL pole is located in right half of S-plane i.e. OLTF is unstable.
As N = Z – P
N = Z – 1
For CL system to be stable the only criteria is (Z=0) i.e.
N = -1
Which means q(S) contour should encircle the origin one’s in CW direction.
Key takeaway:
(1). When OL system is unstable then corresponding CL will be stable only when q(S) contour will encircle origin in CW direction.
(2). The no of encirclements should be equal to no of open loop poles located in right half of S-plane.
** the no of encirclements(N) can also be calculated by using G(S) contour (instead of q(S) contour) but the reference is -1+j0 instead of 0+j0 i.e. the no of encirclements should be considered w.r.t -1+j0 and not with the origin.
Explanation Mapping
q(S) = 1 + G(S)
G(S) is always given to us, so we can relate G(S) with q(S).
G(S) = q(S) – 1
But q(S) can be drawn by adding 1 real part to the q(S).
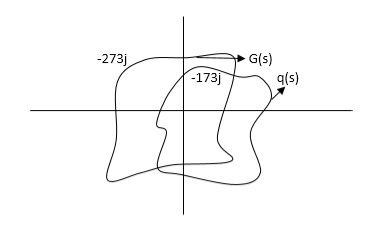
Fig 10. Mapping
G(S) given then q(S) shift to right side.
Nyquist criterion
Nyquist plots are the continuation of polar plots for finding the stability of the closed loop control systems by varying ω from −∞ to ∞. That means, Nyquist plots are used to draw the complete frequency response of the open loop transfer function.
The Nyquist stability criterion works on the principle of argument. It states that if there are P poles and Z zeros are enclosed by the ‘s’ plane closed path, then the corresponding G(s)H(s) plane must encircle the origin P−Z times. So, we can write the number of encirclements N as,
N=P-Z
Nyquist Contour: is the contour in the s-plane that includes the entire right half plane. Now, let’s consider F (s) = 1 + G(s)H(s) and the contour in the s-plane is the Nyquist contour (i.e., the entire right half plane).
Applying the Cauchy’s Principle of Argument, we should have
The number of rotations about the origin of the mapping through 1+ G(s) (H)
N = The number of zeros of 1+ G(s) (H) in the right half plane, Z - The number of poles of 1+ G(s) (H) in the right half plane, P
Please note
The mapping through G(s) (H) is virtually the same as the one through 1+ G(s) (H)
except that the contour is shifted one unit to the left. Thus, we can count rotations
about -1 instead of rotations about the origin in the above statement.
The zeros of 1+ G(s) (H) = the closed-loop poles.
The poles of 1+ G(s) (H) = the open-loop poles or the poles of 1+ G(s) (H)
Therefore
The number of rotations about -1 of the mapping through 1+ G(s) (H),
N = The number of closed-loop poles in the right half plane, Z - The number of open-loop poles in the right half plane, P
The above relationship is called the Nyquist Criterion; and the mapping through G(S)H(S) is called the Nyquist Diagram of G(S)H(S)
For a system to be stable, Z must be zero.
Sketching the Nyquist Diagram
Suppose the open-loop transfer function
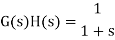
Sketch its Nyquist diagram
| | GH | | GH |
= 0 | 1 | 0 |
= | o | 
|
Cross re: = 0 = | See above | See above |
= 1 rad/s | 0.707 | 
|
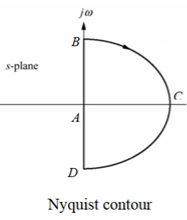
Sketching the Nyquist diagram includes two steps:
(1) Sketch the mapping of Point A to Point B, which is the same as the polar plot of frequency response for G(S)H(S).
Note that the semicircle with an infinite radius, i.e., B-C-D, is mapped to the origin if the order the denominator of G(S)H(S) is greater than the order the numerator of G(S)H(S).
(2) Sketch the mapping of Point A to Point D, which is the mirror image about the real axis of the mapping of Point A to Point B.
Plotting
Q1. For the transfer function below plot the Nyquist plot and also comment on stability?
G(S) = 1/S+1
Sol: N = Z – P ( No pole of right half of S plane P = 0 )
P = 0, N = Z
NYQUIST PATH:
P1 = W – (0 to - ∞)
P2 = ϴ( - π/2 to 0 to π/2 )
P3 = W(+∞ to 0)

Fig 11. Nyquist path
Substituting S = jw
G(jw) = 1/jw + 1
M = 1/√1+W2
Φ = -tan-1(W/I)
For P1 :- W(0 to -∞)
W M φ
0 1 0
-1 1/√2 +450
-∞ 0 +900
Path P2:
W = Rejϴ R ∞ϴ -π/2 to 0 to π/2
G(jw) = 1/1+jw
= 1/1+j(Rejϴ) (neglecting 1 as R ∞)
M = 1/Rejϴ = 1/R e-jϴ
M = 0 e-jϴ = 0
Path P3:
W = -∞ to 0
M = 1/√1+W2, φ = -tan-1(W/I)
W M φ
∞ 0 -900
1 1/√2 -450
0 1 00
The Nyquist Plot is shown in fig 12.
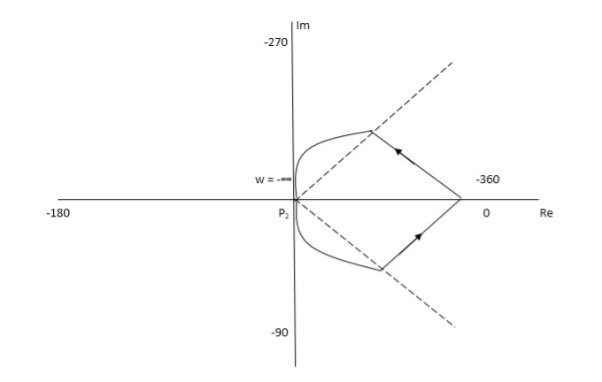
Fig 12. Nyquist Plot G(S) = 1/S+1
From plot we can see that -1 is not encircled so, N = 0
But N = Z, Z = 0
So, system is stable.
Q.2. For the transfer function below plot the Nyquist Plot and comment on stability G(S) = 1/(S + 4)(S + 5)
Soln: N = Z – P, P = 0, No pole on right half of S-plane
N = Z
NYQUIST PATH
P1 = W(0 to -∞)
P2 = ϴ(-π/2 to 0 to +π/2)
P3 = W(∞ to 0)
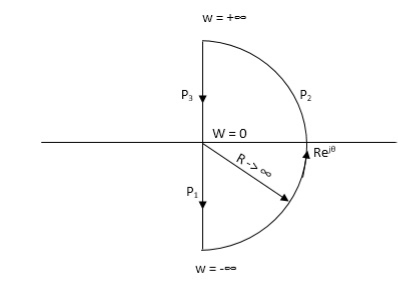
Fig 13. Nyquist Path
Path P1 W(0 to -∞)
M = 1/√42 + w2 √52 + w2
Φ = -tan-1(W/4) – tan-1(W/5)
W M Φ
0 1/20 00
-1 0.047 25.350
-∞ 0 +1800
Path P3 will be the mirror image across the real axis.
Path P2: ϴ(-π/2 to 0 to +π/2)
S = Rejϴ
G(S) = 1/(Rejϴ + 4)( Rejϴ + 5)
R∞
= 1/ R2e2jϴ = 0.e-j2ϴ = 0
The plot is shown in fig 14. From plot N=0, Z=0, system stable.
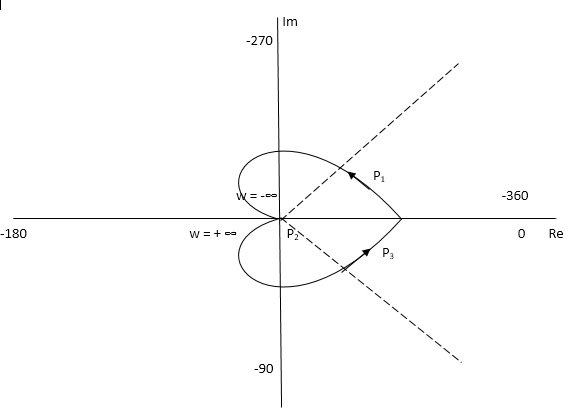
Fig 14. Nyquist Plot G(S) = 1/(S + 4)(S + 5)
Q.3. For the given transfer function, plot the Nyquist plot and comment on stability G(S) = k/S2(S + 10)?
Soln: As the poles exists at origin. So, first time we do not include poles in Nyquist plot. Then check the stability for second case we include the poles at origin in Nyquist path. Then again check the stability.
PART – 1: Not including poles at origin in the Nyquist Path.
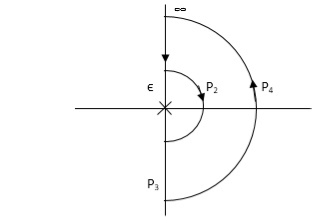
Fig 15. Nyquist Path
P1 W(∞ Ɛ) where Ɛ 0
P2 S = Ɛejϴ ϴ(+π/2 to 0 to -π/2)
P3 W = -Ɛ to -∞
P4 S = Rejϴ, R ∞, ϴ = -π/2 to 0 to +π/2
For P1
M = 1/w.w√102 + w2 = 1/w2√102 + w2
Φ = -1800 – tan-1(w/10)
W M Φ
∞ 0 -3 π/2
Ɛ ∞ -1800
Path P3 will be mirror image of P1 about Real axis.
G(Ɛ ejϴ) = 1/( Ɛ ejϴ)2(Ɛ ejϴ + 10)
Ɛ 0, ϴ = π/2 to 0 to -π/2
= 1/ Ɛ2 e2jϴ(Ɛ ejϴ + 10)
= ∞. e-j2ϴ [ -2ϴ = -π to 0 to +π ]
Path P2 will be formed by rotating through -π to 0 to +π
Path P4 S = Rejϴ R ∞ ϴ = -π/2 to 0 to +π/2
G(Rejϴ) = 1/ (Rejϴ)2(10 + Rejϴ)
= 0
N = Z – P
No poles on right half of S plane so, P = 0
N = Z – 0
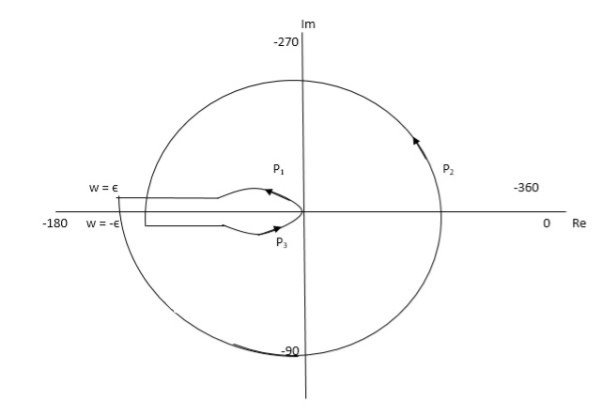
Fig 16. Nyquist Plot for G(S) = k/S2(S + 10)
But from plot shown in fig 16. It is clear that number of encirclements in Anticlockwise direction. So,
N = 2
N = Z – P
2 = Z – 0
Z = 2
Hence, system unstable.
PART 2 Including poles at origin in the Nyquist Path.
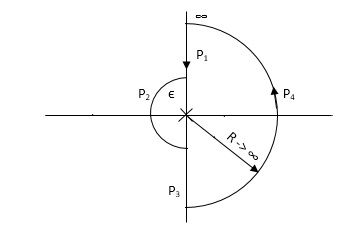
Fig 17. Nyquist Path
P1 W(∞ to Ɛ) Ɛ 0
P2 S = Ɛejϴ Ɛ 0 ϴ(+π/2 to +π to +3π/2)
P3 W(-Ɛ to -∞) Ɛ 0
P4 S = Rejϴ, R ∞, ϴ(3π/2 to 2π to +5π/2)
M = 1/W2√102 + W2 , φ = - π – tan-1(W/10)
P1 W(∞ to Ɛ)
W M φ
∞ 0 -3 π/2
Ɛ ∞ -1800
P3 (mirror image of P1)
P2 S = Ɛejϴ
G(Ɛejϴ) = 1/ Ɛ2e2jϴ(10 + Ɛejϴ)
Ɛ 0
G(Ɛejϴ) = 1/ Ɛ2e2jϴ(10)
= ∞. e-j2ϴϴ(π/2 to π to 3π/2)
-2ϴ = (-π to -2π to -3π)
P4 = 0
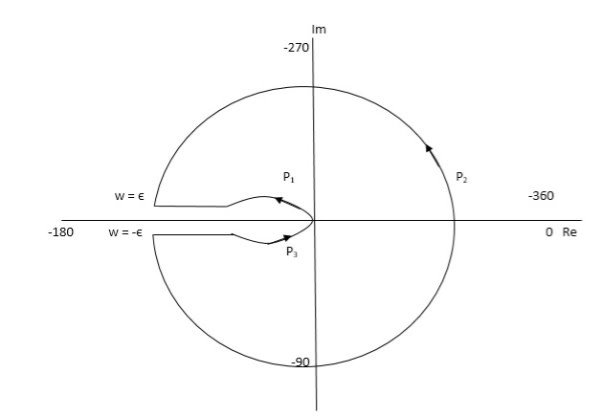
Fig 18. Nyquist Plot G(S) = k/S2(S + 10)
The plot is shown in fig 18. From the plot it is clear that there is no encirclement of -1 in Nyquist path. (N = 0). But the two poles at origin lies to the right half of S-plane in Nyquist path.(P = 2)[see path P2]
N = Z – P
0 = Z – 2
Z = 2
Hence, system is unstable.
Path P2 will be formed by rotating through -π to -2π to -3π
NOTE: The sign convention for angles is shown
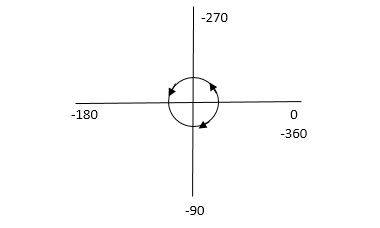
Fig 19. Sign for Angle Directions
NOTE: Angles are considered –ve for anticlockwise directions and +ve for clockwise directions.
Bode Plot
In polar plot any point gives the magnitude phase of the transfer function in bode we split magnitude and  plot.
plot.
Advantages
By looking at bode plot we can write the transfer function of system
Q. G(S) = 
Substitute S = j
G(j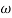 ) =
) = 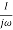
M = 
 = tan-1
= tan-1 = -900
= -900
Magnitude varies with ‘w’ but phase is constant.
MdB = +20 log10
MdB = -20 log10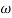
Decade frequency:
W present = 10 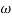 past
past
Then 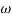 present is called decade frequency of
present is called decade frequency of 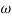 past
past
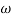 2 = 10
2 = 10  1
1
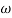 2 is decade frequency of
2 is decade frequency of  1
1
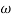 MdB
MdB
0.0140
0.120
10 (shows pole at origin)
0-20
10-40
100-60
Slope = (20db/decade)

MAGNITUDE PLOT
PHASE PLOT
Q.G(S) = 
G(j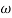 ) =
) = 
M = 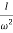 ;
;  = -1800 (-20tan-1
= -1800 (-20tan-1 )
)
MdB = +20 log  -2
-2
MdB = -40 log10
 MdB
MdB
0.0180
0.140
10(pole at origin)
10-40
100-80
Slope = 40dbdecade
Q. G(S) = S
M= W
 = 900
= 900
MdB = 20 log10
 MdB
MdB
0.01-40
0.1-20
10
1020
10090
100060
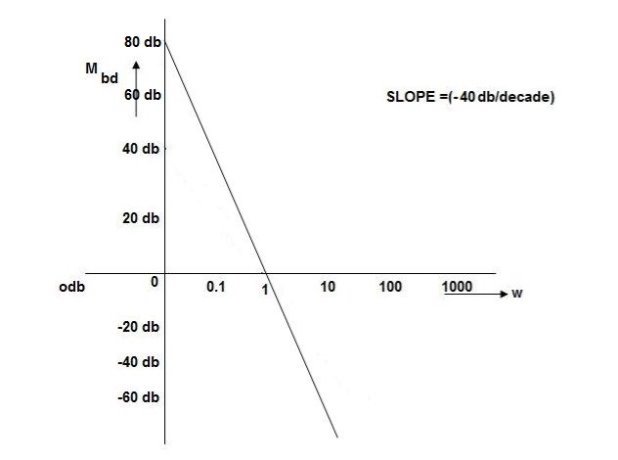
Q. G(S) = S2
M=  2MdB = 20 log10
2MdB = 20 log10 2
2
 = 1800 = 40 log10
= 1800 = 40 log10
WMdB
0.01-80
0.1-40
10
1040
10080

Q. (S) = 
G(j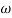 ) =
) = 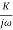
M = 
MdB = 20 log10 K-20 log10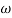
 = tan-1(
= tan-1( ) –tan-1(
) –tan-1(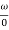 )
)
 = 0-900 = -900
= 0-900 = -900
K=1K=10  =-20 log10   0.014060 0.12040 1020 10-200 100-40-20 |
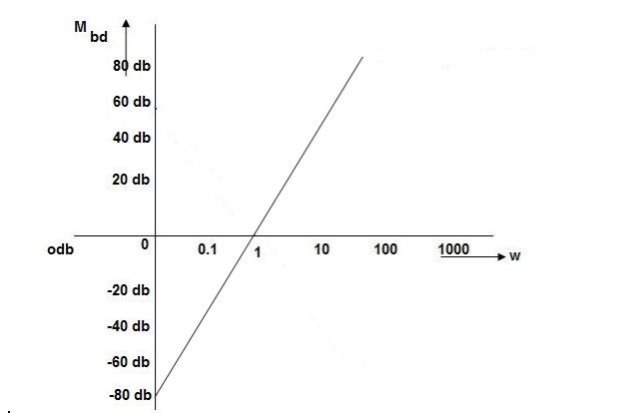
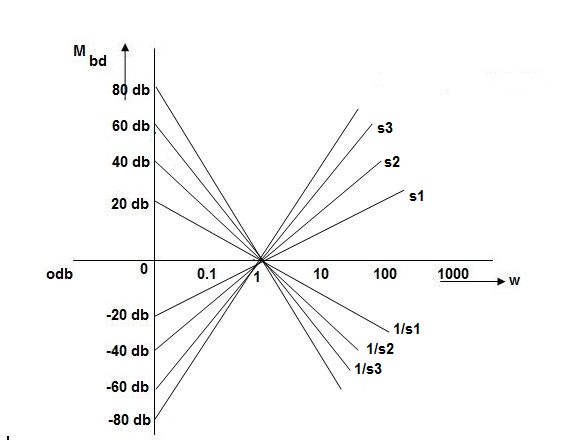
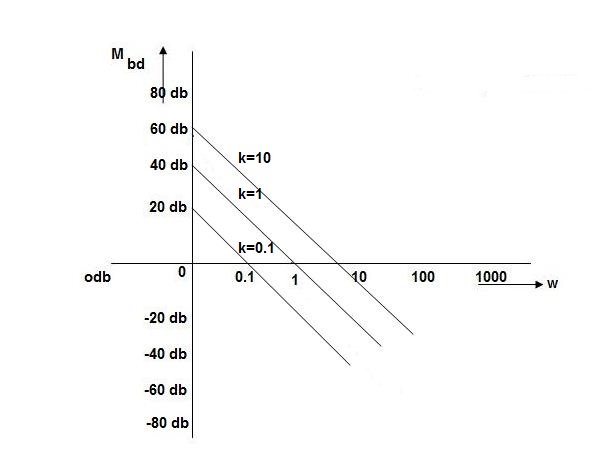
As we vary K  then plot shift by 20 log10K
then plot shift by 20 log10K
i.e adding a d.c. To a.c. Quantity
Approximation of Bode Plot:
IF poles and zeros are not located at origin
G(S) = 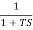
TF = 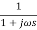
M = 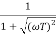
MdB = -20 log10 (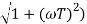
 = -tan-1
= -tan-1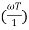
Approximation: 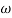 T >> 1. So, we can neglect 1.
T >> 1. So, we can neglect 1.
MdB = -20 log10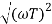
MdB = -20 log10 T . ;
T . ;  = -tan-1(
= -tan-1( T)
T)
Approximation: 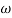 T << 1. So, we can neglecting
T << 1. So, we can neglecting 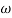 T.
T.
MdB= 0dB,  = 00
= 00
At a point both meet so equal i.e a time will come hence both approx become equal
-20 log10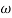 T= 0
T= 0
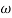 T= 1
T= 1
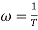 corner frequency
corner frequency
At this frequency both the cases are equal
MdB = -20 log10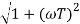
Now for 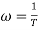
MdB = -20 log10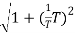
= -20 log10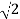
= -10 log102
MdB = 10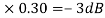
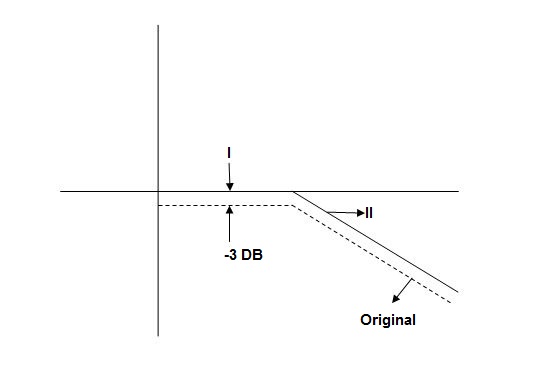
When we increase the value of  in app 2 and decrease the
in app 2 and decrease the 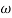 of app 1 so a RT comes when both cases are equal and hence for that value of
of app 1 so a RT comes when both cases are equal and hence for that value of  where both app are equal gives max. Error we found above and is equal to 3dB
where both app are equal gives max. Error we found above and is equal to 3dB
At corner frequency we have max error of -3dB
Gain margin (GM): The gain margin is the change in open-loop gain, expressed in decibels (dB), required at 180◦ of phase shift to make the closed-loop system unstable.
Phase margin (PM): The phase margin is the change in open-loop phase shift, required at unity gain to make the closed-loop system unstable.
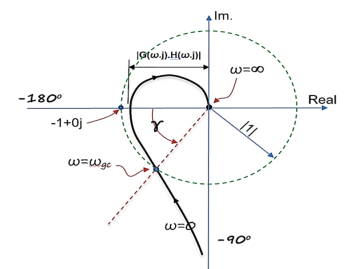
GM = 1/|G(jw)H(jw)| for w=wpc
=20log10(1/|G(jw)H(jw)|)
=-20 log10 (|G(jw)H(jw)|)
For PM refer figure
PM = 1800+ɸ
Gain crossover frequency (ωgc):
The frequency at which magnitude of G(wj)H(wj) is unity (i.e. |G(wj)H(wj)| =1) called gain frequency crossover.
ωpc > ωgc
GM & PM are stable (+ve) Stable system

Phase crossover frequency (ωpc):
The frequency at which phase angle of G(wj)H(wj) is -180o
ωgc > ωpc GM & PM are stable (-ve) Unstable system.
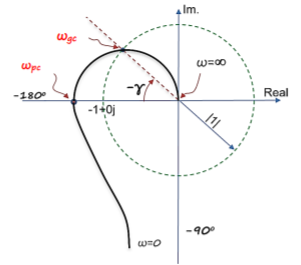
Closed loop frequency response
The closed-loop frequency response reveals important information about the relative stability and the speed of response in the time-domain. For unity-gain feedback configuration (H(s)=1), the closed-loop frequency response is computed as
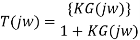
To proceed further, use rectangular form for the open loop frequency response:
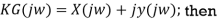
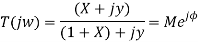
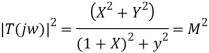
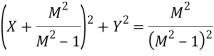
The above relation represents the equation of a circle with centre at
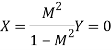
And radius; 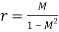
These are described as constant M circles on the
Frequency response plot
Further, as M→1, X=−1/2, which is a vertical line that separates the circles for M<1 from those with M>1.
The phase relationship similarly reveals an equation for constant phase circles:
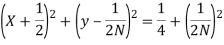
Where N = tan  . The constant phase circle is centred at X =
. The constant phase circle is centred at X = , Y=
, Y= 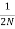 , and have radius
, and have radius
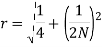
Resonance Peak
The resonance peak in the frequency response occurs at ω=ωr for ζ<0.7. For a prototype second-order system, we have
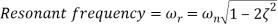

When the polar plot of the loop gain, KGH(jω), is superimposed onto the constant M and constant N contours, it reveals the magnitude peak Mr in T(jω).
The magnitude peak represents a measure of relative stability, while the resonant frequency associated with it is a measure of speed of response in the time-domain. A value of Mr=1.3 (or 2.5dB) is considered a good compromise between speed and stability.
Open loop frequency response
“Open Loop Gain” which is defined as the amplifiers output amplification without any external feedback signals connected to it and for a typical operational amplifier is about 100dB at DC (zero Hz). This output gain decreases linearly with frequency down to “Unity Gain” or 1, at about 1MHz and this is shown in the following open loop gain response curve.
Open-loop Frequency Response Curve
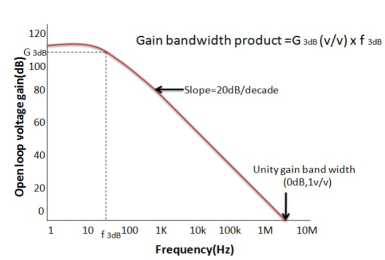
Fig 20. Frequency Response Curve
From this frequency response curve, we can see that the product of the gain against frequency is constant at any point along the curve. Also, that the unity gain (0dB) frequency also determines the gain of the amplifier at any point along the curve. This constant is generally known as the Gain Bandwidth Product or GBP. Therefore:
GBP = Gain x Bandwidth = A x BW
For example, from the graph above the gain of the amplifier at 100kHz is given as 20dB or 10, then the gain bandwidth product is calculated as:
GBP = A x BW = 10 x 100,000Hz = 1,000,000.
Similarly, the operational amplifiers gain at 1kHz = 60dB or 1000, therefore the GBP is given as:
GBP = A x BW = 1,000 x 1,000Hz = 1,000,000.
The Voltage Gain (AV) of the operational amplifier can be found using the following formula:
Av = Vout/ Vin
And in Decibels or (dB) is given as:
20 log (A) or 20 log (Vout/ Vin ) in dB
An Op- Amp Bandwidth
The operational amplifiers bandwidth is the frequency range over which the voltage gain of the amplifier is above 70.7% or -3dB (where 0dB is the maximum) of its maximum output value.
Fig 21. Frequency Response
Example-1
Using the formula 20 log (A), we can calculate the bandwidth of the amplifier as:
37 = 20 log (A) therefore, A = anti-log (37 /20) = 70.8
GBP/ A = Bandwidth, therefore, 1,000,000 / 70.8 = 14,124Hz, or 14kHz
Then the bandwidth of the amplifier at a gain of 40dB is given as 14kHz as previously predicted from the graph.
Key takeaways
“Open Loop Gain” which is defined as the amplifiers output amplification without any external feedback signals connected to it and for a typical operational amplifier is about 100dB at DC (zero Hz).
Que. G(S) = 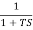
TF = 
M = 
MdB = -20 log10 (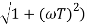 at T=2
at T=2
 MdB
MdB
1-20 log10
10-20 log10
100-20 log10
 MdB
MdB =
= =
= 
0.1-20 log10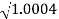 = 1.73
= 1.73  10-3
10-3
0.1-20 log10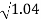 = -0.1703
= -0.1703
0.5-20 log10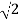 = -3dB
= -3dB
1-20 log10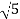 = -6.98
= -6.98
10-20 log10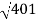 = -26.03
= -26.03
100 -20 log10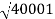 = -46.02
= -46.02
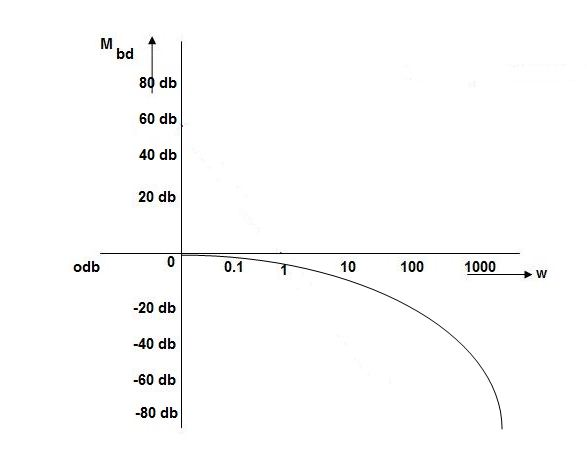
Fig 22. Magnitude Plot with approximation
Without approximation
For second order system
TF = 
TF = 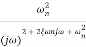
= 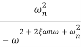
= 
= 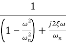
M= 
MdB= 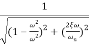
Case 1 <<
<<
 << 1
<< 1
MdB= 20 log10 = 0 dB
= 0 dB
Case 2  >>
>>
 >> 1
>> 1
MdB = -20 log10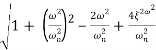
= -20 log10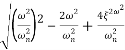
= -20 log10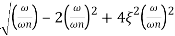
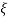 < 1
< 1  is very large so neglecting other two terms
is very large so neglecting other two terms
MdB = -20 log10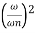
= -40 log10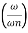
Case 3 . When case 1 is equal to case 2
-40 log10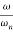 = 0
= 0
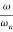 = 1
= 1
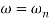
The natural frequency is our corner frequency
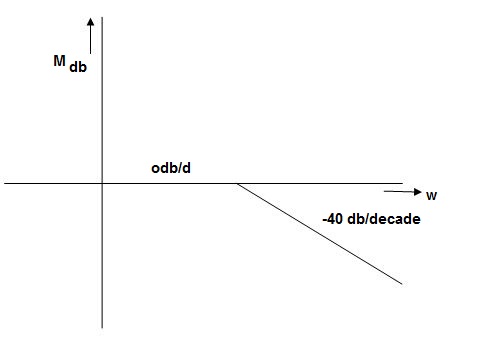
Fig 23. Magnitude Plot
Max error at 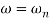 i.e at corner frequency
i.e at corner frequency
MdB = -20 log10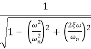
For 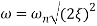
MdB = -20 log10 
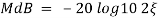 error for
error for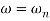
Completely the error depends upon the value of  (error at corner frequency)
(error at corner frequency)
The maximum error will be
MdB = -20 log10 
M = -20 log10 
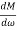 = 0
= 0
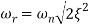
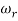 is resonant frequency and at this frequency we are getting the maximum error so the magnitude will be
is resonant frequency and at this frequency we are getting the maximum error so the magnitude will be
M = -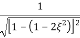 +
+ 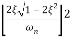
= 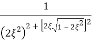
Mr =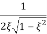
MdB = -20 log10
MdB = -20 log10 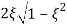
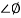 = tan-1
= tan-1
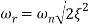
Mr = 
Type of system | Initial slope | Intersection |
0 | 0 dB/decade | Parallel to 0 axis |
1 | -20 dB/decade | =K1 |
2 | -40 dB/decade | =K1/2 |
3 | -60 dB/decade | =K1/3 |
. | . | 1 |
. | . | 1 |
. | . | 1 |
N | -20N dB/decade | =K1/N |
Q.1 Sketch the bode plot for transfer function
G(S) = 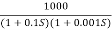
- Replace S = j
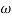
G(j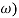 =
= 
This is type 0 system. So initial slope is 0 dB decade. The starting point is given as
20 log10 K = 20 log10 1000
= 60 dB
Corner frequency 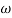 1 =
1 = 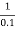 = 10 rad/sec
= 10 rad/sec
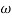 2 =
2 = 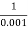 = 1000 rad/sec
= 1000 rad/sec
Slope after 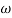 1 will be -20 dB/decade till second corner frequency i.e
1 will be -20 dB/decade till second corner frequency i.e 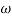 2 after
2 after 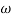 2 the slope will be -40 dB/decade (-20+(-20)) as there are poles
2 the slope will be -40 dB/decade (-20+(-20)) as there are poles
2. For phase plot
 = tan-1 0.1
= tan-1 0.1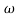 - tan-1 0.001
- tan-1 0.001 
For phase plot

100-900
200-9.450
300-104.80
400-110.360
500-115.420
600-120.00
700-124.170
800-127.940
900-131.350
1000 -134.420
The plot is shown in figure 24.
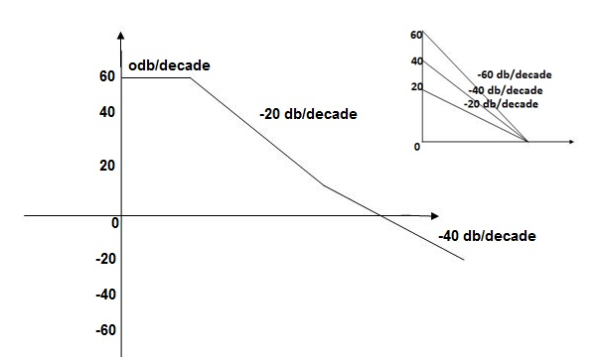
Fig 24. Magnitude Plot for G(S) = 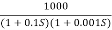
Q.2 For the given transfer function determine
G(S) = 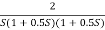
Gain cross over frequency phase cross over frequency phase mergence and gain margin
Initial slope = 1
N = 1, (K)1/N = 2
K = 2
Corner frequency
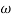 1 =
1 =  = 2 (slope -20 dB/decade
= 2 (slope -20 dB/decade
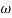 2 =
2 = 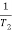 = 20 (slope -40 dB/decade
= 20 (slope -40 dB/decade
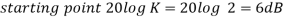
Phase
 = tan-1
= tan-1 - tan-1 0.5
- tan-1 0.5  - tan-1 0.05
- tan-1 0.05 
 = 900- tan-1 0.5
= 900- tan-1 0.5 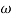 - tan-1 0.05
- tan-1 0.05 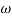
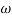

1-119.430
5-172.230
10-195.250
15-209.270
20-219.30
25-226.760
30-232.490
35-236.980
40-240.570
45-243.490
50-245.910
Finding 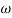 gc (gain cross over frequency
gc (gain cross over frequency
M = 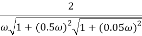
4 =  2 (
2 (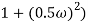 (
(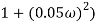
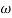 6 (6.25
6 (6.25 104) + 0.252
104) + 0.252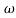 4 +
4 +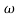 2 = 4
2 = 4
Let 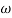 2 = x
2 = x
X3 (6.25 104) + 0.252
104) + 0.252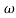 2 + x = 4
2 + x = 4
X1 = 2.46
X2 = -399.9
X3 = -6.50
For x1 = 2.46
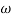 gc = 3.99 rad/sec(from plot )
gc = 3.99 rad/sec(from plot )
For phase margin
PM = 1800 - 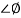
 = 900 – tan-1 (0.5×
= 900 – tan-1 (0.5× gc) – tan-1 (0.05 ×
gc) – tan-1 (0.05 × 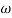 gc)
gc)
= -164.50
PM = 1800 - 164.50
= 15.50
For phase cross over frequency (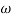 pc)
pc)
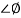 = 900 – tan-1 (0.5
= 900 – tan-1 (0.5  ) – tan-1 (0.05
) – tan-1 (0.05 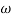 )
)
-1800 = -900 – tan-1 (0.5 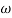 pc) – tan-1 (0.05
pc) – tan-1 (0.05 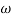 pc)
pc)
-900 – tan-1 (0.5  pc) – tan-1 (0.05
pc) – tan-1 (0.05  pc)
pc)
Taking than on both sides
Tan 900 = tan-1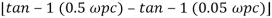
Let tan-1 0.5  pc = A, tan-1 0.05
pc = A, tan-1 0.05  pc = B
pc = B
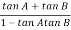 = 00
= 00
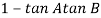 = 0
= 0
1 =0.5  pc 0.05
pc 0.05 pc
pc
 pc = 6.32 rad/sec
pc = 6.32 rad/sec
The plot is shown in figure 25.
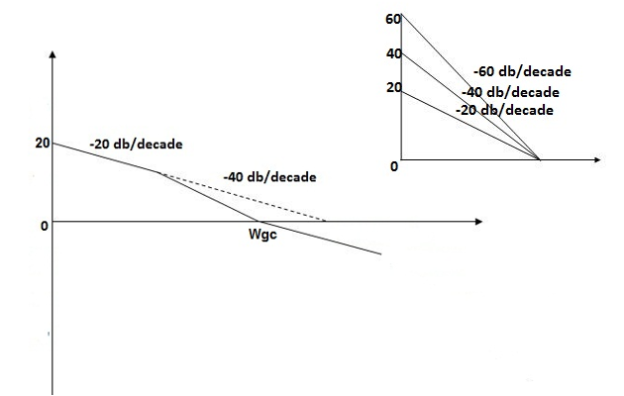
Fig 25. Magnitude Plot G(S) = 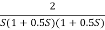
Q3. For the given transfer function
G(S) = 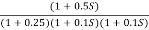
Plot the rode plot find PM and GM
T1 = 0.5  1 =
1 = 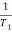 = 2 rad/sec
= 2 rad/sec
Zero so, slope (20 dB/decade)
T2 = 0.2 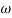 2 =
2 =  = 5 rad/sec
= 5 rad/sec
Pole, so slope (-20 dB/decade)
T3 = 0.1 = T4 = 0.1
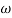 3 =
3 =  4 = 10 (2 pole) (-40 db/decade)
4 = 10 (2 pole) (-40 db/decade)
- Initial slope 0 dB/decade till
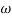 1 = 2 rad/sec
1 = 2 rad/sec - From
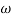 1 to
1 to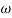 2 (i.e. 2 rad /sec to 5 rad/sec) slope will be 20 dB/decade
2 (i.e. 2 rad /sec to 5 rad/sec) slope will be 20 dB/decade - From
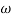 2 to
2 to  3 the slope will be 0 dB/decade (20 + (-20))
3 the slope will be 0 dB/decade (20 + (-20)) - From
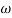 3,
3, 4 the slope will be -40 dB/decade (0-20-20)
4 the slope will be -40 dB/decade (0-20-20)
Phase plot
 = tan-1 0.5
= tan-1 0.5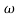 - tan-1 0.2
- tan-1 0.2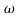 - tan-1 0.1
- tan-1 0.1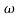 - tan-1 0.1
- tan-1 0.1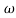

500-177.30
1000-178.60
1500-179.10
2000-179.40
2500-179.50
3000-179.530
3500-179.60
GM = 00
PM = 61.460
The plot is shown in figure 26.
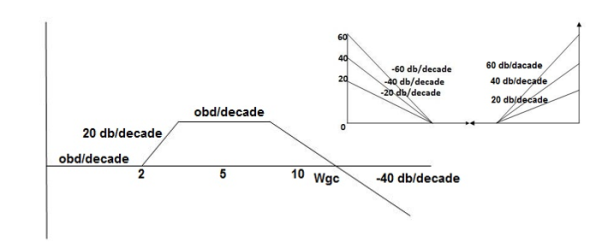
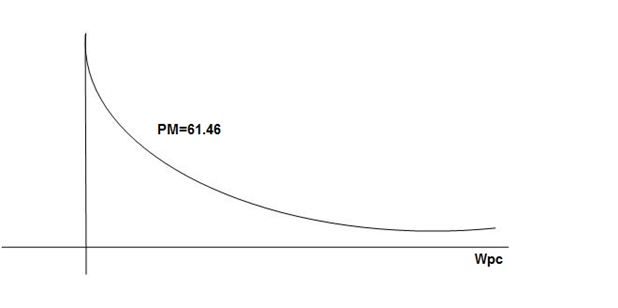
Fig 26. Magnitude and phase Plot for G(S) = 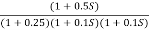
Q4. For the given transfer function plot the bode plot (magnitude plot)
G(S) = 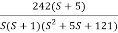
Given transfer function
G(S) = 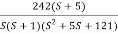
Converting above transfer function to standard from
G(S) = 
= 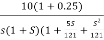
1. As type 1 system, so initial slope will be -20 dB/decade
2. Final slope will be -60 dB/decade as order of system decides the final slope
3. Corner frequency
T1 =  ,
, 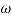 11= 5 (zero)
11= 5 (zero)
T2 = 1, 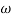 2 = 1 (pole)
2 = 1 (pole)
4. Initial slope will cut zero dB axis at
(K)1/N = 10
i.e 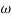 = 10
= 10
5. Finding 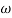 n and
n and 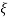
T(S) = 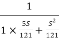
T(S)= 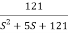
Comparing with standard second order system equation
S2+2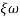 ns +
ns +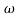 n2
n2
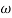 n = 11 rad/sec
n = 11 rad/sec
 n = 5
n = 5
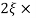 11 = 5
11 = 5
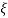 =
= 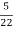 = 0.27
= 0.27
6. Maximum error
M = -20 log 2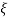
= +6.5 dB
7. As K = 10, so whole plot will shift by 20 log 10 10 = 20 dB
The plot is shown in figure 27.
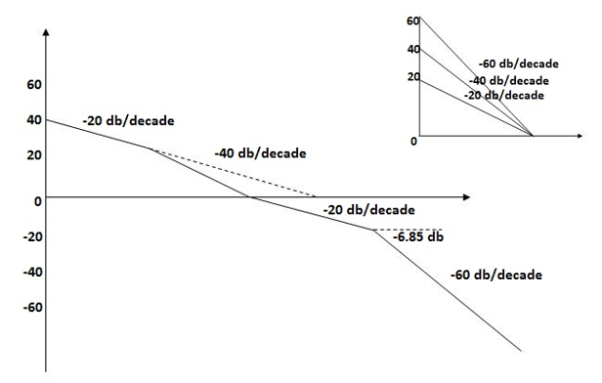
Fig 27. Magnitude Plot for G(S) = 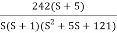
Q5. For the given plot determine the transfer function
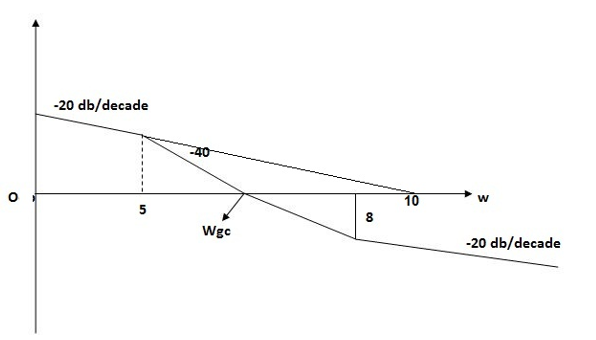
From above figure we can conclude that
1. Initial slope = -20 dB/decade so type -1
2. Initial slope alls 0 dB axis at  = 10 so
= 10 so
K1/N N = 1
(K)1/N = 10.
3. Corner frequency
 1 =
1 =  = 0.2 rad/sec
= 0.2 rad/sec
 2 =
2 =  = 0.125 rad/sec
= 0.125 rad/sec
4. At  = 5 the slope becomes -40 dB/decade, so there is a pole at
= 5 the slope becomes -40 dB/decade, so there is a pole at 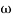 = 5 as slope changes from -20 dB/decade to -40 dB/decade
= 5 as slope changes from -20 dB/decade to -40 dB/decade
5. At 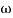 = 8 the slope changes from -40 dB/decade to -20 dB/decade hence is a zero at
= 8 the slope changes from -40 dB/decade to -20 dB/decade hence is a zero at 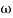 = 8 (-40+(+20)=20)
= 8 (-40+(+20)=20)
6. Hence transfer function is
T(S) = 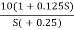
Gain Cross Over Frequency:
The frequency at which the bode plot culls the 0db axis is called Gain Cross Over Frequency.
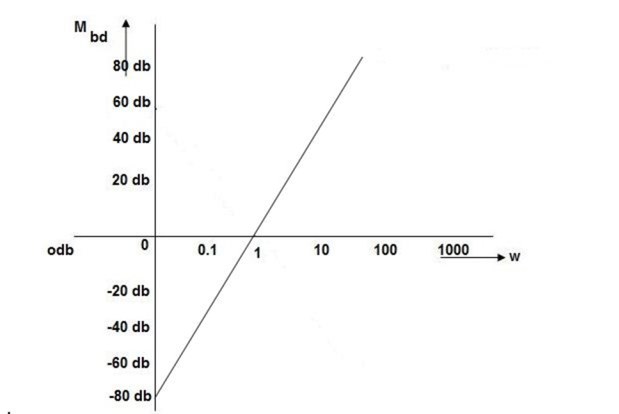
Phase Cross Over Frequency-:
The frequency at which the phase plot culls the -1800 axis.
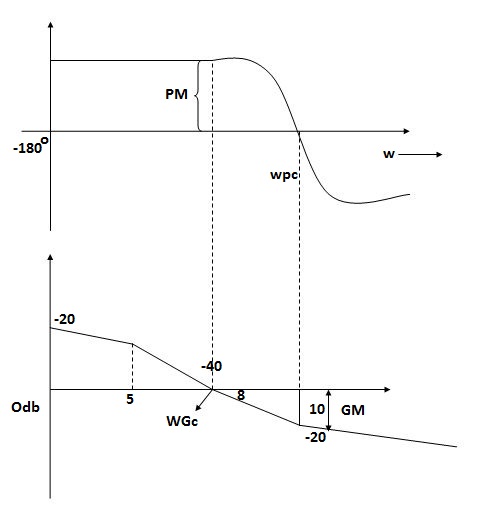
GM=MdB= -20 log [ G (jw)]
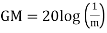 .:
.: 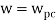
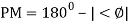 .:
.: 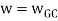
When gain cross over frequency is smaller than phase curves over frequency the system is stable and vice versa.
Key takeaway:
- More the difference between b/WPC and WGC core is the stability of the system
- If GM is below 0dB axis then take ilb +ve and stable. If GM above 0dB axis, that takes -ve
GM= ODB - 20 log M
3. The IM should also lie above -1800 for making the system (i.e. pm=+ve
4. For a stable system, GM and PM should be -ve
5. GM and PM both should be +ve more the value of GM and PM more the system is stable.
6. If Wpc and Wgc are in the same line Wpc= Wgc then the system is marginally stable. As we get GM=0dB.
References:
1. Control Systems Engineering, I.J. Nagrath, M. Gopal
2. Modern Control system (II Edition) – Katsuhiko Ogata
3. Control systems by Smarajit Ghosh (second Edition, Pearson Education)