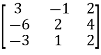UNIT 3
Matrices
A matrix is an ordered rectangular array of numbers or functions. The number or the functions are called the element or the entries of the matrix.
Notation: Let 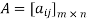 i.e. A is a matrix of order
i.e. A is a matrix of order 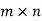 .
.
Or 
Is a matrix of order 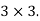 It has 3 rows and 3 columns.
It has 3 rows and 3 columns.
TYPES OF MATRICES
a) Row matrix: A matrix with only one single row and many columns can be possible.
A = 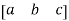
b) Column matrix: A matrix with only one single column and many rows can be possible.
A = 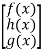
c) Square matrix: A matrix in which number of rows is equal to number of columns is called a square matrix. Thus an 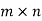 matrix is square matrix then m=n and is said to be of order n.
matrix is square matrix then m=n and is said to be of order n.
The determinant having the same elements as the square matrix A is called the determinant of the matrix A. Denoted by |A|.
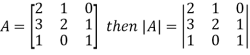
The diagonal elements of matrix A are 2, 2 and 1 is the leading and the principal diagonal.
The sum of the diagonal elements of square matrix A is called the trace of A.
A square matrix is said to be singular if its determinant is zero otherwise non-singular.
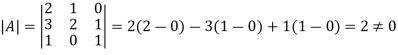
Hence the square matrix A is non-singular.
d) Diagonal matrix:A square matrix is said to be diagonal matrix if all its non diagonal elements are zero.
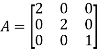
e) Scalar matrix:A diagonal matrix is said to be scalar matrix if its diagonal elements are equal.
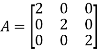
f) Identity matrix: A square matrix in which elements in the diagonal are all 1 and rest are all zero is called an identity matrix or Unit matrix.
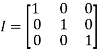
h) Null Matrix: If all the elements of a matrix are zero, it is called a null or zero matrixes.
Ex: 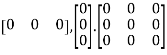 etc.
etc.
If A be any matrix, then a matrix B if it exists, such that
AB=BA=I
Is called inverse of A. The matrix A and B should both be square matrices of the same order.
|AB|=|BA|=|I|=1
i.e. both |A| and |B| must be non zero or non singular.
The inverse of a matrix A is denoted by 
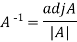
Note: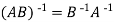
Example: let A = 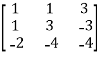
Then 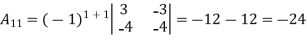
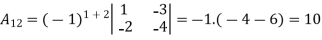
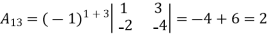
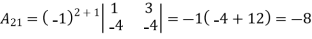
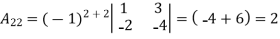
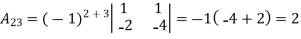
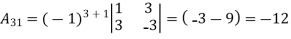
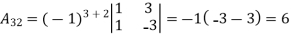
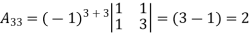
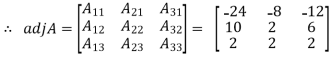
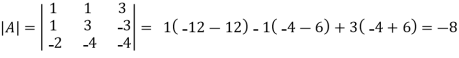
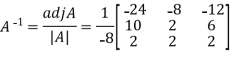
Let An+1An+1 be a matrix of order (n+1)(n+1) (i.e. it has (n+1)(n+1) rows and the same number of columns).
We can express the matrix An+1 An+1 in block form as
An+1 = 
= 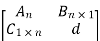
Where
An = 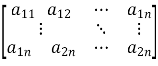
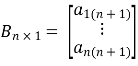
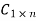 =[a(n+1)1a(n+1)2⋯a(n+1)n]d=a(n+1)(n+1)C1×n=[a(n+1)1a(n+1)2⋯
=[a(n+1)1a(n+1)2⋯a(n+1)n]d=a(n+1)(n+1)C1×n=[a(n+1)1a(n+1)2⋯
a(n+1)n]d=a(n+1)(n+1)
The subscripts used for the matrices above denote their order. Let's now assume that An is invertible and we also know its inverse. Also let I and O denote identity and zero matrices respectively (their order will be indicated by subscripts). If An+1 is also invertible then we can write the inverse A -1n+1 in the block form (in the same way as we wrote An+1) as:
A -1n+1= 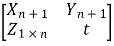
Now we have
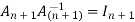
So that
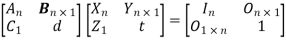
Multiplication above gives the following matrix equations:
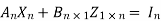
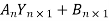 t =
t = 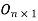
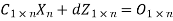
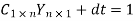
From (2) we get 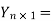 -
- 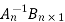 t and putting this in (4)we get
t and putting this in (4)we get
(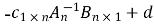 )t =1
)t =1
Or
t =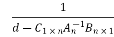
So that we have 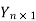 given by
given by
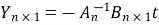
Again from (1)we have 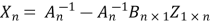 and putting this value in (3) we get
and putting this value in (3) we get
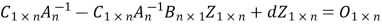
So that
(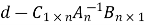 )
)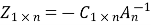
Or
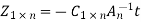
And finally
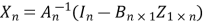
To aid the memory it makes sense to drop subscripts and then if we have
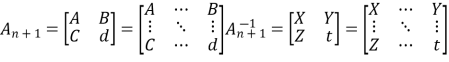
Where A is invertible square matrix of order n, B,Yare matrices of order n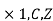 are matrices of order 1
are matrices of order 1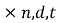 are numbers then,
are numbers then,
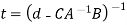
Y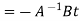
Z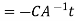
X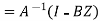
Where I is identity matrix of order n. Note that if d=C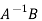 then the number t is not defined. In this case it can be easily seen that the matrix
then the number t is not defined. In this case it can be easily seen that the matrix 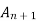 is singular and hence not invertible.
is singular and hence not invertible.
Demonstration of Partition Method
We demonstrate the method by a simple example where n=2n=2 i.e. assuming the inverse of a second order matrix we will calculate the inverse of a third order matrix. Let us then apply this method on the following matrix
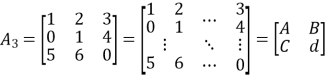
Here we have
A=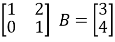 C=
C=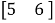 d=0
d=0
Clearly A is invertible as its determinant is 1 and the inverse is easily found by the adjoint method as
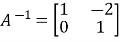
We now have
T=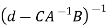
=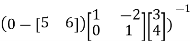
=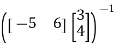
=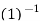
Y = 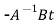
= 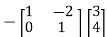
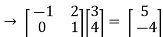
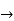 -CA-1 t
-CA-1 t
= -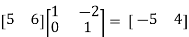
X=A-1(I-BZ)
= 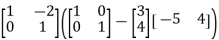
=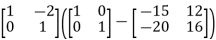
=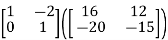 =
= 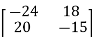
The final inverse is given by
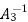 =
= 
The standard form of system of homogenous linear equation is
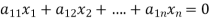
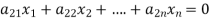 (1)
(1)
…………………………………
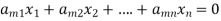
It has m number of equations and n number of unknowns.
Let the coefficient matrix be A = 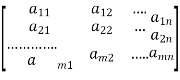
By elementary transformation we reduce the matrix A in triangular form we calculate the rank of matrix A, let rank of matrix A be r.
The following condition helps us to know the solution (if exists consistent otherwise inconsistent) of system of above equations:
- If r = n i.e. rank of coefficient matrix is equal to number of unknowns then system of equations has trivial zero solution by
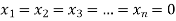
II. If r < n i.e. rank of coefficient matrix is less than the number of unknowns then system of equations has (n-r) linearly independent solutions.
In this case we assume the value of (n-r) variables and other are expressed in terms of these assumed variables. The system has infinite number of solutions.
III. If m < n i.e. number of equations is less than the number of unknowns then system of equations has non zero and infinite number of solutions.
IV. If m=n number of equations is equal to the number of unknowns then system of equations has non zero unique solution if and only if |A|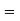 0. The solution is consistent. The |A| is called eliminant of equations.
0. The solution is consistent. The |A| is called eliminant of equations.
Example1: Solve the equations:
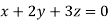
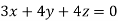
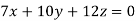
Let the coefficient matrix be A = 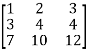
Apply 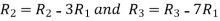
A 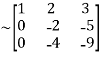
Apply 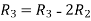
A 
Since |A|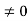 ,
, 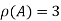
Also number of equation is m=3 and number of unknowns n=3
Since rank of coefficient matrix A = n number of unknowns
The system of equation is consistent and has trivial zero solution.
That is 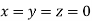
Example2: Solve completely the system of equations
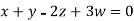
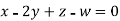
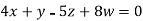
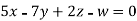
Solution: We can write the given system of equation as AX=0
Or 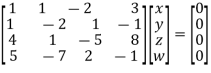
Where coefficient matrix A = 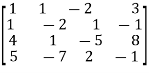
Apply 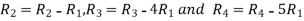
A 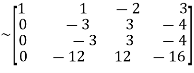
Apply 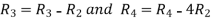
A 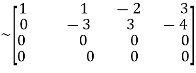 …(i)
…(i)
Since |A|=0 and also 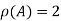 , number of equations m =4 and number of unknowns n=4.
, number of equations m =4 and number of unknowns n=4.
Here 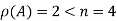
So that the system has (n-r) linearly independent solution.
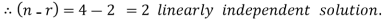
Let 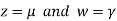
Then from equation (i) we get
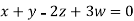
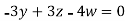
Putting 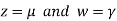
We get 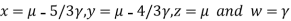 has infinite number solution.
has infinite number solution.
Example 3: find the value of λ for which the equations
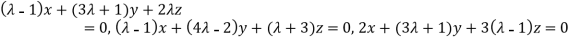
Are consistent, and find the ratio of x: y: z when λ has the smallest of these values. What happen when λ has the greatest o these values?
The system of equation is consistent only if the determinant of coefficient matrix is zero.
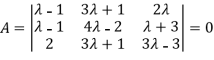
Apply 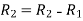
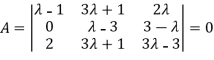
Apply 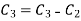
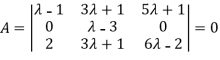
Or 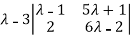 =0
=0
Or 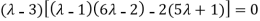
Or (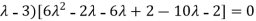
Or (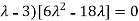
Or 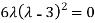
Or 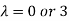 ………….(i)
………….(i)
- When λ =0, the equation become
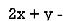 3z=0
3z=0
On solving we get
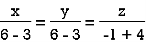
Hence x=y=z
II. When λ=3, equation become identical.
System of linear Non-homogeneous equations:
The standard form of system of non- homogenous linear equation is
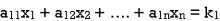
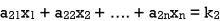 (1)
(1)
…………………………………
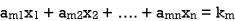
It has m number of equations and n number of unknowns.
Let the coefficient matrix be A = 
And the augmented matrix be K = 
By elementary transformation we reduce the matrix A and K in triangular form we calculate the rank of matrix A and K.
Rouche’s Theorem: The system of equations(1) is consistent if and only if the coefficient matrix A and the augmented matrix K are the same rank otherwise the system is inconsistent.
The following condition helps us to know the solution (if exists consistent otherwise inconsistent) of system of above equations:
Let the rank of matrix A is r and matrix K is r’, number of equations be m and number of unknowns be n.
- If
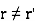 , then system of equations is inconsistent i.e. has no solution.
, then system of equations is inconsistent i.e. has no solution. - If
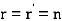 , then system of equations is consistent i.e. has unique solution.
, then system of equations is consistent i.e. has unique solution. - If
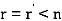 , then system of equations is consistent i.e. has infinite number solution. It has (n-r) linearly independent solutions i.e. we assume arbitrary values for (n-r) variable and rest variable are expressed in terms of these.
, then system of equations is consistent i.e. has infinite number solution. It has (n-r) linearly independent solutions i.e. we assume arbitrary values for (n-r) variable and rest variable are expressed in terms of these.
Example1: Solve the system of equations:
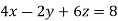
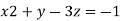
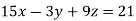
We can write the system as 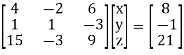
Apply 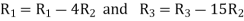
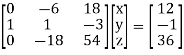
Apply 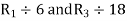
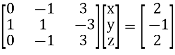
Apply 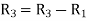
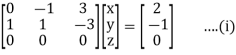
Here coefficient matrix A= 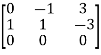 then
then 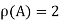
And augmented matrix K= 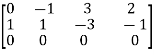 then
then 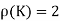
Since rank of coefficient matrix and augmented matrix are equal and is less than the number of unknowns. Therefore system have (n-r) =3-2=1, linearly independent solutions.
From equation (i) we have
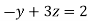
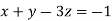
Let 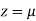
So, 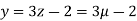
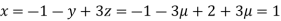
Hence 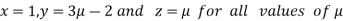
Hence system has infinite number of solutions.
Example2: Investigate for what value of λ and µ the simultaneous equations:
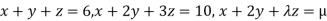
Have (i) no solution
(ii) Unique solution
(iii) An infinite number of solutions.
We can write the given system as
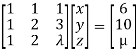
Apply 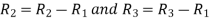
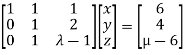
Apply 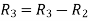
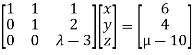
Here the coefficient matrix is A= 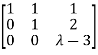 and augmented matrix K=
and augmented matrix K=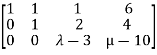
- The system has no solution if rank of coefficient matrix is not equal to rank of augmented matrix. This is possible only if
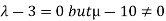 .
.
So, λ=3 and µ≠10 in case of no solution.
II. In case of unique solution we have rank of coefficient matrix, augmented matrix and number of unknowns must be equal.
This is possible only if 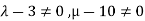 as n=3
as n=3
This implies that 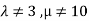 for unique solution.
for unique solution.
III. In case of infinite solution we have rank of coefficient matrix, augmented matrix are equal but less than number of unknowns
This is possible only if 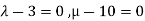 as n=3.
as n=3.
This implies that 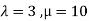 for infinite solution.
for infinite solution.
Example3: Find the values of a and b for which the equations
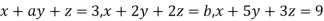
Are consistent. When will these equations have a unique solution?
We can write the above system as
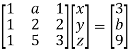
Apply 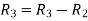
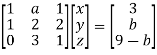
Apply 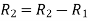
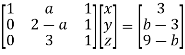
Apply 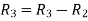
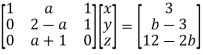
Here the coefficient matrix is A = 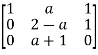
And augmented matrix K is 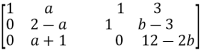
- The system has no solution if rank of coefficient matrix is not equal to rank of augmented matrix. This is possible only if
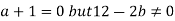 .
.
So, a=-1 and b≠6 in case of no solution
II. In case of unique solution we have rank of coefficient matrix, augmented matrix and number of unknowns must be equal.
This is possible only if 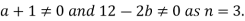
So, 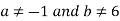 for unique solution.
for unique solution.
III. In case of infinite solution we have rank of coefficient matrix, augmented matrix are equal but less than number of unknowns
This is possible only if 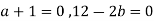 as n=3.
as n=3.
This implies that 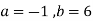 for infinite solution.
for infinite solution.
A matrix is said to be of rank r when
(i) It has at least one nonzero minor of order r,
(ii) Every minor of higher order than order r vanishes.
Equivalently the rank of a matrix is the largest order of any non vanishing minor of the matrix.
Elementary transformation n of a matrix:
- The interchange of any two rows (columns).
- The multiplication of any row (column) by a nonzero number.
- The addition of a constant multiple of the elements of any row(column)to the corresponding elements of any other row(column).
Echelon form of a matrix:
The echelon form of a matrix consist of row echelon form and any matrix can be reduced into row echelon form with help of elementary transformation. The row echelon form consists of:
- The first non zero in each row i.e. leading element is 1.
- Each leading entry is in a column to the right of the leading entry of the previous row.
- Rows with all zero elements, if any, are below to the rows with non zeros entries.
Example: 
Example1: Find the rank of the following matrices?
Let A = 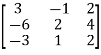
Applying 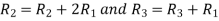
A 
Applying 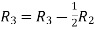
A 
Applying 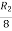
A 
Applying 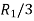
A 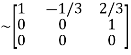
It is clear that minor of order 3 vanishes but minor of order 2 exists as 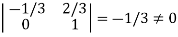
Hence rank of a given matrix A is 2 denoted by 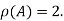
2. 
Let A = 
Applying 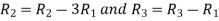

Applying 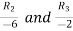
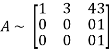
Applying 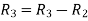
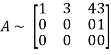
The minor of order 3 vanishes but minor of order 2 non zero as 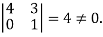
Hence the rank of matrix A is 2 denoted by 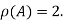
3. 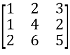
Let A = 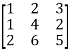
Apply 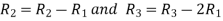

Apply 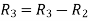

Apply 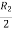
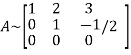
It is clear that the minor of order 3 vanishes where as the minor of order 2 is non zero as 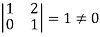
Hence the rank of given matrix is 2 i.e. 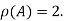
The standard form of system of homogenous linear equation is
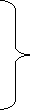
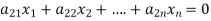 (1)
(1)
…………………………………
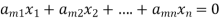
It has m number of equations and n number of unknowns.
Let the coefficient matrix be A = 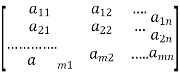
By elementary transformation we reduce the matrix A in triangular form we calculate the rank of matrix A, let rank of matrix A be r.
The following condition helps us to know the solution (if exists consistent otherwise inconsistent) of system of above equations:
V. If r = n i.e. rank of coefficient matrix is equal to number of unknowns then system of equations has trivial zero solution by
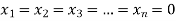
VI. If r < n i.e. rank of coefficient matrix is less than the number of unknowns then system of equations has (n-r) linearly independent solutions.
In this case we assume the value of (n-r) variables and other are expressed in terms of these assumed variables. The system has infinite number of solutions.
VII. If m < n i.e. number of equations is less than the number of unknowns then system of equations has non zero and infinite number of solutions.
VIII. If m=n number of equations is equal to the number of unknowns then system of equations has non zero unique solution if and only if |A|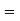 0. The solution is consistent. The |A| is called eliminant of equations.
0. The solution is consistent. The |A| is called eliminant of equations.
Example1: Solve the equations:
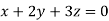
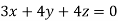
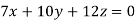
Let the coefficient matrix be A = 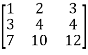
Apply 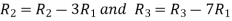
A 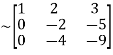
Apply 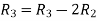
A 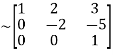
Since |A|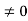 ,
, 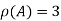
Also number of equation is m=3 and number of unknowns n=3
Since rank of coefficient matrix A = n number of unknowns
The system of equation is consistent and has trivial zero solution.
That is 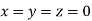
Example2: Solve completely the system of equations
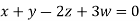
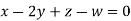
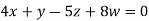
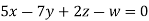
Solution: We can write the given system of equation as AX=0
Or 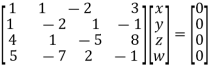
Where coefficient matrix A = 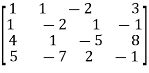
Apply 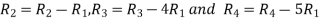
A 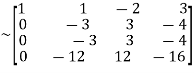
Apply 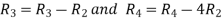
A 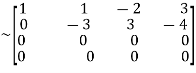 …(i)
…(i)
Since |A|=0 and also 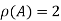 , number of equations m =4 and number of unknowns n=4.
, number of equations m =4 and number of unknowns n=4.
Here 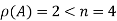
So that the system has (n-r) linearly independent solution.
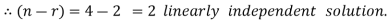
Let 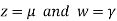
Then from equation (i) we get
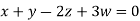
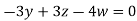
Putting 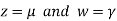
We get 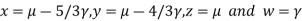 has infinite number solution.
has infinite number solution.
Example 3: find the value of λ for which the equations
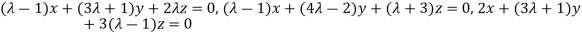
Are consistent, and find the ratio of x: y: z when λ has the smallest of these values. What happen when λ has the greatest o these values?
The system of equation is consistent only if the determinant of coefficient matrix is zero.
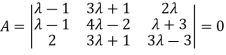
Apply 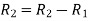
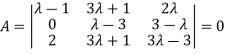
Apply 
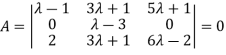
Or 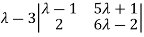 =0
=0
Or 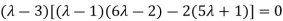
Or (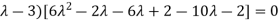
Or (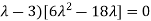
Or 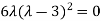
Or 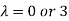 ………….(i)
………….(i)
III. When λ =0, the equation become 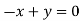
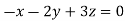
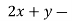 3z=0
3z=0
On solving we get
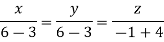
Hence x=y=z
IV. When λ=3, equation become identical.