UNIT 4
First Order Differential Equations
A differential equation is a linear differential equation if it can be expressed in the following form
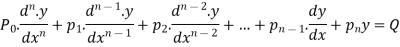
Where
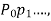and Q are either constants or functions of a independent variable x
Thus ,if a differential equation when expressed in the form of a polynomial involves the derivatives and also the co-efficient of the various terms are either constants or functions of the independent variable,then it is said to be differential equation .otherwise it is non-linear equation.
A non-linear differential equation contains the following:
- If the degree is more than one
- Any of the differential co-efficient has exponent more than one.
- Exponent of the dependent variable is more than one
- Products containg dependent variable and its diferential co-effficients are present
Linear differential equation of first order:
The general form of a linear differential equation of first order is
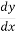+ Py =Q ....(1)
Where p and Q are functions of x(or constants)
Multiplying both sides of eq(1) by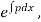 
we get
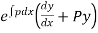=Q
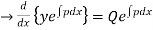
On integrating on both sides w.r.t.x., we get
.....(2)
Therefore eq(2) can also be written as y(I.F)=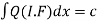
Example 1:
The equation of the curve passing through the origin and satisfying the equation
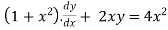is
Solution:
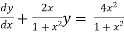
It is the linear equation of the form
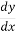+ Py =Q
Here p=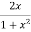
and Q=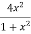 
I.F = 
the general solution is given by
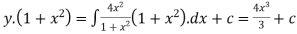
But it passes through(0,0) ,therefore c=0, hence the curve is
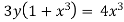
Example 2:
Find the solution for the following differential equation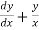 
=
Solution:
The given D.E is of the form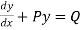 
SO I.F is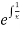 
=
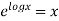
Hence the required solution is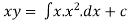 
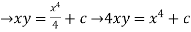
Example 3:
Find the solution for the following D.E
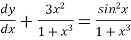
Solution:
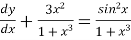
Here p=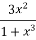 
I.F =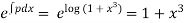 
Thus the solution is,
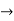
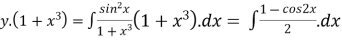
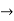
Differential equations of reducible to linear form (Bernouli’s differential equations)
The differential equations of the type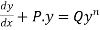 
.....(1)
Where P and Q are constants or functions of x alone and n is a constant other than zero or unity ,can be reduced to thelinear form by dividing by yn and then yn+1=v,as below
Dividing eq(1) by yn on both the sides we get.,
By putting y-n+1 =v so that (-n+1)y-n.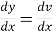
we get
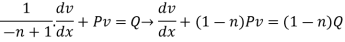
Which is a linear differential equation.
Example 1:
Solve the following D.E
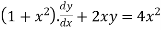
Solution:
It is the linear equation of the form 
Dividing the given D.E on both sides by (1+x2)
So we get,
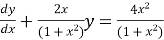
Now we have P= 
and Q=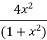 
It is in the linear equation of the form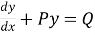 
I.F =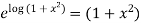
The required reduced linear equation is,
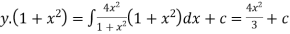
But it passes through(0,0) therefore c=0,hence the curve is 3y(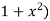
=4x3
Example 2:
Solve the D.E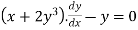 
Solution:
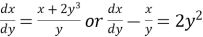, which is a linear equation of the form
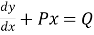
So I.F is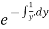 
and the general solution is,
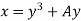
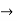
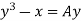
Where A can be positive or negative.
Exact differential equations:
A differential equation of type
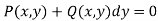is an exact differential equation if there exists a function of two variables u(x,y) with continuous partial derivatives such that,
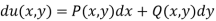
The general solution of an exact equation is given by
U(x,y)=c
Where c is an arbitrary constant.
Test for exactness
Let functions P(x,y) and Q(x,y) have continuous partial derivatives in a certain domain D
The differential equation P(x,y)dx+Q(x,y)dy =0 is an exact equation if
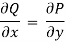
Algorithm in solving an exact equation:
*check for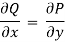 
*Then we write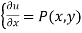 
and
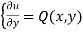
*integrating the first equation w.r.to x
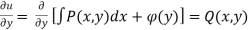
*from here we get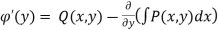 
*By integrating the above expression we get
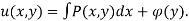
*The general solution of the exact differential equation is given by,
u(x,y)=c.
Example 1:
Solve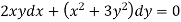 
Solution:
The given equation is exact because the partial derivatives are the same:
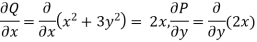
We have the following system of equations ,
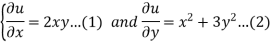
By integrating equation 1 w.r.to x.,
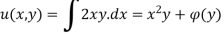
Substituting this expression for u(x,y) in eq(2) we get,
By integrating the above equation we get an unknown function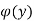 
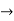
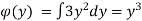
Then the general equation is,
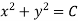,where c is an arbitrary constant.
Example 2:
Solve the given D.E and test for convergence: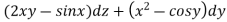 
Solution:
Test for exactness:
Consider,
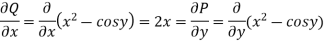
We have the following system of equations ,
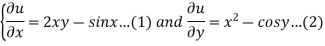
By integrating equation 1 w.r.to x.,
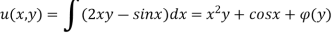
Substituting this expression for u(x,y) in eq(2) we get,
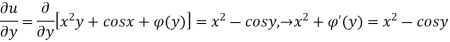
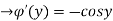
By integrating the above equation we get an unknown function 
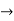
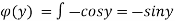
Then the general equation is,
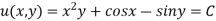
First Order Differential Equations Solutions
Usually, there are two methods considered to solve the linear differential equation of first order.
- Using Integrating Factor
- Method of variation of constant
Let us discuss each method one by one to get the solutions for differential equations of the first order.
Integrating Factor
If a linear differential equation is written in the standard form:
y’ + a(x)y = 0
Then, the integrating factor is defined by the formula
u(x) = exp (∫a(x) dx)
Multiplying the integrating factor u(x) on the left side of the equation that converts the left side into the derivative of the product y(x) u(x).
The general solution of the differential equation is expressed as follows:
y=∫u(x) f(x)dx +Cu(x)
Where C is an arbitrary constant.
Method of Variation of a Constant
This method is similar to the integrating factor method. Finding the general solution of the homogeneous equation is the first necessary step.
y’ + a(x)y = 0
The general solution of the homogeneous equation always contains a constant of integration C. We can replace the constant C with a certain unknown function C(x). When substituting this solution into the non-homogeneous differential equation, we can be able to determine the function C(x). This approach of the algorithm is called the method of variation of a constant. However, both methods lead to the same solution.
Properties of First-order Differential Equations
The Linear first-order differential equation possesses the following properties.
- It does not have any transcendental functions like trigonometric functions and logarithmic functions.
- The products of y and any of its derivatives are not present.
Applications of First-order Differential Equation
Some of the applications which use the first-order differential equation are as follows:
- Newton’s law of cooling
- Growth and decay
- Orthogonal trajectories
- Electrical circuits
- Falling Body Problems
- Dilution Problems
Example:
Solve the given D.E y’-y-ex =0
Solution:
Given y’-y-xex=0
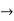y’-y=xex
Using the integrating factor
u(x)=
General solution is,
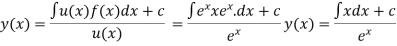
Higher order differential equations:
Here is a brief listing of the topics
Basic Concepts for nth Order Linear Equations – In this section we’ll start the chapter off with a quick look at some of the basic ideas behind solving higher order linear differential equations. Included will be updated definitions/facts for the Principle of Superposition, linearly independent functions and the Wronskian.
Linear Homogeneous Differential Equations – In this section we will extend the ideas behind solving 2nd order, linear, homogeneous differential equations to higher order. As we’ll most of the process is identical with a few natural extensions to repeated real roots that occur more than twice. We will also need to discuss how to deal with repeated complex roots, which are now a possibility. In addition, we will see that the main difficulty in the higher order cases is simply finding all the roots of the characteristic polynomial.
Undetermined Coefficients – In this section we work a quick example to illustrate that using undetermined coefficients on higher order differential equations is no different that when we used it on 2nd order differential equations with only one small natural extension.
Variation of Parameters – In this section we will give a detailed discussion of the process for using variation of parameters for higher order differential equations. We will also develop a formula that can be used in these cases. We will also see that the work involved in using variation of parameters on higher order differential equations can be quite involved on occasion.
Laplace Transforms – In this section we will work a quick example using Laplace transforms to solve a differential equation on a 3rd order differential equation just to say that we looked at one with order higher than 2nd. As we’ll see, outside of needing a formula for the Laplace transform of y‴, which we can get from the general formula, there is no real difference in how Laplace transforms are used for higher order differential equations.
Systems of Differential Equations – In this section we’ll take a quick look at extending the ideas we discussed for solving 2×2 systems of differential equations to systems of size 3×3. As we will see they are mostly just natural extensions of what we already know who to do. We will also make a couple of quick comments about 4×4 systems.
Series Solutions – In this section we are going to work a quick example illustrating that the process of finding series solutions for higher order differential equations is pretty much the same as that used on 2nd order differential equations.
Example 1:
Solve the differential equation y’’’+2y’’-y’-2y=0
Solution:
The corresponding characteristic equation is,
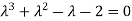
Solving it, we find the roots
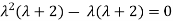
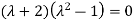
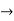
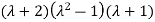=0
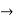
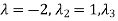=-1
The general solution for the differential equation is
Y(x)= 
Where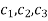 
are arbitrary constants.
Example 2:
Solve the equation y’’’+11y’-5y=0
Solution:
The characterstic equation of the give D.E is
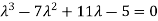
Here one of the root is 
then factorising the term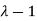 
from the equation we obtain
(
(
(
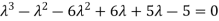
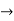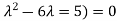
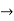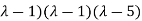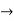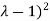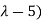=0
(
(
=0
Thus the equation has two roots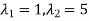 
Hence the general equation of the D.E is
Y(x)=(
Where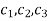 
are arbitrary constants.
Example 3:
To find the general solution of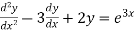 
Solution:
The characteristic equation is r2 -3r+2 =0
The factors are (r-1)(r-2)=0
r=1or r=2
Hence the general solution is A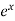
+B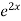
So in this case the fundamental solutions and their derivatives are as follows:
Y1(x) = ex
Y1’(x) = ex
Y2(x) =e2x
Y2’(x) =2.e2x
Example 4:
Find the general solution of the following D.E
-y=2
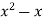-3
Solution :
Consider ,
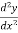-y=0
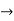The characteristic equation is r2 -1 =0
The factors are (r-1)(r+1)=0
r= 1or-1
Hence the general solution is A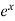
+B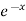
Y1(x) = ex
Y1’(x) =ex
Y2(x) =e-x
Y2’(x) =-e-x
Introduction
In “real-world,” there are many physical quantities that can be represented by functions. Involving only one of the four variables e.g., (x, y, z, t). Equations involving highest order derivatives of order one = 1st order differential equations. Examples Function σ(x) = the stress in a uni – axial stretched tapered metal rod .
Function v(x) =the velocity of fluid flowing a straight channel with varying cross-section.
Solution Method of First Order ODEs Solution of Linear (Homogeneous Equation)
Typical form of the equation
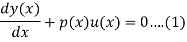
The solution u(x) in eq(1) is given by,
U(x) =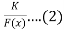
Where k= constant to be determined by given condition and the function F(x) has the form:
F(x)=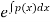 
...(3)
In which p(x) is given in differential equation.
Type 2
Solution Method of First Order ODEs Solution of Linear (Non-Homogeneous Equation)
Typical form of the equation
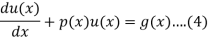
The appearance of g(x) in eq(4) tends to non-homogenous
The solution u(x) in eq(4) is given by,
U(x) =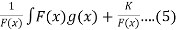
Where k= constant to be determined by given condition and the function F(x) has the form:
F(x)=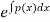 
Some important terms to be considered to solve the electrical circuit problems:
*If a current i(t) is flowing through a resistor R ohms, then the voltage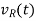 
across
*the resistor is given by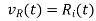 
*for an inductor of L Hentry, the voltage-current relationship is given by
*For a capacity of c farad, the voltage current relationship is given by
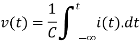
Example:
Finding the optimal current of an electrical circuit (RL circuits) in which the initial condition is i=0 at t=0
Solution:
By Kirchhoff voltage law(KVL) method, we get
The differential equation for the RL circuit will be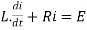 
In which initial conditions are i=0 at t=0
The standard form of the equation is,
Dividing the differential equation by L to obtain
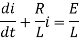
The integrating factor is
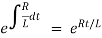
Multiplying the above equation with standard form gives rise to
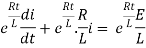
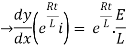
By applying integration on both sides we get
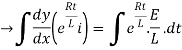
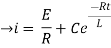
Now applying i=0 at t-0 gives us
0=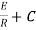
C=-
NOW
i=
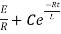
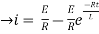
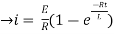= t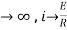 
Therefore by finding current of the RL circuits is i=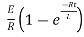
Hence we complete the solution by first order differential equation of first order and even several types of networking circuits and fluid mechanics uses this metod.
