Unit - 1

Fundamentals of Digital Circuit

1.1 Number System

A digital system understands positional number system where there are few symbols called digits and these symbol represents different values depending on their position in the number.

A value of the digit is determined by using

• The digit
• Its position
• The base of the number system

Decimal Number System

• Its the system that we use in our daily life. It has a base 10 and uses 10 digits from 0 to 9.
• Here, the successive positions towards the left of the decimal point represent units, tens, hundreds, thousands and so on.
• Each and every position represents a specific power of the base (10). For example, the decimal number 4321 consists of the digit 1 in the units position, 2 in the tens position, 3 in the hundreds position, and 4 in the thousands position, and its value can be written as

(1×1000) + (2×100) + (3×10) + (4×l)

(1×103) + (2×102) + (3×101) + (4×l00)

1000 + 200 + 30 + 1

1234

• As a computer programmer, we should understand the following number systems used in computers.

Binary Number System

• It uses two digits 0 and 1.
• It is also called as base 2 number system.
• Here, each position in any binary number represents a power of the base (2). Example: 23
• The last position represents a y power of the base (2). Example: 2y where y represents the last position.

Example

Binary Number: 101112

Calculating the Decimal Equivalent of binary number −

Note: 101112 is normally written as 10111.

Octal Number System

• It consists of eight digits 0, 1,2,3,4,5,6,7.
• It is also named as base 8 number system.
• Here each position represents a power of the base (8). Example: 82
• The last position represents a y power of the base (8). Example: 8y where y represents the last position.

Example

Octal Number − 125758

Calculating Decimal Equivalent −

Note: 125758 is normally written as 12575 in octal.

Hexadecimal Number System

• It uses 10 digits starting from 0,1,2,3,4,5,6,7,8,9 and 6 letters A,B,C,D,E,F.
• These letters represents numbers as A = 10, B = 11, C = 12, D = 13, E = 14, F = 15.
• It is also known as base 16 number system.
• Here each position represents a power of the base (16). Example 161.
• The last position represents a y power of the base (16). Example: 16y where y represents the last position.

Example −

Hexadecimal Number: 19FDA16

Calculating Decimal Equivalent −

Note − 19FDA16 is normally written as 19FDA in hexa decimal.

Key Takeaways:

      Binary number system: 0 and 1

      Decimal number system: 0 to 9

      Octal number system: 0 to 7

      Hexa Decimal number system: 0 to 9 and A to F

1.2 Boolean Algebra

The three basic laws of Boolean Algebra are:

• Commutative law
• Associative law
• Distributive law

Commutative Law

• The logical operation carried between two Boolean variables when gives the same result irrespective of the order the two variables, then that operation is said to be Commutative. The logical OR & logical AND operations between x & y are shown below

x + y = y + x

x.y = y.x

• The symbol ‘+’ and ‘.’ indicates logical OR operation and logical AND operation.
• Commutative law holds good for logical OR & logical AND operations.

Associative Law

• If a logical OR operation of any two Boolean variables is performed first and then the same operation is performed with the remaining variable providing the same result, then that operation is said to be Associative. The logical OR & logical AND operations of x, y & z are:

x + (y + z) = (x + y) + z

x.(y.z) = (x.y).z

• Associative law holds good for logical OR & logical AND operations.

Distributive Law

• If a logical OR operation of any two Boolean variables is performed first and then AND operation is performed with the remaining variable, then that logical operation is said to be Distributive. The distribution of logical OR & logical AND operations between variables x, y & z are :

x.(y + z) = x.y + x.z

x + (y.z) = (x + y).(x + z)

• Distributive law holds good for logical OR and logical AND operations.
• These are the Basic laws of Boolean algebra and we can verify them by substituting the Boolean variables with ‘0’ or ‘1’.

1.3 Logic Gates and their truth tables

AND gate

It is a digital circuit that consists of two or more inputs and a single output which is the logical AND of all those inputs. It is represented with the symbol ‘.’.

The following is the truth table of 2-input AND gate.

Here A, B are the inputs and Y is the output of two input AND gate.

If both inputs are ‘1’, then only the output, Y is ‘1’. For remaining combinations of inputs, the output, Y is ‘0’.

The figure below shows the symbol of an AND gate, which is having two inputs A, B and one output, Y.

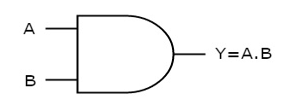
Fig: AND gate (ref. 1)

Timing Diagram:

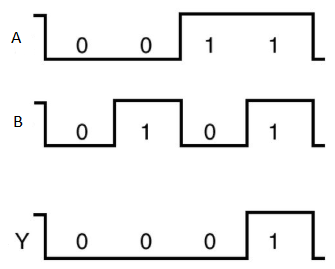
OR gate

It is a digital circuit which has two or more inputs and a single output which is the logical OR of all those inputs. It is represented with the symbol ‘+’.

The truth table of 2-input OR gate is:

Here A, B are the inputs and Y is the output of two input OR gate.

When both inputs are ‘0’, then only the output, Y is ‘0’. For remaining combinations of inputs, the output, Y is ‘1’.

The figure below shows the symbol of an OR gate, which is having two inputs A, B and one output, Y.

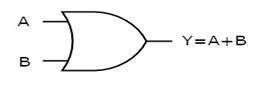
Fig.: OR gate (ref. 1)

Timing Diagram:

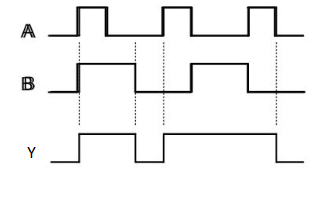
NOT gate

It is a digital circuit that has one input and one output. Here the output is the logical inversion of input. Hence, it is also called as an inverter.

The truth table of NOT gate is:

Here A and Y are the corresponding input and output of NOT gate. When A is ‘0’, then, Y is ‘1’. Similarly, when, A is ‘1’, then, Y is ‘0’.

The figure below shows the symbol of NOT gate, which has one input, A and one output, Y.

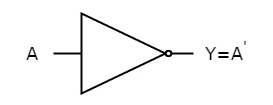
Fig: NOT gate (ref. 1)

Timing Diagram:

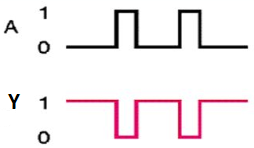
Universal gates

• NAND & NOR gates are known as universal gates.
• We can implement any Boolean function by using NAND gates and NOR gates alone.

NAND gate

It is a digital circuit which has two or more inputs and single output and it is the inversion of logical AND gate.

The truth table of 2-input NAND gate is:

Here A, B are the inputs and Y is the output of two input NAND gate. When both inputs are ‘1’, then the output, Y is ‘0’. If at least one of the input is zero, then the output, Y is ‘1’. This is just the inverse of AND operation.

The image shows the symbol of NAND gate:

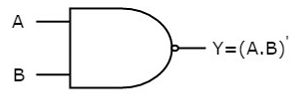
Fig.: NAND gate (ref. 1)

NAND gate works same as AND gate followed by an inverter.

Timing Diagram:

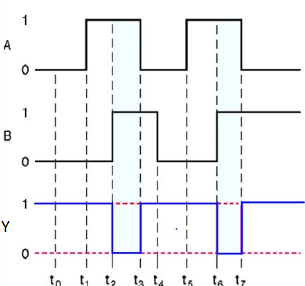
NOR gate

It is a digital circuit that has two or more inputs and a single output which is the inversion of logical OR of all inputs.

The truth table of 2-input NOR gate is:

Here A and B are the two inputs and Y is the output. If both inputs are ‘0’, then the output is ‘1’. If any one of the input is ‘1’, then the output is ‘0’. This is exactly opposite to two input OR gate operation.

The symbol of NOR gate is:

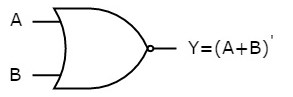
Fig.: NOR gate (ref. 1)

NOR gate works exactly same as that of OR gate followed by an inverter.

Timing Diagram:

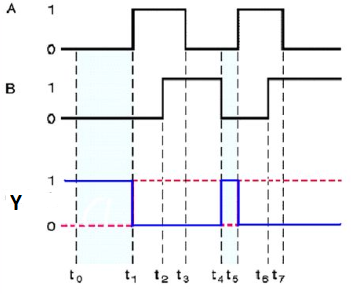
Special Gates

Ex-OR gate

It stands for Exclusive-OR gate. Its function varies when the inputs have even number of ones.

The truth table of 2-input Ex-OR gate is:

Here A, B are the inputs and Y is the output of two input Ex-OR gate. The output (Y) is zero instead of one when both the inputs are one.

Therefore, the output of Ex-OR gate is ‘1’, when only one of the two inputs is ‘1’. And it is zero, when both inputs are same.

The symbol of Ex-OR gate is as follows:

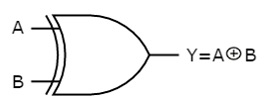
Fig.: XOR gate (ref. 1)

It is similar to that of OR gate with an exception for few combination(s) of inputs. Hence, the output is also known as an odd function.

Timing Diagram:

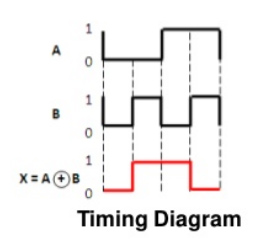
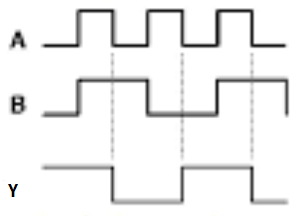
Ex-NOR gate

It stands for Exclusive-NOR gate. Its function is same as that of NOR gate except when the inputs having even number of ones.

The truth table of 2-input Ex-NOR gate is:

Here A, B are the inputs and Y is the output. It is same as Ex-NOR gate with the only modification in the fourth row. The output is 1 instead of 0, when both the inputs are one.

Hence the output of Ex-NOR gate is ‘1’, when both inputs are same and 0, when both the inputs are different.

The symbol of Ex-NOR gate is:

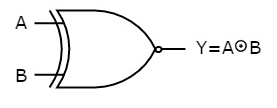
Fig.: XNOR gate (ref. 1)

It is similar to NOR gate except for few combination(s) of inputs. Here the output is ‘1’, when even number of 1 is present at the inputs. Hence is also called as an even function.

Timing Diagram:

1.4 D Morgan’s Laws

De Morgan’s theorem

• It is useful in finding the complement of Boolean function.
• It states that “The complement of logical OR of at least two Boolean variables is equal to the logical AND of each complemented variable”.
• It can be represented using 2 Boolean variables x and y as

(x + y)’ = x’. y’

• The dual of the above Boolean function is

(x.y)’ = x’ + y’

• Therefore, the complement of logical AND of the two Boolean variables is equivalent to the logical OR of each complemented variable.
• Similarly, De Morgan’s theorem can be applied for more than 2 Boolean variables also.

Numerical

Find the complement of the Boolean function,

f = p’q + pq’.

Solution:

Using De Morgan’s theorem, (x + y)’ = x’. y’ we get

⇒ f’ = (p’q)’. (pq’)’

Then by second law, (x.y)’ = x’ + y’ we get

⇒ f’ = {(p’)’ + q’}. {p’ + (q’)’}

Then by using, (x’)’=x we get

⇒ f’ = {p + q’}. {p’ + q}

⇒ f’ = pp’ + pq + p’q’ + qq’

Using x.x’=0 we get

⇒ f = 0 + pq + p’q’ + 0

⇒ f = pq + p’q’

Therefore, the complement of Boolean function, p’q + pq’ is pq + p’q’.

1.5 k-map representation (SOP & POS forms)

K map

• Karnaugh map method or K-map method is the pictorial representation of the Boolean equations and Boolean manipulations are used to reduce the complexity in solving them. These can be considered as a special or extended version of the ‘Truth table’.
• Karnaugh map can be explained as “An array containing 2k cells in a grid like format, where k is the number of variables in the Boolean expression that is to be reduced or optimized”. As it is evaluated from the truth table method, each cell in the K-map will represent a single row of the truth table and a cell is represented by a square.
• The cells in the k-map are arranged in such a way that there are conjunctions, which differ in a single variable, are assigned in adjacent rows. The K-map method supports the elimination of potential race conditions and permits the rapid identification.
• By using Karnaugh map technique, we can reduce the Boolean expression containing any number of variables, such as 2-variable Boolean expression, 3-variable Boolean expression, 4-variable Boolean expression and even 7-variable Boolean expressions, which are complex to solve by using regular Boolean theorems and laws.

Minimization with Karnaugh Maps and advantages of K-map:

• K-maps are used to convert the truth table of a Boolean equation into minimized SOP form.
• Easy and simple basic rules for the simplification.
• The K-map method is faster and more efficient than other simplification techniques of Boolean algebra.
• All rows in the K-map are represented by using square shaped cells, in which each square in that will represent a minterms.
• It is easy to convert a truth table to k-map and k-map to Sum of Products form equation.

Grouping of K-map variables

• There are some rules to follow while we are grouping the variables in K-maps. They are
• The square that contains ‘1’ should be taken in simplifying, at least once.
• The square that contains ‘1’ can be considered as many times as the grouping is possible with it.
• Group shouldn’t include any zeros (0).
• A group should be the as large as possible.
• Groups can be horizontal or vertical. Grouping of variables in diagonal manner is not allowed.

• If the square containing ‘1’ has no possibility to be placed in a group, then it should be added to the final expression.
• Groups can overlap.
• The number of squares in a group must be equal to powers of 2, such as 1, 2, 4, 8 etc.
• Groups can wrap around. As the K-map is considered as spherical or folded, the squares at the corners (which are at the end of the column or row) should be considered as they adjacent squares.
• The grouping of K-map variables can be done in many ways, so they obtained simplified equation need not to be unique always.
• The Boolean equation must be in must be in canonical form, in order to draw a K-map.

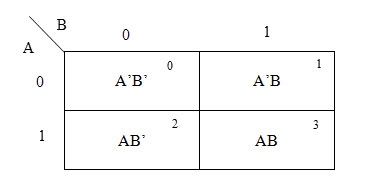
2 variable K-maps

There are 4 cells (22) in the 2-variable k-map. It will look like (see below image)

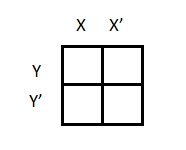
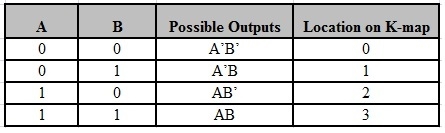
The possible min terms with 2 variables (A and B) are A.B, A.B’, A’. B and A’. B’. The conjunctions of the variables (A, B) and (A’, B) are represented in the cells of the top row and (A, B’) and (A’, B’) in cells of the bottom row. The following table shows the positions of all the possible outputs of 2-variable Boolean function on a K-map.

A general representation of a 2 variable K-map plot is shown below. 

When we are simplifying a Boolean equation using Karnaugh map, we represent each cell of K-map containing the conjunction term with 1. After that, we group the adjacent cells with possible sizes as 2 or 4. In case of larger k-maps, we can group the variables in larger sizes like 8 or 16.

The groups of variables should be in rectangular shape that means the groups must be formed by combining adjacent cells either vertically or horizontally. Diagonal shaped or L-shaped groups are not allowed. The following example demonstrates a K-map simplification of a 2-variable Boolean equation.

Example

Simplify the given 2-variable Boolean equation by using K-map.

F = X Y’ + X’ Y + X’Y’

First, let’s construct the truth table for the given equation,

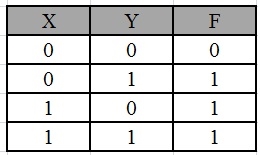
We put 1 at the output terms given in equation.

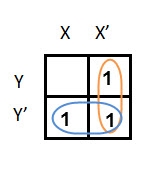
In this K-map, we can create 2 groups by following the rules for grouping, one is by combining (X’, Y) and (X’, Y’) terms and the other is by combining (X, Y’) and (X’, Y’) terms. Here the lower right cell is used in both groups.
After grouping the variables, the next step is determining the minimized expression.

By reducing each group, we obtain a conjunction of the minimized expression such as by taking out the common terms from two groups, i.e., X’ and Y’. So, the reduced equation will be X’ +Y’.

3 variable K-maps

For a 3-variable Boolean function, there is a possibility of 8 output min terms. The general representation of all the min terms using 3-variables is shown below.

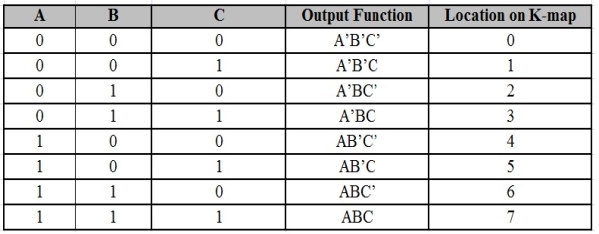
A typical plot of a 3-variable K-map is shown below. It can be observed that the positions of columns 10 and 11 are interchanged so that there is only change in one variable across adjacent cells. This modification will allow in minimizing the logic.

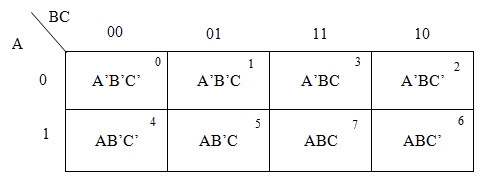
Up to 8 cells can be grouped in case of a 3-variable K-map with other possibilities being 1, 2 and 4.

Example

Simplify the given 3-variable Boolean equation by using k-map.

F = X’ Y Z + X’ Y’ Z + X Y Z’ + X’ Y’ Z’ + X Y Z + X Y’ Z’

First, let’s construct the truth table for the given equation,

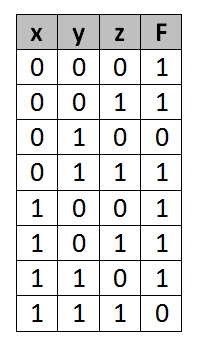
We put 1 at the output terms given in equation.

There are 8 cells (23) in the 3-variable k-map. It will look like (see below image).

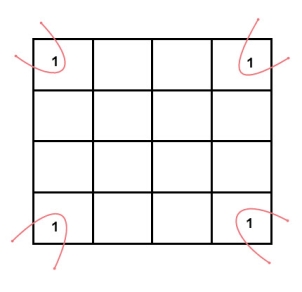
The largest group size will be 8 but we can also form the groups of size 4 and size 2, by possibility. In the 3 variable Karnaugh map, we consider the left most column of the k-map as the adjacent column of rightmost column. So, the size 4 group is formed as shown below.

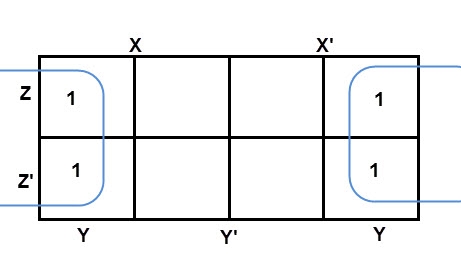
And in both the terms, we have ‘Y’ in common. So, the group of size 4 is reduced as the conjunction Y. To consume every cell which has 1 in it, we group the rest of cells to form size 2 group, as shown below.

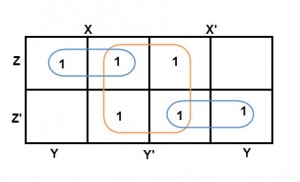
The 2-size group has no common variables, so they are written with their variables and its conjugates. So, the reduced equation will be X Z’ + Y’ + X’ Z. In this equation, no further minimization is possible.

4 variable K-maps

There are 16 possible min terms in case of a 4-variable Boolean function. The general representation of minterms using 4 variables is shown below.

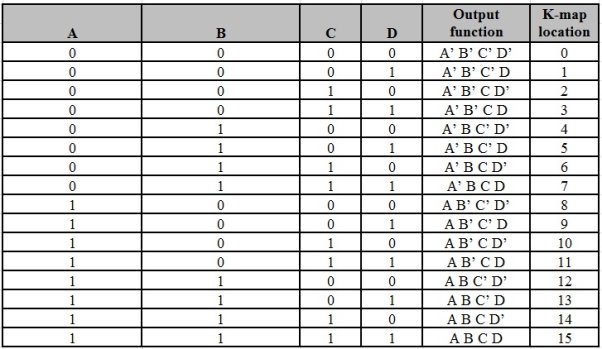
A typical 4-variable K-map plot is shown below. It can be observed that both the columns and rows of 10 and 11 are interchanged.

The possible numbers of cells that can be grouped together are 1, 2, 4, 8 and 16.

Example

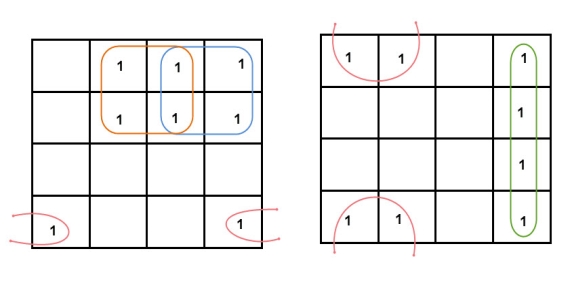
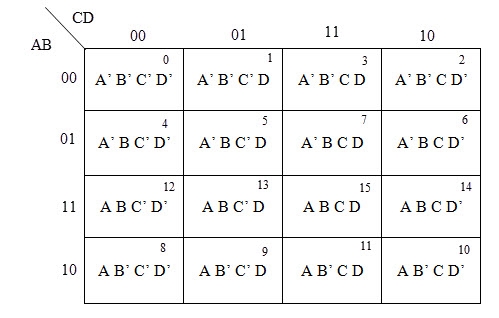
Simplify the given 4-variable Boolean equation by using k-map. F (W, X, Y, Z) = (1, 5, 12, 13)

Sol: F (W, X, Y, Z) = (1, 5, 12, 13)

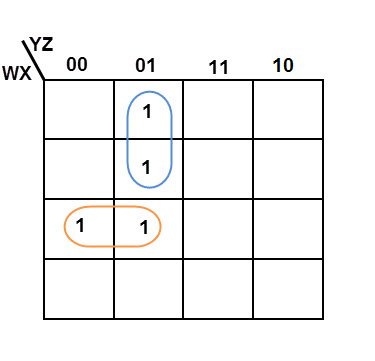
By preparing k-map, we can minimize the given Boolean equation as

F = W Y’ Z + W ‘Y’ Z

Key Takeaways:

1. The range of voltages as logic ‘High’ is represented with ‘1’ and logic ‘Low’ is represented with ‘0’.
2. Logical OR is summing of the literals and logical AND is multiplication of the two literals.

Canonical SoP and PoS forms

• A truth table comprises of a set of inputs and output(s).
• If there are ‘n’ input variables, then there shall be 2n possible combinations comprising of zeros and ones.
• So the value of every output variable depends on the combination of input variables.
• Hence, each output variable have ‘1’ for some combination and ‘0’ for other combination of input variables.

Therefore, we can express each output variable in two ways.

• Canonical SoP form
• Canonical PoS form

Canonical SoP form

• It means Canonical Sum of Products form.
• In this, each product term contains all literals.
• So that these product terms are nothing but the min terms.
• Hence is also known as sum of min terms form.
• Firstly, identification of the min terms is done and then the logical OR of those min terms is taken in order to get the Boolean expression (function) corresponding to that output variable.
• This Boolean function will be in sum of min terms form.
• Then following the same procedure for other output variables too.

Example

Considering the following truth table.

• Here, the output (f) is ‘1’ for only four combinations of inputs.
• The corresponding min terms are given as p’qr, pq’r, pqr’, pqr.
• By doing logical OR, we get the Boolean function of output (f).
• Hence, the Boolean function of output is,

f = p’qr + pq’r + pqr’ + pqr.

• This is the desired canonical SoP form of output, f.
• It can also be represented as:

f=m3+m5+m6+m7f=m3+m5+m6+m7

f=∑m(3,5,6,7)f=∑m(3,5,6,7)

• First, we represented the function as sum of respective min terms and then, the symbol for summation of those min terms is used.

Canonical PoS form

• It means Canonical Product of Sums form.
• Here In this form, each sum term contains all literals.
• These sum terms are the Max terms.
• Hence, canonical PoS form is also known as product of Max terms form.
• Identification of the Max terms for which the output variable is zero is done and then the logical AND of those Max terms is done in order to get the Boolean expression corresponding to that output variable.
• This Boolean function is in the form of product of Max terms.
• Following the same procedure for other output variables too.

Standard SoP and PoS forms

Standard SoP form

• It stands for Standard Sum of Products form.
• In this, each product term need not contain all literals.
• So, the product terms can or cannot be the min terms.
• Therefore, it is therefore the simplified form of canonical SoP form.

Standard SoP of output variable can be obtained by two steps.

• Getting the canonical SoP form of output variable
• Simplification the above Boolean function.

The same procedure is followed for other output variables too, if there is more than one output variable.

Numerical

Convert the Boolean function into Standard SoP form.

f = p’qr + pq’r + pqr’ + pqr

Solution:

Step 1 – By using the Boolean postulate, x + x = x and also writing the last term pqr two more times we get

⇒ f = p’qr + pq’r + pqr’ + pqr + pqr + pqr

Step 2 – By Using Distributive law for 1st and 4th terms, 2nd and 5th terms, 3rdand 6th terms.

⇒ f = qr(p’ + p) + pr(q’ + q) + pq(r’ + r)

Step 3 – Then Using Boolean postulate, x + x’ = 1 we get

⇒ f = qr(1) + pr(1) + pq(1)

Step 4 – hence using Boolean postulate, x.1 = x we get

⇒ f = qr + pr + pq

⇒ f = pq + qr + pr

This is the required Boolean function.

Standard PoS form

• It stands for Standard Product of Sum form.
• Here, each sum term need not contain all literals.
• So, the sum terms can or cannot be the Max terms.
• Therefore, it is the desired simplified form of canonical PoS form.

Standard PoS form of output variable is obtained by two steps.

• Getting the canonical PoS form of output variable
• Simplification of the above Boolean function.

The same procedure is followed for other output variables too.

Numerical

Convert the Boolean function into Standard PoS form.

f = (p + q + r).(p + q + r’).(p + q’ + r).(p’ + q + r)

Solution:

Step 1 – By using the Boolean postulate, x.x = x and  writing the first term p+q+r two more times we get

⇒ f = (p + q + r).(p + q + r).(p + q + r).(p + q + r’).(p +q’ + r).(p’ + q + r)

Step 2 – Now by using Distributive law, x + (y.z) = (x + y).(x + z) for 1st and 4thparenthesis, 2nd and 5th parenthesis, 3rd and 6th parenthesis.

⇒ f = (p + q + rr’).(p + r + qq’).(q + r + pp’)

Step 3 − Applying Boolean postulate, x.x’=0 for simplifying of the terms present in each parenthesis.

⇒ f = (p + q + 0).(p + r + 0).(q + r + 0)

Step 4 − Using Boolean postulate, x + 0 = x we get

⇒ f = (p + q).(p + r).(q + r)

⇒ f = (p + q).(q + r).(p + r)

This is the simplified Boolean function.

Hence, both Standard SoP and Standard PoS forms are Dual to one another.

1.6 Minimization of logical functions for min-terms and maxterms (upto 5 variables)

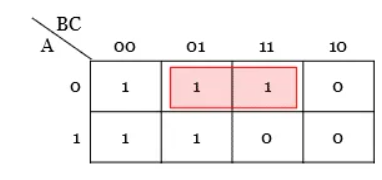
Q1) Minimize the expression Y = AB’C + A’B’C + A’BC + AB’C’ + A’B’C’

Solution:

Step 1: The given function has three variables and hence 23 = 8 cells K-map is necessary to minimize the expression.

Step 2: Plotting of k-map.

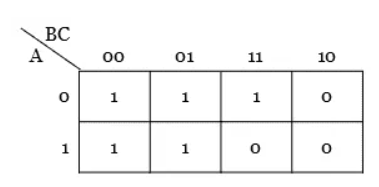
Step 3: No isolated 1s are there in the K-map.

Step 4: Group the pair of 1s in the K-map. 

Step 5: Group the Quad of 1s in the K-map.

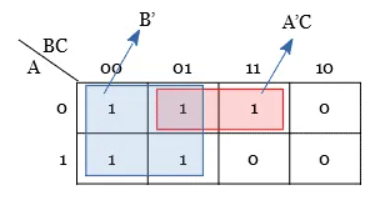
Step 6: There is no octet group.

Hence, from the K-map, the simplified output expression is Y = A’C + B’

Q2) Minimize the Boolean expression Y = ABC’D + ABC’D’ + ABCD + A’BCD + ABCD’ + A’BCD’?

Step 1: The given function has four variables and hence 24 = 16 cells K-map is necessary to minimize the expression.

Step 2: Plotting of k-map.

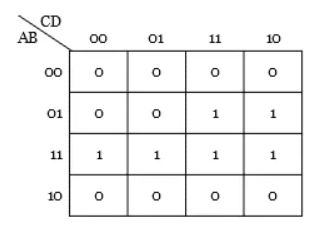
Step 3: No isolated 1s are there in the K-map.

Step 4: Group the pair of 1s in the K-map. But here, two quad groups can be formed. [Thus the number of groups are minimized by grouping the quad cells instead of pairing two cells].

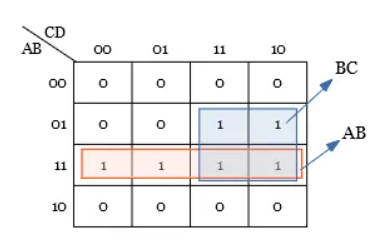
Step 5: There is no octet group.

Hence, from the K-map, the simplified output expression is Y = AB + BC.

Q3) Simplify the Boolean expression Y (A, B, C, D) = ∑ m (0, 1, 2, 3, 4, 7, 8, 9, 10, 11, 12, 14)

Solution:

Step 1: The given function has four variables and hence 24 = 16 cells K-map is necessary to minimize the expression.

Step 2: Plotting of k-map.

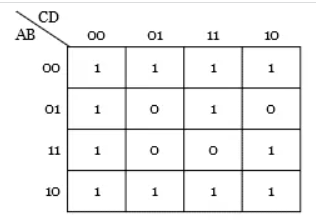
Step 3: No isolated 1s are there in the K-map.

Step 4: Group the pair of 1s in the K-map.

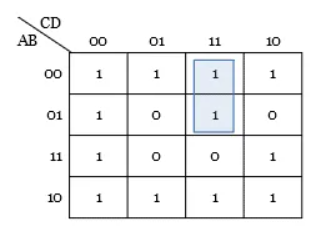
Step 5: Group the Quad and octet of 1s in the K-map.

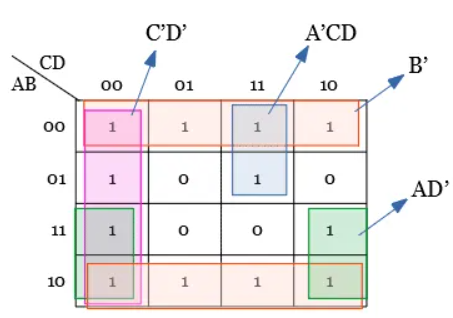
Hence, from the K-map, the simplified output expression is Y = B’ + C’D’ + AD’ + A’CD

Q4) Minimize the Boolean function Y = (A’+B’+C+D) (A+B’+C+D) (A+B+C+D’) (A+B+C’+D’) (A’+B+C+D’) (A+B+C’+D).

Solution

Step 1: The given function has four variables and hence 24 = 16 cells K-map is necessary to minimize the expression.

Step 2: Plotting of k-map.

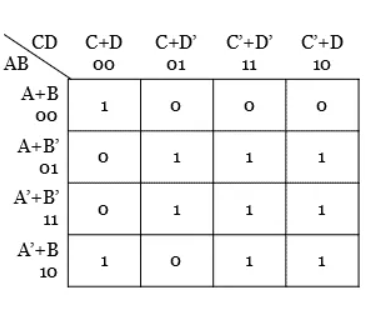
Step 3: No isolated 0s are there in the K-map.

Step 4: Group the pair of 0s in the K-map.

Step 5: There is no Quad and octet group of 0s.

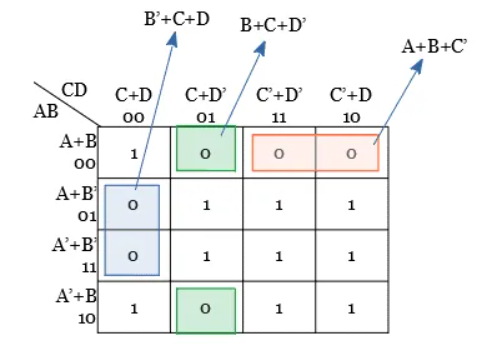
Hence, from the K-map, the simplified output expression is Y = (B’+C+D) (B+C+D’) (A+B+C’)

Q5) Simplify the Boolean function Y(A, B, C, D) = Π M (2, 3, 8, 9, 11, 13, 15).

Solution:

Step 1: The given function has four variables and hence 24 = 16 cells K-map is necessary to minimize the expression.

Step 2: Plotting of k-map.

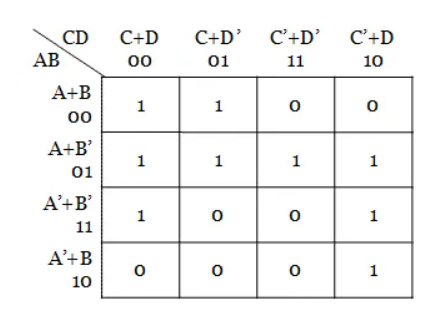
Step 3: No isolated 0s are there in the K-map.

Step 4: Group the pair and quad of 0s in the K-map. There is no octet group of 0s here.

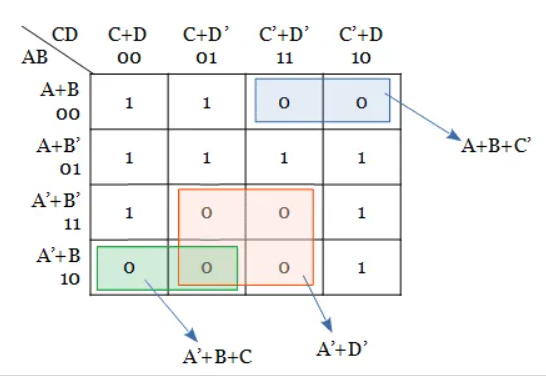
Hence, from the K-map, the simplified output expression is Y = (A’+B+C) (A’+D’) (A+B+C’)

Q6) Simplify the boolean function with don’t care conditions Y(A, B, C, D) = ∑ m (1, 3, 7, 11, 15) + d (0, 2, 5).

Solution:

Step 1: The given function has four variables and hence 24 = 16 cells K-map is necessary to minimize the expression.

Step 2: Plotting of k-map.

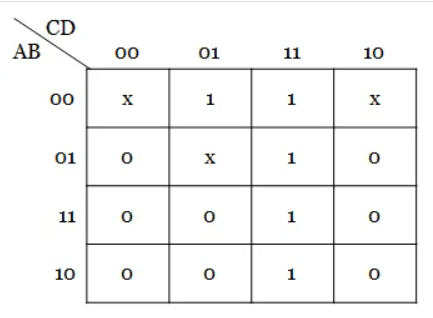
Step 3: Here, instead of pairing cells, quad group can be formed. To form a quad group of 1s, the don’t care outputs of cells 0, 2 are replaced by 1s and grouping is done. The remaining don’t care outputs are left alone or replaced by 0s.

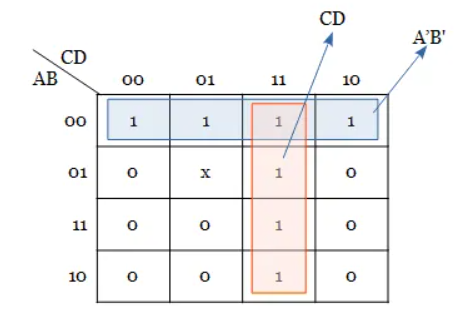
Hence, from the K-map, the simplified output expression is Y = A’B’ + CD
 

Q7) Simplify the boolean function with don’t care conditions Y(A, B, C, D) = Π M (4, 5, 6, 7, 8, 12) + d (1, 2, 3, 9, 11, 14).

Solution:

Step 1: The given function has four variables and hence 24 = 16 cells K-map is necessary to minimize the expression.

Step 2: Plotting of k-map.

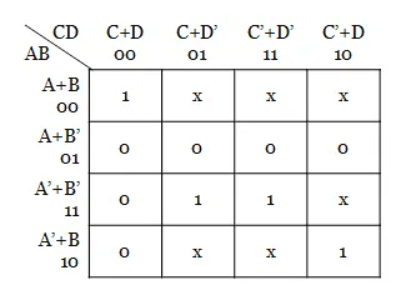
Step 3: Here, instead of pairing cells, quad group can be formed. To form a quad group of 0s, the don’t care outputs of cells 0, 2 are replaced by 0s and grouping is done. The remaining don’t care outputs are left alone or replaced by 1s.

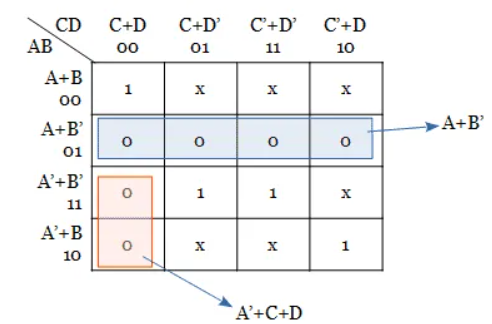
Hence, from the K-map, the simplified output expression is Y = (A+B’) (A’+C+D)

1.7 Introduction of logic families based on characteristics

CMOS Inverter

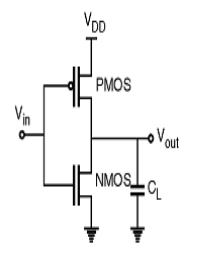
Fig: CMOS inverter

• It consists of PMOS and NMOS FET.
• The input A serves as the gate voltage for both transistors.
• The NMOS transistor has an input from Vss (ground) and PMOS transistor has an input from Vdd. The terminal Y is output.
• When a high voltage (~ Vdd) is given at input terminal (A) of the inverter, the PMOS becomes open circuit and NMOS switched OFF so the output will be pulled down to Vss.
• The truth table of inverter is:

Fig: NOT gate (ref. 1)

CMOS characteristics

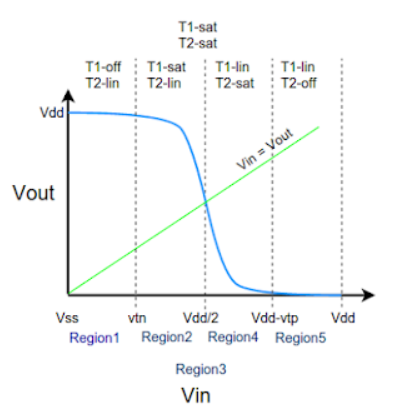
The VTC is divided into five regions(1-5) for easy of understanding. The above shown curve is possible when both T1 and T2 are matched for optimum operation. Optimum operation is achieved when Vin = Vdd/2 we get Vout = Vdd/2 . This can be achieved by adjusting width and length of both T1 and T2 as other parameters like mobility, oxide capacitance vary between different technologies. 

Region-1

In this, the input is in the range of (0,Vtn).

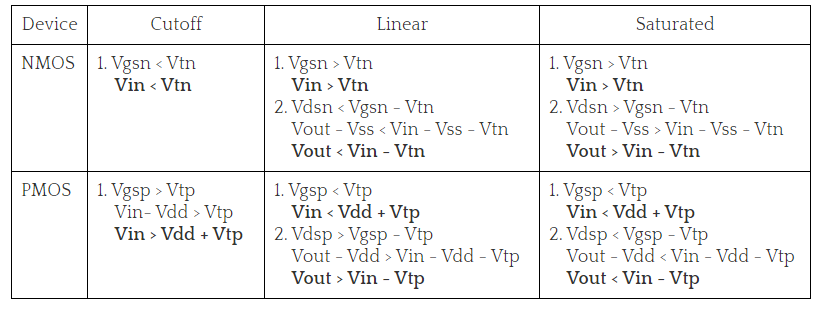
• NMOS is in cutoff as Vgs<Vtn
• PMOS is in linear as Vgsp<Vtp and Vdsp>Vgsp -Vtp.
• Zero current flows from supply voltage and the power dissipation is zero.

Region-2

Here, the input is in the range of (Vtn,Vdd/2).

• NMOS is in saturation as Vgs>Vtn and Vout>Vin – Vtn.
• PMOS is in linear region as Vdsp>Vgsp -Vtp.
• Since both the transistors are conducting some amount of current flows from supply in this region.

Region-3

Here the input voltage is Vdd/2. At this point the output voltage is Vdd/2. Here both the NMOS and PMOS are in saturation and the output drops drastically from Vdd to Vdd/2. At this point a large amount of current flows from the supply.

• NMOS is in saturation as Vgs>Vtn and Vout>Vin - Vtn.
• PMOS is in saturation as Vgsp<Vtp and Vdsp<Vgsp -Vtp.
• Large amount of current is drawn from supply and hence large power dissipation.

Region-4

In this region the input voltage is in the range of (Vdd/2 ,Vdd-Vtp). Here the PMOS remains in saturation as Vout< Vin - Vtp and Vgsp<Vtp. But the NMOS moves from saturation to linear region since the drain to source voltage now is less than Vgsn-Vtn.

• NMOS is in linear as Vgs>Vtn and Vout< Vin - Vtn.
• PMOS is in saturation as Vgsp<Vtp and Vdsp<Vgsp -Vtp.
• A medium amount of current is drawn as NMOS is in linear region and power dissipation is low.

Region-5

In this region the input voltage is in the range of (Vdd-Vtp,Vdd). Here the PMOS moves from saturation to cutoff as the Vgsp is so high that Vgsp>Vtp. The NMOS still remains in linear as the drain to source voltage now is less than Vgsn-Vtn.

• NMOS is in linear as Vgs>Vtn and Vout< Vin - Vtn.
• PMOS is in cutoff as Vgsp>Vtp.
• Zero current flows from the supply and hence the power dissipation is zero.

CMOS configurations- Wired Logic, Open-drain outputs

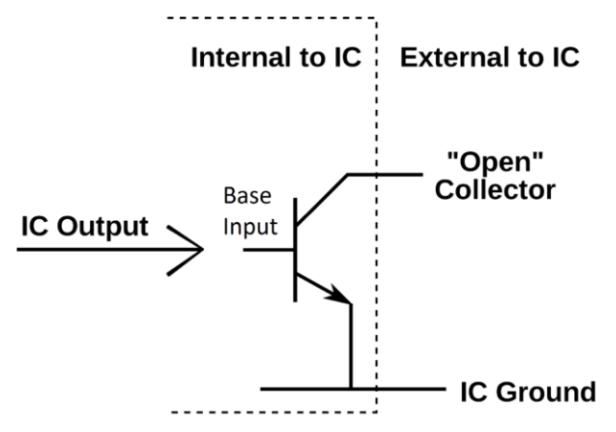
Open Drain is a type of programmable output port configuration with push pull, input only, and quasi-bidirectional configurations. Open-collector/open-drain is a circuit technique which allows multiple devices to communicate bidirectionally on a single wire. This is basically a mode which provides just a pull down operation.

An open collector/open drain is a common type of output found on many integrated circuits (IC). Instead of outputting a signal of a specific voltage or current, the output signal is applied to the base of an internal NPN transistor whose collector is externalized (open) on a pin of the IC. The emitter of the transistor is connected internally to the ground pin. If the output device is a MOSFET the output is called open drain and it functions in a similar way.

ECL

Emitter Coupled Logic or ECL emitter-coupled logic (ECL) is a high-speed integrated circuit bipolar transistor logic family. ECL uses an overdriven BJT differential amplifier with single-ended input and limited emitter current to avoid the saturated (fully on) region of operation and its slow turn-off behavior.

Emitter Coupled Logic (ECL), also referred to as Current Mode Logic families, is a digital technology with extremely high-speed. Transistors are not allowed to go into deep saturation thus, eliminating storage delays like in TTL logic families.

Fig: Motorola ECL 10,000 basic gate circuit diagram. Image source: Wikipedia

As the current is steered between two legs of an emitter-coupled pair, ECL is sometimes called current-steering logic (CSL), current-mode logic (CML)or current-switch emitter-follower (CSEF) logic.

ECL's major disadvantage is that each gate continuously draws current, which means that it requires (and dissipates) significantly more power than those of other logic families, especially when quiescent.

They are built only with the help of transistors.

It has been improved to meet performance requirements.

TTL family comprises of:

• Standard TTL.
• High-Speed TTL
• Low Power TTL.
• Schhottky TTL.

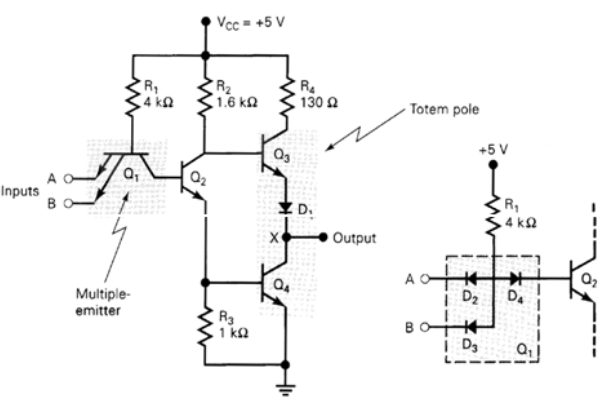
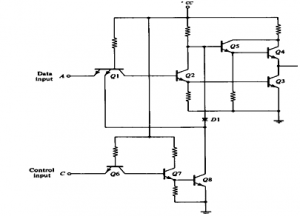
Operation of TTL NAND Gate (Two input )

The circuit diagram of a 2 input TTL NAND gate is as follows:

• A two input TTL NAND is shown above. A and B are two inputs while Y is the output.
• Operation of the gate:

a) A and B both low: both B-E junctions of Q1 are forward biased. Hence D1 and D2 will conduct to force the voltage at point C to 0.7V. This voltage is insufficient to forward bias B-E junction of Q2. Hence Q2 remains OFF. Therefore its collector voltage rises to VCCVCC. As Q3 is operating in emitter follower mode, output Y will be pulled up to high voltage Y= 1

b) Either A or B low: If any one input is connected to ground with other left open or connected to VCCVCC the corresponding diode (D1 or D2) will conduct. This will pull down voltage at C o 0.7V. This voltage is insufficient to turn on Q2 so it remains OFF. So collector voltage of Q2 will be equal to VCC. This voltage acts as base voltage for Q3. As Q3 acts as an emitter follower, output Y will be pulled to VCCVCC. Y= 1

c) A and B both high: If both A and B are connected to then both diodes D1 and D2 will be reverse biased and do not conduct. Therefore D3 is forward biased and base current is supplied to transistor Q2 via R1 and D3. As Q2 conducts, the voltage at X will drop down and Q3 will be OFF, whereas voltage at Z will increase to turn ON Q4. As Q4 goes into saturation, the output voltage Y will be pulled down to low. Y = 0

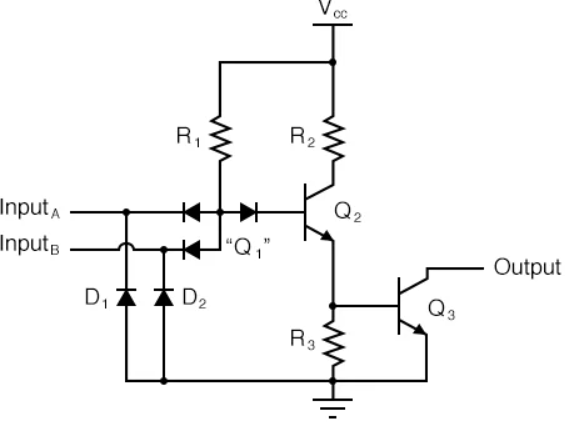
TTL with active pull up

It is possible in TTL gates the charging of output capacitance without corresponding increase in power dissipation with the help of an output circuit arrangement referred to as an active pull-up or totem-pole output. In this case,

• Outputs must never be connected together.
• Connecting outputs causes excessively high currents to flow.
• Outputs will eventually be damaged.
• The standard TTL output configuration with a HIGH output and a LOW output transistor, only one of which is active at any time.
• A phase splitter transistor controls which transistor is active.

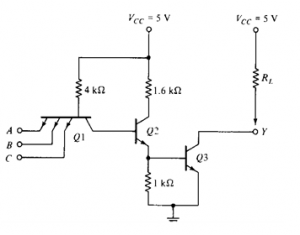
TTL with open collector output

The main feature is that its output is 0 when low and floating when high. Usually, an external Vcc may be applied.

Transistor Q1 behaves as a cluster of diodes placed back to back. With any of the input at logic low, the corresponding emitter-base junction is forward biased and the voltage drop across the base of Q1 is around 0.9V, not enough for the transistors Q2 and Q3 to conduct. Thus the output is either floating or Vcc, i.e. High level.

Similarly, when all inputs are high, all base-emitter junctions of Q1 are reverse biased and transistor Q2 and Q3 get enough base current and are in saturation mode. The output is at logic low. (For a transistor to go to saturation, collector current should be greater than β times the base current).

Totem Pole Output:

Totem Pole means the addition of an active pull up the circuit in the output of the Gate which results in a reduction of propagation delay.

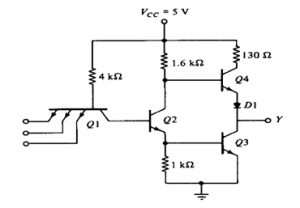
Logic operation is the same as the open collector output. The use of transistors Q4 and diode is to provide quick charging and discharging of parasitic capacitance across Q3. The resistor is used to keep the output current to a safe value.

Three state Gate:

It provides 3 state output.

1. Low-level state when a lower transistor is ON and an upper transistor is OFF.
2. High-level state when the lower transistor is OFF and the upper transistor is ON.
3. Third state when both transistors are OFF. It allows a direct wire connection of many outputs.

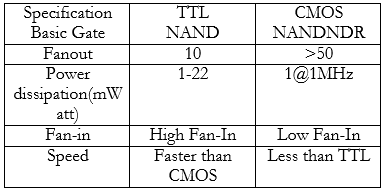
Comparison of Specifications of Logic Families

1.8 Speed of operation

Speed of a logic circuit is determined by the time between the application of input and change in the output of the circuit.

1.9 Power dissipation

Every gate is connected to a power supply VCC (VDD in the case of CMOS).

A certain amount of current is drawn during its operation. Since each gate can be in a High, Transition or Low state, hence there are three types of currents drawn from power supply:

• ICCH: Current drawn during the HIGH state.
• ICCT: Current drawn during HIGH to LOW, LOW to the HIGH transition state.
• ICCL: Current drawn during the LOW state.

For TTL,

Average Power Dissipation = Vcc * (ICCH + ICCL)/2

For CMOS,

Average Power Dissipation = Vcc * ICCT.

For the TTL logic family, power dissipation does not depend on the frequency of operation.

For CMOS, power dissipation depends on the frequency of operation.

Power Dissipation:

Power dissipation of a circuit defines its battery life: the greater the power dissipation, the shorter the battery life.

It is directly proportional to the heat generated by the chip or system hence excessive heat dissipation may increase operating temperature and cause gate circuitry to drift out of its normal operating range.

Total power dissipation = static power dissipation + dynamic power dissipation.

1.10 Figure of merit

Figure of merit is a product of propagation delay and power dissipation. It is measured in terms of Pico-Joules (ns ´mW = pJ). Current and voltage parameters define the minimum and maximum limit of current and voltage for input and output of a logic family.

1.11 Fan in

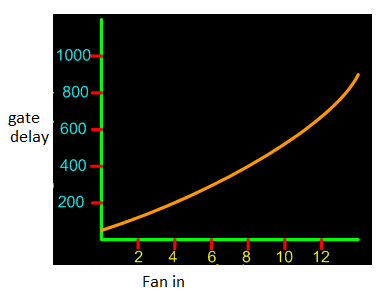
• It is the number of inputs that a gate can have like a two input AND gate has fan-in of two, a three input NAND gate as a fan-in of three etc.
• Hence a NOT gate has a fan-in of one.
• The figure below shows the effect of fan-in on a CMOS based gate.
• Normally delay increases as a quadratic function of fan-in.

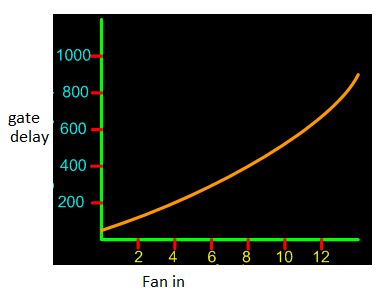
Fig: Effects of Fan-in

1.12 Fan out

• The number of gates that each gate can drive, while providing voltage levels in the specified range is called the standard load or fan-out.
• It depends on the amount of electric current a gate can source or sink while driving other gates.

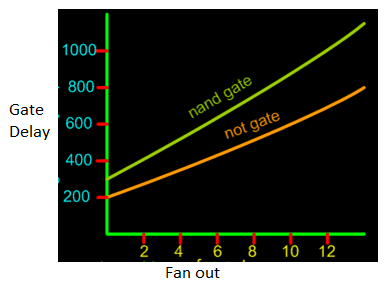
Fig: Effects of Fan-out

References:

1. Wakerly Pearon: “Digital Design: Principles and Practices”, Pearon Education Publications.

2. Mark Bach: “Complete Digital Design”, Tata MCGraw Hill Publications.

3. W. Fletcher: “Engg. Approach to Digital Design”, PHI Publications.