Unit - 1

Sources and Mesh Analysis

1.1 Sources and Mesh Analysis: Voltage source

Categories of sources

1. Voltage source and current source
2. A.C. Source and D.C. Source
3. Dependent source and independent source
4. Constant and function of time source

Few either

AC or DC                             v(t) = e-t(time source)

AC → sin wt                        dc → 5V

Equivalent circuit diagram of

1. Voltage Source: A voltage source always have a resistance in series. 

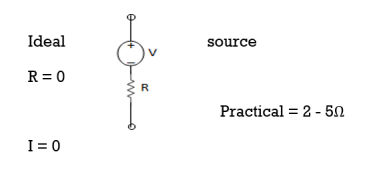
A voltage source is a device which provides a constant voltage to load at any instance of time and is independent of the current drawn from it. This type of source is known as an ideal voltage source. Practically, the ideal voltage source cannot be made. It has zero internal resistance. It is denoted by this symbol.

Fig:  Voltage source symbol

Ideal Voltage Source

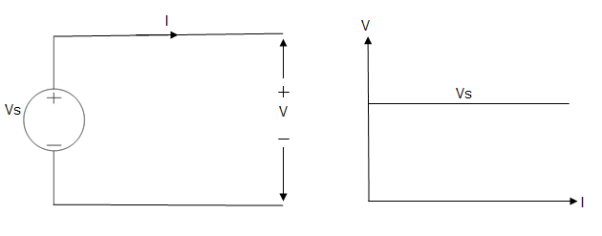
Fig: Ideal Voltage Source

The graph represents the change in voltage of the voltage source with respect to time. It is constant at any instance of time.

Voltage sources that have some amount of internal resistance are known as a practical voltage source. Due to this internal resistance, voltage drop takes place. If the internal resistance is high, less voltage will be provided to load and if the internal resistance is less, the voltage source will be closer to an ideal voltage source. A practical voltage source is thus denoted by a resistance in series which represents the internal resistance of source.

Practical Voltage source

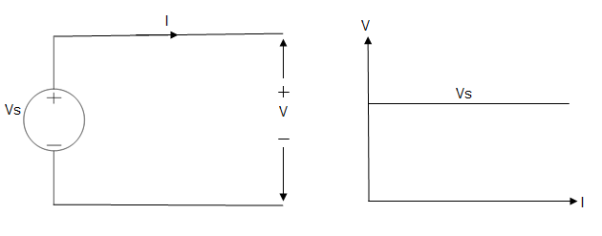
Fig: Practical Voltage source

The graph represents the voltage of the voltage source with respect to time. It is not constant but it keeps on decreasing as the time passes.

1.2 Current source

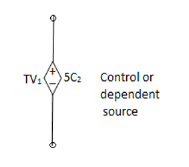
Dependent current source

Dependent current source changes its available current depending upon the voltage across, or the current through, and some other element connected to the circuit.

That is the output of a dependent current source is controlled by another voltage or current.

A current source that depends on a voltage input is generally referred to as a Voltage Controlled Current Source or VCCS. A current source that depends on a current input is generally referred as a Current Controlled Current Source or CCCS.

Dependent Current Source Symbols

A voltage source that depends on a voltage input is generally referred to as a Voltage Controlled Voltage Source or VCVS. A voltage source that depends on a current input is referred as a Current Controlled Voltage Source or CCVS.

Ideal dependent sources are commonly used in the analysing the input/output characteristics or the gain of circuit elements such as operational amplifiers, transistors and integrated circuits. 

An ideal dependent voltage-controlled current source, VCCS, maintains an output current, IOUT that is proportional to the controlling input voltage, VIN.

That is the output current “depends” on the value of input voltage making it a dependent current source. Then, the VCCS output current is defined by

IOUT = αVIN.

This multiplying constant α has the SI units of mhos, ℧  becauseα = IOUT/VIN, and its units will therefore be amperes/volt.

1.3 Source transformation and reduction

Source Transformation

Electrical source transformation is a method of replacing voltage source in a circuit by its equivalent current source and current source by its equivalent voltage source.

Let us take a simple voltage source along with a resistance connected in series with it. This series resistance normally represents the internal resistance of a practical voltage source.

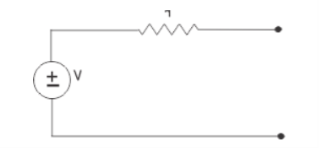
Short circuit the output terminals of the voltage source circuit as shown below,

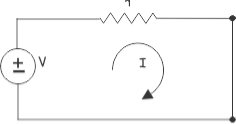
Now applying Kirchhoff Voltage law in the circuit, we get

V = Ir ---------------------(i)

Where, I is the current which delivers by the voltage source when it is short circuited.

Now, let us take a current source of same current I which produces same open circuit voltage at its open terminals as shown below,

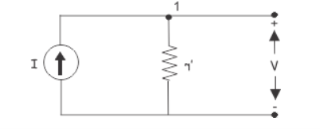
Now, applying Kirchhoff’s current law at node 1, of the above circuit, we get,

I = V / r’ ----- V = I r’ --------(ii)

From equation (i) and (ii) we get

r = r’

The open circuit voltage of both the sources is V and short circuit current of both sources is I. The same resistance is connected in series in voltage source is connected in parallel in its equivalent current source.

So, these voltage source and current source are equivalent to each other.

A current source is dual form of a voltage source and a voltage source is dual form of a current source. A voltage source can be converted into an equivalent current source and a current source can also be converted into an equivalent voltage source.

Voltage Source to Current Source Conversion

Assume a voltage source with terminal voltage V and the internal resistance r. This resistance is in series. The current supplied by the source is equal to:

I = V / r

When the source of the terminals are shorted.

This current is supplied by the equivalent current source and the same resistance r will be connected across the source. The voltage source to current source conversion is shown in the following figure.

Current source to Equivalent voltage source:

Assume a current source with the value I and internal resistance r. Now according to the Ohms law the voltage across the source can be calculated as

V = Ir

Hence, voltage appearing, across the source, when terminals are open, is V.

Current source                                    Equivalent voltage source

Source reduction

Q1) Find the output voltage using source transformation technique. For the given circuit?

A1) The 12 V Voltage source transfers into Current source:

I =12/3 =4 mA

After source transformation the circuit will be

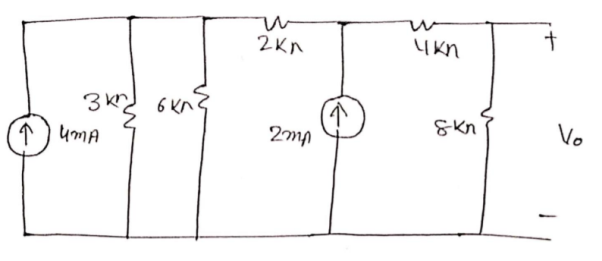
The 3KΩ and 6 KΩ are parallel to each other so equivalent resistance = (3x6)/(3+6) = 2k

The equivalent circuit will now be

The 4mA current source transfers voltage of =4x2 =8V

The reduced circuit diagram is

Now 2k and 2k are in series

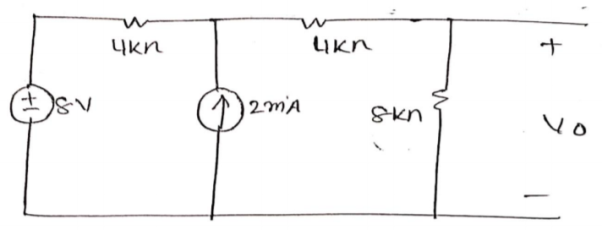
The 8V voltage source convert into current source: = 8/4 = 2A

The circuit diagram is

The both current source are in same direction so add the both current sources.

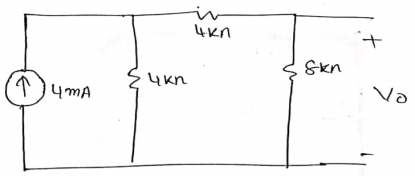
The 4mA current source transfer into a voltage source: = 4 × 4 = 16 V

So, calculate the output voltage across 8 ohm using voltage divider rule:

𝑉0 = 16 × 8/(8 + 8) = 8 V

Example 1. For the circuits given below write the voltage equations:

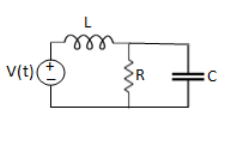
Solution: Let current i1be in loop 1 current and i2 for loop 2 

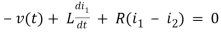
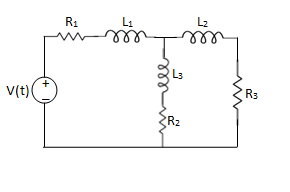
Solution:

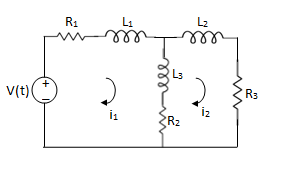
For loop 1 

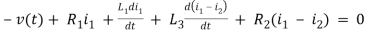
For loop 2 

Example: Using nodal analysis find voltage across 5resistor.

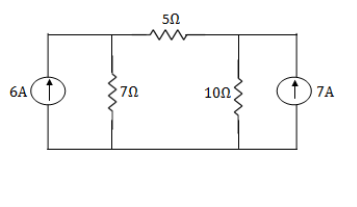
Solution:

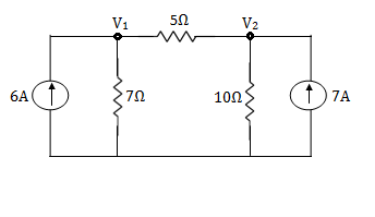
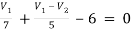
For V1

1

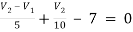
For V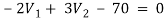2

2

Solving 1 and 2:

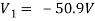
For 5 voltage =

= -50.9 + 57.27

= 6.37V

1.4 Mesh basis equilibrium approach for complicated network containing independent sources and reactance

Concept of Super nodes

We are primarily interested in node voltages. We may avoid utilizing the voltage source branch that is causing difficulty. To do this we may treat N2, N3 and the voltage source together as a type of super node and apply KCL to both nodes at same time.

This is possible since total current leaving node 2 is zero and total current leaving node 3 is also zero. Thus, the current leaving both the nodes in totality must be zero.

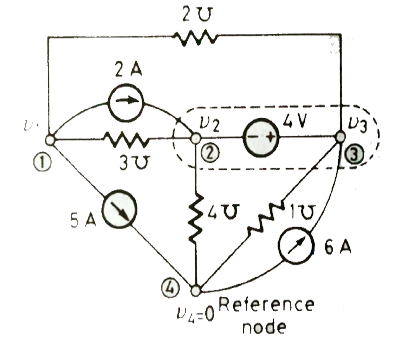
Fig. Circuit with super node

A simple way of identifying the super node is to think of the voltage source as a short circuit physically joining the two nodes together.

Solving the above circuit for finding node voltage

KCL for V1

2+5+ [(V1-V2)/(1/3)]+[(V1-V3)(1/2)]=0

5V1 -3V2-2V3+7=0     (1)

KCL at V4

-5+6+ [(V4-V2)/(1/4)]+[(V4-V3)/1] = 0

4V2+V3+4V4+1=0                 (2)

Applying KCL for both N2 and N3 simultaneously we get

[(V2-V1)/(1/3)]-2+(4V2)+[2(V3-V1)]+V3-6=0

-5V1 + 7V2 + 3V3 = 8       (3)

We get one more relation as

V3-V2 = 4                         (4)

Solving equations 1,2,3 and 4 we get

V2= -3/5 V

V3 = 17/5 V

V1= -2/5 V

Concept of Super mesh

If the current source is also present in the network than we face difficulty in writing mesh equations. A better approach is we assume the current source to be open circuited and create a new mesh called super mesh. We than apply KVL only to those meshes in the modified network.

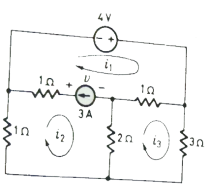
Fig. Ciruit (a) 3A in circuit                         circuit (b) with super mesh

Let the mesh current be i1, i2 and i3. The current source be mentally open circuited. Thus, creating a new mesh called super mesh shown by dotted lines. Applying KVL around this mesh we get

-4+ (i1-i3)1 + 2(i2-i3)+i2 = 0

i1+3i2-3i3=4         (1)

2(i3-i2)+i3-i1+3i3=0

i1+2i2-6i3=0       (2)

i1-i2=3     (3)

Solving above equations we get

i1= 4A

i2= 1A

i3= 1A

Key takeaway

When a current source creates problem while applying mesh, we use super mesh by open circuiting the current source. When a voltage source creates problem while applying node, we use super node by short circuiting the voltage source.

1.5 Node Voltage Analysis: Nodal Basis equilibrium equation

Nodal analysis

In the nodal method we are finding the node voltages with the following steps:

1. Select a reference node. Assign all the rest nodes voltages , with respect to reference node.
2. Use Kirchhoff’s and Ohm’s Laws to each non-reference node and branch currents.
3. Resolve the system of equations and obtain node voltages.

Consider the following circuit.

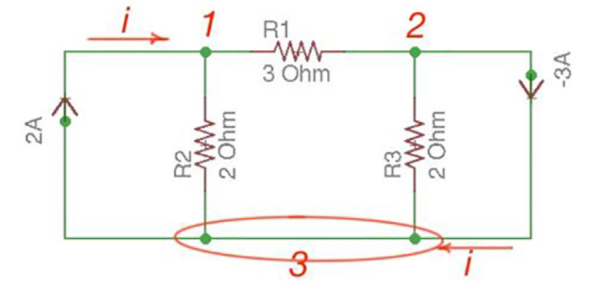
Let us consider a reference node – 3.

In a real circuit a reference node is ground is assumed to have potential.

By the Kirchhoff’s Law having the following current relation:

I1 = i1 + i2

I2 = i2 -i3

Let us represent currents like ratio of voltage and resistance by the Ohm’s Law:

i 1 = v1 /R1 ;i 2 = v1 -v2 /R2 ; i3 = v2/R3;

Or

i 1= v1 * G1 ; i2 =(v1 -v2)*G2 ; i3 =v2 * G3

i1 = v1 * G1 + (v1-v2) * G2 ;

i2 = (v1-v2) * G2 – v2 * G3

i1= v1 * (G1 +G2) – v2 * G2

i2 = v1 *G2 – v2 *(G3 +G2)

Or

And we achieve the following matrix equation, which can be resolved by the Cramer’s rule:

[ G1 + G2 -G3 -G3 ] [v1] = [I1]

[G2 -G2][v2] =[I2]

Consider the following figure:

There are two possibilities that exist:

1. If the voltage source is between reference node and non-reference node, the non-reference voltage is considered equal to the voltage source.
2. If the voltage source is between two non-reference nodes, these two nodes are generalised nodes. To determine its voltage Kirchhoff’s Laws must be applied.

Applying Kirchhoff’s Law we achieve the following equations:

i  1 + i4 = i2 + i3

-v2 +5+v3 =0

v 1 =10

By Ohm’s Law

These equations will help determine node voltages.

1.6 Matrix for electrical network containing independent sources and reactance

Matrix Analysis of Networks

When we solve circuit problems, we need to write the equations corresponding to the Ohm’s Law and the Kirchoff’s Laws. These same equations need to be used even when there are a large number of branches, and as such when using Matrix analysis of networks.

Kirchoff’s current Law in matrix form Let Ij be the current in the jth branch. Consider any node k in the network, as shown in the figure. The jth branch may either be directed away from kth node, may be directed towards kth node, or may not be incident on the kth node. From Kirchoff’s current Law,

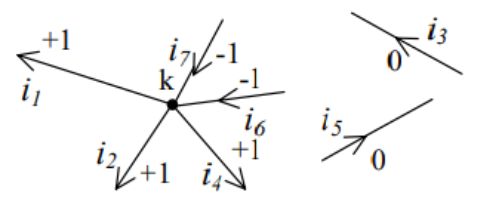
-i1-i2-i4+i6+i7=0

i1 + i2 + i4 = i6 + i7

Branch currents directed away from the node are associated with a coefficient of +1, while current directed towards the node are associated with a coefficient –1. Branches not connected to (or incident on) the node are obviously associated with a coefficient of 0. These coefficients are defined as ajk so that Kirchoff’s current law may thus be written as

a1k . i1 + a2k . i­2 + a3k . i3 + a4k . i4 + . . . . . . . . . a7k . i7 = 0

Or for kth node we can write

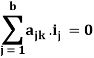
The collection of such equations for each node k would give the matrix equation

In the matrix [A]t, the row vectors are dependant, since their sum is zero. For this reason, the matrix [A]t is written with one row less, usually the last row for convenience, so that there are only (n-1) rows.

The matrix [A]t of dimension (n-1)×b is referred to as the node-branch incidence matrix. The matrix [A] of dimension b× (n-1) is then referred to as the branch-node incidence matrix. The elements of the matrix [A] are

ajk = +1 if jth current is directed away from the kth node

ajk = −1 if jth current is directed towards the kth node

ajk = 0 if jth current is not incident on the kth node

Kirchoff’s voltage Law in matrix form

Similarly, the Kirchoff’s voltage law may be applied for the sth loop. The coefficients brs of the voltages are defined as +1, −1 or 0 depending on whether the loop direction is the same as the branch direction or not.

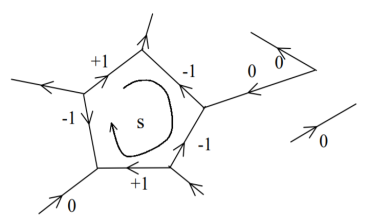
For sth node, for all s;

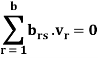
Where brs = −1, 0, or +1

In matrix form this becomes

The matrix [B]t of dimension l×b is referred to as the mesh-branch incidence matrix. The matrix [B] of dimension b×l is then referred to as the branch-mesh incidence matrix. The elements of the matrix [B] are

The elements of the matrix [B] are brs = +1 if rth current is in the same direction as the sth loop

brs = −1 if rth current is in the opposite direction to the sth loop

brs = 0 if rth current is in the not part of the sth loop

Ohm’s Law in matrix form

A general branch may contain a voltage source and/or a current source in addition to the branch impedance/admittance.

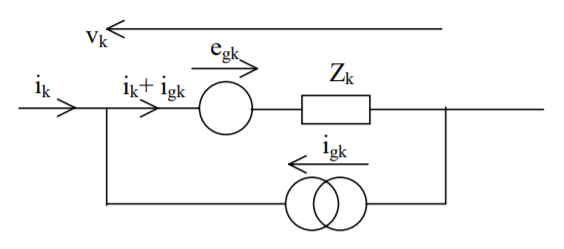
Applying Ohm’s Law

vk = - egk + Zkigk + Zkik for all branches k = 1, 2, .... ... b

However, using Thevenin’s Theorem or Norton’s Theorem, a current generator may be converted to a voltage generator or vice versa, except when ideal. Thus, analysis can be done with only either a voltage source or a current source. Thus, we may either write

vk = - egk + Zkik for all branches k = 1, 2, .... ... b

Which may be written in matrix form as

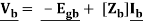
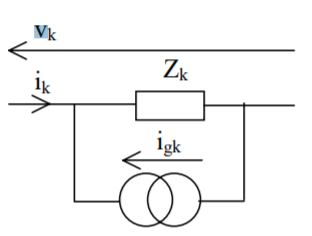
Or we may write vk = Zkigk + Zkik or Ykvk = YkZkigk + YkZkiki.e.ik = Ykvk - igk

Or in matrix form as

Where:

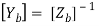
Mesh Analysis

In mesh analysis, we eliminate the branch voltages from the equations. We further reduce the number of remaining currents to the minimum using Kirchoff’s current law and apply Kirchoff’s voltage law for solution. Let us define a set of mesh currents, Im

The branch currents Ib can be seen to be related to the mesh currents Im by an algebraic summation. In fact, if an example is considered, it will be easily seen that the relation corresponds to the matrix [B].

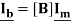
We can eliminate Vb from the equations, by pre-multiplying equation by [B]t

It is seen that [B]tVb = 0 Also Ib = [B] Im

[B]tVb = 0 corresponds to the sum of the voltages around a loop is zero. [B]tVb must correspond to the sum of the voltages around a loop. Since [B]t is constant, and Egb is the branch source voltage vector, [B]tEgb must correspond to the sum of the source voltages around a loop. This is defined as the mesh source voltage vector

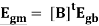
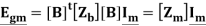
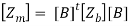
This corresponds to only l equations, and the only unknowns in that equation is Im which corresponds to l unknowns. Thus, the original problem of 2b equations and 2b unknowns has been reduced to that of l equations and l unknowns. The elements of the matrix [Zm] can be obtained either by going through the above mathematical considerations, or by inspection in the following manner for the simple problems.

zjj = self impedance of mesh

j = sum of all branch impedances in mesh j

zjk = mutual impedance between mesh j and mesh k

= sum of all branch impedances common to mesh j and mesh k and traversed in mesh direction − sum of all branch impedances common to mesh j and mesh k and traversed in opposite direction ej = algebraic sum of the branch voltage sources in mesh j in mesh direction.

Note: Matrix [B] is also known as the tie-set matrix (as its elements tie the loop together).

Key takeaway

From Kirchoff’s Laws we have

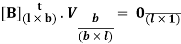
And from Ohm’s Law

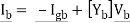
Thus, the total number of independent equations is n – 1 + l + b = b + b = 2 b It is seen that there is a total of 2b independent equations and 2b unknowns (corresponding to b branch currents and b branch voltages). However, it is not usual to solve the equations for both current and voltage simultaneously.

So let us see how these may be reduced for solution. The reductions can be done in one of two ways. The first is to eliminate the voltages and solve for currents. The second method is to eliminate the currents and solve for the voltages. These two methods are known as mesh analysis and nodal analysis respectively.

Examples

Q1) Solve the circuit using Mesh matrix analysis. Work from first principles.

A1) Let us first number the branches and the loops.

Let us write the loop currents in terms of the branch currents.

i1 = I1

i2 = - I3

i3 = I1 – I2

i4 = I2

i5 = I2 – I3

i6 = I3

Or in matrix form we can write it as

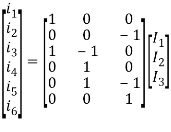
This gives us the [B] matrix or the Branch-Mesh incidence matrix. We can also write the Mesh–Branch incidence matrix [B]t matrix as follows, independent of the above, by writing the relation between the mesh direction and the branch direction.

The vector of branch currents Egb can be written as follows.

We now need to write the branch impedance matrix. Then we can write expressions for the mesh voltage vector and the mesh impedance matrix using the derived equations.

Egm = [B]tEgb , and [Zm] = [B]t [Zb] [B]

The Branch impedance matrix is

Thus we can write the mesh source voltage vector

This could also have been written by inspection by writing down the sources effectively driving the mesh currents round the loops. If first principles is not asked for, writing by inspection would generally be sufficient. The mesh impedance matrix can be written as

This matrix too could have been written by inspection, and would normally have been done that way, if first principles were not required. Thus, we may now write the mesh analysis equation as

The equations may be solved by inversion or otherwise.

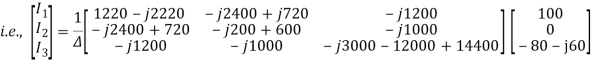
The discriminant ∆ is given by

Δ = (1220 - j2220) × (-j100) + (720 - j2400)×(j120) +(-j1200)×0

Δ = - j 122000 - 222000 + j 86400 + 288000 = 66000 - j35600 = 74989 ∠-28.34o

Thus, I1 is given as

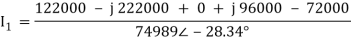
Currents I2 and I3 can be similarly determined. The branch currents i1, i2, ..... May then be determined from the matrix equation.

Nodal Analysis

In nodal analysis, we eliminate the branch currents from the equations. We further reduce the number of remaining voltages to the minimum using Kirchoff’s voltage law and apply Kirchoff’s current law for solution. Let us define a set of nodal voltages, VN which are node pair voltages (i.e. voltage across a pair of nodes) The branch voltages Vb can be seen to be related to the nodal voltages VN by an algebraic summation. In fact, if an example is considered, it will be easily seen that the relation corresponds to the matrix [A].

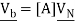
This gives

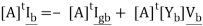
But, [A]tIb = 0.

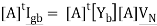
Where:

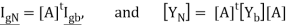
As in the case of mesh analysis, the source nodal current vector IgN and the nodal admittance matrix [YN] could be written by inspection as follows.

yii = sum of all branch admittances incident at node i

yij = negative of the sum of all branch admittances connecting node i and nodej.

The reason why the negative sign appears can be understood as follows. Consider the simple circuit shown.

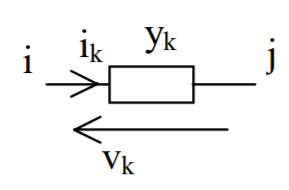
ik = ykvk = yk (Vi – Vj)

At any node i, from Kirchoff’s current law, nodal injected current at the node i is equal to the sum of the branch currents going out from the node

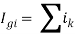
Also,

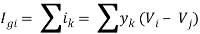
At node i for all j (different k actually correspond to different j)

Since Vi is a constant for a given i,

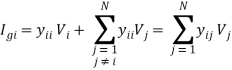
Thus, we see that the final equation derived in this manner actually corresponds to the nodal equation, and that the diagonal term of the matrix actually corresponds to the branch admittances connected to the node, and that the off diagonal terms actually correspond to the negative of the branch admittance.

As in the case of mesh analysis, the nodal equation IgN = [YN]VN is first solved to give VN and the branch voltages and branch currents can then be obtained using the matrix equations.

Example

Q1) Solve the circuit using Mesh matrix analysis. Work from first principles.

A1) Let us first convert the above circuit with current sources. The network may also be drawn in terms of admittances as follows.

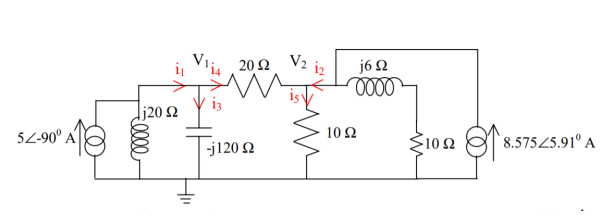
The branch-node incidence matrix [A], branch injected current Igb, and the branch admittance matrix may be written, with the reference selected as the earthed node as

As in the case of mesh analysis, the nodal current injection vector and the nodal admittance matrix may be written from first principles.

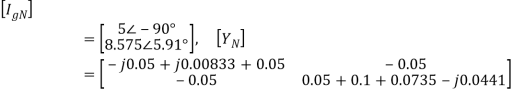
Δ = (-j 0.05 + j0.00833 +0.05)(0.05 +0.1 + 0.0735-j0.0441) - 0.052

= (0.05 - j0.04167)(0.2235 - j0.0441) - 0.0025

= 0.06509 ∠-39.81o×0.2278∠-11.16o - 0.0025

= 0.01483∠-5097 - 0.0025 = 0.00934 - 0.0025 - j0.01152 = 0.00684 - j0.01152

= 0.0134∠-59.30o

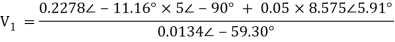
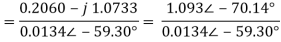
V1 = 81.6∠-19.84V

The branch current will be

i1 = 1.384 -j1.165 = 1.809∠-40.09o A

1.7 Duality

The two networks are said to be dual if mesh equation of one network is equal to node equation of other.

Let us consider RLC circuit

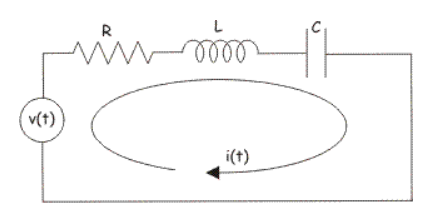
Fig. RLC Circuit

Applying KVL we have

v(t) = ri(t) + L +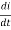 

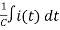
So, dual of above network will be

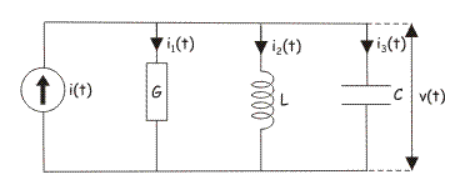
Fig. Dual of RLC circuit

i(t) = Gv(t) + C +

Steps for construction of Dual Network:

i)          In each loop place a dot. This internal dot corresponds to independent node in the dual network.

Ii)        Outside network place a dot. This is called datum node is dual network

Iii)     Connect all the adjacent loops by dashed lines crossing common branches.

Iv)     In dual network this common branch is replaced by its dual element.

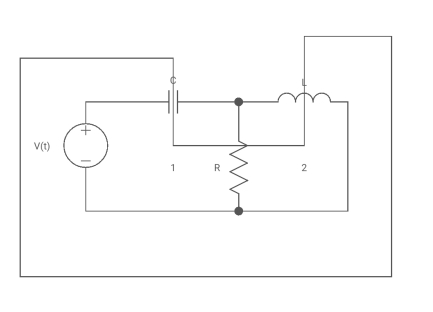
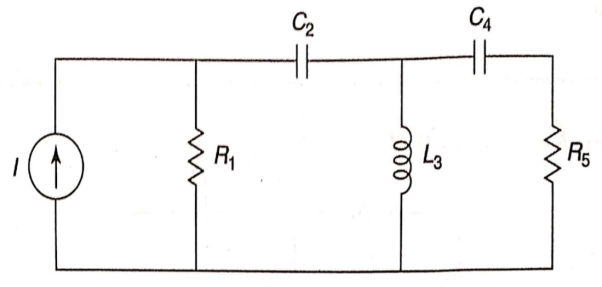
Fig. Circuit whose dual is to made

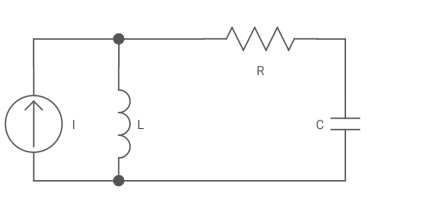
Fig. Dual of above circuit

Example

Q1) Draw the dual of the network shown in figure

A1) For drawing the dual network, mark the node and dashed lines

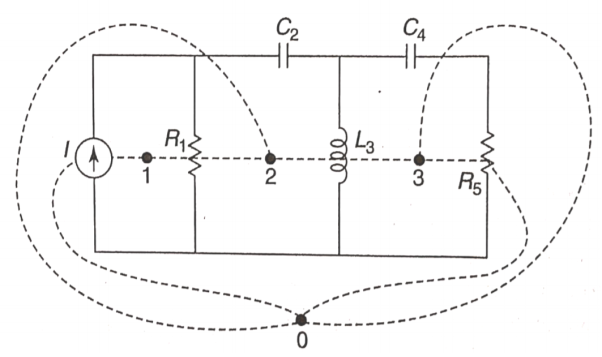
The dual network is shown in figure

Key takeaway

Some important duals are given below.

Solved Examples

Q1. For the circuits given below write the voltage equations:

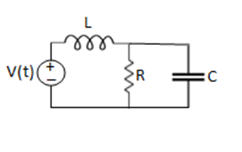
Solution: Let current i1be in loop 1 current and i2 for loop 2 

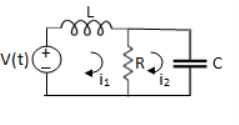
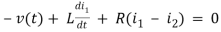
Que Write the loop equations for the given circuit below?

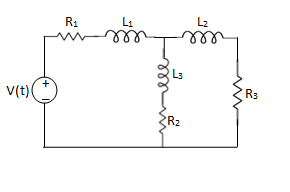
Solution:

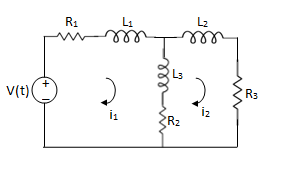
For loop 1 

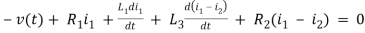
For loop 2 

Example: Using nodal analysis find voltage across 5resistor.

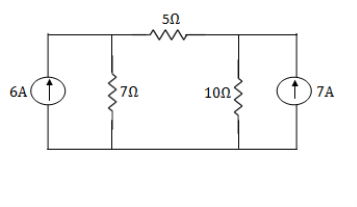
Solution:

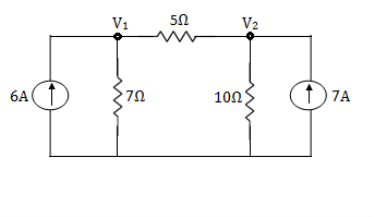
For V1

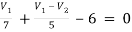
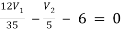
1

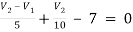
For V2

2

Solving 1 and 2:

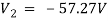
For 5 voltage =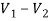

= -50.9 + 57.27

= 6.37V

Q) Find the node voltage in the network shown in figure.

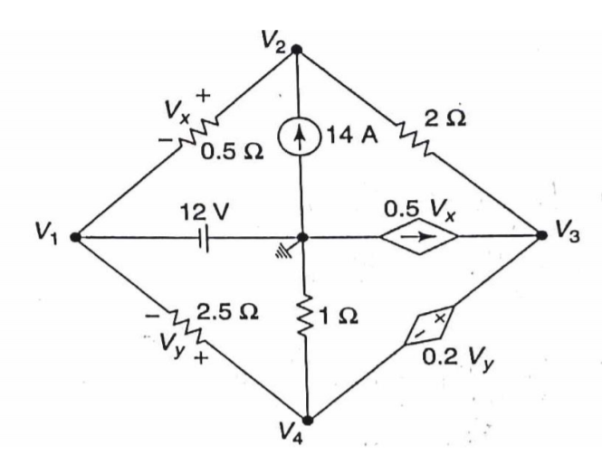
A) The node voltage V1 is

V1 = - 12 V

Applying KCL at node 2,

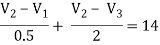
-2V1 + 2.5 V2 - 0.5 V3 = 14

Nodes 3 and 4 will form a super node. The voltage equation for the super node.

V3 - V4 = 0.2Vy = 0.2 (V4 - V1)

0.2V1 + V3 - 1.2 V4 = 0

Solving above equation for given node voltages we get

V1 = -12V

V2 = -4V

V3 = 0

V4 = -2V

Q) For the circuit shown in figure, Find the voltage across 4Ω resistor by using nodal analysis.

A) Let the voltage at node 1 and 2 be V1 and V2.

Vx = V1 + 5 - V2

Now applying KCL at node 1

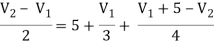
6(V2 - V1 ) = 60 + 4V1 + 3(V1 + 5 - V2)

9V2 - 13V1 = 75

Applying KCL at node 2 we get

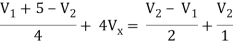
V1 + 5 - V2 + 16Vx = 2(V2 - V1) +4V2

3V1 -7V2 + 16Vx = -5

Solving

3V1 - 7V2 + 16(V1 + 5 - V2) = - 5

19V1 - 23V2 = -85

Again we have the following set of equations

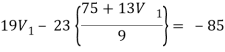
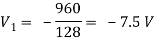
Again we have

9V2 = 75 + 13(-7.5)

The value Vx will be

Vx = - 7.5 + 5 + 2.5 = 0

Q) Draw the dual of the network shown in figure

A) For drawing the dual network, mark the node and dashed lines

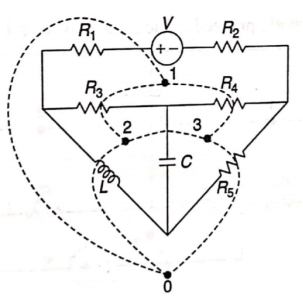
The dual network is shown in figure

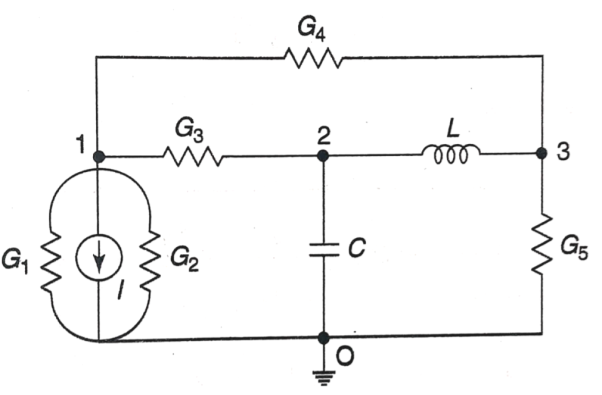
Q) Find dual for the series RLC circuit?

Sol: Let us consider RLC circuit

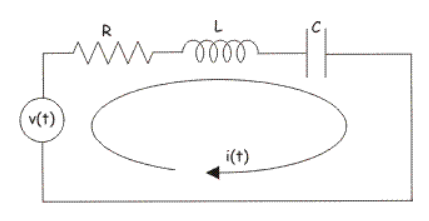
Applying KVL we have

v(t) = ri(t) + L + 

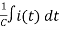
So, dual of above network will be

i(t) = Gv(t) + C +

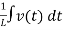
Q) For the characteristics given below comment about the type of element?

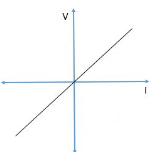
Sol: It is Linear, Bilateral and Passive element

Q) For the figure below comment on the type of element?

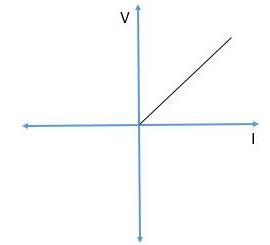
Sol: The element is Non-Linear, Passive and Unilateral.

References:

1. Mahmood Nahvi, Joseph A Edminister, “Schaum’s outline of Electric Circuits”, 6th Edition, Tata McGraw-Hill, 6th Edition, 2013

2. W. H. Hayt and J. E. Kemmerly, “Engineering Circuit Analysis”, McGraw Hill Education, 2013.

3. C. K. Alexander and M. N. O. Sadiku, “Electric Circuits”, McGraw Hill Education, 2004.

4. K. V. V. Murthy and M. S. Kamath, “Basic Circuit Analysis”, Jaico Publishers, 1999.

5. K. Sureshkumar, “Electric Circuits & Network”, Pearson Publication

6. Del Toro, “Electrical circuit”, Prentice Hall