Unit - 1
Data Structures
A data structure is a collection of data pieces that provides an efficient method for storing and organizing data in a computer so that it may be used effectively. Arrays, Linked Lists, Stacks, Queues, and other Data Structures are examples. Data Structures are employed in practically every element of computer science, including operating systems, compiler design, artificial intelligence, graphics, and many more applications.
Data Structures are an important aspect of many computer science algorithms because they allow programmers to efficiently handle data. It is critical to improving the performance of a software or program because the software's primary duty is to save and retrieve user data as quickly as feasible.
Basic terminology
The building blocks of every program or software are data structures. The most challenging challenge for a programmer is deciding on a suitable data structure for a program. When it comes to data structures, the following terminology is utilized.
Data: The data on a student can be defined as an elementary value or a set of values, for example, the student's name and id.
Group items: Group items are data items that include subordinate data items, such as a student's name, which can have both a first and a last name.
Record: A record can be characterized as a collection of several data objects. For example, if we consider the student entity, the name, address, course, and grades can all be gathered together to constitute the student's record.
File: A file is a collection of various records of one type of entity; for example, if there are 60 employees in the class, the relevant file will contain 20 records, each containing information about each employee.
Attribute and Entity: A class of objects is represented by an entity. It has a number of characteristics. Each attribute represents an entity's specific property.
Key takeaway
A data structure is a collection of data pieces that provides an efficient method for storing and organizing data in a computer so that it may be used effectively.
As applications become more complicated and the amount of data collected grows, the following issues may arise:
● Processor speed: High-speed processing is essential to manage vast amounts of data, however as data grows by the day to billions of files each entity, processors may be unable to handle that much data.
● Data Search: Consider a store with a 106-item inventory. If our programme needs to search for a specific item, it must traverse all 106 items each time, which slows down the search process.
● Multiple requests: If thousands of users are searching for data on a web server at the same time, there is a potential that a very large server will fail during the process.
Data structures are used to solve the difficulties listed above. Data is grouped into a data structure in such a way that not all things must be searched and essential data can be found quickly.
Advantages of Data Structures
● Efficiency: The efficiency of a programme is determined by the data structures used. Consider the following scenario: we have certain data and need to find a specific record. If we structure our data in an array, we will have to search element by element in such a scenario. As a result, employing an array may not be the most efficient solution in this case. There are more efficient data structures for searching, such as an ordered array, a binary search tree, or hash tables.
● Reusability: Data structures are reusable, which means that after we've implemented one, we can use it somewhere else. Data structure implementations can be compiled into libraries that can be utilized by a variety of clients.
● Abstraction: The ADT specifies the data structure, which provides a level of abstraction. The client software only interacts with the data structure through an interface, thus it isn't concerned with the implementation details.
The abstract data type is a special kind of datatype, whose behavior is defined by a set of values and set of operations. The keyword “Abstract” is used as we can use these data types, we can perform different operations. But how those operations are working is totally hidden from the user. The ADT is made of primitive data types, but operation logics are hidden.
Here we will see the stack ADT. These are a few operations or functions of the Stack ADT.
● isFull(), This is used to check whether stack is full or not
● isEmpty(), This is used to check whether stack is empty or not
● push(x), This is used to push x into the stack
● pop(), This is used to delete one element from top of the stack
● peek(), This is used to get the top most element of the stack
● size(), this function is used to get number of elements present into the stack
Example
#include<iostream>
#include<stack>
Using namespace std;
Main(){
stack<int> stk;
if(stk.empty()){
cout << "Stack is empty" << endl;
} else {
cout << "Stack is not empty" << endl;
}
//insert elements into stack
stk.push(10);
stk.push(20);
stk.push(30);
stk.push(40);
stk.push(50);
cout << "Size of the stack: " << stk.size() << endl;
//pop and display elements
while(!stk.empty()){
int item = stk.top(); // same as peek operation
stk.pop();
cout << item << " ";
}
}
Output
Stack is empty
Size of the stack: 5
50 40 30 20 10
Key takeaway
The abstract data type is a special kind of datatype, whose behavior is defined by a set of values and set of operations.
The keyword “Abstract” is used as we can use these data types, we can perform different operations. But how those operations are working is totally hidden from the user.
The ADT is made of primitive data types, but operation logics are hidden.
What is an Algorithm?
An algorithm is a process or a set of rules required to perform calculations or some other problem-solving operations especially by a computer. The formal definition of an algorithm is that it contains the finite set of instructions which are being carried in a specific order to perform the specific task. It is not the complete program or code; it is just a solution (logic) of a problem, which can be represented either as an informal description using a Flowchart or Pseudocode.
Characteristics of an Algorithm
The following are the characteristics of an algorithm:
● Input: An algorithm has some input values. We can pass 0 or some input value to an algorithm.
● Output: We will get 1 or more output at the end of an algorithm.
● Unambiguity: An algorithm should be unambiguous which means that the instructions in an algorithm should be clear and simple.
● Finiteness: An algorithm should have finiteness. Here, finiteness means that the algorithm should contain a limited number of instructions, i.e., the instructions should be countable.
● Effectiveness: An algorithm should be effective as each instruction in an algorithm affects the overall process.
● Language independent: An algorithm must be language-independent so that the instructions in an algorithm can be implemented in any of the languages with the same output.
Dataflow of an Algorithm
● Problem: A problem can be a real-world problem or any instance from the real-world problem for which we need to create a program or the set of instructions. The set of instructions is known as an algorithm.
● Algorithm: An algorithm will be designed for a problem which is a step by step procedure.
● Input: After designing an algorithm, the required and the desired inputs are provided to the algorithm.
● Processing unit: The input will be given to the processing unit, and the processing unit will produce the desired output.
● Output: The output is the outcome or the result of the program.
Why do we need Algorithms?
We need algorithms because of the following reasons:
● Scalability: It helps us to understand scalability. When we have a big real-world problem, we need to scale it down into small-small steps to easily analyze the problem.
● Performance: The real-world is not easily broken down into smaller steps. If the problem can be easily broken into smaller steps means that the problem is feasible.
Let's understand the algorithm through a real-world example. Suppose we want to make a lemon juice, so following are the steps required to make a lemon juice:
Step 1: First, we will cut the lemon into half.
Step 2: Squeeze the lemon as much as you can and take out its juice in a container.
Step 3: Add two tablespoons of sugar in it.
Step 4: Stir the container until the sugar gets dissolved.
Step 5: When sugar gets dissolved, add some water and ice in it.
Step 6: Store the juice in a fridge for 5 to minutes.
Step 7: Now, it's ready to drink.
The above real-world can be directly compared to the definition of the algorithm. We cannot perform step 3 before step 2, we need to follow the specific order to make lemon juice. An algorithm also says that each and every instruction should be followed in a specific order to perform a specific task.
Now we will look at an example of an algorithm in programming.
We will write an algorithm to add two numbers entered by the user.
The following are the steps required to add two numbers entered by the user:
Step 1: Start
Step 2: Declare three variables a, b, and sum.
Step 3: Enter the values of a and b.
Step 4: Add the values of a and b and store the result in the sum variable, i.e., sum=a+b.
Step 5: Print sum
Step 6: Stop
Key takeaway
An algorithm is a process or a set of rules required to perform calculations or some other problem-solving operations especially by a computer.
The formal definition of an algorithm is that it contains the finite set of instructions which are being carried in a specific order to perform the specific task.
Efficiency of an Algorithm
Following are the conditions where we can analyze the algorithm:
● Time efficiency: indicates how fast algorithm is running
● Space efficiency: how much extra memory the algorithm needs to complete its execution
● Simplicity: - generating sequences of instruction which are easy to understand.
● Generality: - It fixes the range of inputs it can accept. The generality of problems which algorithms can solve.
The time efficiencies of a large number of algorithms fall into only a few classes
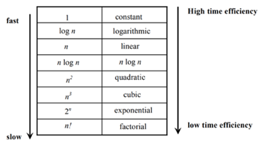
Fig 1: Time efficiency
Time complexity:
The time complexity of an algorithm is the amount of time required to complete the execution. The time complexity of an algorithm is denoted by the big O notation. Here, big O notation is the asymptotic notation to represent the time complexity. The time complexity is mainly calculated by counting the number of steps to finish the execution.
Let's understand the time complexity through an example.
- Sum=0;
- // Suppose we have to calculate the sum of n numbers.
- For i=1 to n
- Sum=sum+i;
- // when the loop ends then sum holds the sum of the n numbers
- Return sum;
In the above code, the time complexity of the loop statement will be at least n, and if the value of n increases, then the time complexity also increases. While the complexity of the code, i.e., return sum will be constant as its value is not dependent on the value of n and will provide the result in one step only. We generally consider the worst-time complexity as it is the maximum time taken for any given input size.
Space complexity: An algorithm's space complexity is the amount of space required to solve a problem and produce an output. Similar to the time complexity, space complexity is also expressed in big O notation.
For an algorithm, the space is required for the following purposes:
- To store program instructions
- To store constant values
- To store variable values
To track the function calls, jumping statements, etc.
Key takeaway
The time complexity of an algorithm is the amount of time required to complete the execution.
An algorithm's space complexity is the amount of space required to solve a problem and produce an output.
Big Oh (O) Notation:
- It is the formal way to express the time complexity.
- It is used to define the upper bound of an algorithm’s running time.
- It shows the worst-case time complexity or largest amount of time taken by the algorithm to perform a certain task.
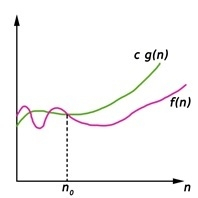
Fig 2: Big Oh notation
Here, f (n) <= g (n) …………….(eq1)
where n>= k, C>0 and k>=1
If any algorithm satisfies the eq1 condition then it becomes f (n)= O (g (n))
Big Omega (ῼ) Notation
- It is the formal way to express the time complexity.
- It is used to define the lower bound of an algorithm’s running time.
- It shows the best-case time complexity or best of time taken by the algorithm to perform a certain task.
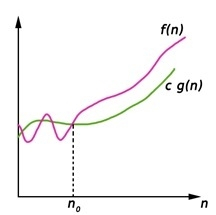
Fig 3: Big omega notation
Here, f (n) >= g (n)
Where n>=k and c>0, k>=1
If any algorithm satisfies the eq1 condition then it becomes f (n)= ῼ (g (n))
Theta (Θ) Notation
- It is the formal way to express the time complexity.
- It is used to define the lower as well as upper bound of an algorithm’s running time.
- It shows the average case time complexity or average of time taken by the algorithm to perform a certain task.
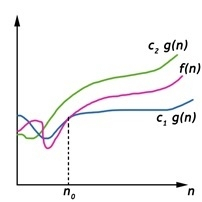
Fig 4: Theta notation
Let C1 g(n) be upper bound and C2 g(n) be lower bound.
C1 g(n)<= f (n)<=C2 g(n)
Where C1, C2>0 and n>=k
Key takeaway
- Big Oh is used to define the upper bound of an algorithm’s running time.
- Big Omega is used to define the lower bound of an algorithm’s running time.
- Theta is used to define the lower as well as upper bound of an algorithm’s running time.
- It is also known as time memory tradeoff.
- It is a way of solving problems in less time by using more storage space.
- It can be used with the problem of data storage.
- For example: time complexity of merge sort is O(n log n)in all cases. But requires an auxiliary array.
- In quick sort complexity is O(n log n) for best and average case but it doesn’t require auxiliary space.
- Two Space-for-Time Algorithm Varieties:
- Input enhancement - To store some info, preprocess the input (or its portion) to be used in solving the issue later
- Counting sorts
- String searching algorithms
- Pre-structuring-preprocessing the input to access its components
1) hashing 2) indexing schemes simpler (e.g., B-trees)
Key takeaway
- It is also known as time memory tradeoff.
- It is a way of solving problems in less time by using more storage space.
Searching is the process of looking for a certain item in a list. If the element is found in the list, the process is considered successful, and the location of that element is returned; otherwise, the search is considered unsuccessful.
Linear Search and Binary Search are two prominent search strategies. So, we'll talk about a popular search strategy called the Linear Search Algorithm.
The linear search algorithm is also known as the sequential search algorithm. It is the most basic search algorithm. We just traverse the list in linear search and match each element of the list with the object whose position has to be discovered. If a match is found, the algorithm delivers the item's location; otherwise, NULL is returned.
It's commonly used to find an element in an unordered list, or one in which the items aren't sorted. The time complexity of linear search in the worst-case scenario is O(n).
The following are the steps involved in implementing Linear Search:
● We must first use a for loop to traverse the array elements.
● Compare the search element with the current array element in each iteration of the for loop, and -
○ Return the index of the related array entry if the element matches.
○ If the element you're looking for doesn't match, move on to the next one.
● Return -1 if there is no match or the search element is not found in the given array.
Let's look at the linear search algorithm now.
Algorithm
Linear_Search(a, n, val) // 'a' is the given array, 'n' is the size of given array, 'val' is the value to search
Step 1: set pos = -1
Step 2: set i = 1
Step 3: repeat step 4 while i <= n
Step 4: if a[i] == val
Set pos = i
Print pos
Go to step 6
[end of if]
Set ii = i + 1
[end of loop]
Step 5: if pos = -1
Print "value is not present in the array "
[end of if]
Step 6: exit
Time Complexity
Case | Time Complexity |
Best Case | O(1) |
Average Case | O(n) |
Worst Case | O(n) |
Space Complexity
Space Complexity | O(1) |
Application of Linear Search Algorithm
The linear search algorithm is useful for the following tasks:
● Both single-dimensional and multi-dimensional arrays can benefit from linear search.
● When the array has only a few elements, linear search is simple to implement and effective.
● When performing a single search in an unordered-List, Linear Search is also quite efficient.
Binary Search
Binary search is the search technique which works efficiently on the sorted lists. Hence, in order to search an element into some list by using binary search technique, we must ensure that the list is sorted.
Binary search follows a divide and conquer approach in which the list is divided into two halves and the item is compared with the middle element of the list. If the match is found then, the location of the middle element is returned; otherwise, we search into either of the halves depending upon the result produced through the match.
Binary search algorithm is given below.
BINARY_SEARCH(A, lower_bound, upper_bound, VAL)
● Step 1: [INITIALIZE] SET BEG = lower_bound
END = upper_bound, POS = - 1
● Step 2: Repeat Steps 3 and 4 while BEG <=END
● Step 3: SET MID = (BEG + END)/2
● Step 4: IF A[MID] = VAL
SET POS = MID
PRINT POS
Go to Step 6
ELSE IF A[MID] > VAL
SET END = MID - 1
ELSE
SET BEG = MID + 1
[END OF IF]
[END OF LOOP]
● Step 5: IF POS = -1
PRINT "VALUE IS NOT PRESENT IN THE ARRAY"
[END OF IF]
● Step 6: EXIT
Complexity
SN | Performance | Complexity |
1 | Worst case | O(log n) |
2 | Best case | O(1) |
3 | Average Case | O(log n) |
4 | Worst case space complexity | O(1) |
Example
Let us consider an array arr = {1, 5, 7, 8, 13, 19, 20, 23, 29}. Find the location of the item 23 in the array.
In 1st step:
- BEG = 0
- END = 8ron
- MID = 4
- a[mid] = a[4] = 13 < 23, therefore
In Second step:
- Beg = mid +1 = 5
- End = 8
- Mid = 13/2 = 6
- a[mid] = a[6] = 20 < 23, therefore;
In third step:
- Beg = mid + 1 = 7
- End = 8
- Mid = 15/2 = 7
- a[mid] = a[7]
- a[7] = 23 = item;
- Therefore, set location = mid;
- The location of the item will be 7.
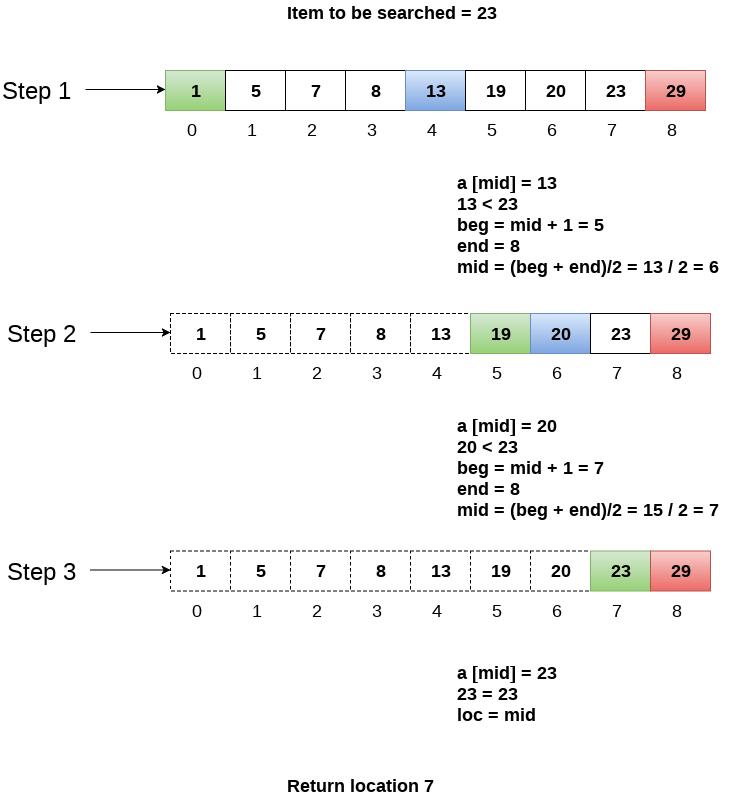
Fig 3 - Example
Bubble sort
Bubble Sort is a simple algorithm for sorting a collection of n elements that is provided in the form of an array with n elements. Bubble Sort compares each element individually and sorts them according to their values.
If an array must be sorted in ascending order, bubble sort will begin by comparing the first and second members of the array, swapping both elements if the first element is greater than the second, and then moving on to compare the second and third elements, and so on.
If there are n elements in total, we must repeat the method n-1 times.
It's called bubble sort because the largest element in the given array bubbles up to the last position or highest index with each full iteration, similar to how a water bubble rises to the sea surface.
Although it is simple to use, bubble sort is largely employed as an educational tool because its performance in the actual world is low. It isn't designed to handle huge data collections. Bubble sort has an average and worst-case complexity of O(n2), where n is the number of elements.
Sorting is done by going through all of the items one by one, comparing them to the next closest element, and swapping them if necessary.
Algorithm
Assume arr is an array of n elements in the algorithm below. The algorithm's presumed swap function will swap the values of specified array members.
Begin BubbleSort(arr)
for all array elements
if arr[i] > arr[i+1]
swap(arr[i], arr[i+1])
end if
end for
return arr
End BubbleSort
Working of Bubble Sort
Assume we're attempting to arrange the elements in ascending order.
1. First Iteration (Compare and Swap)
● Compare the first and second elements starting with the first index.
● The first and second elements are swapped if the first is bigger than the second.
● Compare and contrast the second and third elements now. If they aren't in the right order, swap them.
● The process continues until the last piece is added.
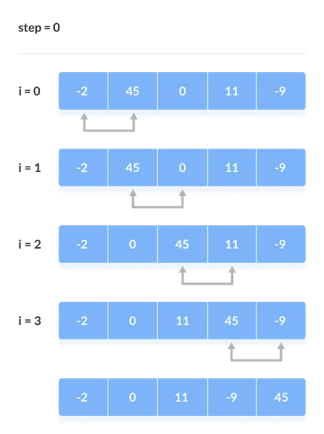
2. Remaining Iteration
For the remaining iterations, the same procedure is followed.
The largest element among the unsorted items is placed at the conclusion of each iteration.
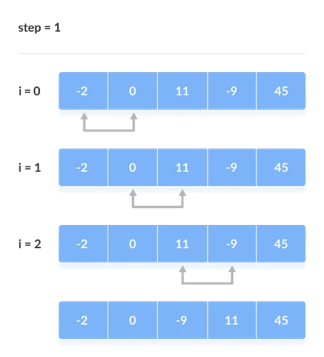
The comparison takes place up to the last unsorted element in each iteration.
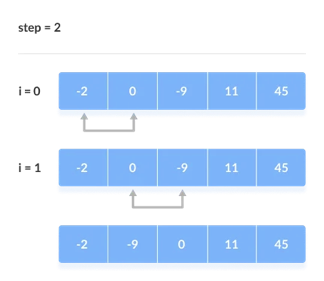
When all of the unsorted elements have been placed in their correct placements, the array is said to be sorted.
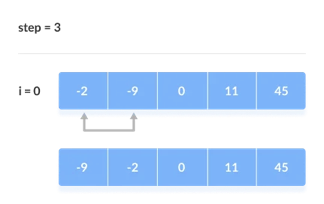
Key takeaway
- Compare and swap adjacent elements of the list if they are out of order.
- After repeating the procedure, we end up 'bubbling up' the largest element to the last place on the list by doing it repeatedly.
Insertion sort
Insertion style is a decrease & conquer technique application. It is a sort based on comparison in which the sorted array is constructed on one entry at a time.
Insertion sorting is a very basic process for sorting numbers in an ascending or descending order. The gradual method is accompanied by this method. It can be contrasted with the method of sorting cards at the time of playing a game.
The numbers that are needed to be sorted are known as keys. Here is the insertion sort method algorithm.
Algorithm:
Algorithm: Insertion-Sort (A)
For j = 2 to A.length
Key = A[j]
// Insert A[j] into the sorted sequence A[1.. j - 1]
i = j - 1
While i > 0 and A[i] > key
A[i + 1] = A[i]
i = i -1
A[i + 1] = key
Analysis:
This algorithm's run time is very dependent on the input given.
If the numbers given are sorted, this algorithm runs in O(n) time. If the numbers given are in reverse order, the algorithm runs in O(n2) time.
Example:
Using insertion sort to sort the following list of elements:
89, 45, 68, 90, 29, 34, 17
89 |45 68 90 29 34 17
45 89 |68 90 29 34 17
45 68 89 |90 29 34 17
45 68 89 90 |29 34 17
29 45 68 89 90 |34 17
29 34 45 68 89 90 |17
17 29 34 45 68 89 90
Application:
In the following instances, the insertion sort algorithm is used:
- When only a few elements are in the list.
- When there are few elements for sorting.
Advantages:
- Straightforward implementation. Three variants exist.
● Left to right scan
● Right to left scan
● Binary insertion sort
2. Effective on a small list of components, on a nearly sorted list.
3. In the best example, running time is linear.
4. This algorithm is stable.
5. Is the on-the-spot algorithm
Key takeaways
- Insertion sorting is a very basic process for sorting numbers in an ascending or descending order.
- Insertion style is a decrease & conquer technique application.
- It is a sort based on comparison in which the sorted array is constructed on one entry at a time.
Selection sort
In the selection sort, the smallest value among the array's unsorted items is chosen in each pass and inserted into the proper spot.
To begin, locate the array's smallest element and set it in the first position. Then locate the array's second smallest element and set it in the second spot. The procedure is repeated till the sorted array is obtained.
The n-1 pass of the selection sort algorithm is used to sort the array of n entries.
● The smallest element of the array, as well as its index pos, must be identified in the first run. Swap A[0] and A[pos] after that. As a result of sorting A[0], we now have n -1 elements to sort.
● The location pos of the smallest element in the sub-array A[n-1] is obtained in the second pass. Swap A[1] and A[pos] after that. After sorting A[0] and A[1], we're left with n-2 unsorted elements.
● The position pos of the smaller element between A[n-1] and A[n-2] must be found in the n-1st pass. Swap A[pos] and A[n-1] after that.
As a result, the items A[0], A[1], A[2],...., A[n-1] are sorted using the procedure described above.
Example
Consider the following six-element array. Using selection sort, sort the array's elements.
A = {10, 2, 3, 90, 43, 56}.
Pass | Pos | A[0] | A[1] | A[2] | A[3] | A[4] | A[5] |
1 | 1 | 2 | 10 | 3 | 90 | 43 | 56 |
2 | 2 | 2 | 3 | 10 | 90 | 43 | 56 |
3 | 2 | 2 | 3 | 10 | 90 | 43 | 56 |
4 | 4 | 2 | 3 | 10 | 43 | 90 | 56 |
5 | 5 | 2 | 3 | 10 | 43 | 56 | 90 |
Sorted A = {2, 3, 10, 43, 56, 90}
Algorithm
SELECTION SORT(ARR, N)
● Step 1: Repeat Steps 2 and 3 for K = 1 to N-1
● Step 2: CALL SMALLEST(ARR, K, N, POS)
● Step 3: SWAP A[K] with ARR[POS]
[END OF LOOP]
● Step 4: EXIT
SMALLEST (ARR, K, N, POS)
● Step 1: [INITIALIZE] SET SMALL = ARR[K]
● Step 2: [INITIALIZE] SET POS = K
● Step 3: Repeat for J = K+1 to N -1
IF SMALL > ARR[J]
SET SMALL = ARR[J]
SET POS = J
[END OF IF]
[END OF LOOP]
● Step 4: RETURN POS
Key takeaway
- In the selection sort, the smallest value among the array's unsorted items is chosen in each pass and inserted into the proper spot.
- To begin, locate the array's smallest element and set it in the first position.
- Then locate the array's second smallest element and set it in the second spot.
It becomes easier to solve the complete problem if we can separate a single major problem into smaller sub-problems, solve the smaller sub-problems, and integrate their solutions to find the solution for the original huge problem.
Let's look into Divide and Rule as an example.
When the British arrived in India, they encountered a country where many religions coexisted peacefully, hardworking but ignorant individuals, and unity in variety, making it difficult for them to establish their empire. As a result, they chose the Divide and Rule strategy. Where the population of India was a single large difficulty for them, they divided it into smaller ones by inciting rivalries amongst local monarchs and pitting them against one another, which worked extremely well for them.
That was history and a socio-political policy (Break and Rule), but the notion here is that if we can divide a problem into smaller sub-problems, it becomes easier to tackle the total problem in the end.
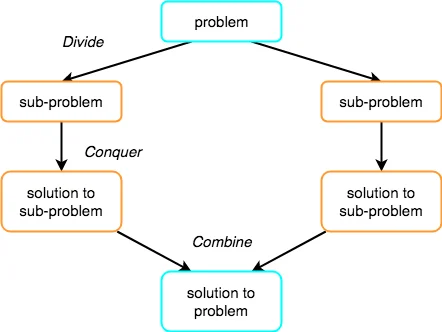
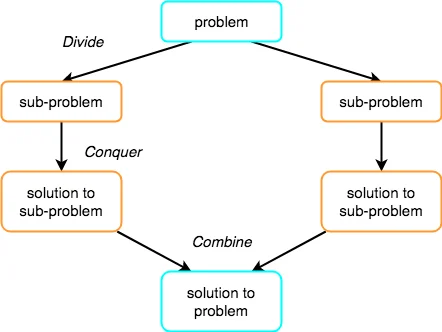
The Divide and Conquer strategy consists of three steps:
● Break the problem down into smaller chunks.
● Solve the subproblems to defeat them. The goal is to break down the problem into atomic subproblems that can be solved individually.
● To obtain the solution to the actual problem, combine the solutions of the subproblems.
Merge sort
Merge Sort is based on a divide and conquer strategy. It divides the unsorted list into n sublists such that each sublist contains one element. Each sublist is then sorted and merged until there is only one sublist.
Step 1: Divide the list into sublists such that each sublist contains only one element.
Step 2: Sort each sublist and Merge them.
Step 3: Repeat Step 2 till the entire list is sorted.
Example: Apply Merge Sort on array A= {85,24,63,45,17,31,96,50}
Step1: A contains 8 elements. First we divide the list into two sublists such that each sublist contains 4 elements. Then we divide each sublist of 4 elements into sublist of two elements each. Finally every sublist contains only one element.
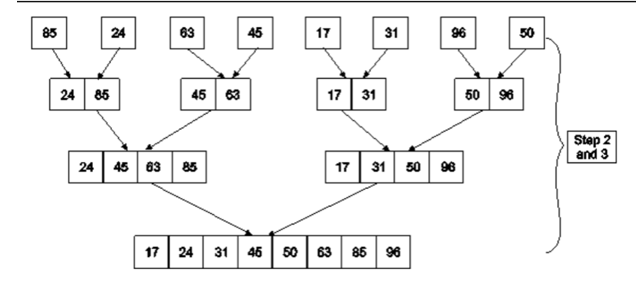
Fig. 4: Example
Step 2: Now we start from the bottom. Compare 1st and 2nd element. Sort and merge them. Apply this for all bottom elements.
Thus we got 4 sublists as follows
24 | 85 |
| 45 | 63 |
| 17 | 31 |
| 50 | 96 |
Step 3: Repeat this sorting and merging until the entire list is sorted. The above four sublists are sorted and merged to form 2 sublists.
24 | 85 | 63 | 85 |
| 17 | 31 | 50 | 96 |
Finally, the above 2 sublists are again sorted and merged in one sublist.
17 | 24 | 31 | 45 | 50 | 63 | 85 | 96 |
We will see one more example on merge sort.
Example: Apply merge Sort on array A={10,5,7,6,1,4,8,3,2,9,12,11}
Step 1:
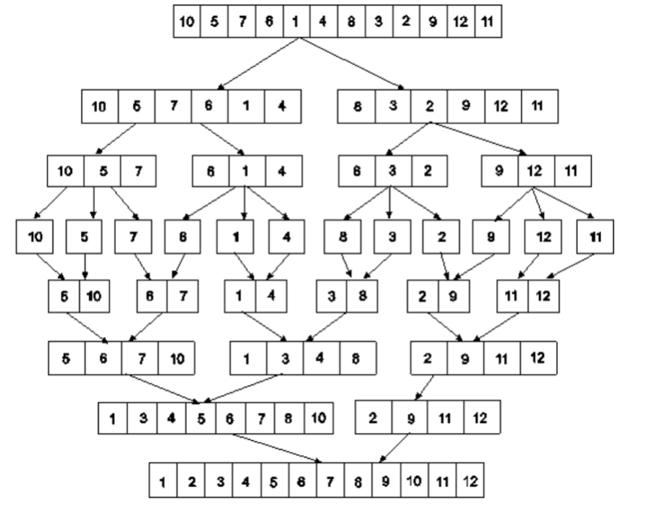
Fig 5: Merge sort
Algorithm for Merge Sort:
Let x = no. Of elements in array A
y = no. Of elements in array B
C = sorted array with no. Of elements n
n = x+y
Following algorithm merges a sorted x element array A and sorted y element array B into a sorted array C, with n = x + y elements. We must always keep track of the locations of the smallest element of A and the smallest element of B which have not yet been placed in C. Let LA and LB denote these locations, respectively. Also, let LC denote the location in C to be filled. Thus, initially, we set
LA : = 1,
LB : = 1 and
LC : = 1.
At each step, we compare A[LA] and B[LB] and assign the smaller element to C[LC].
Then
LC:= LC + 1,
LA: = LA + 1, if a new element has come from A .
LB: = LB + 1, if a new element has come from B.
Furthermore, if LA> x, then the remaining elements of B are assigned to C;
LB >y, then the remaining elements of A are assigned to C.
Thus the algorithm becomes
MERGING ( A, x, B, y, C)
1. [Initialize ] Set LA : = 1 , LB := 1 AND LC : = 1
2. [Compare] Repeat while LA <= x and LB <= y
If A[LA] < B[LB] , then
(a) [Assign element from A to C ] set C[LC] = A[LA]
(b) [Update pointers ] Set LC := LC +1 and LA = LA+1
Else
(a) [Assign element from B to C] Set C[LC] = B[LB]
(b) [Update Pointers] Set LC := LC +1 and LB = LB +1
[End of loop]
3. [Assign remaining elements to C]
If LA > x , then
Repeat for K= 0 ,1,2,........,y–LB
Set C[LC+K] = B[LB+K]
[End of loop]
Else
Repeat for K = 0,1,2,......,x–LA
Set C[LC+K] = A[LA+K]
[End of loop]
4. Exit
Quick sort
Quick sort is the most efficient method of sorting .It uses the divide and conquer strategy to sort the elements. In quicksort, we divide the array of items to be sorted into two partitions and then call the quicksort procedure recursively to sort the two partitions. For this we choose a pivot element and arrange all elements such that all the elements in the left part are less than the pivot and all those in the right part are greater than it.
Algorithm to implement Quick Sort is as follows.
Consider array A of size n to be sorted. p is the pivot element. Index positions of the first and last element of array A are denoted by ‘first’ and ‘last’.
- Initially first=0 and last=n–1.
- Increment first till A[first]<=p
- Decrement last till A[last]>=p
- If first < last then swap A[first] with A[last].
- If first > last then swap p with A[last] and thus the position of p is found. Pivot p is placed such that all elements to its left are less than it and all elements right to it are greater than it. Let us assume that j is the final position of p. Then A[0] to A[j–1] are less than p and A [j + 1] to A [n–1]are greater than p.
- Now we consider the left part of array A i.e A[0] to A[j–1].Repeat step 1,2,3 and 4. Apply the same procedure for the right part of the array.
- We continue with the above steps till no more partitions can be made for every subarray.
Algorithm
PARTITION (ARR, BEG, END, LOC)
● Step 1: [INITIALIZE] SET LEFT = BEG, RIGHT = END, LOC = BEG, FLAG =
● Step 2: Repeat Steps 3 to 6 while FLAG =
● Step 3: Repeat while ARR[LOC] <=ARR[RIGHT]
AND LOC != RIGHT
SET RIGHT = RIGHT – 1
[END OF LOOP]
● Step 4: IF LOC = RIGHT
SET FLAG = 1
ELSE IF ARR[LOC] > ARR[RIGHT]
SWAP ARR[LOC] with ARR[RIGHT]
SET LOC = RIGHT
[END OF IF]
● Step 5: IF FLAG = 0
Repeat while ARR[LOC] >= ARR[LEFT] AND LOC != LEFT
SET LEFT = LEFT + 1
[END OF LOOP]
● Step 6:IF LOC = LEFT
SET FLAG = 1
ELSE IF ARR[LOC] < ARR[LEFT]
SWAP ARR[LOC] with ARR[LEFT]
SET LOC = LEFT
[END OF IF]
[END OF IF]
● Step 7: [END OF LOOP]
● Step 8: END
QUICK_SORT (ARR, BEG, END)
● Step 1: IF (BEG < END)
CALL PARTITION (ARR, BEG, END, LOC)
CALL QUICKSORT(ARR, BEG, LOC - 1)
CALL QUICKSORT(ARR, LOC + 1, END)
[END OF IF]
● Step 2: END
Key takeaways
- Merge sort consisting two phases as divide and merge.
- In divide phase, each time it divides the given unsorted list into two sub list until each sub list get single element then sorts the elements.
- In merge phase, it merges all the solution of sub lists and find the original sorted list.
- Quick sort is the most efficient method of sorting .It uses the divide and conquer strategy to sort the elements.
- In quicksort, we divide the array of items to be sorted into two partitions and then call the quicksort procedure recursively to sort the two partitions.
Bubble Sort, Selection Sort, Insertion Sort, Merge Sort, Quick Sort, Heap Sort, Counting Sort, Radix Sort, and Bucket Sort have all had their time and space difficulties discussed.
Bubble sort
Each nearby pair is compared in bubble sort. We swap them if they aren't in the right order. We repeat the preceding procedure until no more swaps are required, indicating that all of the components have been sorted.
Worse case: O(n2)
We iterate through the array (n - 1) times once it is reverse-sorted. We do (n - 1) swaps in the first iteration, (n - 2) swaps in the second, and so on until we only do one swap in the last iteration. As a result, the total number of swaps equals n * (n - 1) / 2.
Average case: O(n2)
The total number of swaps for a truly random array averages out to roughly n2 / 4, which is again O(n2).
Best case: O(n)
In the first iteration of the array, if no swaps are performed, we know that the array is already sorted and hence cease sorting, resulting in a linear time complexity.
Space Complexity:
The space complexity is O(1) since we only use a constant amount of additional memory away from the input array.
Selection Sort
Selection sort is a straightforward sorting method that divides an array into two parts: a subarray of already sorted elements and a subarray of unsorted elements. Initially, the sorted subarray is empty. The array is iterated over (n - 1) times. We find the smallest element from the unsorted subarray and set it at the end of the sorted subarray in each iteration.
Time Complexity:
Worst case = Average Case = Best Case = O(n2)
For an array of whatever size, we conduct the same number of comparisons.
We execute (n - 1) comparisons in the first iteration, (n - 2) in the second, and so on until the last iteration, when we only perform one comparison. As a result, the total number of comparisons is n * (n - 1) / 2. The number of swaps performed is at most n - 1. So the overall time complexity is quadratic.
Space Complexity:
The space complexity is O(1) because we don't use any other data structures except the input array.
Insertion Sort
The insertion sort method, like selection sort, separates the array into two parts: a subarray of already sorted elements and a subarray of unsorted elements. Only the first member of the array is originally stored in the sorted subarray. We go over each of the remaining elements one by one, putting them in their proper places in the sorted subarray.
Time Complexity:
Worse case: O(n2)
When we use insertion sort on a reverse-sorted array, each element is inserted at the beginning of the sorted subarray, which has the highest temporal complexity.
Average case: O(n2)
The average running time is O(n2 / 4) = O(n2). When the array members are in random order.
Best case: O(n)
When we run insertion sort on an array that has previously been sorted, it merely compares each element to its predecessor, needing n steps to sort the already sorted array of n elements.
Space Complexity:
The space complexity is O(1) since we only use a constant amount of additional memory away from the input array.
Merge Sort
We partition the unsorted array into n subarrays, each of size one, that can be considered sorted trivially in merge sort. Then, until there is only one sorted array of size n left, we merge the sorted subarrays to make new sorted subarrays.
Time Complexity:
Worst case = Average Case = Best Case = O(n log n)
For any input array of a certain size, merge sort performs the same number of operations.
We divide the array into two subarrays repeatedly in this approach, resulting in O(log n) rows with each element appearing exactly once in each row.
Merging every pair of subarrays takes O(n) time for each row. As a result, the entire time complexity is O(n log n).
Space Complexity:
The space complexity is O(n) since we store the merged subarray in an auxiliary array of size at most n.
Quick Sort
Quick sort is a more complicated algorithm. It divides the array into two subarrays using a divide-and-conquer approach. We pick an element called pivot and place it at its proper index before reordering the array by moving all elements less than pivot to the left and all elements greater than it to the right.
The subarrays of these subarrays are then sorted recursively until the entire array is sorted. The pivot element's selection has a significant impact on the quick sort algorithm's efficiency.
Time Complexity:
Worse case: O(n2)
When the array is sorted and the leftmost element is chosen as pivot, or when the array is reverse-sorted and the rightmost element is chosen as pivot, the time complexity increases quadratically because dividing the array produces extremely unbalanced subarrays.
When the array has a high number of identical members, splitting becomes difficult, resulting in quadratic time complexity.
Average case and best case: O(n log n)
The best case scenario for quick-sort is when we consistently use the median element for partitioning. As a result of this partitioning, we can always divide the array in half.
Space Complexity:
Although rapid sort does not need auxiliary space to store array elements, recursive calls require additional space to create stack frames.
Worst case: O(n)
This occurs when the pivot element in each recursive call is the largest or smallest element of the array. After partitioning, the size of the subarray will be n-1 and 1. The recursive tree will be n in size in this situation.
Best case: O(log n)
This occurs when the right position of the pivot element in the partitioned array is always in the middle. Subarrays will have a size of half that of the parent array. The size of the recursive tree will be O in this situation (log n).
References:
- Data Structures with C, Seymour Lipschutz, Schaum's Outlines, Tata McGraw Hill Education.
- Fundamentals of Computer Algorithms by Horowitz, Sahni,Galgotia Pub. 2001 ed.
- Data Structures and program design in C by Robert Kruse, Bruce Leung & Clovis Tondo.
- Data Structures: A Pseudocode Approach with C by Richard F. Gilberg and
Behrouz Forouzan.
Unit - 1
Data Structures
A data structure is a collection of data pieces that provides an efficient method for storing and organizing data in a computer so that it may be used effectively. Arrays, Linked Lists, Stacks, Queues, and other Data Structures are examples. Data Structures are employed in practically every element of computer science, including operating systems, compiler design, artificial intelligence, graphics, and many more applications.
Data Structures are an important aspect of many computer science algorithms because they allow programmers to efficiently handle data. It is critical to improving the performance of a software or program because the software's primary duty is to save and retrieve user data as quickly as feasible.
Basic terminology
The building blocks of every program or software are data structures. The most challenging challenge for a programmer is deciding on a suitable data structure for a program. When it comes to data structures, the following terminology is utilized.
Data: The data on a student can be defined as an elementary value or a set of values, for example, the student's name and id.
Group items: Group items are data items that include subordinate data items, such as a student's name, which can have both a first and a last name.
Record: A record can be characterized as a collection of several data objects. For example, if we consider the student entity, the name, address, course, and grades can all be gathered together to constitute the student's record.
File: A file is a collection of various records of one type of entity; for example, if there are 60 employees in the class, the relevant file will contain 20 records, each containing information about each employee.
Attribute and Entity: A class of objects is represented by an entity. It has a number of characteristics. Each attribute represents an entity's specific property.
Key takeaway
A data structure is a collection of data pieces that provides an efficient method for storing and organizing data in a computer so that it may be used effectively.
As applications become more complicated and the amount of data collected grows, the following issues may arise:
● Processor speed: High-speed processing is essential to manage vast amounts of data, however as data grows by the day to billions of files each entity, processors may be unable to handle that much data.
● Data Search: Consider a store with a 106-item inventory. If our programme needs to search for a specific item, it must traverse all 106 items each time, which slows down the search process.
● Multiple requests: If thousands of users are searching for data on a web server at the same time, there is a potential that a very large server will fail during the process.
Data structures are used to solve the difficulties listed above. Data is grouped into a data structure in such a way that not all things must be searched and essential data can be found quickly.
Advantages of Data Structures
● Efficiency: The efficiency of a programme is determined by the data structures used. Consider the following scenario: we have certain data and need to find a specific record. If we structure our data in an array, we will have to search element by element in such a scenario. As a result, employing an array may not be the most efficient solution in this case. There are more efficient data structures for searching, such as an ordered array, a binary search tree, or hash tables.
● Reusability: Data structures are reusable, which means that after we've implemented one, we can use it somewhere else. Data structure implementations can be compiled into libraries that can be utilized by a variety of clients.
● Abstraction: The ADT specifies the data structure, which provides a level of abstraction. The client software only interacts with the data structure through an interface, thus it isn't concerned with the implementation details.
The abstract data type is a special kind of datatype, whose behavior is defined by a set of values and set of operations. The keyword “Abstract” is used as we can use these data types, we can perform different operations. But how those operations are working is totally hidden from the user. The ADT is made of primitive data types, but operation logics are hidden.
Here we will see the stack ADT. These are a few operations or functions of the Stack ADT.
● isFull(), This is used to check whether stack is full or not
● isEmpty(), This is used to check whether stack is empty or not
● push(x), This is used to push x into the stack
● pop(), This is used to delete one element from top of the stack
● peek(), This is used to get the top most element of the stack
● size(), this function is used to get number of elements present into the stack
Example
#include<iostream>
#include<stack>
Using namespace std;
Main(){
stack<int> stk;
if(stk.empty()){
cout << "Stack is empty" << endl;
} else {
cout << "Stack is not empty" << endl;
}
//insert elements into stack
stk.push(10);
stk.push(20);
stk.push(30);
stk.push(40);
stk.push(50);
cout << "Size of the stack: " << stk.size() << endl;
//pop and display elements
while(!stk.empty()){
int item = stk.top(); // same as peek operation
stk.pop();
cout << item << " ";
}
}
Output
Stack is empty
Size of the stack: 5
50 40 30 20 10
Key takeaway
The abstract data type is a special kind of datatype, whose behavior is defined by a set of values and set of operations.
The keyword “Abstract” is used as we can use these data types, we can perform different operations. But how those operations are working is totally hidden from the user.
The ADT is made of primitive data types, but operation logics are hidden.
What is an Algorithm?
An algorithm is a process or a set of rules required to perform calculations or some other problem-solving operations especially by a computer. The formal definition of an algorithm is that it contains the finite set of instructions which are being carried in a specific order to perform the specific task. It is not the complete program or code; it is just a solution (logic) of a problem, which can be represented either as an informal description using a Flowchart or Pseudocode.
Characteristics of an Algorithm
The following are the characteristics of an algorithm:
● Input: An algorithm has some input values. We can pass 0 or some input value to an algorithm.
● Output: We will get 1 or more output at the end of an algorithm.
● Unambiguity: An algorithm should be unambiguous which means that the instructions in an algorithm should be clear and simple.
● Finiteness: An algorithm should have finiteness. Here, finiteness means that the algorithm should contain a limited number of instructions, i.e., the instructions should be countable.
● Effectiveness: An algorithm should be effective as each instruction in an algorithm affects the overall process.
● Language independent: An algorithm must be language-independent so that the instructions in an algorithm can be implemented in any of the languages with the same output.
Dataflow of an Algorithm
● Problem: A problem can be a real-world problem or any instance from the real-world problem for which we need to create a program or the set of instructions. The set of instructions is known as an algorithm.
● Algorithm: An algorithm will be designed for a problem which is a step by step procedure.
● Input: After designing an algorithm, the required and the desired inputs are provided to the algorithm.
● Processing unit: The input will be given to the processing unit, and the processing unit will produce the desired output.
● Output: The output is the outcome or the result of the program.
Why do we need Algorithms?
We need algorithms because of the following reasons:
● Scalability: It helps us to understand scalability. When we have a big real-world problem, we need to scale it down into small-small steps to easily analyze the problem.
● Performance: The real-world is not easily broken down into smaller steps. If the problem can be easily broken into smaller steps means that the problem is feasible.
Let's understand the algorithm through a real-world example. Suppose we want to make a lemon juice, so following are the steps required to make a lemon juice:
Step 1: First, we will cut the lemon into half.
Step 2: Squeeze the lemon as much as you can and take out its juice in a container.
Step 3: Add two tablespoons of sugar in it.
Step 4: Stir the container until the sugar gets dissolved.
Step 5: When sugar gets dissolved, add some water and ice in it.
Step 6: Store the juice in a fridge for 5 to minutes.
Step 7: Now, it's ready to drink.
The above real-world can be directly compared to the definition of the algorithm. We cannot perform step 3 before step 2, we need to follow the specific order to make lemon juice. An algorithm also says that each and every instruction should be followed in a specific order to perform a specific task.
Now we will look at an example of an algorithm in programming.
We will write an algorithm to add two numbers entered by the user.
The following are the steps required to add two numbers entered by the user:
Step 1: Start
Step 2: Declare three variables a, b, and sum.
Step 3: Enter the values of a and b.
Step 4: Add the values of a and b and store the result in the sum variable, i.e., sum=a+b.
Step 5: Print sum
Step 6: Stop
Key takeaway
An algorithm is a process or a set of rules required to perform calculations or some other problem-solving operations especially by a computer.
The formal definition of an algorithm is that it contains the finite set of instructions which are being carried in a specific order to perform the specific task.
Efficiency of an Algorithm
Following are the conditions where we can analyze the algorithm:
● Time efficiency: indicates how fast algorithm is running
● Space efficiency: how much extra memory the algorithm needs to complete its execution
● Simplicity: - generating sequences of instruction which are easy to understand.
● Generality: - It fixes the range of inputs it can accept. The generality of problems which algorithms can solve.
The time efficiencies of a large number of algorithms fall into only a few classes
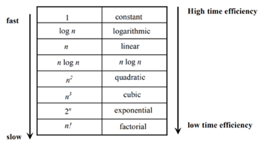
Fig 1: Time efficiency
Time complexity:
The time complexity of an algorithm is the amount of time required to complete the execution. The time complexity of an algorithm is denoted by the big O notation. Here, big O notation is the asymptotic notation to represent the time complexity. The time complexity is mainly calculated by counting the number of steps to finish the execution.
Let's understand the time complexity through an example.
- Sum=0;
- // Suppose we have to calculate the sum of n numbers.
- For i=1 to n
- Sum=sum+i;
- // when the loop ends then sum holds the sum of the n numbers
- Return sum;
In the above code, the time complexity of the loop statement will be at least n, and if the value of n increases, then the time complexity also increases. While the complexity of the code, i.e., return sum will be constant as its value is not dependent on the value of n and will provide the result in one step only. We generally consider the worst-time complexity as it is the maximum time taken for any given input size.
Space complexity: An algorithm's space complexity is the amount of space required to solve a problem and produce an output. Similar to the time complexity, space complexity is also expressed in big O notation.
For an algorithm, the space is required for the following purposes:
- To store program instructions
- To store constant values
- To store variable values
To track the function calls, jumping statements, etc.
Key takeaway
The time complexity of an algorithm is the amount of time required to complete the execution.
An algorithm's space complexity is the amount of space required to solve a problem and produce an output.
Big Oh (O) Notation:
- It is the formal way to express the time complexity.
- It is used to define the upper bound of an algorithm’s running time.
- It shows the worst-case time complexity or largest amount of time taken by the algorithm to perform a certain task.
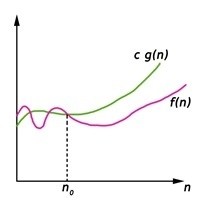
Fig 2: Big Oh notation
Here, f (n) <= g (n) …………….(eq1)
where n>= k, C>0 and k>=1
If any algorithm satisfies the eq1 condition then it becomes f (n)= O (g (n))
Big Omega (ῼ) Notation
- It is the formal way to express the time complexity.
- It is used to define the lower bound of an algorithm’s running time.
- It shows the best-case time complexity or best of time taken by the algorithm to perform a certain task.
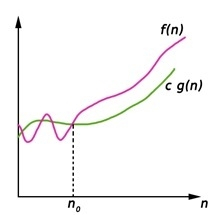
Fig 3: Big omega notation
Here, f (n) >= g (n)
Where n>=k and c>0, k>=1
If any algorithm satisfies the eq1 condition then it becomes f (n)= ῼ (g (n))
Theta (Θ) Notation
- It is the formal way to express the time complexity.
- It is used to define the lower as well as upper bound of an algorithm’s running time.
- It shows the average case time complexity or average of time taken by the algorithm to perform a certain task.
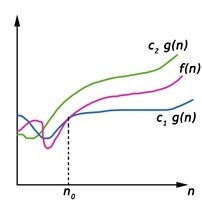
Fig 4: Theta notation
Let C1 g(n) be upper bound and C2 g(n) be lower bound.
C1 g(n)<= f (n)<=C2 g(n)
Where C1, C2>0 and n>=k
Key takeaway
- Big Oh is used to define the upper bound of an algorithm’s running time.
- Big Omega is used to define the lower bound of an algorithm’s running time.
- Theta is used to define the lower as well as upper bound of an algorithm’s running time.
- It is also known as time memory tradeoff.
- It is a way of solving problems in less time by using more storage space.
- It can be used with the problem of data storage.
- For example: time complexity of merge sort is O(n log n)in all cases. But requires an auxiliary array.
- In quick sort complexity is O(n log n) for best and average case but it doesn’t require auxiliary space.
- Two Space-for-Time Algorithm Varieties:
- Input enhancement - To store some info, preprocess the input (or its portion) to be used in solving the issue later
- Counting sorts
- String searching algorithms
- Pre-structuring-preprocessing the input to access its components
1) hashing 2) indexing schemes simpler (e.g., B-trees)
Key takeaway
- It is also known as time memory tradeoff.
- It is a way of solving problems in less time by using more storage space.
Searching is the process of looking for a certain item in a list. If the element is found in the list, the process is considered successful, and the location of that element is returned; otherwise, the search is considered unsuccessful.
Linear Search and Binary Search are two prominent search strategies. So, we'll talk about a popular search strategy called the Linear Search Algorithm.
The linear search algorithm is also known as the sequential search algorithm. It is the most basic search algorithm. We just traverse the list in linear search and match each element of the list with the object whose position has to be discovered. If a match is found, the algorithm delivers the item's location; otherwise, NULL is returned.
It's commonly used to find an element in an unordered list, or one in which the items aren't sorted. The time complexity of linear search in the worst-case scenario is O(n).
The following are the steps involved in implementing Linear Search:
● We must first use a for loop to traverse the array elements.
● Compare the search element with the current array element in each iteration of the for loop, and -
○ Return the index of the related array entry if the element matches.
○ If the element you're looking for doesn't match, move on to the next one.
● Return -1 if there is no match or the search element is not found in the given array.
Let's look at the linear search algorithm now.
Algorithm
Linear_Search(a, n, val) // 'a' is the given array, 'n' is the size of given array, 'val' is the value to search
Step 1: set pos = -1
Step 2: set i = 1
Step 3: repeat step 4 while i <= n
Step 4: if a[i] == val
Set pos = i
Print pos
Go to step 6
[end of if]
Set ii = i + 1
[end of loop]
Step 5: if pos = -1
Print "value is not present in the array "
[end of if]
Step 6: exit
Time Complexity
Case | Time Complexity |
Best Case | O(1) |
Average Case | O(n) |
Worst Case | O(n) |
Space Complexity
Space Complexity | O(1) |
Application of Linear Search Algorithm
The linear search algorithm is useful for the following tasks:
● Both single-dimensional and multi-dimensional arrays can benefit from linear search.
● When the array has only a few elements, linear search is simple to implement and effective.
● When performing a single search in an unordered-List, Linear Search is also quite efficient.
Binary Search
Binary search is the search technique which works efficiently on the sorted lists. Hence, in order to search an element into some list by using binary search technique, we must ensure that the list is sorted.
Binary search follows a divide and conquer approach in which the list is divided into two halves and the item is compared with the middle element of the list. If the match is found then, the location of the middle element is returned; otherwise, we search into either of the halves depending upon the result produced through the match.
Binary search algorithm is given below.
BINARY_SEARCH(A, lower_bound, upper_bound, VAL)
● Step 1: [INITIALIZE] SET BEG = lower_bound
END = upper_bound, POS = - 1
● Step 2: Repeat Steps 3 and 4 while BEG <=END
● Step 3: SET MID = (BEG + END)/2
● Step 4: IF A[MID] = VAL
SET POS = MID
PRINT POS
Go to Step 6
ELSE IF A[MID] > VAL
SET END = MID - 1
ELSE
SET BEG = MID + 1
[END OF IF]
[END OF LOOP]
● Step 5: IF POS = -1
PRINT "VALUE IS NOT PRESENT IN THE ARRAY"
[END OF IF]
● Step 6: EXIT
Complexity
SN | Performance | Complexity |
1 | Worst case | O(log n) |
2 | Best case | O(1) |
3 | Average Case | O(log n) |
4 | Worst case space complexity | O(1) |
Example
Let us consider an array arr = {1, 5, 7, 8, 13, 19, 20, 23, 29}. Find the location of the item 23 in the array.
In 1st step:
- BEG = 0
- END = 8ron
- MID = 4
- a[mid] = a[4] = 13 < 23, therefore
In Second step:
- Beg = mid +1 = 5
- End = 8
- Mid = 13/2 = 6
- a[mid] = a[6] = 20 < 23, therefore;
In third step:
- Beg = mid + 1 = 7
- End = 8
- Mid = 15/2 = 7
- a[mid] = a[7]
- a[7] = 23 = item;
- Therefore, set location = mid;
- The location of the item will be 7.
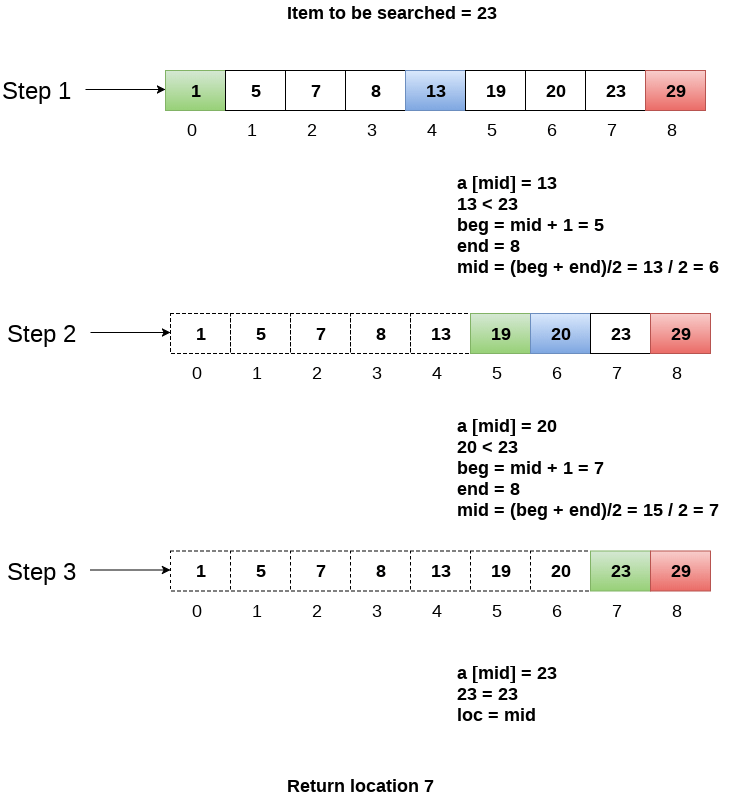
Fig 3 - Example
Bubble sort
Bubble Sort is a simple algorithm for sorting a collection of n elements that is provided in the form of an array with n elements. Bubble Sort compares each element individually and sorts them according to their values.
If an array must be sorted in ascending order, bubble sort will begin by comparing the first and second members of the array, swapping both elements if the first element is greater than the second, and then moving on to compare the second and third elements, and so on.
If there are n elements in total, we must repeat the method n-1 times.
It's called bubble sort because the largest element in the given array bubbles up to the last position or highest index with each full iteration, similar to how a water bubble rises to the sea surface.
Although it is simple to use, bubble sort is largely employed as an educational tool because its performance in the actual world is low. It isn't designed to handle huge data collections. Bubble sort has an average and worst-case complexity of O(n2), where n is the number of elements.
Sorting is done by going through all of the items one by one, comparing them to the next closest element, and swapping them if necessary.
Algorithm
Assume arr is an array of n elements in the algorithm below. The algorithm's presumed swap function will swap the values of specified array members.
Begin BubbleSort(arr)
for all array elements
if arr[i] > arr[i+1]
swap(arr[i], arr[i+1])
end if
end for
return arr
End BubbleSort
Working of Bubble Sort
Assume we're attempting to arrange the elements in ascending order.
1. First Iteration (Compare and Swap)
● Compare the first and second elements starting with the first index.
● The first and second elements are swapped if the first is bigger than the second.
● Compare and contrast the second and third elements now. If they aren't in the right order, swap them.
● The process continues until the last piece is added.
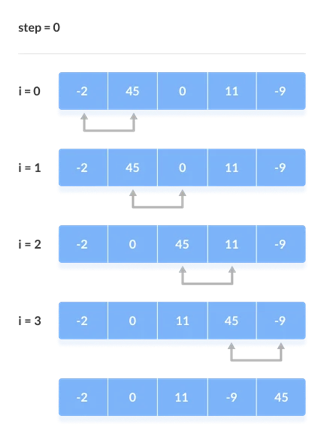
2. Remaining Iteration
For the remaining iterations, the same procedure is followed.
The largest element among the unsorted items is placed at the conclusion of each iteration.
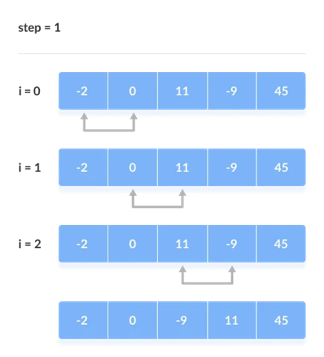
The comparison takes place up to the last unsorted element in each iteration.
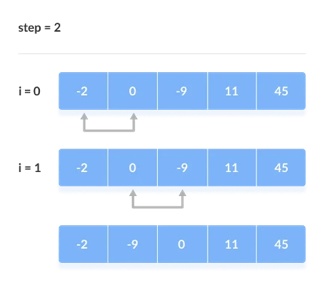
When all of the unsorted elements have been placed in their correct placements, the array is said to be sorted.
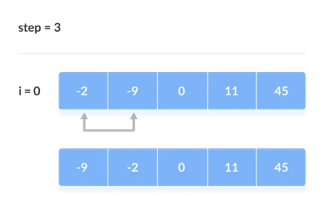
Key takeaway
- Compare and swap adjacent elements of the list if they are out of order.
- After repeating the procedure, we end up 'bubbling up' the largest element to the last place on the list by doing it repeatedly.
Insertion sort
Insertion style is a decrease & conquer technique application. It is a sort based on comparison in which the sorted array is constructed on one entry at a time.
Insertion sorting is a very basic process for sorting numbers in an ascending or descending order. The gradual method is accompanied by this method. It can be contrasted with the method of sorting cards at the time of playing a game.
The numbers that are needed to be sorted are known as keys. Here is the insertion sort method algorithm.
Algorithm:
Algorithm: Insertion-Sort (A)
For j = 2 to A.length
Key = A[j]
// Insert A[j] into the sorted sequence A[1.. j - 1]
i = j - 1
While i > 0 and A[i] > key
A[i + 1] = A[i]
i = i -1
A[i + 1] = key
Analysis:
This algorithm's run time is very dependent on the input given.
If the numbers given are sorted, this algorithm runs in O(n) time. If the numbers given are in reverse order, the algorithm runs in O(n2) time.
Example:
Using insertion sort to sort the following list of elements:
89, 45, 68, 90, 29, 34, 17
89 |45 68 90 29 34 17
45 89 |68 90 29 34 17
45 68 89 |90 29 34 17
45 68 89 90 |29 34 17
29 45 68 89 90 |34 17
29 34 45 68 89 90 |17
17 29 34 45 68 89 90
Application:
In the following instances, the insertion sort algorithm is used:
- When only a few elements are in the list.
- When there are few elements for sorting.
Advantages:
- Straightforward implementation. Three variants exist.
● Left to right scan
● Right to left scan
● Binary insertion sort
2. Effective on a small list of components, on a nearly sorted list.
3. In the best example, running time is linear.
4. This algorithm is stable.
5. Is the on-the-spot algorithm
Key takeaways
- Insertion sorting is a very basic process for sorting numbers in an ascending or descending order.
- Insertion style is a decrease & conquer technique application.
- It is a sort based on comparison in which the sorted array is constructed on one entry at a time.
Selection sort
In the selection sort, the smallest value among the array's unsorted items is chosen in each pass and inserted into the proper spot.
To begin, locate the array's smallest element and set it in the first position. Then locate the array's second smallest element and set it in the second spot. The procedure is repeated till the sorted array is obtained.
The n-1 pass of the selection sort algorithm is used to sort the array of n entries.
● The smallest element of the array, as well as its index pos, must be identified in the first run. Swap A[0] and A[pos] after that. As a result of sorting A[0], we now have n -1 elements to sort.
● The location pos of the smallest element in the sub-array A[n-1] is obtained in the second pass. Swap A[1] and A[pos] after that. After sorting A[0] and A[1], we're left with n-2 unsorted elements.
● The position pos of the smaller element between A[n-1] and A[n-2] must be found in the n-1st pass. Swap A[pos] and A[n-1] after that.
As a result, the items A[0], A[1], A[2],...., A[n-1] are sorted using the procedure described above.
Example
Consider the following six-element array. Using selection sort, sort the array's elements.
A = {10, 2, 3, 90, 43, 56}.
Pass | Pos | A[0] | A[1] | A[2] | A[3] | A[4] | A[5] |
1 | 1 | 2 | 10 | 3 | 90 | 43 | 56 |
2 | 2 | 2 | 3 | 10 | 90 | 43 | 56 |
3 | 2 | 2 | 3 | 10 | 90 | 43 | 56 |
4 | 4 | 2 | 3 | 10 | 43 | 90 | 56 |
5 | 5 | 2 | 3 | 10 | 43 | 56 | 90 |
Sorted A = {2, 3, 10, 43, 56, 90}
Algorithm
SELECTION SORT(ARR, N)
● Step 1: Repeat Steps 2 and 3 for K = 1 to N-1
● Step 2: CALL SMALLEST(ARR, K, N, POS)
● Step 3: SWAP A[K] with ARR[POS]
[END OF LOOP]
● Step 4: EXIT
SMALLEST (ARR, K, N, POS)
● Step 1: [INITIALIZE] SET SMALL = ARR[K]
● Step 2: [INITIALIZE] SET POS = K
● Step 3: Repeat for J = K+1 to N -1
IF SMALL > ARR[J]
SET SMALL = ARR[J]
SET POS = J
[END OF IF]
[END OF LOOP]
● Step 4: RETURN POS
Key takeaway
- In the selection sort, the smallest value among the array's unsorted items is chosen in each pass and inserted into the proper spot.
- To begin, locate the array's smallest element and set it in the first position.
- Then locate the array's second smallest element and set it in the second spot.
It becomes easier to solve the complete problem if we can separate a single major problem into smaller sub-problems, solve the smaller sub-problems, and integrate their solutions to find the solution for the original huge problem.
Let's look into Divide and Rule as an example.
When the British arrived in India, they encountered a country where many religions coexisted peacefully, hardworking but ignorant individuals, and unity in variety, making it difficult for them to establish their empire. As a result, they chose the Divide and Rule strategy. Where the population of India was a single large difficulty for them, they divided it into smaller ones by inciting rivalries amongst local monarchs and pitting them against one another, which worked extremely well for them.
That was history and a socio-political policy (Break and Rule), but the notion here is that if we can divide a problem into smaller sub-problems, it becomes easier to tackle the total problem in the end.
The Divide and Conquer strategy consists of three steps:
● Break the problem down into smaller chunks.
● Solve the subproblems to defeat them. The goal is to break down the problem into atomic subproblems that can be solved individually.
● To obtain the solution to the actual problem, combine the solutions of the subproblems.
Merge sort
Merge Sort is based on a divide and conquer strategy. It divides the unsorted list into n sublists such that each sublist contains one element. Each sublist is then sorted and merged until there is only one sublist.
Step 1: Divide the list into sublists such that each sublist contains only one element.
Step 2: Sort each sublist and Merge them.
Step 3: Repeat Step 2 till the entire list is sorted.
Example: Apply Merge Sort on array A= {85,24,63,45,17,31,96,50}
Step1: A contains 8 elements. First we divide the list into two sublists such that each sublist contains 4 elements. Then we divide each sublist of 4 elements into sublist of two elements each. Finally every sublist contains only one element.
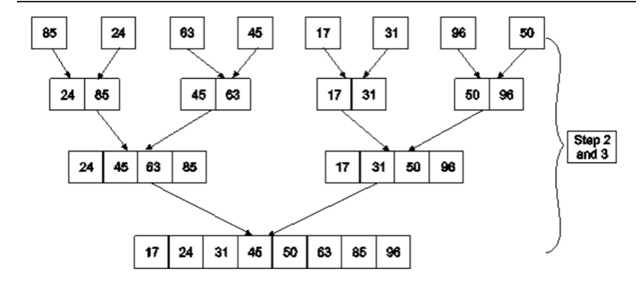
Fig. 4: Example
Step 2: Now we start from the bottom. Compare 1st and 2nd element. Sort and merge them. Apply this for all bottom elements.
Thus we got 4 sublists as follows
24 | 85 |
| 45 | 63 |
| 17 | 31 |
| 50 | 96 |
Step 3: Repeat this sorting and merging until the entire list is sorted. The above four sublists are sorted and merged to form 2 sublists.
24 | 85 | 63 | 85 |
| 17 | 31 | 50 | 96 |
Finally, the above 2 sublists are again sorted and merged in one sublist.
17 | 24 | 31 | 45 | 50 | 63 | 85 | 96 |
We will see one more example on merge sort.
Example: Apply merge Sort on array A={10,5,7,6,1,4,8,3,2,9,12,11}
Step 1:
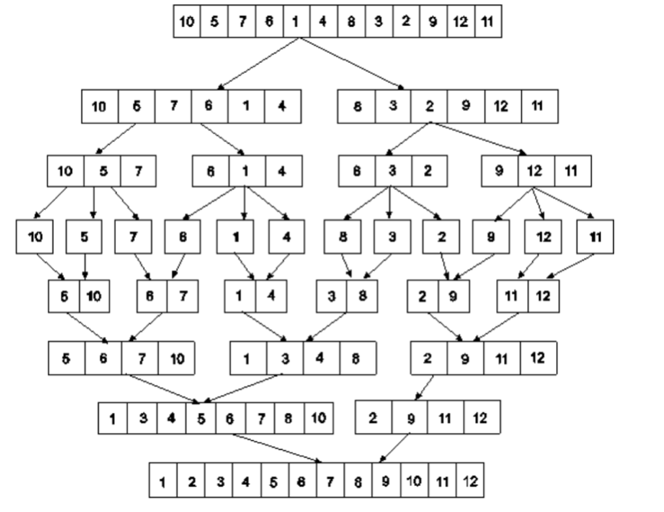
Fig 5: Merge sort
Algorithm for Merge Sort:
Let x = no. Of elements in array A
y = no. Of elements in array B
C = sorted array with no. Of elements n
n = x+y
Following algorithm merges a sorted x element array A and sorted y element array B into a sorted array C, with n = x + y elements. We must always keep track of the locations of the smallest element of A and the smallest element of B which have not yet been placed in C. Let LA and LB denote these locations, respectively. Also, let LC denote the location in C to be filled. Thus, initially, we set
LA : = 1,
LB : = 1 and
LC : = 1.
At each step, we compare A[LA] and B[LB] and assign the smaller element to C[LC].
Then
LC:= LC + 1,
LA: = LA + 1, if a new element has come from A .
LB: = LB + 1, if a new element has come from B.
Furthermore, if LA> x, then the remaining elements of B are assigned to C;
LB >y, then the remaining elements of A are assigned to C.
Thus the algorithm becomes
MERGING ( A, x, B, y, C)
1. [Initialize ] Set LA : = 1 , LB := 1 AND LC : = 1
2. [Compare] Repeat while LA <= x and LB <= y
If A[LA] < B[LB] , then
(a) [Assign element from A to C ] set C[LC] = A[LA]
(b) [Update pointers ] Set LC := LC +1 and LA = LA+1
Else
(a) [Assign element from B to C] Set C[LC] = B[LB]
(b) [Update Pointers] Set LC := LC +1 and LB = LB +1
[End of loop]
3. [Assign remaining elements to C]
If LA > x , then
Repeat for K= 0 ,1,2,........,y–LB
Set C[LC+K] = B[LB+K]
[End of loop]
Else
Repeat for K = 0,1,2,......,x–LA
Set C[LC+K] = A[LA+K]
[End of loop]
4. Exit
Quick sort
Quick sort is the most efficient method of sorting .It uses the divide and conquer strategy to sort the elements. In quicksort, we divide the array of items to be sorted into two partitions and then call the quicksort procedure recursively to sort the two partitions. For this we choose a pivot element and arrange all elements such that all the elements in the left part are less than the pivot and all those in the right part are greater than it.
Algorithm to implement Quick Sort is as follows.
Consider array A of size n to be sorted. p is the pivot element. Index positions of the first and last element of array A are denoted by ‘first’ and ‘last’.
- Initially first=0 and last=n–1.
- Increment first till A[first]<=p
- Decrement last till A[last]>=p
- If first < last then swap A[first] with A[last].
- If first > last then swap p with A[last] and thus the position of p is found. Pivot p is placed such that all elements to its left are less than it and all elements right to it are greater than it. Let us assume that j is the final position of p. Then A[0] to A[j–1] are less than p and A [j + 1] to A [n–1]are greater than p.
- Now we consider the left part of array A i.e A[0] to A[j–1].Repeat step 1,2,3 and 4. Apply the same procedure for the right part of the array.
- We continue with the above steps till no more partitions can be made for every subarray.
Algorithm
PARTITION (ARR, BEG, END, LOC)
● Step 1: [INITIALIZE] SET LEFT = BEG, RIGHT = END, LOC = BEG, FLAG =
● Step 2: Repeat Steps 3 to 6 while FLAG =
● Step 3: Repeat while ARR[LOC] <=ARR[RIGHT]
AND LOC != RIGHT
SET RIGHT = RIGHT – 1
[END OF LOOP]
● Step 4: IF LOC = RIGHT
SET FLAG = 1
ELSE IF ARR[LOC] > ARR[RIGHT]
SWAP ARR[LOC] with ARR[RIGHT]
SET LOC = RIGHT
[END OF IF]
● Step 5: IF FLAG = 0
Repeat while ARR[LOC] >= ARR[LEFT] AND LOC != LEFT
SET LEFT = LEFT + 1
[END OF LOOP]
● Step 6:IF LOC = LEFT
SET FLAG = 1
ELSE IF ARR[LOC] < ARR[LEFT]
SWAP ARR[LOC] with ARR[LEFT]
SET LOC = LEFT
[END OF IF]
[END OF IF]
● Step 7: [END OF LOOP]
● Step 8: END
QUICK_SORT (ARR, BEG, END)
● Step 1: IF (BEG < END)
CALL PARTITION (ARR, BEG, END, LOC)
CALL QUICKSORT(ARR, BEG, LOC - 1)
CALL QUICKSORT(ARR, LOC + 1, END)
[END OF IF]
● Step 2: END
Key takeaways
- Merge sort consisting two phases as divide and merge.
- In divide phase, each time it divides the given unsorted list into two sub list until each sub list get single element then sorts the elements.
- In merge phase, it merges all the solution of sub lists and find the original sorted list.
- Quick sort is the most efficient method of sorting .It uses the divide and conquer strategy to sort the elements.
- In quicksort, we divide the array of items to be sorted into two partitions and then call the quicksort procedure recursively to sort the two partitions.
Bubble Sort, Selection Sort, Insertion Sort, Merge Sort, Quick Sort, Heap Sort, Counting Sort, Radix Sort, and Bucket Sort have all had their time and space difficulties discussed.
Bubble sort
Each nearby pair is compared in bubble sort. We swap them if they aren't in the right order. We repeat the preceding procedure until no more swaps are required, indicating that all of the components have been sorted.
Worse case: O(n2)
We iterate through the array (n - 1) times once it is reverse-sorted. We do (n - 1) swaps in the first iteration, (n - 2) swaps in the second, and so on until we only do one swap in the last iteration. As a result, the total number of swaps equals n * (n - 1) / 2.
Average case: O(n2)
The total number of swaps for a truly random array averages out to roughly n2 / 4, which is again O(n2).
Best case: O(n)
In the first iteration of the array, if no swaps are performed, we know that the array is already sorted and hence cease sorting, resulting in a linear time complexity.
Space Complexity:
The space complexity is O(1) since we only use a constant amount of additional memory away from the input array.
Selection Sort
Selection sort is a straightforward sorting method that divides an array into two parts: a subarray of already sorted elements and a subarray of unsorted elements. Initially, the sorted subarray is empty. The array is iterated over (n - 1) times. We find the smallest element from the unsorted subarray and set it at the end of the sorted subarray in each iteration.
Time Complexity:
Worst case = Average Case = Best Case = O(n2)
For an array of whatever size, we conduct the same number of comparisons.
We execute (n - 1) comparisons in the first iteration, (n - 2) in the second, and so on until the last iteration, when we only perform one comparison. As a result, the total number of comparisons is n * (n - 1) / 2. The number of swaps performed is at most n - 1. So the overall time complexity is quadratic.
Space Complexity:
The space complexity is O(1) because we don't use any other data structures except the input array.
Insertion Sort
The insertion sort method, like selection sort, separates the array into two parts: a subarray of already sorted elements and a subarray of unsorted elements. Only the first member of the array is originally stored in the sorted subarray. We go over each of the remaining elements one by one, putting them in their proper places in the sorted subarray.
Time Complexity:
Worse case: O(n2)
When we use insertion sort on a reverse-sorted array, each element is inserted at the beginning of the sorted subarray, which has the highest temporal complexity.
Average case: O(n2)
The average running time is O(n2 / 4) = O(n2). When the array members are in random order.
Best case: O(n)
When we run insertion sort on an array that has previously been sorted, it merely compares each element to its predecessor, needing n steps to sort the already sorted array of n elements.
Space Complexity:
The space complexity is O(1) since we only use a constant amount of additional memory away from the input array.
Merge Sort
We partition the unsorted array into n subarrays, each of size one, that can be considered sorted trivially in merge sort. Then, until there is only one sorted array of size n left, we merge the sorted subarrays to make new sorted subarrays.
Time Complexity:
Worst case = Average Case = Best Case = O(n log n)
For any input array of a certain size, merge sort performs the same number of operations.
We divide the array into two subarrays repeatedly in this approach, resulting in O(log n) rows with each element appearing exactly once in each row.
Merging every pair of subarrays takes O(n) time for each row. As a result, the entire time complexity is O(n log n).
Space Complexity:
The space complexity is O(n) since we store the merged subarray in an auxiliary array of size at most n.
Quick Sort
Quick sort is a more complicated algorithm. It divides the array into two subarrays using a divide-and-conquer approach. We pick an element called pivot and place it at its proper index before reordering the array by moving all elements less than pivot to the left and all elements greater than it to the right.
The subarrays of these subarrays are then sorted recursively until the entire array is sorted. The pivot element's selection has a significant impact on the quick sort algorithm's efficiency.
Time Complexity:
Worse case: O(n2)
When the array is sorted and the leftmost element is chosen as pivot, or when the array is reverse-sorted and the rightmost element is chosen as pivot, the time complexity increases quadratically because dividing the array produces extremely unbalanced subarrays.
When the array has a high number of identical members, splitting becomes difficult, resulting in quadratic time complexity.
Average case and best case: O(n log n)
The best case scenario for quick-sort is when we consistently use the median element for partitioning. As a result of this partitioning, we can always divide the array in half.
Space Complexity:
Although rapid sort does not need auxiliary space to store array elements, recursive calls require additional space to create stack frames.
Worst case: O(n)
This occurs when the pivot element in each recursive call is the largest or smallest element of the array. After partitioning, the size of the subarray will be n-1 and 1. The recursive tree will be n in size in this situation.
Best case: O(log n)
This occurs when the right position of the pivot element in the partitioned array is always in the middle. Subarrays will have a size of half that of the parent array. The size of the recursive tree will be O in this situation (log n).
References:
- Data Structures with C, Seymour Lipschutz, Schaum's Outlines, Tata McGraw Hill Education.
- Fundamentals of Computer Algorithms by Horowitz, Sahni,Galgotia Pub. 2001 ed.
- Data Structures and program design in C by Robert Kruse, Bruce Leung & Clovis Tondo.
- Data Structures: A Pseudocode Approach with C by Richard F. Gilberg and
Behrouz Forouzan.
Unit - 1
Data Structures
A data structure is a collection of data pieces that provides an efficient method for storing and organizing data in a computer so that it may be used effectively. Arrays, Linked Lists, Stacks, Queues, and other Data Structures are examples. Data Structures are employed in practically every element of computer science, including operating systems, compiler design, artificial intelligence, graphics, and many more applications.
Data Structures are an important aspect of many computer science algorithms because they allow programmers to efficiently handle data. It is critical to improving the performance of a software or program because the software's primary duty is to save and retrieve user data as quickly as feasible.
Basic terminology
The building blocks of every program or software are data structures. The most challenging challenge for a programmer is deciding on a suitable data structure for a program. When it comes to data structures, the following terminology is utilized.
Data: The data on a student can be defined as an elementary value or a set of values, for example, the student's name and id.
Group items: Group items are data items that include subordinate data items, such as a student's name, which can have both a first and a last name.
Record: A record can be characterized as a collection of several data objects. For example, if we consider the student entity, the name, address, course, and grades can all be gathered together to constitute the student's record.
File: A file is a collection of various records of one type of entity; for example, if there are 60 employees in the class, the relevant file will contain 20 records, each containing information about each employee.
Attribute and Entity: A class of objects is represented by an entity. It has a number of characteristics. Each attribute represents an entity's specific property.
Key takeaway
A data structure is a collection of data pieces that provides an efficient method for storing and organizing data in a computer so that it may be used effectively.
As applications become more complicated and the amount of data collected grows, the following issues may arise:
● Processor speed: High-speed processing is essential to manage vast amounts of data, however as data grows by the day to billions of files each entity, processors may be unable to handle that much data.
● Data Search: Consider a store with a 106-item inventory. If our programme needs to search for a specific item, it must traverse all 106 items each time, which slows down the search process.
● Multiple requests: If thousands of users are searching for data on a web server at the same time, there is a potential that a very large server will fail during the process.
Data structures are used to solve the difficulties listed above. Data is grouped into a data structure in such a way that not all things must be searched and essential data can be found quickly.
Advantages of Data Structures
● Efficiency: The efficiency of a programme is determined by the data structures used. Consider the following scenario: we have certain data and need to find a specific record. If we structure our data in an array, we will have to search element by element in such a scenario. As a result, employing an array may not be the most efficient solution in this case. There are more efficient data structures for searching, such as an ordered array, a binary search tree, or hash tables.
● Reusability: Data structures are reusable, which means that after we've implemented one, we can use it somewhere else. Data structure implementations can be compiled into libraries that can be utilized by a variety of clients.
● Abstraction: The ADT specifies the data structure, which provides a level of abstraction. The client software only interacts with the data structure through an interface, thus it isn't concerned with the implementation details.
The abstract data type is a special kind of datatype, whose behavior is defined by a set of values and set of operations. The keyword “Abstract” is used as we can use these data types, we can perform different operations. But how those operations are working is totally hidden from the user. The ADT is made of primitive data types, but operation logics are hidden.
Here we will see the stack ADT. These are a few operations or functions of the Stack ADT.
● isFull(), This is used to check whether stack is full or not
● isEmpty(), This is used to check whether stack is empty or not
● push(x), This is used to push x into the stack
● pop(), This is used to delete one element from top of the stack
● peek(), This is used to get the top most element of the stack
● size(), this function is used to get number of elements present into the stack
Example
#include<iostream>
#include<stack>
Using namespace std;
Main(){
stack<int> stk;
if(stk.empty()){
cout << "Stack is empty" << endl;
} else {
cout << "Stack is not empty" << endl;
}
//insert elements into stack
stk.push(10);
stk.push(20);
stk.push(30);
stk.push(40);
stk.push(50);
cout << "Size of the stack: " << stk.size() << endl;
//pop and display elements
while(!stk.empty()){
int item = stk.top(); // same as peek operation
stk.pop();
cout << item << " ";
}
}
Output
Stack is empty
Size of the stack: 5
50 40 30 20 10
Key takeaway
The abstract data type is a special kind of datatype, whose behavior is defined by a set of values and set of operations.
The keyword “Abstract” is used as we can use these data types, we can perform different operations. But how those operations are working is totally hidden from the user.
The ADT is made of primitive data types, but operation logics are hidden.
What is an Algorithm?
An algorithm is a process or a set of rules required to perform calculations or some other problem-solving operations especially by a computer. The formal definition of an algorithm is that it contains the finite set of instructions which are being carried in a specific order to perform the specific task. It is not the complete program or code; it is just a solution (logic) of a problem, which can be represented either as an informal description using a Flowchart or Pseudocode.
Characteristics of an Algorithm
The following are the characteristics of an algorithm:
● Input: An algorithm has some input values. We can pass 0 or some input value to an algorithm.
● Output: We will get 1 or more output at the end of an algorithm.
● Unambiguity: An algorithm should be unambiguous which means that the instructions in an algorithm should be clear and simple.
● Finiteness: An algorithm should have finiteness. Here, finiteness means that the algorithm should contain a limited number of instructions, i.e., the instructions should be countable.
● Effectiveness: An algorithm should be effective as each instruction in an algorithm affects the overall process.
● Language independent: An algorithm must be language-independent so that the instructions in an algorithm can be implemented in any of the languages with the same output.
Dataflow of an Algorithm
● Problem: A problem can be a real-world problem or any instance from the real-world problem for which we need to create a program or the set of instructions. The set of instructions is known as an algorithm.
● Algorithm: An algorithm will be designed for a problem which is a step by step procedure.
● Input: After designing an algorithm, the required and the desired inputs are provided to the algorithm.
● Processing unit: The input will be given to the processing unit, and the processing unit will produce the desired output.
● Output: The output is the outcome or the result of the program.
Why do we need Algorithms?
We need algorithms because of the following reasons:
● Scalability: It helps us to understand scalability. When we have a big real-world problem, we need to scale it down into small-small steps to easily analyze the problem.
● Performance: The real-world is not easily broken down into smaller steps. If the problem can be easily broken into smaller steps means that the problem is feasible.
Let's understand the algorithm through a real-world example. Suppose we want to make a lemon juice, so following are the steps required to make a lemon juice:
Step 1: First, we will cut the lemon into half.
Step 2: Squeeze the lemon as much as you can and take out its juice in a container.
Step 3: Add two tablespoons of sugar in it.
Step 4: Stir the container until the sugar gets dissolved.
Step 5: When sugar gets dissolved, add some water and ice in it.
Step 6: Store the juice in a fridge for 5 to minutes.
Step 7: Now, it's ready to drink.
The above real-world can be directly compared to the definition of the algorithm. We cannot perform step 3 before step 2, we need to follow the specific order to make lemon juice. An algorithm also says that each and every instruction should be followed in a specific order to perform a specific task.
Now we will look at an example of an algorithm in programming.
We will write an algorithm to add two numbers entered by the user.
The following are the steps required to add two numbers entered by the user:
Step 1: Start
Step 2: Declare three variables a, b, and sum.
Step 3: Enter the values of a and b.
Step 4: Add the values of a and b and store the result in the sum variable, i.e., sum=a+b.
Step 5: Print sum
Step 6: Stop
Key takeaway
An algorithm is a process or a set of rules required to perform calculations or some other problem-solving operations especially by a computer.
The formal definition of an algorithm is that it contains the finite set of instructions which are being carried in a specific order to perform the specific task.
Efficiency of an Algorithm
Following are the conditions where we can analyze the algorithm:
● Time efficiency: indicates how fast algorithm is running
● Space efficiency: how much extra memory the algorithm needs to complete its execution
● Simplicity: - generating sequences of instruction which are easy to understand.
● Generality: - It fixes the range of inputs it can accept. The generality of problems which algorithms can solve.
The time efficiencies of a large number of algorithms fall into only a few classes
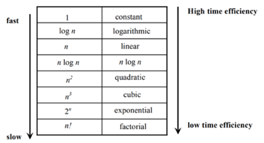
Fig 1: Time efficiency
Time complexity:
The time complexity of an algorithm is the amount of time required to complete the execution. The time complexity of an algorithm is denoted by the big O notation. Here, big O notation is the asymptotic notation to represent the time complexity. The time complexity is mainly calculated by counting the number of steps to finish the execution.
Let's understand the time complexity through an example.
- Sum=0;
- // Suppose we have to calculate the sum of n numbers.
- For i=1 to n
- Sum=sum+i;
- // when the loop ends then sum holds the sum of the n numbers
- Return sum;
In the above code, the time complexity of the loop statement will be at least n, and if the value of n increases, then the time complexity also increases. While the complexity of the code, i.e., return sum will be constant as its value is not dependent on the value of n and will provide the result in one step only. We generally consider the worst-time complexity as it is the maximum time taken for any given input size.
Space complexity: An algorithm's space complexity is the amount of space required to solve a problem and produce an output. Similar to the time complexity, space complexity is also expressed in big O notation.
For an algorithm, the space is required for the following purposes:
- To store program instructions
- To store constant values
- To store variable values
To track the function calls, jumping statements, etc.
Key takeaway
The time complexity of an algorithm is the amount of time required to complete the execution.
An algorithm's space complexity is the amount of space required to solve a problem and produce an output.
Big Oh (O) Notation:
- It is the formal way to express the time complexity.
- It is used to define the upper bound of an algorithm’s running time.
- It shows the worst-case time complexity or largest amount of time taken by the algorithm to perform a certain task.
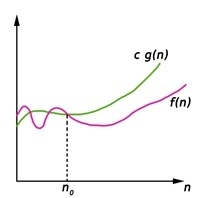
Fig 2: Big Oh notation
Here, f (n) <= g (n) …………….(eq1)
where n>= k, C>0 and k>=1
If any algorithm satisfies the eq1 condition then it becomes f (n)= O (g (n))
Big Omega (ῼ) Notation
- It is the formal way to express the time complexity.
- It is used to define the lower bound of an algorithm’s running time.
- It shows the best-case time complexity or best of time taken by the algorithm to perform a certain task.
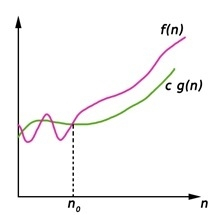
Fig 3: Big omega notation
Here, f (n) >= g (n)
Where n>=k and c>0, k>=1
If any algorithm satisfies the eq1 condition then it becomes f (n)= ῼ (g (n))
Theta (Θ) Notation
- It is the formal way to express the time complexity.
- It is used to define the lower as well as upper bound of an algorithm’s running time.
- It shows the average case time complexity or average of time taken by the algorithm to perform a certain task.
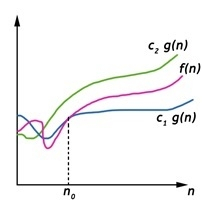
Fig 4: Theta notation
Let C1 g(n) be upper bound and C2 g(n) be lower bound.
C1 g(n)<= f (n)<=C2 g(n)
Where C1, C2>0 and n>=k
Key takeaway
- Big Oh is used to define the upper bound of an algorithm’s running time.
- Big Omega is used to define the lower bound of an algorithm’s running time.
- Theta is used to define the lower as well as upper bound of an algorithm’s running time.
- It is also known as time memory tradeoff.
- It is a way of solving problems in less time by using more storage space.
- It can be used with the problem of data storage.
- For example: time complexity of merge sort is O(n log n)in all cases. But requires an auxiliary array.
- In quick sort complexity is O(n log n) for best and average case but it doesn’t require auxiliary space.
- Two Space-for-Time Algorithm Varieties:
- Input enhancement - To store some info, preprocess the input (or its portion) to be used in solving the issue later
- Counting sorts
- String searching algorithms
- Pre-structuring-preprocessing the input to access its components
1) hashing 2) indexing schemes simpler (e.g., B-trees)
Key takeaway
- It is also known as time memory tradeoff.
- It is a way of solving problems in less time by using more storage space.
Searching is the process of looking for a certain item in a list. If the element is found in the list, the process is considered successful, and the location of that element is returned; otherwise, the search is considered unsuccessful.
Linear Search and Binary Search are two prominent search strategies. So, we'll talk about a popular search strategy called the Linear Search Algorithm.
The linear search algorithm is also known as the sequential search algorithm. It is the most basic search algorithm. We just traverse the list in linear search and match each element of the list with the object whose position has to be discovered. If a match is found, the algorithm delivers the item's location; otherwise, NULL is returned.
It's commonly used to find an element in an unordered list, or one in which the items aren't sorted. The time complexity of linear search in the worst-case scenario is O(n).
The following are the steps involved in implementing Linear Search:
● We must first use a for loop to traverse the array elements.
● Compare the search element with the current array element in each iteration of the for loop, and -
○ Return the index of the related array entry if the element matches.
○ If the element you're looking for doesn't match, move on to the next one.
● Return -1 if there is no match or the search element is not found in the given array.
Let's look at the linear search algorithm now.
Algorithm
Linear_Search(a, n, val) // 'a' is the given array, 'n' is the size of given array, 'val' is the value to search
Step 1: set pos = -1
Step 2: set i = 1
Step 3: repeat step 4 while i <= n
Step 4: if a[i] == val
Set pos = i
Print pos
Go to step 6
[end of if]
Set ii = i + 1
[end of loop]
Step 5: if pos = -1
Print "value is not present in the array "
[end of if]
Step 6: exit
Time Complexity
Case | Time Complexity |
Best Case | O(1) |
Average Case | O(n) |
Worst Case | O(n) |
Space Complexity
Space Complexity | O(1) |
Application of Linear Search Algorithm
The linear search algorithm is useful for the following tasks:
● Both single-dimensional and multi-dimensional arrays can benefit from linear search.
● When the array has only a few elements, linear search is simple to implement and effective.
● When performing a single search in an unordered-List, Linear Search is also quite efficient.
Binary Search
Binary search is the search technique which works efficiently on the sorted lists. Hence, in order to search an element into some list by using binary search technique, we must ensure that the list is sorted.
Binary search follows a divide and conquer approach in which the list is divided into two halves and the item is compared with the middle element of the list. If the match is found then, the location of the middle element is returned; otherwise, we search into either of the halves depending upon the result produced through the match.
Binary search algorithm is given below.
BINARY_SEARCH(A, lower_bound, upper_bound, VAL)
● Step 1: [INITIALIZE] SET BEG = lower_bound
END = upper_bound, POS = - 1
● Step 2: Repeat Steps 3 and 4 while BEG <=END
● Step 3: SET MID = (BEG + END)/2
● Step 4: IF A[MID] = VAL
SET POS = MID
PRINT POS
Go to Step 6
ELSE IF A[MID] > VAL
SET END = MID - 1
ELSE
SET BEG = MID + 1
[END OF IF]
[END OF LOOP]
● Step 5: IF POS = -1
PRINT "VALUE IS NOT PRESENT IN THE ARRAY"
[END OF IF]
● Step 6: EXIT
Complexity
SN | Performance | Complexity |
1 | Worst case | O(log n) |
2 | Best case | O(1) |
3 | Average Case | O(log n) |
4 | Worst case space complexity | O(1) |
Example
Let us consider an array arr = {1, 5, 7, 8, 13, 19, 20, 23, 29}. Find the location of the item 23 in the array.
In 1st step:
- BEG = 0
- END = 8ron
- MID = 4
- a[mid] = a[4] = 13 < 23, therefore
In Second step:
- Beg = mid +1 = 5
- End = 8
- Mid = 13/2 = 6
- a[mid] = a[6] = 20 < 23, therefore;
In third step:
- Beg = mid + 1 = 7
- End = 8
- Mid = 15/2 = 7
- a[mid] = a[7]
- a[7] = 23 = item;
- Therefore, set location = mid;
- The location of the item will be 7.
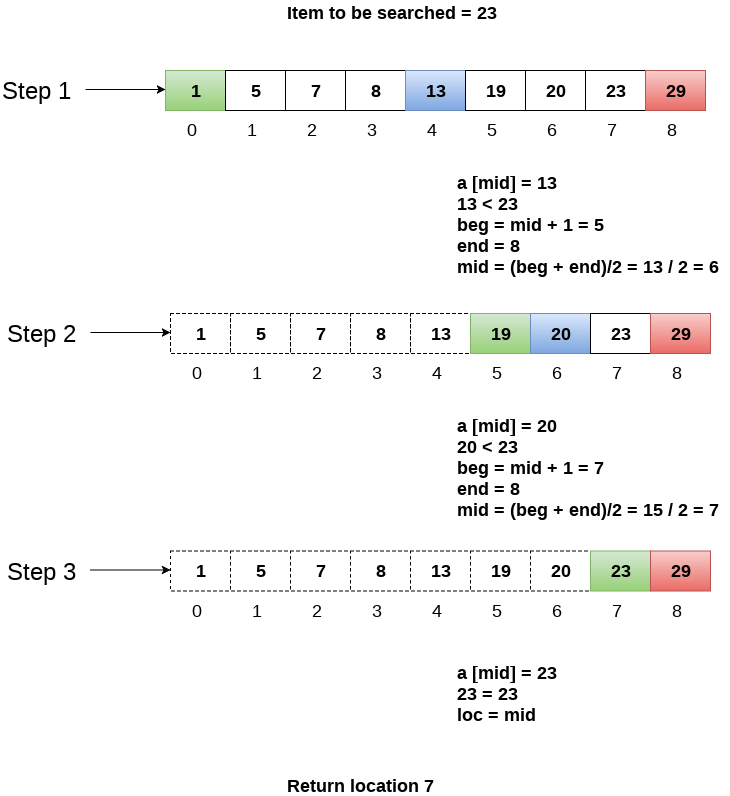
Fig 3 - Example
Bubble sort
Bubble Sort is a simple algorithm for sorting a collection of n elements that is provided in the form of an array with n elements. Bubble Sort compares each element individually and sorts them according to their values.
If an array must be sorted in ascending order, bubble sort will begin by comparing the first and second members of the array, swapping both elements if the first element is greater than the second, and then moving on to compare the second and third elements, and so on.
If there are n elements in total, we must repeat the method n-1 times.
It's called bubble sort because the largest element in the given array bubbles up to the last position or highest index with each full iteration, similar to how a water bubble rises to the sea surface.
Although it is simple to use, bubble sort is largely employed as an educational tool because its performance in the actual world is low. It isn't designed to handle huge data collections. Bubble sort has an average and worst-case complexity of O(n2), where n is the number of elements.
Sorting is done by going through all of the items one by one, comparing them to the next closest element, and swapping them if necessary.
Algorithm
Assume arr is an array of n elements in the algorithm below. The algorithm's presumed swap function will swap the values of specified array members.
Begin BubbleSort(arr)
for all array elements
if arr[i] > arr[i+1]
swap(arr[i], arr[i+1])
end if
end for
return arr
End BubbleSort
Working of Bubble Sort
Assume we're attempting to arrange the elements in ascending order.
1. First Iteration (Compare and Swap)
● Compare the first and second elements starting with the first index.
● The first and second elements are swapped if the first is bigger than the second.
● Compare and contrast the second and third elements now. If they aren't in the right order, swap them.
● The process continues until the last piece is added.
2. Remaining Iteration
For the remaining iterations, the same procedure is followed.
The largest element among the unsorted items is placed at the conclusion of each iteration.
The comparison takes place up to the last unsorted element in each iteration.
When all of the unsorted elements have been placed in their correct placements, the array is said to be sorted.
Key takeaway
- Compare and swap adjacent elements of the list if they are out of order.
- After repeating the procedure, we end up 'bubbling up' the largest element to the last place on the list by doing it repeatedly.
Insertion sort
Insertion style is a decrease & conquer technique application. It is a sort based on comparison in which the sorted array is constructed on one entry at a time.
Insertion sorting is a very basic process for sorting numbers in an ascending or descending order. The gradual method is accompanied by this method. It can be contrasted with the method of sorting cards at the time of playing a game.
The numbers that are needed to be sorted are known as keys. Here is the insertion sort method algorithm.
Algorithm:
Algorithm: Insertion-Sort (A)
For j = 2 to A.length
Key = A[j]
// Insert A[j] into the sorted sequence A[1.. j - 1]
i = j - 1
While i > 0 and A[i] > key
A[i + 1] = A[i]
i = i -1
A[i + 1] = key
Analysis:
This algorithm's run time is very dependent on the input given.
If the numbers given are sorted, this algorithm runs in O(n) time. If the numbers given are in reverse order, the algorithm runs in O(n2) time.
Example:
Using insertion sort to sort the following list of elements:
89, 45, 68, 90, 29, 34, 17
89 |45 68 90 29 34 17
45 89 |68 90 29 34 17
45 68 89 |90 29 34 17
45 68 89 90 |29 34 17
29 45 68 89 90 |34 17
29 34 45 68 89 90 |17
17 29 34 45 68 89 90
Application:
In the following instances, the insertion sort algorithm is used:
- When only a few elements are in the list.
- When there are few elements for sorting.
Advantages:
- Straightforward implementation. Three variants exist.
● Left to right scan
● Right to left scan
● Binary insertion sort
2. Effective on a small list of components, on a nearly sorted list.
3. In the best example, running time is linear.
4. This algorithm is stable.
5. Is the on-the-spot algorithm
Key takeaways
- Insertion sorting is a very basic process for sorting numbers in an ascending or descending order.
- Insertion style is a decrease & conquer technique application.
- It is a sort based on comparison in which the sorted array is constructed on one entry at a time.
Selection sort
In the selection sort, the smallest value among the array's unsorted items is chosen in each pass and inserted into the proper spot.
To begin, locate the array's smallest element and set it in the first position. Then locate the array's second smallest element and set it in the second spot. The procedure is repeated till the sorted array is obtained.
The n-1 pass of the selection sort algorithm is used to sort the array of n entries.
● The smallest element of the array, as well as its index pos, must be identified in the first run. Swap A[0] and A[pos] after that. As a result of sorting A[0], we now have n -1 elements to sort.
● The location pos of the smallest element in the sub-array A[n-1] is obtained in the second pass. Swap A[1] and A[pos] after that. After sorting A[0] and A[1], we're left with n-2 unsorted elements.
● The position pos of the smaller element between A[n-1] and A[n-2] must be found in the n-1st pass. Swap A[pos] and A[n-1] after that.
As a result, the items A[0], A[1], A[2],...., A[n-1] are sorted using the procedure described above.
Example
Consider the following six-element array. Using selection sort, sort the array's elements.
A = {10, 2, 3, 90, 43, 56}.
Pass | Pos | A[0] | A[1] | A[2] | A[3] | A[4] | A[5] |
1 | 1 | 2 | 10 | 3 | 90 | 43 | 56 |
2 | 2 | 2 | 3 | 10 | 90 | 43 | 56 |
3 | 2 | 2 | 3 | 10 | 90 | 43 | 56 |
4 | 4 | 2 | 3 | 10 | 43 | 90 | 56 |
5 | 5 | 2 | 3 | 10 | 43 | 56 | 90 |
Sorted A = {2, 3, 10, 43, 56, 90}
Algorithm
SELECTION SORT(ARR, N)
● Step 1: Repeat Steps 2 and 3 for K = 1 to N-1
● Step 2: CALL SMALLEST(ARR, K, N, POS)
● Step 3: SWAP A[K] with ARR[POS]
[END OF LOOP]
● Step 4: EXIT
SMALLEST (ARR, K, N, POS)
● Step 1: [INITIALIZE] SET SMALL = ARR[K]
● Step 2: [INITIALIZE] SET POS = K
● Step 3: Repeat for J = K+1 to N -1
IF SMALL > ARR[J]
SET SMALL = ARR[J]
SET POS = J
[END OF IF]
[END OF LOOP]
● Step 4: RETURN POS
Key takeaway
- In the selection sort, the smallest value among the array's unsorted items is chosen in each pass and inserted into the proper spot.
- To begin, locate the array's smallest element and set it in the first position.
- Then locate the array's second smallest element and set it in the second spot.
It becomes easier to solve the complete problem if we can separate a single major problem into smaller sub-problems, solve the smaller sub-problems, and integrate their solutions to find the solution for the original huge problem.
Let's look into Divide and Rule as an example.
When the British arrived in India, they encountered a country where many religions coexisted peacefully, hardworking but ignorant individuals, and unity in variety, making it difficult for them to establish their empire. As a result, they chose the Divide and Rule strategy. Where the population of India was a single large difficulty for them, they divided it into smaller ones by inciting rivalries amongst local monarchs and pitting them against one another, which worked extremely well for them.
That was history and a socio-political policy (Break and Rule), but the notion here is that if we can divide a problem into smaller sub-problems, it becomes easier to tackle the total problem in the end.
The Divide and Conquer strategy consists of three steps:
● Break the problem down into smaller chunks.
● Solve the subproblems to defeat them. The goal is to break down the problem into atomic subproblems that can be solved individually.
● To obtain the solution to the actual problem, combine the solutions of the subproblems.
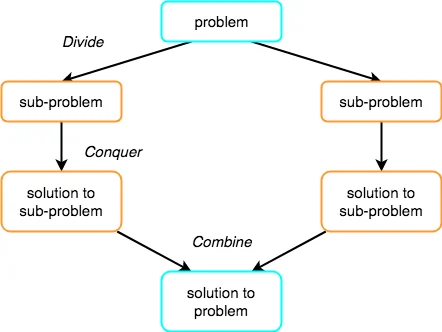
Merge sort
Merge Sort is based on a divide and conquer strategy. It divides the unsorted list into n sublists such that each sublist contains one element. Each sublist is then sorted and merged until there is only one sublist.
Step 1: Divide the list into sublists such that each sublist contains only one element.
Step 2: Sort each sublist and Merge them.
Step 3: Repeat Step 2 till the entire list is sorted.
Example: Apply Merge Sort on array A= {85,24,63,45,17,31,96,50}
Step1: A contains 8 elements. First we divide the list into two sublists such that each sublist contains 4 elements. Then we divide each sublist of 4 elements into sublist of two elements each. Finally every sublist contains only one element.
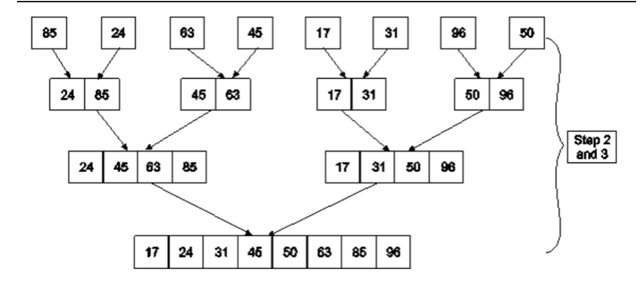
Fig. 4: Example
Step 2: Now we start from the bottom. Compare 1st and 2nd element. Sort and merge them. Apply this for all bottom elements.
Thus we got 4 sublists as follows
24 | 85 |
| 45 | 63 |
| 17 | 31 |
| 50 | 96 |
Step 3: Repeat this sorting and merging until the entire list is sorted. The above four sublists are sorted and merged to form 2 sublists.
24 | 85 | 63 | 85 |
| 17 | 31 | 50 | 96 |
Finally, the above 2 sublists are again sorted and merged in one sublist.
17 | 24 | 31 | 45 | 50 | 63 | 85 | 96 |
We will see one more example on merge sort.
Example: Apply merge Sort on array A={10,5,7,6,1,4,8,3,2,9,12,11}
Step 1:
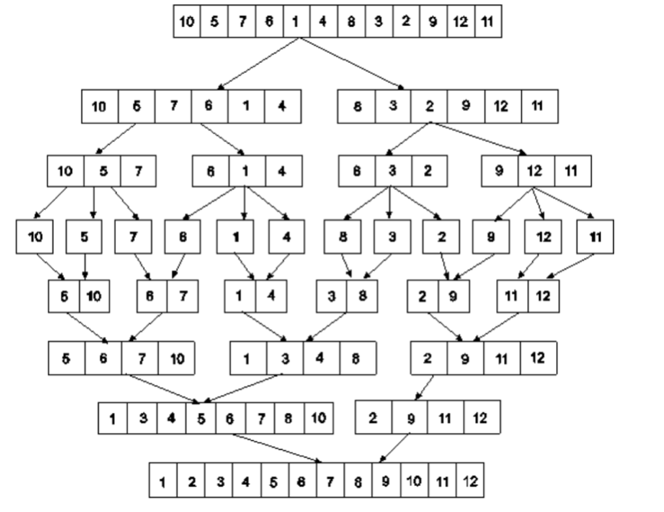
Fig 5: Merge sort
Algorithm for Merge Sort:
Let x = no. Of elements in array A
y = no. Of elements in array B
C = sorted array with no. Of elements n
n = x+y
Following algorithm merges a sorted x element array A and sorted y element array B into a sorted array C, with n = x + y elements. We must always keep track of the locations of the smallest element of A and the smallest element of B which have not yet been placed in C. Let LA and LB denote these locations, respectively. Also, let LC denote the location in C to be filled. Thus, initially, we set
LA : = 1,
LB : = 1 and
LC : = 1.
At each step, we compare A[LA] and B[LB] and assign the smaller element to C[LC].
Then
LC:= LC + 1,
LA: = LA + 1, if a new element has come from A .
LB: = LB + 1, if a new element has come from B.
Furthermore, if LA> x, then the remaining elements of B are assigned to C;
LB >y, then the remaining elements of A are assigned to C.
Thus the algorithm becomes
MERGING ( A, x, B, y, C)
1. [Initialize ] Set LA : = 1 , LB := 1 AND LC : = 1
2. [Compare] Repeat while LA <= x and LB <= y
If A[LA] < B[LB] , then
(a) [Assign element from A to C ] set C[LC] = A[LA]
(b) [Update pointers ] Set LC := LC +1 and LA = LA+1
Else
(a) [Assign element from B to C] Set C[LC] = B[LB]
(b) [Update Pointers] Set LC := LC +1 and LB = LB +1
[End of loop]
3. [Assign remaining elements to C]
If LA > x , then
Repeat for K= 0 ,1,2,........,y–LB
Set C[LC+K] = B[LB+K]
[End of loop]
Else
Repeat for K = 0,1,2,......,x–LA
Set C[LC+K] = A[LA+K]
[End of loop]
4. Exit
Quick sort
Quick sort is the most efficient method of sorting .It uses the divide and conquer strategy to sort the elements. In quicksort, we divide the array of items to be sorted into two partitions and then call the quicksort procedure recursively to sort the two partitions. For this we choose a pivot element and arrange all elements such that all the elements in the left part are less than the pivot and all those in the right part are greater than it.
Algorithm to implement Quick Sort is as follows.
Consider array A of size n to be sorted. p is the pivot element. Index positions of the first and last element of array A are denoted by ‘first’ and ‘last’.
- Initially first=0 and last=n–1.
- Increment first till A[first]<=p
- Decrement last till A[last]>=p
- If first < last then swap A[first] with A[last].
- If first > last then swap p with A[last] and thus the position of p is found. Pivot p is placed such that all elements to its left are less than it and all elements right to it are greater than it. Let us assume that j is the final position of p. Then A[0] to A[j–1] are less than p and A [j + 1] to A [n–1]are greater than p.
- Now we consider the left part of array A i.e A[0] to A[j–1].Repeat step 1,2,3 and 4. Apply the same procedure for the right part of the array.
- We continue with the above steps till no more partitions can be made for every subarray.
Algorithm
PARTITION (ARR, BEG, END, LOC)
● Step 1: [INITIALIZE] SET LEFT = BEG, RIGHT = END, LOC = BEG, FLAG =
● Step 2: Repeat Steps 3 to 6 while FLAG =
● Step 3: Repeat while ARR[LOC] <=ARR[RIGHT]
AND LOC != RIGHT
SET RIGHT = RIGHT – 1
[END OF LOOP]
● Step 4: IF LOC = RIGHT
SET FLAG = 1
ELSE IF ARR[LOC] > ARR[RIGHT]
SWAP ARR[LOC] with ARR[RIGHT]
SET LOC = RIGHT
[END OF IF]
● Step 5: IF FLAG = 0
Repeat while ARR[LOC] >= ARR[LEFT] AND LOC != LEFT
SET LEFT = LEFT + 1
[END OF LOOP]
● Step 6:IF LOC = LEFT
SET FLAG = 1
ELSE IF ARR[LOC] < ARR[LEFT]
SWAP ARR[LOC] with ARR[LEFT]
SET LOC = LEFT
[END OF IF]
[END OF IF]
● Step 7: [END OF LOOP]
● Step 8: END
QUICK_SORT (ARR, BEG, END)
● Step 1: IF (BEG < END)
CALL PARTITION (ARR, BEG, END, LOC)
CALL QUICKSORT(ARR, BEG, LOC - 1)
CALL QUICKSORT(ARR, LOC + 1, END)
[END OF IF]
● Step 2: END
Key takeaways
- Merge sort consisting two phases as divide and merge.
- In divide phase, each time it divides the given unsorted list into two sub list until each sub list get single element then sorts the elements.
- In merge phase, it merges all the solution of sub lists and find the original sorted list.
- Quick sort is the most efficient method of sorting .It uses the divide and conquer strategy to sort the elements.
- In quicksort, we divide the array of items to be sorted into two partitions and then call the quicksort procedure recursively to sort the two partitions.
Bubble Sort, Selection Sort, Insertion Sort, Merge Sort, Quick Sort, Heap Sort, Counting Sort, Radix Sort, and Bucket Sort have all had their time and space difficulties discussed.
Bubble sort
Each nearby pair is compared in bubble sort. We swap them if they aren't in the right order. We repeat the preceding procedure until no more swaps are required, indicating that all of the components have been sorted.
Worse case: O(n2)
We iterate through the array (n - 1) times once it is reverse-sorted. We do (n - 1) swaps in the first iteration, (n - 2) swaps in the second, and so on until we only do one swap in the last iteration. As a result, the total number of swaps equals n * (n - 1) / 2.
Average case: O(n2)
The total number of swaps for a truly random array averages out to roughly n2 / 4, which is again O(n2).
Best case: O(n)
In the first iteration of the array, if no swaps are performed, we know that the array is already sorted and hence cease sorting, resulting in a linear time complexity.
Space Complexity:
The space complexity is O(1) since we only use a constant amount of additional memory away from the input array.
Selection Sort
Selection sort is a straightforward sorting method that divides an array into two parts: a subarray of already sorted elements and a subarray of unsorted elements. Initially, the sorted subarray is empty. The array is iterated over (n - 1) times. We find the smallest element from the unsorted subarray and set it at the end of the sorted subarray in each iteration.
Time Complexity:
Worst case = Average Case = Best Case = O(n2)
For an array of whatever size, we conduct the same number of comparisons.
We execute (n - 1) comparisons in the first iteration, (n - 2) in the second, and so on until the last iteration, when we only perform one comparison. As a result, the total number of comparisons is n * (n - 1) / 2. The number of swaps performed is at most n - 1. So the overall time complexity is quadratic.
Space Complexity:
The space complexity is O(1) because we don't use any other data structures except the input array.
Insertion Sort
The insertion sort method, like selection sort, separates the array into two parts: a subarray of already sorted elements and a subarray of unsorted elements. Only the first member of the array is originally stored in the sorted subarray. We go over each of the remaining elements one by one, putting them in their proper places in the sorted subarray.
Time Complexity:
Worse case: O(n2)
When we use insertion sort on a reverse-sorted array, each element is inserted at the beginning of the sorted subarray, which has the highest temporal complexity.
Average case: O(n2)
The average running time is O(n2 / 4) = O(n2). When the array members are in random order.
Best case: O(n)
When we run insertion sort on an array that has previously been sorted, it merely compares each element to its predecessor, needing n steps to sort the already sorted array of n elements.
Space Complexity:
The space complexity is O(1) since we only use a constant amount of additional memory away from the input array.
Merge Sort
We partition the unsorted array into n subarrays, each of size one, that can be considered sorted trivially in merge sort. Then, until there is only one sorted array of size n left, we merge the sorted subarrays to make new sorted subarrays.
Time Complexity:
Worst case = Average Case = Best Case = O(n log n)
For any input array of a certain size, merge sort performs the same number of operations.
We divide the array into two subarrays repeatedly in this approach, resulting in O(log n) rows with each element appearing exactly once in each row.
Merging every pair of subarrays takes O(n) time for each row. As a result, the entire time complexity is O(n log n).
Space Complexity:
The space complexity is O(n) since we store the merged subarray in an auxiliary array of size at most n.
Quick Sort
Quick sort is a more complicated algorithm. It divides the array into two subarrays using a divide-and-conquer approach. We pick an element called pivot and place it at its proper index before reordering the array by moving all elements less than pivot to the left and all elements greater than it to the right.
The subarrays of these subarrays are then sorted recursively until the entire array is sorted. The pivot element's selection has a significant impact on the quick sort algorithm's efficiency.
Time Complexity:
Worse case: O(n2)
When the array is sorted and the leftmost element is chosen as pivot, or when the array is reverse-sorted and the rightmost element is chosen as pivot, the time complexity increases quadratically because dividing the array produces extremely unbalanced subarrays.
When the array has a high number of identical members, splitting becomes difficult, resulting in quadratic time complexity.
Average case and best case: O(n log n)
The best case scenario for quick-sort is when we consistently use the median element for partitioning. As a result of this partitioning, we can always divide the array in half.
Space Complexity:
Although rapid sort does not need auxiliary space to store array elements, recursive calls require additional space to create stack frames.
Worst case: O(n)
This occurs when the pivot element in each recursive call is the largest or smallest element of the array. After partitioning, the size of the subarray will be n-1 and 1. The recursive tree will be n in size in this situation.
Best case: O(log n)
This occurs when the right position of the pivot element in the partitioned array is always in the middle. Subarrays will have a size of half that of the parent array. The size of the recursive tree will be O in this situation (log n).
References:
- Data Structures with C, Seymour Lipschutz, Schaum's Outlines, Tata McGraw Hill Education.
- Fundamentals of Computer Algorithms by Horowitz, Sahni,Galgotia Pub. 2001 ed.
- Data Structures and program design in C by Robert Kruse, Bruce Leung & Clovis Tondo.
- Data Structures: A Pseudocode Approach with C by Richard F. Gilberg and
Behrouz Forouzan.
Unit - 1
Data Structures
A data structure is a collection of data pieces that provides an efficient method for storing and organizing data in a computer so that it may be used effectively. Arrays, Linked Lists, Stacks, Queues, and other Data Structures are examples. Data Structures are employed in practically every element of computer science, including operating systems, compiler design, artificial intelligence, graphics, and many more applications.
Data Structures are an important aspect of many computer science algorithms because they allow programmers to efficiently handle data. It is critical to improving the performance of a software or program because the software's primary duty is to save and retrieve user data as quickly as feasible.
Basic terminology
The building blocks of every program or software are data structures. The most challenging challenge for a programmer is deciding on a suitable data structure for a program. When it comes to data structures, the following terminology is utilized.
Data: The data on a student can be defined as an elementary value or a set of values, for example, the student's name and id.
Group items: Group items are data items that include subordinate data items, such as a student's name, which can have both a first and a last name.
Record: A record can be characterized as a collection of several data objects. For example, if we consider the student entity, the name, address, course, and grades can all be gathered together to constitute the student's record.
File: A file is a collection of various records of one type of entity; for example, if there are 60 employees in the class, the relevant file will contain 20 records, each containing information about each employee.
Attribute and Entity: A class of objects is represented by an entity. It has a number of characteristics. Each attribute represents an entity's specific property.
Key takeaway
A data structure is a collection of data pieces that provides an efficient method for storing and organizing data in a computer so that it may be used effectively.
As applications become more complicated and the amount of data collected grows, the following issues may arise:
● Processor speed: High-speed processing is essential to manage vast amounts of data, however as data grows by the day to billions of files each entity, processors may be unable to handle that much data.
● Data Search: Consider a store with a 106-item inventory. If our programme needs to search for a specific item, it must traverse all 106 items each time, which slows down the search process.
● Multiple requests: If thousands of users are searching for data on a web server at the same time, there is a potential that a very large server will fail during the process.
Data structures are used to solve the difficulties listed above. Data is grouped into a data structure in such a way that not all things must be searched and essential data can be found quickly.
Advantages of Data Structures
● Efficiency: The efficiency of a programme is determined by the data structures used. Consider the following scenario: we have certain data and need to find a specific record. If we structure our data in an array, we will have to search element by element in such a scenario. As a result, employing an array may not be the most efficient solution in this case. There are more efficient data structures for searching, such as an ordered array, a binary search tree, or hash tables.
● Reusability: Data structures are reusable, which means that after we've implemented one, we can use it somewhere else. Data structure implementations can be compiled into libraries that can be utilized by a variety of clients.
● Abstraction: The ADT specifies the data structure, which provides a level of abstraction. The client software only interacts with the data structure through an interface, thus it isn't concerned with the implementation details.
The abstract data type is a special kind of datatype, whose behavior is defined by a set of values and set of operations. The keyword “Abstract” is used as we can use these data types, we can perform different operations. But how those operations are working is totally hidden from the user. The ADT is made of primitive data types, but operation logics are hidden.
Here we will see the stack ADT. These are a few operations or functions of the Stack ADT.
● isFull(), This is used to check whether stack is full or not
● isEmpty(), This is used to check whether stack is empty or not
● push(x), This is used to push x into the stack
● pop(), This is used to delete one element from top of the stack
● peek(), This is used to get the top most element of the stack
● size(), this function is used to get number of elements present into the stack
Example
#include<iostream>
#include<stack>
Using namespace std;
Main(){
stack<int> stk;
if(stk.empty()){
cout << "Stack is empty" << endl;
} else {
cout << "Stack is not empty" << endl;
}
//insert elements into stack
stk.push(10);
stk.push(20);
stk.push(30);
stk.push(40);
stk.push(50);
cout << "Size of the stack: " << stk.size() << endl;
//pop and display elements
while(!stk.empty()){
int item = stk.top(); // same as peek operation
stk.pop();
cout << item << " ";
}
}
Output
Stack is empty
Size of the stack: 5
50 40 30 20 10
Key takeaway
The abstract data type is a special kind of datatype, whose behavior is defined by a set of values and set of operations.
The keyword “Abstract” is used as we can use these data types, we can perform different operations. But how those operations are working is totally hidden from the user.
The ADT is made of primitive data types, but operation logics are hidden.
What is an Algorithm?
An algorithm is a process or a set of rules required to perform calculations or some other problem-solving operations especially by a computer. The formal definition of an algorithm is that it contains the finite set of instructions which are being carried in a specific order to perform the specific task. It is not the complete program or code; it is just a solution (logic) of a problem, which can be represented either as an informal description using a Flowchart or Pseudocode.
Characteristics of an Algorithm
The following are the characteristics of an algorithm:
● Input: An algorithm has some input values. We can pass 0 or some input value to an algorithm.
● Output: We will get 1 or more output at the end of an algorithm.
● Unambiguity: An algorithm should be unambiguous which means that the instructions in an algorithm should be clear and simple.
● Finiteness: An algorithm should have finiteness. Here, finiteness means that the algorithm should contain a limited number of instructions, i.e., the instructions should be countable.
● Effectiveness: An algorithm should be effective as each instruction in an algorithm affects the overall process.
● Language independent: An algorithm must be language-independent so that the instructions in an algorithm can be implemented in any of the languages with the same output.
Dataflow of an Algorithm
● Problem: A problem can be a real-world problem or any instance from the real-world problem for which we need to create a program or the set of instructions. The set of instructions is known as an algorithm.
● Algorithm: An algorithm will be designed for a problem which is a step by step procedure.
● Input: After designing an algorithm, the required and the desired inputs are provided to the algorithm.
● Processing unit: The input will be given to the processing unit, and the processing unit will produce the desired output.
● Output: The output is the outcome or the result of the program.
Why do we need Algorithms?
We need algorithms because of the following reasons:
● Scalability: It helps us to understand scalability. When we have a big real-world problem, we need to scale it down into small-small steps to easily analyze the problem.
● Performance: The real-world is not easily broken down into smaller steps. If the problem can be easily broken into smaller steps means that the problem is feasible.
Let's understand the algorithm through a real-world example. Suppose we want to make a lemon juice, so following are the steps required to make a lemon juice:
Step 1: First, we will cut the lemon into half.
Step 2: Squeeze the lemon as much as you can and take out its juice in a container.
Step 3: Add two tablespoons of sugar in it.
Step 4: Stir the container until the sugar gets dissolved.
Step 5: When sugar gets dissolved, add some water and ice in it.
Step 6: Store the juice in a fridge for 5 to minutes.
Step 7: Now, it's ready to drink.
The above real-world can be directly compared to the definition of the algorithm. We cannot perform step 3 before step 2, we need to follow the specific order to make lemon juice. An algorithm also says that each and every instruction should be followed in a specific order to perform a specific task.
Now we will look at an example of an algorithm in programming.
We will write an algorithm to add two numbers entered by the user.
The following are the steps required to add two numbers entered by the user:
Step 1: Start
Step 2: Declare three variables a, b, and sum.
Step 3: Enter the values of a and b.
Step 4: Add the values of a and b and store the result in the sum variable, i.e., sum=a+b.
Step 5: Print sum
Step 6: Stop
Key takeaway
An algorithm is a process or a set of rules required to perform calculations or some other problem-solving operations especially by a computer.
The formal definition of an algorithm is that it contains the finite set of instructions which are being carried in a specific order to perform the specific task.
Efficiency of an Algorithm
Following are the conditions where we can analyze the algorithm:
● Time efficiency: indicates how fast algorithm is running
● Space efficiency: how much extra memory the algorithm needs to complete its execution
● Simplicity: - generating sequences of instruction which are easy to understand.
● Generality: - It fixes the range of inputs it can accept. The generality of problems which algorithms can solve.
The time efficiencies of a large number of algorithms fall into only a few classes
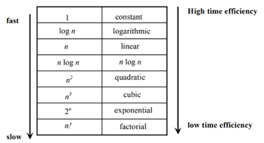
Fig 1: Time efficiency
Time complexity:
The time complexity of an algorithm is the amount of time required to complete the execution. The time complexity of an algorithm is denoted by the big O notation. Here, big O notation is the asymptotic notation to represent the time complexity. The time complexity is mainly calculated by counting the number of steps to finish the execution.
Let's understand the time complexity through an example.
- Sum=0;
- // Suppose we have to calculate the sum of n numbers.
- For i=1 to n
- Sum=sum+i;
- // when the loop ends then sum holds the sum of the n numbers
- Return sum;
In the above code, the time complexity of the loop statement will be at least n, and if the value of n increases, then the time complexity also increases. While the complexity of the code, i.e., return sum will be constant as its value is not dependent on the value of n and will provide the result in one step only. We generally consider the worst-time complexity as it is the maximum time taken for any given input size.
Space complexity: An algorithm's space complexity is the amount of space required to solve a problem and produce an output. Similar to the time complexity, space complexity is also expressed in big O notation.
For an algorithm, the space is required for the following purposes:
- To store program instructions
- To store constant values
- To store variable values
To track the function calls, jumping statements, etc.
Key takeaway
The time complexity of an algorithm is the amount of time required to complete the execution.
An algorithm's space complexity is the amount of space required to solve a problem and produce an output.
Big Oh (O) Notation:
- It is the formal way to express the time complexity.
- It is used to define the upper bound of an algorithm’s running time.
- It shows the worst-case time complexity or largest amount of time taken by the algorithm to perform a certain task.
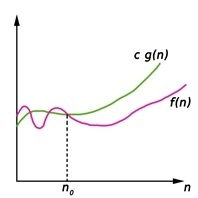
Fig 2: Big Oh notation
Here, f (n) <= g (n) …………….(eq1)
where n>= k, C>0 and k>=1
If any algorithm satisfies the eq1 condition then it becomes f (n)= O (g (n))
Big Omega (ῼ) Notation
- It is the formal way to express the time complexity.
- It is used to define the lower bound of an algorithm’s running time.
- It shows the best-case time complexity or best of time taken by the algorithm to perform a certain task.
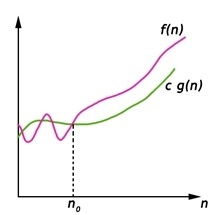
Fig 3: Big omega notation
Here, f (n) >= g (n)
Where n>=k and c>0, k>=1
If any algorithm satisfies the eq1 condition then it becomes f (n)= ῼ (g (n))
Theta (Θ) Notation
- It is the formal way to express the time complexity.
- It is used to define the lower as well as upper bound of an algorithm’s running time.
- It shows the average case time complexity or average of time taken by the algorithm to perform a certain task.
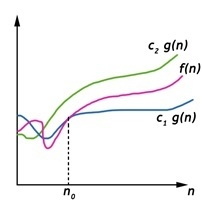
Fig 4: Theta notation
Let C1 g(n) be upper bound and C2 g(n) be lower bound.
C1 g(n)<= f (n)<=C2 g(n)
Where C1, C2>0 and n>=k
Key takeaway
- Big Oh is used to define the upper bound of an algorithm’s running time.
- Big Omega is used to define the lower bound of an algorithm’s running time.
- Theta is used to define the lower as well as upper bound of an algorithm’s running time.
- It is also known as time memory tradeoff.
- It is a way of solving problems in less time by using more storage space.
- It can be used with the problem of data storage.
- For example: time complexity of merge sort is O(n log n)in all cases. But requires an auxiliary array.
- In quick sort complexity is O(n log n) for best and average case but it doesn’t require auxiliary space.
- Two Space-for-Time Algorithm Varieties:
- Input enhancement - To store some info, preprocess the input (or its portion) to be used in solving the issue later
- Counting sorts
- String searching algorithms
- Pre-structuring-preprocessing the input to access its components
1) hashing 2) indexing schemes simpler (e.g., B-trees)
Key takeaway
- It is also known as time memory tradeoff.
- It is a way of solving problems in less time by using more storage space.
Searching is the process of looking for a certain item in a list. If the element is found in the list, the process is considered successful, and the location of that element is returned; otherwise, the search is considered unsuccessful.
Linear Search and Binary Search are two prominent search strategies. So, we'll talk about a popular search strategy called the Linear Search Algorithm.
The linear search algorithm is also known as the sequential search algorithm. It is the most basic search algorithm. We just traverse the list in linear search and match each element of the list with the object whose position has to be discovered. If a match is found, the algorithm delivers the item's location; otherwise, NULL is returned.
It's commonly used to find an element in an unordered list, or one in which the items aren't sorted. The time complexity of linear search in the worst-case scenario is O(n).
The following are the steps involved in implementing Linear Search:
● We must first use a for loop to traverse the array elements.
● Compare the search element with the current array element in each iteration of the for loop, and -
○ Return the index of the related array entry if the element matches.
○ If the element you're looking for doesn't match, move on to the next one.
● Return -1 if there is no match or the search element is not found in the given array.
Let's look at the linear search algorithm now.
Algorithm
Linear_Search(a, n, val) // 'a' is the given array, 'n' is the size of given array, 'val' is the value to search
Step 1: set pos = -1
Step 2: set i = 1
Step 3: repeat step 4 while i <= n
Step 4: if a[i] == val
Set pos = i
Print pos
Go to step 6
[end of if]
Set ii = i + 1
[end of loop]
Step 5: if pos = -1
Print "value is not present in the array "
[end of if]
Step 6: exit
Time Complexity
Case | Time Complexity |
Best Case | O(1) |
Average Case | O(n) |
Worst Case | O(n) |
Space Complexity
Space Complexity | O(1) |
Application of Linear Search Algorithm
The linear search algorithm is useful for the following tasks:
● Both single-dimensional and multi-dimensional arrays can benefit from linear search.
● When the array has only a few elements, linear search is simple to implement and effective.
● When performing a single search in an unordered-List, Linear Search is also quite efficient.
Binary Search
Binary search is the search technique which works efficiently on the sorted lists. Hence, in order to search an element into some list by using binary search technique, we must ensure that the list is sorted.
Binary search follows a divide and conquer approach in which the list is divided into two halves and the item is compared with the middle element of the list. If the match is found then, the location of the middle element is returned; otherwise, we search into either of the halves depending upon the result produced through the match.
Binary search algorithm is given below.
BINARY_SEARCH(A, lower_bound, upper_bound, VAL)
● Step 1: [INITIALIZE] SET BEG = lower_bound
END = upper_bound, POS = - 1
● Step 2: Repeat Steps 3 and 4 while BEG <=END
● Step 3: SET MID = (BEG + END)/2
● Step 4: IF A[MID] = VAL
SET POS = MID
PRINT POS
Go to Step 6
ELSE IF A[MID] > VAL
SET END = MID - 1
ELSE
SET BEG = MID + 1
[END OF IF]
[END OF LOOP]
● Step 5: IF POS = -1
PRINT "VALUE IS NOT PRESENT IN THE ARRAY"
[END OF IF]
● Step 6: EXIT
Complexity
SN | Performance | Complexity |
1 | Worst case | O(log n) |
2 | Best case | O(1) |
3 | Average Case | O(log n) |
4 | Worst case space complexity | O(1) |
Example
Let us consider an array arr = {1, 5, 7, 8, 13, 19, 20, 23, 29}. Find the location of the item 23 in the array.
In 1st step:
- BEG = 0
- END = 8ron
- MID = 4
- a[mid] = a[4] = 13 < 23, therefore
In Second step:
- Beg = mid +1 = 5
- End = 8
- Mid = 13/2 = 6
- a[mid] = a[6] = 20 < 23, therefore;
In third step:
- Beg = mid + 1 = 7
- End = 8
- Mid = 15/2 = 7
- a[mid] = a[7]
- a[7] = 23 = item;
- Therefore, set location = mid;
- The location of the item will be 7.
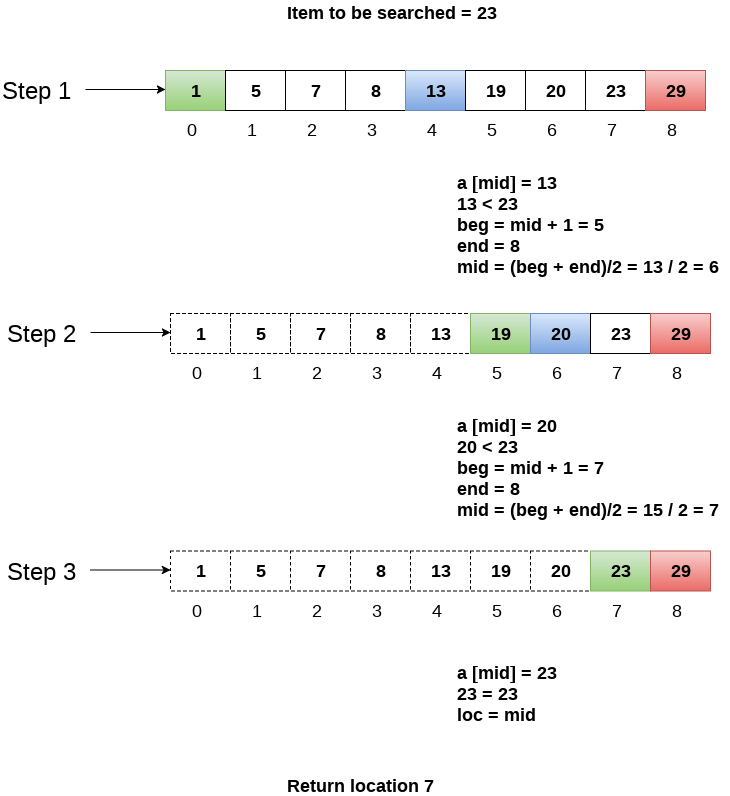
Fig 3 - Example
Bubble sort
Bubble Sort is a simple algorithm for sorting a collection of n elements that is provided in the form of an array with n elements. Bubble Sort compares each element individually and sorts them according to their values.
If an array must be sorted in ascending order, bubble sort will begin by comparing the first and second members of the array, swapping both elements if the first element is greater than the second, and then moving on to compare the second and third elements, and so on.
If there are n elements in total, we must repeat the method n-1 times.
It's called bubble sort because the largest element in the given array bubbles up to the last position or highest index with each full iteration, similar to how a water bubble rises to the sea surface.
Although it is simple to use, bubble sort is largely employed as an educational tool because its performance in the actual world is low. It isn't designed to handle huge data collections. Bubble sort has an average and worst-case complexity of O(n2), where n is the number of elements.
Sorting is done by going through all of the items one by one, comparing them to the next closest element, and swapping them if necessary.
Algorithm
Assume arr is an array of n elements in the algorithm below. The algorithm's presumed swap function will swap the values of specified array members.
Begin BubbleSort(arr)
for all array elements
if arr[i] > arr[i+1]
swap(arr[i], arr[i+1])
end if
end for
return arr
End BubbleSort
Working of Bubble Sort
Assume we're attempting to arrange the elements in ascending order.
1. First Iteration (Compare and Swap)
● Compare the first and second elements starting with the first index.
● The first and second elements are swapped if the first is bigger than the second.
● Compare and contrast the second and third elements now. If they aren't in the right order, swap them.
● The process continues until the last piece is added.
2. Remaining Iteration
For the remaining iterations, the same procedure is followed.
The largest element among the unsorted items is placed at the conclusion of each iteration.
The comparison takes place up to the last unsorted element in each iteration.
When all of the unsorted elements have been placed in their correct placements, the array is said to be sorted.
Key takeaway
- Compare and swap adjacent elements of the list if they are out of order.
- After repeating the procedure, we end up 'bubbling up' the largest element to the last place on the list by doing it repeatedly.
Insertion sort
Insertion style is a decrease & conquer technique application. It is a sort based on comparison in which the sorted array is constructed on one entry at a time.
Insertion sorting is a very basic process for sorting numbers in an ascending or descending order. The gradual method is accompanied by this method. It can be contrasted with the method of sorting cards at the time of playing a game.
The numbers that are needed to be sorted are known as keys. Here is the insertion sort method algorithm.
Algorithm:
Algorithm: Insertion-Sort (A)
For j = 2 to A.length
Key = A[j]
// Insert A[j] into the sorted sequence A[1.. j - 1]
i = j - 1
While i > 0 and A[i] > key
A[i + 1] = A[i]
i = i -1
A[i + 1] = key
Analysis:
This algorithm's run time is very dependent on the input given.
If the numbers given are sorted, this algorithm runs in O(n) time. If the numbers given are in reverse order, the algorithm runs in O(n2) time.
Example:
Using insertion sort to sort the following list of elements:
89, 45, 68, 90, 29, 34, 17
89 |45 68 90 29 34 17
45 89 |68 90 29 34 17
45 68 89 |90 29 34 17
45 68 89 90 |29 34 17
29 45 68 89 90 |34 17
29 34 45 68 89 90 |17
17 29 34 45 68 89 90
Application:
In the following instances, the insertion sort algorithm is used:
- When only a few elements are in the list.
- When there are few elements for sorting.
Advantages:
- Straightforward implementation. Three variants exist.
● Left to right scan
● Right to left scan
● Binary insertion sort
2. Effective on a small list of components, on a nearly sorted list.
3. In the best example, running time is linear.
4. This algorithm is stable.
5. Is the on-the-spot algorithm
Key takeaways
- Insertion sorting is a very basic process for sorting numbers in an ascending or descending order.
- Insertion style is a decrease & conquer technique application.
- It is a sort based on comparison in which the sorted array is constructed on one entry at a time.
Selection sort
In the selection sort, the smallest value among the array's unsorted items is chosen in each pass and inserted into the proper spot.
To begin, locate the array's smallest element and set it in the first position. Then locate the array's second smallest element and set it in the second spot. The procedure is repeated till the sorted array is obtained.
The n-1 pass of the selection sort algorithm is used to sort the array of n entries.
● The smallest element of the array, as well as its index pos, must be identified in the first run. Swap A[0] and A[pos] after that. As a result of sorting A[0], we now have n -1 elements to sort.
● The location pos of the smallest element in the sub-array A[n-1] is obtained in the second pass. Swap A[1] and A[pos] after that. After sorting A[0] and A[1], we're left with n-2 unsorted elements.
● The position pos of the smaller element between A[n-1] and A[n-2] must be found in the n-1st pass. Swap A[pos] and A[n-1] after that.
As a result, the items A[0], A[1], A[2],...., A[n-1] are sorted using the procedure described above.
Example
Consider the following six-element array. Using selection sort, sort the array's elements.
A = {10, 2, 3, 90, 43, 56}.
Pass | Pos | A[0] | A[1] | A[2] | A[3] | A[4] | A[5] |
1 | 1 | 2 | 10 | 3 | 90 | 43 | 56 |
2 | 2 | 2 | 3 | 10 | 90 | 43 | 56 |
3 | 2 | 2 | 3 | 10 | 90 | 43 | 56 |
4 | 4 | 2 | 3 | 10 | 43 | 90 | 56 |
5 | 5 | 2 | 3 | 10 | 43 | 56 | 90 |
Sorted A = {2, 3, 10, 43, 56, 90}
Algorithm
SELECTION SORT(ARR, N)
● Step 1: Repeat Steps 2 and 3 for K = 1 to N-1
● Step 2: CALL SMALLEST(ARR, K, N, POS)
● Step 3: SWAP A[K] with ARR[POS]
[END OF LOOP]
● Step 4: EXIT
SMALLEST (ARR, K, N, POS)
● Step 1: [INITIALIZE] SET SMALL = ARR[K]
● Step 2: [INITIALIZE] SET POS = K
● Step 3: Repeat for J = K+1 to N -1
IF SMALL > ARR[J]
SET SMALL = ARR[J]
SET POS = J
[END OF IF]
[END OF LOOP]
● Step 4: RETURN POS
Key takeaway
- In the selection sort, the smallest value among the array's unsorted items is chosen in each pass and inserted into the proper spot.
- To begin, locate the array's smallest element and set it in the first position.
- Then locate the array's second smallest element and set it in the second spot.
It becomes easier to solve the complete problem if we can separate a single major problem into smaller sub-problems, solve the smaller sub-problems, and integrate their solutions to find the solution for the original huge problem.
Let's look into Divide and Rule as an example.
When the British arrived in India, they encountered a country where many religions coexisted peacefully, hardworking but ignorant individuals, and unity in variety, making it difficult for them to establish their empire. As a result, they chose the Divide and Rule strategy. Where the population of India was a single large difficulty for them, they divided it into smaller ones by inciting rivalries amongst local monarchs and pitting them against one another, which worked extremely well for them.
That was history and a socio-political policy (Break and Rule), but the notion here is that if we can divide a problem into smaller sub-problems, it becomes easier to tackle the total problem in the end.
The Divide and Conquer strategy consists of three steps:
● Break the problem down into smaller chunks.
● Solve the subproblems to defeat them. The goal is to break down the problem into atomic subproblems that can be solved individually.
● To obtain the solution to the actual problem, combine the solutions of the subproblems.
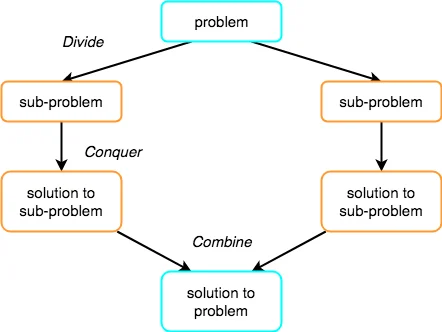
Merge sort
Merge Sort is based on a divide and conquer strategy. It divides the unsorted list into n sublists such that each sublist contains one element. Each sublist is then sorted and merged until there is only one sublist.
Step 1: Divide the list into sublists such that each sublist contains only one element.
Step 2: Sort each sublist and Merge them.
Step 3: Repeat Step 2 till the entire list is sorted.
Example: Apply Merge Sort on array A= {85,24,63,45,17,31,96,50}
Step1: A contains 8 elements. First we divide the list into two sublists such that each sublist contains 4 elements. Then we divide each sublist of 4 elements into sublist of two elements each. Finally every sublist contains only one element.
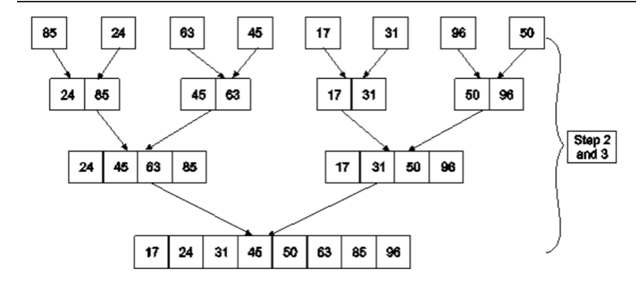
Fig. 4: Example
Step 2: Now we start from the bottom. Compare 1st and 2nd element. Sort and merge them. Apply this for all bottom elements.
Thus we got 4 sublists as follows
24 | 85 |
| 45 | 63 |
| 17 | 31 |
| 50 | 96 |
Step 3: Repeat this sorting and merging until the entire list is sorted. The above four sublists are sorted and merged to form 2 sublists.
24 | 85 | 63 | 85 |
| 17 | 31 | 50 | 96 |
Finally, the above 2 sublists are again sorted and merged in one sublist.
17 | 24 | 31 | 45 | 50 | 63 | 85 | 96 |
We will see one more example on merge sort.
Example: Apply merge Sort on array A={10,5,7,6,1,4,8,3,2,9,12,11}
Step 1:
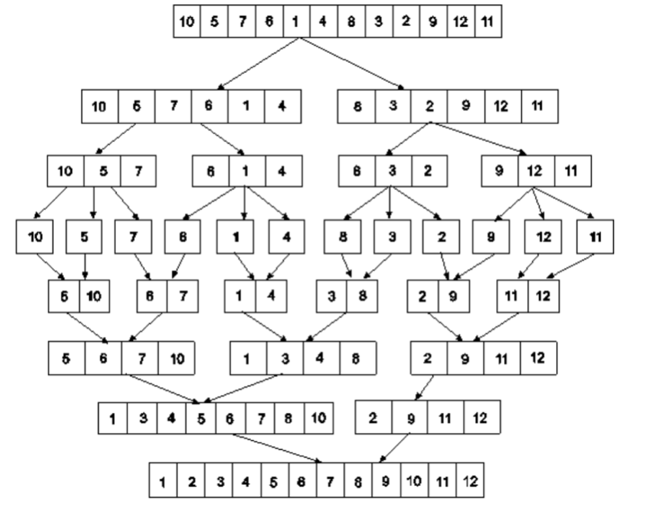
Fig 5: Merge sort
Algorithm for Merge Sort:
Let x = no. Of elements in array A
y = no. Of elements in array B
C = sorted array with no. Of elements n
n = x+y
Following algorithm merges a sorted x element array A and sorted y element array B into a sorted array C, with n = x + y elements. We must always keep track of the locations of the smallest element of A and the smallest element of B which have not yet been placed in C. Let LA and LB denote these locations, respectively. Also, let LC denote the location in C to be filled. Thus, initially, we set
LA : = 1,
LB : = 1 and
LC : = 1.
At each step, we compare A[LA] and B[LB] and assign the smaller element to C[LC].
Then
LC:= LC + 1,
LA: = LA + 1, if a new element has come from A .
LB: = LB + 1, if a new element has come from B.
Furthermore, if LA> x, then the remaining elements of B are assigned to C;
LB >y, then the remaining elements of A are assigned to C.
Thus the algorithm becomes
MERGING ( A, x, B, y, C)
1. [Initialize ] Set LA : = 1 , LB := 1 AND LC : = 1
2. [Compare] Repeat while LA <= x and LB <= y
If A[LA] < B[LB] , then
(a) [Assign element from A to C ] set C[LC] = A[LA]
(b) [Update pointers ] Set LC := LC +1 and LA = LA+1
Else
(a) [Assign element from B to C] Set C[LC] = B[LB]
(b) [Update Pointers] Set LC := LC +1 and LB = LB +1
[End of loop]
3. [Assign remaining elements to C]
If LA > x , then
Repeat for K= 0 ,1,2,........,y–LB
Set C[LC+K] = B[LB+K]
[End of loop]
Else
Repeat for K = 0,1,2,......,x–LA
Set C[LC+K] = A[LA+K]
[End of loop]
4. Exit
Quick sort
Quick sort is the most efficient method of sorting .It uses the divide and conquer strategy to sort the elements. In quicksort, we divide the array of items to be sorted into two partitions and then call the quicksort procedure recursively to sort the two partitions. For this we choose a pivot element and arrange all elements such that all the elements in the left part are less than the pivot and all those in the right part are greater than it.
Algorithm to implement Quick Sort is as follows.
Consider array A of size n to be sorted. p is the pivot element. Index positions of the first and last element of array A are denoted by ‘first’ and ‘last’.
- Initially first=0 and last=n–1.
- Increment first till A[first]<=p
- Decrement last till A[last]>=p
- If first < last then swap A[first] with A[last].
- If first > last then swap p with A[last] and thus the position of p is found. Pivot p is placed such that all elements to its left are less than it and all elements right to it are greater than it. Let us assume that j is the final position of p. Then A[0] to A[j–1] are less than p and A [j + 1] to A [n–1]are greater than p.
- Now we consider the left part of array A i.e A[0] to A[j–1].Repeat step 1,2,3 and 4. Apply the same procedure for the right part of the array.
- We continue with the above steps till no more partitions can be made for every subarray.
Algorithm
PARTITION (ARR, BEG, END, LOC)
● Step 1: [INITIALIZE] SET LEFT = BEG, RIGHT = END, LOC = BEG, FLAG =
● Step 2: Repeat Steps 3 to 6 while FLAG =
● Step 3: Repeat while ARR[LOC] <=ARR[RIGHT]
AND LOC != RIGHT
SET RIGHT = RIGHT – 1
[END OF LOOP]
● Step 4: IF LOC = RIGHT
SET FLAG = 1
ELSE IF ARR[LOC] > ARR[RIGHT]
SWAP ARR[LOC] with ARR[RIGHT]
SET LOC = RIGHT
[END OF IF]
● Step 5: IF FLAG = 0
Repeat while ARR[LOC] >= ARR[LEFT] AND LOC != LEFT
SET LEFT = LEFT + 1
[END OF LOOP]
● Step 6:IF LOC = LEFT
SET FLAG = 1
ELSE IF ARR[LOC] < ARR[LEFT]
SWAP ARR[LOC] with ARR[LEFT]
SET LOC = LEFT
[END OF IF]
[END OF IF]
● Step 7: [END OF LOOP]
● Step 8: END
QUICK_SORT (ARR, BEG, END)
● Step 1: IF (BEG < END)
CALL PARTITION (ARR, BEG, END, LOC)
CALL QUICKSORT(ARR, BEG, LOC - 1)
CALL QUICKSORT(ARR, LOC + 1, END)
[END OF IF]
● Step 2: END
Key takeaways
- Merge sort consisting two phases as divide and merge.
- In divide phase, each time it divides the given unsorted list into two sub list until each sub list get single element then sorts the elements.
- In merge phase, it merges all the solution of sub lists and find the original sorted list.
- Quick sort is the most efficient method of sorting .It uses the divide and conquer strategy to sort the elements.
- In quicksort, we divide the array of items to be sorted into two partitions and then call the quicksort procedure recursively to sort the two partitions.
Bubble Sort, Selection Sort, Insertion Sort, Merge Sort, Quick Sort, Heap Sort, Counting Sort, Radix Sort, and Bucket Sort have all had their time and space difficulties discussed.
Bubble sort
Each nearby pair is compared in bubble sort. We swap them if they aren't in the right order. We repeat the preceding procedure until no more swaps are required, indicating that all of the components have been sorted.
Worse case: O(n2)
We iterate through the array (n - 1) times once it is reverse-sorted. We do (n - 1) swaps in the first iteration, (n - 2) swaps in the second, and so on until we only do one swap in the last iteration. As a result, the total number of swaps equals n * (n - 1) / 2.
Average case: O(n2)
The total number of swaps for a truly random array averages out to roughly n2 / 4, which is again O(n2).
Best case: O(n)
In the first iteration of the array, if no swaps are performed, we know that the array is already sorted and hence cease sorting, resulting in a linear time complexity.
Space Complexity:
The space complexity is O(1) since we only use a constant amount of additional memory away from the input array.
Selection Sort
Selection sort is a straightforward sorting method that divides an array into two parts: a subarray of already sorted elements and a subarray of unsorted elements. Initially, the sorted subarray is empty. The array is iterated over (n - 1) times. We find the smallest element from the unsorted subarray and set it at the end of the sorted subarray in each iteration.
Time Complexity:
Worst case = Average Case = Best Case = O(n2)
For an array of whatever size, we conduct the same number of comparisons.
We execute (n - 1) comparisons in the first iteration, (n - 2) in the second, and so on until the last iteration, when we only perform one comparison. As a result, the total number of comparisons is n * (n - 1) / 2. The number of swaps performed is at most n - 1. So the overall time complexity is quadratic.
Space Complexity:
The space complexity is O(1) because we don't use any other data structures except the input array.
Insertion Sort
The insertion sort method, like selection sort, separates the array into two parts: a subarray of already sorted elements and a subarray of unsorted elements. Only the first member of the array is originally stored in the sorted subarray. We go over each of the remaining elements one by one, putting them in their proper places in the sorted subarray.
Time Complexity:
Worse case: O(n2)
When we use insertion sort on a reverse-sorted array, each element is inserted at the beginning of the sorted subarray, which has the highest temporal complexity.
Average case: O(n2)
The average running time is O(n2 / 4) = O(n2). When the array members are in random order.
Best case: O(n)
When we run insertion sort on an array that has previously been sorted, it merely compares each element to its predecessor, needing n steps to sort the already sorted array of n elements.
Space Complexity:
The space complexity is O(1) since we only use a constant amount of additional memory away from the input array.
Merge Sort
We partition the unsorted array into n subarrays, each of size one, that can be considered sorted trivially in merge sort. Then, until there is only one sorted array of size n left, we merge the sorted subarrays to make new sorted subarrays.
Time Complexity:
Worst case = Average Case = Best Case = O(n log n)
For any input array of a certain size, merge sort performs the same number of operations.
We divide the array into two subarrays repeatedly in this approach, resulting in O(log n) rows with each element appearing exactly once in each row.
Merging every pair of subarrays takes O(n) time for each row. As a result, the entire time complexity is O(n log n).
Space Complexity:
The space complexity is O(n) since we store the merged subarray in an auxiliary array of size at most n.
Quick Sort
Quick sort is a more complicated algorithm. It divides the array into two subarrays using a divide-and-conquer approach. We pick an element called pivot and place it at its proper index before reordering the array by moving all elements less than pivot to the left and all elements greater than it to the right.
The subarrays of these subarrays are then sorted recursively until the entire array is sorted. The pivot element's selection has a significant impact on the quick sort algorithm's efficiency.
Time Complexity:
Worse case: O(n2)
When the array is sorted and the leftmost element is chosen as pivot, or when the array is reverse-sorted and the rightmost element is chosen as pivot, the time complexity increases quadratically because dividing the array produces extremely unbalanced subarrays.
When the array has a high number of identical members, splitting becomes difficult, resulting in quadratic time complexity.
Average case and best case: O(n log n)
The best case scenario for quick-sort is when we consistently use the median element for partitioning. As a result of this partitioning, we can always divide the array in half.
Space Complexity:
Although rapid sort does not need auxiliary space to store array elements, recursive calls require additional space to create stack frames.
Worst case: O(n)
This occurs when the pivot element in each recursive call is the largest or smallest element of the array. After partitioning, the size of the subarray will be n-1 and 1. The recursive tree will be n in size in this situation.
Best case: O(log n)
This occurs when the right position of the pivot element in the partitioned array is always in the middle. Subarrays will have a size of half that of the parent array. The size of the recursive tree will be O in this situation (log n).
References:
- Data Structures with C, Seymour Lipschutz, Schaum's Outlines, Tata McGraw Hill Education.
- Fundamentals of Computer Algorithms by Horowitz, Sahni,Galgotia Pub. 2001 ed.
- Data Structures and program design in C by Robert Kruse, Bruce Leung & Clovis Tondo.
- Data Structures: A Pseudocode Approach with C by Richard F. Gilberg and
Behrouz Forouzan.