Unit - 2
Time Domain analysis
The Response of the system as a function of time, to the applied excitation is called Time Response. The time response of a system can be fully studied by studying the following two responses
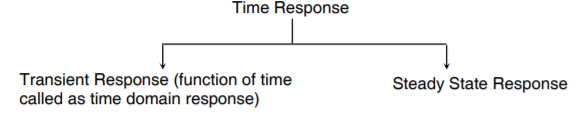
The total time response C(t) is given by
C(t) = Ctr(t) + Css(t)
Where Ctr(t) = transient response
Css(t) = steady state response
Consider the class of differential equation
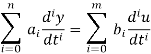
Where the coefficient ai and bi are constant, u = u(t) (the input) is a known time function, and y = y(t) (the output) is the unknown solution of the equation. Generally, m ≤ n, and n is called the order of the differential equation.
The Free Response
The Free response of a differential equation is the solution of the differential equation when the input u(t) is identically zero. If the input u(t) is identically zero, then the differential equation has the form:

The solution y(t) of such an equation depends only on the initial conditions.
The Forced Response
The forced response yb(t) of a differential equation is the solution of the differential equation when all the initial conditions are identically zero.
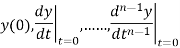
The Total Response
The total response of a linear constant −coefficient differential equation is the sum of the free response and the forced response.
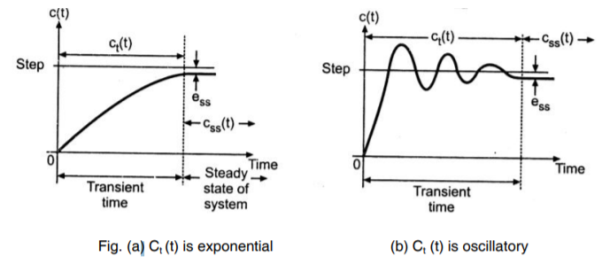
The Steady State and Transient Response
The steady state response and transient response are another pair of quantities whose sum is equal to the total response. These terms are often used for specifying control system performance. They are defined as follows. The steady state response is that part of the total response which does not approach zero as time approaches infinity. The transient response is that part of the total response which approaches zero as time approaches infinity
For stable system Transient response vanishes after some time to get final value closer to the desired value.
Steady State Response: The part of the time response which remains after complete transient response vanishes from the system output. The steady state response is generally the final value achieved by the system output. The difference between the desired output and the actual output of the system is called as Steady state error (ess) and the time taken to reach steady state is called Settling time.

Transient Analysis of First Order System:
OLTF G(s) = 1/TS
CLTF c(s)/R(s) = 1/1+TS
CE: HTS = 0
S= -1/T
C(s) = R(s) [G(S)/1+G(s)]
C(s) = R(s)/1+TS
So, Calculating value of c(s), c(t) for different input
Unit Step:
R(t) = u(t)
R(s) = 1/s
C(s) = 1/s(1+ST)
1/s(1+ST) = A/s + o/1+TS
1/s(1+ST) = A/S + 0/1+TS
1= A(1+ST) + BS
AT +B =0
A = 1
B= -T
C(s) = 1/s + (-T)/1+TS
= 1+ (-T)/1-(-T)s = 1-I/n/1+ass+1/T =e-t/s
C(t) = [ 1-e-t/T]
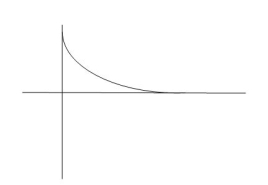
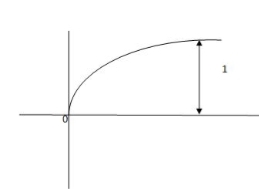
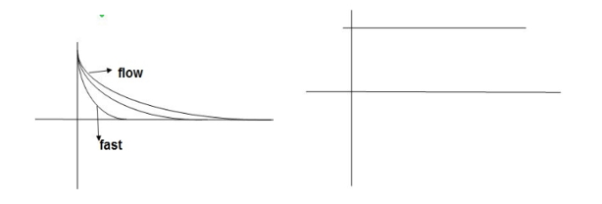
Fig 1. Output response for Unit Step input
Ramp
R(t) = t
R(s) = 1/s2
C(s) = R(s) [G(s)/1+G(s)]
C(s) = 1/s2 1/(1+TS) + c
1/s2 (1+TS) = A/(s) + B/s2 + c(1+TS)
1= A (s+s2. T) + B(1+TS) +cs2
TA +c = 0
A+TB =0
B =1
A = -T
C = T2
C(s) = -T/s + 1/s2 +T2/1+ST
=(-T) u(t) + t(u) + T e-t/T u(t)
= [ -T + t +Te-t/T u(t)
= [ -T+ t+Te-t/T] u(t)
C(s) = t- T+ Te-t/T
ess = R(t) – c(t)
R(t) – c(t)
=  [ t- t+ 7-Te –t/T]
[ t- t+ 7-Te –t/T]
= 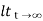 T( 1-e-t/T]
T( 1-e-t/T]
ess = The less the value of T the less in the errors.
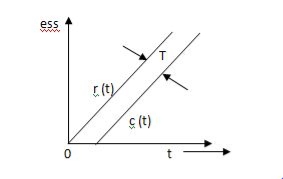
Fig 2. Output response for ramp input
Key takeaway
From both the Cases input unit step, ramp Unit step
Unit Step Ramp
c(t) = 1-e-t/T r(t) = t
ess = e-t/T (r/t)-(t) c(t) = t- T+te-t/T
ess= e-t/T (r/t) (t) ess = T- Te-t/T
For t for t
ess =0 ess = T
In both the cases (values of T) must be as small as possible (so, that e-t/T) must be as small as possible which gives us
Fig 3. Location of poles
G(s) = 1/Ts
ATf = 1/1+TS
1st order system
Poles must be situated as far as possible from origin i.e. deeper and deeper into the left half of s-place. Thus, we get less errors.
Transient Analysis of Second Order System:
OLTF G(s) = k/s(1+TS)
CLTFC(s)/R(s) = k/k+s(1+Ts)
= k/s2+ s/T +k/T
Comparing above equation with standard 2nd order eqn
CLTF = wn2/s2+2rs wns+wn2
Standard 2nd order equation
CEs2+2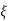 wn s+wn2= 0
wn s+wn2= 0
S= -2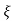 wn±
wn±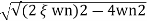 /2
/2
=2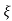 wn±2wn
wn±2wn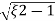 /2
/2
S= wn±wn
wn±wn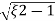
S= -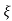 wn±wn
wn±wn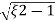
S= -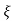 wn ±wn
wn ±wn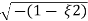
S= -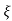 wn ±gwn
wn ±gwn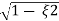
Standard eqn:
T(s) = wn2/s2+2 wns+wn2
wns+wn2
Our eqn T(s) = K/T/s2+1/T s+ K/T
Wn2 = k/T
2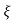 wn = 1/T
wn = 1/T
2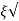 k/T = 1/T
k/T = 1/T
 k/T = 1/2T
k/T = 1/2T
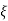 = 1/2T
= 1/2T 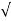 T/K
T/K
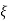 = 1
= 1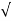 2KT
2KT
Graphically showing the position of loops s1, s2 for offered of
As the characteristic Equation (location of poles) is dependent only on (wn constant for a given system.
S1 = - wn + jwn
wn + jwn 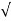 1-
1-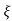 2
2
S2= -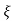 wn - jwn
wn - jwn 1-
1- 2
2
CASE 1: ( =0)
=0)
S1=jwn, S2, = -jwn
Fig 4. Location of poles for  =0
=0
Undamped
CASE 2:(0<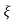 <1)
<1)
S1= -wn + jwn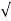 0.75
0.75
=-wn/2 +jwn(0.26)
S2 = -wn/2 – jwn (0.86)
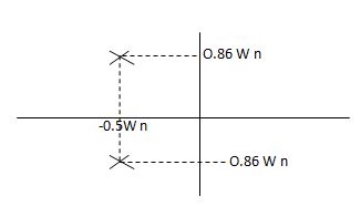
Fig 5. Location of poles for 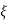 <1
<1
CASE:3 (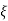 -1)
-1)
S1= S2 = -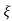 wn = -wn
wn = -wn
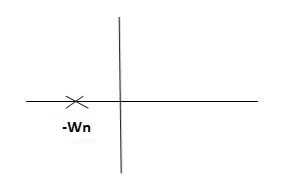
Fig 6. Location of poles for  =1
=1
CASE4: ( -1)
-1)
S1 = -2wn +jwn -3
-3
=-2wn – jwn (1.73)
S1 = -3.73wn
S2 = -2wn –jwn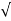 -3
-3
= -2wn + jwn (1.73)
= -0.27 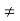 wn
wn
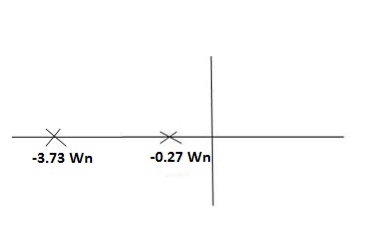
Fig 7. Location of poles for 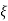 >1
>1
Overdamped
All practical systems are 2 order to, if R(e) =  (t) R(s) = 1. CLTF = 2nd order st eqn and hence already the system is possible.
(t) R(s) = 1. CLTF = 2nd order st eqn and hence already the system is possible.
CLTF = e(s)/ R(s) = wn2/s2+2 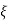 wns+wn2
wns+wn2
Now calculating c(s), c(t) for different values of input
Impulse I/p
R(t) = 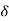 (t)
(t)
R(t) =  (t)
(t)
R(s) = 1
C(s) = R(s) wn2/s2+2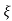 wns+wn2
wns+wn2
C(s) = wn2/s2 +2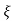 wn+wn2
wn+wn2
Under this i/p (R(t) = 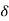 (t)) the output varies with different values of
(t)) the output varies with different values of  . So,
. So,
CONDITION 1: (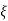 =0)
=0)
C(s) =wn2/s2 +wn2
Os2 +wn2 =0
S=+-jwn
C(t) = wnsinwnt
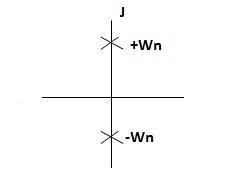
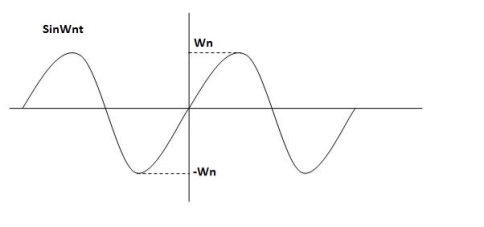
Fig 8. Undamped oscillations
As there in no damping i.e. oscillations at t= 0 are some at t  so, called UNDAMPED
so, called UNDAMPED
CONDITION 2: 0<<1
c(s) = R(s) wn2/s22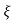 wn+wn2 R(t) =
wn+wn2 R(t) = 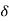 (t)
(t)
R(s) =1
C(s) = wn2/s2+2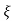 wns+wn2
wns+wn2
CE
S2+2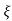 wns +wn2 =0
wns +wn2 =0
S2, S1 = -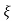 wn ±jwn
wn ±jwn 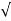 1-
1-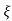 2
2
C(t) = e- wntsin(wn
wntsin(wn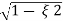 )t
)t
Wd=wn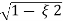 )
)
C(t)=e-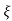 wnt sin (wdt)
wnt sin (wdt)
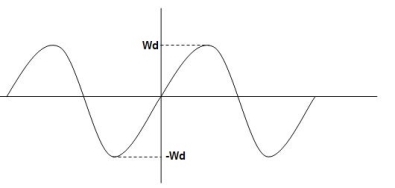
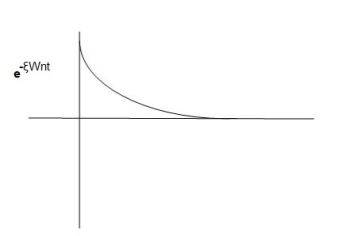
Fig 9. Underdamped oscillations
The oscillations are present but at t- infinity the Oscillations are 0 so, it is UNDERDAMPED
CONDITION 3: =1
=1
C(s) = R(s) wn2/s2+2 wns+wn2
wns+wn2
C(s)=wn2/S2 +2wns+wn2
=wn2/(s +wn)2
CE S= -Wn
C(t)= w2n/(
w2n/( )2
)2
C(t)=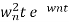
Diagram
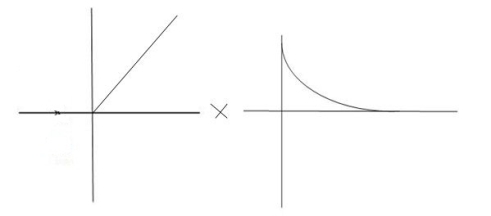
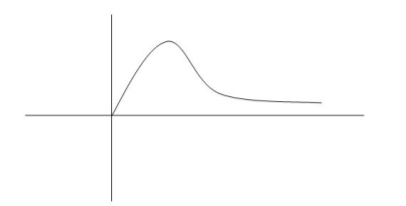
Fig 10. Critically damped oscillations
No damping obtained at 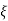 =1so is called CRITICALLY DAMPED.
=1so is called CRITICALLY DAMPED.
CONDITION 4- 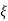 >1
>1
C(s) = wn2/s22 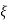 wnS+Wn2
wnS+Wn2
S1,s2 = 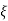 WN+-jwn
WN+-jwn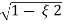 )
)
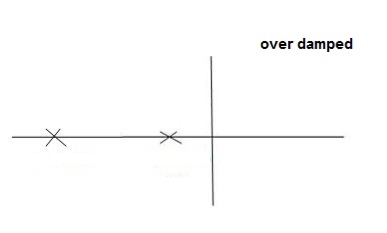
Fig 11. Location of poles for over damped oscillations
UNIT Step Input:
R(s) = 1/s
C(s)/R(s) = wn2/s2+2 wns+wn2
wns+wn2
C(s) = R(s) wn2 /s2 +2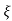 wns+wn2
wns+wn2
C(s) = R(s) wn2/s2+2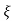 wns+wn2
wns+wn2
C(s) = R(s) wn2/s2+2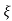 wns+wn2
wns+wn2
C(s) = wn2s(s2+2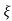 wns+wn2)
wns+wn2)
C(t) = 1- e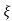 wnt/
wnt/ 1-es2sin (wdt + ø)
1-es2sin (wdt + ø)
Wd = wn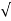 1-
1-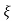 2
2
Ø= 
Where
Wd = Damping frequency of oscillations
Wn = natural frequency of oscillations
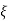 wn = damping coefficient.
wn = damping coefficient.
T= Time constant
Condition 1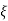 = 0
= 0
C(s) = wn2 /s(s2+wn2)
C(t) = 1- e° sin wdt +ø
C(t)= 1- sin( wn +90)
C(t) = 1+cos wnt
Constant
C(t) = 1+constant
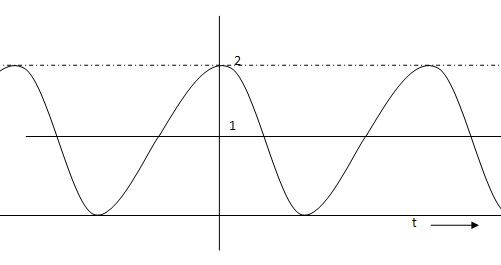
Fig 12. C(t) = 1+cos wnt
Condition 2: 0<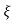 <1
<1
C(s) =  /s2+
/s2+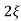 wns +wn2
wns +wn2
C(s) =1/s – s+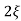 wn/s2+
wn/s2+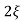 wns +wn2
wns +wn2
=1/s – s+ wn/(s+
wn/(s+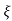 wn)2+wd2-
wn)2+wd2- 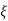 wn/(s+
wn/(s+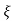 wn2) +wd2
wn2) +wd2
Wd = wn 1-
1-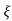 2
2
Taking Laplace inverse of above equation
L --1 s+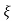 wn/(s+
wn/(s+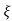 wn) +wd2= e-
wn) +wd2= e-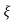 wnt coswdt
wnt coswdt
L-1 s+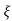 wn/(s+
wn/(s+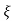 wn)2+wd2 = e-
wn)2+wd2 = e-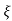 wnt sinWdt
wnt sinWdt
C(t) = 1-e-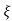 wnt [coswdt +
wnt [coswdt + /
/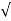 1-
1-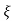 2sinwdt]
2sinwdt]
= 1-e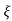 wnt /
wnt /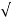 1-
1-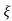 2 sin [wdt +
2 sin [wdt + 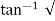 1-
1-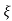 2/
2/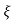 ] t>=0
] t>=0
C(t) = 1-e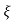 wnt/
wnt/ 1-
1-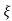 2 sin(wdt+ø)
2 sin(wdt+ø)
Ø = 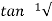 1+
1+ 2/
2/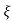
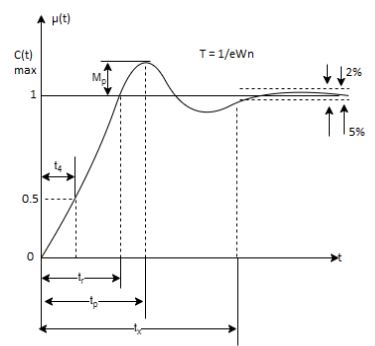
Fig 13. Transient Response of second order system
Specifications:
1) Rise Time (tp)
The time taken by the output to reach the already status value for the first time is known as Rise time.
C(t) = 1-e-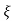 wnt/
wnt/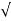 1-
1- 2 sin (wdt+ø)
2 sin (wdt+ø)
Sin (wd +ø) = 0
Wdt +ø = n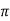
tr = n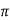 -ø/wd
-ø/wd
For first time so, n=1.
tr = 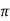 -ø/wd
-ø/wd
T=1/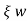
2) Peak Time (tp)
The peak value attained by the output is called peak time. The time required by the output to reach this value is lp.
d(cct) /dt = 0 (maxima)
d(t)/dt = peak value
tp = n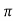 /wd for n=1
/wd for n=1
tp =  wd
wd
3) Peak Overshoot Value:
Maximum deviation of output from steady state value is called peak overshoot value (Mp).
(ltp) = 1 = Mp
(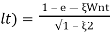 Sin(Wat + φ )
Sin(Wat + φ )
(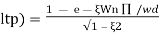 Sin( Wd∏/Wd + φ)
Sin( Wd∏/Wd + φ)
Mp = e-∏ξ / √1 –ξ2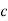
Condition 3 ξ = 1
C( S ) = R( S ) Wn2 / S2 + 2ξWnS + Wn2
C( S ) = Wn2 / S(S2 + 2WnS + Wn2) [ R(S) = 1/S ]
C( S ) = Wn2 / S( S2 + Wn2 )
C( t ) = 1 – e-Wnt + tWne-Wnt
The response is critically damped.
4) Settling Time (ts):
ts = 3 / ξWn ( 5% )
ts = 4 / ξWn ( 2% )
Examples
Q.1. The open loop transfer function of a system with unity feedback gain G( S ) = 20 / S2 + 5S + 4. Determine the ξ, Mp, tr, tp.
Soln: Finding closed loop transfer function,
C(S) / R( S ) = G( S ) / 1 + G( S ) + H( S )
As it is unity feedback so, H(S) = 1
C(S)/R(S) = G(S)/1 + G(S)
= 20/S2 + 5S + 4/1 + 20/S2 + 5S + 4
C(S)/R(S) = 20/S2 + 5S + 24
Standard equation for second order system,
S2 + 2ξWnS + Wn2 = 0
We have,
S2 + 5S + 24 = 0
Wn2 = 24
Wn = 4.89 rad/sec
2ξWn = 5
(a). ξ = 5/2 x 4.89 = 0.511
(b). Mp% = e-∏ξ / √1 –ξ2 x 100
= e-∏ x 0.511 / √1 – (0.511)2 x 100
Mp% = 15.4%
(c). tr = ∏ - φ / Wd
φ = tan-1√1 – ξ2 / ξ
φ= tan-1√1 – (0.511)2 / (0.511)
φ = 1.03 rad.
tr = ∏ - 1.03/Wd
Wd = Wn√1 – ξ2
= 4.89 √1 – (0.511)2
Wd = 4.20 rad/sec
tr = ∏ - 1.03/4.20
tr = 502.34 msec
(d). tp = ∏/4.20 = 747.9 msec
Q.2. A second order system has Wn = 5 rad/sec and is ξ = 0.7 subjected to unit step input. Find (i) closed loop transfer function. (ii) Peak time (iii) Rise time (iv) Settling time (v) Peak overshoot.
Soln: The closed loop transfer function is
C(S)/R(S) = Wn2 / S2 + 2ξWnS + Wn2
= (5)2 / S2 + 2 x 0.7 x S + (5)2
C(S)/R(S) = 25 / S2 + 7s + 25
(ii). tp = ∏ / Wd
Wd = Wn√1 - ξ2
= 5√1 – (0.7)2
= 3.571 sec
(iii). tr = ∏ - φ/Wd
φ= tan-1√1 – ξ2 / ξ = 0.795 rad
tr = ∏ - 0.795 / 3.571
tr = 0.657 sec
(iv). For 2% settling time
ts = 4 / ξWn = 4 / 0.7 x 5
ts = 1.143 sec
(v). Mp = e-∏ξ / √1 –ξ2 x 100
Mp = 4.59%
Q.3. The open loop transfer function of a unity feedback control system is given by G(S) = K/S(1 + ST)
Calculate the value by which k should be multiplied so that damping ratio is increased from 0.2 to 0.4?
Soln:
C(S)/R(S) = G(S) / 1 + G(S)H(S) H(S) = 1
C(S)/R(S) = K/S(1 + ST) / 1 + K/S(1 + ST)
C(S)/R(S) = K/S(1 + ST) + K
C(S)/R(S) = K/T / S2 + S/T + K/T
For second order system,
S2 + 2ξWnS + Wn2
2ξWn = 1/T
ξ = 1/2WnT
Wn2 = K/T
Wn =√K/T
ξ = 1 / 2√K/T T
ξ = 1 / 2 √KT
Forξ1 = 0.2, for ξ2 = 0.4
ξ1 = 1 / 2 √K1T
ξ2 = 1 / 2 √K2T
ξ1/ ξ2 = √K2/K1
K2/K1 = (0.2/0.4)2
K2/K1 = 1 / 4
K1 = 4K2
Q.4. Consider the transfer function C(S)/R(S) = Wn2 / S2 + 2ξWnS + Wn2
Find ξ, Wn so that the system responds to a step input with 5% overshoot and settling time of 4 sec?
Soln:
Mp = 5% = 0.05
Mp = e-∏ξ / √1 –ξ2
0.05 = e-∏ξ / √1 –ξ2
Cn 0.05 = - ∏ξ / √1 –ξ2
-2.99 = - ∏ξ / √1 –ξ2
8.97(1 – ξ2) = ξ2∏2
0.91 – 0.91 ξ2 = ξ2
0.91 = 1.91 ξ2
ξ2 = 0.69
(ii). ts = 4/ ξWn
4 = 4/ ξWn
Wn = 1/ ξ = 1/ 0.69
Wn = 1.45 rad/sec
The Impulse signal, Ramp signal, unit step and parabolic signals are used as the standard test signals. All these signals are explained below.
(a) Impulse Signal:
This signal has zero amplitude everywhere except at the origin. Fig below shown the representation of Impulse signal.
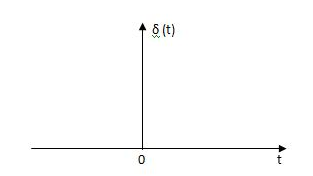
Fig 14. Unit Impulse Signal
The mathematical representations
A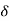 (t) = 0 for t ≠0
(t) = 0 for t ≠0
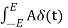 dt = A e
dt = A e 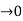
Where A represent energy or area of the Laplace Transform of Impulse signal is
L [A (t)] = A
(t)] = A
Unit Impulse Signal:
If A = 1
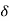 (t) = 0 for t ≠0
(t) = 0 for t ≠0
L [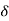 (t)] = 1
(t)] = 1
The transfer function of a linear time invariant
System is the Laplace transform of the impulse response of the system. If a unit impulse signal is applied to system then Laplace transform of the output c(s) is the transfer function G(s)
As we know G(s) = c(s)/R(S)
r(t) =  (t)
(t)
R(s) = L [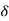 (t)] = 1
(t)] = 1
:. G(S) = C(s)
(b) Step signal:
Step signal of size A is a signal that change from zero level to A in zero time and stays there forever.
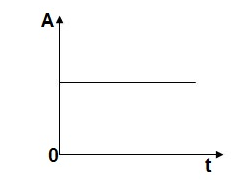
Fig 15. Unit Step Signal
r(t)= A t >=0
=0 t<0
L[r(t)] = R(s) = A/s
Unit Step Signal:
If the magnitude of the slip signal is I then it is called unit step signal.
u(t) = 1
t>=0
t<0
L[u(t)] = 1/s
(c) Ramp Signal:
The vamp signal increase linearly with time from initial value of zero at t= 0 as shown in fig is below

Fig 16. Ramp Signal
r(t) = At t>=0
=0 t<0
A is the slope of the line The Laplace transform of ramp signal is
L[r(t)] = R(s) = A/s2
(d) Parabolic Signal:
The instantaneous value of a parabolic signal varies as square of the time from an initial value of zero t=0. The signal representation in fig 14 below.
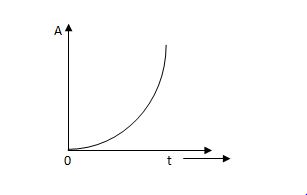
Fig 17. Parabolic Signal
r(t) At2 t>=0
=0 t<0
Then Laplace Transform is given as
R(s) = L[At2] = 2A/s3
If no error then E(t) =0, :. R(t) = c(t), output is tracking the input.
Steady state Errors signal (ess): - (t  )
)
Ess = t  e(t)
e(t)
Using final values, the theorem
 = ess =
= ess = 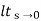 S.E (s)
S.E (s)
ess= 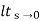 S[R(s)/1+G/(s)]
S[R(s)/1+G/(s)]
Key takeaway
If no error then E(t) =0,: R(t) = c(t), output is tracking the input.
Steady state Errors signal (ess): - (t 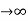 )
)
Ess = t 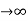 e(t)
e(t)
Using final values, the theorem
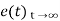 = ess =
= ess = 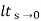 S.E (s)
S.E (s)
Examples
Q1) Find the initial value for the function f(t) = 2u(t)+3cost u(t)?
Sol:
f(t) = 2u(t)+3cost u(t)
F(s) = 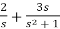
SF(s) = 2+ 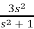
By initial value theorem
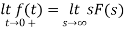 = f(0+)
= f(0+)
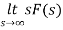 =
= 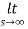 2+
2+ 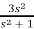 = 5 = f(0+)
= 5 = f(0+)
Hence, initial value of the function is 5
Q2) Find final value of the function F(s) = 
Sol:
F(s) = 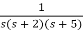
SF(s) = 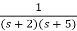
By final value theorem
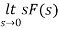 =
= 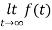
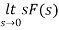 =
= 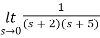 = 0.1
= 0.1
So, final value of the function is 0.1
Key takeaway
By initial value theorem
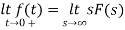 = f(0+)
= f(0+)
By final value theorem
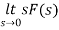 =
= 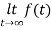
So, for difficult input, ess will be different Input still be
1) R(s) = unit step (3) R(s) = parabolic
2) R (s) = Ramp
1) R(s)= Unit step
R(t) = u(t)
R(s) = 1/s
ess = 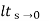 s[ R(s)/1+G(s)]
s[ R(s)/1+G(s)]
= 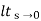 s[ys/1+G(s)]
s[ys/1+G(s)]
ess= 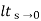 1+1/1+G(s)
1+1/1+G(s)
=1/1+lt G(s) s- 0
Kp = 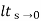 G(s)
G(s)
(Position error coefficient)
ess = 1/1+kp
2) R(s) = Ramp
R(t) = t
R(s) = 1/s2
ess=  s[ R(s)/1+G(s)]
s[ R(s)/1+G(s)]
= 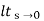 s[ys2/1+G(s)]
s[ys2/1+G(s)]
= 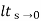 1/s(1+G(S)
1/s(1+G(S)
= 1/s+SG(s)
1/s+SG(s)
ess=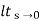 l/s-0 SG (s)
l/s-0 SG (s)
ess = 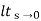 t L/SG (s)
t L/SG (s)
Kv = 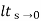 SG(s)
SG(s)
Velocity errors coefficient
ess = L/Kv
3) Parabolic
R(t) = t2
R(s) =1/s3
Ess = 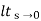 s[ R(s)/1+G(s)]
s[ R(s)/1+G(s)]
= 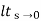 s(1/s3)/1+G(s)
s(1/s3)/1+G(s)
= 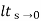 1/s2+s2G(s)
1/s2+s2G(s)
Ess = 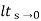 1/s2G(s)
1/s2G(s)
Ka = 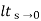 s2 G(s)
s2 G(s)
Acceleration error coefficient
Ess = 1/ka
I/p error coefficient
(1) Unit step ess= 1/1+kv kv = 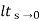 G(S)
G(S)
(2) Ramp ess= 1/kvkv = 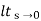 sG(s)
sG(s)
(3) Parabolic ess= 1/ka ka =  s2 G(s)
s2 G(s)
Now finding errors in type 0,1,2 system
1) Type 0:
G(s) = 1/(s+a) (s+b)
(a) Kp:
Kp =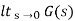
=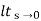 1/(s+a)(s+b)
1/(s+a)(s+b)
Kp= 1/ab
Ess=1/1+np = 1/1+(1/ab) 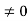
o/p not locking the input
(b) kv:
Kv = 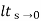 s G(s)
s G(s)
= 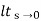 s/(s+a) (s+b)
s/(s+a) (s+b)
=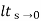 s/(s+a) (s+b)
s/(s+a) (s+b)
Kv = 0
ess = 1/kv = 
o/p not locating the input
(c) ka:
Ka = 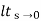 s2 G(s)
s2 G(s)
= 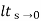 s2 /(s+a) (s+b)
s2 /(s+a) (s+b)
Ka =0
ess = 1/ka = 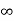
o/p not locking the input
2) Type I:
G(s) = 1/s(s+a) (s+b)
(a) Kp:
Kp = 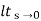 G(s)
G(s)
=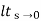 1/s(s2+as+ab)
1/s(s2+as+ab)
Kp = 1/0 = 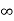
ess = 1/1+kp = 0
o/p is tracking the input
(b) kv:
Kv = 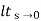 S G(s)
S G(s)
=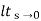 1/(s+a) (s+b)
1/(s+a) (s+b)
=1/ab
Kv = 1/ab
ess =1/ka = ab 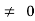
o/p is not tracking the input
(c) ka:
Ka=  s2G(s)
s2G(s)
= 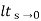 s2 /s(s+a)(s+b)
s2 /s(s+a)(s+b)
= 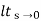 s/(s+a)(s+b)
s/(s+a)(s+b)
Ka= 0
Ess = 1/ka =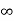
O/p is not tracking the input
3) Type 2:
G(s) = 1+/(s2(s+a) (s+b)
a) Kp:
Kp = 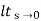 G(s)
G(s)
= 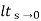 1/s2 (s+a) (s+b)
1/s2 (s+a) (s+b)
Kp = 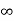
ess = 1/1+kp = 0
o/p tracking the i/p
b) kv:
Kv =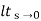 s G(s)
s G(s)
=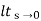 1/s(s+a) (1+b)
1/s(s+a) (1+b)
kv = 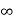
ess =1/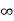 = 0
= 0
o/p tracking the o/p
c) ka:
Ka= 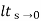 s2G(s)
s2G(s)
=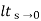 1/(s+a) (s+b)
1/(s+a) (s+b)
Ka = 1/ab
ess = 1/(yab) ≠0
o/p not locking the i/p
ess | Type 0 | Type 1 | Type 2 |
Unit step | ≠0 | 0 | 0 |
Ramp |  | ≠0 | 0 |
Parabolic |  |  | ≠0 |
Open loop systems:
This is the loop of control system without any feedback. In this the control action is not dependent on the desired output.

Fig 18. Open loop control system
Example of open Loop systems are the traffic signals, Automatic washing machine and in fields control d.c. Motor.
Closed loop systems:
This is a type of control system with feedback. In this type of system, the control action is dependent on the desired output.

Fig 19. Closed Loop control system
The error signal is again fed to controller to the error and get desired output.
Key takeaway:
- The open loop systems are without feedback.
- The closed loop systems use feedback.
The time domain analysis for second order system can be extended to third order system. Let transfer function for third order system be,
C(S)/R(S) = Wn2/(1 + ST)(S2 + 2ξWnS + Wn2)
Let 1/T = P
C(S)/R(S) = Wn2P/(S + P) (S2 + 2ξWnS + Wn2)
Taking Laplace inverse of above equation (for unit step response will be)
Cp(t) = 1 – K1e-pt + K2e-ξWnt Sin[ Wn√(1-ξ2)t - φ ]
Where K1 = Wn2 / Wn2 - 2ξWnp + p2
K2 = 1 / √1 – ξ2(1 - 2ξWn/p + Wn2/p2)
φ = tan-1√(1 – ξ2) / -ξ + tan-1Wn√1- ξ2/p – ξWn
From above equations we can conclude that:
(1). The system has three poles S = -p and S = - ξWn+-√(1 – ξ2). So the position of these poles effect the system. As the pole S = -p moves towards the origin, the output Cp(t) is dominated by only this pole.
(2). As the pole S = -p moves away from the origin, the response Cp(t) is dominated by the complex poles at S = -ξWn+-(√1-ξ2)jWn.
The response of third order system is shown in figure.
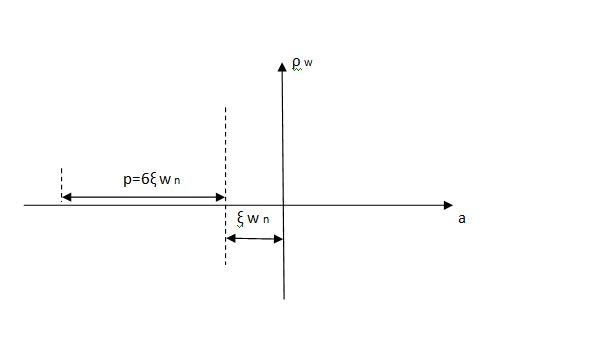
The relative location of dominant poles of the third order system is shown below in fig.
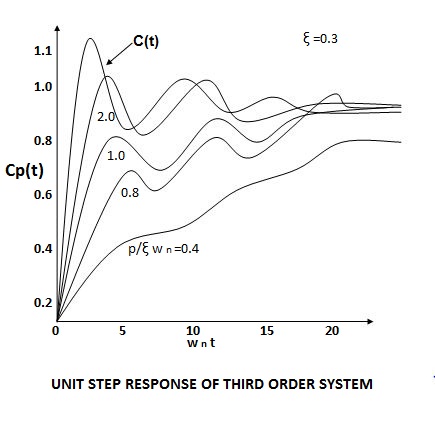
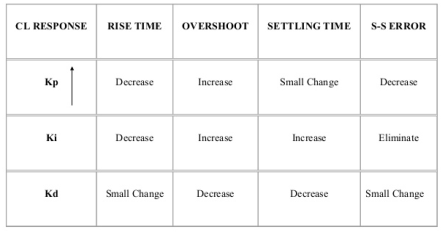
Effects of controller are viewed on time response and stability.
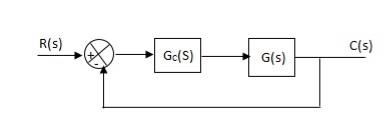
Fig 20. Controller with unity feedback system
Gc(S) = TF of the controller
G(S) = OLTF without controller
G’(S) = Gc(S).G(S)
= OLTF with controller
1. Proportional (P) Controller –
Proportional means scalar Multiplier.
Gc(S) = Kp Stability can be controlled
Q. G(S) = 1/S(S + 8)
CLTF = 1/S2 + 8S + 1
w2n = 1
wn = 1
2ξWn = 8
ξ = 4
ξ>/1 so, overdamped.
Now introducing Gc(S) = K
G’(S) = Kp/S(S + 8)
CLTF = Kp/S2 + 8S + Kp
wn = √Kp
2 ξwn = 8
ξ = 4/√Kp
If,
Kp = 16; ξ = 1; critically damped
Kp> 16; ξ< 1; undamped
Kp< 16; ξ> 1; overdamped
2. Integral (I) controller –
The transfer function of this controller is
Gc(S) = Ki/S
Integral controller is used to improve the steady state response or reduce the steady state error.
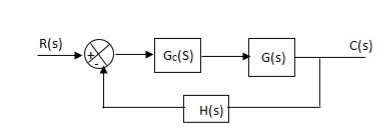
Fig 21. Integral Controller
G’(S) = Gc(S).G(S)
G(S) = 1/S + 5, Gc(S) = Ki/S
G’(S) = Ki/S(S + 5). After applying the Gc(S) the type of system is increasing and hence, the steady state error is decreasing (Refer Time Response).
Disadvantage -
By using integral controller, the stability of closed loop system decreases.
G(S) = 1/S + 5
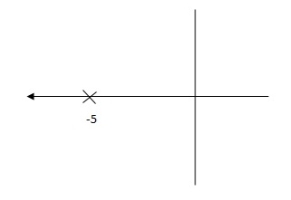
Fig 22. Pole Locations For given system
G’(S) = Ki/S(S + 5)
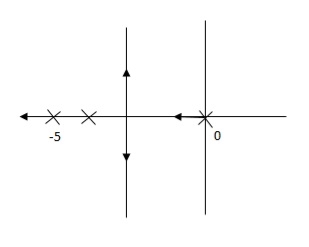
Fig 23. Pole Location after Integral controller
Fig(23), is more stable than (22) as more the away the pole from origin (imaginary axis) more is the stability.
Q. G(S) = 1/(S + 5)(S + 10)
G’(S) = Kp/S(S + 5)(S + 10)
G(S) = 1/(S + 5)(S + 10)

Fig 24. Root Locus Without controller
G’(S) = Ki/S(S + 5)(S + 10)
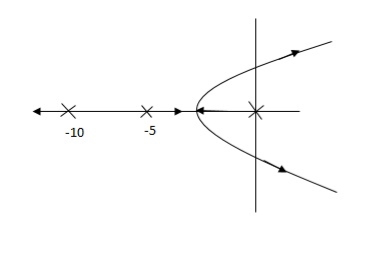
Fig 25. Root Locus Without controller
So, Fig 25 is less stable at root locus lies on the R.H.S
3. Derivative (D) Controller -
Gc(S) = Kd(S)
They are used to improve the stability.
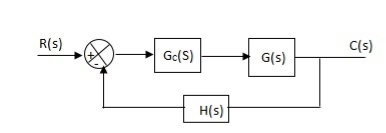
Fig 26. Derivative controller system
G’(S) = KdS/S2(S + 10)
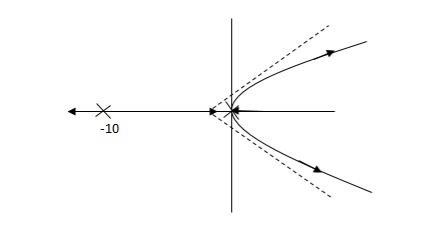
Fig 27. Root Locus for system without controller
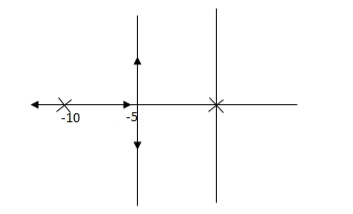
Fig 28. Root locus with controller
Fig 28 is stable i.e. more stable than the Fig 27.
Disadvantage –
It increases the steady state i.e. o/p will not track the input at steady state.
4. Proportional Plus Integral [PI] controller -
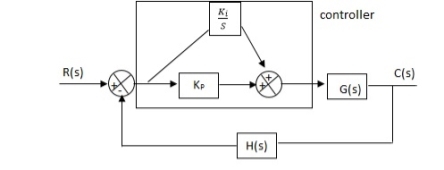
Fig 29. PI controller
Gc(S) = KpS + Ki/S
The steady state error will decrease and the stability will depend on Kp i.e. if Kp is increased/decreased than according to it stability will change (Kpα stability).
Used to reduce ess without much affecting the stability.
5. Proportional Plus Derivative (PD) Controller -
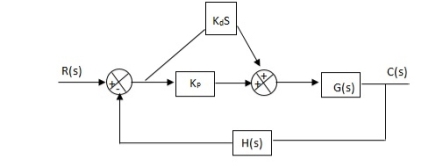
Fig 30. PD controller
Used to improve the stability without affecting much the steady state error.
6. PID controller -
Gc(S) = Kp + Ki/S + KdS
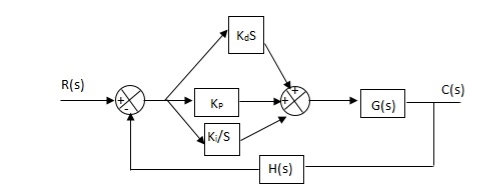
Fig 31. PID Controller
It improves the stability. It decreases the steady state error and both are proportional to Kp.
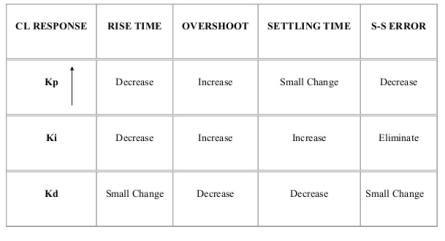
Key takeaway
Example-1 The block diagram of a system using PI controllers is shown in the figure below Calculate:
(a). The steady state without and with controller for unit step input?
(b). Determine TF of newly constructed sys. With controller so, that a CL Poles is located at -5?

Fig 32. Block diagram with PI controller
(a). Without:
C(S)/R(S) = 0.2/(S + 1)
C(S) = R(S) 0.2/(S + 1) + 0.2
For unit step
Ess = 1/1 + Kp
Kp = lt G(S)
S 0
= lt 0.2/(S + 1)
S 0
Kp = 0.2
Ess = 1/1.2 = 5/6 = 0.8
(b). With controller:
Gc(S) = Kp + Ki/S
G’(S) = Gc(S).G(S)
= ( Kp + Ki/S )0.2/(S + 1)
= (KpS + Ki)0.2/S(S + 1)
Ess = 1/1 + Kp = 0
So, the value of ess is decreased.
(b). Given
Kpi/Kp = 0.1
G’(S) = (Kp + Ki/S)(0.2/S + 1)
= (KpS + Ki)0.2/S(S + 1)
As a pole is to be added so, we have to examine the CE,
1 + G’(S) = 0
1 + (Kp + Ki)0.2/S(S + 1) = 0
S2 + S + 0.2KpS + 0.2Ki = 0
S2 + (0.2Kp + 1)S + 0.2Ki = 0
Given,
Kpi = 0.1Ki
Kp = 10Ki
S2 + (2Ki + 1)S + 0.2Ki = 0
Pole at S = -5
25 + (2Ki + 1)(-5) + 0.2Ki = 0
-10Ki – 5 + 25 + 0.2Ki = 0
-9.8Ki = -20
Ki = 2.05
Kp = 10Ki
= 20.5
Now,
G’(S) = (KpS + Ki)(0.2)/S(S + 1)
= (20.5S + 2.05)(0.2)/S(S + 1)
G’(S) = 4.1S + 0.41/S(S + 1)
Example-2 The block diagram of a system using Pd controller is shown, the PD is used to increase ξ to 0.8. Determine the T.F of controller?
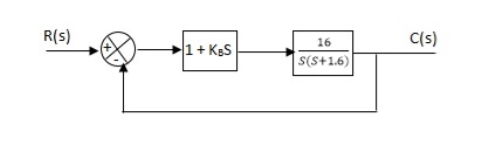
Fig 33. Block diagram with PD controller
(1). Kp = 1
Without controller:
C(S)/R(S) = 16/S2 + 1.6S + 16
wn = 4
2 ξwn = 16
ξ = 1.6/2 x 4 = 0.2
(b). With derivative:
ξS = 0.2 to 0.8
Undamped to critically damped,
G’(S) = (1 + KdS)(16)/(S2 + 1.6S)
CE:
S2 + 1.6S + 16(1 + KdS) = 0
S2 + (1.6 + Kd)S + 16 = 0
2 ξwn = 1.6 + Kd1.6
wn = 4
ξS = 0.8
2 x 4 x 0.8 = 1.6 + Kd1.6
6.4 – 1.6 = Kd1.6
4.8/16 = Kd
Kd = 0.3
TF = (1 + 0.3S)16/S(S + 16)
References:
1. Automatic Control system (II Edition) – Benjamin C, Kuo, PHI
2. Modern Control System, Drof, Bishop, Wesly Publication
3. Control system Engineering, S.K. Bhattacharya, Pearson Education.
Unit - 2
Time Domain analysis
The Response of the system as a function of time, to the applied excitation is called Time Response. The time response of a system can be fully studied by studying the following two responses

The total time response C(t) is given by
C(t) = Ctr(t) + Css(t)
Where Ctr(t) = transient response
Css(t) = steady state response
Consider the class of differential equation
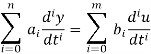
Where the coefficient ai and bi are constant, u = u(t) (the input) is a known time function, and y = y(t) (the output) is the unknown solution of the equation. Generally, m ≤ n, and n is called the order of the differential equation.
The Free Response
The Free response of a differential equation is the solution of the differential equation when the input u(t) is identically zero. If the input u(t) is identically zero, then the differential equation has the form:
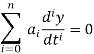
The solution y(t) of such an equation depends only on the initial conditions.
The Forced Response
The forced response yb(t) of a differential equation is the solution of the differential equation when all the initial conditions are identically zero.

The Total Response
The total response of a linear constant −coefficient differential equation is the sum of the free response and the forced response.
The Steady State and Transient Response
The steady state response and transient response are another pair of quantities whose sum is equal to the total response. These terms are often used for specifying control system performance. They are defined as follows. The steady state response is that part of the total response which does not approach zero as time approaches infinity. The transient response is that part of the total response which approaches zero as time approaches infinity
For stable system Transient response vanishes after some time to get final value closer to the desired value.
Steady State Response: The part of the time response which remains after complete transient response vanishes from the system output. The steady state response is generally the final value achieved by the system output. The difference between the desired output and the actual output of the system is called as Steady state error (ess) and the time taken to reach steady state is called Settling time.
Transient Analysis of First Order System:
OLTF G(s) = 1/TS
CLTF c(s)/R(s) = 1/1+TS
CE: HTS = 0
S= -1/T
C(s) = R(s) [G(S)/1+G(s)]
C(s) = R(s)/1+TS
So, Calculating value of c(s), c(t) for different input
Unit Step:
R(t) = u(t)
R(s) = 1/s
C(s) = 1/s(1+ST)
1/s(1+ST) = A/s + o/1+TS
1/s(1+ST) = A/S + 0/1+TS
1= A(1+ST) + BS
AT +B =0
A = 1
B= -T
C(s) = 1/s + (-T)/1+TS
= 1+ (-T)/1-(-T)s = 1-I/n/1+ass+1/T =e-t/s
C(t) = [ 1-e-t/T]

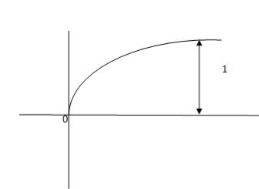
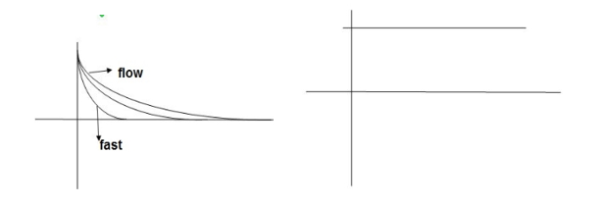
Fig 1. Output response for Unit Step input
Ramp
R(t) = t
R(s) = 1/s2
C(s) = R(s) [G(s)/1+G(s)]
C(s) = 1/s2 1/(1+TS) + c
1/s2 (1+TS) = A/(s) + B/s2 + c(1+TS)
1= A (s+s2. T) + B(1+TS) +cs2
TA +c = 0
A+TB =0
B =1
A = -T
C = T2
C(s) = -T/s + 1/s2 +T2/1+ST
=(-T) u(t) + t(u) + T e-t/T u(t)
= [ -T + t +Te-t/T u(t)
= [ -T+ t+Te-t/T] u(t)
C(s) = t- T+ Te-t/T
ess = R(t) – c(t)
R(t) – c(t)
=  [ t- t+ 7-Te –t/T]
[ t- t+ 7-Te –t/T]
=  T( 1-e-t/T]
T( 1-e-t/T]
ess = The less the value of T the less in the errors.
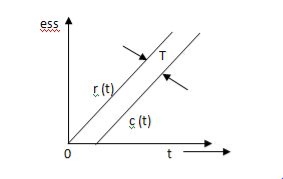
Fig 2. Output response for ramp input
Key takeaway
From both the Cases input unit step, ramp Unit step
Unit Step Ramp
c(t) = 1-e-t/T r(t) = t
ess = e-t/T (r/t)-(t) c(t) = t- T+te-t/T
ess= e-t/T (r/t) (t) ess = T- Te-t/T
For t for t
ess =0 ess = T
In both the cases (values of T) must be as small as possible (so, that e-t/T) must be as small as possible which gives us
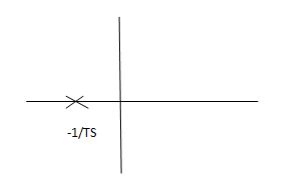
Fig 3. Location of poles
G(s) = 1/Ts
ATf = 1/1+TS
1st order system
Poles must be situated as far as possible from origin i.e. deeper and deeper into the left half of s-place. Thus, we get less errors.
Transient Analysis of Second Order System:
OLTF G(s) = k/s(1+TS)
CLTFC(s)/R(s) = k/k+s(1+Ts)
= k/s2+ s/T +k/T
Comparing above equation with standard 2nd order eqn
CLTF = wn2/s2+2rs wns+wn2
Standard 2nd order equation
CEs2+2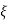 wn s+wn2= 0
wn s+wn2= 0
S= -2 wn±
wn±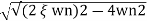 /2
/2
=2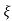 wn±2wn
wn±2wn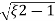 /2
/2
S=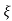 wn±wn
wn±wn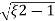
S= - wn±wn
wn±wn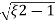
S= -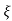 wn ±wn
wn ±wn
S= -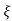 wn ±gwn
wn ±gwn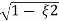
Standard eqn:
T(s) = wn2/s2+2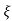 wns+wn2
wns+wn2
Our eqn T(s) = K/T/s2+1/T s+ K/T
Wn2 = k/T
2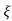 wn = 1/T
wn = 1/T
2 k/T = 1/T
k/T = 1/T
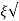 k/T = 1/2T
k/T = 1/2T
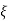 = 1/2T
= 1/2T 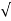 T/K
T/K
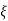 = 1
= 1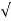 2KT
2KT
Graphically showing the position of loops s1, s2 for offered of
As the characteristic Equation (location of poles) is dependent only on (wn constant for a given system.
S1 = -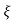 wn + jwn
wn + jwn 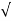 1-
1-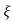 2
2
S2= - wn - jwn
wn - jwn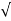 1-
1-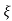 2
2
CASE 1: (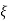 =0)
=0)
S1=jwn, S2, = -jwn
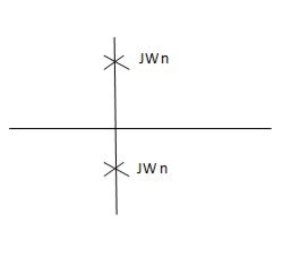
Fig 4. Location of poles for  =0
=0
Undamped
CASE 2:(0< <1)
<1)
S1= -wn + jwn 0.75
0.75
=-wn/2 +jwn(0.26)
S2 = -wn/2 – jwn (0.86)

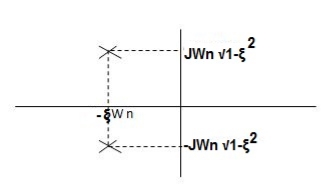
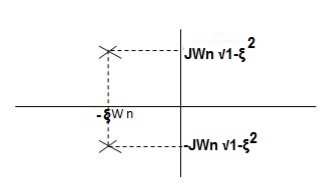
Fig 5. Location of poles for 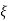 <1
<1
CASE:3 (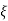 -1)
-1)
S1= S2 = -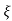 wn = -wn
wn = -wn
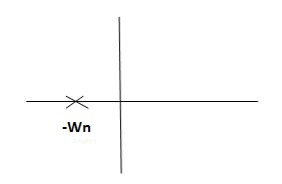
Fig 6. Location of poles for  =1
=1
CASE4: (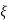 -1)
-1)
S1 = -2wn +jwn -3
-3
=-2wn – jwn (1.73)
S1 = -3.73wn
S2 = -2wn –jwn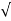 -3
-3
= -2wn + jwn (1.73)
= -0.27 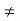 wn
wn
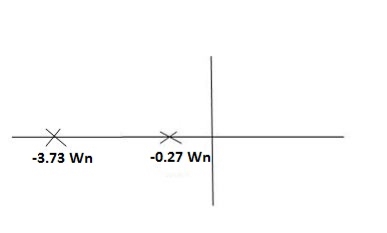
Fig 7. Location of poles for 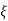 >1
>1
Overdamped
All practical systems are 2 order to, if R(e) = 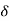 (t) R(s) = 1. CLTF = 2nd order st eqn and hence already the system is possible.
(t) R(s) = 1. CLTF = 2nd order st eqn and hence already the system is possible.
CLTF = e(s)/ R(s) = wn2/s2+2 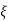 wns+wn2
wns+wn2
Now calculating c(s), c(t) for different values of input
Impulse I/p
R(t) = 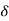 (t)
(t)
R(t) =  (t)
(t)
R(s) = 1
C(s) = R(s) wn2/s2+2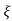 wns+wn2
wns+wn2
C(s) = wn2/s2 +2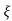 wn+wn2
wn+wn2
Under this i/p (R(t) = 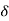 (t)) the output varies with different values of
(t)) the output varies with different values of 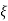 . So,
. So,
CONDITION 1: (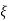 =0)
=0)
C(s) =wn2/s2 +wn2
Os2 +wn2 =0
S=+-jwn
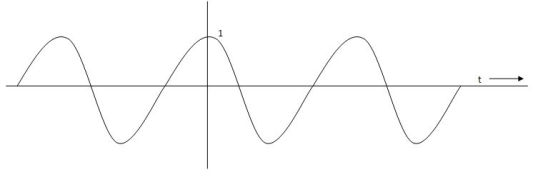
C(t) = wnsinwnt

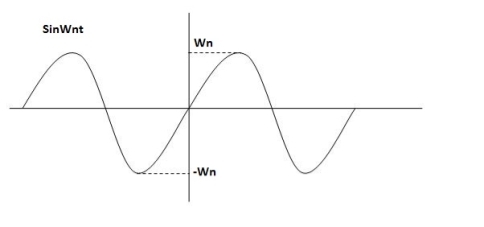
Fig 8. Undamped oscillations
As there in no damping i.e. oscillations at t= 0 are some at t  so, called UNDAMPED
so, called UNDAMPED
CONDITION 2: 0<<1
c(s) = R(s) wn2/s22 wn+wn2 R(t) =
wn+wn2 R(t) =  (t)
(t)
R(s) =1
C(s) = wn2/s2+2 wns+wn2
wns+wn2
CE
S2+2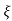 wns +wn2 =0
wns +wn2 =0
S2, S1 = -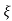 wn ±jwn
wn ±jwn 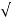 1-
1-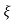 2
2
C(t) = e-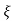 wntsin(wn
wntsin(wn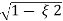 )t
)t
Wd=wn )
)
C(t)=e- wnt sin (wdt)
wnt sin (wdt)
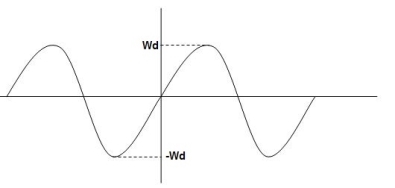
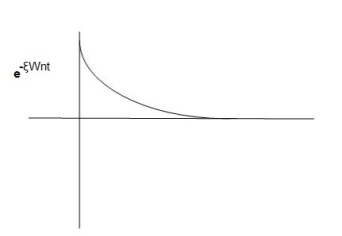
Fig 9. Underdamped oscillations
The oscillations are present but at t- infinity the Oscillations are 0 so, it is UNDERDAMPED
CONDITION 3: =1
=1
C(s) = R(s) wn2/s2+2 wns+wn2
wns+wn2
C(s)=wn2/S2 +2wns+wn2
=wn2/(s +wn)2
CE S= -Wn
C(t)= w2n/(
w2n/(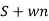 )2
)2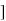
C(t)=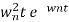
Diagram
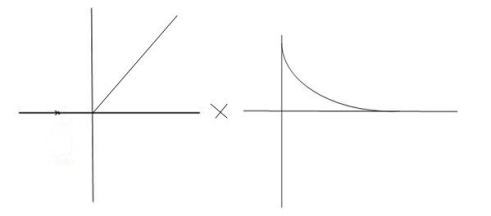
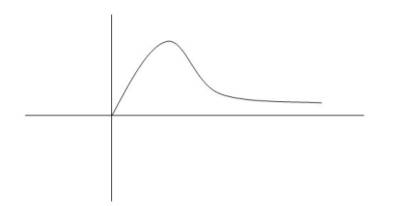
Fig 10. Critically damped oscillations
No damping obtained at 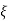 =1so is called CRITICALLY DAMPED.
=1so is called CRITICALLY DAMPED.
CONDITION 4- 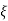 >1
>1
C(s) = wn2/s22 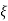 wnS+Wn2
wnS+Wn2
S1,s2 = 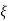 WN+-jwn
WN+-jwn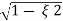 )
)
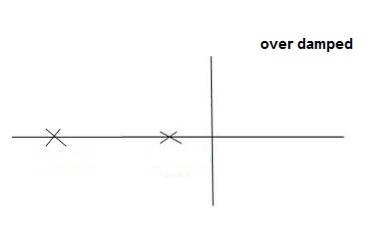
Fig 11. Location of poles for over damped oscillations
UNIT Step Input:
R(s) = 1/s
C(s)/R(s) = wn2/s2+2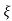 wns+wn2
wns+wn2
C(s) = R(s) wn2 /s2 +2 wns+wn2
wns+wn2
C(s) = R(s) wn2/s2+2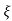 wns+wn2
wns+wn2
C(s) = R(s) wn2/s2+2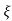 wns+wn2
wns+wn2
C(s) = wn2s(s2+2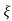 wns+wn2)
wns+wn2)
C(t) = 1- e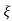 wnt/
wnt/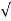 1-es2sin (wdt + ø)
1-es2sin (wdt + ø)
Wd = wn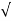 1-
1- 2
2
Ø= 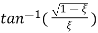
Where
Wd = Damping frequency of oscillations
Wn = natural frequency of oscillations
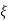 wn = damping coefficient.
wn = damping coefficient.
T= Time constant
Condition 1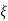 = 0
= 0
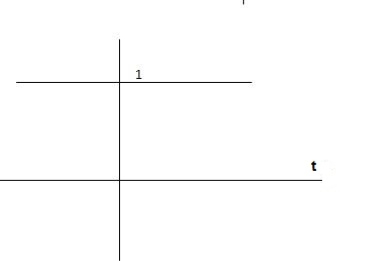
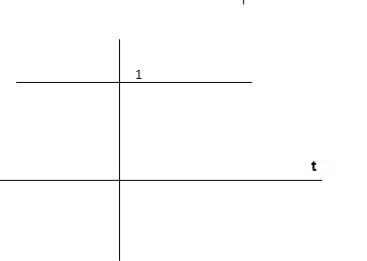
C(s) = wn2 /s(s2+wn2)
C(t) = 1- e° sin wdt +ø
C(t)= 1- sin( wn +90)
C(t) = 1+cos wnt
Constant

C(t) = 1+constant
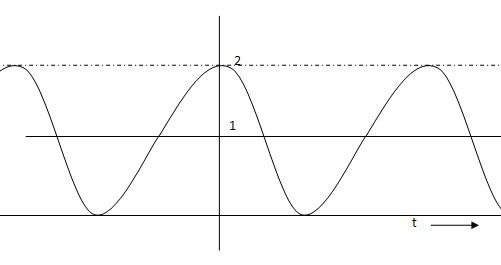
Fig 12. C(t) = 1+cos wnt
Condition 2: 0<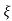 <1
<1
C(s) = 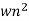 /s2+
/s2+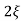 wns +wn2
wns +wn2
C(s) =1/s – s+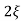 wn/s2+
wn/s2+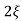 wns +wn2
wns +wn2
=1/s – s+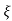 wn/(s+
wn/(s+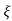 wn)2+wd2-
wn)2+wd2- 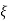 wn/(s+
wn/(s+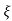 wn2) +wd2
wn2) +wd2
Wd = wn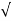 1-
1- 2
2
Taking Laplace inverse of above equation
L --1 s+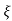 wn/(s+
wn/(s+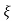 wn) +wd2= e-
wn) +wd2= e-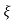 wnt coswdt
wnt coswdt
L-1 s+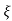 wn/(s+
wn/(s+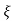 wn)2+wd2 = e-
wn)2+wd2 = e-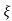 wnt sinWdt
wnt sinWdt
C(t) = 1-e-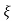 wnt [coswdt +
wnt [coswdt +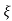 /
/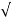 1-
1- 2sinwdt]
2sinwdt]
= 1-e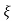 wnt /
wnt / 1-
1-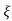 2 sin [wdt +
2 sin [wdt + 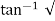 1-
1-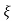 2/
2/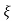 ] t>=0
] t>=0
C(t) = 1-e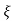 wnt/
wnt/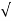 1-
1-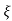 2 sin(wdt+ø)
2 sin(wdt+ø)
Ø = 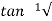 1+
1+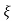 2/
2/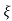
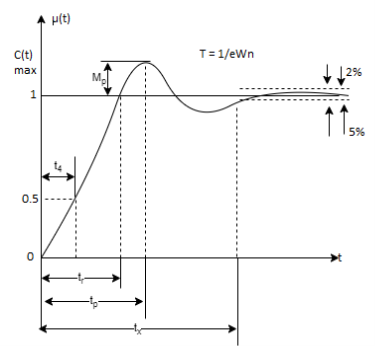
Fig 13. Transient Response of second order system
Specifications:
1) Rise Time (tp)
The time taken by the output to reach the already status value for the first time is known as Rise time.
C(t) = 1-e-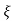 wnt/
wnt/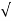 1-
1-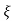 2 sin (wdt+ø)
2 sin (wdt+ø)
Sin (wd +ø) = 0
Wdt +ø = n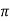
tr = n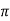 -ø/wd
-ø/wd
For first time so, n=1.
tr = 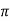 -ø/wd
-ø/wd
T=1/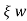
2) Peak Time (tp)
The peak value attained by the output is called peak time. The time required by the output to reach this value is lp.
d(cct) /dt = 0 (maxima)
d(t)/dt = peak value
tp = n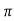 /wd for n=1
/wd for n=1
tp = 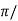 wd
wd
3) Peak Overshoot Value:
Maximum deviation of output from steady state value is called peak overshoot value (Mp).
(ltp) = 1 = Mp
(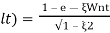 Sin(Wat + φ )
Sin(Wat + φ )
( Sin( Wd∏/Wd + φ)
Sin( Wd∏/Wd + φ)
Mp = e-∏ξ / √1 –ξ2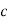
Condition 3 ξ = 1
C( S ) = R( S ) Wn2 / S2 + 2ξWnS + Wn2
C( S ) = Wn2 / S(S2 + 2WnS + Wn2) [ R(S) = 1/S ]
C( S ) = Wn2 / S( S2 + Wn2 )
C( t ) = 1 – e-Wnt + tWne-Wnt
The response is critically damped.
4) Settling Time (ts):
ts = 3 / ξWn ( 5% )
ts = 4 / ξWn ( 2% )
Examples
Q.1. The open loop transfer function of a system with unity feedback gain G( S ) = 20 / S2 + 5S + 4. Determine the ξ, Mp, tr, tp.
Soln: Finding closed loop transfer function,
C(S) / R( S ) = G( S ) / 1 + G( S ) + H( S )
As it is unity feedback so, H(S) = 1
C(S)/R(S) = G(S)/1 + G(S)
= 20/S2 + 5S + 4/1 + 20/S2 + 5S + 4
C(S)/R(S) = 20/S2 + 5S + 24
Standard equation for second order system,
S2 + 2ξWnS + Wn2 = 0
We have,
S2 + 5S + 24 = 0
Wn2 = 24
Wn = 4.89 rad/sec
2ξWn = 5
(a). ξ = 5/2 x 4.89 = 0.511
(b). Mp% = e-∏ξ / √1 –ξ2 x 100
= e-∏ x 0.511 / √1 – (0.511)2 x 100
Mp% = 15.4%
(c). tr = ∏ - φ / Wd
φ = tan-1√1 – ξ2 / ξ
φ= tan-1√1 – (0.511)2 / (0.511)
φ = 1.03 rad.
tr = ∏ - 1.03/Wd
Wd = Wn√1 – ξ2
= 4.89 √1 – (0.511)2
Wd = 4.20 rad/sec
tr = ∏ - 1.03/4.20
tr = 502.34 msec
(d). tp = ∏/4.20 = 747.9 msec
Q.2. A second order system has Wn = 5 rad/sec and is ξ = 0.7 subjected to unit step input. Find (i) closed loop transfer function. (ii) Peak time (iii) Rise time (iv) Settling time (v) Peak overshoot.
Soln: The closed loop transfer function is
C(S)/R(S) = Wn2 / S2 + 2ξWnS + Wn2
= (5)2 / S2 + 2 x 0.7 x S + (5)2
C(S)/R(S) = 25 / S2 + 7s + 25
(ii). tp = ∏ / Wd
Wd = Wn√1 - ξ2
= 5√1 – (0.7)2
= 3.571 sec
(iii). tr = ∏ - φ/Wd
φ= tan-1√1 – ξ2 / ξ = 0.795 rad
tr = ∏ - 0.795 / 3.571
tr = 0.657 sec
(iv). For 2% settling time
ts = 4 / ξWn = 4 / 0.7 x 5
ts = 1.143 sec
(v). Mp = e-∏ξ / √1 –ξ2 x 100
Mp = 4.59%
Q.3. The open loop transfer function of a unity feedback control system is given by G(S) = K/S(1 + ST)
Calculate the value by which k should be multiplied so that damping ratio is increased from 0.2 to 0.4?
Soln:
C(S)/R(S) = G(S) / 1 + G(S)H(S) H(S) = 1
C(S)/R(S) = K/S(1 + ST) / 1 + K/S(1 + ST)
C(S)/R(S) = K/S(1 + ST) + K
C(S)/R(S) = K/T / S2 + S/T + K/T
For second order system,
S2 + 2ξWnS + Wn2
2ξWn = 1/T
ξ = 1/2WnT
Wn2 = K/T
Wn =√K/T
ξ = 1 / 2√K/T T
ξ = 1 / 2 √KT
Forξ1 = 0.2, for ξ2 = 0.4
ξ1 = 1 / 2 √K1T
ξ2 = 1 / 2 √K2T
ξ1/ ξ2 = √K2/K1
K2/K1 = (0.2/0.4)2
K2/K1 = 1 / 4
K1 = 4K2
Q.4. Consider the transfer function C(S)/R(S) = Wn2 / S2 + 2ξWnS + Wn2
Find ξ, Wn so that the system responds to a step input with 5% overshoot and settling time of 4 sec?
Soln:
Mp = 5% = 0.05
Mp = e-∏ξ / √1 –ξ2
0.05 = e-∏ξ / √1 –ξ2
Cn 0.05 = - ∏ξ / √1 –ξ2
-2.99 = - ∏ξ / √1 –ξ2
8.97(1 – ξ2) = ξ2∏2
0.91 – 0.91 ξ2 = ξ2
0.91 = 1.91 ξ2
ξ2 = 0.69
(ii). ts = 4/ ξWn
4 = 4/ ξWn
Wn = 1/ ξ = 1/ 0.69
Wn = 1.45 rad/sec
The Impulse signal, Ramp signal, unit step and parabolic signals are used as the standard test signals. All these signals are explained below.
(a) Impulse Signal:
This signal has zero amplitude everywhere except at the origin. Fig below shown the representation of Impulse signal.
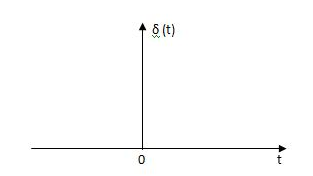
Fig 14. Unit Impulse Signal
The mathematical representations
A (t) = 0 for t ≠0
(t) = 0 for t ≠0
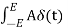 dt = A e
dt = A e 
Where A represent energy or area of the Laplace Transform of Impulse signal is
L [A (t)] = A
(t)] = A
Unit Impulse Signal:
If A = 1
 (t) = 0 for t ≠0
(t) = 0 for t ≠0
L [ (t)] = 1
(t)] = 1
The transfer function of a linear time invariant
System is the Laplace transform of the impulse response of the system. If a unit impulse signal is applied to system then Laplace transform of the output c(s) is the transfer function G(s)
As we know G(s) = c(s)/R(S)
r(t) =  (t)
(t)
R(s) = L [ (t)] = 1
(t)] = 1
:. G(S) = C(s)
(b) Step signal:
Step signal of size A is a signal that change from zero level to A in zero time and stays there forever.

Fig 15. Unit Step Signal
r(t)= A t >=0
=0 t<0
L[r(t)] = R(s) = A/s
Unit Step Signal:
If the magnitude of the slip signal is I then it is called unit step signal.
u(t) = 1
t>=0
t<0
L[u(t)] = 1/s
(c) Ramp Signal:
The vamp signal increase linearly with time from initial value of zero at t= 0 as shown in fig is below
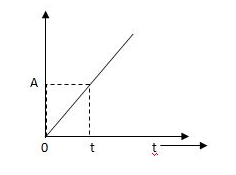
Fig 16. Ramp Signal
r(t) = At t>=0
=0 t<0
A is the slope of the line The Laplace transform of ramp signal is
L[r(t)] = R(s) = A/s2
(d) Parabolic Signal:
The instantaneous value of a parabolic signal varies as square of the time from an initial value of zero t=0. The signal representation in fig 14 below.
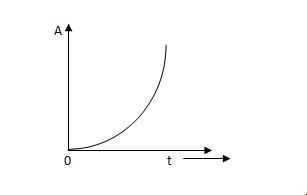
Fig 17. Parabolic Signal
r(t) At2 t>=0
=0 t<0
Then Laplace Transform is given as
R(s) = L[At2] = 2A/s3
If no error then E(t) =0, :. R(t) = c(t), output is tracking the input.
Steady state Errors signal (ess): - (t  )
)
Ess = t 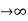 e(t)
e(t)
Using final values, the theorem
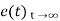 = ess =
= ess = 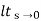 S.E (s)
S.E (s)
ess= 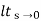 S[R(s)/1+G/(s)]
S[R(s)/1+G/(s)]
Key takeaway
If no error then E(t) =0,: R(t) = c(t), output is tracking the input.
Steady state Errors signal (ess): - (t 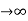 )
)
Ess = t 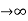 e(t)
e(t)
Using final values, the theorem
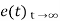 = ess =
= ess = 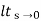 S.E (s)
S.E (s)
Examples
Q1) Find the initial value for the function f(t) = 2u(t)+3cost u(t)?
Sol:
f(t) = 2u(t)+3cost u(t)
F(s) = 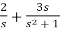
SF(s) = 2+ 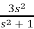
By initial value theorem
 = f(0+)
= f(0+)
 =
= 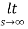 2+
2+ 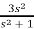 = 5 = f(0+)
= 5 = f(0+)
Hence, initial value of the function is 5
Q2) Find final value of the function F(s) = 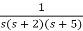
Sol:
F(s) = 
SF(s) = 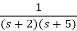
By final value theorem
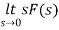 =
= 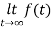
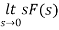 =
= 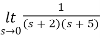 = 0.1
= 0.1
So, final value of the function is 0.1
Key takeaway
By initial value theorem
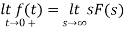 = f(0+)
= f(0+)
By final value theorem
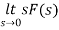 =
= 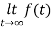
So, for difficult input, ess will be different Input still be
1) R(s) = unit step (3) R(s) = parabolic
2) R (s) = Ramp
1) R(s)= Unit step
R(t) = u(t)
R(s) = 1/s
ess = 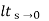 s[ R(s)/1+G(s)]
s[ R(s)/1+G(s)]
= 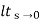 s[ys/1+G(s)]
s[ys/1+G(s)]
ess= 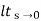 1+1/1+G(s)
1+1/1+G(s)
=1/1+lt G(s) s- 0
Kp = 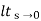 G(s)
G(s)
(Position error coefficient)
ess = 1/1+kp
2) R(s) = Ramp
R(t) = t
R(s) = 1/s2
ess=  s[ R(s)/1+G(s)]
s[ R(s)/1+G(s)]
= 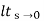 s[ys2/1+G(s)]
s[ys2/1+G(s)]
= 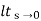 1/s(1+G(S)
1/s(1+G(S)
=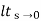 1/s+SG(s)
1/s+SG(s)
ess=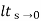 l/s-0 SG (s)
l/s-0 SG (s)
ess = 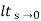 t L/SG (s)
t L/SG (s)
Kv = 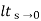 SG(s)
SG(s)
Velocity errors coefficient
ess = L/Kv
3) Parabolic
R(t) = t2
R(s) =1/s3
Ess = 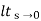 s[ R(s)/1+G(s)]
s[ R(s)/1+G(s)]
=  s(1/s3)/1+G(s)
s(1/s3)/1+G(s)
= 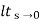 1/s2+s2G(s)
1/s2+s2G(s)
Ess = 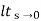 1/s2G(s)
1/s2G(s)
Ka = 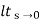 s2 G(s)
s2 G(s)
Acceleration error coefficient
Ess = 1/ka
I/p error coefficient
(1) Unit step ess= 1/1+kv kv = 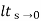 G(S)
G(S)
(2) Ramp ess= 1/kvkv = 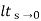 sG(s)
sG(s)
(3) Parabolic ess= 1/ka ka =  s2 G(s)
s2 G(s)
Now finding errors in type 0,1,2 system
1) Type 0:
G(s) = 1/(s+a) (s+b)
(a) Kp:
Kp =
=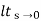 1/(s+a)(s+b)
1/(s+a)(s+b)
Kp= 1/ab
Ess=1/1+np = 1/1+(1/ab) 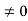
o/p not locking the input
(b) kv:
Kv = 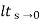 s G(s)
s G(s)
= 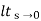 s/(s+a) (s+b)
s/(s+a) (s+b)
=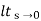 s/(s+a) (s+b)
s/(s+a) (s+b)
Kv = 0
ess = 1/kv = 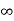
o/p not locating the input
(c) ka:
Ka = 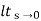 s2 G(s)
s2 G(s)
= 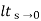 s2 /(s+a) (s+b)
s2 /(s+a) (s+b)
Ka =0
ess = 1/ka = 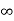
o/p not locking the input
2) Type I:
G(s) = 1/s(s+a) (s+b)
(a) Kp:
Kp = 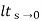 G(s)
G(s)
=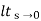 1/s(s2+as+ab)
1/s(s2+as+ab)
Kp = 1/0 = 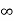
ess = 1/1+kp = 0
o/p is tracking the input
(b) kv:
Kv = 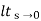 S G(s)
S G(s)
=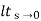 1/(s+a) (s+b)
1/(s+a) (s+b)
=1/ab
Kv = 1/ab
ess =1/ka = ab 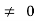
o/p is not tracking the input
(c) ka:
Ka=  s2G(s)
s2G(s)
= 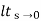 s2 /s(s+a)(s+b)
s2 /s(s+a)(s+b)
= 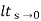 s/(s+a)(s+b)
s/(s+a)(s+b)
Ka= 0
Ess = 1/ka =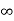
O/p is not tracking the input
3) Type 2:
G(s) = 1+/(s2(s+a) (s+b)
a) Kp:
Kp = 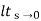 G(s)
G(s)
= 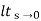 1/s2 (s+a) (s+b)
1/s2 (s+a) (s+b)
Kp = 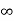
ess = 1/1+kp = 0
o/p tracking the i/p
b) kv:
Kv = s G(s)
s G(s)
=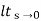 1/s(s+a) (1+b)
1/s(s+a) (1+b)
kv = 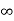
ess =1/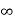 = 0
= 0
o/p tracking the o/p
c) ka:
Ka= 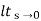 s2G(s)
s2G(s)
=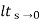 1/(s+a) (s+b)
1/(s+a) (s+b)
Ka = 1/ab
ess = 1/(yab) ≠0
o/p not locking the i/p
ess | Type 0 | Type 1 | Type 2 |
Unit step | ≠0 | 0 | 0 |
Ramp | 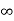 | ≠0 | 0 |
Parabolic |  |  | ≠0 |
Open loop systems:
This is the loop of control system without any feedback. In this the control action is not dependent on the desired output.

Fig 18. Open loop control system
Example of open Loop systems are the traffic signals, Automatic washing machine and in fields control d.c. Motor.
Closed loop systems:
This is a type of control system with feedback. In this type of system, the control action is dependent on the desired output.
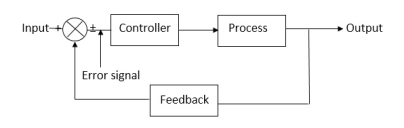
Fig 19. Closed Loop control system
The error signal is again fed to controller to the error and get desired output.
Key takeaway:
- The open loop systems are without feedback.
- The closed loop systems use feedback.
The time domain analysis for second order system can be extended to third order system. Let transfer function for third order system be,
C(S)/R(S) = Wn2/(1 + ST)(S2 + 2ξWnS + Wn2)
Let 1/T = P
C(S)/R(S) = Wn2P/(S + P) (S2 + 2ξWnS + Wn2)
Taking Laplace inverse of above equation (for unit step response will be)
Cp(t) = 1 – K1e-pt + K2e-ξWnt Sin[ Wn√(1-ξ2)t - φ ]
Where K1 = Wn2 / Wn2 - 2ξWnp + p2
K2 = 1 / √1 – ξ2(1 - 2ξWn/p + Wn2/p2)
φ = tan-1√(1 – ξ2) / -ξ + tan-1Wn√1- ξ2/p – ξWn
From above equations we can conclude that:
(1). The system has three poles S = -p and S = - ξWn+-√(1 – ξ2). So the position of these poles effect the system. As the pole S = -p moves towards the origin, the output Cp(t) is dominated by only this pole.
(2). As the pole S = -p moves away from the origin, the response Cp(t) is dominated by the complex poles at S = -ξWn+-(√1-ξ2)jWn.
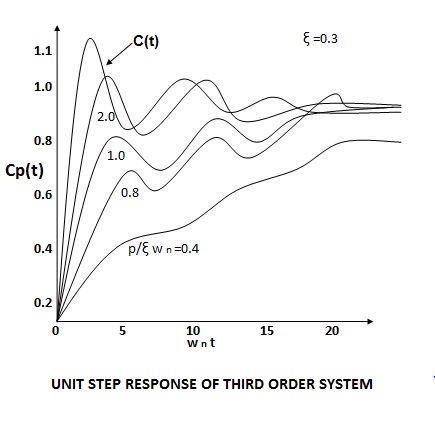
The response of third order system is shown in figure.
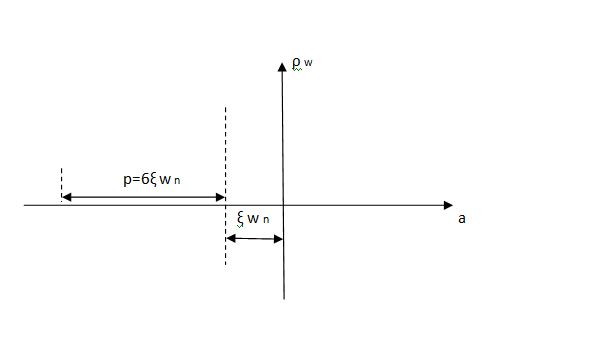
The relative location of dominant poles of the third order system is shown below in fig.
Effects of controller are viewed on time response and stability.
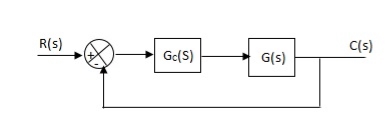
Fig 20. Controller with unity feedback system
Gc(S) = TF of the controller
G(S) = OLTF without controller
G’(S) = Gc(S).G(S)
= OLTF with controller
1. Proportional (P) Controller –
Proportional means scalar Multiplier.
Gc(S) = Kp Stability can be controlled
Q. G(S) = 1/S(S + 8)
CLTF = 1/S2 + 8S + 1
w2n = 1
wn = 1
2ξWn = 8
ξ = 4
ξ>/1 so, overdamped.
Now introducing Gc(S) = K
G’(S) = Kp/S(S + 8)
CLTF = Kp/S2 + 8S + Kp
wn = √Kp
2 ξwn = 8
ξ = 4/√Kp
If,
Kp = 16; ξ = 1; critically damped
Kp> 16; ξ< 1; undamped
Kp< 16; ξ> 1; overdamped
2. Integral (I) controller –
The transfer function of this controller is
Gc(S) = Ki/S
Integral controller is used to improve the steady state response or reduce the steady state error.
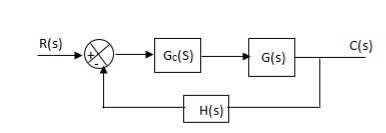
Fig 21. Integral Controller
G’(S) = Gc(S).G(S)
G(S) = 1/S + 5, Gc(S) = Ki/S
G’(S) = Ki/S(S + 5). After applying the Gc(S) the type of system is increasing and hence, the steady state error is decreasing (Refer Time Response).
Disadvantage -
By using integral controller, the stability of closed loop system decreases.
G(S) = 1/S + 5
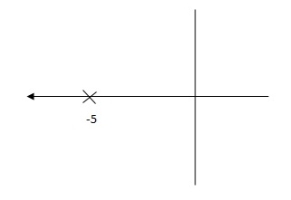
Fig 22. Pole Locations For given system
G’(S) = Ki/S(S + 5)
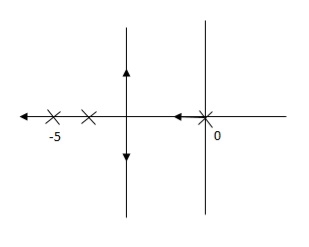
Fig 23. Pole Location after Integral controller
Fig(23), is more stable than (22) as more the away the pole from origin (imaginary axis) more is the stability.
Q. G(S) = 1/(S + 5)(S + 10)
G’(S) = Kp/S(S + 5)(S + 10)
G(S) = 1/(S + 5)(S + 10)

Fig 24. Root Locus Without controller
G’(S) = Ki/S(S + 5)(S + 10)
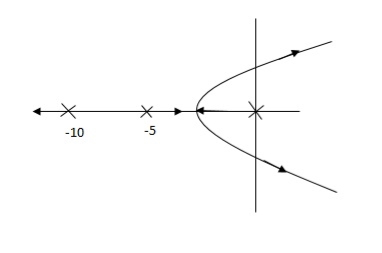
Fig 25. Root Locus Without controller
So, Fig 25 is less stable at root locus lies on the R.H.S
3. Derivative (D) Controller -
Gc(S) = Kd(S)
They are used to improve the stability.
Fig 26. Derivative controller system
G’(S) = KdS/S2(S + 10)
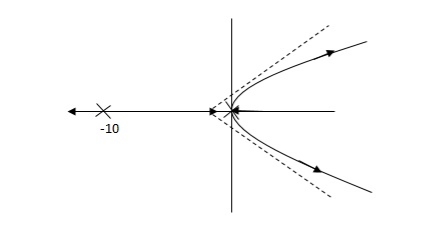
Fig 27. Root Locus for system without controller
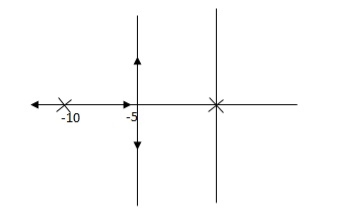
Fig 28. Root locus with controller
Fig 28 is stable i.e. more stable than the Fig 27.
Disadvantage –
It increases the steady state i.e. o/p will not track the input at steady state.
4. Proportional Plus Integral [PI] controller -
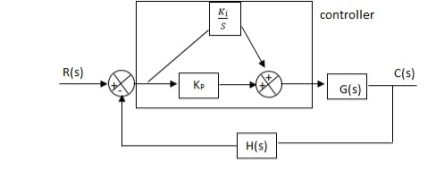
Fig 29. PI controller
Gc(S) = KpS + Ki/S
The steady state error will decrease and the stability will depend on Kp i.e. if Kp is increased/decreased than according to it stability will change (Kpα stability).
Used to reduce ess without much affecting the stability.
5. Proportional Plus Derivative (PD) Controller -
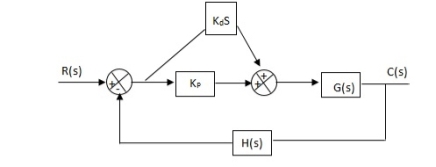
Fig 30. PD controller
Used to improve the stability without affecting much the steady state error.
6. PID controller -
Gc(S) = Kp + Ki/S + KdS
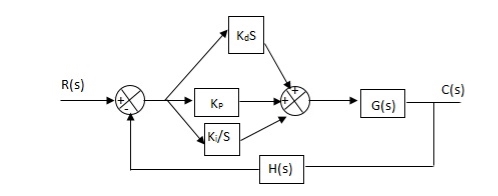
Fig 31. PID Controller
It improves the stability. It decreases the steady state error and both are proportional to Kp.
Key takeaway
Example-1 The block diagram of a system using PI controllers is shown in the figure below Calculate:
(a). The steady state without and with controller for unit step input?
(b). Determine TF of newly constructed sys. With controller so, that a CL Poles is located at -5?
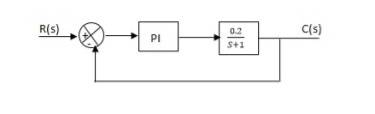
Fig 32. Block diagram with PI controller
(a). Without:
C(S)/R(S) = 0.2/(S + 1)
C(S) = R(S) 0.2/(S + 1) + 0.2
For unit step
Ess = 1/1 + Kp
Kp = lt G(S)
S 0
= lt 0.2/(S + 1)
S 0
Kp = 0.2
Ess = 1/1.2 = 5/6 = 0.8
(b). With controller:
Gc(S) = Kp + Ki/S
G’(S) = Gc(S).G(S)
= ( Kp + Ki/S )0.2/(S + 1)
= (KpS + Ki)0.2/S(S + 1)
Ess = 1/1 + Kp = 0
So, the value of ess is decreased.
(b). Given
Kpi/Kp = 0.1
G’(S) = (Kp + Ki/S)(0.2/S + 1)
= (KpS + Ki)0.2/S(S + 1)
As a pole is to be added so, we have to examine the CE,
1 + G’(S) = 0
1 + (Kp + Ki)0.2/S(S + 1) = 0
S2 + S + 0.2KpS + 0.2Ki = 0
S2 + (0.2Kp + 1)S + 0.2Ki = 0
Given,
Kpi = 0.1Ki
Kp = 10Ki
S2 + (2Ki + 1)S + 0.2Ki = 0
Pole at S = -5
25 + (2Ki + 1)(-5) + 0.2Ki = 0
-10Ki – 5 + 25 + 0.2Ki = 0
-9.8Ki = -20
Ki = 2.05
Kp = 10Ki
= 20.5
Now,
G’(S) = (KpS + Ki)(0.2)/S(S + 1)
= (20.5S + 2.05)(0.2)/S(S + 1)
G’(S) = 4.1S + 0.41/S(S + 1)
Example-2 The block diagram of a system using Pd controller is shown, the PD is used to increase ξ to 0.8. Determine the T.F of controller?
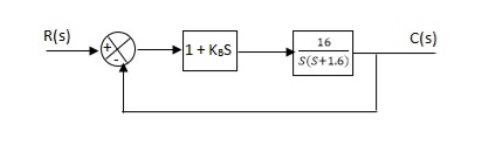
Fig 33. Block diagram with PD controller
(1). Kp = 1
Without controller:
C(S)/R(S) = 16/S2 + 1.6S + 16
wn = 4
2 ξwn = 16
ξ = 1.6/2 x 4 = 0.2
(b). With derivative:
ξS = 0.2 to 0.8
Undamped to critically damped,
G’(S) = (1 + KdS)(16)/(S2 + 1.6S)
CE:
S2 + 1.6S + 16(1 + KdS) = 0
S2 + (1.6 + Kd)S + 16 = 0
2 ξwn = 1.6 + Kd1.6
wn = 4
ξS = 0.8
2 x 4 x 0.8 = 1.6 + Kd1.6
6.4 – 1.6 = Kd1.6
4.8/16 = Kd
Kd = 0.3
TF = (1 + 0.3S)16/S(S + 16)
References:
1. Automatic Control system (II Edition) – Benjamin C, Kuo, PHI
2. Modern Control System, Drof, Bishop, Wesly Publication
3. Control system Engineering, S.K. Bhattacharya, Pearson Education.