Unit - 3

Discrete and Fast Fourier Transforms

3.1 Definition and properties of DFT

The discrete Fourier transform transforms a sequence of N complex numbers

xn = x0, x1, ... xN-1into another sequence of complex numbers [Xk]: = X0, X1,..XN-1

Which is defined by

Xk =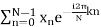

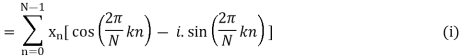
Example:

Let N =4 and

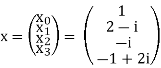
Here we demonstrate how to calculate the DFT of x using equation (1)

X0 = e-i2π 0.0/4.1+ e-i2π 0.1/4.(2-i)+ e-i2π 0.2/4.(-i)+ e-i2π 0.3/4.(-1+2i) = 2

X1 = e-i2π 1.0/4.1+ e-i2π 1.1/4.(2-i)+ e-i2π 1.2/4.(-i)+ e-i2π 1.3/4.(-1+2i) = 2 – 2i

X2 = e-i2π 1.2/4.1+ e-i2π 2.1/4.(2-i)+ e-i2π 2.2/4.(-i)+ e-i2π 2.3/4.(-1+2i) = - 2i

X3 = e-i2π 3.2/4.1+ e-i2π 3.1/4.(2-i)+ e-i2π 3.2/4.(-i)+ e-i2π 3.3/4.(-1+2i) = 4 + 4i

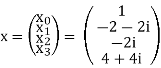
Properties of DFT

Linear Property

If x(t) -> X(w)

Y(t) -> Y(w)  then

a x(t) + b y(t)  -> a X(w) +b Y(w)

Time Shifting Property

If  x(t)⟷F.TX(ω)

Then Time shifting property states that

x(t−t0)⟷F.T   e−jω0t X(ω)

Frequency Shifting Property

If x(t)⟷X(ω)

Then frequency shifting property states that

Ejω0t.x(t)⟷X(ω−ω0)

Time Reversal Property

If x(t)⟷X(ω)

Then Time reversal property states that

x(−t)⟷X(−ω)

Differentiation Property

If x(t)⟷X(ω)

Then Differentiation property states that

Dx(t)dt⟷jω.X(ω)

dnx(t)dtn⟷(jω)n.X(ω)

Integration Property

Integration property states that

∫x(t)dt⟷1jω X(ω)

Then

∭...∫x(t)dt⟷(jω)n X(ω)

Multiplication and Convolution Properties

If x(t)⟷X(ω)

y(t)⟷Y(ω)

Then multiplication property states that

x(t).y(t)⟷X(ω)∗Y(ω)

And convolution property states that

x(t)∗y(t)⟷1/2πX(ω).Y(ω)

Numericals:

1. Compute the N-point DFT of x(n)=3δ(n).

x(k) =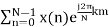

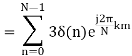
= 3δ(0) × e0 =1

x(k0 = 3,0 ≤ k ≤ N – 1

2.     Compute the N-point DFT of x(n)=7(n−n0)

Solution − We know that,

x(k) =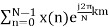

Substituting the value of x(n),

3.2 IDFT

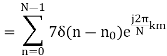
The inverse DFT (IDFT) transforms N discrete-frequency samples to the same number of discrete-time samples. The IDFT has a form very similar to the DFT and can thus also be computed efficiently using FFTs.

x(n) =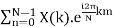

3.3 Relation between DFT and Z–Transform

Discrete-time signal: x[n] where n is an integer.

Z transform:

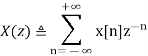
Discrete-time Fourier transform (DTFT):

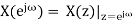
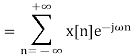
That is how the DTFT is related to the Z transform.

DFT:-

=

=

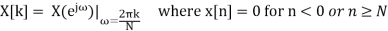
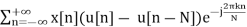
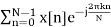
Here k is an integer and u[n] is the discrete unit step function.

u[n]​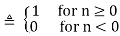

3.4 Radix- 2 FFT algorithms

Usually, we calculate N point DFT as N is an important factor. It can also be considered as N= r1, r2, r3, …… rv

r is selected because it represents Radix of FFT algorithm.

N = rv

For instance, if N= 8 and r =2 we can write

N = rv = 2v

8=2v

v= 3

v represents the number of stages in the FFT algorithm. But in signal processing we only relate to the number of samples. For DFT we select number of samples N and we divide by r. For example

Let N= 8

N’ = N/2 =4

N’ is still divisible by 2. N’=N/2=4/2 =2

Now N’’=r=2 and stop the process.

3.5 Linear filtering methods based on DFT

Linear Convolution states that

y(n) = x(n) * h(n)

y(n) = x(n) ×  h(n)

y(n) =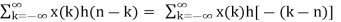

Example 1: h(n) = { 1 , 2 , 1, -1 } & x(n) = { 1, 2, 3, 1 } Find y(n).

METHOD 1: GRAPHICAL REPRESENTATION

Step 1) Find the value of n = nx+ nh = -1 (Starting Index of x(n)+ starting index of h(n))

Step 2) y(n)= { y(-1) , y(0) , y(1), y(2), ….} It goes up to length(xn)+ length(yn) -1. i.e n=-1

y(-1) = x(k) ×  h(-1-k)                                                                          y(0) = x(k) ×  h(0-k)

n=0                                                                                            y(1) = x(k) ×  h(1-k)

n=1                                                                                         y(n) = { 1,4,8,8,3,-2,-1}

METHOD 2: MATHEMATICAL FORMULA

Use Convolution formula

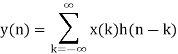
k= 0 to 3     (start index to end index of x(n))

y(n) = x(0) h(n) + x(1) h(n-1) + x(2) h(n-2) + x(3) h(n-3)

METHOD 3: VECTOR FORM (TABULATION METHOD)

X(n)= {x1,x2,x3} &       h(n) ={ h1,h2,h3}

y(-1) = h1 x1

y(0) = h2 x1 + h1 x2

y(1) = h1 x3 + h2x2 + h3 x1 …………

METHOD 4: SIMPLE MULTIPLICATION FORM

Xn = {x1, x2, x3}     and h(n) = {h1, h2, h3}

y(n) = x          x1, x2, x3

y1, y2, y3

3.6 Circular convolution

Let us take two finite duration sequences x1n and x2n,having integer length as N. Their DI are X1K and X2K respectively which is shown below

X1(K) = 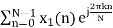, k = 0, 1, 2, ... N - 1

X2(K) = 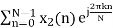, k = 0, 1, 2, ... N - 1

Now we will try to find the DFT of another sequence x3n, which is given by X3K

X3K = X1K × X2K

By taking the IDFT of the above we get

x3n = =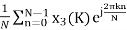

After solving the above equation finally we get

x3(K) = 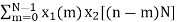, m = 0, 1, 2, ... N - 1 

Methods of Circular Convolution

Generally, there are two methods, which are adopted to perform circular convolution and they are −

• Concentric circle method
• Matrix multiplication method

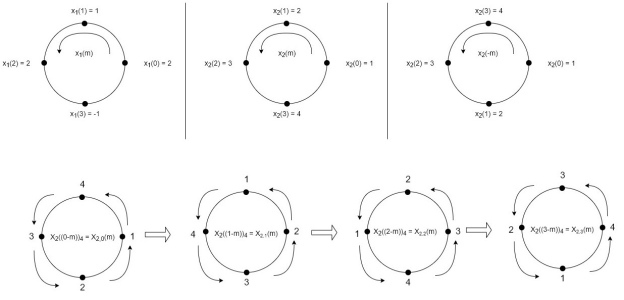
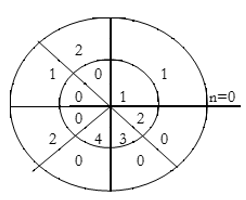
Concentric Circle Method

Let x1(n) and x2(n) be two given sequences. The steps followed for circular convolution of x1(n) and x2(n) are

• Take two concentric circles. Plot N samples of x1(n) on the circumference of the outer circle maintaining equal distance successive points maintaining equal distance successive points in anti-clockwise direction.
• For plotting x2(n), plot N samples of x2(n) in clockwise direction on the inner circle, starting sample placed at the same point as 0th sample of x1(n)
• Multiply corresponding samples on the two circles and add them to get output.
• Rotate the inner circle anti-clockwise with one sample at a time.

Matrix Multiplication Method

Matrix method represents the two given sequence x1(n) and x2(n) in matrix form.

• One of the given sequences is repeated via circular shift of one sample at a time to form a N X N matrix.
• The other sequence is represented as column matrix.
• The multiplication of two matrices give the result of circular convolution.

Numerical:

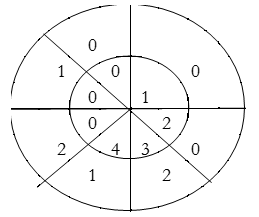
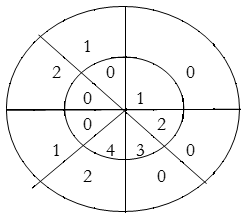
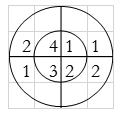
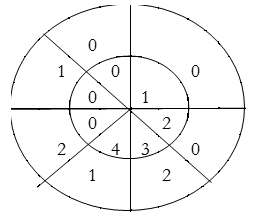
Perform circular convolution of the two sequences, x1(n)= {2,1,2,-1} and x2(n)= {1,2,3,4}

x3(n) =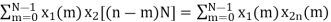

(2) x3(n) =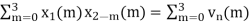

When n=0;

x3(0) =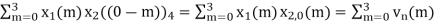

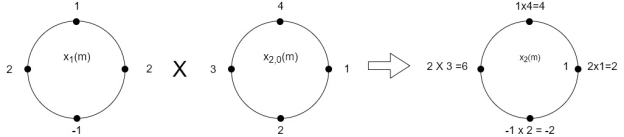
The sum of samples of v0(m) gives x3(0)

⸫ x3(0)=2+4+6-2=10

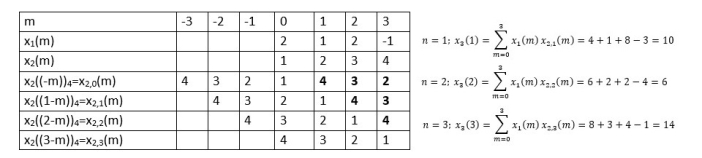
When n=1; x3(1) =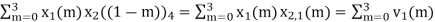

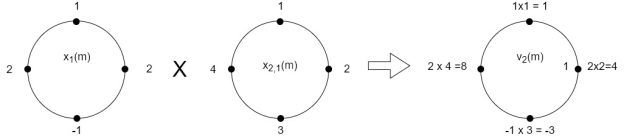
The sum of samples of v1(m) gives x2(1)

⸫ x3(1)=4 + 1 +8-3=10

(3) When n=2;

x3(2) =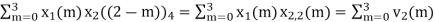

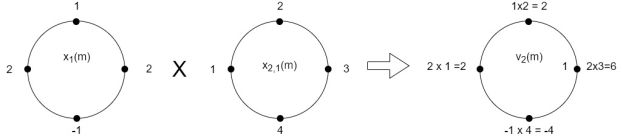
The sum of samples of v2(m) gives x3(2)

⸫ x3(2)=6+2+2-4=6

(4) When n=3;

x3(3) =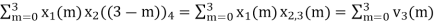

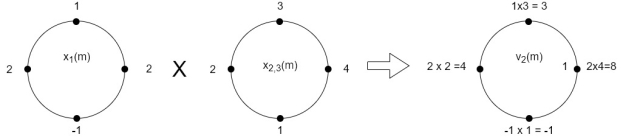
The sum of samples of v3(m) gives x3(3)

⸫ x3(3)=8+ 3+ 4-1= 14

x3(n)={10,10,6,14}

x3(n) =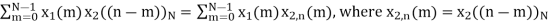

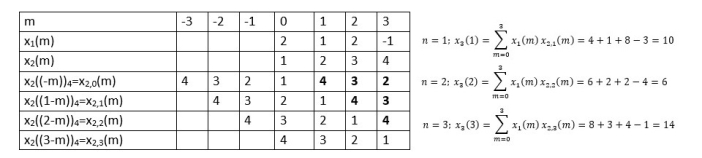
n=1; x3(1) =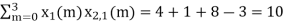

n=2; x3(2) =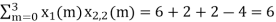

n=3; x3(3) =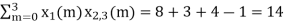

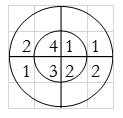
n=0; x3(0) =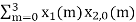

= x1(0) x x2,0(0) + x1(1) x2,0(1) + x1(2) x2,0(2) + x1(3) x2,0(3)

= 2 x 1 + 1 x 4 + 2 x 3 + (-1) x 2 = 2 +4 +6 -2 =10

Computation of linear convolution using circular convolution

Find circular convolution and linear using circular convolution for the following sequences x1(n) = {1, 2, 3, 4} and x2(n) = {1, 2, 1, 2}. Using Time Domain formula method.

Solution:

Circular convolution using circular convolution:

x1x1(n) = {1, 2, 3, 4}

And x2x2 (n) = {1, 2, 1, 2}

L=4, M=4

Length of y(n) = L+M-1=4+4-1=7

∴,x1(n) = {1, 2, 3, 4, 0, 0, 0}

& x2(n) = {1, 2, 1, 2, 0, 0, 0}

For y(0),

∴ y(0)= 1×1=1

For y(1),

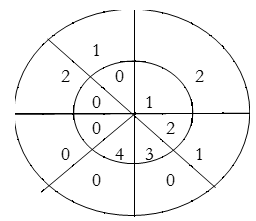
∴ y(1)= 2×1+1×2=4

For y(2),

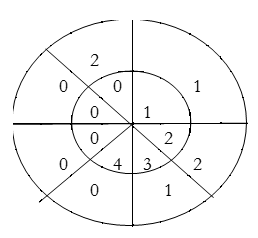
∴ y(2)= 1×1+2×2+3×1=8

For y(3),

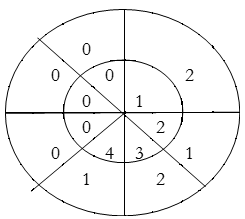
y(3)=1×2+2×1+3×2+4×1=14

For y(4),

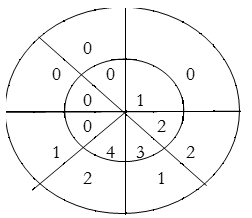
∴ y(4)= 4×2+3×1+2×2=15

For y(5),

∴ y(5) = 4×1+3×2=10

For y(6),

∴ y(6) = 4×2=8

∴y(n) = {1, 4, 8, 14, 15, 10, 8}

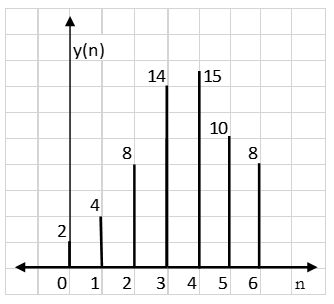
Result: y(n) = {2, 4, 8, 14, 15, 10, 8}

Linear using circular convolution:

For y(0),

∴ y(0)= 1+4+3+8=16

For y(1),

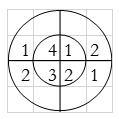
∴ y(1)= 2+2+6+4=14

For y(2),

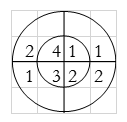
∴ y(2)= 1+4+3+8=16

For y(3),

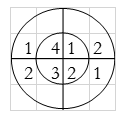
∴ y(3)= 2+2+6+4=14

y(n) = {16, 14, 16, 14}

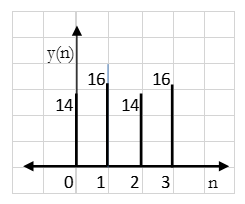
Result: y(n) = {14, 16, 14, 16}

3.7 Gortzel algorithm

FFT algorithms are used to compute N point DFT for N samples of the sequence x(n). This requires N/2 log2N number of complex multiplications and N log2N complex additions. In some applications DFT is to be computed only at selected values of frequencies and selected values are less than log2N, then direct computations of DFT becomes more efficient than FFT. This direct computations of DFT can be realized through linear filtering of x(n). Such linear filtering for computation of DFT can be implemented using Goertzel algorithm.

By definition N point DFT is given as

N-1

X(k) =

Multiplying both sides by 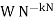(which is always equal to 1).

X(k) =

Thus for LSI system which has input x(n) and having unit sample response

Hk(n) = WNkn u(n)

X(n) → hk(n) = WN-kn u(n) →  yk(n)

Linear convolution is given by

y(n) =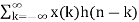

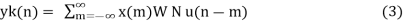
As x(m) is given for N values

Yk(n)

The output of LSI system at n=N is given by

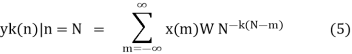
Thus comparing equation (2) and (5), X(k)

= yk(n)|n=N

Thus DFT can be obtained as the output of LSI system at n=N. Such systems can give X(k) at selected values of k. Thus, DFT is computed as linear filtering operations by Gortzel Algorithm.

References:

1. Digital signal processing- A practical approach Second Edition, 2002.E. C. Ifeachar, B. W. Jarvis Pearson Education

2. Sanjit K. Mitra, ‘Digital Signal Processing – A Computer based approach’

3. S. Salivahanan, A Vallavaraj, C. Gnanapriya, ‘Digital Signal Processing’, 2nd Edition McGraw Hill.

4. A. Nagoor Kani, ‘Digital Signal Processing’, 2nd Edition McGraw Hill.

5.P. Ramesh Babu, ‘Digital Signal Processing’ Scitech

Unit - 3

Discrete and Fast Fourier Transforms

3.1 Definition and properties of DFT

The discrete Fourier transform transforms a sequence of N complex numbers

xn = x0, x1, ... xN-1into another sequence of complex numbers [Xk]: = X0, X1,..XN-1

Which is defined by

Xk =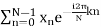

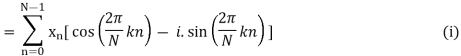
Example:

Let N =4 and

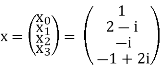
Here we demonstrate how to calculate the DFT of x using equation (1)

X0 = e-i2π 0.0/4.1+ e-i2π 0.1/4.(2-i)+ e-i2π 0.2/4.(-i)+ e-i2π 0.3/4.(-1+2i) = 2

X1 = e-i2π 1.0/4.1+ e-i2π 1.1/4.(2-i)+ e-i2π 1.2/4.(-i)+ e-i2π 1.3/4.(-1+2i) = 2 – 2i

X2 = e-i2π 1.2/4.1+ e-i2π 2.1/4.(2-i)+ e-i2π 2.2/4.(-i)+ e-i2π 2.3/4.(-1+2i) = - 2i

X3 = e-i2π 3.2/4.1+ e-i2π 3.1/4.(2-i)+ e-i2π 3.2/4.(-i)+ e-i2π 3.3/4.(-1+2i) = 4 + 4i

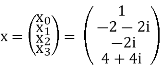
Properties of DFT

Linear Property

If x(t) -> X(w)

Y(t) -> Y(w)  then

a x(t) + b y(t)  -> a X(w) +b Y(w)

Time Shifting Property

If  x(t)⟷F.TX(ω)

Then Time shifting property states that

x(t−t0)⟷F.T   e−jω0t X(ω)

Frequency Shifting Property

If x(t)⟷X(ω)

Then frequency shifting property states that

Ejω0t.x(t)⟷X(ω−ω0)

Time Reversal Property

If x(t)⟷X(ω)

Then Time reversal property states that

x(−t)⟷X(−ω)

Differentiation Property

If x(t)⟷X(ω)

Then Differentiation property states that

Dx(t)dt⟷jω.X(ω)

dnx(t)dtn⟷(jω)n.X(ω)

Integration Property

Integration property states that

∫x(t)dt⟷1jω X(ω)

Then

∭...∫x(t)dt⟷(jω)n X(ω)

Multiplication and Convolution Properties

If x(t)⟷X(ω)

y(t)⟷Y(ω)

Then multiplication property states that

x(t).y(t)⟷X(ω)∗Y(ω)

And convolution property states that

x(t)∗y(t)⟷1/2πX(ω).Y(ω)

Numericals:

1. Compute the N-point DFT of x(n)=3δ(n).

x(k) =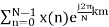

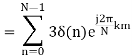
= 3δ(0) × e0 =1

x(k0 = 3,0 ≤ k ≤ N – 1

2.     Compute the N-point DFT of x(n)=7(n−n0)

Solution − We know that,

x(k) =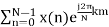

Substituting the value of x(n),

3.2 IDFT

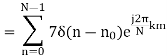
The inverse DFT (IDFT) transforms N discrete-frequency samples to the same number of discrete-time samples. The IDFT has a form very similar to the DFT and can thus also be computed efficiently using FFTs.

x(n) =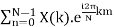

3.3 Relation between DFT and Z–Transform

Discrete-time signal: x[n] where n is an integer.

Z transform:

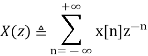
Discrete-time Fourier transform (DTFT):

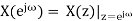
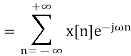
That is how the DTFT is related to the Z transform.

DFT:-

=

=

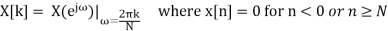
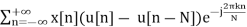
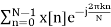
Here k is an integer and u[n] is the discrete unit step function.

u[n]​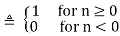

3.4 Radix- 2 FFT algorithms

Usually, we calculate N point DFT as N is an important factor. It can also be considered as N= r1, r2, r3, …… rv

r is selected because it represents Radix of FFT algorithm.

N = rv

For instance, if N= 8 and r =2 we can write

N = rv = 2v

8=2v

v= 3

v represents the number of stages in the FFT algorithm. But in signal processing we only relate to the number of samples. For DFT we select number of samples N and we divide by r. For example

Let N= 8

N’ = N/2 =4

N’ is still divisible by 2. N’=N/2=4/2 =2

Now N’’=r=2 and stop the process.

3.5 Linear filtering methods based on DFT

Linear Convolution states that

y(n) = x(n) * h(n)

y(n) = x(n) ×  h(n)

y(n) =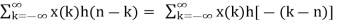

Example 1: h(n) = { 1 , 2 , 1, -1 } & x(n) = { 1, 2, 3, 1 } Find y(n).

METHOD 1: GRAPHICAL REPRESENTATION

Step 1) Find the value of n = nx+ nh = -1 (Starting Index of x(n)+ starting index of h(n))

Step 2) y(n)= { y(-1) , y(0) , y(1), y(2), ….} It goes up to length(xn)+ length(yn) -1. i.e n=-1

y(-1) = x(k) ×  h(-1-k)                                                                          y(0) = x(k) ×  h(0-k)

n=0                                                                                            y(1) = x(k) ×  h(1-k)

n=1                                                                                         y(n) = { 1,4,8,8,3,-2,-1}

METHOD 2: MATHEMATICAL FORMULA

Use Convolution formula

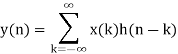
k= 0 to 3     (start index to end index of x(n))

y(n) = x(0) h(n) + x(1) h(n-1) + x(2) h(n-2) + x(3) h(n-3)

METHOD 3: VECTOR FORM (TABULATION METHOD)

X(n)= {x1,x2,x3} &       h(n) ={ h1,h2,h3}

y(-1) = h1 x1

y(0) = h2 x1 + h1 x2

y(1) = h1 x3 + h2x2 + h3 x1 …………

METHOD 4: SIMPLE MULTIPLICATION FORM

Xn = {x1, x2, x3}     and h(n) = {h1, h2, h3}

y(n) = x          x1, x2, x3

y1, y2, y3

3.6 Circular convolution

Let us take two finite duration sequences x1n and x2n,having integer length as N. Their DI are X1K and X2K respectively which is shown below

X1(K) = 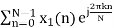, k = 0, 1, 2, ... N - 1

X2(K) = 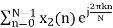, k = 0, 1, 2, ... N - 1

Now we will try to find the DFT of another sequence x3n, which is given by X3K

X3K = X1K × X2K

By taking the IDFT of the above we get

x3n = =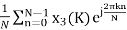

After solving the above equation finally we get

x3(K) = 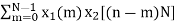, m = 0, 1, 2, ... N - 1 

Methods of Circular Convolution

Generally, there are two methods, which are adopted to perform circular convolution and they are −

• Concentric circle method
• Matrix multiplication method

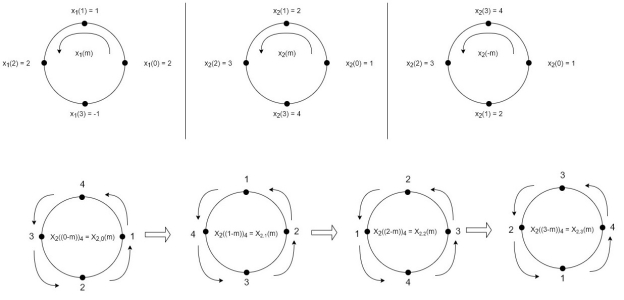
Concentric Circle Method

Let x1(n) and x2(n) be two given sequences. The steps followed for circular convolution of x1(n) and x2(n) are

• Take two concentric circles. Plot N samples of x1(n) on the circumference of the outer circle maintaining equal distance successive points maintaining equal distance successive points in anti-clockwise direction.
• For plotting x2(n), plot N samples of x2(n) in clockwise direction on the inner circle, starting sample placed at the same point as 0th sample of x1(n)
• Multiply corresponding samples on the two circles and add them to get output.
• Rotate the inner circle anti-clockwise with one sample at a time.

Matrix Multiplication Method

Matrix method represents the two given sequence x1(n) and x2(n) in matrix form.

• One of the given sequences is repeated via circular shift of one sample at a time to form a N X N matrix.
• The other sequence is represented as column matrix.
• The multiplication of two matrices give the result of circular convolution.

Numerical:

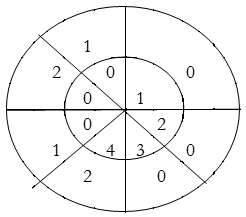
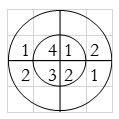
Perform circular convolution of the two sequences, x1(n)= {2,1,2,-1} and x2(n)= {1,2,3,4}

x3(n) =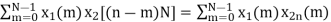

(2) x3(n) =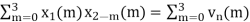

When n=0;

x3(0) =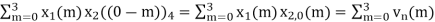

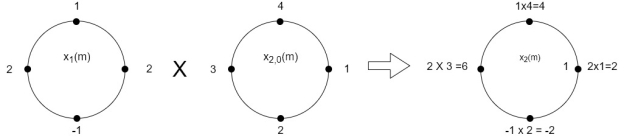
The sum of samples of v0(m) gives x3(0)

⸫ x3(0)=2+4+6-2=10

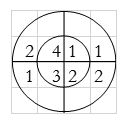
When n=1; x3(1) =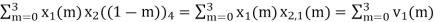

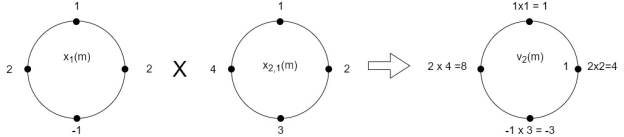
The sum of samples of v1(m) gives x2(1)

⸫ x3(1)=4 + 1 +8-3=10

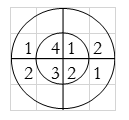
(3) When n=2;

x3(2) =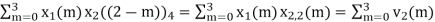

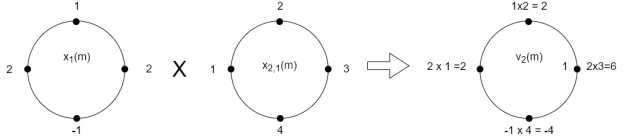
The sum of samples of v2(m) gives x3(2)

⸫ x3(2)=6+2+2-4=6

(4) When n=3;

x3(3) =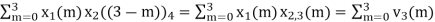

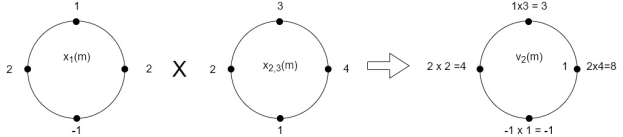
The sum of samples of v3(m) gives x3(3)

⸫ x3(3)=8+ 3+ 4-1= 14

x3(n)={10,10,6,14}

x3(n) =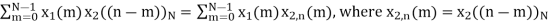

n=1; x3(1) =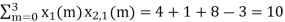

n=2; x3(2) =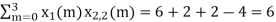

n=3; x3(3) =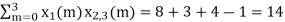

n=0; x3(0) =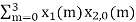

= x1(0) x x2,0(0) + x1(1) x2,0(1) + x1(2) x2,0(2) + x1(3) x2,0(3)

= 2 x 1 + 1 x 4 + 2 x 3 + (-1) x 2 = 2 +4 +6 -2 =10

Computation of linear convolution using circular convolution

Find circular convolution and linear using circular convolution for the following sequences x1(n) = {1, 2, 3, 4} and x2(n) = {1, 2, 1, 2}. Using Time Domain formula method.

Solution:

Circular convolution using circular convolution:

x1x1(n) = {1, 2, 3, 4}

And x2x2 (n) = {1, 2, 1, 2}

L=4, M=4

Length of y(n) = L+M-1=4+4-1=7

∴,x1(n) = {1, 2, 3, 4, 0, 0, 0}

& x2(n) = {1, 2, 1, 2, 0, 0, 0}

For y(0),

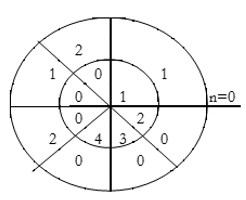
∴ y(0)= 1×1=1

For y(1),

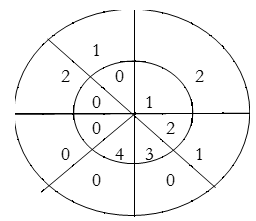
∴ y(1)= 2×1+1×2=4

For y(2),

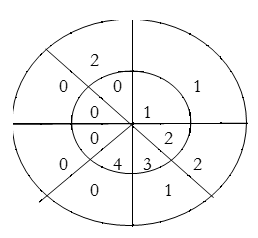
∴ y(2)= 1×1+2×2+3×1=8

For y(3),

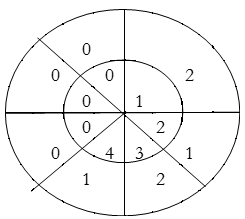
y(3)=1×2+2×1+3×2+4×1=14

For y(4),

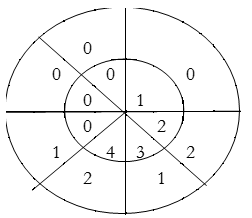
∴ y(4)= 4×2+3×1+2×2=15

For y(5),

∴ y(5) = 4×1+3×2=10

For y(6),

∴ y(6) = 4×2=8

∴y(n) = {1, 4, 8, 14, 15, 10, 8}

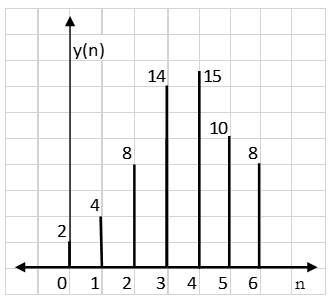
Result: y(n) = {2, 4, 8, 14, 15, 10, 8}

Linear using circular convolution:

For y(0),

∴ y(0)= 1+4+3+8=16

For y(1),

∴ y(1)= 2+2+6+4=14

For y(2),

∴ y(2)= 1+4+3+8=16

For y(3),

∴ y(3)= 2+2+6+4=14

y(n) = {16, 14, 16, 14}

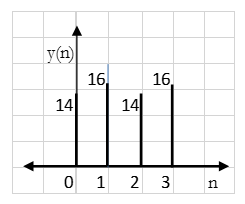
Result: y(n) = {14, 16, 14, 16}

3.7 Gortzel algorithm

FFT algorithms are used to compute N point DFT for N samples of the sequence x(n). This requires N/2 log2N number of complex multiplications and N log2N complex additions. In some applications DFT is to be computed only at selected values of frequencies and selected values are less than log2N, then direct computations of DFT becomes more efficient than FFT. This direct computations of DFT can be realized through linear filtering of x(n). Such linear filtering for computation of DFT can be implemented using Goertzel algorithm.

By definition N point DFT is given as

N-1

X(k) =

Multiplying both sides by 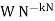(which is always equal to 1).

X(k) =

Thus for LSI system which has input x(n) and having unit sample response

Hk(n) = WNkn u(n)

X(n) → hk(n) = WN-kn u(n) →  yk(n)

Linear convolution is given by

y(n) =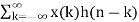

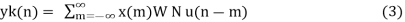
As x(m) is given for N values

Yk(n)

The output of LSI system at n=N is given by

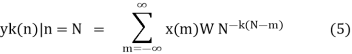
Thus comparing equation (2) and (5), X(k)

= yk(n)|n=N

Thus DFT can be obtained as the output of LSI system at n=N. Such systems can give X(k) at selected values of k. Thus, DFT is computed as linear filtering operations by Gortzel Algorithm.

References:

1. Digital signal processing- A practical approach Second Edition, 2002.E. C. Ifeachar, B. W. Jarvis Pearson Education

2. Sanjit K. Mitra, ‘Digital Signal Processing – A Computer based approach’

3. S. Salivahanan, A Vallavaraj, C. Gnanapriya, ‘Digital Signal Processing’, 2nd Edition McGraw Hill.

4. A. Nagoor Kani, ‘Digital Signal Processing’, 2nd Edition McGraw Hill.

5.P. Ramesh Babu, ‘Digital Signal Processing’ Scitech